2. 哈尔滨工业大学 土木学院, 哈尔滨 150001
2. School of Civil Egnineering, Harbin Institute of Technology, Harbin 150001, China
持续充足的石油天然气供应对于我国经济的发展和人民生活水平的提高具有重大意义.进入21世纪以来,我国陆上多数油田的储量下降,开采难度不断增大,而新发现的油气田不足,海上油田勘探开发技术也尚待提高. 这迫切需要提出新的勘探测量方法,以便更深入地认识储层岩石的物理特性. 近年来一种利用固液界面弹性场与电磁场之间耦合关系(动电效应)的测量方法受到学者们的重视,可望成为一项新技术——动电测井(胡恒山和王克协,1999,2000),它由声源换能器发射声波信号,然后记录声波诱导的转换电场. 人们期望这种新方法能够获得一些传统测量技术无法获取的信息,从而更好地描述储层特性. 国内外诸多学者也相继开展了与动电效应有关的理论(Pride,1994;戴世坤,1996;胡恒山等2003;崔志文,2004;Haartsen et al,2007;高永新和胡恒山,2009 ;关威等,2011; Gao et al,2013; Guan et al,2013)和测量(刘洪,1994;刘洪和李幼铭,1994;Zhu et al,1999;严洪瑞等,1999;石昆法,2001;陈本池等,2003;王军等,2010,2011)工作.
随着研究的不断深入,人们逐渐认识到了动电效应在地层参数(如地层波速、渗透率等)的测量与反演方面的应用价值。Pride和Haartsen(1997)分析了动电耦合波场的传播特性并说明声波伴随电磁场的视速度与声波的传播速度相同,可用于地层波速的井下测量. Berryman(2003)通过理论说明孔隙介质动电效应可用于地层渗透率的现场测量. 胡恒山和王克协(2000)模拟了井中动电信号与地层参数之间的关系,指出伴随井孔声场中斯通利波的电场对地层渗透率较敏感. 关威等(2011)进一步提出了利用动电测井中斯通利波电声比的相位反演地层渗透率方法. Dupuis和Butler(2006)针对冰川结构地层的垂直动电剖面研究表明:同震的电磁场信号可用于评价地层孔隙度和渗透率. Pengra等(1999)和王军等(2010)先后在实验室内利用低频准静态的动电效应(流动电势效应和电渗效应)测量了小岩样的渗透率.
渗透率是评价地层特性的重要参数,上述研究表明动电效应可用于地层渗透率的评估,但考虑到动电效应的转换能力很低,通常为10-9V/Pa量级(王军等,2010,2011),以及电磁波在导电介质中衰减很快等原因,制约了动电测井技术在实际油气勘探中的应用. 因此,关于井中动电效应的实验或现场测量研究极少,而且已有的实验报道只观测到测井全波中部分分波的动电转换信号(Mikhailov et al,2000;陈本池等,2003).此外,能否利用动电测井数据评价地层参数,实现渗透率的井下动电测量以及对渗透率不同地层的区分,缺乏相应测量数据的支持. 本文则从实验角度出发,开展了井中动电效应的测量研究工作,记录到了单极源动电测井的全波波形(包括纵波、横波和斯通利波的转换电场),给出了井中动电信号的幅值,并定量分析了渗透率不同模型井中动电信号的差异.
2 动电测井实验系统 2.1 实验模型井及测井探头实验选用2种渗透率不同的材料制作模型井,其物理参数如表 1所示,实验用自来水对岩样进行饱和. 实验探头如图 1所示,包括声源和接收器两部分,分别用于声波测井(图 1a)和动电测井实验(图 1b). 用于声波测井和动电测井的声源相同,它由4块材料相同的圆盘状压电片构成,间隔90°放置在同一圆周上构成单极源激发模式. 声波测井接收器为6组压电片,其材料与声源相同,每组2片,嵌于钢管圆周凹槽内,表面用环氧树脂封装. 动电测井接收器为6组镀银点电极,电极突出接收器外壳2 mm,且与外壳绝缘.
| | 表 1 模型井物理参数表 Table 1 Parameters of borehole models |
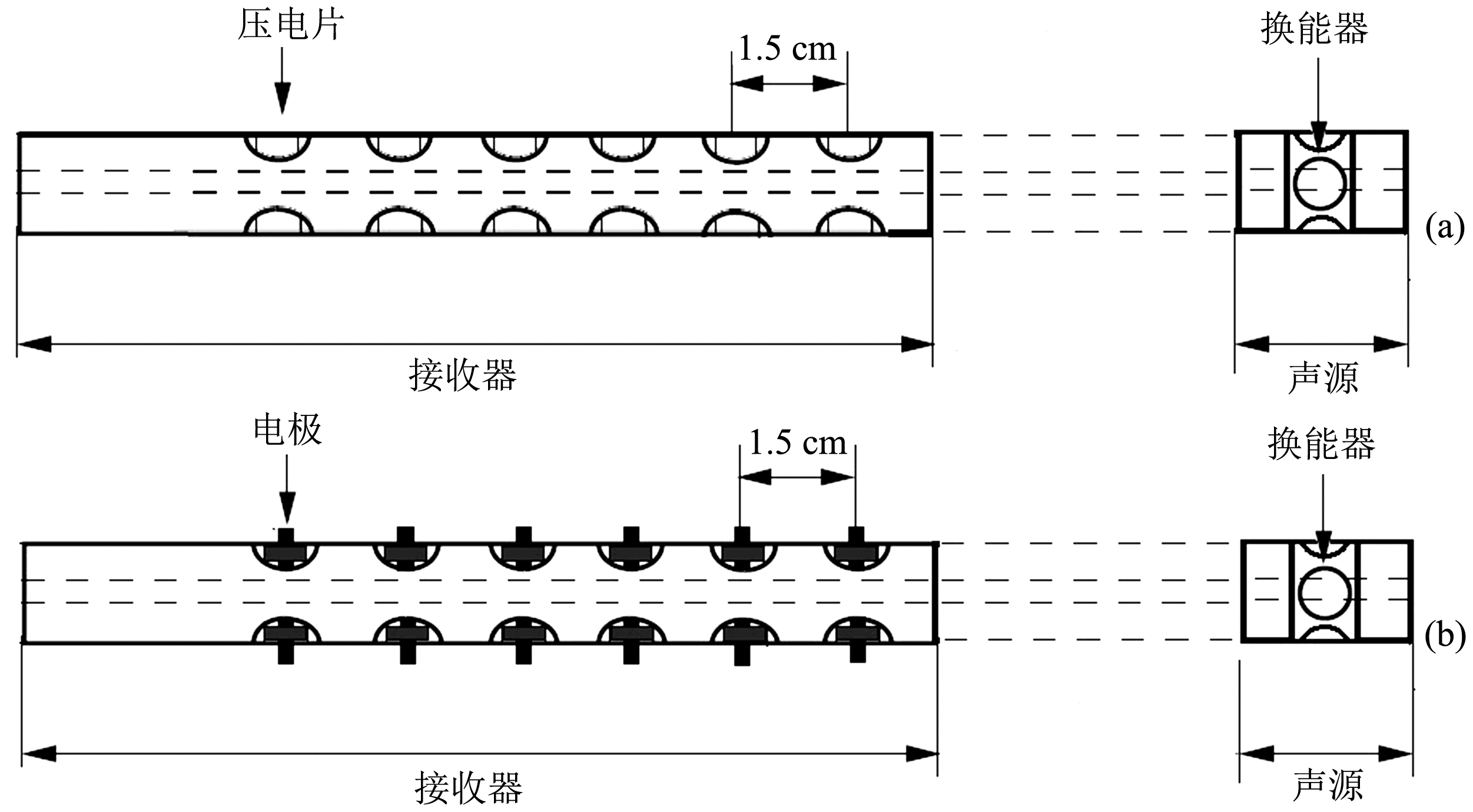 | 图 1 声波测井探头(a)和动电测井探头(b) Fig. 1 The acoustic logging detector (a) and seismoelectric logging detector (b) |
已有实验表明动电转换信号非常微弱,因此,实验测量系统的性能是动电测量的关键和前提,其测 量精度直接决定动电信号的有效性. 本文实验测量系统主要由脉冲源(5077PR)、前置放大器(5660C)、滤波器(NF3628)、NI数据采集卡(5922)、函数信号发生器(AFG3022B)构成. 下面分别介绍各仪器的功能及其在实验测量中的作用.
脉冲源:为声源换能器提供电压激励,其输出为负方波脉冲信号. 中心频率由实验用井孔尺寸与实际井孔尺寸的几何相似关系确定(本文模型井内径约为实际井孔的10倍缩小模型),因此,实验用声源频率约为实际测井频率(2~20 kHz)的10倍. 通过粗略的实验观测得出:当声源中心频率选为90 kHz时,斯通利波幅度达到最大. 因此,本文中声源的中心频率选为90 kHz. 前人研究表明声场越强,得到的动电转换也越强(Pengra et al,1999),但由于高压脉冲会在空间中产生电磁辐射,并被电极接收到,该辐射对动电转换信号的测量具有较大干扰(见下文动电信号中0时刻的波形),很难消除. 而且电压越高,它在时域上的延续越长,可能会掩盖到时较早的动电信号,因此,实验没有采用实际测井的千伏电压作为激励,而是选用200 V.
前置放大器:对高于其阈值的信号进行放大,可有效提高信号的信噪比,由于动电信号十分微弱,实验中使用前置放大器对被测信号进行放大.
滤波器:实验选用双通道的滤波器构成一个带通滤波器,滤波范围在1~300 kHz之间,用于滤除工频和高频干扰.
NI数据采集卡:用于采集和存储数据,其最大分辨率为24位,考虑此时的采样率不高,实验选择的分辨率为20位,对应采样率为5 MS/s. 而且通过Labview软件采用多次叠加取平均的方式来减弱随机噪声.
函数信号发生器:实验测量时为脉冲源和采集卡提供触发信号,保证两者同步工作,同时还在声波测井时为声源换能器提供激励信号.
此外,针对表 1给出2种模型进行同一种测井实验时,如声波测井实验,所用设备的参数(脉冲激励电压,放大倍数,滤波器带宽,采样率等)均不变. 这样保证了实验条件的一致性,排除了实验环境、仪器参数不同等因素对测量数据的影响,使得不同模型实验结果的对比更加有意义.
实验测量流程如图 2所示,高压脉冲源给声源换能器供电,使其激发声波信号.当声波在井孔中传播时,由于动电效应的作用,在井孔中能够产生电场,此信号为声波在地层中传播引起的动电转换信号. 由电极接收该信号,并经过放大、滤波等过程,以减弱噪声,提高信号的幅度和信噪比,之后由采集卡将数据记录并存储,以便做进一步的数据分析.
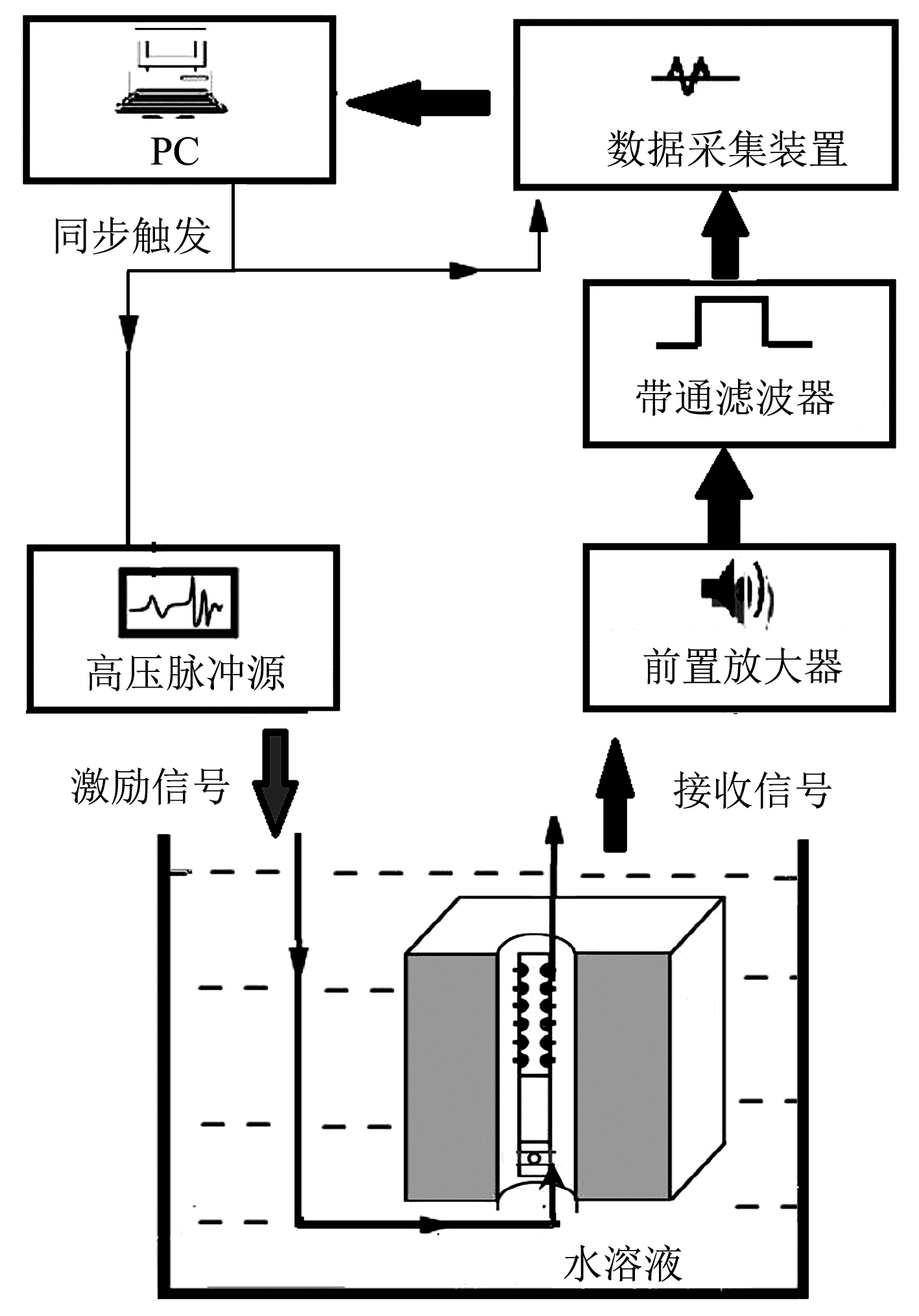 | 图 2 动电测井实验测量流程图 Fig. 2 The measuring diagram for seismoelectric experiment |
实验时,将声源和接收器(换能器或电极)置于井孔中,并进行居中处理. 由于实验设备的限制,本文测量系统每次只能记录一个通道的信号,如进行声波测井实验时,根据图 1接收器所示结构先在距离声源最近的位置接收井中声波信号,然后通过波段开关选择下一个较远位置进行测量,以此类推,实验共记录了6条曲线. 之后,将接收换能器改为电极,重复上述测量,以完成动电测井实验. 虽然测量过程没有实现多通道同步采集,但实验过程中,保持声源和接收器的位置不动,同时保持各设备的参数不变,只通过波段开关的变化来完成不同源距的实验测量,这样单通道多次测量与多通道同步测量的结果是一样的.
本节主要针对岩样1和岩样2模型井,进行单极源电缆声波测井和动电测井实验研究,观测了井中的声波信号和声波诱导的动电转换信号,并对比分析了两者之间的关系,比较了不同渗透率模型井中动电转换信号的差异. 详细实验结果如下.
(1)岩样1模型井中实验测量
图 3给出了岩样1模型井中声波测井和动电测井归一化的测量结果. 图 3a声波测井全波中清楚地看到3个波群,它们分别对应地层的纵波(P波)、横波(S波)和斯通利波(ST波),而且通过图中各分波到时计算出的传播速度与表 1中结果吻合. 图 3b动电测井全波中除了0时刻的波群之外也有3个波群存在,首先从视觉上看,它们的形状与声波测井中3个分波(P波、S波和ST波)相似,到时也基本一致. 其次,通过计算3个波群的传播速度可知,它们分别对应地层纵波、横波和斯通利波的传播速度. 理论计算表明:声波在井中传播时能够产生伴随动电场(胡恒山和王克协,1999,2000),它的传播速度与引起动电效应的声波速度相同,因此,图 3b中3个波群是地层纵波、横波和斯通利波在井中传播时产生的动电转换信号,即伴随纵波电场、伴随横波电场和伴随斯通利波电场.
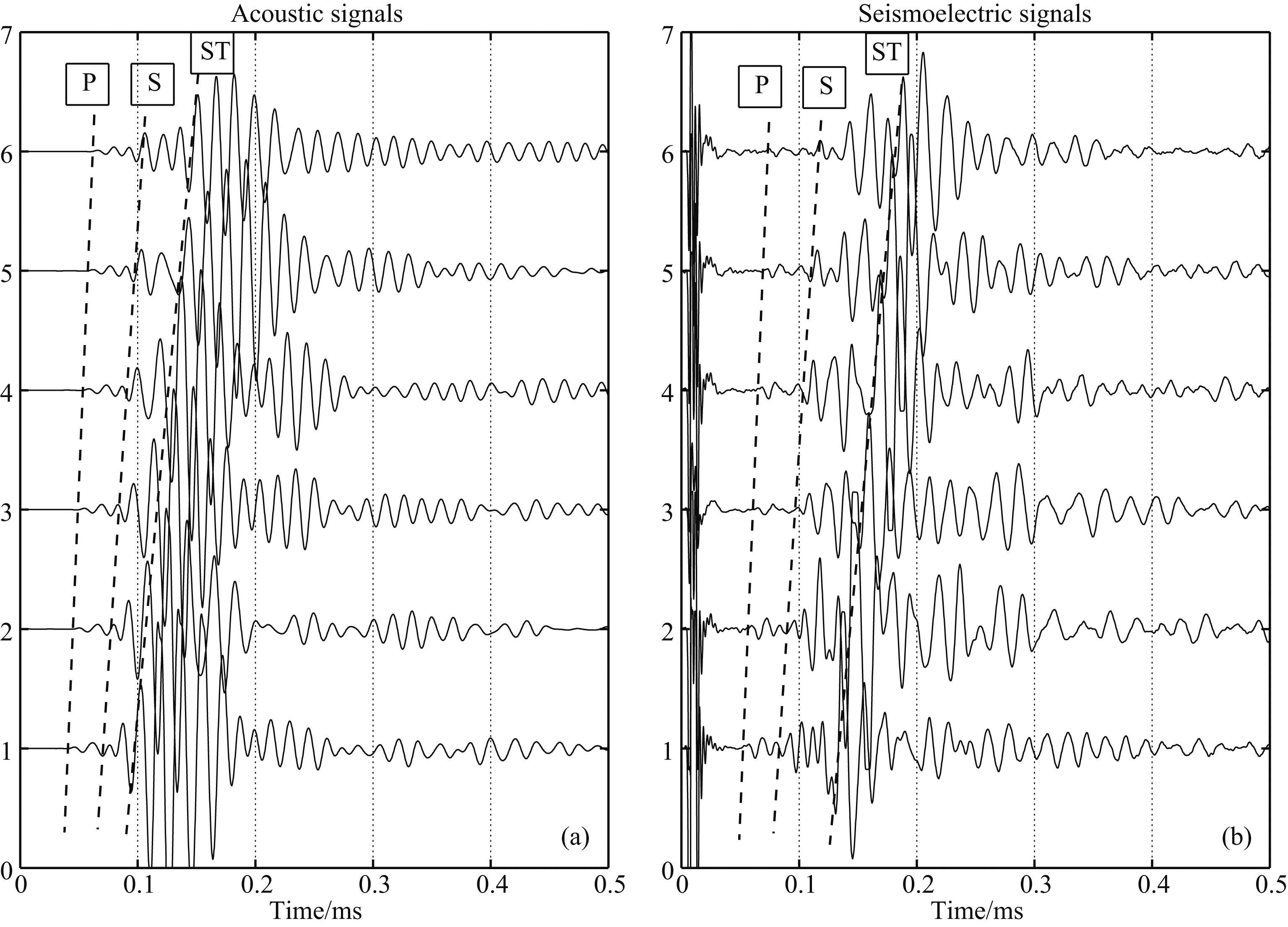 |
图 3 岩样1模型井中归一化实验结果 (a) 声波测井实验; (b) 动电测井实验. Fig. 3 The normalized waves of well logging in rock 1 (a) Acoustic well logging; (b) Seismoelectric well logging. |
此外,图 3b中0时刻出现一个幅度很大的波群,那是高压脉冲在空间形成的电磁辐射干扰,因为它们同时到达6个接收电极,没有体现出6次测量源距的差异,目前还没有找到办法将它消除,只能通过共地的方法尽量缩短它在时域上的延续时间,使其不对后面到达的动电信号产生干扰. 不过该波群的存在给我们提供一个区分声波场和动电场的依据. 而动电测井理论计算中还有一种在井壁处产生 的界面动电转换信号(胡恒山和王克协,1999,2000),本文实验结果中没有看到该信号,那是因为界面动电信号的到时很早(声波沿径向由声源传播到井壁的时间),被0时刻的干扰掩盖掉了.
图 4是单次声波测井和动电测井的实验结果,由于手动更换接收器,声波和动电测井的源距不可能完全相同,导致两种情况下各分波到时有些偏差,但这不影响实验数据分析. 图 4a声场中纵波、横波和斯通利波的峰峰值分别为0.237 V,1.499 V和4.945 V. 图 4b动电场中伴随纵波、横波和斯通利 波电场的峰峰值分别为0.859 V,3.036 V和11.593 V.
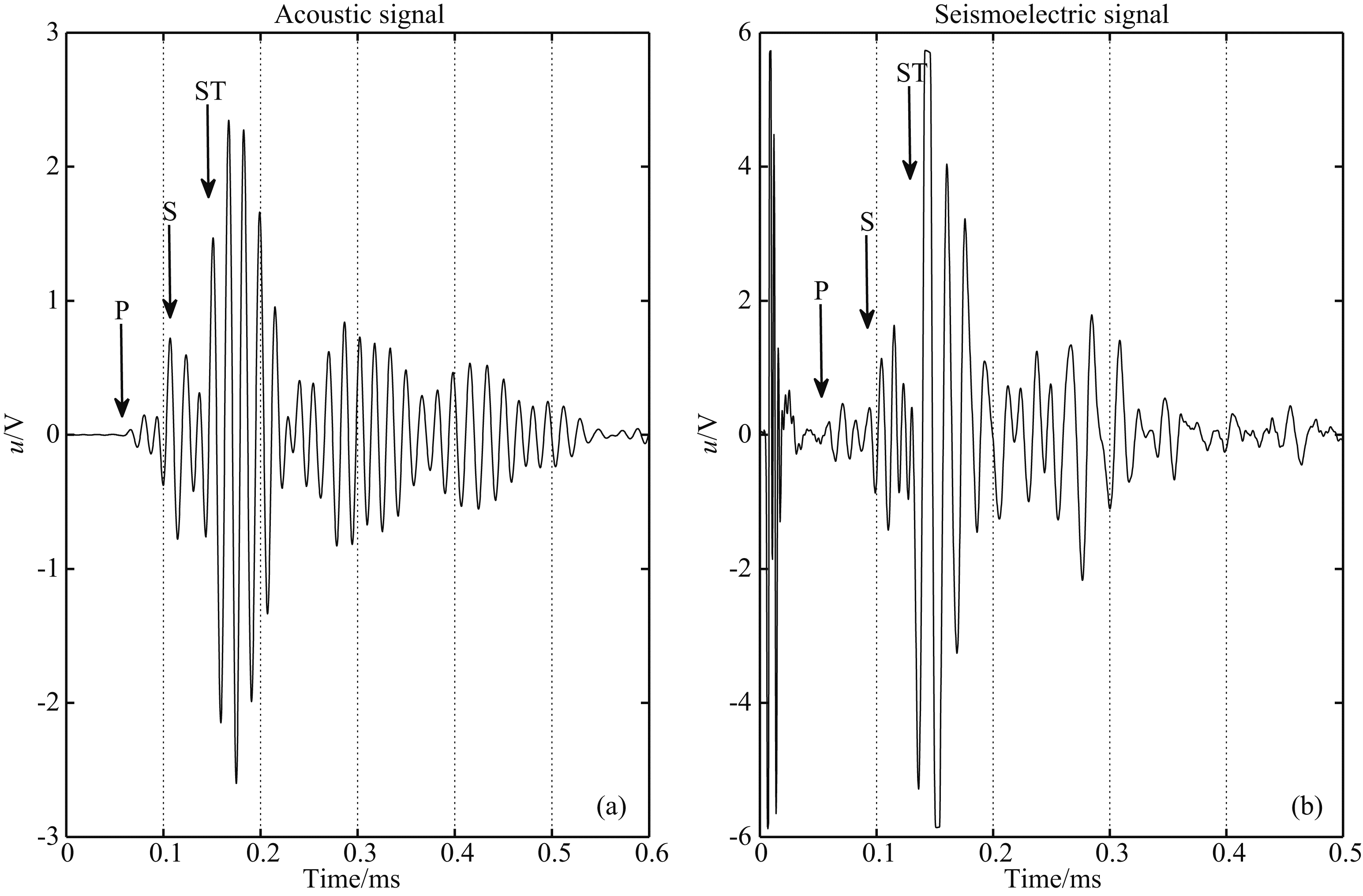 |
图 4 岩样1模型中测井信号的幅值 (a) 声波测井实验; (b) 动电测井实验. Fig. 4 The values of well logging signals in rock 1 (a) Acoustic well logging; (b) Seismoelectric well logging. |
综上,岩样1模型中的动电测井实验观测到了声波在井孔中传播产生的动电转换信号,并能从测井全波中清晰地区分伴随纵波、横波和斯通利波动电场,给出了本文实验条件下记录到各伴随动电信号的幅度. 另外,图 3和图 4实验结果证明了本文实验测量系统对动电测量的有效性以及动电测井的可行性. 但由于模型结构关系,本文实验无法观测界面动电信号,因此,在王军等(2015)工作中针对多种实验模型,详细地分析伴随动电信号和界面动电信号的传播特性.
(2)岩样2模型井中实验测量
图 5和图 6给出了岩样2模型井中声波测井和动电测井的实验结果.从图 5a和6a声波测井全波中能够清楚地看到单极源在井中激发的纵波(P波)、横波(S波)和斯通利波(ST波)波群,而且通过时域波形计算出它们的传播速度也与表 1中结果吻合. 但由于岩样2模型井的渗透率较低,动电测井全波中(图 5b和6b),只有伴随ST波的动电信号幅度较大,波形比较清晰,不同源距情况下记录波形的到时一致性较好.伴随P波和S波的动电信号幅度与背景噪声相当,只能勉强将两者从动电测井全波中提取出来.图 6是单次声波测井和动电测井的实验结果,其中纵波、横波和斯通利波的峰峰值分别为0.144 V,1.322 V和5.161 V.动电场中伴随纵波、 横波和斯通利波动电信号的峰峰值分别为0.096 V,0.156 V和0.722 V.
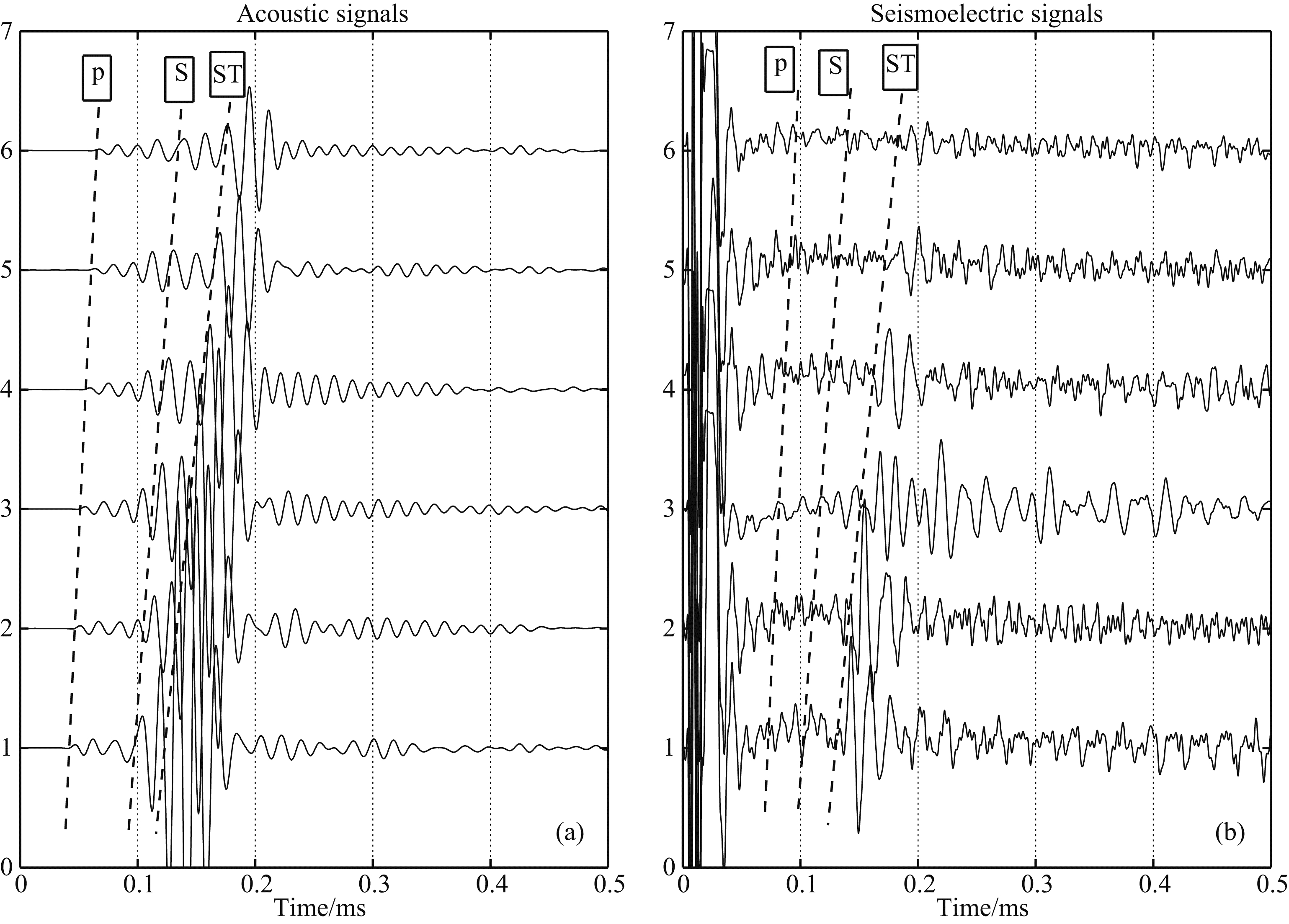 |
图 5 岩样2模型井中归一化实验结果 (a) 声波测井实验; (b) 动电测井实验. Fig. 5 The normalized waves of well logging in rock 2 (a) Acoustic well logging; (b) Seismoelectric well logging. |
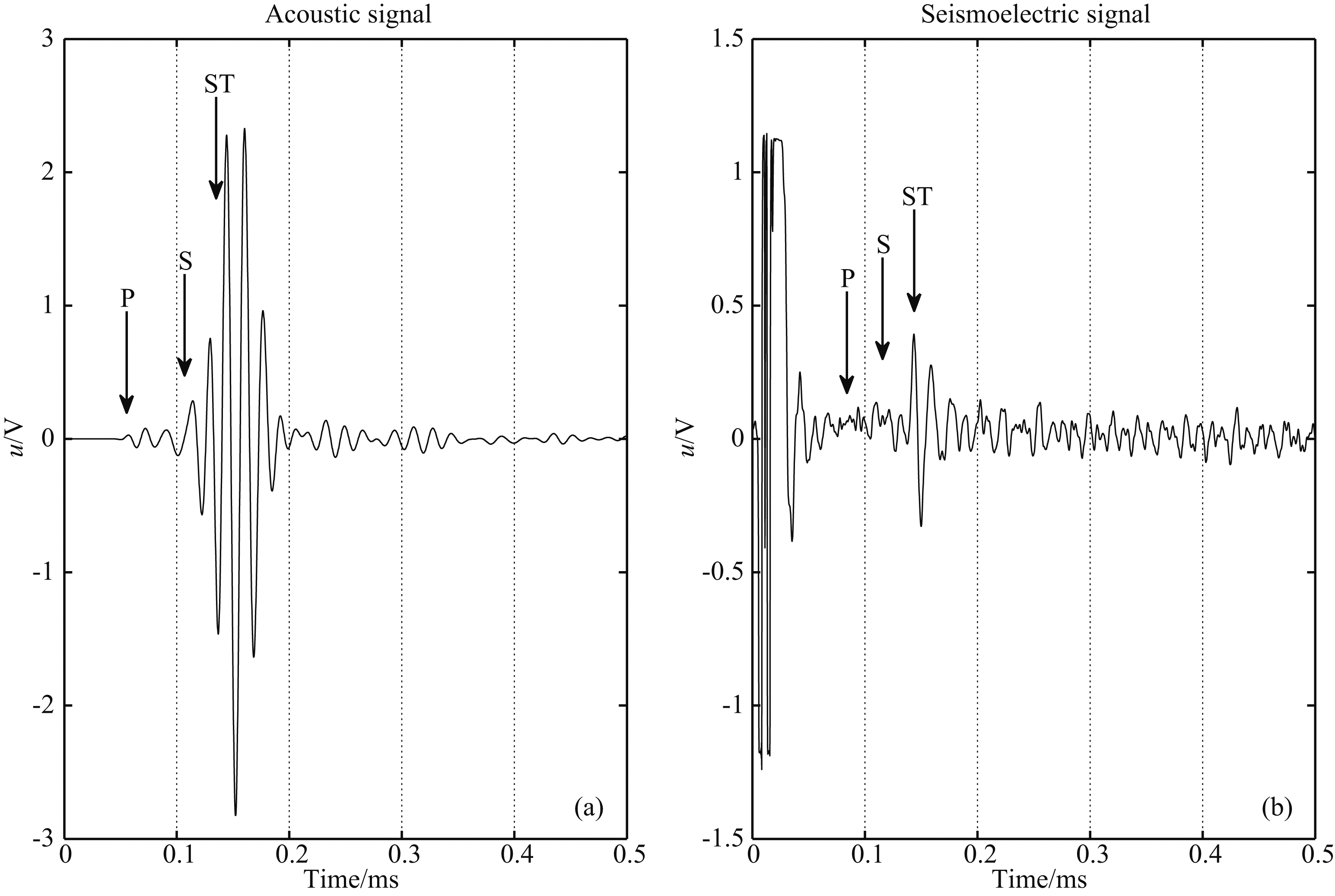 |
图 6 岩样2模型中测井信号的幅值 (a) 声波测井实验; (b) 动电测井实验. Fig. 6The values of well logging signals in rock 2 (a) Acoustic well logging; (b) Seismoelectric well logging. |
为了分析渗透率对动电效应的影响,我们对比分析了2种模型中的实验测量结果(图 4和图 6). 从这2幅图形中(图 4a和图 6a)可以看出:在相同实验条件下,接收换能器记录到声波测井信号中对应分波的幅度相差不大,基本都在同一个量级上,但动电测井信号的幅度却相差很大,比如两岩样声波测井实验中横波波群的峰峰值约为1.5 V,而动电测井实验中伴随横波动电信号的峰峰值分别为3 V和0.15 V左右,这种差别说明不同分波的动电耦合能力不同. 由于动电测井无法获得地层的动电耦合系数,胡恒山和王克协(2000)提出了“电声比”(REP)的概念,用于分析每个分波的动电转换效率. 电声比表示电场强度最大幅度与声场最大幅度的比值,虽然与动电耦合系数不同(Pride,1994;王军等,2010,2011),但它在一定程度上反映了孔隙介质的动电耦合能力,而且电声比越大,表明该分波的动电转换能力越强. 因此,对动电测井中电声比的分析是非常有意义的.
基于实验测量数据,本文计算了2种砂岩模型井中各分波的电声比:岩样1模型井中纵波、横波和斯通利波波的电声比分别为3.62,2.03,2.34;岩样2中纵波、横波和斯通利波波的电声比分别为0.67,0.12,0.14. 通过计算数据知:两种砂岩模型中实验结果具有相同的规律,即纵波的电声比最大,如岩样1中结果为3.62;其次是斯通利波,为2.34;横波电声比最小,为2.03,此结果表明了3种分波动电耦合能力的强弱关系,它们由强而弱依次为纵波、斯通利波和横波,该规律与胡恒山和王克协(2000)的动电测井模拟分析结果相同.
值得注意的是,动电信号非常微弱,虽然理论和实验结果均表明:在动电测井过程中纵波的电声比最大,但由于纵波在测井全波中的幅度相对最小,使得全波中伴随纵波电场的幅度并不是最大的,横波也有类似的问题,如图 6b岩样2中实验结果,图中伴随纵波和横波的动电信号因幅度太小导致这两个信号的信噪比较低,这不利于动电信号的测量和分析. 因此,利用伴随纵波和横波的动电信号评估渗透率等地层参数不是最佳的选择. 但通过实验发现:伴随斯通利波动电场的幅度最大,而且它对地层渗透率也非常敏感,详见图 4b和图 6b中动电信号的幅度. 本文还给出了两模型中伴随斯通利波电场幅度的定量结果,其中岩样1和岩样2的渗透率分别为15 mD和0.12 mD,声波测井记录到斯通利波的幅度为4.945 V和5.161 V,两者非常接近,没有体现出渗透率不同引起的斯通利波幅度变化. 而伴随斯通利波动电场的幅度为11.593 V和0.722 V,两者相差约16.1倍,电声比为2.34和0.14,相差约16.7倍. 这说明伴随斯通利波动电信号的幅度能够反映地层渗透率的大小关系,在高渗透率的地层中获得的动电信号更强,此结果也与Wang等(2015)在实验室内针对多块不同渗透率小岩样(非井孔模型)的测量结果一致. 因此,井中斯通利波引起的动电转换信号可用于地层渗透率的评价,而且通过声波测井和动电测井中斯通利波幅度和伴随斯通利波电场幅度的对比可以得出:与声波测井相比,动电测井信号对地层渗透率更加敏感.
5 结论针对流体饱和孔隙介质的动电效应,本文在实验室内建立了能进行动电测量的实验装置和实验测量系统,并在砂岩模型井中开展了单极源动电测井实验研究,清晰地观测到了井中伴随声场的动电转换信号,包括伴随地层纵波、横波和斯通利波的电场. 实验结果还表明:声场中引起动电效应的各分波(纵波、横波和斯通利波)的动电转换能力不同,通过计算他们的电声比得出,纵波的动电转换能力最强,斯通利波次之,横波最弱.
通过对比渗透率不同模型中动电测井信号的幅度可知:动电信号与地层渗透率密切相关,在高渗透率模型井中获得动电转换信号的幅度较大. 这一特性可用于地层渗透率的井下动电评估,而且实验结果表明:在动电测井全波中,伴随斯通利波动电转换信号的幅度最大,进而最有利于现场测量(其信噪比最高). 因此,综合比较纵波、横波和斯通利波的幅度大小关系及其动电转换能力,利用伴随斯通利波的动电转换信号来评价地层渗透率更合适. 此外,考虑到实际测井仪器的性能要更好一些,如放大倍数可达110 dB,且设备噪声更低的前置放大器;功率更大(激励电压几千伏,换能器直径更大)的换能器等因素,利用动电测井信号评价地层渗透率是有望实现的. 本文结果为渗透率等地层参数的井下动电测量奠定了实验基础.
另外,将两岩样声波测井和动电测井数据分别进行比较可知:两岩样声场中对应分波的幅度基本处于同一个量级上,由渗透率引起的声场幅度差异很小;但伴随声波的动电信号幅度却相差十几倍,这说明动电信号的幅度对渗透率更加敏感,因此,与声波测井相比,利用动电测井数据更利于地层渗透率的评价.
| [1] | Berryman J G. 2003. Electrokinetic effects and fluid permeability. Physics B., 338: 270-273. |
| [2] | Chen B C,Mu Y G,Di B R. 2003. Seismoelectric measurements in a borehole model. GPP,42 (1):35-38. |
| [3] | Cui Z W. 2004. Theoretical and numerical study of modified Biot's models, acoustoelectric well logging and acoustic logging while drilling excited by multipole acoustic sources (in Chinese). Changchun: Jilin University. |
| [4] | Dupuis J C,Butler K E. 2006. Vertical seismoelectric profiling in a borehole penetrating glaciofluvial sediments. Geophys. Res. Lett., 33(16): L16301. |
| [5] | Dai S K. 1996. Seismoelectric effect in porous medium and seismoelectric wave theory (in Chinese). Beijing: University of Petroleum. |
| [6] | Gao Y X, Hu H S. 2009. Numerical simulation and analysis of seismoelectromagnetic wave field excited by a point source in layered porous media. Chinese J. Geophysics.(in Chinese),52(8): 2093-2104. |
| [7] | Gao Y, Chen X, Hu H S, et al. 2013. Early electromagnetic waves from earthquake rupturing: I.theoretical formulations. Geophys. J. Int., 192 (3), 1288-1307. |
| [8] | Gao Y, Chen X, Hu H S,et al. 2013. Early electromagnetic waves from earthquake rupturing: Ⅱ. validation and numerical experiments. Geophys. J. Int, 192(3), 1308-1323. |
| [9] | Guan W, Hu H S, Tang T Z, et al. 2011.The ratio of the acoustoelectric field to the acoustic pressure in the borehole and its dependence on permeability. Chinese J. Geophysics (in Chinese), 54(6): 1660-1671. |
| [10] | Guan W, Hu H S, Zheng X B. 2013a. Theoretical simulation of the multipole seismoelectric logging while drilling. Geophysical Journal International. 195:1239-1250. |
| [11] | Guan W, Hu H S, Wang Z. 2013b. Permeability inversion from the low-frequency seismoelectric logs in fluid-saturated porous formations. Geophysical Prospecting, 61:120-133. |
| [12] | Hu H S,Wang K X. 1999. Coupled acoustic and electromagnetic waves around a borehole embedded in a porous formation: Part 1. theory. Well Logging Technology (in Chinese),23(6): 427-432. |
| [13] | Hu H S, Wang K X. 2000. Coupled acoustic and electromagnetic waves around a borehole embedded in a porous formation : part 2. numerical simulation of acoustically induced fields. Well Logging Technology,24(1) : 3-13. |
| [14] | Hu H S, Liu J Q, Wang H B,et al. 2003. Simulation of acoustic-electric well logging based on simplified pride equations. Chinese J. Geophysics (in Chinese),46(2):259-264 |
| [15] | Haartsen M W, Pride S R. 1997. Electroseismic waves from point sources in layered media. J. Geophys.Res.,102:24745-24769. |
| [16] | Haines S S,Pride S R, Klemperer S L. 2007. Seismoelectric imaging of shallow targets. Geophysics,72: G9-G20. |
| [17] | Liu H. 1994. The possibility of high resolution detection for subsurface oil,gas and water by means of natural electromagnetic field. Chinese J. Geophys.(in Chinese), 37(6) :828-835. |
| [18] | Liu H,Li Y M. 1994.Comments on exploring oil, gas and water using seismoelectric effects. GPP,33(2):94-101. |
| [19] | Mikhailov O V ,Queen J,Toksöz M N. 2000. Using borehole electroseismic measurements to detect and characterize fractured (Permeable) zones. Geophysics,65: 1098-1112. |
| [20] | Pengra D B, Li S X, Wong P Z. 1999. Determination of rock properties by low-frequency AC electrokinetics. J.Geo.Res.,104:29485-29508. |
| [21] | Pride S R. 1994. Governing equations for the coupled electromagnetics and acoustics of porous media. Phys. Rev. B.,50:15678-15696. |
| [22] | Shi K F. 2001. Seismo-electric effect theory and preliminary experimental results. Chinese J. Geophysics.(in Chinese),44(5):720-728. |
| [23] | Wang J,Hu H S,Xu X R,et al. 2010. Experimental measurement study on rock permeability based on the electrokinetic effect. Chinese J. Geophys. (in Chinese),53(8): 1953-1960. |
| [24] | Wang J,Hu H S,Yang G,et al. 2011. Experimental measurements on streaming current and zeta-potential of core samples under the excitation of low-frequency sinusoidal pressure. Chinese J. Geophysics.(in Chinese),54 (8): 2169-2176. |
| [25] | Wang J,Hu H S,Guan W,Li H. 2015. Electrokinetic experimental study on saturated rock samples: zeta potential and surface conductance. Geophys. J. Int., 201: 869-877. |
| [26] | Wang J,Guan W,Hu H S,Zhu Z. 2015. Electrokinetic experimental studies in borehole model II: localized and radiated seismoelectric field. Chinese J. Geophysics.(in Chinese), Accepted. |
| [27] | Yan H R,Liu H, Li Y M ,et al. 1999. Daqing oilfield experiment of seismo-electric exploration. Chinese J. Geophys. ( in Chinese),42(2) : 257-267. |
| [28] | Zhu Z,Haartsen M W,Toksöz M N. 1999. Experimental studies of electrokinetic conversions in fluid-saturated borehole models. Geophysics,64:1349-1356. |
| [29] | 崔志文. 2004. 多孔介质声学模型与多极源声电效应测井和多极随钻声测井的理论与数值研究[博士论文].长春:吉林大学. |
| [30] | 陈本池,牟永光,狄帮让. 2003. 井中震电勘探模型实验研究.石油物探,42 (1):35-38. |
| [31] | 戴世坤. 1996. 双相介质中的震电效应和震电波场传播理论[博士后研究工作报告] . 北京:石油大学. |
| [32] | 高永新,胡恒山. 2009. 水平分层孔隙介质中点源激发的震电波场数值模拟及分析.地球物理学报,52(8):2093-2104. |
| [33] | 关威,胡恒山,汤天知等. 2011. 声电效应测井电声比及其与地层渗透率的关系.地球物理学报,54(6):1660-1671. |
| [34] | 胡恒山,王克协. 1999. 井孔周围轴对称声电耦合波:理论(Ⅰ).测井技术,23 (6):427-432. |
| [35] | 胡恒山, 王克协. 2000. 井孔周围轴对称声电耦合波: (Ⅱ) 声电效应测井数值模拟. 测井技术,24(1) :3-13. |
| [36] | 胡恒山,刘家琦,王洪滨等.2003.基于简化的Pride理论声电效应测井响应 地球物理学报,46(2):259-264. |
| [37] | 刘洪. 1994. 利用天然电磁场高分辨率探测地下油气水的可能性. 地球物理学报, 37(6) :828-835. |
| [38] | 刘洪,李幼铭. 1994. 对利用震电效应勘探油气水的几点看法.石油物探,33(2):94-101. |
| [39] | 石昆法. 2001. 震电效应原理和初步实验结果. 地球物理学报,44(5):720-728. |
| [40] | 王军, 胡恒山,徐小蓉等. 2010. 基于动电效应的岩心渗透率实验测量. 地球物理学报,53(8): 1953-1960. |
| [41] | 王军, 胡恒山,杨光等. 2011. 低频交变压差作用下岩心流动电流和zeta电势实验测量. 地球物理学报,54 (8): 2169-2176. |
| [42] | 王军,关威,胡恒山,Zhenya Zhu. 2015. 动电测井实验研究Ⅱ:伴随动电场和界面辐射场.地球物理学报,已录用. |
| [43] | 严洪瑞, 刘洪, 李幼铭等. 1999. 震电勘探方法在大庆油田的实验研究. 地球物理学报,42(2) :257-267. |
 2015, Vol. 58
2015, Vol. 58


