2. 国土资源部沉积盆地与油气资源重点实验室, 成都 610081;
3. 油气资源与探测国家重点实验室, 北京 102249;
4. 北京市地球探测与信息技术重点实验室, 北京 102249;
5. 新疆油田公司勘探开发研究院, 新疆克拉玛依 834000
2. Key Laboratory of Sedimentary Basin and Oil and Gas Resources, Ministry of Land and Resources, Chengdu 610081, China;
3. State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum, Beijing 102249, China;
4. Key Laboratory of Earth Prospecting and Information Technology (Beijing), China University of Petroleum, Beijing 102249, China;
5. Research Institute of Exploration and Development, Xinjiang Oilfield Company, PetroChina, Xinjiang Karamay 834000, China
In this study, based on the assumption that the shaly sand can be simplified as a capillary tubes model, a expression of fluid permeability in terms of the surface area, tortuosity of throat, total porosity, and bound water porosity of clay is deduced. In addition, according to the physics volume model, the relationship of bound water porosity of clay to cation exchange capacity and salinity of solution is derived. Finally, by means of introducing the bound water porosity of clay to the expression of fluid permeability, a theoretical model of fluid permeability in terms of total porosity, cation exchange capacity, salinity of solution, surface area, and tortuosity of throat is deduced. The theoretical model and two sets of experimental data of fluid permeability show that the fluid permeability decreases with the increasing cation exchange capacity, and increases with the growing salinity of solution.
However, in the application of the model of fluid permeability, it is difficult to calculate the parameters of the surface area and tortuosity of throat. So the application of the theoretical model to calculate the fluid permeability is limited. Based on the analysis of the models of fluid permeability and air permeability, a transformation model of fluid permeability and air permeability is established. Then, with the help of the transformation model, a new method for calculating fluid permeability is suggested. In order to verify the accuracy of the transformation model of fluid permeability and air permeability, two sets of experimental data are used to calculate fluid permeability. Comparison of the calculated fluid permeability and core measured fluid permeability shows that the calculated fluid permeability matches fairly well with core measured results, which indicates that the transformation model in this study is credible.
渗透率描述了流体在岩石内部流动的难易程度,是评价泥质砂岩渗流特性与预测油气产能的重要参数.目前,对泥质砂岩渗透率的评价主要集中在绝对渗透率与液相渗透率的评价两个方面(匡立春等,2002).绝对渗透率是指单一流体在岩石孔隙中流动而与岩石没有发生物理化学作用时所测得的渗透率(孙建孟和闫国亮,2012; 景成等,2013; 闫国亮等,2014).在渗透率实验测量中,由于空气与岩石难以发生物理化学作用;因此,通常将空气渗透率作为岩石的绝对渗透率.液相渗透率是指盐水溶液在岩石孔隙中流动且与岩石孔隙表面黏土矿物发生物理化学作用时所测得的渗透率(匡立春等,2002).由于液相渗透率的测量条件更加接近实际地层泥质砂岩的条件,使得液相渗透率更能反映地层条件下泥质砂岩的渗流特性(Macary,1999; 谢伟彪等,2014).
对绝对渗透率计算方法的研究国内外众多学者做了大量工作,研究的思路可总结为:①根据岩石物理实验数据,在分析影响绝对渗透率主控因素的基础上,建立绝对渗透率的统计模型.②基于毛管束模型与Darcy定律,推导建立绝对渗透率的理论模型.大量岩心实验数据表明,影响绝对渗透率的参数较多,主要有孔隙度、束缚水饱和度、颗粒分选性与平均粒径、矿物组分、岩石比表面、孔隙曲折度、喉道半径等.基于这些影响因素,众多学者建立了大量的渗透率统计模型.Jennings与Lucia(2001)、焦翠华与徐朝晖(2006)根据孔隙度与渗透率的幂函数与指数函数关系,分别建立了基于孔隙度参数的绝对渗透率统计模型.Krumbein和Monk(1943)提出了考虑颗粒分选性与平均粒径的绝对渗透率统计模型.Herron(1987)提出了考虑矿物组成的绝对渗透率统计模型.Timur(1968)、Coates与Denoo(1981)建立了基于孔隙度、束缚水饱和度等参数的绝对渗透率评价模型.Kenyon(1997)、Kenyon等(1988)、Coates等(1991)、陈刚等(2012)在Timur公式的基础上,提出了SDR模型、Coates模型与孔隙空间集中分布模型.考虑喉道半径对绝对渗透率的作用,Schowalter(1979)、Thompson与Raschke(1987)、Pittman(1992)、Swanson(1981)、成志刚等(2014)根据压汞曲线分别用R10、R35、Swanson等参数计算绝对渗透率.Waxman 与Smits(1968)提出阳离子交换容量(Qv)对泥质砂岩导电性的影响以后,众多学者注意到了阳离子交换容量对渗透率的影响.De Lima(1995)、Sen等(1990)根据阳离子交换容量与绝对渗透率之间的统计关系,建立了绝对渗透率的统计模型.对渗透率理论模型的研究主要体现在Kozeny-Carman(KC)模型的建立.Kozeny(1927)基于毛管束理论,提出了Kozeny绝对渗透率计算公式.Carman(1937)对Kozeny公式进行了证明,并进一步修改得到了KC模型.由于KC模型中比表面与喉道曲折度等参数求取困难,KC模型的使用受到限制.Nooruddin与Hossain(2012)根据喉道曲折度与胶结指数、地层因素的关系,提出了基于胶结指数、地层因素等参数的改进KC模型.Amaefule等(1993)、宋宁等(2013)在分析KC模型的基础上,提出了基于划分流动单元的绝对渗透率计算方法.Shan和Chen(1993)、Grunau等(1993)、Chen等(1998)、He等(1999)基于格子Boltzmann方法探索了流体的流动及多相渗透率.
目前,对液相渗透率计算方法的研究还不够深入.液相渗透率的计算模型较少,且均为统计模型.Macary(1999)建立了液相渗透率与空气渗透率之间的关系式.Goode与Sen(1988)根据Waxman与Smits(1968)测量的液相渗透率、阳离子交换容量等实验数据,提出了利用阳离子交换容量、孔隙度等参数计算液相渗透率的统计模型.匡立春等(2002)对泥质砂岩岩心开展多矿化度溶液液相渗透率实验测量发现,溶液矿化度对液相渗透率有较大影响.但是,Macary(1999)、Goode与Sen(1988)建立的液相渗透率计算模型均未能体现溶液矿化度对液相渗透率的影响.
本文综合考虑了阳离子交换容量、溶液矿化度、喉道曲折度、比表面等因素对渗透率的影响,在毛管束模型与岩石物理体积模型的基础上,推导建立了基于阳离子交换容量、溶液矿化度、比表面、喉道曲折度等参数的液相渗透率理论计算模型.同时,考虑到运用理论模型计算液相渗透率时,模型中比表面、喉道曲折度等参数求取困难的问题,进一步建立了空气渗透率与液相渗透率的转换模型.最终,确立了在准确求取空气渗透率的基础上,利用空气渗透率与液相渗透率转换模型计算液相渗透率的新方法.
2 泥质砂岩液相渗透率理论计算模型 2.1 泥质砂岩液相渗透率与黏土束缚水饱和度的关系将长度为L,截面积为A的多孔介质岩石等效 为个数为n,半径为r的平行毛细管束模型(Kozeny,1927; Carmen,1937; Nooruddin and Hossain,2011; 葛新明等,2011).基于泊肃叶方程,可得到纯岩石的毛细管模型:
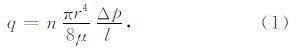
通常情况下,多孔介质岩石中毛细管渗流长度大于岩石的长度.为此,引入曲折度τ,表示孔隙的复杂程度:

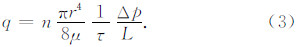
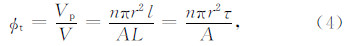
基于达西渗透率定律,可得到毛细管模型的绝对渗透率:

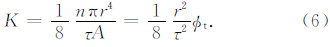
在泥质砂岩中,当泥质或者黏土分散地存在于孔隙空间时,认为泥质或黏土附着在岩石孔隙的表面(葛新明等,2011).由于黏土矿物表面带负电,因而一旦把它放入溶液中,溶液中的阳离子就会被吸附到黏土矿物表面以保持电中性,在黏土矿物表面形成水膜,这些水膜中的水称为黏土束缚水(Hill and Millburn,1956;Clavier et al.,1984;Juhasz,1979,1986;Sen et al.,1990;Lonnes et al.,2003).假设 水膜厚度为d,则有效的毛细管渗流半径减小为r-d(图 1).此时,得到泥质砂岩的液相渗透率为
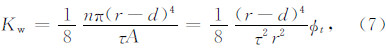
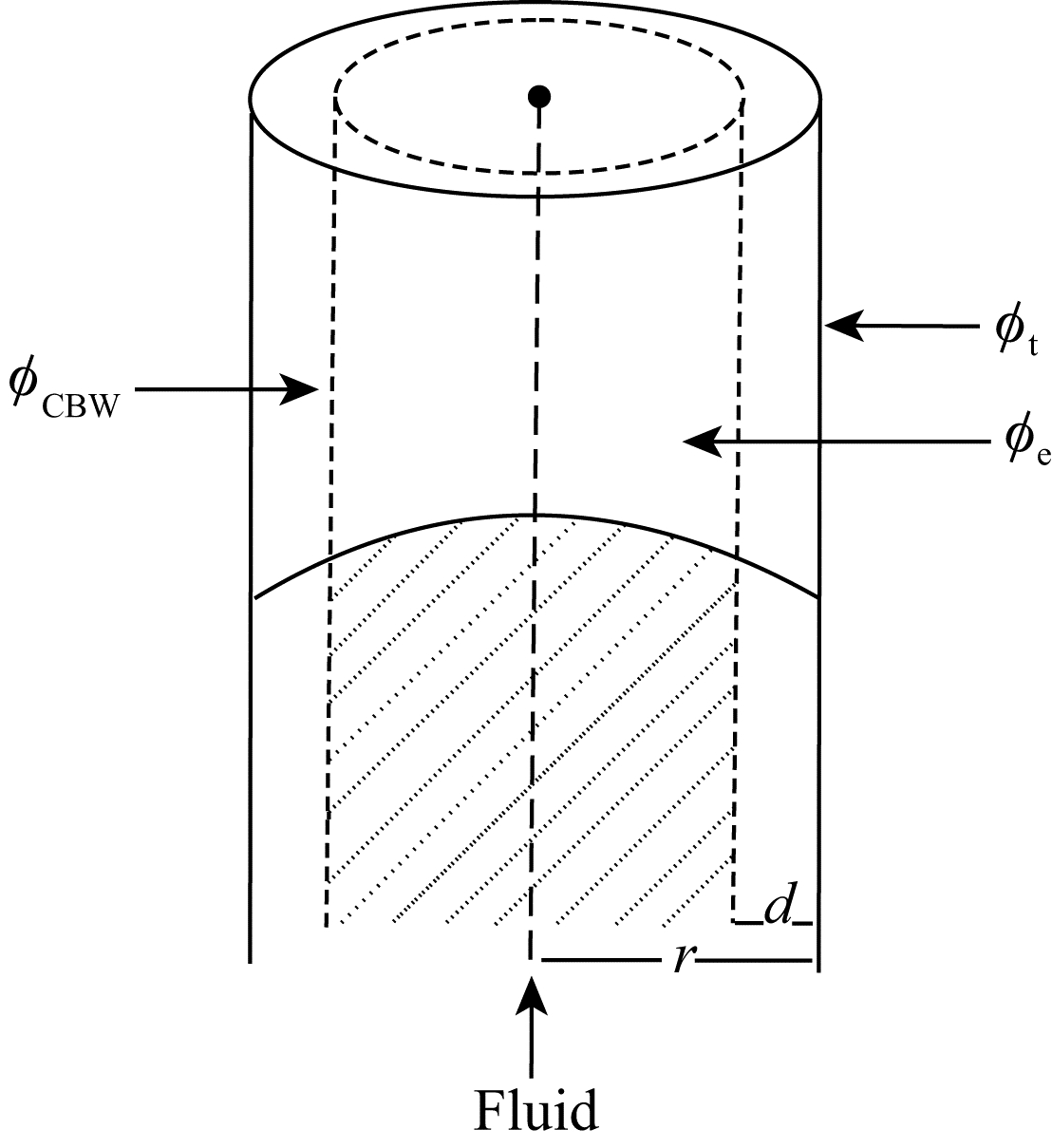 | 图 1 泥质砂岩毛细管模型示意图 Fig. 1 Capillary model of shaly sandstone |
将公式(7)代入式(6)可得:
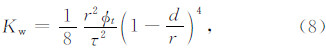
根据图 1中的泥质砂岩模型,黏土表面束缚水孔隙度可表示为
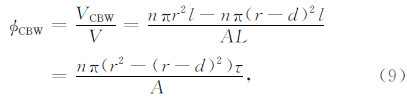
将式(9)代入式(4)可得黏土束缚水孔隙度与总孔隙度的比值:
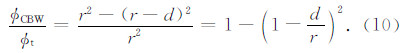
将式(10)代入式(8),并整理可得:
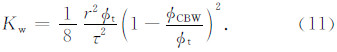
定义Svp为以岩石孔隙体积为基准的比面(cm2/cm3).则多孔岩石中Svp可以表示为
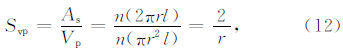
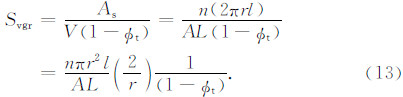
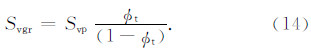

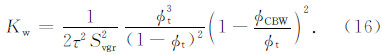
根据泥质砂岩岩石物理体积模型(图 2),可以将泥质砂岩看成由砂岩骨架、干黏土和总孔隙度三部分组成,其中总孔隙度et可以进一步分为黏土束缚水孔隙度eCBW和有效孔隙度φe.
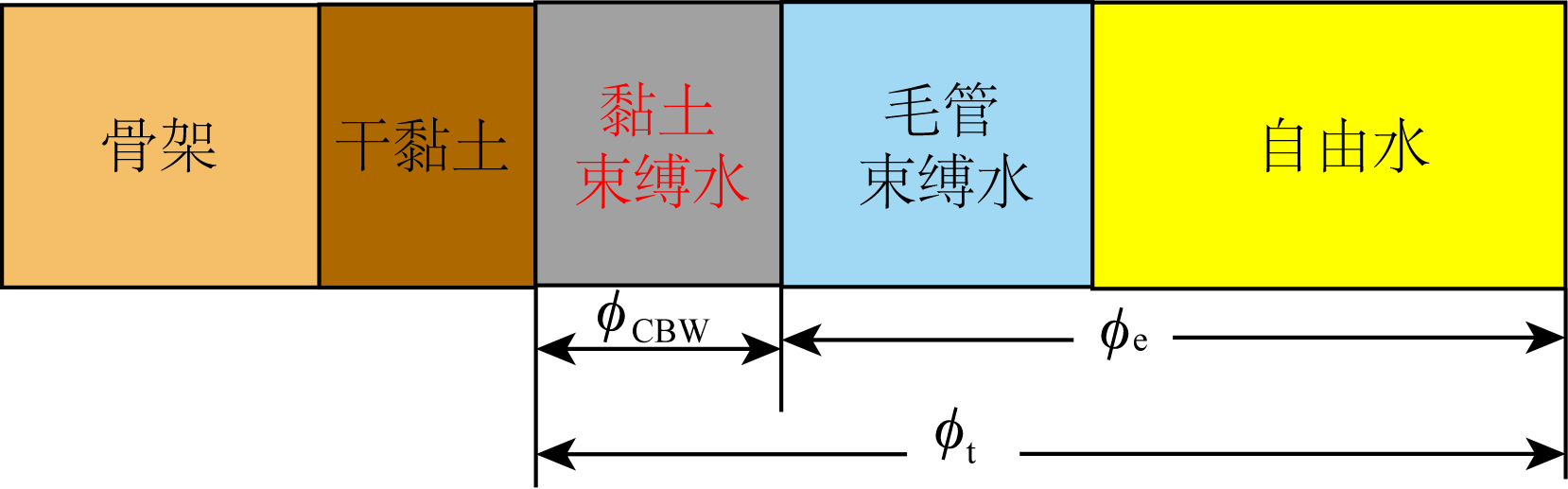 | 图 2 泥质砂岩岩石物理体积模型 Fig. 2 Physical volume model of shaly sandstone |
根据黏土束缚水孔隙度的定义,可知:
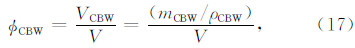

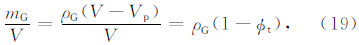
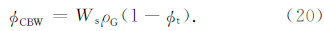
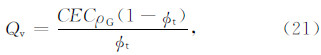
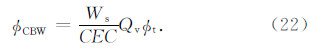
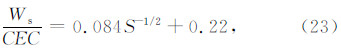
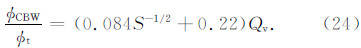
将式(24)代入式(16),并整理可得
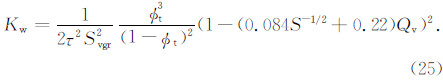
将式(25)写成一般形式,可以表示为
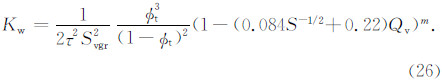
式(26)等式右边第一部分:
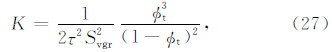
| | 表 1 岩心基本物性参数与两种不同溶液矿化度液相渗透率测量结果( 匡立春等,2002) Table 1 Physical parameters of cores and its fluid permeability with two salinity |
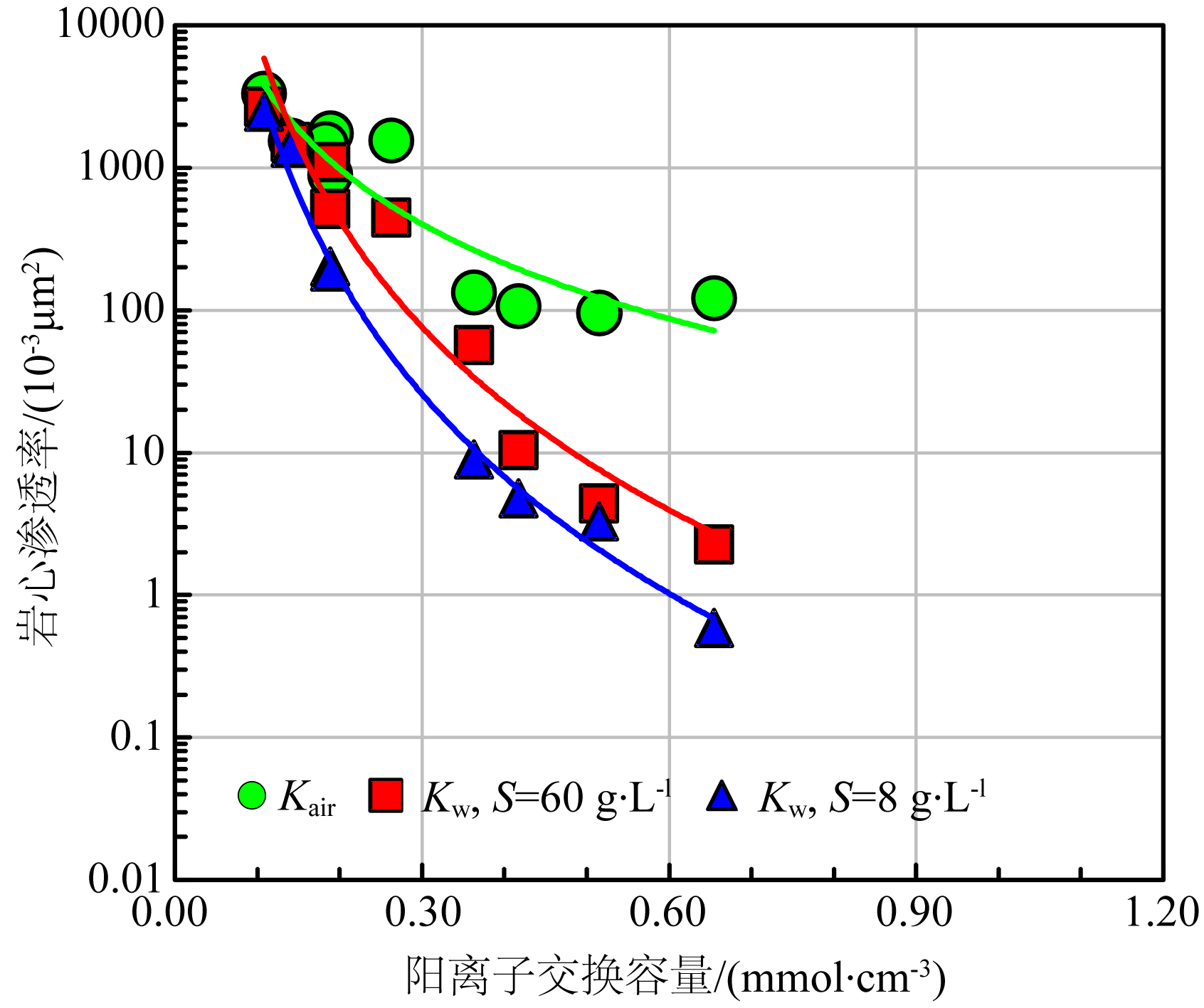 | 图 3 液相渗透率与阳离子交换容量的关系 Fig. 3 Relationship between cation exchange capacity and fluid permeability |
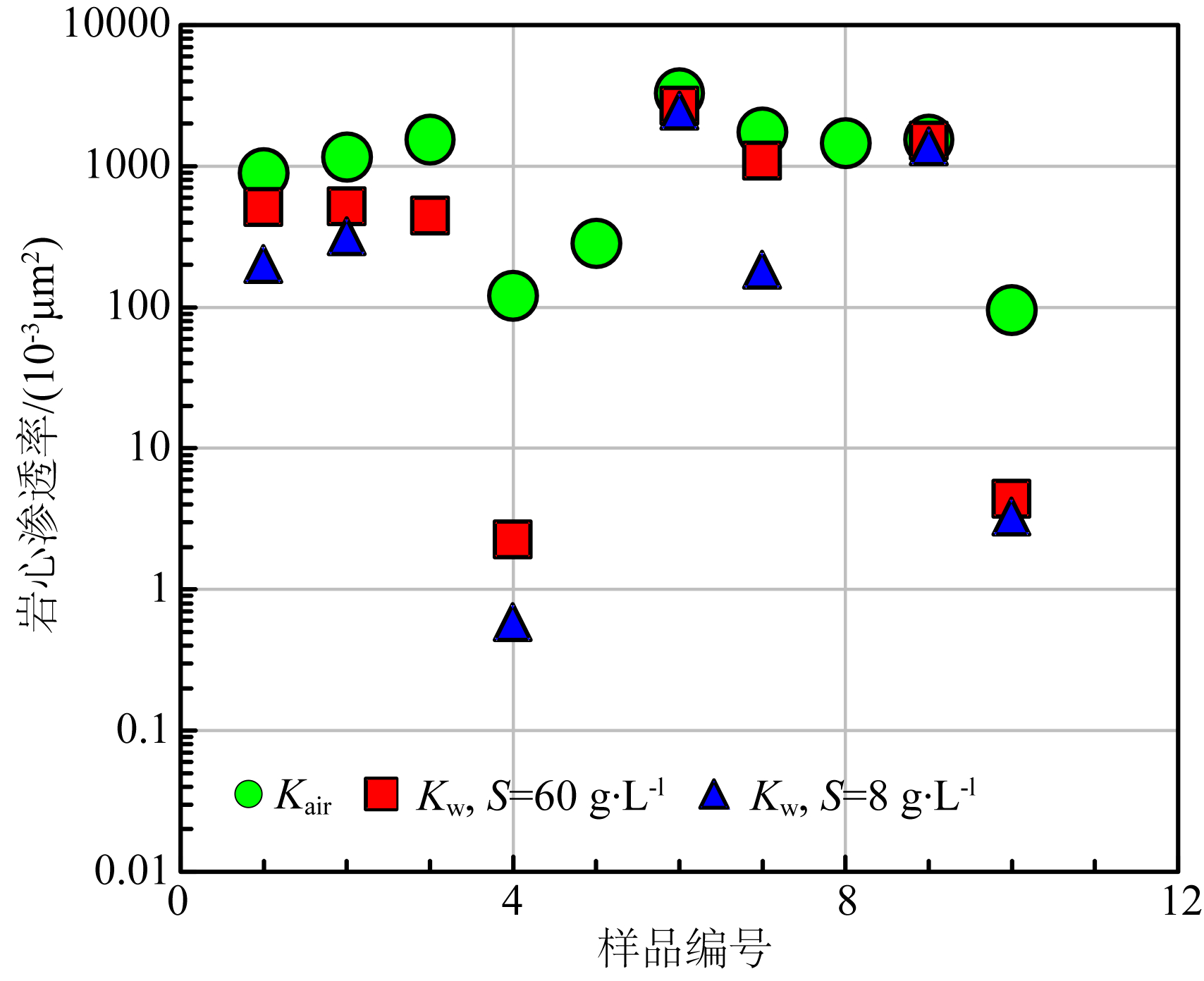 | 图 4 不同溶液矿化度条件下的渗透率变化特征 Fig. 4 Characteristics of fluid permeability with different salinity |
液相渗透率理论计算模型揭示了孔隙度、曲折度、比表面、阳离子交换容量、溶液矿化度与液相渗透率之间的理论关系.但是,在实际液相渗透率评价过程中,由于模型中曲折度、比表面等参数求取困难,直接利用理论模型计算液相渗透率困难.因此,为解决液相渗透率因理论模型中部分参数不易求取,造成计算液相渗透率困难的问题,可采用如下的思路:①准确求取空气渗透率;②在液相渗透率理论模型的基础上,建立液相渗透率与空气渗透率的转换模型;利用空气渗透率与液相渗透率之间的转换模型计算液相渗透率.
3.1 液相渗透率与空气渗透率的转换模型在岩心空气渗透率测量过程中,由于空气与黏土不发生电化学反应,在黏土表面不会形成水膜,即空气渗透率不受黏土表面束缚水的影响(Juhasz,1979;Hill et al.,1979).此时,公式(26)中(1-(0.084S-1/2+0.22)Qv)m值为1.因此,空气渗透率可以表示为
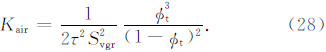
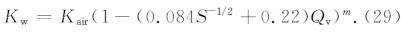
式(29)表明,在确定模型系数m以后,可通过式(29)评价液相渗透率.根据表 1中的实验测量结果,采用回归分析方法确定了模型系数m,得到液相渗透率与空气渗透率的转化模型:
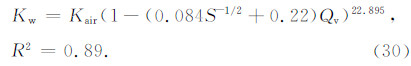
为进一步验证液相渗透率与空气渗透率转化模 型的准确性,根据表 1以及Waxman与Smits(1968)文献中的岩心实验数据(表 2),利用空气渗透率、溶液矿化度以及阳离子交换容量计算了液相渗透率,将液相渗透率计算结果与岩心液相渗透率实验结果进行对比(图 5).图 5中模型计算结果与实验测量结果对比显示,液相渗透率计算结果与实际岩心测量吻合较好.表明文中建立的液相渗透率与空气渗透率转化模型合理可靠,模型计算结果精度较高.
| | 表 2 岩心基本物性参数与液相渗透率测量结果 (S=12 g·L-1) (Waxman与Smits(1968)) Table 2 Physical parameters of cores and its fluid permeability with one salinity (S=12 g·L-1) |
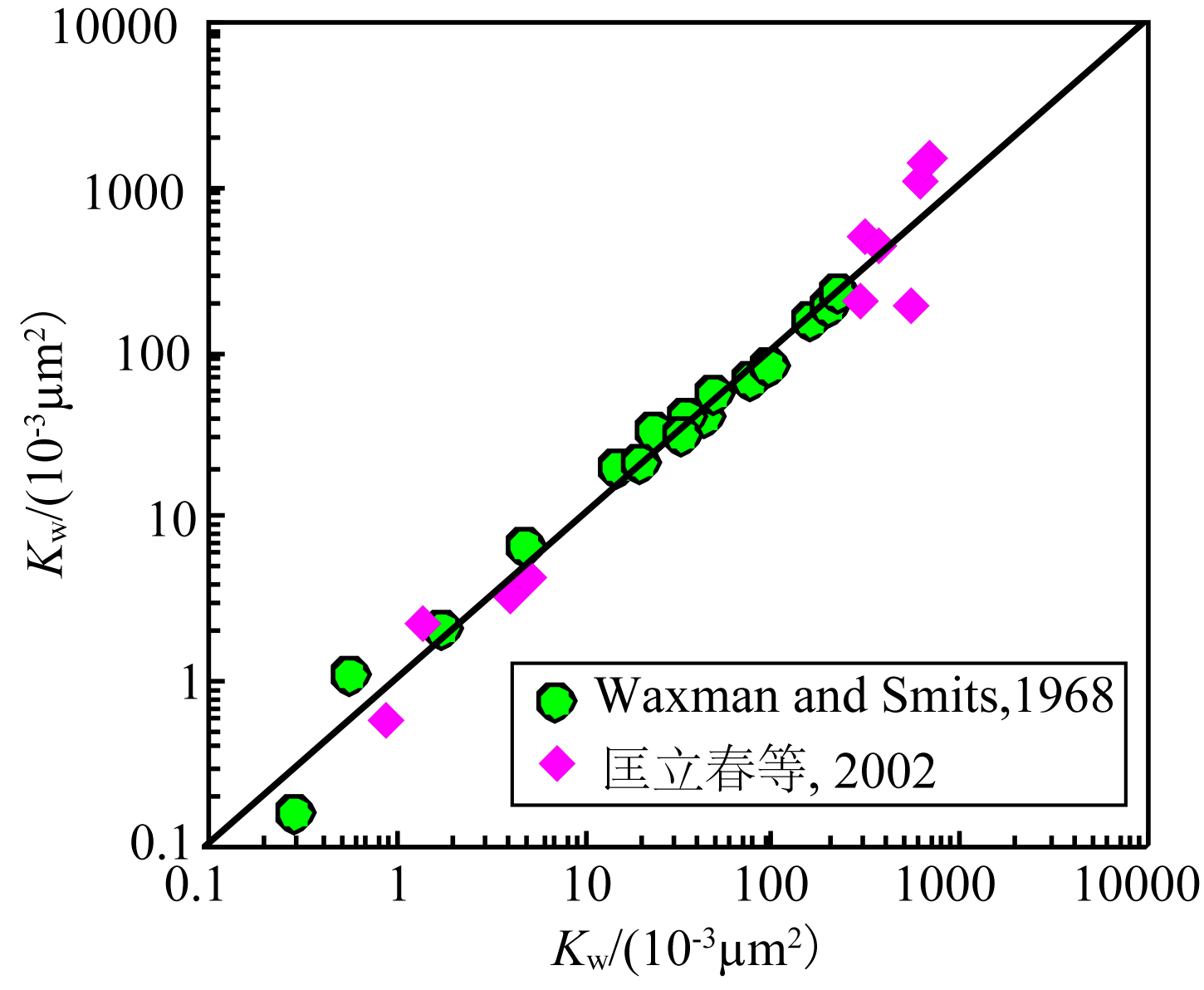 | 图 5 岩心液相渗透率与模型计算液相渗透率交会图 Fig. 5 Cross plot of core analyzed fluid permeability and estimated fluid permeability |
1)液相渗透率理论计算模型由KC模型与(1-(0.084S-1/2+0.22)Qv)m两部分组成;与绝对渗透率相比,液相渗透率除了受到岩石孔隙度、比表面、喉道曲折度等影响因素外,还受溶液矿化度、岩石阳离子交换容量的影响.液相渗透率随阳离子交换容量的增大而降低,随溶液矿化度的降低而降低.
2)液相渗透率理论计算模型中喉道曲折度、比表面等参数求取困难,直接利用理论模型计算液相渗透率困难.利用液相渗透率与空气渗透率之间的转换模型,可有效计算液相渗透率.
| [1] | Amaefule J O, Altunbay M, Tiab D, et al. 1993. Enhanced reservoir description: using core and log data to identify hydraulic (flow) units and predict permeability in uncored intervals/wells. SPE 26436. |
| [2] | Carmen P C. 1937. Fluid flow through granular beds. Transactions of the Institution of Chemical Engineers, 15: 150-166. |
| [3] | Chen S Y, Doolen G D. 1998. Lattice Boltzmann method for fluid flows. Annual Review of Fluid Mechanics, 30(1): 329-364. |
| [4] | Chen G, Pan B Z, Wang C P, et al. 2012. Permeability evaluation method for complex pore structure reservoir. Well Logging Technology (in Chinese), 36(4): 382-386. |
| [5] | Cheng Z G, Luo S C, Du Z W, et al. 2014. The method to calculate tight sandstone reservoir permeability using pore throat characteristic parameters. Well Logging Technology (in Chinese), 38(2): 185-189. |
| [6] | Clavier C, Coates G, Dumanoir J. 1984. Theoretical and experimental bases for the dual-water model for interpretation of shaly sands. Society of Petroleum Engineers Journal, 24(2): 153-158. |
| [7] | Coates G, Denoo S. 1981. The producibility answer product. The Technical Review, 29(2): 54-63. |
| [8] | Coates R G, Miller M, Gillen M, et al. 1991. An investigation of a new magnetic resonance imaging log.//SPWLA 32nd Annual Logging Symposium. Midland, Texas. |
| [9] | De Lima O A L. 1995. Water saturation and permeability from resistivity, dielectric, and porosity logs. Geophysics, 60(6): 1756-1764. |
| [10] | Ge X M, Fan Y Y, Deng S G. 2011. Research on T2 cutoff-value determination method for shaly sand based on experiments. Well Logging Technology (in Chinese), 35(4): 308-313. |
| [11] | Goode P, Sen P N. 1988. Charge density and permeability in clay-bearing sandstones. Geophysics, 53(12): 1610-1612. |
| [12] | Grunau D, Chen S Y, Eggert K. 1993. A lattice Boltzmann model for multiphase fluid flows. Phys. Fluids A, 5(10): 2557-2562. |
| [13] | He X Y, Chen S Y, Zhang R Y. 1999. A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh-Taylor instability. Journal of Computational Physics, 152(2): 642-663. |
| [14] | Herron M M. 1987. Estimating the intrinsic permeability of clastic sediments from geochemical data.//SPWLA 28th Annual Logging Symposium. London, England. |
| [15] | Hill H J, Millburn J D. 1956. Effect of clay and water salinity on electrochemical behavior of reservoir rocks. AIME Petroleum Transaction, 207(3): 65-72. |
| [16] | Hill H J, Shirley O J, Klein G E. 1979. Bound water in shaly sands-its relation to Qv and other formation properties. The Log Analyst, 20(3): 13-19. |
| [17] | Jennings J W Jr, Lucia F J. 2001. Predicting permeability from well logs in carbonates with a link to geology for interwell permeability mapping. Society of Petroleum Engineers Journal, 6(4): 215-225. |
| [18] | Jiao C H, Xu C H. 2006. An approach to permeability prediction based on flow zone index. Well Logging Technology (in Chinese), 30(4): 317-319. |
| [19] | Jing C, Song Z Q, Pu C S, et al. 2013. Refined permeability of tight gas reservoir based on petrophysical facies classification — taking the study of tight gas reservoir permeability in the eastern of Sulige for an example. Progress in Geophysics (in Chinese), 28(6): 3222-3230, doi: 10.6038/pg20130649. |
| [20] | Juhasz I. 1979. The central role of Qv and formation-water salinity in the evaluation of shaly formations. The Log Analyst, 20(4): 3-13. |
| [21] | Juhasz I. 1986. Conversion of routine air permeability data into stressed brine permeability data.//10th European Formation Evaluation Symposium. |
| [22] | Kenyon W E, Day P I, Straley C, et al. 1988. A three-part study of NMR longitudinal relaxation properties of water-saturated sandstones. SPE Formation Evaluation, 3(3): 622-636. |
| [23] | Kenyon W E. 1997. Petrophysical principles of applications of NMR logging. The Log Analyst, 38(2): 21-43. |
| [24] | Kozeny J. 1927. Vber kapillare leitung des wassers im boden. Sitzungsberichte der Wiener Akademie der Wissenschaften, 136(2a): 271-306. |
| [25] | Krumbein W C, Monk G D. 1943. Permeability as a function of the size parameters of unconsolidated sand. Transactions of the AIME, 151(1): 153-163. |
| [26] | Kuang L C, Mao Z Q, Sun Z C. 2002. On the controlling factors of irreducible water saturation in the low resistivity pay zone of cretaceous formation in Lu 9 area, Junggar basin. Well Logging Technology (in Chinese), 26(1): 14-17. |
| [27] | Lonnes S, Angel G, Holland R. 2003. NMR petrophysical predictions on cores.//SPWLA 44th Annual Logging Symposium. |
| [28] | Macary S M. 1999. Conversion of air permeability to liquid permeabilities extracts huge source of information for reservoir studies.//Middle East Oil Show and Conference. February, Bahrain: SPE. |
| [29] | Martin P, Dacy J. 2004. Effective Qv by NMR tests.//SPWLA 45th Annual Logging Symposium. Noordwijk, Netherlands. |
| [30] | Nooruddin H A, Hossain M E. 2011. Modified Kozeny-Carmen correlation for enhanced hydraulic flow unit characterization. Journal of Petroleum Science and Engineering, 80(1): 107-115. |
| [31] | Pittman E D. 1992. Relationship of porosity and permeability to various parameters derived from mercury injection capillary pressure curves for sandstones. AAPG Bulletin, 76(2): 191-198. |
| [32] | Schofield R K. 1947. Calculation of surface areas from measurements of negative adsorption. Nature, 160(4064): 408-410. |
| [33] | Schowalter T T. 1979. Mechanics of secondary hydrocarbon migration and entrapment. AAPG Bulletin, 63(5): 723-760. |
| [34] | Sen P N, Straley C, Kenyon W E, et al. 1990. Surface-to-volume ratio, charge density, nuclear magnetic relaxation, and permeability in clay-bearing sandstones. Geophysics, 55(1): 61-69. |
| [35] | Shan X W, Chen H D. 1993. Lattice Boltzmann model for simulating flows with multiple phases and components. Physical Review E, 47(3): 1815-1819. |
| [36] | Song N, Liu Z, Zhang J F, et al. 2013. Permeability prediction of heterogeneous sand reservoir based on flow units classification. Science & Technology Review (in Chinese), 31(2): 68-71. |
| [37] | Sun J M, Yan G L. 2012. Review on absolute permeability model. Well Logging Technology (in Chinese), 36(4): 329-335. |
| [38] | Swanson B F. 1981. A simple correlation between permeabilities and mercury capillary pressures. Journal of Petroleum Technology, 33(12): 2498-2504. |
| [39] | Thompson A H, Raschke R A. 1987. Estimation of absolute permeability from capillary pressure measurements.//SPE Annual Technical Conference and Exhibition. Dallas, Texas: SPE. |
| [40] | Timur A. 1968. An investigation of permeability, porosity, and residual water saturation relationship for sandstone reservoirs. The Log Analyst, 9(4): 8-17. |
| [41] | Waxman M H, Smits L J M. 1968. Electrical conductivities in oil-bearing shaly sands. Society of Petroleum Engineers Journal, 8(3): 107-122. |
| [42] | Xie W B, Zhou F M, Si Z W, et al. 2014. New calculation model of permeability in sandstone formation by the mathematical derivation. Well Logging Technology (in Chinese), 38(5): 553-557. |
| [43] | Yan G L, Sun J M, Liu X F, et al. 2014. Characterization of microscopic pore structure of reservoir rock and its effect on permeability. Well Logging Technology (in Chinese), 38(1): 28-32. |
| [44] | 陈刚, 潘保芝, 王翠平等. 2012. 复杂孔隙结构储层渗透率评价方法研究. 测井技术, 36(4): 382-386. |
| [45] | 成志刚, 罗少成, 杜支文等. 2014. 基于储层孔喉特征参数计算致密砂岩渗透率的新方法. 测井技术, 38(2): 185-189. |
| [46] | 葛新民, 范宜仁, 邓少贵. 2011. 基于实验分析的泥质砂岩T2截止值确定方法研究. 测井技术, 35(4): 308-313. |
| [47] | 焦翠华, 徐朝晖. 2006. 基于流动单元指数的渗透率预测方法. 测井技术, 30(4): 317-319. |
| [48] | 景成, 宋子齐, 谱春生等. 2013. 基于岩石物理相分类确定致密气储层渗透率—以苏里格东区致密气储层渗透率研究为例. 地球物理学进展, 28(6): 3222-3230, doi: 10.6038/pg20130649. |
| [49] | 匡立春, 毛志强, 孙中春. 2002. 准噶尔盆地Lu9井区白垩系低电阻率油层束缚水饱和度控制因素研究. 测井技术, 26(1): 14-17. |
| [50] | 宋宁, 刘振, 张剑风等. 2013. 基于流动单元分类的非均质砂岩储集层渗透率预测. 科技导报, 31(2): 68-71. |
| [51] | 孙建孟, 闫国亮. 2012. 渗透率模型研究进展. 测井技术, 36(4): 329-335. |
| [52] | 谢伟彪, 周凤鸣, 司兆伟等. 2014. 基于数理推导的砂岩地层渗透率计算新模型. 测井技术, 38(5): 553-557. |
| [53] | 闫国亮, 孙建孟, 刘学锋等. 2014. 储层岩石微观孔隙结构特征及其对渗透率影响. 测井技术, 38(1): 28-32. |
 2015, Vol. 58
2015, Vol. 58

