地球物理学报  2015, Vol. 58 Issue (1): 267-276   PDF    
引用本文
黄建平, 袁茂林, 李振春, 岳玉波. 2015. 双复杂条件下非倾斜叠加精确束偏移方法及应用I——声波方程. 地球物理学报, 58(1): 267-276, doi: 10.6038/cjg20150124   
HUANG Jian-Ping, YUAN Mao-Lin, LI Zhen-Chun, YUE Yu-Bo. 2015. The accurate beam migration method without slant stack under dual-complexity conditions and its application (I): Acoustic equation. Chinese J. Geophysics, 58(1): 267-276, doi: 10.6038/cjg20150124   
双复杂条件下非倾斜叠加精确束偏移方法及应用I——声波方程
黄建平1, 袁茂林1, 李振春1, 岳玉波2    
1. 中国石油大学(华东)地球科学与技术学院地球物理系, 青岛 266555;
2. 中石油东方地球物理公司物探技术研究中心, 河北涿州 072750
投稿时间:2014-01-02    最后修改时间: 2014-05-28 .
基金项目：国家重点基础研究发展计划(973计划)项目(2014CB239006,2011CB202402),国家自然科学基金(41104069,41274124)及山东省自然科学基金(ZR2011DQ016),中央高校基本科研业务费专项基金(R1401005A, R1401038A)及骨干教师人才支持计划联合资助.
作者简介：黄建平,1982年生,副教授,主要从事地震波正演及偏移成像工作. E-mail:jphuang@mail.ustc.edu.cn
通讯作者：袁茂林,男,1990年生,硕士在读,主要从事高斯束正演与反演成像工作.E-mail:yml3290432@163.com
摘要：近年来,油气勘探的重心正转向具有复杂地表和复杂地质体的双复杂区域.本文发展了一种精确的双复杂条件下基于地表倾角信息的非倾斜叠加束偏移方法,相对于传统束成像方法无需进行三方面处理:(1)高程静校正;(2)相位校正;(3)束中心与接收点之间关于速度和束出射角的近似替换,因而具有更高的成像精度.通过加拿大逆掩断层模型、中原油田断层模型及实际资料的偏移试算,并与传统束偏移及波动方程偏移成像结果对比可知:本文非近似束偏移方法在近地表、高陡倾等构造处的成像精度、反射界面成像振幅等方面优于传统的偏移方法,以此验证了本文非倾斜叠加精确束偏移方法的正确性、优越性及适应性.
关键词： 双复杂     倾角信息     非倾斜叠加     束偏移     波动方程偏移    
The accurate beam migration method without slant stack under dual-complexity conditions and its application (I): Acoustic equation
HUANG Jian-Ping1, YUAN Mao-Lin1, LI Zhen-Chun1, YUE Yu-Bo2    
1. Geophysics Department of China University of Petroleum, Qingdao 266555, China;
2. Geophysical Technich Research Center, BGP Inc. of CNP, Hebei Zhuozhou 072750, China
Abstract: Recent trends in seismic exploration have transferred to lands where both topography and subsurface targets are complex, leading to challenges for both acquisition and processing methods. Compared with one-way or two-way wave-equation migration, ray-based migration is an efficient and flexible method, especially for complex topography. In general, Gaussian beam migration (GBM) is more accurate than single-arrival Kirchhoff migration, although there are some issues resulting in dissatisfactory GBM images. For example, static correction will lead to the distortion of wavefields when near-surface elevation and velocity vary drastically. Worse still, unbalanced amplitude will emerge in migrated images when receivers are not placed within some neighborhood of the beam center, that is, GBM is slightly inflexible for the irregular acquisition system. For the irregular surface, both near-surface velocity and takeoff angle of an individual beam at the beam center are different from those at each receiver, so GBM usually produces non-ignorable migration artifacts. In order to improve the flexibility and accuracy of GBM, we propose an accurate beam migration method without slant stack based on acoustic wave equation.
An accurate acoustic beam migration algorithm based on surface dip angle information for complex topography is presented. Unlike the conventional GBM migration method, the proposed method shoots beams directly from receivers without elevation static correction, phase correction, as well as approximate velocity and takeoff angle of an individual beam. Based on acoustic wave equation, we first derive the acoustic backward-continued wavefields from receivers by using surface dip angle information and then derive the acoustic beam migration formula by using the deconvolution imaging condition. Finally, we use a real data and two synthetic datasets separately from the 2D Canadian Foothills model and the Zhongyuan oilfield fault model to verify the proposed algorithm.
In the example of 2D Canadian Foothills model, our method suppresses the near-surface noise. Meanwhile, it images near-surface, extremely steep, and overturned structures more clearly, compared to other methods such as wave-equation migration, the Gray's method and Yue's method. Furthermore, our method efficiently eliminates imaging energy error caused by the large distance between the beam centre and receivers in both Gray's method and Yue's method, and thus improves the imaging amplitude. In the example of Zhongyuan oilfield fault model, the image generated by our method shows fewer migration artifacts and better continuity for the reflectors than those generated by the Yue's method. Our method is capable of producing a higher resolution of images and better S/N of profiles. In the example of real data, compared to the Yue's method, our method produces more continuous reflectors on both flanks of the buried hill and sharper faults on the left side of the area. Moreover, our method generates more interpretable image profiles with more balanced amplitude, especially in the deep formation, while the Yue's method can hardly accomplish this because of the amplitude error caused by the large distance between the beam center and receivers.
One feature of our method is that beams for backward-continued wavefields are emitted directly from the receivers, without implementing the following procedures: (1) elevation statics; (2) phase correction; (3) approximation of both velocity and takeoff angle of an individual beam between receivers and the beam centre. While in the traditional beam migration methods, those procedures will lower the imaging quality, especially when the near-surface velocity and elevation vary drastically. Compared to wave equation migration (WEM) and other ray-based methods, our method is more effective in suppressing the near-surface noise and improving imaging quality on the near-surface, extremely steep, and overturned structures. Moreover, our method effectively reduces the imaging energy error that is caused by the large distance between the beam centre and receivers, which usually occurs in conventional beam migration methods, and has great potential in improving amplitude and S/N. However, our method is relatively costly because it requires shooting beams from each receiver. We will develop the algorithm for elastic wave equation and then apply it to multicomponent data processing.
Key words: Dual-complexity     Dip angle information     Non slant stack     Beam migration     Wave equation migration    
1 引言

研究复杂地表和复杂地下地质体双重复杂条件下的处理技术是地震勘探领域的热点.复杂地表对地震数据的采集与处理都带来了不小的困难，尤其是在中国西部和南方山前带探区尤为突出(王华忠等，2013).在近地表速度远小于地下介质速度且地形变化较平缓的条件下，简单的静校正可以满足要求；但当地表高程起伏较大且近地表速度变化剧烈时，静校正的假设条件不成立，采用简单的静校正对波场造成的畸变会影响偏移成像的质量.为此，发展双复杂条件下的地震偏移成像方法成为解决上述问题的关键.

目前，针对起伏地表条件下的地震成像问题，国内外学者提出并发展了一系列有效的处理方法：第一类是基于波动方程的偏移成像方法.Berryhill(1979，1984)较早提出了波动方程基准面校正的方 法.随后，Yilmaz和Lucas(1986)，Schneider等(1995)，Bevc(1997)以及 Yang等(1999)在此基础上结合层替代思想进一步发展了此方法.虽然波动方程基准面校正能够有效地消除起伏地表对同相轴造成的扭曲.但是，近地表速度的横向变化会严重影 响基准面校正的精度.针对上述缺陷，Reshef(1991)，Beasley和Lynn(1992)，何英等(2002)，Shragge和Paul(2005)，程玖兵(2006)，叶月明等(2008)以及吕彬等(2011)提出了多种改进的基于波动理论的偏移成像方法来解决复杂地表问题.然而，在复杂的地表条件下，波场延拓很难适应不规则的观测系统，并且运算量较大.第二类是基于射线的偏移成像方法.射线类方法具有更加灵活，易于实现，计算效率高等优点.Wiggins(1984)提出了适用于起伏地表条件的Kirchhoff偏移方法，Gray和Marfurt(1995)实现了直接在起伏地表进行Kirchhoff 偏移的方法且成像效果较好，Jäger等(2003)提出了起伏地表条件下的保幅Kirchhoff偏移方法，而董春晖和张剑锋(2009)及刘国峰等(2010)先后基于Kirchhoff 算子提出了起伏地表直接时间偏移的流程与应用.

Gray(2005)发展了一种适用于起伏地表的局部静校正的束偏移方法，但是当地表高程及速度变化剧烈时，静校正方法会造成地震波场发生畸变从而影响成像质量.Yue等(2010)提出了一种适用于起伏地表条件的保幅高斯束偏移方法，该方法通过考虑起伏地表平面波的传播特点，直接在起伏地表进行局部平面波的分解.Yue等(2010)提出的方法在成像精度方面相较于Kirchhoff偏移以及基于局部静校正的高斯束偏移有一定的优势，且在高陡倾以及倒转构造处成像效果优于单程波方法.然而，由于束中心出射位置与接收点位置之间有水平距离差和高程差，需要引入相位校正因子以近似表征格林函数，当水平距离差较大时，这种近似所带来的振幅误差不能忽略，尤其当地形起伏较大且近地表速度变化剧烈时，上述近似处理会极大地降低偏移成像的质量.

针对已有起伏地表条件高斯束成像方法存在的两个主要问题：(1)Gray(2005)静校正方法在地表高程变化剧烈时，会造成地震波场发生畸变从而影响成像质量；(2)Yue等(2010)方法由于束中心位置与接收点位置不一致，一系列近似处理会降低偏移成像的质量.本文通过考虑地表倾角信息，推导了波场反向延拓公式，并结合反褶积成像条件，实现了一种非倾斜叠加的双复杂条件下精确的束偏移方法.在实现基于倾角信息的起伏地表非近似束偏移成像方法的基础上，通过加拿大逆掩断层模型、中原油田断层模型和某探区实际资料的试算，验证方法的正确性、适应性和实用性. 2 方法原理 2.1 双复杂条件下波场反向延拓公式

如图 1所示的复杂地表模型，假设S为复杂地表面，由震源xs激发，接收点xr接收到的地震记录 为u(xr，ω)，则x处反向延拓的地震波场u(x，xr，ω) 可以通过 Kirchhoff-Helmholtz积分来表示，在自由地表S上简化为(Claerbout，1971; Schneider，1978; Wapenarr et al., 1989; Docherty，1991; Geiger，2002)：

其中，θr=βr－αr为接收点xr处射线出射方向同法线之间的角度，βr和αr分别为出射到达地下成像点x处射线的出射角以及地表倾角，ω为角频率，Vr为xr处速度，*表示复共轭.
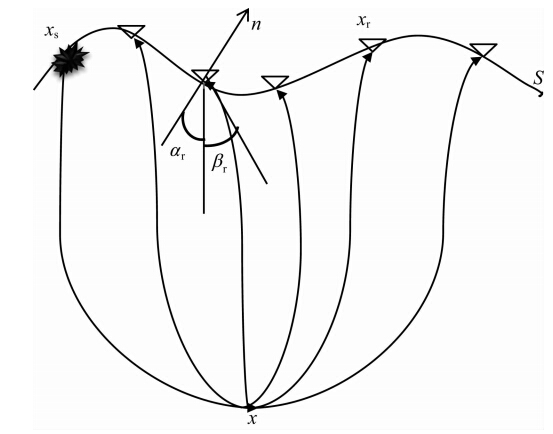图 1 复杂地表条件下的地震波场反向延拓 Fig. 1 Backward-continued seismic wavefields under complex topographic conditions

如图 2所示，将(1)式中格林函数G(x，xr，ω)通过接收点xr处出射的高斯束uGB(x，xr，ω)的叠加积分来表示：

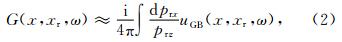
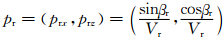此处，为束初始慢度.
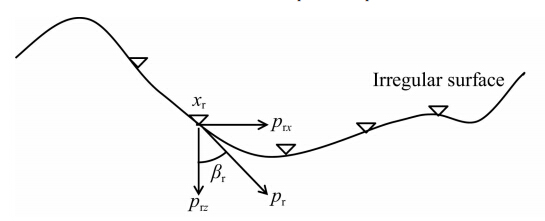图 2 接收点xr处出射高斯束 Fig. 2 Gaussian beam emitted from receiverxr

将(2)式代入(1)式，反向延拓波场的公式可重写为：

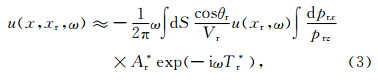
式中，Ar和Tr分别为高斯束的复值振幅和复值走时. 2.2 双复杂条件下束偏移成像公式

由高斯束表征的从震源到地下某个成像点x的格林函数为：

应用反褶积成像条件：

其中，I(x)为单炮成像值.将(3)式，(4)式代入(5)式得到共炮域的单炮成像结果表达式：

要计算关于prx和psx的二维复值积分，效率较低.为此，本文采用最速下降法进行降维处理.

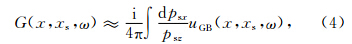
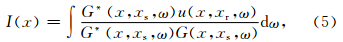
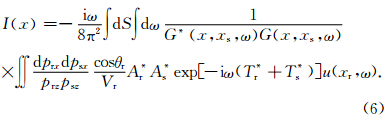
首先，将震源与接收点射线参数的水平分量psx和prx变换到中心点与偏移距射线参数的水平分量pmx和phx，则式(6)可表示为：

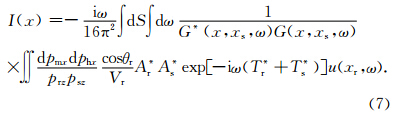
进一步，利用最速下降法求取式(7)中G*(x，xs，ω)G(x，xs，ω)以及关于phx的积分，Hill(2001)指出式(7)中积分的鞍点对应着令Tr+Ts的虚值走时最小的phx0，Gray和Bleistein(2009)给出了此时积分及G*(x，xs，ω)G(x，xs，ω)的渐进解.得到双复杂条件下最终的用于编程计算的单炮偏移成像公式：

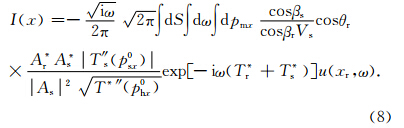
式中，Vs为震源xs处速度，βs为震源到成像点的束 出射角度；T″ s(p0sx)和T*″(phx0)为走时的二阶导数. 2.3 地表倾角的近似求取

本文给出了一种近似求取地表倾角αr的方法.如图 3a—3d所示，黑色弧线代表起伏地表，五角星代表接收点(计算点)在起伏地表的位置，两个黑色圆点代表接收点两侧相邻的网格点，三个网格点之间由虚线构成一个三角形.图 3a—3d分别展示了起伏地表的四种形态，经过计算点(五角星)且平分此计算点所在顶角的直线(图中虚线)与竖直方向(z方向)之间的夹角i可以近似表示地表倾角αr.在此求取过程中，以逆时针方向为正方向，图 3a和图 3c所示的地表倾角为负，图 3b和图 3d所示的地表倾角为正.

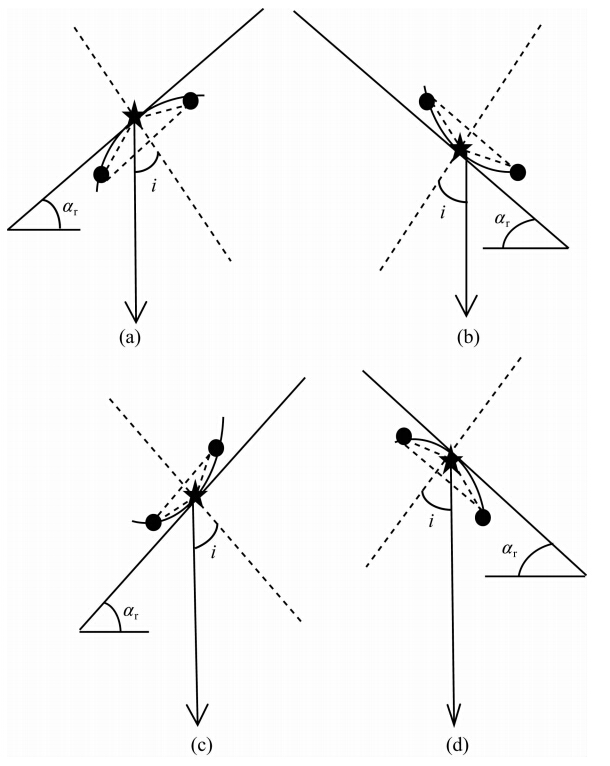图 3 地表倾角的近似计算 Fig. 3 The approximate calculation of surface dip angle
3 模型试算 3.1 加拿大逆掩断层模型

本文在上述理论推导的基础上，用程序对加拿大逆掩断层模型进行了试算，并将其成像结果与其他偏移方法进行了对比分析.速度模型如图 4所示，模型网格为1668×1000，横纵向间隔距离分别为15 m和10 m.本文采用Amoco和BP公司提供的地震模拟数据，此数据共有278炮，单炮最大和最小接收道数分别为481和241，每道2000个采样点，采样间隔为4 ms，道间距为15 m，炮间隔为90 m.

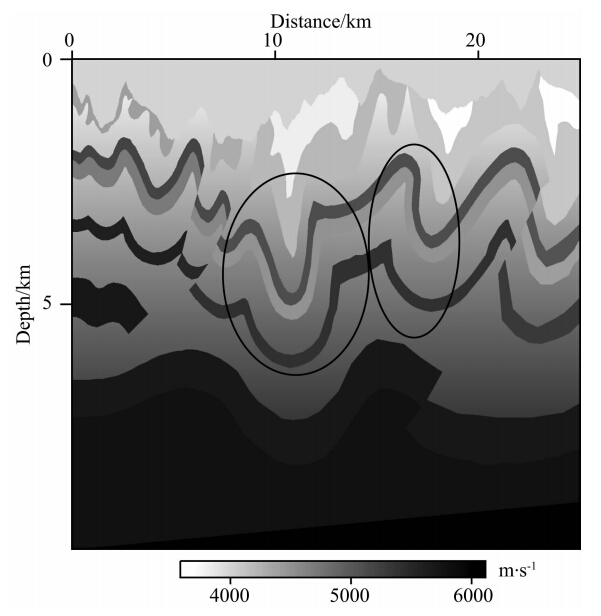图 4 加拿大山麓模型 Fig. 4 Canadian Foothills model

该模型的地表高程和速度都存在极强的横向变化，地表最大高程差接近1800 m，地表高程分布结果如图 5所示.图 6给出了地震模拟数据中的一个 典型的小于4 s的局部放大炮记录示意图，由图 6可以清晰地发现：由于起伏地表的存在，所采集到的 炮记录同相轴较明显地偏离双曲特征.此外，该模型速度横向变化也非常剧烈，速度变化范围从3600 m·s-1 到6000 m·s-1，且模型中含有高陡倾及倒转等典型复杂构造，如图 4中椭圆线圈所示.

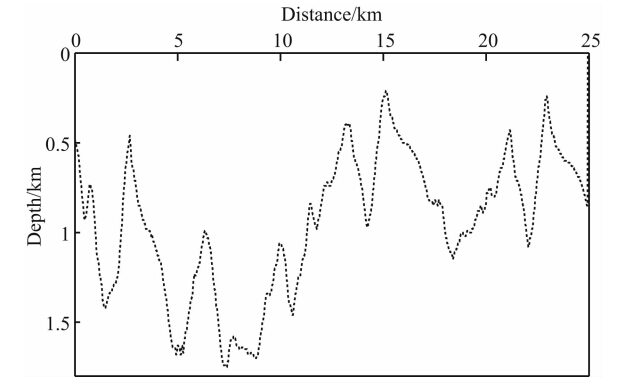图 5 复杂地表高程 Fig. 5 The sketch of topography

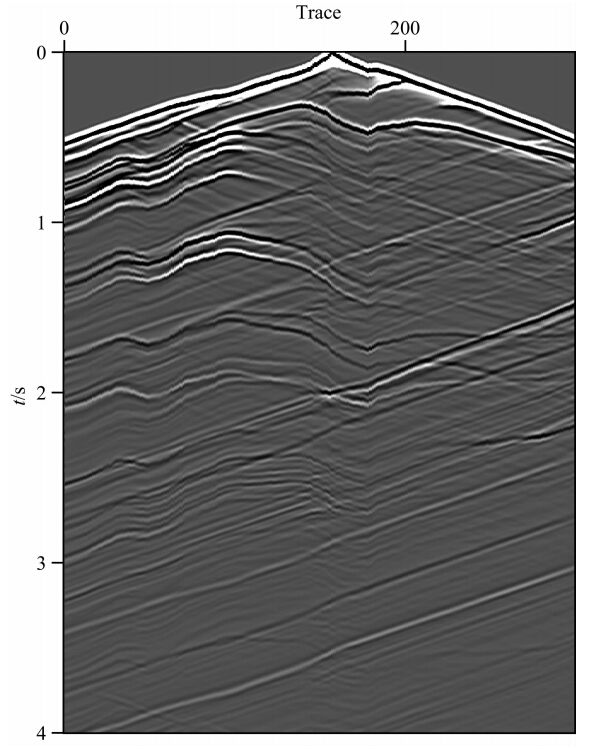图 6 炮记录局部放大 Fig. 6 The local zoom of shot gather

为了比较本方法与传统起伏地表偏移方法成像效果的差异，针对相同的观测系统和炮记录，本文也用其他偏移方法进行试算.不同偏移方法的成像结果如图 7所示.其中，图 7a是基于单程波傅里叶有限差分(FFD)偏移成像结果，图 7b为Gray(2005)提出的基于倾斜叠加的局部静校正束偏移方法的成 像结果，图 7c为Yue等(2010)提出的基于倾斜叠加的保幅延拓束偏移方法成像结果，而图 7d为本文非倾斜叠加的精确束偏移方法成像结果.通过对比图 7a—7d可以看到：总的说来，这些方法都能较好地适应起伏地表成像，且断层及深部倾斜反射层都能得到良好成像.在如图所示的椭圆线圈内两个地层之间存在一组竖直的“同相轴”，为偏移假象.这种偏移假象在本文所述四种方法的偏移成像中有不同程度的显现，产生这种假象的原因可能是：①地震波场在双复杂介质中的传播过程尤为复杂，导致记录到的波场中也存在干扰波，比如多次波，复杂地表角点处形成的散射波，复杂地表二次或多次源产生的规则干扰波同相轴；②高斯束偏移不能够处理所有的波至信息，剩余的波至信息便成为了噪声成分；③在复杂介质中，高斯束叠加积分近似表征格林函数，地震波场存在误差.然而，不同方法在近地表、高陡倾以及倒转构造等区域的成像能力存在明显差异.在图 7a所示的FFD法成像结果中，近地表构造成像结果较为清晰(图中方框所示)，但是由于单程波算子的局限，在高陡倾以及倒转构造处成像效果较差(图中椭圆线圈所示).在图 7b所示的基于倾斜叠加的局部静校正束偏移方法成像结果中，由于局部静校正对波场造成畸变而产生了较多的成像噪声，尤其在近地表偏移噪声较为明显.图 7c所示的基于倾斜叠加的保幅延拓法束偏移成像结果，同Gray提出的方法相比，削弱了成像噪声且提高了近地表成像质量，然而其高陡构造成像振幅较弱，连续性较差.相较于前三种方法，本方法的主要优点是：(1)有效地压制了近地 表成像噪声；(2)弥补了Gray(2005)和Yue等(2010)高斯束偏移方法中由于束中心位置与接收点位置之间存在水平距离差和高度差引起的振幅误差，在高陡倾、倒转等构造处的成像振幅较 强，连续性较好，成像结果更加清晰；(3)对比中深层 成像振幅，其改善效果更加明显(图 7d黑色箭头所指).

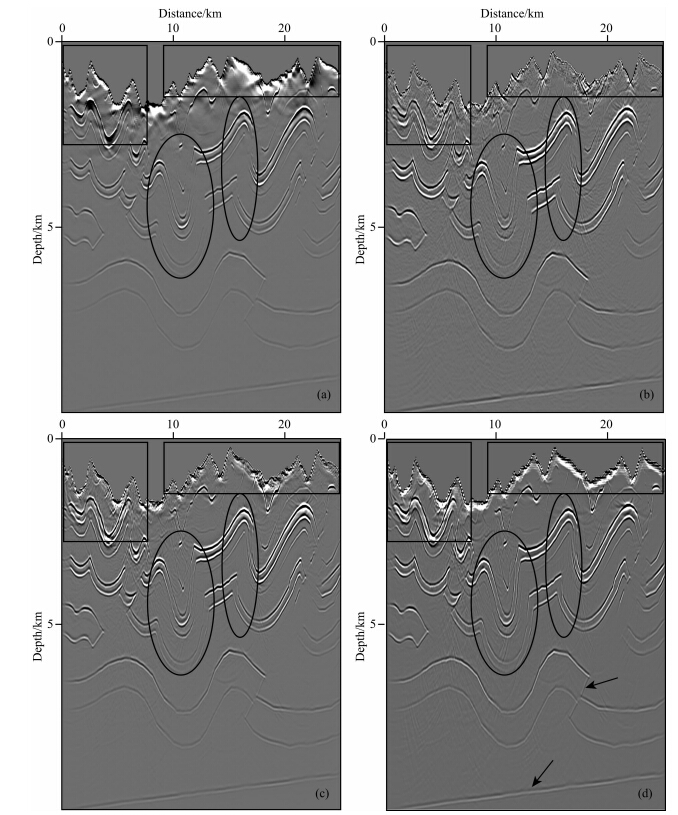图 7 偏移成像结果：(a)傅里叶有限差分(FFD)；(b)Gray(2005)所提出局部静校正法；(c)Yue(2010)所提出保幅延拓法；(d)本文方法 Fig. 7 The migration results generated by(a)FFD migration method;(b)Gray′s method(2005); (c)Yue′s method(2010) and (d)our method
3.2 中原油田断层模型

为了验证方法的适应性，本文进一步对国内某探区典型起伏地表模型进行了成像试算.模型的速度场如图 8所示，此模型具有典型的山谷地表，并且模型的中深部包含发育良好的断层构造.模型网格大小为871×1000，横纵向间隔距离为12.5 m和4 m.正演计算采用的野外模拟放炮方式为中间放炮两边接收，共80炮，每炮120道接收，道间隔为50 m，每道采样点数为1500，采样间隔为2 ms.正演模拟采用高阶交错网格有限差分算法，炮记录均切去直达波，第一炮记录如图 9所示，由于存在较为明显的起伏地形，炮记录中反射波同 相轴出现较为明显的扭曲现象(图中黑色线圈所示).

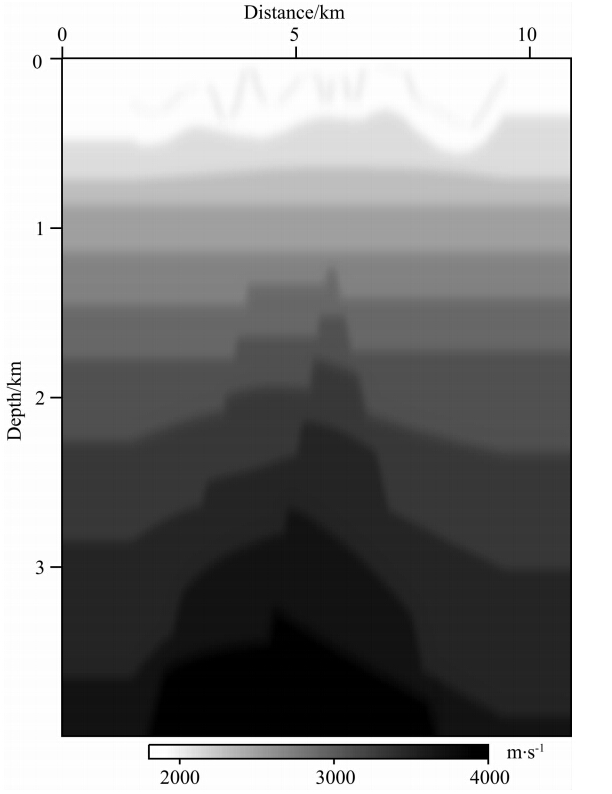图 8 中原油田断层模型速度场 Fig. 8 Zhongyuan oilfield faults velocity model

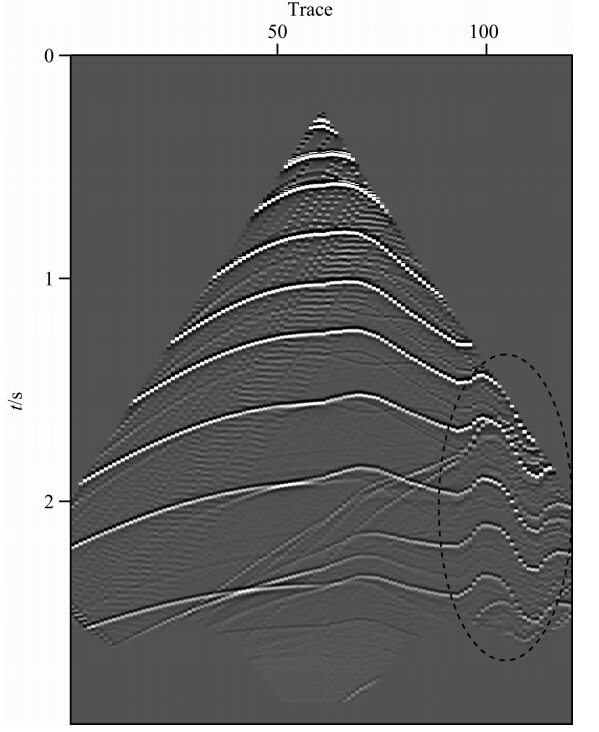图 9 单炮记录 Fig. 9 Single-shot gather

图 10a，10b分别给出了Yue(2010)所提出的基于倾斜叠加的保幅延拓法和本文方法在目标勘探区域的偏移成像结果，相比之下，本方法产生了分辨率和信噪比更高的偏移剖面，目标区域的断层构造成像更清晰，如图中黑色线圈所示.本方法成像效果具有以下主要特点：(1)成像振幅较强，同相轴连续性更好；(2)成像噪声较小.

图 10 偏移成像结果：(a)Yue(2010)所提出保幅延拓法；(b)本文方法 Fig. 10 The migration results generated by(a)Yue′s method(2010) and (b)our method
4 实际资料

在模型测试的基础上，进一步对某探区实际资料进行了试算，验证了本方法对实际资料处理的适应性.

偏移速度场如图 11所示，此地区地下构造较为复杂，主要典型构造包括潜山、断层和凹陷等.图 12给出了地表高程示意图，地表最大高程差为58 m，局部变化比较剧烈.图 13为其中两炮原始记录，从炮记录中可以明显地看出：同相轴因起伏地表而出现扭曲、间断等现象(图 13中黑色线圈所示).

图 11 偏移速度场 Fig. 11 The migration velocity

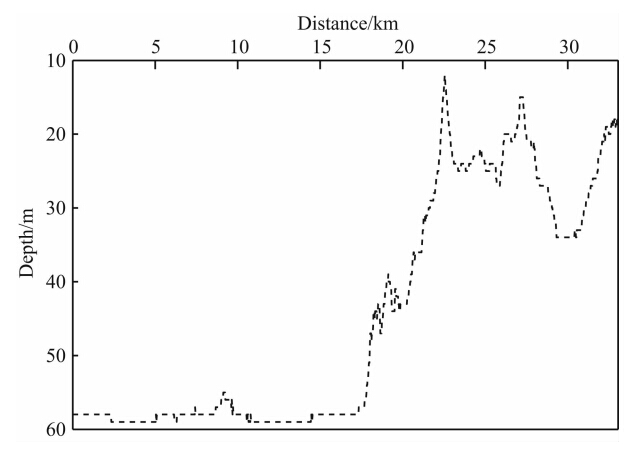图 12 地表高程 Fig. 12 The sketch of topography

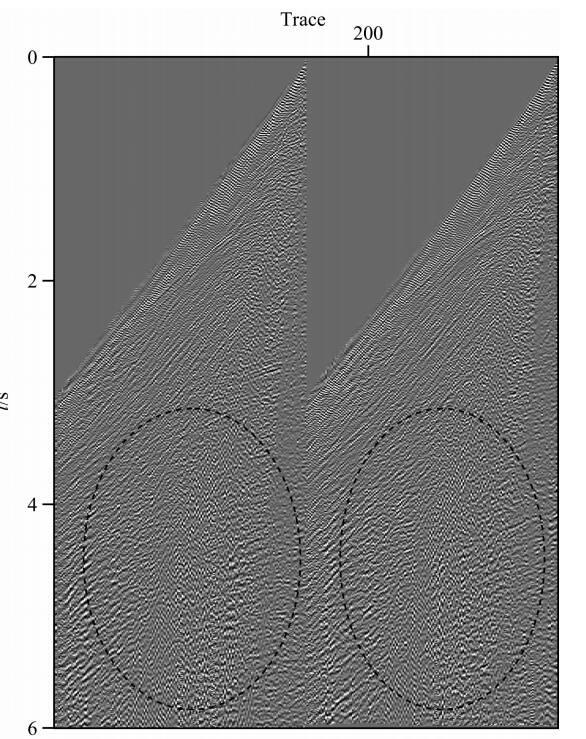图 13 原始炮记录 Fig. 13 Original shot gathers

图 14a，14b分别为Yue(2010)提出的基于倾 斜叠加的保幅延拓法成像结果和本方法偏移结果. 从本方法偏移结果(图 14b)可以看出：同相轴的连续性强，没有出现由于绕射波不能完全归位的绕射画弧现象，成像结果图中潜山两翼侧的凹陷构造也得到了较好地成像.对比Yue等所提出的方法，本文精确方法深部反射层成像能量明显较强，成像保幅性更好(图中黑色方框所示)；同时，潜山两翼同相轴也更加连续(图中黑色箭头所示).需要指出的是，虽然本文方法弥补了Yue等方法中由于束中心位置与接收点位置之间存在水平距离差和高度差引起的振幅误差，在深层表现得尤为明显.但是，本文方法也存在不足，例如不能够处理所有波至信息，计算地震波场仍然存在误差.对于低信噪比的野外资料而言，干扰波或噪声成为偏移假象的诱因，与真实反射层一样得到凸显.综上所述：本文方法在处理基于起伏地表条件下的采集数据，较传统方法在成像精度和中深部储层保幅性等方面都有一定的提高.

图 14 偏移成像结果：(a)Yue(2010)所提出保幅延拓法；(b)本文方法 Fig. 14 The migration results generated by(a)Yue′s method(2010) and (b)our method
5 结论

本文以一种非倾斜叠加的束偏移思路实现了双复杂条件下的地震成像，并且对加拿大逆掩断层模型、中原油田断层模型以及某探区实际资料进行了试算，得到以下几点认识：
(1)本方法通过考虑地表倾角信息，在接收点处直接出射高斯束，既无须进行高程静校正，也无须引入相位校正因子来近似表征反向延拓波场，更不需要进行束中心与接收点之间关于速度和束出射角的近似替代处理，在理论上是一种更为准确的束偏移思路；
(2)通过模型与实际资料试算可以看出：本方法能够有效地压制偏移噪声，相比于波动方程FFD方法与其他射线类方法，具有更高的成像质量，尤其在近地表、高陡倾以及倒转构造处的成像具有明显的改进；此外，本方法能够有效地增强反射界面成像振幅，且同相轴连续性更好.

应当指出的是，本方法需要计算每个接收点处反向延拓的波场，因此需要额外的计算量.另外，本文方法是基于声波方程提出的，故只能处理声波资料.基于此，下一步研究重点：(1)改进偏移算子，以 获得更高的计算效率和更好的成像效果；(2)从声波方程延伸到弹性波方程，求解基于弹性波动方程的非倾斜叠加束偏移算子，以处理多波多分量资料.

致谢     作者感谢Amoco和BP公司提供加拿大逆掩断层模型数据.
参考文献
[1] Beasley B, Lynn W. 1992. The zero-velocity layer: Migration from irregular surfaces. Geophysics, 57(11): 1435-1443.
[2] Berryhill J R. 1979. Wave-equation datuming. Geophysics, 44(8): 1329-1341.
[3] Berryhill J R. 1984. Wave-equation datuming before stack. Geophysics, 49(11): 2064-2066.
[4] Bevc D. 1997. Flooding the topography: Wave-equation datuming of land data with rugged acquisition topography. Geophysics, 62(5): 1558-1569.
[5] Cheng J B, Ma Z T, Tao Z X, et al. 2006. Imaging study of piedmont complex structures. Oil Geophysical Prospecting (in Chinese), 41(5): 525-529.
[6] Claerbout J F. 1971. Toward a unified theory of reflector mapping. Geophysics, 36(3): 467-481.
[7] Docherty P. 1991. A brief comparison of some Kirchhoff integral formulas for migration and inversion. Geophysics, 56(8): 1164-1169.
[8] Dong C H, Zhang J F. 2009. Prestack time migration including surface topography. Chinese Journal of Geophysics (in Chinese), 52(1): 239-244.
[9] Geiger H D. 2002. Relative-amplitude-preserving prestack time migration by the equivalent offset method. Calgary: University of Calgary.
[10] Gray A H, Marfurt K J. 1995. Migration from topography: Improving the near-surface image. Canadian Journal of Exploration Geophysics, 31(1-2): 18-24.
[11] Gray S H. 2005. Gaussian beam migration of common-shot records. Geophysics, 70(4): S71-S77.
[12] Gray S H, Bleistein N. 2009. True-amplitude Gaussian-beam migration. Geophysics, 74(2): S11-S23.
[13] He Y, Wang H Z, Ma Z T, et al. 2002. Wave-equation pre-stack depth migration under complex topography conditions. Progress in Exploration Geophysics (in Chinese), 25(3): 13-19.
[14] Hill N R. 2001. Prestack Gaussian-beam depth migration. Geophysics, 66(4): 1240-1250.
[15] Jäger C, Hertweck T, Spinner M. 2003. True-amplitude Kirchhoff migration from topography. 69th Annual International Meeting, SEG, Expanded Abstracts: 1239-1248.
[16] Liu G F, Liu H, Li B, et al. 2010. Directly pre-stack time migration for irregular surface. Oil Geophysical Prospecting (in Chinese), 45(2): 196-200.
[17] Lü B, Wang X W, Wang Y C, et al. 2011. Amplitude-preserved FFD pre-stack depth migration of piedmont overthrust structures. Oil Geophysical Prospecting (in Chinese), 46(5): 720-724.
[18] Reshef M. 1991. Depth migration from irregular surfaces with depth extrapolation methods. Geophysics, 56(1): 119-122.
[19] Schneider W A. 1978. Integral formulation for migration in two and three dimensions. Geophysics, 43(1): 49-76.
[20] Schneider W A, Pillip L D, Paal E F. 1995. Wave-equation velocity replacement of the low-velocity layer for overthrust-belt data. Geophysics, 60(2): 573-579.
[21] Shragge J, Paul S. 2005. Wave-equation migration from topography. Expanded Abstracts of 75th Annual Internat SEG Mtg: 1842-1845.
[22] Wang H Z, Liu S Y, Yang Q Y, et al. 2013. Seismic exploration strategy and image processing method of piedmont. Oil Geophysical Prospecting (in Chinese), 48(1): 151-159.
[23] Wapenarr C P A, Peels G L, Budejicky V, et al. 1989. Inverse extrapolation of primary seismic waves. Geophysics, 54(7): 853-863.
[24] Wiggins J W. 1984. Kirchhoff integral extrapolation and migration of nonplanar data. Geophysics, 49(8): 1239-1248.
[25] Yang K, Wang H Z, Ma Z T. 1999. Wave equation datuming from irregular surfaces using finite difference scheme. Expanded Abstracts of 69th Annual Internat SEG Mtg: 1465-1468.
[26] Ye Y M, Li Z C, Tong Z Q, et al. 2008. Xwfd pre-stack depth migration based on dual-complexity with error compensation correction. Progress in Geophysics (in Chinese), 23(1): 136-145.
[27] Yilmaz O, Lucas D. 1986. Prestack layer replacement. Geophysics, 51(7): 1355-1369.
[28] Yue Y B, Li Z C, Zhang P, et al. 2010. Prestack Gaussian beam depth migration under complex surface conditions. Applied Geophysics, 7(2): 143-148.
[29] 程玖兵, 马在田, 陶正喜等. 2006. 山前带复杂构造成像方法研究. 石油地球物理勘探, 41(5): 525-529.
[30] 董春晖, 张剑锋. 2009. 起伏地表下的直接叠前时间偏移. 地球物理学报, 52(1): 239-244.
[31] 何英, 王华忠, 马在田等. 2002. 复杂地形条件下波动方程叠前深度成像. 勘探地球物理进展, 25(3): 13-19.
[32] 刘国峰, 刘洪, 李博等. 2010. 起伏地表直接叠前时间偏移. 石油地球物理勘探, 45(2): 196-200.
[33] 吕彬, 王西文, 王宇超等. 2011. 山前带逆掩构造保幅FFD叠前深度偏移. 石油地球物理勘探, 46(5): 720-724.
[34] 王华忠, 刘少勇, 杨勤勇等. 2013. 山前带地震勘探策略与成像处理方法. 石油地球物理勘探, 48(1): 151-159.
[35] 叶月明, 李振春, 仝兆岐等. 2008. 双复杂条件下带误差补偿的频率空间域有限差分法叠前深度偏移. 地球物理学进展, 23(1): 136-145.