2. 哈尔滨工业大学深圳研究生院, 深圳 518055
2. Harbin Institute of Technology Shenzhen Graduate School, Shenzhen 518055, China
The theoretical analysis is carried out by using mass-spring-damping model and TDF-mass-spring-damping model. Firstly, the vibration of the rockfill system is analyzed by using a mass-spring-damping model considering the rockfill damping. The influence of the damping of the rockfill body on the measured vibration frequency and the mass-frequency curve are analyzed. Secondly, the vibration of the rockfill system is analyzed by using a two-degree-of-freedom mass-spring-damping model considering the non-rigid connecting between the additive mass and rockfill body. The influence of the non-rigid connecting on the measured vibration frequency and the mass-frequency curve are also analyzed.
Based on mass-spring-damping model, the formula of received signal spectrum is presented. It shows that the received signal dominant frequency varies with source frequency and also the damping value of the rockfill body. For a given model, the theoretical computed received signal dominant frequencies fit well with the FEM simulated received signal dominant frequencies. It also shows that the received signal dominant frequency becomes higher with the increasing additive mass for low source frequency and small additive mass. This cause some abnormal mass-frequency curves. On the other hand, based on TDF-mass-spring-damping model, another formula of received signal spectrum is presented. This formula causes different received signal spectrum results from the results for simple mass-spring-damping model. The mass-frequency curve obtained from a small stiffness connection TDF-mass-spring-damping model has a very small intercept which means small vibration mass of the rockfill body. These results fit well with some FEM simulated mass-frequency curve. For a moderate stiffness connection TDF-mass-spring-damping model, the theoretical computed received signal spectrum has two peaks when source frequency is high. The first peak fits well with the natural frequency of total mass of the rockfill vibration system for small additive mass. For a big stiffness connection TDF-mass-spring-damping model, the theoretical computed received signal spectrum only has one peak near the natural frequency of total mass of the rockfill vibration system.
The mass-spring-damping model can be used to explain the phenomenon that the received signal frequency varies with source frequency and rainwater. It can also be used to explain the down-to-up type and decreasing type of abnormal mass-frequency curve in the additive mass testing. The TDF-mass-spring-damping model can be used to explain the phenomenon that the received signal frequency varies with the offset and the contacting area of the additive mass. It can also be used to explain the small-intercept type of abnormal mass-frequency curve and double-peak spectrum of the received signal.
1 引言
在堆石体大坝的建设过程中,密度检测是保证大坝质量合格的重要因素.李丕武等(1999)根据附加质量改变物体振动频率的思想(周传荣,1989;Nakazaki和Yamaguchi,1999)提出了堆石体大坝密度检测的附加质量法.此方法的基本原理是将堆石体系统等效为质弹模型,通过施加不同级数附加质量块,测试对应的堆石体振动频率,进而分析堆石体的参振质量以及密度.
此方法相比传统的坑测法具有简便、快速、原位、非破坏性等优点,已经被广泛地应用于水坝(宋先海等,2004;郑庆举等,2005;张智等,2009)、路堤(于德介等,2005)和机场填料(谭峰屹等,2010)等场地的堆石体密度检测中.最初的附加质量法的密度公式中涉及到参振质量、波衰减系数和波长三个测试参数(李丕武等,1999),测试过程略显复杂.经过实践发展,目前常用的密度公式则直接基于密度与刚度或者参振体积一个测试参数的相关性(谭峰屹等,2010;张建清等,2012),测试过程更为简单.
但是附加质量法在应用中也遇到了一些问题,例如重复性不是很好.不同高度的锤击震源、下雨前后以及附加质量块偏移距的变化等都会影响堆石体振动主频的测量结果(张智等,2013).实际上这是由于目前的附加质量法基于的理论模型(质弹模型)过于理想的原因,此模型没有考虑实际工程中堆石体振动的阻尼因素,也没有考虑附加质量块和堆石体非刚性连接问题,故限制了附加质量法的应用范围.李丕武等(1993)曾考虑过堆石体振动的阻尼因素,但仅仅给出了简单的自由振动公式,并没有分析阻尼对于堆石体振动主频等测试结果的影响.
本文则深入考虑堆石体振动的阻尼因素,将堆石体系统等效为质弹阻模型,分析阻尼对测试频率以及Δm-D曲线的影响.在此基础上,再考虑附加质量块与堆石体的非刚性连接问题,参照检波器多自由度模型(石战结等,2010),将堆石体系统等效为双自由度-质弹阻模型,分析附加质量块和堆石体的非 刚性连接对测试的频谱分布及Δm-D曲线的影响.同时,本文利用分析结果尝试解释附加质量法应用中出现的一些特别现象,并对测试方法的改进提出了建议.
2 堆石体系统的质弹阻模型及分析李丕武(1993)曾以6个简单的自由振动公式考虑过阻尼因素,但没有进一步分析阻尼对于堆石体振动主频等测试结果的影响,也没有考虑堆石体上动荷载作用.为此,我们深入考虑了堆石体系统振动中阻尼的影响,首先将堆石体系统等效为一个考虑动荷载的质弹阻模型,然后利用此模型分析和解释附加质量法测试中出现的震源、雨水、质量块个数的影响问题.
2.1 堆石体系统的质弹阻模型参照经典的基础振动模型(Das,1984),将堆石体系统等效为质量-弹簧-阻尼器体系(质弹阻模型),如图 1所示.其中c为阻尼系数,k为刚度,m0为堆石体的参振质量,Δm为附加质量,f(t)为作用在堆石体上的动载荷,v(t)为检波器接收的速度振动信号.地震波数值模拟中经常用Ricker子波函数来模拟震源(周红和陈晓非,2007),类似地,本文也选择Ricker子波函数模拟作用在堆石体上的动荷载.
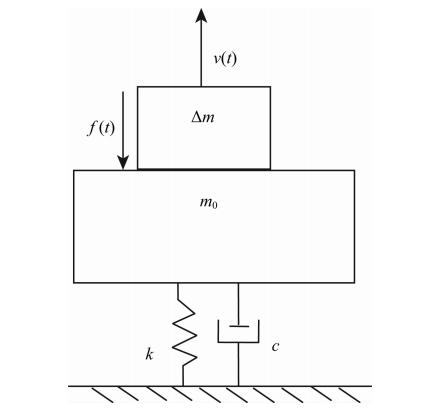 | 图 1 堆石体系统的质弹阻模型 Fig. 1 Mass-spring-damping model for rockfill system |
参照经典的基础振动力学公式(Das,1984),给出图 1中堆石体系统质弹阻模型的振动方程表达形式:
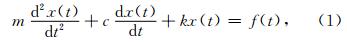
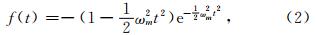
实际工程应用中,张智等(2013)发现不同的震源频率将导致接收信号主频发生变化.而我们基于有限元对黏弹性堆石体模型的附加质量法测试进行了数值模拟,其结果表明,震源主频对接收信号的主频有较大影响,如表 1所示.
|
|
表 1 不同震源主频对应的接收信号主频值(Hz) Table 1 The received signal dominant frequencies for different source dominant frequencies(Hz) |
由表 1可以看出,接收信号随震源主频的增大而增大,最后趋向于一个定值.这个现象基于简单的质弹模型是无法解释的,因为质弹模型的振动主频是一个恒定值,不会随震源频率的变化而变化.我们 将尝试基于本文的质弹阻模型对以上现象给予解释.
对本文质弹阻模型的振动方程(1)及其震源函数(2)式做Fourier变换,则有:
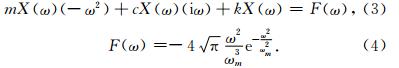
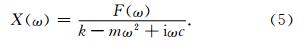
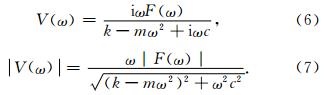
由公式(7)可知  ,而|V(ω)|为连续函数,故|V(ω)|存在极大值ωmax,使得
,而|V(ω)|为连续函数,故|V(ω)|存在极大值ωmax,使得
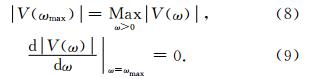
由式(4)、(7)、(9)可得,ωmax满足下面的求解公式:
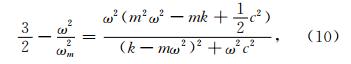
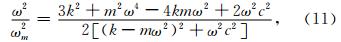
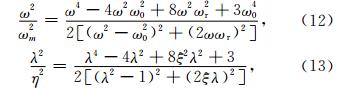
其中,ω0=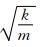 为系统的固有频率,ωr= c/2m 为系统的阻尼频率.λ= ω/ω0 为系统的频率比,ξ= c/2mω0 为系统的阻尼比,η= ωm/ω0 为震源频率比.
为系统的固有频率,ωr= c/2m 为系统的阻尼频率.λ= ω/ω0 为系统的频率比,ξ= c/2mω0 为系统的阻尼比,η= ωm/ω0 为震源频率比.
公式(11)、(12)或(13)即为本文基于质弹阻模型得到的接收信号主频求解方程.根据三次方程通用的求根公式及相关性质,可以得到接收信号主频的显示表达式为
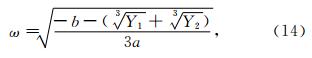
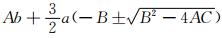 ,A=b2-3ac,B=bc-9ad,C=c2-3bd;a=1,b=4ωr2
,A=b2-3ac,B=bc-9ad,C=c2-3bd;a=1,b=4ωr2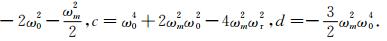
考虑一质弹阻模型(记为MSD-1),其中质量m0取250 kg,刚度k取为100 MN·m-1,阻尼c取为3000 kg·s-1,Δm取为6级,每级75 kg.通过公式(14)计算了模型MSD-1在4块质量块时的接收信号主频ωmax随震源主频ωm变化的曲线,如图 2中实线所示.
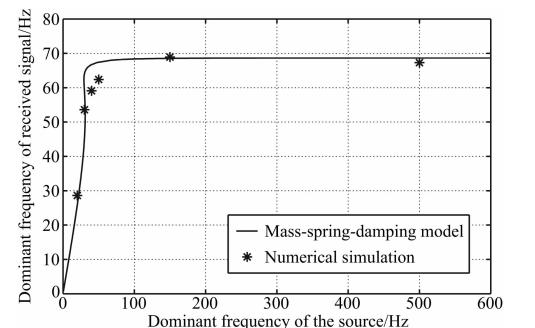 | 图 2 质弹阻模型MSD-1的接收信号主频随震源主频的变化曲线 Fig. 2 The received signal dominant frequency curve varying with source frequency for MSD-1 |
图 2中的星号点为数值模拟的结果,可以看出本文质弹阻模型的理论公式可以较好地拟合数值模拟的结果.故本文质弹阻模型可以较好地解释震源的影响问题.
另外,在附加质量法实际工程应用中发现雨水对测量结果有较大影响.对同一测点,下雨前后测试的接收信号主频会存在较大的差异.此现象基于质弹模型则无法给予解释,但可以通过质弹阻模型进行定性的分析解释,因为下雨前后堆石体系统对应的阻尼c会发生较大的变化,而根据本文的质弹阻模型的接收信号主频求解公式(11),接收信号主频也将发生变化.
2.3 利用质弹阻模型分析附加质量块个数的影响 附加质量法的基本原理中假定所测的接收信号主频为系统的固有频率ω0,由公式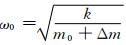 可知,附加质量Δm与接收信号主频的平方倒数(D=1/ω2)大致呈线性递增关系,通过设置几级附加质量块从而得到一条Δm-D曲线,计算其斜率和截距可以得到堆石体参振质量m0及刚度k,进而根据经验公式得到堆石体密度.但是在实际工程应用及数值模拟研究中有时出现以下情况:Δm级数较小测得的(Δm,D)点往往偏离直线,Δm-D曲线呈先减后增甚至递减关系,如图 3和图 4所示.
可知,附加质量Δm与接收信号主频的平方倒数(D=1/ω2)大致呈线性递增关系,通过设置几级附加质量块从而得到一条Δm-D曲线,计算其斜率和截距可以得到堆石体参振质量m0及刚度k,进而根据经验公式得到堆石体密度.但是在实际工程应用及数值模拟研究中有时出现以下情况:Δm级数较小测得的(Δm,D)点往往偏离直线,Δm-D曲线呈先减后增甚至递减关系,如图 3和图 4所示.
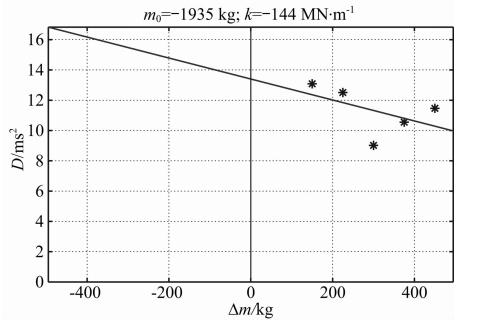 | 图 3 附加质量法数值模拟中得到的异常Δm-D曲线(先减后增型) Fig. 3 The abnormal Δm-D curve occurred in additive mass method simulation(Down-to-up type) |
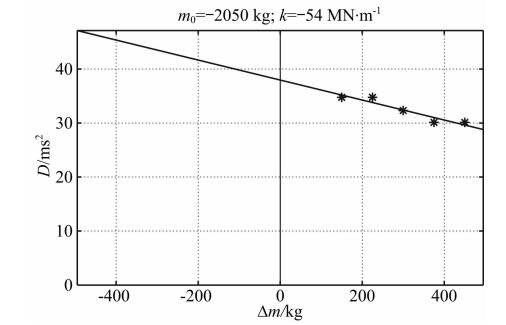 | 图 4 附加质量法数值模拟中得到的异常Δm-D曲线(递减型) Fig. 4 The abnormal Δm-D curve occurred in additive mass method simulation(Decreasing type) |
根据质弹阻模型对应的接收信号主频求解公式(11),不同的附加质量Δm会引起总质量m的变化,接收信号主频也将随之变化.同样考虑质弹阻模型MSD-1,分别计算此模型的震源频率在10 Hz、20、30、40、50 Hz和60 Hz时接收信号主频随总质量的变化曲线,如图 5所示,其中星号点为不同级数附加质量块对应的总质量-接收信号主频点.
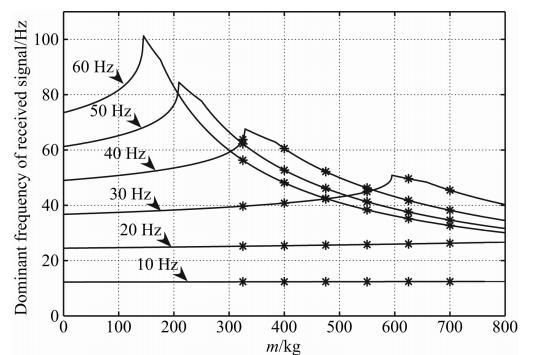 | 图 5 质弹阻模型MSD-1的接收信号主频随总质量的变化曲线 Fig. 5 The received signal dominant frequency curve varying with total mass for MSD-1 |
由图 5中各曲线可以看出,接收信号的主频随总质量m的变化呈先增后减关系.转折点的位置与 震源主频有关,震源频率越高,转折点频率越低.在 图 5中,对于40 Hz的Ricker子波,Δm由2块增至 6块时,接收信号主频单调递减,故Δm-D曲线单调 递增,这与正常的Δm-D曲线是吻合的;对于30 Hz的Ricker子波,Δm由2块增至6块时,接收信号主频先增后减,故Δm-D曲线先减后增,这与图 3 的先减后增型异常Δm-D曲线相吻合;对于20 Hz的Ricker子波,附加质量Δm由2块增加到6块时,接收信号的主频单调递增,故Δm-D曲线单调递减,这与图 4的递减型异常Δm-D曲线相吻合.
综上所述,基于质弹阻模型可以较好地解释实际工程应用及数值模拟中出现的几个现象,同时我们提出以下建议:(1)采用可控震源,使得每次测量采用的震源频率基本相同,从而去除震源的影响.(2)尽量选择干燥的测点进行测量,避免雨水的影响.(3)尽量选择频率相对较高的震源,以保证低级 别附加质量Δm对应的接收信号主频也落在总质 量-接收频率曲线的下降段,从而获取正常的Δm-D曲线.
3 堆石体系统的双自由度-质弹阻模型及分析质弹阻模型虽然较好地解释了质弹模型无法解释的几个现象,但对于另外一些特殊的现象质弹阻模型则不能给予很好地解释,如附加质量块的触地面积的影响问题等.为此本文在质弹阻模型的基础上,进一步考虑附加质量块和堆石体之间的非刚性连接问题,借鉴石战结(2010)提出的岩石检波器系统的等效模型,把附加质量块分离出来作为另一个自由度来考虑,即把堆石体系统等效为一个双自由度-质弹阻模型.根据此模型,分析和解释附加质量块的偏移距及触地面积对接收信号主频的影响以及接收信号频谱有时出现“双峰”现象的原因.
3.1 双自由度-质弹阻模型本文建立的堆石体系统的双自由度-质弹阻模型如图 6所示.其中k1和c1分别为附加质量块与堆石体之间的连接刚度和阻尼系数,k2和c2则为堆石体的等效刚度和阻尼系数,Δm为附加质量,f(t)为作用在堆石体上的动载荷,v1(t)为检波器接收的速度振动信号,v2(t)为堆石体振动的速度.
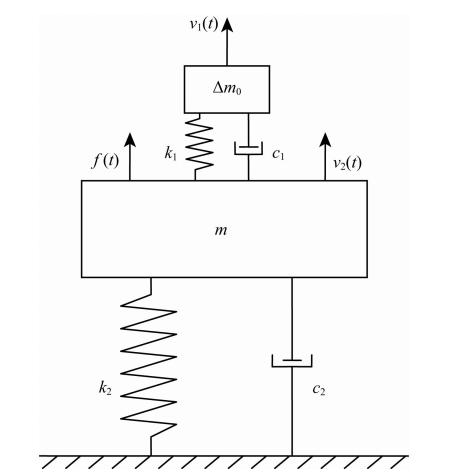 | 图 6 堆石体系统的双自由度-质弹阻模型 Fig. 6 TDF-mass-spring-damping model for rockfill system |
参照经典的基础振动力学公式(Das,1984),给出了图 6中堆石体系统的双自由度-质弹阻模型的振动方程表达形式:
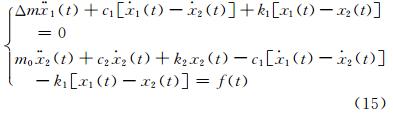
基于有限元对附加质量法的质量块偏移距和触地面积问题进行了数值模拟研究,发现当偏移距较大或触地面积较小时,所测的接收信号主频会发生明显变化.特别是当触地面积较小时接收信号主频变化非常明显,会出现异常的Δm-D曲线(图 7).
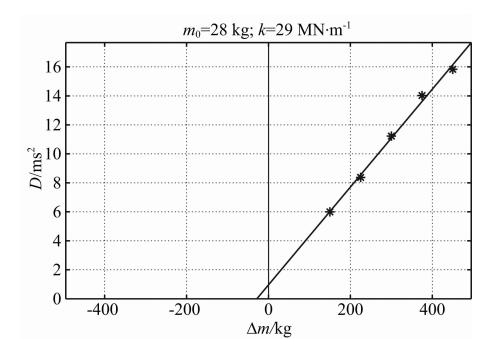 | 图 7 附加质量法数值模拟中得到的异常Δm-D曲线(小截距型) Fig. 7 The abnormal Δm-D curve occurred in additive mass method simulation(Small-intercept type) |
图 7中Δm-D曲线的截距很小,即测得的堆石体参振质量m0很小(为28 kg).此结果与正常情况测得的m0相差比较大,正常测得的Δm-D曲线如图 8所示,其m0为250 kg.
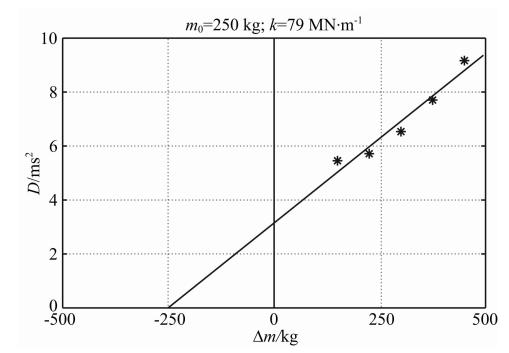 | 图 8 附加质量法数值模拟中得到的正常Δm-D曲线 Fig. 8 The normal Δm-D curve occurred in additive mass method simulation |
如何在理论上解释这一现象?下面基于双自由度-质弹阻模型进行解释,并在此基础上对测试方法提出建议.对双自由度-质弹阻模型的振动方程(15)做Fourier变换,得到:
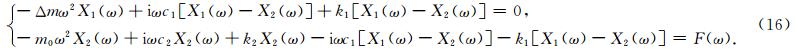
公式(16)中利用第一个方程将X2(ω)用X1(ω)表示,再代入第二个方程得到X1(ω)的表达式为
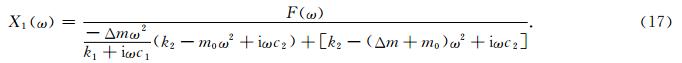
利用公式(17)分析质量块与堆石体的连接刚度k1对此双自由度模型的动力学响应X1(ω)的影响.一般情况下,由于附加质量块和地面接触面积大,接触界面层厚度薄,则根据柱体刚度的计算公式EA/H(A为截面积,H为厚度,E为模量),此连接刚度k1相比堆石体的刚度k2比较大,近似认为k1>> k2,故(17)式中的X1(ω)的表达式的分母的第一项很小,故得到下面的近似表达式:
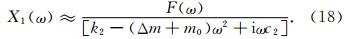
比较(18)式和单自由度-质弹阻模型对应的接收信号频谱公式(5),发现两者的表达是相同的.即若k1>>k2,双自由度的质弹阻模型退化为单自由度的质弹阻模型.实际上,比较图 6和图 1,若k1>>k2,则表示质量块和堆石体耦合得比较紧密,质量块的振动与堆石体的振动近似保持同步,近似认为它们之间是刚性连接,故退化为质弹阻模型.
但是,附加质量法测试中若出现附加质量块和堆石体的振动耦合出现不够同步的情况,即k1不够大,则公式(18)不能退化为公式(5),由其求得的频谱将和由公式(5)求得的频谱相差较大,使得测试结果出现异常.例如,偏移距较大时,质量块偏离堆石体的参振中心较远,相当于它们之间连接得不够紧密,即对应双自由度-质弹阻模型中的k1较小,测试主频相对于质弹阻模型则会有一定的偏差.
另外,质量块触地面积较小时,质量块与堆石体的连接刚度k1会明显变小,这样会出现质量块和堆石体之间明显的振动不同步,而质量块振动的频率主要表现出其自身的固有振动频率,从而使得接收到的信号主频约等于质量块本身的固有主频ω1= 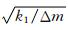 ,故Δm-D曲线近似为D=
,故Δm-D曲线近似为D=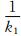 Δm,其截距 近似为0,即m0相对很小.例如,我们考虑一小刚度 连接的双自由度-质弹阻模型(记为TDFMSD-1),其中取堆石体参振质量m0为250 kg,取刚度k2为 100 MN·m-1,取阻尼c2为3000 kg·s-1,取质量块Δm为6级,每级75 kg,取质量块与地面的连接刚度k1为37 MN·m-1,取质量块与地面的连接阻尼c1为 3000 kg·s-1,取震源为68 Hz的Ricker子波.通过公式(17)计算得到此模型在附加2到6块质量块时的接收信号主频分别为63、53、46、42 Hz和38 Hz,进而得到Δm-D曲线,如图 9所示.
Δm,其截距 近似为0,即m0相对很小.例如,我们考虑一小刚度 连接的双自由度-质弹阻模型(记为TDFMSD-1),其中取堆石体参振质量m0为250 kg,取刚度k2为 100 MN·m-1,取阻尼c2为3000 kg·s-1,取质量块Δm为6级,每级75 kg,取质量块与地面的连接刚度k1为37 MN·m-1,取质量块与地面的连接阻尼c1为 3000 kg·s-1,取震源为68 Hz的Ricker子波.通过公式(17)计算得到此模型在附加2到6块质量块时的接收信号主频分别为63、53、46、42 Hz和38 Hz,进而得到Δm-D曲线,如图 9所示.
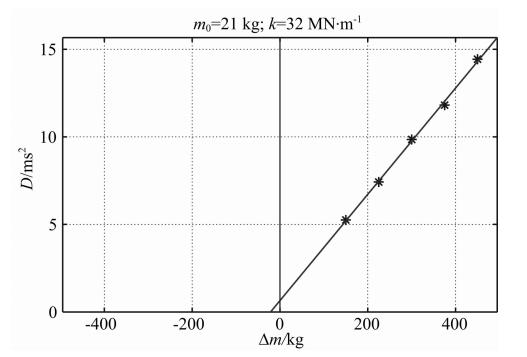 | 图 9 小刚度连接双自由度-质弹阻模型TDFMSD-1的Δm-D曲线 Fig. 9 The Δm-D curve for TDFMSD-1 with small stiffness connection |
基于以上分析,为避免出现小截距型的异常 Δm-D曲线,附加质量块距离震源中心的偏移距应 尽可能小一些,应尽可能使用较大触地面积的附加质量块,应使附加质量块与地面连接紧密.
3.3 利用双自由度-质弹阻模型解释接收信号频谱出现的“双峰”现象在实际工程应用中,张智等(2013)发现接收信号的频谱往往会出现“双峰”现象,即出现两个频率峰值,这往往导致主频出现误判.目前对这一问题的解决办法是反复激震,直到出现单峰频谱为止.
考虑一中等刚度连接的双自由度-质弹阻模型(记为TDFMSD-2),其中取堆石体参振质量m0为250 kg,取刚度k2为100 MN·m-1,取阻尼c2为3000 kg·s-1,取质量块Δm为6级,每级75 kg,取质量块与地面的连接刚度k1为150 MN·m-1,取质量块与地面的连接阻尼c1为 750 kg·s-1.通过公式(17)计算此模型在震源分别取为68、150 Hz和300 Hz时,1块附加质量块和6块质量块对应的接收信号频谱.如图 10所示.
 | 图 10 中等刚度连接双自由度-质弹阻模型TDFMSD-2在不同震源频率下的接收信号频谱 (a)68 Hz Ricker子波-1块质量块;(b)68 Hz Ricker子波-6块质量块;(c)150 Hz Ricker子波-1块质量块; (d)150 Hz Ricker子波-6块质量块;(e)300 Hz Ricker子波-1块质量块;(f)300 Hz Ricker子波-6块质量块. Fig. 10 The received signal spectra under different source frequencies for TDFMSD-2 with moderate stiffness connection (a)68 Hz Ricker wavelet,one mass block;(b)68 Hz Ricker wavelet,six mass blocks;(c)150 Hz Ricker wavelet,one mass block; (d)150 Hz Ricker wavelet,six mass blocks;(e)300 Hz Ricker wavelet,one mass block;(f)300 Hz Ricker wavelet,six mass blocks. |
由图 10可以看出,在中等刚度连接情况下,不论质量块的个数为1块还是6块,接收信号的频谱在震源频率较高时均出现了“双峰”现象(图 10(c、d、e、f)),其中震源频率为150 Hz时的低频峰值为主峰(图 10(c、d)),而震源频率为300 Hz时的高频峰值为主峰(图 10(e、f)).说明高频震源是“双峰”出现的主要因素.另外,由图 10还可以看出,虽然高频震源出现“双峰”,但是低频峰对应的频率却基本保持不变,1块质量块时为86 Hz左右,6块质量块为52 Hz左右.故出现双峰时,应选择低频峰的频率为接收信号的主频.
另外,我们再考虑连接刚度较大的双自由度-质 弹阻模型(记为TDFMSD-3),其中取堆石体参振质 量m0为250 kg,取刚度k2为100 MN·m-1,取阻 尼c2为3000 kg·s-1,取质量块Δm为6级,每级 75 kg,取质量块与地面的连接刚度k1为600 MN·m-1,取质量块与地面的连接阻尼c1为 187.5 kg·s-1.通过公式(17)计算此模型在震源分别取为68、150 Hz和300 Hz时,1块附加质量块和6块质量块对应的接收信号频谱.如图 11所示.
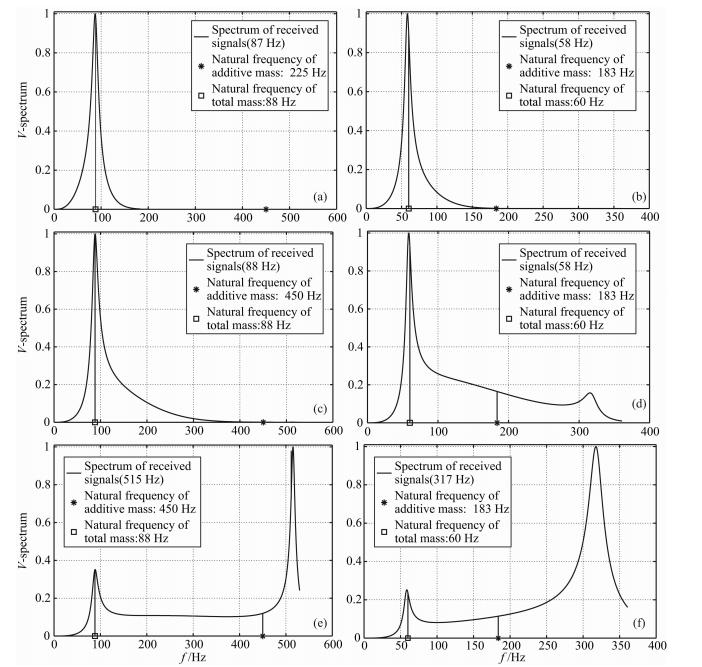 | 图 11 大刚度连接双自由度-质弹阻模型TDFMSD-3在不同震源频率下的接收信号频谱 (a)68 Hz Ricker子波-1块质量块;(b)68 Hz Ricker子波-6块质量块;(c)150 Hz Ricker子波-1块质量块; (d)150 Hz Ricker子波-6块质量块;(e)300 Hz Ricker子波-1块质量块;(f)300 Hz Ricker子波-6块质量块. Fig. 11 The received signal spectra under different source frequencies for TDFMSD-3 with big stiffness connection (a)68 Hz Ricker wavelet,one mass block;(b)68 Hz Ricker wavelet,six mass blocks;(c)150 Hz Ricker wavelet,one mass block; (d)150 Hz Ricker wavelet,six mass blocks;(e)300 Hz Ricker wavelet,one mass block;(f)300 Hz Ricker wavelet,six mass blocks. |
对比图 11和图 10可以看出,在大刚度连接情 况下,接收信号频谱不易出现 “双峰”现象,仅在较 高频率时才出现两个相距较远的“双峰”(图 11(e、f)),故比较容易判别.
综上所述,基于双自由度质弹阻模型,我们可以较好地解释实际工程应用及数值模拟中出现的一些现象,同时提出以下建议:(1)尽量选择较小偏移距和触地面积大的质量块,采取措施增大质量块与堆石体之间的连接刚度,以便质量块和堆石体达到同步振动.(2)在质量块和堆石体的连接刚度不够大时,不要选择频率过高的震源.(3)当出现“双峰”频谱现象时,应取低频峰为接收信号的主频.
4 结论本文考虑堆石体系统振动的阻尼因素,以及附加质量块与堆石体之间的非刚性连接问题,分别基于质弹阻模型和双自由度-质弹阻模型对附加质量 法应用中出现的一些问题进行了理论分析和解释,结论如下:
(1)基于质弹阻模型可以较好地解释附加质量法接收信号主频随震源频率和下雨而变化、先增后减型异常Δm-D曲线和递减性异常Δm-D曲线等现象.建议附加质量法测试中应采用可控震源,尽量选择干燥的测点进行测量,尽量选择频率相对较高的震源.
(2)基于双自由度-质弹阻模型可以较好地解释附加质量法接收信号主频随质量块偏移距和触地面积而变化、小截距型异常Δm-D曲线以及接收信号频谱出现“双峰”等现象.建议附加质量法测试中应尽量选择较小偏移距和触地面积大的质量块,采取措施增大质量块与堆石体之间的连接刚度,不要选择频率过高的震源,当无法避免“双峰”频谱时,应选取低频峰为接收信号的主频峰.
| [1] | Das B M. 1984. Fundamentals of Soil Dynamics (in Chinese). Wu S M, Gu Y Z Trans. Hangzhou: Zhejiang University Press, 1-15. |
| [2] | Li P W. 1993. Additive mass method measured dynamically foundation bearing capacity. Chinese J. Geophys. (in Chinese), 36(5): 683-687. |
| [3] | Li P W, Leng Y B, Yuan J H. 1999. The density measurement of rock fill object by additive mass method. Chinese J. Geophys. (in Chinese), 42(3): 422-427, doi: 10.3321/j.issn:0001-5733.1999.03.016. |
| [4] | Nakazaki S, Yamaguchi H. 1999. Preliminary design of super long suspension bridges using the temporary additional mass method against a storm. Journal of Wind Engineering and Industrial Aerodynamics, 83(1-3): 317-326. |
| [5] | Shi Z J, Tian G, Shen H L, et al. 2010. Theoretical studies of the geophone coupling influence in the limestone out crops area. Chinese J. Geophys. (in Chinese), 53(5): 1234-1246, doi: 10.3969/j.issn.0001-5733.2010.05.026. |
| [6] | Song X H, Xiao B X, Gu H M, et al. 2004. Application of method of additive mass to density measurement of rock fill object in Shuibuya water control project. Coal Geology & Exploration (in Chinese), 32(3): 40-43. |
| [7] | Tan F Y, Jiang Z Q, Li Z Q, et al. 2010. Application of additive mass method to testing compacted density of filling material in Kunming new airport. Rock and Soil Mechanics (in Chinese), 31(7): 2214-2218. |
| [8] | Xue Y F, Cui L, Li P W, et al. 2010. Density measurement of rock fill by use of rigidity correlation method. Chinese Journal of Geotechnical Engineering (in Chinese), 32(6): 987-990. |
| [9] | Yu D J, Zhao M H, Zhao J, et al. 2005. A research on the measure of the compactness of a model of high embankment using dynamic test method. Carsologica Sinica (in Chinese), 24(2): 124-127. |
| [10] | Zhang J Q, Zhou Z Q, Cai J X, et al. 2012. Technique of additional Mass method for rockfill body density measurement and evaluation of its application. Journal of Yangtze River Scientific Research Institute (in Chinese), 29(8): 45-51. |
| [11] | Zhang Z, Liu J Q, Min X L, et al. 2009. Applied research on density measurement of rockfill object by additive mass method. // The Progress of Modern Rockfill Object Technology: 2009.The Memoir of the First International Seminar on Rockfill Object. Beijing: China Water & Power Press, 263-268. |
| [12] | Zhang Z, Liu X F, Cai J X, et al. 2013. A experimental study on density measurement of rock fill object by additive mass method. Progress in Geophys. (in Chinese), 28(1): 498-506, doi: 10.6038/pg20130157. |
| [13] | Zheng Q J, Tang R M, Cen Z S. 2005. Applications of Shuibuya rock fill dam detection method. Yangze River (in Chinese), 36(5): 25-26. |
| [14] | Zhou C R. 1989. How to eliminate the influence of additional mass, stiffness and damping on the frequency response function. Journal of Vibration, Measurement & Diagnosis (in Chinese), 9(2): 13-17. |
| [15] | Zhou H, Chen X F. 2007. A study on the effect of depressed topography on Rayleigh surface wave. Chinese J. Geophys. (in Chinese), 50(4): 1182-1189, doi: 10.3321/j.issn:0001-5733.2007.04.027. |
| [16] | 达斯B M. 1984. 土动力学原理. 吴世明, 顾尧章译. 杭州: 浙江大学出版社, 1-15. |
| [17] | 李丕武. 1993. 地基承载力动测的附加质量法. 地球物理学报, 36(5): 683-687. |
| [18] | 李丕武, 冷元宝, 袁江华. 1999. 堆石体密度测定的附加质量法. 地球物理学报, 42(3): 422-427, doi: 10.3321/j.issn:0001-5733.1999.03.016. |
| [19] | 石战结, 田钢, 沈洪垒等. 2010. 灰岩裸露区检波器三自由度耦合系统理论的研究. 地球物理学报, 53(5): 1234-1246, doi: 10.3969/j.issn.0001-5733.2010.05.026. |
| [20] | 宋先海, 肖柏勋, 顾汉明等. 2004. 附加质量法在水布垭堆石体密度测定中的应用. 煤田地质与勘探, 32(3): 40-43. |
| [21] | 谭峰屹, 姜志全, 李仲秋等. 2010. 附加质量法在昆明新机场填料压实密度检测中的应用研究. 岩土力学, 31(7): 2214-2218. |
| [22] | 薛云峰, 崔琳, 李丕武等. 2010. 刚度相关法测试堆石体密度. 岩土工程学报, 32(6): 987-990. |
| [23] | 于德介, 赵明华, 赵江等. 2005. 高填石路堤模型密实度动测方法的研究. 中国岩溶, 24(2): 124-127. |
| [24] | 张建清, 周正全, 蔡加兴等. 2012. 附加质量法检测堆石体密度技术及应用评价. 长江科学院院报, 29(8): 45-51. |
| [25] | 张智, 刘家琦, 闵晓莉等. 2009. 堆石体施工堆石体密度附加质量法检测技术应用研究. //现代堆石体技术进展: 2009.第一届堆石体国际研讨会论文集. 北京: 中国水利水电出版社, 263-268. |
| [26] | 张智, 刘雪峰, 蔡加兴等. 2013. 测定堆石体密度的附加质量法的实验研究. 地球物理学进展, 28(1): 498-506, doi: 10.6038/pg20130157. |
| [27] | 郑庆举, 唐儒敏, 岑中山. 2005. 水布垭面板堆石坝填筑检测方法应用. 人民长江, 36(5): 25-26. |
| [28] | 周传荣. 1989. 如何消除附加质量、刚度及阻尼对频响函数的影响. 振动、测试与诊断, 9(2): 13-17. |
| [29] | 周红, 陈晓非. 2007. 凹陷地形对Rayleigh面波传播影响的研究. 地球物理学报, 50(4): 1182-1189, doi: 10.3321/j.issn:0001-5733.2007.04.027. |
 2015, Vol. 58
2015, Vol. 58


