地球物理学报  2014, Vol. 57 Issue (9): 2946-2960   PDF    
引用本文
王雄文, 王华忠. 2014. 基于压缩感知的高分辨率平面波分解方法研究. 地球物理学报, 57(9): 2946-2960, doi: 10.6038/cjg20140920   
WANG Xiong-Wen, WANG Hua-Zhong. 2014. A research of high-resolution plane-wave decomposition based on compressed sensing. Chinese J. Geophysics, 57(9): 2946-2960, doi: 10.6038/cjg20140920   
基于压缩感知的高分辨率平面波分解方法研究
王雄文, 王华忠     
同济大学海洋与地球科学学院, 上海 200092
投稿时间:2013-12-9    最后修改时间: 2014-5-9 .
基金项目：国家重点基础研究发展计划项目（2011 CB201002）、国家自然科学基金（41374117）以及国家重大专项（2011ZX05005-005-008HZ ，2011ZX05006-002，2011ZX05023）资助.
作者简介：王雄文，男，1983年生，同济大学海洋与地球科学学院在读博士.主要从事地震信号处理和速度分析的研究.E-mail：xiongwenwang@gmail.com
摘要：平面波分解方法是地震资料处理中的一项关键技术，它广泛地运用在平面波偏移、各类Beam偏移等成像方法中.平面波分解不仅可以提高偏移成像的效率，而且可以压制地震资料中的随机噪音，提高地震数据的信噪比.线性Radon变换（LRT）是一种常见的实现平面波分解的方法，但常规的LRT存在以下两个缺点：（1）分辨率受测不准原理限制；（2）变换结果存在很多噪音和空间假频.为了克服LRT的上述缺点，本文提出一种基于压缩感知的高分辨率平面波分解方法，并利用加权匹配追踪（WMP）技术实现了该方法.该方法将LRT视为一个参数估计问题，并将LRT结果的稀疏性作为约束条件，在压缩感知理论的指导下利用WMP方法得到高分辨率、高信噪比的平面波分解结果.另外，该方法还可以用于提取地震数据的线性信号、压制随机噪音、实现高维地震数据规则化等地震资料处理技术.数值实验结果证明：WMP方法可以有效地提取地震数据中的线性信号，提高LRT的分辨率和信噪比，从而改善平面波分解的质量.
关键词： 平面波分解     压缩感知(CS)     线性Radon变换(LRT)     加权匹配追踪(WMP)    
A research of high-resolution plane-wave decomposition based on compressed sensing
WANG Xiong-Wen, WANG Hua-Zhong     
School of Ocean and Earth Science, Tongji University, Shanghai 200092, China
Abstract: Plane-wave decomposition is a useful technique of seismic data processing, it is widely used in plane-wave migration and all kinds of Beam migration. Plane-wave decomposition can improve the efficiency of migration, attenuate the noise of field data and improve the signal to noise ratio of field data. Linear Radon Transform (LRT) is a most common method to realize plane-wave decomposition. But it has two defects which impact the effect of plane-wave decomposition: (1) The resolution of LRT is decided by uncertainty principle; (2) The result of LRT contains a lot of space aliasing and other noise caused by sample pattern. In order to overcome these defects and improve the quality of plane-wave decomposition, in this paper we present a new method to achieve high-resolution plane-wave decomposition based on compressed sensing, which is realized by weighted matching pursuit(WMP) algorithm. The presented method considers LRT as an inverse problem, and uses the sparsity of LRT's result as the constraint of this problem. Under the framework of compressed sensing theory, this method achieves high resolution and high signal to noise ratio plane-wave decomposition by WMP algorithm. In addition to plane-wave decomposition, this method can also be used to get the linear events of seismic data, attenuate noise of field data, realize high dimension seismic data regularization and other seismic data processing techniques. The numerical examples show that WMP algorithm can forecast the linear events of seismic data effectively, improve the resolution and signal to noise ratio of LRT's result and then get a high quality of plane-wave decomposition.
Key words: Plane-wave decomposition     Compressed sensing (CS)     Linear Radon Transform (LRT)     Weighted marching pursuit (WMP)    
 1 引言

平面波分解方法广泛地运用于平面波波动方程偏移成像(陈生昌，2003；冯波和王华忠，2011)、Beam类偏移成像(陈凌等，2004；Gao et al., 2006)、高维地震数据规则化(Wang et al., 2011)等其他地震资料处理环节中，是地震资料处理中的一项关键技术.平面波分解方法最早是一项雷达信号处理技术，主要用来增强某个方向上的线性信号并压制其他方向的噪音(Capon，1969).后来勘探地震学运用该项技术提取地震数据中的线性信号、压制数据中的随机噪音(Özbek，2000; Hu et al., 2002)，提高地震数据的信噪比.随着平面波偏移方法、Beam类偏移方法的发展，平面波分解再一次被广泛地运用于偏移前提取局部平面波的数据预处理中.由于平面波的分解结果会严重影响地震偏移成像、速度反演等的计算效率和计算结果，因此研究一种高分辨率、高信噪比的平面波分解方法是一项具有重要意义和实用价值的研究工作.

局部倾斜叠加是一种常见的平面波分解方法，它是线性Radon变换(LRT)的一种具体实现方式.与Fourier变换(FT)、正交小波变换等其他常用的完备正交变换不同，LRT的基函数是非完备正交的.LRT基函数的非正交性会导致LRT结果包含大量的噪音，这些噪音会严重降低LRT结果的分辨率.LRT基函数的非完备性导致LRT经常是不可逆的(即无法通过反LRT得到原始数据)，在这种情况下平面波的分解结果与原始数据是不等价的.空间采样不足同样会导致LRT结果出现很多空间假频能量，它是降低LRT结果分辨率和信噪比的另一个重要因素，该现象在实际地震资料处理中表现得更加明显.为了克服LRT的这些问题，学者们提出了各种各样实现LRT的方法，其中以参数估计类的方法最为有效.该类方法用实际数据与预测数据的差作为误差范函，在最小二乘意义下估计LRT的结果(Hampson，1986; Beylkin，1987; Hu et al., 2012).最小二乘意义下估计的LRT结果在信噪比方面有比较显著的改善，但其分辨率依然受测不准原理限制，主要表现为：空间积分孔径越小，分辨率越低.由于地震数据的有效信号仅在局部范围内才满足线性假设，这就决定了LRT的空间积分孔径不宜太大，因此LRT只能得到低分辨率的结果.为了提高LRT结果的分辨率，Claerbout(1985)提出了随机反演的方法，提高了时间域LRT的分辨率(Thorson and Claerbout， 1985)； Sacchi和Ulrych(1995)提出了用柯西范数代替二范数的方法，利用有效信号的稀疏性作为约束条件，实现了频率域高分辨率的LRT(Sacchi and Ulrych， 1995).在这之后，许多研究工作都在讨论如何在参数估计框架下获得高分辨率的LRT结果：Cary(1998)在他的文章中表明时间域的LRT结果具有更强的稀疏性，并且特别适合描述地震数据中的时变信号，但他同样指出频率域的LRT可以更准确地刻画有效信号的频率特征，更准确地提取地震数据的子波(Cary，1998)；Herrmann等(2000)提出了一种在频率域实现的反空间假频LRT方法(Herrmann，2000)，该方法先利用无假频的低频数据实现LRT，然后用LRT结果构造加权算子并利用该加权算子压制高频数据LRT结果中的空间假频能量，进而提高LRT结果的信噪比和分辨率.这些方法表明，利用地震数据有效信号的稀疏性特征作为约束条件，构造出合理的正则化方式，可以有效地提高LRT结果的分辨率和信噪比.高分辨率的LRT方法可以有效地压缩地震数据中的线性信号，压制数据中的随机噪音，减小后续资料处理的成本，是一项实用价值很高的处理技术.

但这些高分辨率LRT方法同样存在很多问题.首先，这些方法都增加了LRT的计算成本.由于这些方法都需要求解一个反问题，在反问题的每一次迭代求解过程中都需要实现一次正、反LRT，因此计算代价要远远高于常规的LRT.其次，这些方法得到的LRT结果受正则化方法的影响比较大.不同的正则化方法描述了LRT结果不同的信号特征，因此得到的LRT结果也都各不相同.最后，这些方法并不是在所有的情况下都可以获得稳定的LRT结果.由于这些方法构造的反问题经常是极度不适定的，因此如果正则化方式不合理，该反问题就会存在多个极值点，从而导致这些方法无法得到稳定的LRT结果.

本文介绍了一种新的基于压缩感知理论的高分辨率LRT方法，该方法充分利用了地震数据有效信号的稀疏性特征，并利用该特征将常规的LRT转化为一个压缩感知问题，在压缩感知的理论框架下实现了高分辨率的LRT.本文首先介绍如何利用有效信号的稀疏性作为约束条件，在压缩感知的理论框架下将常规的LRT转换为一个压缩感知问题；然后，考虑到LRT在时间域具有更好的稀疏性，本文接着分析了时间域LRT结果中噪音和有效信号的分布特征，并根据该分布特征构造一个加权算子W ；最后，本文利用加权算子W设计了加权匹配追踪(WMP)算法求解该压缩感知问题，该算法有效地压制了时间域LRT的噪音，并在时频域提取地震子波，实现了高分辨率的LRT.本文介绍的高分辨率LRT方法充分利用了时间域LRT的稀疏性和频率域LRT的准确性，并用加权算子W有效地压制了LRT结果中由于基函数的非正交性、空间采样不足等因素而引入的噪音，有效地提高了LRT的分辨率和信噪比.本文最后的数值实验结果证明该方法可以获得稀疏的、高分辨率的平面波分解结果，大大压缩了地震数据中的有效信号、提高了地震数据的信噪比，是一项比较理想的平面波分解技术.

2 理论与方法 2.1 压缩感知框架下平面波分解的表达方法

假设地震数据中平面波的子波频谱可以表示为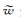(f，p)，其中f表示子波的频率，p表示子波传播的方向，则地震数据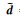(f，x)可以表示为

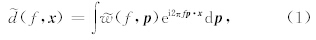
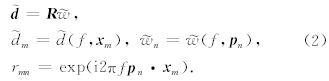
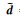其中x表示地震数据的空间采样坐标.方程(1)即为平面波数据的预测模型，该方程为Fredholm第一类积分方程，相移项ei2πfp·x 为该积分方程的积分核.将方程(1)离散化后可以得到下面的矩阵方程：

其中向量和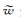分别表示频率域的地震数据和平面波子波，矩阵R为平面波数据的预测算子，该算子由方程(1)的积分核构成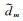，为向量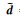的第m个分量，x m为数据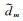的空间采样坐标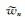，为向量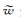的第n个分量，p n为子波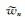的传播方向，rmn表示矩阵R第m行、第n列的元素.矩阵R的列向量组构成了LRT的一组基函数，该基函数完备正交的交要条件为R H R = I，即矩阵R是一个酉矩阵.但在实际数据的LRT处理中，会对平面波的倾角范围做假设，只考虑小倾角范围的平面波，使得矩阵R无法描述大倾角的平面波，因此矩阵R的核空间是一个非空集合，即LRT的基函数是非完备的；另外，即使在平面波的倾角范围内，矩阵R对倾角的采样也经常是过采样的，从而导致R的列向量组是非正交的，甚至是线性相关的.基于上述的两个原因，LRT在处理实际数据时经常是不可逆的.当LRT的基函数蜕化成Fourier基函数的时候，LRT才是可逆的，这时候矩阵R实现了对全倾角范围的采样，并且在采样范围内保持了基函数的正交性.

在平面波分解问题中，方程(2)的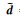和R是已知的，要求取的是子波的频谱和子波的传播方向(即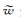)，因此平面波分解问题可以理解为方程(2)的求解问题.由于方程(2)经常是一个欠定的矩阵方程，因此该方程不存在唯一解.常规的LRT通过下面的方式获取方程(2)的近似解：

其中矩阵R H表示矩阵R的共轭转置.由于矩阵R不是酉矩阵，即LRT的基函数是非标准正交的，因此利用方程(3)得到的平面波分解结果只是方程(2)的一个近似解.该近似解的分辨率不仅受测不准原理的限制，而且还受基函数的非正交性所引入的噪音的影响，因此其分辨率和信噪比都比较低.为了改善平面波分解结果的质量，可以在最小二乘意义下估计方程(2)的近似解：

反问题(4)以向量 的L2范数最小作为约束条件求解地震数据的平面波分解问题.利用反问题(4)获得的平面波分解结果可以有效地压制基函数的非正交性所引入的噪音，但其分辨率依然受测不准原理的限制.为了进一步提高平面波分解结果的分辨率，可以利用平面波子波的稀疏性作为约束条件，将平面波分解问题转换为压缩感知问题，在压缩感知的理论框架下求解平面波分解结果.

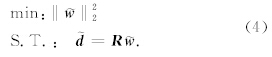
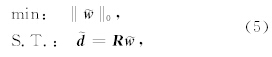
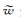压缩感知(CS，Compressed Sensing)问题其实是一类特殊的反问题，它是利用解的稀疏性特征作为约束条件求解欠定方程组的一类方法.由于利用解的稀疏性特征作为反问题的约束条件，因此压缩感知方法在求解欠定方程组的过程中以寻找最稀疏的解(即非零元素最少)为目的，得到的解具有较高的分辨率.L0、L1和Lp，00和L1范数的使用更加普遍.这里我们用L0范数来刻画平面波分解结果的稀疏性，因此压缩感知框架下的平面波分解问题可以用下面的优化问题来表示：

范数‖‖0表示方程的解中非0元素的个数，定量地描述了平面波分解结果的稀疏性.由于平面波分解结果在时间域具有更强的稀疏性，因此利用时间域的稀疏性作为约束条件可以获得分辨率更高的平面波分解结果：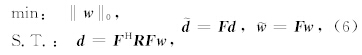

其中矩阵F表示正Fourier变换算子，F H表示反Fourier变换算子，d表示时间域的地震数据，w表示时间域的平面波子波.

压缩感知问题(6)式描述了数据d不包含噪音情况下的平面波分解问题.由于实际地震数据含有各种各样的噪音，因此无法直接用式(6)实现实际地震数据的平面波分解.为了能够处理实际地震数据，可以对式(6)做如下的修改：

其中e表示地震数据d中噪音的能量，矩阵T表示平面波数据在时间域的预测算子.压缩感知问题(7)考虑了地震数据所包含的噪音，因此可以用来实现实际地震数据的平面波分解并压制地震数据d中的非线性噪音.但与数据空间d的噪音相比，模型空间(即w所在的空间)的噪音对平面波分解结果的分辨率影响更严重.因此，用模型空间的噪音代替数据空间的噪音作为压缩感知问题的约束条件可以获得分辨率更高的平面波分解结果：

其中矩阵T H表示矩阵T的共轭转置矩阵.如果能够获得模型空间中解的能量分布情况，则可以用该能量分布构造一个加权因子W，然后利用该加权因子进一步压制模型空间中的噪音、提高平面波分解结果的分辨率.加入加权因子W后的压缩感知问题可以表示成如下形式：

其中ε表示模型空间的噪音能量大小，加权因子W为一个对角矩阵，其对角线上的元素wii=ei表示解的第i个分量能量的大小，范数‖·‖2w W表示加权的二范数，其计算方式如(9)式所示.(9)式即为本文最终用来实现地震数据平面波分解的压缩感知问题.与其它平面波分解方法相比，(9)式有以下的两个优点：(1)引入了L0范数，用解的稀疏性作为约束条件，将平面波分解问题转换为压缩感知问题，有效提高了平面波分解结果的分辨率；(2)引入加权因子W，加权因子W使(9)式具有更强的抗噪能力，并且有效地压制了由于采样不足而引入的空间假频，提高了压缩感知问题(9)在求解过程中的稳定性.因此，本文在后面两部分将详细介绍加权因子W的构造方法以及压缩感知问题(9)的求解方法.

2.2 加权因子W的计算方法

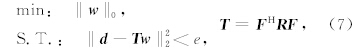
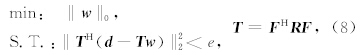
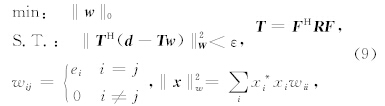
构造加权因子W的主要目的是预测问题中解的能量分布情况，并根据该能量分布情况辨别每次迭代过程中近似解的噪音成分和有效信号成分.由于问题的解为时间域高分辨率线性Radon变换(HR-LRT)结果，因此需要分析常规LRT结果中噪音和有效信号的分布特征，并根据该分布特征设计出有效的滤波器压制LRT中的假频能量、提高LRT的分辨率.为了简化分析过程，本文运用单平面波数据模型推导LRT中信号的分布特征.由于LRT是线性变换，因此其分析结果在多平面波数据模型中同样成立.

假设平面波的子波可以表示为

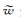其中w(t)表示子波在时间域的函数，(f)表示子波的频谱，f表示子波的频率.假设信号s(t)是对子波时移t0后得到的信号，则s(t)可以表示为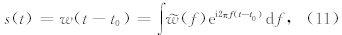

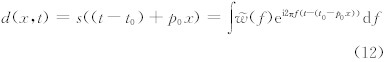
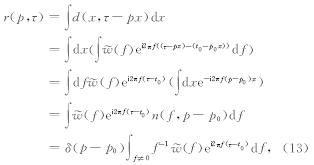
若在x=0处子波的时移量为t0，子波的入射方向为p0，并且数据中只包含该平面波，则该单平面波数据可以表示为

其中d(x，t)表示包含平面波的数据.数据d(x，t)的LRT变换结果可以解析地表示为

其中r(p，τ)表示LRT结果.从式(13)可以看出，当数据d(x，t)满足下面两个条件时：(1)在x方向上是连续的；(2)在x方向上的积分孔径为无穷大，LRT结果r(p，τ)可以达到最高的分辨率，即除方向p0外其他方向p上的值都为0.但实际地震数据并不满足上述的两个条件:首先，地震数据是离散采样的信号，由于受施工条件、成本预算等因素的影响，经常会出现空间采样不足的现象，导致LRT结果包含大量的空间假频噪音；其次，地震数据的有效信号只在局部范围内满足线性假设条件，这就决定了LRT在空间方向上的积分孔径不能太大，导致LRT得不到一个高分辨率的结果.因此，HR-LRT方法的主要目标就是解决地震数据的实际情况与积分公式(13)获得高分辨率结果所要求的条件之间的矛盾：利用压缩感知问题(9)实现HR-LRT主要是为了解决积分孔径的矛盾对分辨率的影响，通过对解的稀疏性进行约束以求突破测不准原理对分辨率的限制；在此处将引入的加权因子W主要是为了解决空间采样的矛盾对信噪比的影响，通过分析LRT结果的信号特征预测HR-LRT解的能量分布情况，辨别空间假频和有效信号，从而达到压制空间假频 噪音的目的.下面将详细介绍构造加权因子W的方法.

假设(p，t)为(p0，t0)附近的值，因此可以得到下面的结果:

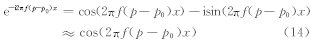
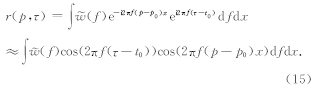
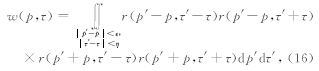
从积分(15)可以看出，LRT结果r(p，τ)在(p0，t0)附近分别关于轴τ=t0和p=p0对称.根据该对称性，可 以利用下面高维的相关方法构造加权因子w(p，τ)：

其中ε和η分别表示沿p和τ方向相关时所用的窗的大小.根据r(p，τ)的对称性可知，当数据d(x，t)包含一个入射方法为p0、在x=0处出现时刻为t0的平面波时，加权因子w(p，τ)具有如下的信号特征：(1)w(p，τ)在(p0，t0)处取得极大值，该极大值的大小由子波的能量决定；(2)在(p0，t0)外的其他地方，由于r(p，τ)不具备对称性，因此w(p，τ)的值会比较小.因此w(p，τ)可以视为HR-LRT有效信号的概率分布函数：w(p，τ)值大的地方表示该处包含有效信号的概率比较大，w(p，τ)值小的地方表示该处包含有效信号的概率比较小.引入加权因子w(p，τ)后就可以在求解压缩感知问题(9)的过程中根据w(p，τ)值的大小辨别假频噪音和有效信号，从而达到压制空间假频的目的.下面用一些简单的数值实验证实这里提到的分析结果.

图 1a为对一个单平面波离散采样后得到的数据，该数据的空间采样间隔为10 m，采样范围为-100~100 m；图 1b为图 1a的LRT结果.从图 1b可以看出空间假频是LRT结果中的主要噪音来源之一，p离p0越远空间假频越严重.并且这种空间假频主要表现为不同频率的振荡噪音，因此可以通过高维相关的方法压制这种振荡噪音.图 2a为扩大采样范围后对该平面波离散采样得到的数据，其采样间隔仍为10 m，采样范围为-200~200 m；图 2b为图 2a的LRT结果.对比图 1b和图 2b可知，扩大采样范围后可以提高LRT的分辨率.但由于图 2a的采样间隔与图 1a相同，因此它们的LRT结果中出现空间假频时p－p0的值是相同的.图 3a为加密采样间隔后对该平面波离散采样得到的 数据，其采样间隔为5 m，采样范围为-100~100 m； 图 3b为图 3a的LRT结果.对比图 1b和图 3b可知，加密采样间隔可以有效地压制LRT结果中的空间假频，提高LRT的信噪比.但由于图 3a的采样范围与图 1a相同，因此它们的LRT结果的分辨率相同.这三个简单的数值实验形象地说明了采样方式对LRT分辨率和信噪比的影响：LRT的分辨率与空间采样范围成正比，空间采样范围越大LRT的分辨率越高；p－p0的值与空间采样间隔成反比(p为LRT结果开始出现假频时的斜率)，空间采样间隔越小LRT的假频噪音越弱.该结果其实是采样定理在LRT中的一种表现形式.而本文提出的实现HR-LRT方法是一种在不改变采样方式的前提下运用压缩感知的方法提高LRT分辨率和信噪比的方法.另外，从图 1b、图 2b、图 3b中可以看出LRT结果具有比较强的轴对称性.LRT结果的该种信号特征特别有利于通过高维相关的方法构造出信噪比高、抗噪能力强的加权因子w(p，τ).

图 1 (a)采样间隔为10 m，采样孔径为200 m的平面波数据；(b)图(a)的LRT结果Fig. 1 (a)Plane-wave data with sample interval is 10 m and sample aperture is 200 m; (b)The result of LRT with data in figure(a)

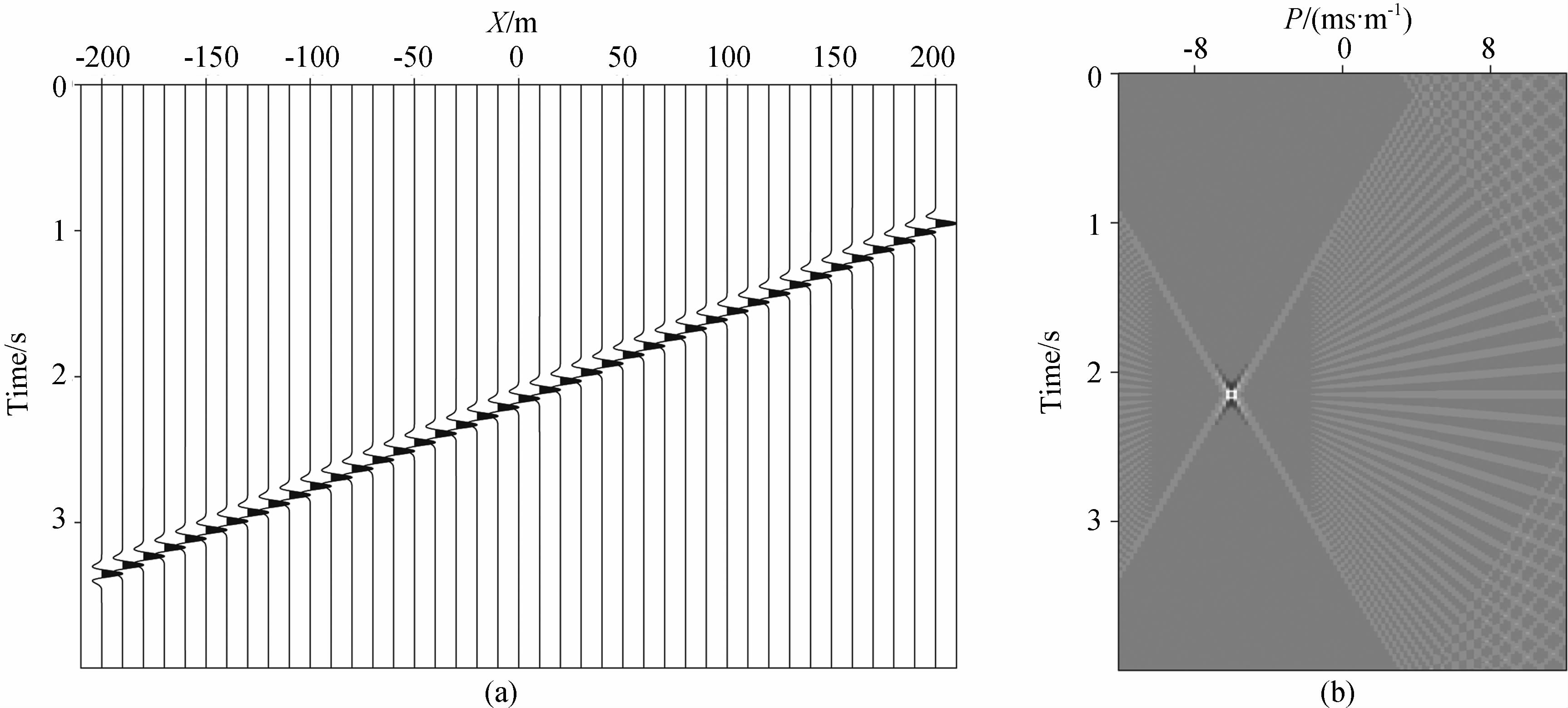图 2 (a)采样间隔为10 m，采样孔径为400 m的平面波数据；(b)图(a)的LRT结果Fig. 2 (a)Plane-wave data with sample interval is 10 m and sample aperture is 400 m; (b)The result of LRT with data in figure(a)

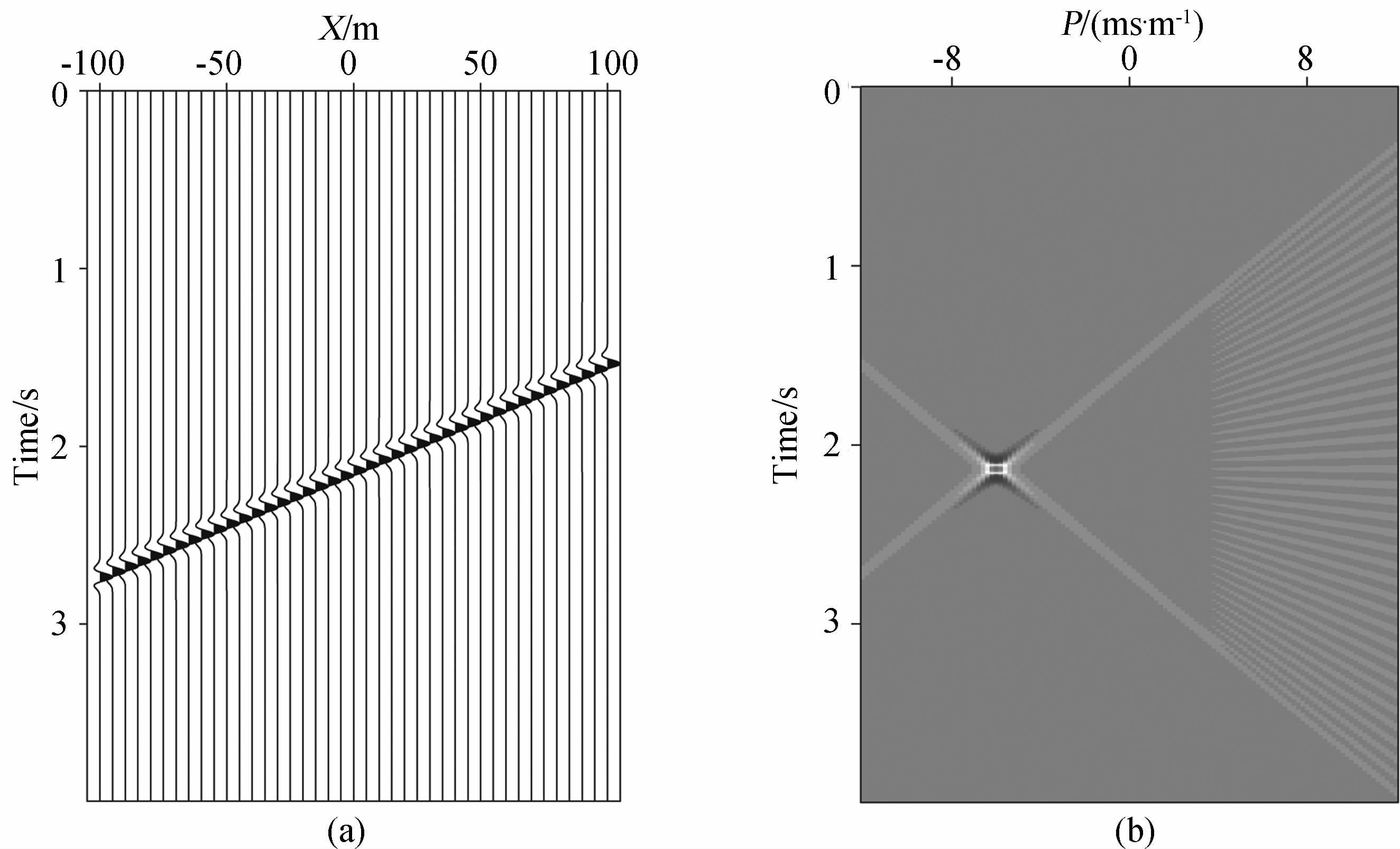图 3 (a)采样间隔为5 m，采样孔径为200 m的平面波数据；(b)图(a)的LRT结果Fig. 3 (a)Plane-wave data with sample interval is 5 m and sample aperture is 200 m; (b)The result of LRT with data in figure(a)

下面的数值实验用来证明通过高维相关方法(16)可以构造出高信噪比、强抗噪能力的加权因子w(p，τ).图 4a为一个包含五个平面波的二维数据；图 4b为图 4a的LRT结果，该图包含大量的空间假频，严重影响LRT结果的信噪比；图 4c为图 4b 根据高维相关方法(16)计算得到的加权因子w(p，τ)，该加权因子具有很高的信噪比.从图 4c中可以看出，高维相关 方法(16)可以有效地压制图 4b中出现的空间假频噪音，并且准确地预测平面波在x=0处出现的时刻和传播方向(如图 4c所示).因此，图 4c的能量分布可以视为数据中平面波出现的概率密度函数，利用图 4c可以辨别图 4b中的空间假频和有效信号，从而达到压制空间假频的目的.为了证明高维相关方法(16)的抗噪能力，我们在图 4a的数据中加入了大量的高斯白噪得到图 5a这样的数据；图 5b为图 5a的LRT结果，在图 5b中除了空间假频外，还包含大量的随机噪音；图 5c为图 5b根据高维相关方法计算得到的加权因子w(p，τ)，该加权因子与图 4c基本一致.从图 5c中可以看出，高维相关方法(16)具有很强的抗噪能力，可以有效地压制地震数据中的随机噪音，预测出平面波出现的时刻和传播方向.

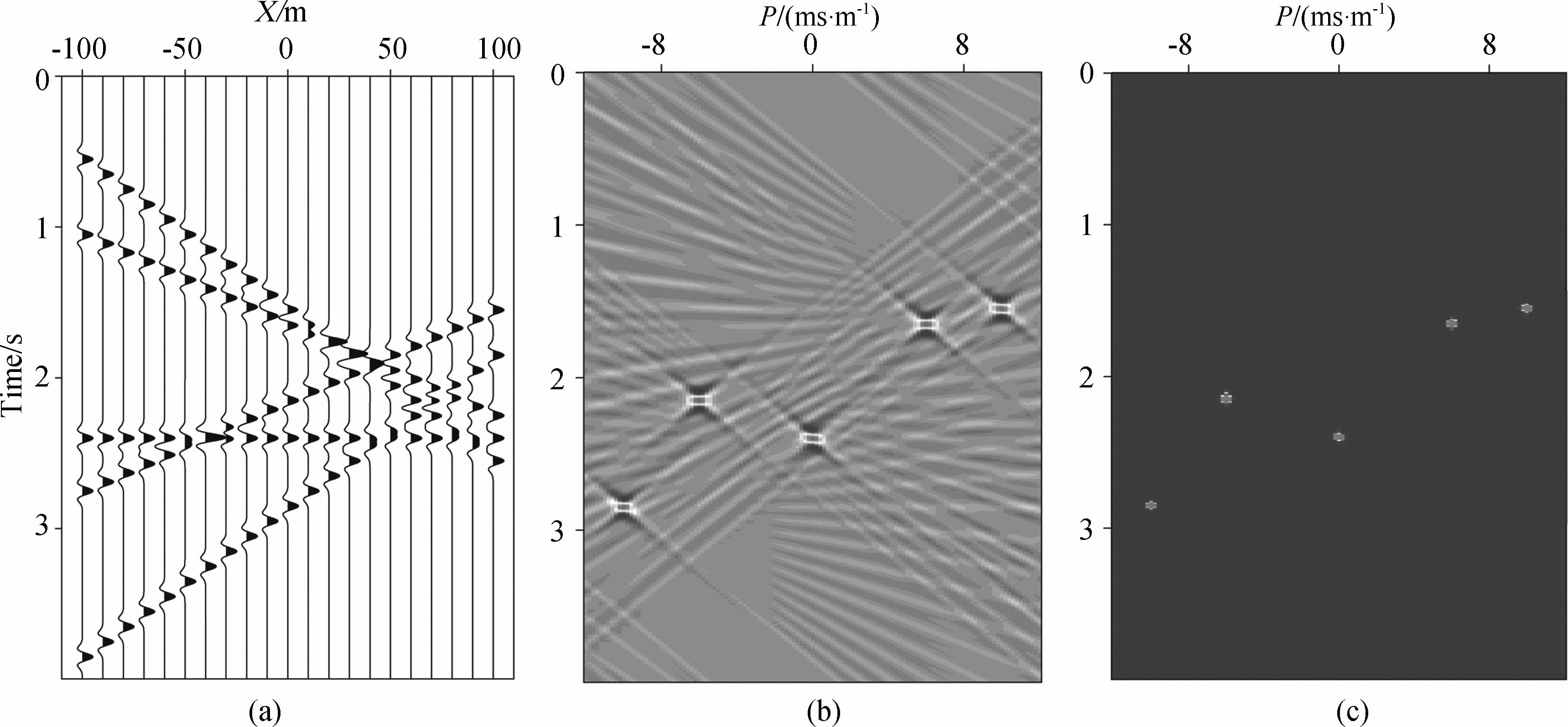图 4 (a)包含五个平面波的二维数据d(x，t)；(b)图(a)的LRT结果r(p，τ);(c)图(b)中根据高维相关方法计算得到的加权因子w(p，τ)Fig. 4 (a)Plane-wave data d(x，t)containing five plane waves in it;(b)The result of LRTr(p，τ)with data in figure(a);(c)The weighted factor w(p，τ)of figure(b)computed with high-dimension corporation method

图 5(a)包含五个平面波和大量高斯白噪的二维数据d(x，t)；(b)图(a)的LRT结果r(p，τ)；(c)图(b)根据高维相关方法计算得到的加权因子w(p，τ)Fig. 5 (a)Plane-wave datad(x，t)containing five plane waves and a lot of noise in it;(b)The result of LRT r(p，τ)with data in figure(a);(c)The weighted factor w(p，τ)of figure(b)computed with high-dimension corporation method

加权因子w(p，τ)只能提高LRT的信噪比，压制LRT结果中的空间假频，其改善LRT分辨率的能力是有限的.压缩感知问题(9)的求解才是提高LRT分辨率的关键，因此本文下面将详细介绍压缩感知问题(9)的求解方法.

2.3 平面波分解的求解方法

高分辨率的平面波分解方法可以抽象成求解压 缩感知问题(9)，该方法用平面波分解结果的L0范数作为约束条件构造平面波分解问题.由于L0范数不是一个严格凸的函数，因此问题(9)有可能存在多个极值点.多极值问题(9)是求解问题的一个难点，它会导致问题出现多解性并影响问题求解过程的稳定性，因此在更多的时候我们用该问题的近似解来代替其真实解.

匹配追踪(MP)算法是求取以L0范数作为约束条件这一类压缩感知问题近似解的方法，但当问题的规模比较大时传统的MP算法会变得不稳定.另外，MP算法比较容易受噪音的影响，抗噪能力比较低.为了提高问题(9)求解过程的稳定性，可以在传统的MP算法中引入加权因子W，利用加权因子W提高MP算法的抗噪能力并使求解过程变得稳定，我们称这种新的方法为加权匹配追踪(WMP).为了区别于常规的LRT，这里将用WMP实现HR-LRT的算法称为WMP-LRT.对于问题(9)，WMP-LRT算法的具体实现方式描述如下.

2.4 WMP-LRT算法的实现方式

任务：求取下面压缩感知问题的近似解:min:‖w‖0S.T.:‖TH(dobs－Tw)‖2W<ε.

问题描述：已知时间域的平面波预测算子T(矩阵)、观测数据dobs(向量)、加权因子W(对角矩阵)以及高分辨率线性Radon变换(HR-LRT)结果中的噪音能量ε，求取平面波分解结果w(向量).

初始化：令k=0，并做如下的初始化：

(1)初始化WMP-LRT结果：w0=0.

(2)初始化数据空间的残差：e0=dobs－Tw0=dobs.

(3)初始化模型空间的残差：ξ0=THe0=THdobs.

(4)初始化WMP-LRT结果的支集：S0=Support(w0)=Φ.

迭代求解过程：令k=k+1，并顺序执行如下操作：

(1)更新子波出现的位置：寻找下标j0，使得j0满足如下的条件：j，wj0ξk－1(j0)≥wjξk－1(j)， 其中wj为加权因子W的第j个分量，ξk－1(j)为模型空间残差ξk－1的第j个分量.

(2)更新子波的长度：在j0处对ξk－1做短时Fourier变换，令ζk－1(j0，f)为变换结果.假设fmax为ζk－1(j0，f)有效频带的最大值，由fmax确定j0处子波的半径：rk－1=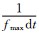 其中dt为信号在时间方向上的采样间隔，rk－1为子波半径的采样点数.此时子波的长度为2rk－1.

(3)更新WMP-LRT结果的支集：根据第1步、第2步确定的子波位置j0和子波长度2rk－1，在ξk－1中选取相应的子波xk，并更新WMP-LRT结果的支集：Sk=Sk+1∪Support(xk).

(4)更新WMP-LRT结果：根据第3步确定的子波xk，更新WMP-LRT变换结果：wk=wk－1+xk.

(5)更新数据空间的残差：根据第4步更新后的WMP-LRT结果wk更新数据域的残差：ek=dobs－Twk.

(6)更新模型空间的残差：根据第5步更新后的数据空间的残差ek更新模型空间的残差：ξk=THek.

(7)检查：如果‖ξk‖2W<ε，迭代结束；否则进入下一次迭代.

输出：问题的近似解为k次迭代后的结果：wk.

该算法在每一次迭代过程中根据加权因子W和模型空间的残差ξk－1先寻找子波出现的位置j0，加权因子W大大增加了这一过程的抗噪能力，增加了j0的可靠性.由于LRT在频率域可以更好地保持子波的信号特征，因此获得j0后WMP-LRT算法在j0处对ξk－1做时频变换，并根据ξk－1在j0处的频率特征计算子波的有效长度.利用在迭代的第1步、第2步中获得的子波xk，算法在迭代的第4步、第5步和第6步分别更新了WMP-LRT的结果wk、数据空间的残差ek和模型空间的残差ξk.迭代以模型空间的残差能量是否小于ε作为终止条件，其中ε为算法一开始就设定的模型空间噪音的能量.该算法在迭代过程的第(1)步和第(2)步中结合了时间域LRT和频率域LRT的优点，并引进加权因子W增加了WMP-LRT的抗噪能力.算法最后得到的问题(9)的近似解为经过k次迭代后得到的WMP-LRT结果wk.

下面的数值实验是根据该WMP-LRT算法实现的HR-LRT，这些数值实验证明了WMP-LRT可以有效地提高LRT的分辨率，并且具有很强的抗噪能力，是平面波分解的有力工具.

3 数值实验

本文首先用一个单平面波合成数据来证明WMP-LRT算法可以提高平面波分解的分辨率和信噪比.图 6a为一单平面波合成数据；图 6b为图 6a的常规LRT结果；图 6c为图 6a的WMP-LRT结果；图 6d为图 6c的波形图.对比图 6b和图 6c可知，WMP-LRT不仅能够压制常规LRT产生的噪音，提高平面波分解的信噪比，而且大大提高了平面波分解的分辨率.图 7是一个只含正振幅的子波的合成数据，图 7a是一个单平面波合成数据；图 7b为 图 7a的常规LRT结果；图 7c为图 7a的WMP-LRT结果；图 7d为图 7c的波形图.从波形图 6d和图 7d中还可以看出，WMP-LRT算法在提高平面波分解的分辨率和信噪比的同时还保持了子波原有 的波形特征，这对后续的保幅偏移成像是极其重要的.

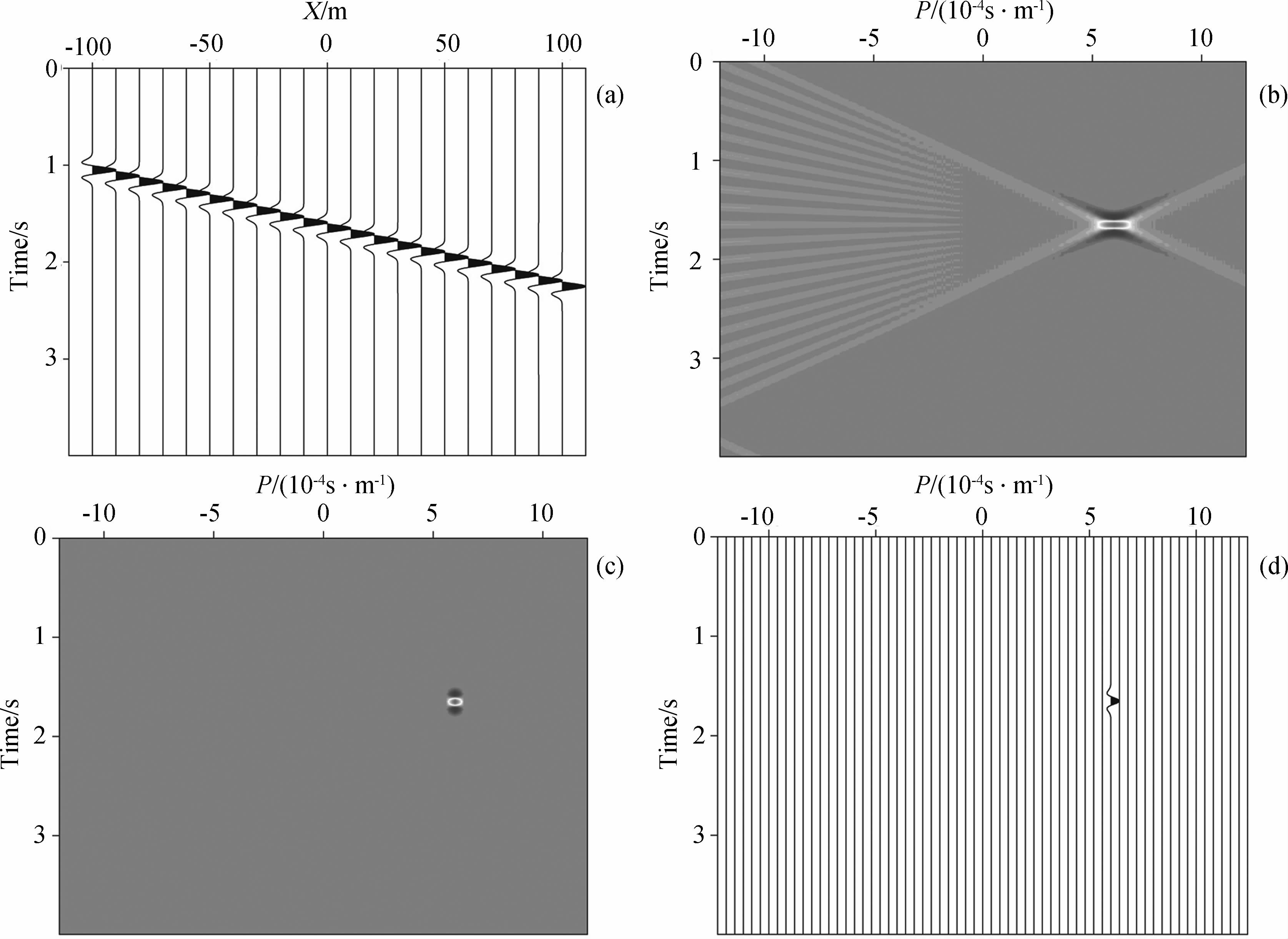图 6 (a)单平面波数据；(b)图(a)的常规LRT结果；(c)图(a)的WMP-LRT结果；(d)图(c)的波形显示图Fig. 6 (a)Plane-wave data with only one plane wave;(b)The result of LRT with data in figure(a);(c)The result of WMP-LRT with data in figure(a);(d)The waveform of figure(c)

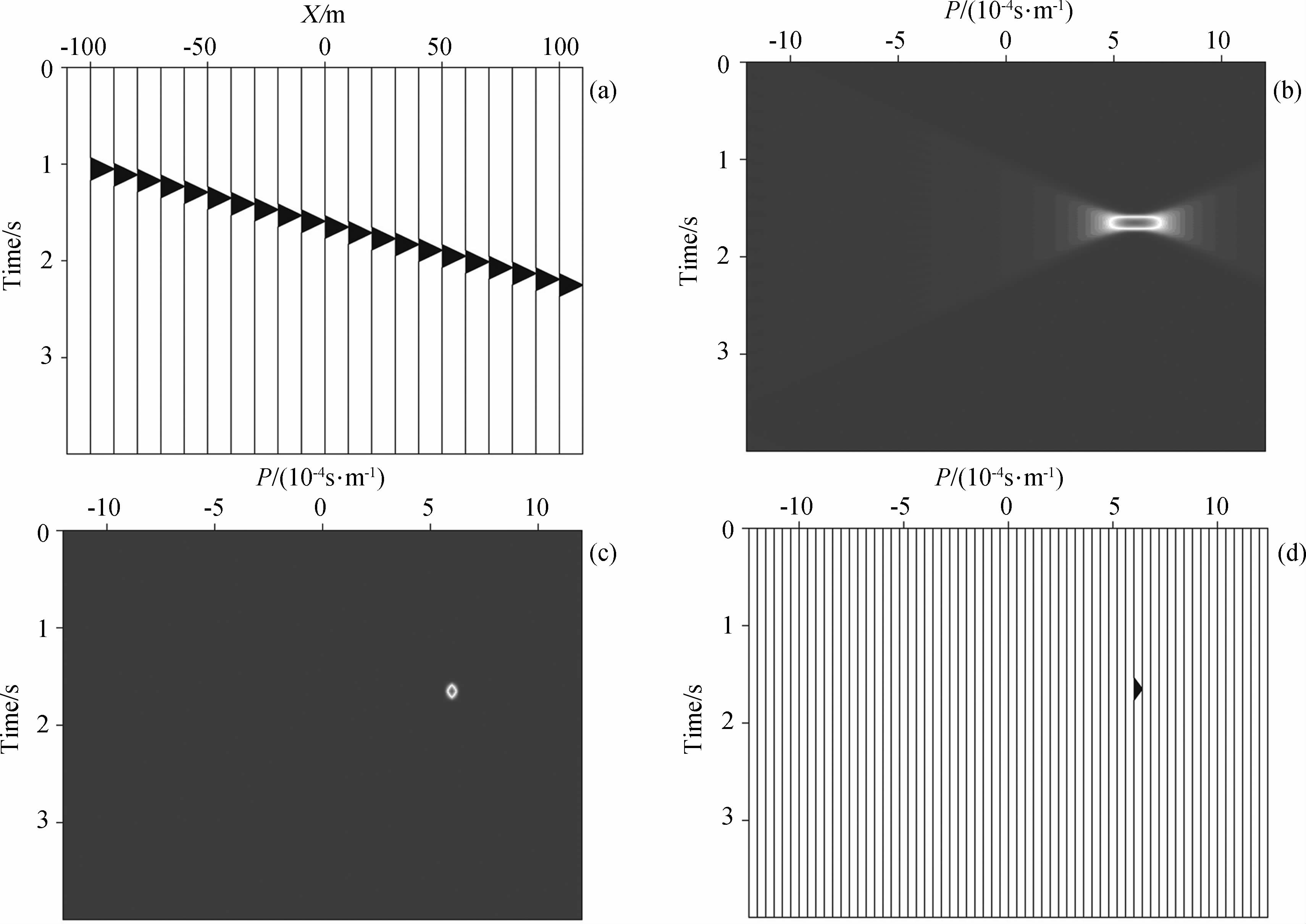图 7 (a)单平面波数据；(b)图(a)的常规LRT结果；(c)图(a)的WMP-LRT结果；(d)图(c)的波形显示图Fig. 7 (a)Plane-wave data with only one plane wave;(b)The result of LRT with data in figure(a);(c)The result of WMP-LRT with data in figure(a);(d)The waveform of figure

第二个数值实验是一个多平面波合成数据的LRT结果与WMP-LRT结果的对比，用来证明WMP-LRT可以同时提取多个平面波、具有处理多平面波数据的能力.其中图 8a为一个包含多个平面波的合成数据；图 8b为图 8a的常规LRT结果，该结果包含大量的空间假频，严重影响平面波分解的质量；图 8c为图 8a的WMP-LRT结果，该结果压制了在图 8b中产生的空间假频，并大大提高了平面波分解的分辨率；图 8d为图 8c的波形显示图，从该图可以看出WMP-LRT的结果很好地保持了每个平面波的子波特征；图 8e为WMP-LRT算法根据图 8b计算得到的加权因子W，该加权因子准确地预测出每个平面波出现的时间和传播方向.从该数值实验可以看出，利用高维相关方法可以有效地压制常规LRT结果中的噪音、辨别平面波出现的时间和传播方向、获得高信噪比的加权因子W，从而增加了WMP-LRT算法的稳定性和抗噪能力，保证WMP-LRT可以获得高信噪比、高分辨率的平面波分解结果.

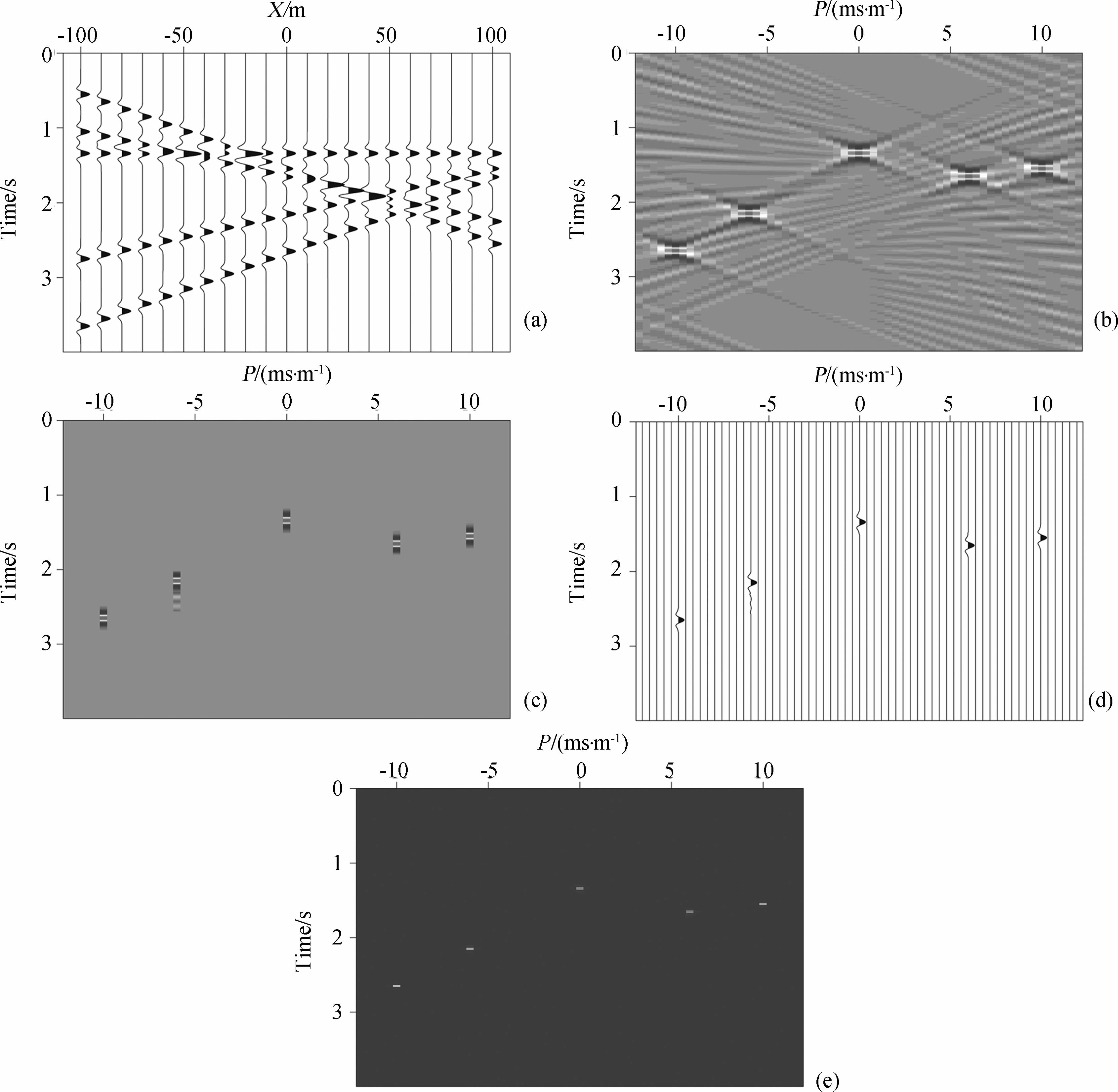图 8 (a)包含多个平面波的合成数据；(b)图(a)的常规LRT结果；(c)图(a)的WMP-LRT结果；(d)图(c)的波形显示图；(e)WMP-LRT算法根据图(b)计算得到的加权因子WFig. 8 (a)Plane-wave data with multi plane waves;(b)The result of LRT with data in figure(a);(c)The result of WMP-LRT with data in figure(a);(d)The waveform of figure(c);(e)The weighted factor W of data in figure(a)

第三个数值实验是一个包含大量随机噪音的多平面波合成数据的LRT结果与WMP-LRT结果的对比，用来证明WMP-LRT具有压制数据空间中的随机噪音、提高平面波数据信噪比的能力.其中图 9a为在图 8a中加入大量高斯白噪后的多平面波合成数据；图 9b为图 9a常规的LRT结果，该结果中除空间假频外还包含大量的随机噪音，大大降低了平面波分解的质量；图 9c为图 9a的WMP-LRT结果，该结果不仅压制了常规LRT产生的空间假频，还消除了原始数据中的随机噪音，有效地提高了数据的信噪比；图 9d为图 9c的波形显示图，从该图中可以看出WMP-LRT具有很强的从低信噪比的平面波数据中提取平面波子波的能力，可以比较理想地压制平面波数据中的随机噪音；图 9e是WMP-LRT算法利用高维相关方法计算得到的加权因子W，该加权因子有效地压制了数据中随机噪音对LRT的影响，准确地预测出每个平面波出现的时间和传播方向，为WMP-LRT算法提供一个高信噪比的滤波器；图 9f为WMP-LRT算法从图 9a中消除的噪音，该图几乎只包含随机噪音，不包含任何有效信号，因此WMP-LRT是一种比较理想的平面波数据去噪方法.从该数值实验可知，借助高维相关方法我们可以得到抗噪能力很强的加权因子W，该加权因子准确地预测了每个平面波的出现时间和传播方向，是WMP-LRT算法成功的重要基础.利用加权因子W并结合压缩感知的思想，我们设计了WMP-LRT算法，成功地消除了数据中的随机噪音，并获得了高信噪比、高分辨率的平面波分解结果.

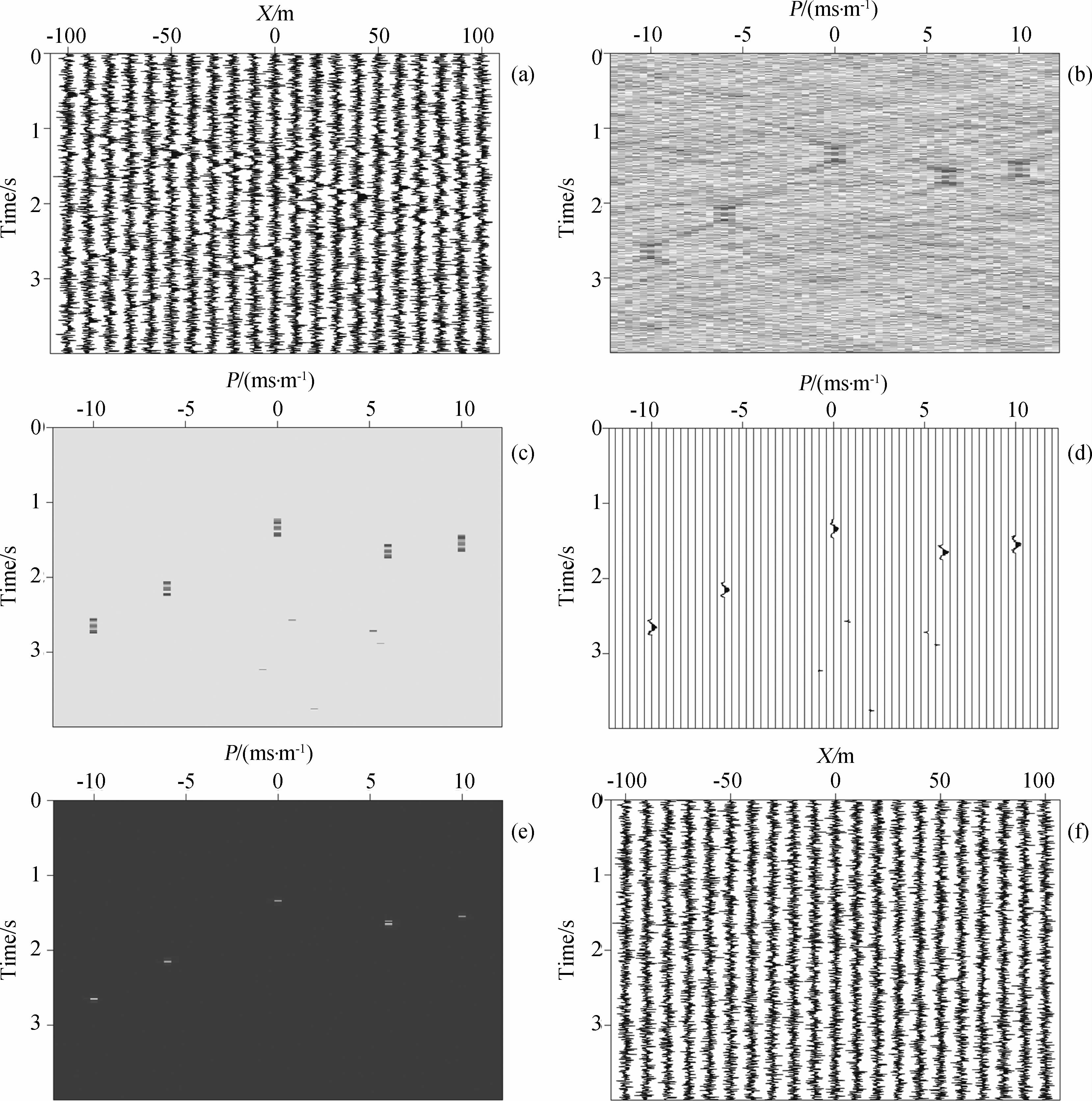图 9 (a)包含大量随机噪音的多平面波合成数据；(b)图(a)的常规LRT结果；(c)图(a)的WMP-LRT结果；(d)图(c)的波形显示图；(e)WMP-LRT算法根据图(b)计算得到的加权因子W ;(f)WMP-LRT算法消除的随机噪音 Fig. 9 (a)Plane-wave data with multi plane waves and a lot of noise;(b)The result of LRT with data in figure(a);(c)The result of WMP-LRT with data in figure(a);(d)The waveform of figure(c);(e)The weighted factor W of data in figure(a);(f)The removed noise with WMP-LRT algorithm

后面的两个数值实验是实际数据的LRT结果与WMP-LRT结果的对比.由于实际地震数据的有效信号只有在局部范围内才满足线性的假设条件，因此对实际数据做平面波分解时需要选择合适的空间窗，使有效信号在该窗内满足线性的假设条件.图 10a为海上某工区CMP道集中的一部分，该部分数据的最大偏移距为940 m，最小偏移距为590 m，道 间距为25 m，总道数为15道，时间采样间隔为5 ms，有效信号在该窗内基本满足线性假设条件.图 10b为图 10a常规LRT的结果.由于受空间窗大小和时间采样方式的影响，图 10b的信噪比和分辨率都很低，获得的平面波分解结果质量比较差.图 10c为图 10a的WMP-LRT结果，该结果消除了图 10b中的各种噪音，并且大大提高了变换结果的分辨率，获得了高质量的平面波分解结果.图 10d是图 10b利用高维相关方法获得的加权因子，该加权因子有效地压制了LRT结果中的各类噪音，准确地预测出实际数据中主要平面波的位置.图 10e是利用WMP-LRT结果重构的CMP道集，该数据重构出图 10a中的各种有效信号，并且很好地保持了平面波原有的子波特征.图 10f是原始数据与重构数据的残差， 为WMP-LRT算法去掉的噪音部分.受浅层强能量 平面波的影响，图 10d中加权因子的能量主要集中 在浅层，在迭代过程中随着浅层数据误差的减小，加权因子的能量分布会发生变化，深层能量所占的比例会越来越大，此时迭代过程会逐渐从以估计浅层强能量的平面波为主过渡到以估计深层弱能量的平面波为主.在图 10中，图 10c相当于公式(9)中的变量w，是WMP-LRT估计的结果，图 10e是利用公式(9)中的d = Tw重构的数据.

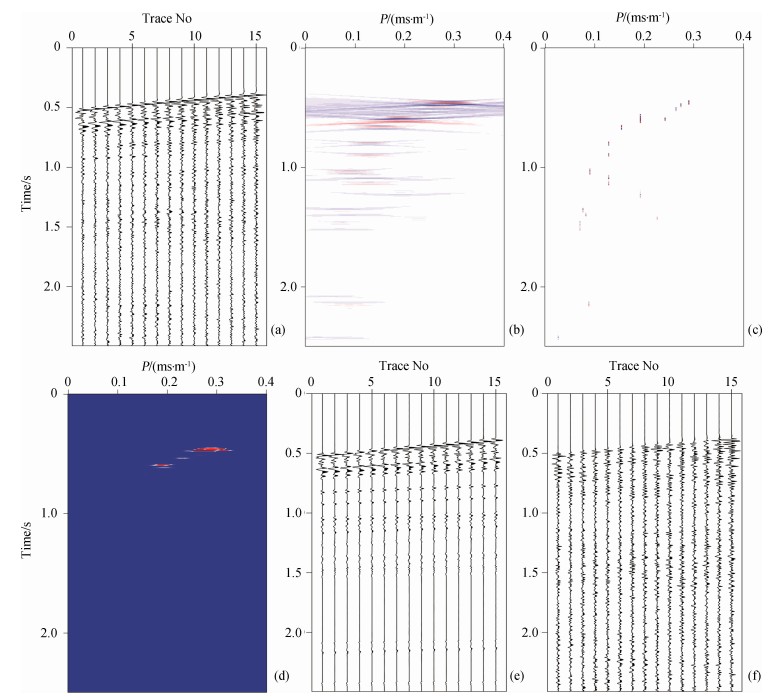图 10 (a)海上某工区的CMP道集，最大偏移距为940m，最小偏移距为590m，道间距为25m，时间采样间隔为5ms；(b)该CMP道集的LRT结果；(c)该CMP道集的WMP-LRT结果；(d)该CMP道集对应的加权因子；(e)利用WMP-LRT结果重构的CMP道集；(f)原始数据与重构数据的残差，WMP-LRT算法去除的随机噪音Fig. 10 (a)The CMP gather of a marine data，the maximum offset is 940 m，minimum offset is 590 m，sample interval of space is 25 m，sample interval of time is 5 micro-second;(b)The LRT result of this CMP gather;(c)The WMP-LRT result of this CMP gather;(d)The weighted factor of this CMP gather;(e)The reconstructed data with WMP-LRT result of this CMP gather;(f)The residual between original data and reconstructed data，it is the removed noise with WMP-LRT algorithm

最后一个数值实验是某实际数据叠前时间偏移结果的LRT和WMP-LRT处理结果的对比.其中图 11a是某实际数据叠前时间偏移结果，由于该剖面中的有效信号只在局部范围内满足线性假设，因此这里先对图 11a中的数据进行分块处理，然后分别对每一小块的数据做LRT和WMP-LRT处理；图 11(b—e)是图 11a中不同空间窗的数据对应的 常规LRT结果，从左到右对应的空间窗的 坐标分别为5.000~5.125 km、10.000~10.125 km、15.000~ 15.125 km、20.000~20.125 km，从这些图可以看出LRT结果经常包含大量的噪音，这些噪音会严重影响平面波分解的分辨率和信噪比；图 11(f—i)是图 11a中不同空间窗的数据对应的WMP-LRT 结果，从左到右对应的空间窗的坐标分别为5.000~ 5.125 km、10.000~10.125 km、15.000~15.125 km、 20.000~20.125 km，从这些图可以看出WMP- LRT算法大大提高了平面波分解结果的稀疏性，改善了平面波分解结果的分辨率和信噪比；图 11(j— m)是图 11a中不同空间窗的数据在WMP-LRT算 法中对应的加权因子，从左到右对应的空间窗的坐标分别为5.000~5.125 km、10.000~10.125 km、15.000~15.125 km、20.000~20.125 km，这些加权因子有效地压制了LRT结果中的各类噪音，并准确地预测了平面波出现的位置，提高了WMP-LRT算法的稳定性；图 11n是利用剖面图 11a的WMP-LRT变换结果及公式(9)中的平波波数据预测算子d = Tw重构的数据.该图说明了WMP-LRT算法不仅改善了平面波分解结果的稀疏性、分辨率和信噪比，而且可以很好地重构原始数据，保证了WMP-LRT算法在正反变换过程中可以保留原始数据中的有效信息.

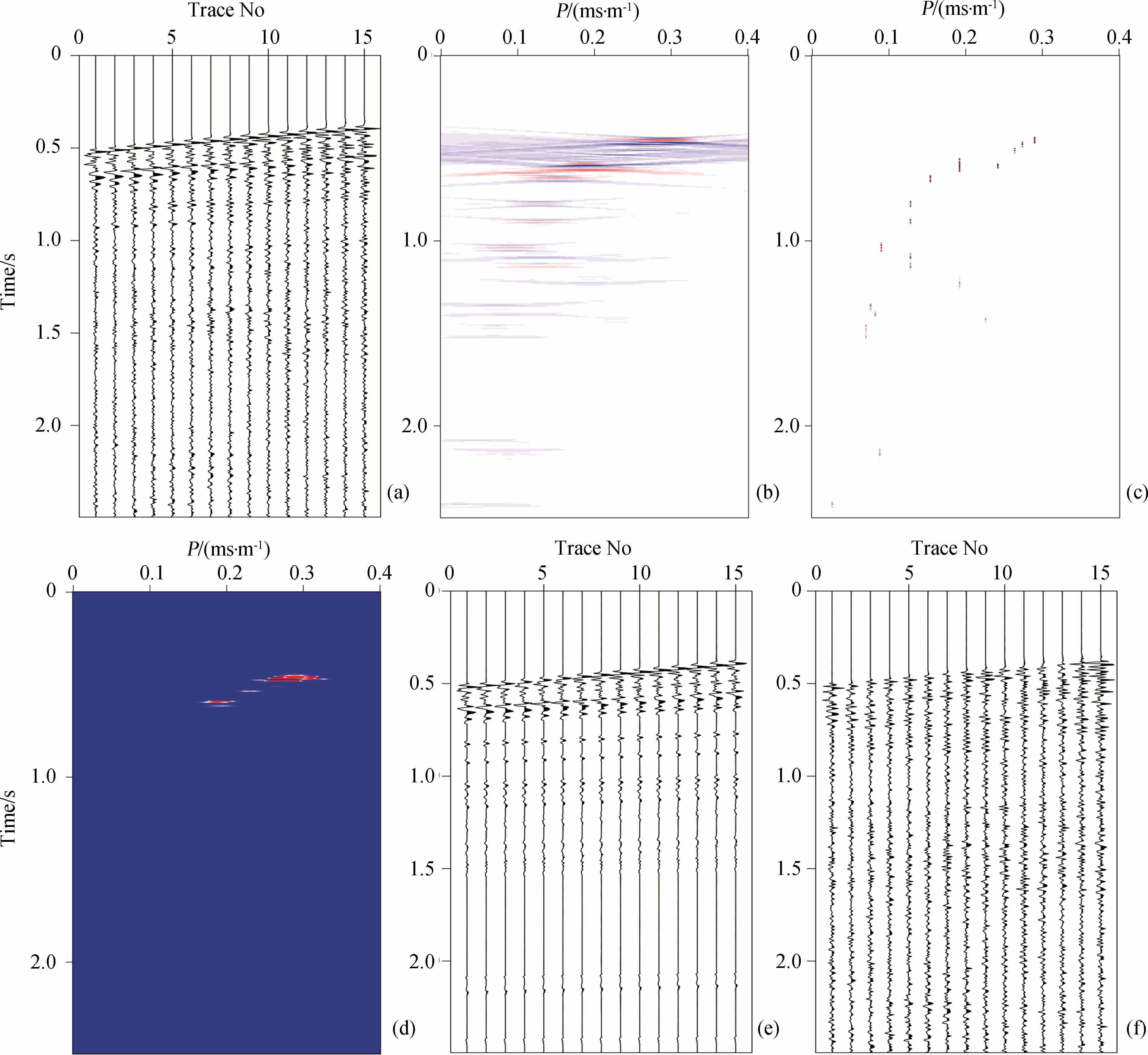图 11(a)某实际数据叠前时间偏移结果；(b)—(e)图(a)中不同空间窗的数据对应的常规LRT结果;(f)—(i)图(a)中不同空间窗的数据对应的WMP-LRT结果；(j)—(m)图(a)中不同空间窗的数据在WMP-LRT算法中对应的加权因子，从左到右对应的空间窗的坐标分别为5.000~5.125 km、10.000~10.125 km、15.000~15.125 km、20.000~20.125 km；(n)利用WMP-LRT变换结果及公式(9)中的d=Tw重构的数据Fig. 11 (a)Some pre-stack time migration profile of field data;(b)—(e)The LRT result of the profile within different space windows;(f)—(i)The WMP-LRT result of the profile within different space windows;(j)—(m)The weight factor of the profile within different space windows in algorithm WMP-LRT，the coordinate of the space windows from left to right are 5.000~5.125 km，10.000~10.125 km，15.000~15.125 km，20.000~20.125 km respectively;(n)The restored data with the result of WMP-LRT and d = Tw informular(9)

从上面的六个数值实验可以看出，WMP-LRT算法成功的一个关键是利用常规LRT结果轴对称的信号特征，并通过高维相关的方法获得高分辨率、高信噪比的加权因子W .该加权因子准确地预测出每个平面波出现的时间和传播方向，压制了常规 LRT结果中各种各样的噪音，提高了WMP-LRT的稳定性及抗噪能力.压缩感知方法的利用是 WMP-LRT算法取得成功的另一个关键.根据压缩 感知的思想，WMP-LRT算法利用结果的稀疏性作为反问题的约束条件，在解空间中寻找稀疏性最好的解作为WMP-LRT的估计结果.压缩感知思想在此处之所以可行是因为平面波数据在线性Radon变换域中是可压缩的，具有很强的稀疏性.平面波数据的该种信号特征保证了WMP-LRT的稀疏约束条件是合理的，因此获得的估计结果与真实解具有很强的相似性.

4 结论与讨论

本文介绍了一种高分辨率、高信噪比的平面波分解方法——WMP-LRT算法，加权因子的构造和压缩感知思想的利用是WMP-LRT算法的核心部分.该算法利用常规LRT结果轴对称的信号特征，通过高维相关的方法构造了一个高信噪比的加权因子W .加权因子W不仅可以压制常规LRT结果中的各类噪音，还能压制平面波数据中的随机噪音，准确地预测出平面波数据中每个平面波出现的时间和传播方向，提高了WMP-LRT算法的抗噪能力，保证了WMP-LRT算法的稳定性和其结果的高信噪比.在提高分辨率方面，WMP-LRT算法利用了压缩感知的思想，将结果的稀疏性作为反问题的约束条件.该约束条件表明WMP-LRT算法以寻找反问题最稀疏的解为目标，保证WMP-LRT算法可以获得一个高分辨率的结果.

另外，由于加权因子W可以准确地预测平面波数据中每个平面波的相关参数，因此可以利用W获得成像剖面上高信噪比的地层倾角信息.提高信噪比后的地层倾角信息可以用在反射层析、RTM角道集生成等地震资料处理技术上，以改善这些技术方法的处理结果.

参考文献
[1] Beylkin G. 1987. Discrete radon transform. IEEE Transactions on Acoustics, Speech and Signal Processing, 35(2): 162-172.
[2] Capon J. 1969. High-resolution frequency-wavenumber spectrum analysis. Proceedings of the IEEE, 57(8): 1408-1418.
[3] Cary P W. 1998. The simplest discrete Radon transform. 1998 SEG Annual Meeting, Society of Exploration Geophysicists: 1999-2002.
[4] Chen L, Wu R S, Wang W J. 2004. Common angle image gathers obtained from gabor-daubechies beamlet prestack depth migration. Chinese J. Geophys. (in Chinese), 2004, 47(5): 876-885.
[5] Chen S C, Cao J Z, Ma Z T. 2003. A method of plane wave depth migration for pre-stack seismic data. Chinese J. Geophys. (in Chinese), 46(6): 821-826.
[6] Feng B, Wang H Z. 2011. 3D offset plane-wave finite-difference pre-stack time migration. Chinese J. Geophys. (in Chinese), 54(11): 2916-2925.
[7] Gao F, Zhang P, Wang B, et al. 2006. Fast Beam migration-a step toward interactive imaging. 2006 SEG Annual Meeting, Society of Exploration Geophysicists: 2470-2473.
[8] Hampson D. 1986. Inverse velocity stacking for multiple elimination. 1986 SEG Annual Meeting, Society of Exploration Geophysicists: 44-55.
[9] Herrmann P, Mojesky T, Magesan M. 2000. Amplitude Preserving Radon Demultiple. Offshore Technology Conference: OTC-12008-MS.
[10] Hu J, Wang X, Wang H. 2012. Beam Forming by Least Square Inversion with Radon Spectrum Constraints. 2012 SEG Annual Meeting, Society of Exploration Geophysicists: PAPR1140.
[11] Hu T Y, Hong F, Wang R Q, et al. 2002. Multiple attenuation using beamforming onshore and offshore China. The Leading Edge, 21(9): 906-910.
[12] Ma B, Wang H Z. 2011. 3D offset plane-wave finite-difference pre-stack time migration. Chinese Journal of Geophysics (in Chinese), 54(11): 2916-2925.
[13] Özbek A. 2000. Adaptive beamforming with generalized linear constraints. 2000 SEG Annual Meeting, Society of Exploration Geophysicists: 2081-2084.
[14] Sacchi M D, Ulrych T J. 1995. High-resolution velocity gathers and offset space reconstruction. Geophysics, 60(4): 1169-1177.
[15] Thorson J R, Claerbout J F. 1985. Velocity-stack and slant-stack stochastic inversion. Geophysics, 50(12): 2727-2741.
[16] Wang X, Wang H Z, Zhou D H, et al. 2011. Minimizing Ellipsoidal Norm Seismic Data Interpolation with Radon Spectrum Constraints. 73rd EAGE Conference & Exhibition: A046.
[17] 陈凌,吴如山,王伟君.2004.基于Gabor Daubechies小波束叠前深度偏移的角度域共成像道集.地球物理学报,47(5):876-885.
[18] 陈生昌,曹景忠,马在田.2003.叠前地震数据的平面波深度偏移法.地球物理学报,46(6):821-826.
[19] 冯波,王华忠.2011.三维偏移距平面波有限差分叠前时间偏移.地球物理学报,54(11):2916-2925.