Radon变换在地震数据处理中有着广泛的应用,诸如多次波衰减(Wang,2003; Schonewille and Aaron, 2007;熊登,2009)、噪声压制(巩向博等,2009)、波场分离(曾有良等,2007;冯晅等,2011)、数据重建(王维红等,2006;王维红等,2007)、速度频散分析(潘冬明等,2010)、偏移成像(黄新武等,2004)等.根据研究问题的特点和需要,Radon变换可以派生出灵活多样的形式,根据积分路径的不同产生多种变换方式,如线性Radon变换(τ-p变换)、抛物Radon变换、双曲Radon变换、多项式Radon变换(牛滨华等,2001)等.根据物理场的不同,可以选择合理的变换方法,以达到最佳解决问题的途径.
Radon域内信号与噪声能量越集中,其信噪分离能力越好.对于水平均匀层状介质来说,常规Radon变换中,双曲Radon变换分辨率最高,在海上多次波压制中也有较多的应用.但真实地下介质是各向异性的,在不同方向上,波场的传播特征、能量的分配是不同的,常见的水平各向同性介质(VTI)下,反射波同相轴已经不是双曲线,而是与各向异性参数相关的非双曲同相轴;另外,对于长偏移距地震数据,即使地下为各向同性水平层状均匀介质,随着偏移距的增大,反射同相轴也呈现非双曲线形态.在这两种情况下,双曲Radon变换已经不能保证反射波能量非常收敛,对于后续的信号与噪声的分离有时就无能为力.
为克服上述难题,我们在Radon变换的积分路径上考虑了非双曲走时影响,引入各向异性介质中非椭圆率η参数,积分路径由原先的偏移距、慢度两参数控制改为由偏移距、慢度、非椭圆率三参数控制,新的变换公式可以精确刻画VTI介质以及长偏移距下地震数据的走时路径,沿此路径进行Radon正反变换,我们称之为各向异性Radon变换(Gong et al., 2013).各向异性和长偏移距的引起的非双曲现象数学表达相同而物理意义不同,故名称可理解为“各向异性介质条件下的Radon变换”,也可理解为“各向异性参数控制下的Radon变换”.
离散求解各向异性Radon变换与双曲Radon变换类似,由于其时变特征,频率分量不能解耦,若直接在时间域采用Sacchi的策略,利用Radon变换的稀疏解来提高Radon变换域分辨率方法,其算子矩阵过大会导致计算量剧增,使其实用性大为降低(Beylkin,1987; Sacchi and Ulrych, 1995; Trad et al., 2002).Ng和Rerz提出的Gauss-Seidel方案为时变积分路径提供了极好的思路(Ng and Perz, 2004; Wang et al., 2010).这种方法对符合积分路径的能量强加权累加,然而不符合积分路径的能量弱加权弱化,通过几次迭代累加后,获得时间域分辨率极高的结果.我们在此算法基础上加入各向异性的相似系数加权函数,突出最大各向异性相似系数下的积分路径能量,使用前次变换结果作为先验信息,避免采用共轭梯度算法的多次迭代计算,正反离散变换并未花费很大的计算量,同时得到很高的时空分辨率.
对于深层陡倾角的成像来说,长偏移距的地震信息十分关键.针对此问题,本文提出各向异性Radon变换,并对模型地震数据与长偏移距海上地震数据的多次波衰减进行处理,计算表明此方法有着很高的分辨率,可以有效的压制多次波,并具有较高的计算效率.
2 各向异性Radon变换 2.1 非双曲时差公式任意水平层状介质模型反射波走时方程可由级数展开,得到的方程是层厚、层速度、偏移距2阶、4阶、6阶等有关的复杂函数.当偏移距较小时(即排列长度小于反射界面深度),可忽略偏移距四阶及其更高项,从而简化为双曲线方程.但对于VTI介质以及较大偏移距的地震数据,其走时方程并不能用简单双曲线方程表示.
对于非双曲时距曲线的逼近,我们并未采用精度最高的VTI方程,因为精度虽高但其复杂性大大增加,增加了求解的难度,权衡计算结果的精度与效率,我们采用了Alkhalifah提出的非双曲时差公式,其偏移距最高4阶,射线慢度参数2阶,并引入各向异性参数η,以逼近VTI介质及长偏移距下的准确走时.
Alkhalifah等提出了非双曲线时差公式为(Alkhalifah and Tsvankin, 1995)
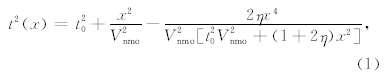
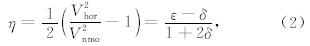
常规线性离散Radon正变换公式可定义为
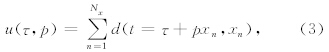
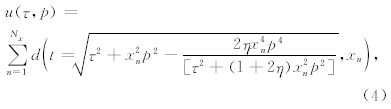
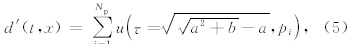
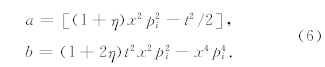
各向异性Radon正反变换形式上虽复杂,但究其本变换过程还是沿曲线进行积分,t-x域的一条曲线对应Radon域内的一个点,t仍对应截距时间τ,变换曲线由常规Radon变换的偏移距、慢度两参数控制,转变为偏移距、慢度、非椭圆率η三参数控制.而增加η参数后离散计算矩阵维数、大小未变,时间域求解时,计算量与双曲Radon变换相当,而非双曲积分路径的精度由高阶偏移距与η参数控制.
2.3 各向异性Radon变换离散求解基于反演理论的Radon变换,先定义反变换,从反变换导出正变换,可以在Radon域内得到分辨率更高的结果.各向异性Radon反变换公式(5)离散化,写成矩阵形式 d ′= Lm,其中算子 L 为各向异性Radon反变换算子,即公式(4)定义的积分路径,其物理意义将Radon域内的一个点变换到时空域内由x、p、η控制的一条曲线.Radon正变换算子为 L T,其物理意义将t-x域内由x、p、η控制的曲线变为Radon域内的一个点.采用最小二乘反演求解,并加入权系数矩阵 W m提高求解的分辨率,得到公式为
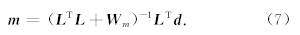
加入控制非双曲积分路径的各向异性参数η,Radon正反变换算子由两参数控制变为三参数控制.从形式上看,各向异性Radon变换要比常规Radon变换要复杂很多,实际上它和时变Radon变换计算过程一致,算子矩阵的维数均与常规Radon变换相同.
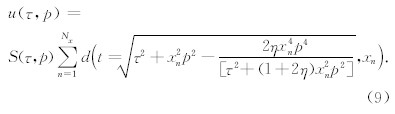
2.4 最优相似系数加权Gauss-Seidel迭代算法为了得到高分辨率的变换结果,我们采用相似 系数加权的Radon变换,其相似系数加权函数定义为

由于公式(7)中算子 L 与其逆算子 L T并不是时变的,不能在频率域求解,基于Sacchi贝叶斯原理的高分辨率求解,往往采用共轭梯度算法实现,需要进行多次稀疏约束迭代,共轭梯度算法本身还需多次迭代以进行最优化反演求解,未压缩前的算子矩阵维数为(nt×nx)×(nτ×np),计算量会随着数据增大成倍增长,计算效率很低.
为了更具有实用性,节约计算量,我们从公式(9)出发,采用最优相似系数加权Gauss-Seidel迭代算法的各向异性Radon变换,此算法利用以前的变换作为先验信息,按照相似系数加权函数计算值大小对离散p值进行排序,最显著能量的p值积分首先计算,当次p轨迹计算后相应的减掉t-x域内积分路径的能量,当前的变换结果可以成为新p轨迹估计的初步结果,随着p轨迹路径积分,t-x域内能量不断衰减,直到所有p值计算完毕.此算法偏重计算最初p轨迹的积分路径能量,确保初始最显著的p轨迹参与叠加计算,因此它会包含这个路径中最强的能量,故得到能量收敛的Radon域变换结果.这样仅用几次迭代过程就可以得到Radon域内很高的分辨率,并且计算量会大为节约.
基于Gauss-Seidel迭代方式的相似系数加权各向异性Radon变换流程如图 1所示,在各向异性 Radon变换时,相似系数加权函数将由非双曲线时差曲线t(t′0,p,η,x)定义,即按公式(9)计算,变换流程可分三个步骤进行:
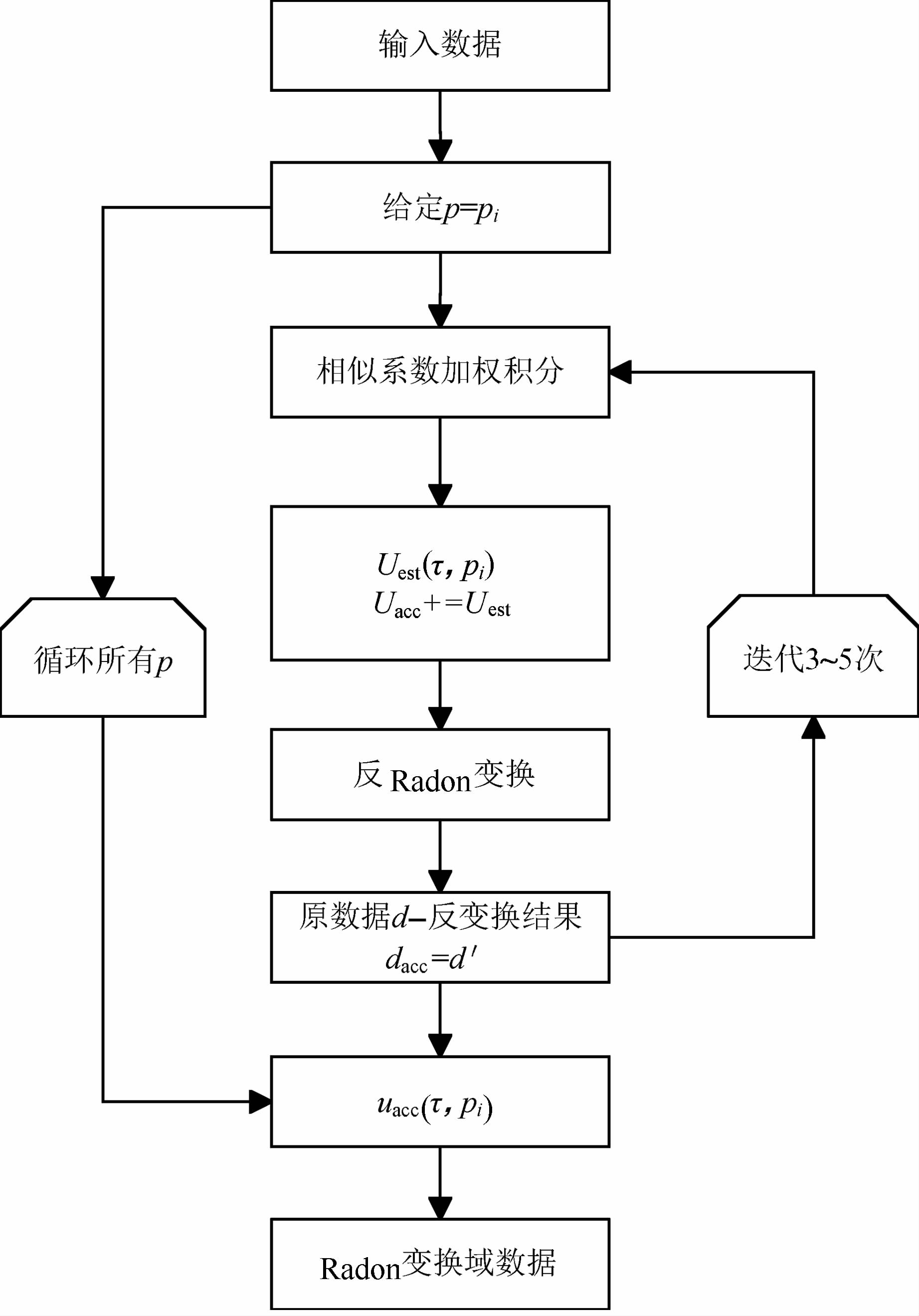 | 图 1 相似系数加权Gauss-Seidel迭代算法的Radon变换流程图Fig. 1 Flowchart of the anisotropic Radon transform with semblance weighting Gauss-Seidel algorithm |
(1)计算当前慢度pi相似系数加权函数,计算当前慢度积分的Radon域内结果uest(τ,pi),并将每次慢度积分结果累加到uacc(τ,pi)之中;
(2)将uacc(τ,pi)做反变换得到dacc,原数据d减掉dacc得到d′,以d′为输入数据,按照步骤(1)累加相似系数加权pi积分路径能量,通常3~5次迭代就可以使t-x域剩余能量降到可接受的水平,即计算完成一次慢度pi积分;
(3)按照步(1)和步(2)的过程,循环所有慢度p的积分,并累加能量至uacc(τ,pi),构成Radon变换域最终结果.
3 实例计算 3.1 各向异性介质模型建立如下的各向异性介质模型,模型参数如表 1 所示,模拟数据为200道数据,偏移距范围为0~4000 m,分别用抛物、双曲与各向异性Radon变换进行正变换,得到的Radon域内数据如图 2,图 2a为VTI介质单炮记录,其中一次波的零偏移距t0分别为0.4 s、0.64 s、0.86 s,多次波零偏移距t0为0.8 s、1.2 s、1.28 s、1.72 s、1.92 s;图 2b为抛物Radon正变换结果,非双曲走时的同相轴经抛物Radon变换之后,能量并不收敛,有明显的拖尾现象;图 2c为双曲Radon正变换结果,Radon域内能量已经收敛较好,但仔细观察细节,能量团仍不集中,能量最强的中心位置两侧有一定的能量延伸;图 2d为各向异性Radon正变换结果,从图中可看到,经各向异性Radon正变换后,变换域内能量收敛几乎与模拟时的子波相同,结果有着极高的分辨率,设置图 2d白线所示的切除线,白线之上为一次波能量,之下为多次波能量;图 2e为在各向异性Radon域内切除多次波后反变换结果,得到的一次波的记录;图 2f为在各向异性Radon域内切除一次波后反变换结果,得到的多次波的记录,可见通过各向异性Radon变换,多次波与一次波可明显分离,且原道集同相轴的振幅保持很好.对比抛物、双曲与各向异性Radon变换的计算效率,环境为Intel Core2,主频2 GHz,Intel C++ Compiler XE 12.1.2.278并行编译器,三者计算时间分别为1.2 s、8.5 s、9.1 s,可见各向异性Radon变换计算量与双曲Radon变 换相当,采用相似系数加权的Gauss-Seidel迭代算法计算效率较高.
| 表 1 各向异性模型参数表格Table 1 Parameters of the anisotropic model |
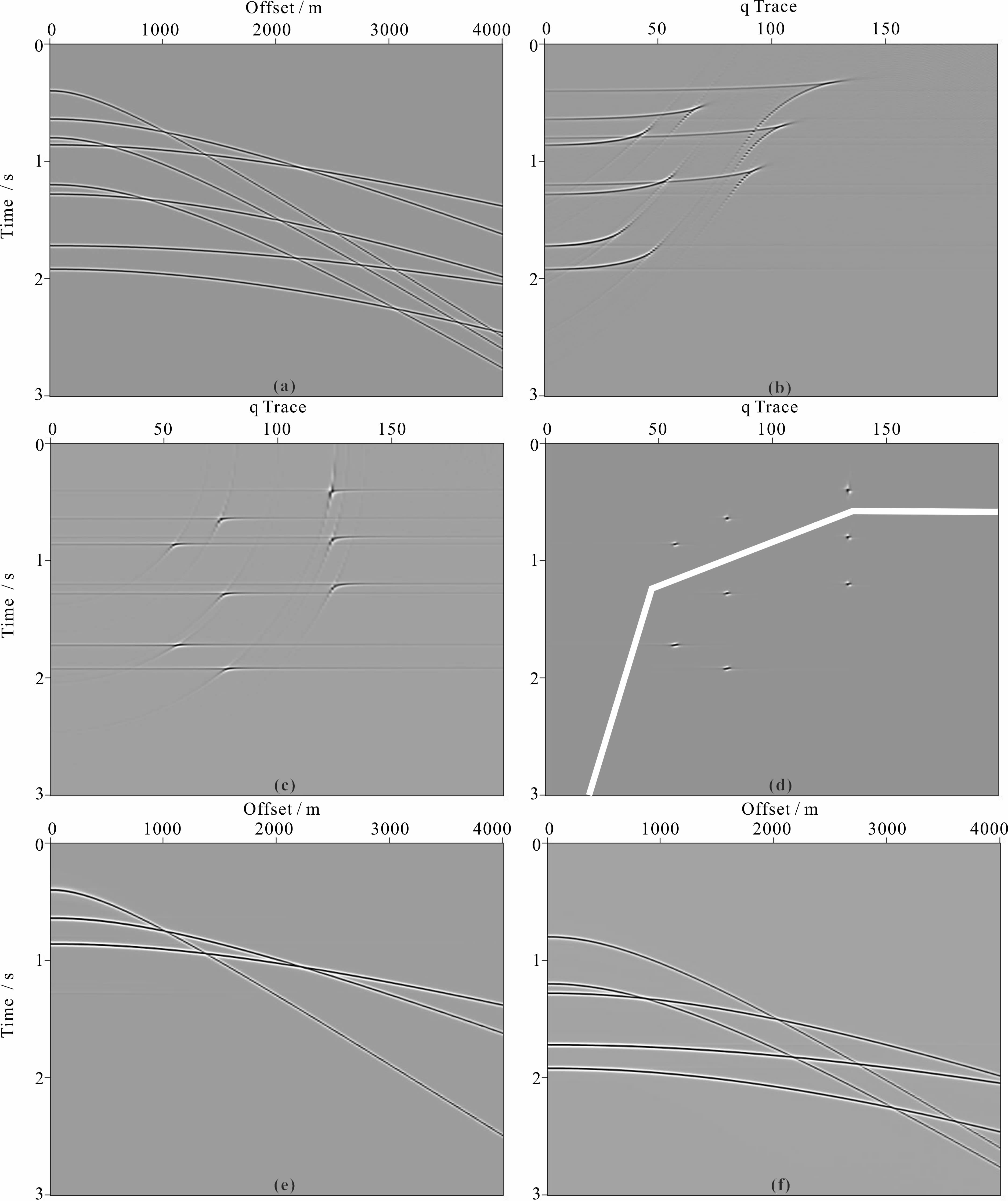 | 图 2 各向异性介质模型Radon域结果(a)VTI介质模型数值模拟记录;(b)抛物Radon正变换结果;(c)双曲Radon正变换结果;(d)各向异性Radon正变换结果;(e)分离的一次波道集;(f)分离的多次波道集.Fig. 2 Results of Radon domain of the anisotropic model(a)Simulated data of the VTI model;(b)Result of parabolic radon transform;(c)Result of hyperbolic radon transform; (d)Result of anisotropic radon transform;(e)Primary gather;(f)Multiples gather. |
由于Radon变换非正交性,其正反变换过程存在振幅损失,但基于2.3节的最小二乘反演算法可较好地恢复原信号.本文对比了模型数据在抛物、双曲与各向异性Radon正反变换的数据振幅特征,并通过式(10)计算振幅失真度,公式为
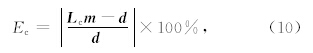
以海上长偏移距地震数据为例进行各向异性Radon变换的应用.图 4a为海上地震数据,采样率 为2 ms,采样长度为12 s,其最大偏移距可达8287 m,浅层的反射走时已不能用双曲时距曲线表示,尤其当偏移距深度比大于1时.从图中可以看出,在3 s以下的反射波能量基本上已经被多次波能量所淹没,若不进行多次波压制,深层的地下构造无法还原.图中用红色箭头标识一次波,黑色箭头标识多次波.
各向异性Radon变换时,首先对当前道集进行双参数速度分析,同时给出动校正速度与η参数,每个拾取能量团(走时同相轴叠加)对应一对动校正速度与η参数,即η参数个数与拾取的同相轴个数相同,我们将η参数沿时间方向进行线性插值,这样在每个离散时间采样上均对应一个η数值.图 3为当前道集进行双参数速度分析并插值后的η参数曲线.需注意的是,η参数的正确性对于各向异性Radon变换分辨率影响较大,不准的η参数导致非双曲走时路径与实际不符,难以达到反射波能量的累加聚焦,导致有效信号不易从多次波能量中进行分离.为了保证η参数的准确,在压制多次波的过程中,我们进行多次双参数速度谱扫描,最终得到准确的η参数.
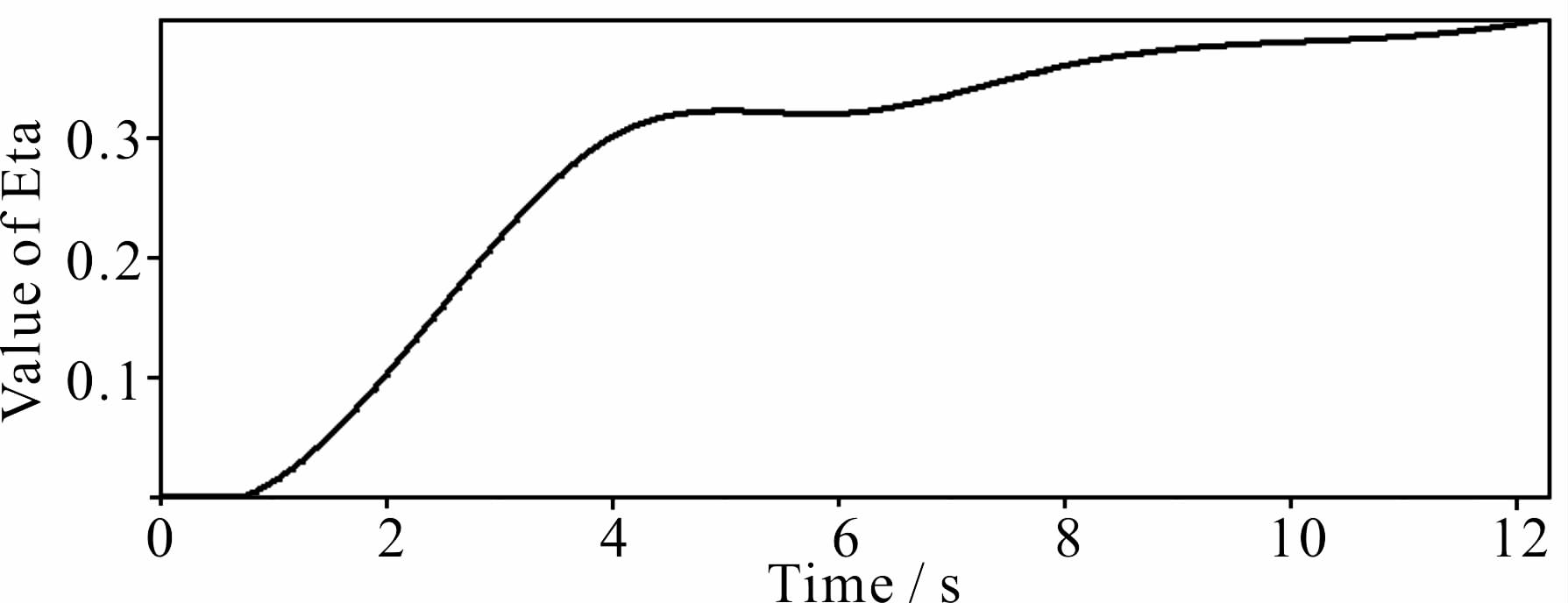 | 图 3 双参数速度分析得到的η参数曲线(a)海上原始记录,最大偏移距可达8287 m;(b)双曲Radon正变换结果;(c)各向异性Radon正变换结果及切除线;(d)(b)图白框所示范围细节放大图;(e)(c)图白框所示范围细节放大图;(f)双曲Radon变换压制多次波后的一次波数据;(g)各向异性Radon变换压制多次波后的一次波数据;(h)(a)图白框所示范围细节放大图;(i)(f)图白框所示范围细节放大图;(j)(g)图白框所示范围细节放大图.Fig. 3 Curve of η by dual-parameter velocity analysis and interpolation |
本文对比常规双曲Radon变换与各向异性Radon变换,其Radon域内变换结果分别如图 4b和图 4c,由于采用了非双曲相似系数加权的高分辨 率Gauss-Seidel迭代算法(2.4节),各向异性Radon 域内有效波与多次波能量相比于常规双曲Radon变换聚焦更好并已得到了有效的分离,见红色箭头所示的一次波与黑色箭头所示的多次波,将图 4b和图 4c中白框所示范围放大得到图 4d和图 4e,细节上对比各向异性Radon域比常规双曲Radon变换能量更为集中,便于设置切除线.设置如图 4b和图 4c所示的切除线,将切除线下方多次波的能量进行切除,反Radon变换后的结果如图 4f和图 4g,与原数据相比,多次波能量压制的很好,大偏移距处一次波的信号并未损失,变换后的地震剖面的信噪比得到了较大的提高.图 4h、4i、4j分别对应图 4a、4f、4g 中白框所示的细节放大图,观测道集波场的细节,双曲Radon变换与各向异性Radon变换均对多次波有较好的衰减,而后者对一次波能量有更好的保护.
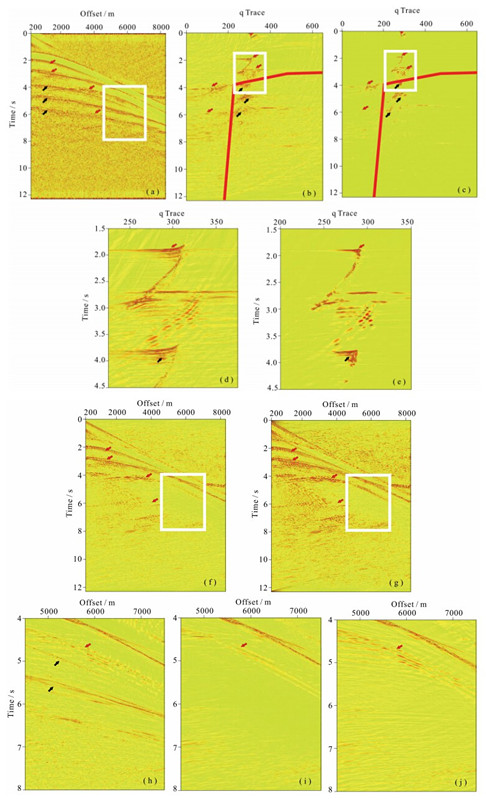 | 图 4 海上长偏移距数据多次波压制实例Fig. 4 Demultiple example of large offset marine data(a)Original gather with the maximum offset of 8287m;(b)Result of hyperbolic radon transform;(c)Result of anisotropic radon transform and cutting line;(d)Zoom of the white frame of(b);(e)Zoom of the white frame of(c);(f)Primary reflection after demultiple of hyperbolic radon transform;(g)Primary reflection after demultiple of anisotropic radon transform;(h)Zoom of the white frame of(a);(i)Zoom in on the white frame of(f);(j)Zoom of the white frame of(g). |
图 5是压制多次波前后的速度谱分析图,图 5a是原始记录的速度谱,1500m/s速度附近沿时间轴多次波的能量团十分明显,表现为速度相同时间等倍数一串相似的能量团;图 5b是各向异性Radon变换衰减掉多次波后一次波的速度谱,图 5a中时间大于4 s多次波的低速度能量团已经消失,在高速度范围出现速度谱能量团,也就是说深层的高速反射同相轴经过多次波压制后可以得到分辨.
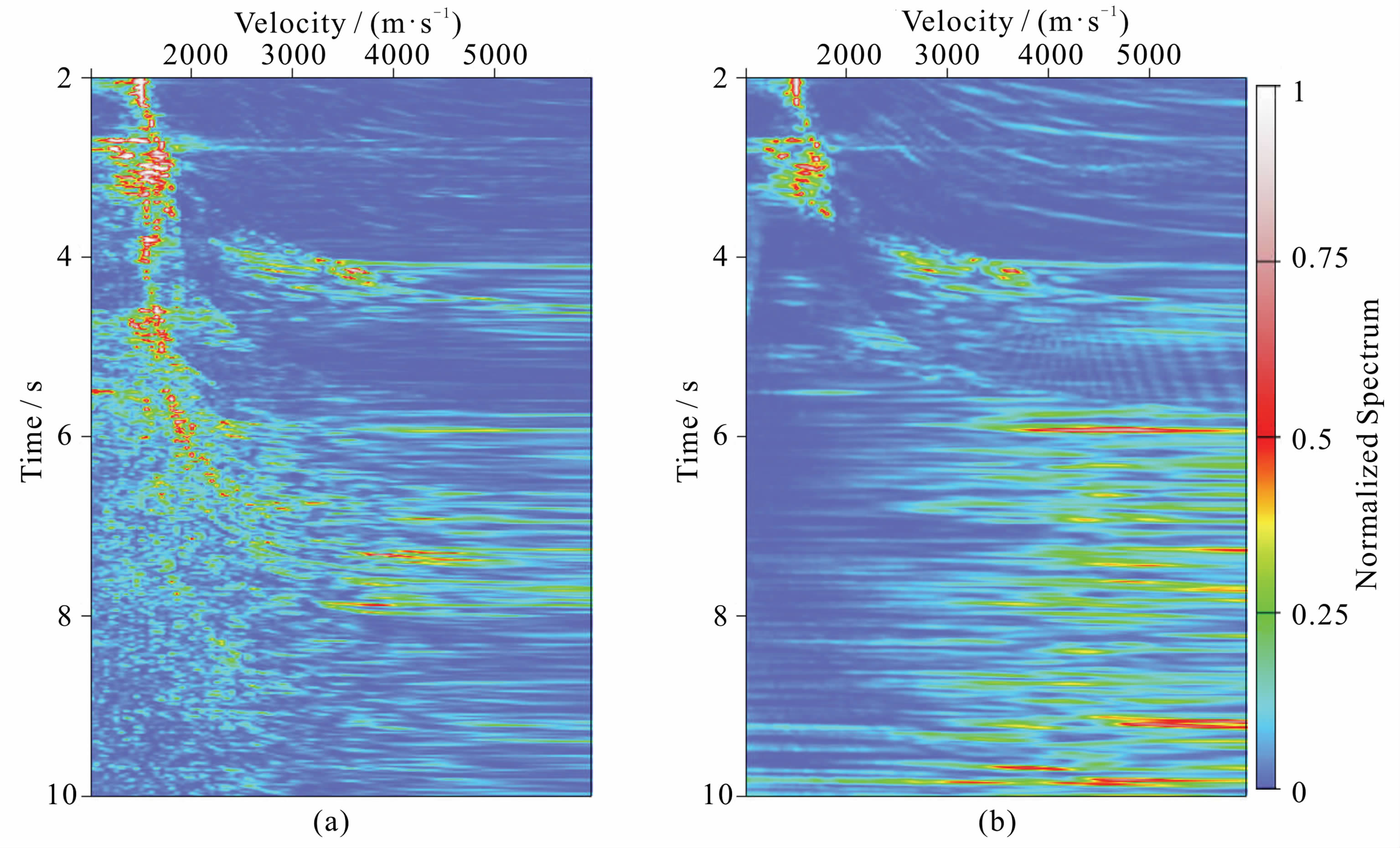 | 图 5 压制多次波前后速度谱分析图(a)原始记录的速度谱;(b)各向异性Radon变换衰减多次波后速度谱.Fig. 5 Comparison of velocity spectra(a)Velocity spectrum of original gather;(b)Velocity spectrum of primary after anisotropic Radon transform demultiple. |
在Radon变换积分路径中加入各向异性参数后,得到由偏移距、慢度、非椭圆率三参数控制的积分曲线,即各向异性Radon变换.本文推导了各向异性Radon变换的正反公式,并采用了最优相似系数加权的Gauss-Seidel迭代算法进行了高分辨率的求解,避免了时间域稀疏脉冲迭代反演中的大矩阵运算,保持很高的精度的同时,提高了计算效率.
各向异性Radon变换处理前,需进行双参数的速度扫描,以选择最佳的非椭圆率η值,离散计算每个t时刻需对应一个η值,其值的选择对于Radon域内的分辨率影响较大,应选择最佳动校正速度下时的η值.
长偏移距的海上地震数据在各向异性Radon变换后,其Radon域内分辨率明显提高,即使有较小时差存在,有效反射信号与多次反射波能量也可以很好的分离,保留了大偏移距的有效反射信息,对于地下深层陡倾角的成像提供了保幅的预处理数据体.
| [1] | Abbad B, Ursin B, Rappin D. 2009. Automatic nonhyperbolic velocity analysis. Geophysics, 74(2): U1-U12. |
| [2] | Alkhalifah T, Tsvankin I. 1995. Velocity analysis for transversely isotropic media. Geophysics, 60(5): 1550-1566. |
| [3] | Beylkin G. 1987. Discrete radon transform. IEEE Transactions on Acoustics, Speech, and Signal Processing, 35(2): 162-712. |
| [4] | Feng X, Zhang X W, Liu C, et al. 2011. Separating P-P and P-SV wave by parabolic Radon transform with multiple coherence. Chinese J. Geophys. (in Chinese), 54(2): 304-309,doi: 10.3969/j.issn.0001-5733.2011.02.005. |
| [5] | Gong X B, Han L G, Wang E L, et al. 2009. Denoising via high resolution Radon transform. Journal of Jilin University(Earth Science Edition) (in Chinese), 39(1): 152-157. |
| [6] | Gong X B, Lv Q T, Han L G. 2013. Anisotropic Radon transform.//75th EAGE Conference & Exhibition Extended Abstracts. |
| [7] | Huang X W, Wu L, Song W. 2004. 3D Pre-Stack depth migration with radon projection. Chinese J. Geophys. (in Chinese), 47(2): 321-326. |
| [8] | Ng M, Perz M. 2004. High resolution Radon transform in the t-x domain using "intelligent" prioritization of the Gauss-Seidel estimation sequence.//74th Ann. Internat Mtg., Soc. Expi. Geophys.. Expanded Abstracts, 2160-2163. |
| [9] | Niu B H, Sun C Y, Zhang Z J, et al. 2001. Polynomial Radon transform. Chinese J. Geophys.(in Chinese), 44(2): 263-271. |
| [10] | Pan D M, Hu M S, Cui R F, et al. 2010. Dispersion analysis of Rayleigh surface waves and application based on Radon transform. Chinese J. Geophys. (in Chinese), 53(11): 2760-2766, doi:10.3969/j.issn.0001-5733.2010.11.025. |
| [11] | Sacchi M D, Ulrych T J. 1995. High-resolution velocity gathers and offset space reconstruction. Geophysics, 60(4): 1169-1177. |
| [12] | Schonewille M A, Aaron P A. 2007. Applications of time-domain high-resolution Radon demultiple.//77th Ann. Internat Mtg., SEG Technical Program Expanded Abstracts, 2565-2569. |
| [13] | Trad D O, Ulrych T J, Sacchi M D. 2002. Accurate interpolation with high-resolution time-variant Radon transforms. Geophysics, 67(2): 644-656. |
| [14] | Wang J F, Ng M, Perz M. 2010. Seismic data interpolation by greedy local Radon transform. Geophysics, 75(6): WB225-WB234. |
| [15] | Wang W H, Shou H, Liu H, et al. 2006. High resolution τ-ρ transform in linear events wavefield separation. Progress in Geophysics (in Chinese), 21(1): 74-78. |
| [16] | Wang W H, Pei J Y, Zhang J F. 2007. Prestack seismic data reconstruction using weighted parabolic Radon transform. Chinese J. Geophys. (in Chinese), 50(3): 851-859. |
| [17] | Wang Y H. 2003. Multiple attenuation: Coping with the spatial truncation effect in the Radon transform domain. Geophysical Prospecting, 51(1): 75-87. |
| [18] | Xiong D, Zhao W, Zhang J F. 2009. Hybrid-domain high-resolution parabolic Radon transform and its application to demultiple. Chinese J. Geophys. (in Chinese), 52(4): 1068-1077. |
| [19] | Zeng Y L, Le Y S, Shan Q T, et al. 2007. VSP wavefield separation based on high-resolution Radon transformation. Geophysical Prospecting for Petroleum (in Chinese), 46(2): 115-119, 173. |
| [20] | 冯晅, 张先武, 刘财等. 2011. 带有多道相关的抛物线Radon变换法分离P-P、P-SV 波. 地球物理学报, 54(2): 304-309 ,doi: 10.3969/j.issn.0001-5733.2011.02.005. |
| [21] | 巩向博, 韩立国, 王恩利等. 2009. 压制噪声的高分辨率Radon变换法. 吉林大学学报(地球科学版), 39(1): 152-157. |
| [22] | 黄新武, 吴律, 宋炜. 2004. 拉东投影法三维叠前深度偏移. 地球物理学报, 47(2): 321-326. |
| [23] | 牛滨华, 孙春岩, 张中杰等. 2001. 多项式Radon变换. 地球物理学报, 44(2): 263-271. |
| [24] | 潘冬明, 胡明顺, 崔若飞等. 2010. 基于拉东变换的瑞雷面波频散分析与应用. 地球物理学报, 53(11): 2760-2766, doi:10.3969/j.issn.0001-5733.2010.11.025. |
| [25] | 王维红, 首皓, 刘洪等. 2006. 线性同相轴波场分离的高分辨率τ-ρ变换法. 地球物理学进展, 21(1): 74-78. |
| [26] | 王维红, 裴江云, 张剑锋. 2007. 加权抛物Radon 变换叠前地震数据重建. 地球物理学报, 50(3): 851-859. |
| [27] | 熊登, 赵伟, 张剑锋. 2009. 混合域高分辨率抛物Radon变换及在衰减多次波中的应用. 地球物理学报, 52(4): 1068-1077. |
| [28] | 曾有良, 乐友善, 单启铜等. 2007. 基于高分辨率Radon变换的VSP波场分离方法. 石油物探, 46(2): 115-119, 173. |
 2014, Vol. 57
2014, Vol. 57

