地球物理学报  2014, Vol. 57 Issue (9): 2918-2927   PDF    
引用本文
唐欢欢, 毛伟建. 2014. 3D高阶抛物Radon变换地震数据保幅重建. 地球物理学报, 57(9): 2918-2927, doi: 10.6038/cjg20140917   
TANG Huan-Huan, MAO Wei-Jian. 2014. Amplitude preserved seismic data reconstruction by 3D high-order parabolic Radon transform. Chinese J. Geophysics, 57(9): 2918-2927, doi: 10.6038/cjg20140917   
3D高阶抛物Radon变换地震数据保幅重建
唐欢欢1,2, 毛伟建1,2    
1. 中国科学院测量与地球物理研究所计算与勘探地球物理研究中心, 武汉 430077;
2. 大地测量与地球动力学国家重点实验室, 武汉 430077
投稿时间:2013-10-30    最后修改时间: 2014-8-1 .
基金项目：中国科学院创新启动基金（Y203701070，Y209131013），国家自然科学基金（41474120）联合资助.
作者简介：唐欢欢，女，1987年生，中国石油大学（北京）地球探测与信息技术专业硕士，主要从事地震数据重建及地震数据处理相关工作.E-mail：tanghuan@whigg.ac.cn
通讯作者：毛伟建，男，研究员，博士生导师，主要从事地震数据处理、成像和反演研究.E-mail：wjmao@whigg.ac.cn
摘要：本文结合传统3D抛物Radon变换（PRT）和AVO数据正交多项式拟合，给出了3D高阶抛物Radon变换方法（HOPRT）.该变换增加了描述AVO数据变化的梯度信息和曲率信息，拓展了传统3D抛物Radon变换方法，使其在具有AVO特征的数据重建中具有更高的准确度，从而提高AVO分析的可靠性.文中给出了3D高阶抛物Radon变换进行地震数据保幅重建的流程.理论模型和实际地震资料的重建结果显示了本文方法的优点.
关键词： 3D高阶Radon变换     AVO数据     保幅重建    
Amplitude preserved seismic data reconstruction by 3D high-order parabolic Radon transform
TANG Huan-Huan1,2, MAO Wei-Jian1,2    
1. Center for Computational & Exploration Geophysics, Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China;
2. State Key Laboratory of Geodesy and Earth's Dynamics, Wuhan 430077, China
Abstract: 3D high-order parabolic Radon transform (HOPRT) method for amplitude preserving reconstruction is proposed on the basis of the traditional 3D parabolic Radon transform and orthogonal polynomial fitting techniques. The information on the amplitude and its gradient and curvature of the AVO data are taken into account in the 3D parabolic Radon transform, which makes the proposed method have higher accuracy for AVO data. We present a workflow for seismic data reconstruction with amplitude preserved by the method of HOPRT. The results of the synthetic model and the field data demonstrate the effectiveness of the method.
Key words: 3D high-order Radon transform     AVO data     Amplitude preserved reconstruction    
1 引言

地震数据采集过程中，当工区内存在障碍物、禁采区，或者为了节约成本加大道间距，这些原因会导致部分采集数据缺失.同时，在地震数据处理时，废炮废道的剔除也会导致数据不规则.不规则地震数据使后续处理产生噪声，降低信噪比，并且会导致偏移处理中产生空间假频.针对这一问题，早在1981年Lamer就地震道的插值和野外观测系统设计进行了深入探讨(Larner et al., 1981)，经过三十多年来的发展，国内外许多学者对此问题进行了研究，提出一系列解决方法.利用同相轴在CMP道集上双曲线的走时特征，双曲Radon变换在地震资料去噪、重建等方面有很好的应用效果，但是由于双曲Radon变换在频率域不解耦，使得其计算量很大.而将双曲同相轴经过部分动校正后，可近似为抛物型同相轴，因此Hampson(1986)引入了抛物Radon变换，抛物Radon变换在频率域是解耦的，可以大幅度提高计算效率，所以大部分基于Radon变换的地震数据重建都是抛物型的.

在2D地震数据重建方面，Kabir和Verschuur(1995)提出基于迭代抛物Radon变换的重建方法.该方法对近偏移距缺失数据能够进行有效重建，但是不能处理不规则空间采样地震数据且迭代次数较多.Sacchi和Ulrych(1995)提出频率域高分辨率抛物Radon变换地震道重建方法，该方法可以得到比传统Radon变换更好的重建效果，但是由于加上了稀疏因子，破坏了反演矩阵的Toeplitz结构，无法运用Levinson递推快速算法求解，使其迭代算法的计算量有所增加且未考虑振幅信息.对于CMP道集而言，远偏移距同相轴的形状更接近于双曲线而非抛物线，所以Trad等(2002)提出基于时变高分辨率双曲Radon变换的地震数据重建方法.但是，由于是时变方法无法运用Levinson递推快速算法求解，尚难用于实际生产.黄新武等(2003)提出了基于抛物Radon变换的地震道内插和外推方法.此方法用零道代替所有待重建道，结合了带限抛物Radon正变换和最小平方抛物Radon反变换，迭代求解出重建结果，但该方法重建结果与原始数据的振幅差异较大.王维红等(2007)给出了加权抛物Radon变换不规则地震数据重建方法.该方法可以使不规则采样数据规则化，完成空缺道及近偏移距数据的重建，可有效用于复杂地质构造的地震数据保幅重建，但是没有给出保幅重建原理.

近年来关于3D地震数据重建也有较大发展，如针对宽方位3D陆地采集数据，Trad(2009)提出基于Fourier变换的MWNI(最小加权范数反演)5D数据重建方法；Cary(2011)提出用3D正交观测系统采样克服基于Fourier变换的MWNI方法的假频问题；Kumar等(2013)提出用SVD低自由度矩阵因子分解法进行地震数据重建和去噪；而在基于Radon变换3D数据重建方面，Donati和Martin(1995)提出了3D τ-p变换地震数据重建；其后Zhang(2013)提出了一个新的高分辨率3D τ-p变换方法；Hugonnet等(2008)提出了高分辨率3D抛物Radon滤波器，解决了2D抛物Radon滤波器在高密度、宽方位地震数据多次波去除上的不适用问题.在这些3D地震数据重建方法中也没有关于保幅重建的研究.

本文研究了3D高阶抛物Radon变换地震数据保幅重建方法.文中在传统3D抛物Radon变换的基础上，引入Johansen等(1995)的正交多项式变换拟合地震数据振幅方法，得到了改进的3D抛物Radon变换.该方法将一个地震剖面变换到三个Radon域剖面，第一个剖面表示振幅的叠加信息，第二个剖面表示振幅的梯度信息，第三个剖面表示振幅的曲率信息，本文将该方法定义为3D高阶抛物Radon变换.该变换既可以描述AVO信息又可以分辨相邻同相轴的曲率信息，利用该方法对3D地震数据重建，可以较好地实现保幅重建.

2 3D高阶抛物Radon变换保幅重建 2.1 3D高阶抛物Radon变换原理

3D 抛物Radon正变换可表达为：

其反变换为：

其中，m为地震数据在τ-qx-qy域中的表达形式，d为3D地震数据体，qx，qy为变换参数.

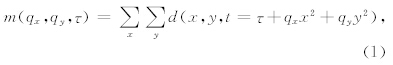
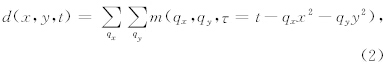
3D 抛物Radon变换是沿着抛物面轨迹分别对不同曲率的地震数据求和，其实质是振幅的叠加运算，不考虑振幅随偏移距的变化情况.因此，当地震数据具有AVO效应时，3D 抛物Radon变换的误差较大.图 1为两种类型3D模拟数据，共有32条测线，每条测线64道，道间距都为25 m，图 1a是inline=1振幅在偏移距方向是常数的数据，图 1b是inline=1振幅在偏移距方向有AVO效应的数据.分别对这两种数据进行正反3D抛物 Radon变换，结果如图 1c和图 1d所示.从图中可以看出，对于常振幅数据3D抛物 Radon变换的误差较小，而对具有AVO效应的数据误差较大.

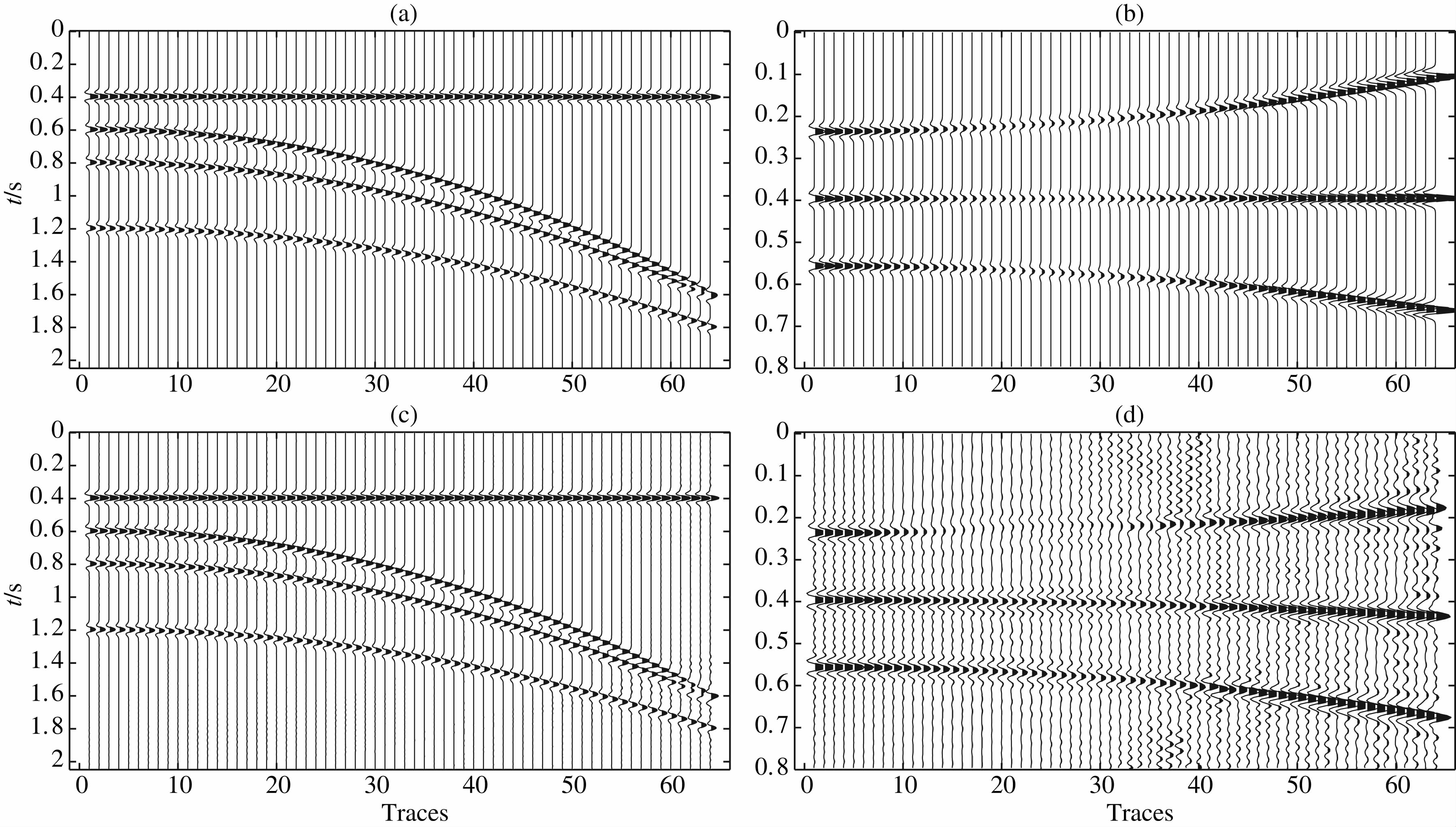图 1 传统3D抛物 Radon正反变换效果(a)常振幅数据;(b)具有AVO效应数据;(c)常振幅数据变换效果;(d)AVO数据变换效果.Fig. 1 Traditional 3D parabolic Radon transform effect(a)Constant amplitude data;(b)AVO data;(c)Result of(a)using 3D PRT;(d)Result of(b)using 3D PRT.

3D抛物 Radon变换对具有AVO效应的地震数据变换误差较大的原因是在变换中缺少描述振幅变化的信息.Johansen(1995)提出了用正交多项式变换拟合地震数据振幅的方法，而正交多项式的系数代表了地震数据的AVO信息(Johansen et al., 1995).因此，本文将该方法引入到3D抛物Radon变换中来.正交多项式系数求取如下：

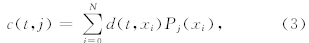
其中，j表示正交多项式的阶数，N为偏移距方向接收点个数，c(t，j)为对应的系数，{j=0，1，…，L}.同相轴的振幅变化信息，可以用较少的前几阶系数表示，通常情况下取其前三个系数，一般L=2.c(t，0)表示叠加信息，c(t，1)表示梯度信息，c(t，2)表示曲率信息.N为空间采样点个数，pj(x)是第j阶正交多项式基函数，满足：pi(x)pj(x)=δij，δij为脉冲函数.正交多项式系数c(t，0)，c(t，1)，c(t，2)可以准确地描述地震数据振幅变化信息.

比较公式(1)和(3)可以看出，Radon变换是使地震数据按照抛物轨迹进行叠加，Johasen的正交多项式变换拟合地震数据振幅是使地震数据以基函数为准则进行叠加.二者形式上不同，而实质上是一致的，即对地震数据按某种规律求和运算.因此，将正交多项式变换拟合地震数据振幅的方法引入到3D抛物Radon中来，就可以对具有AVO效应的数据进行准确的Radon变换.

将3D抛物Radon正变换扩展为：

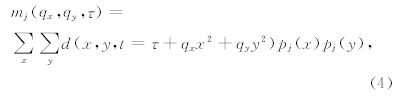
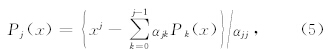
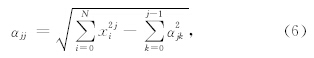
即将沿着路径求和的Radon正变换变为沿着路径的加权求和.这样就将传统Radon正变换的一个τ-p域剖面分解到表示AVO信息的j个剖面.其中，pj(x)，pj(y)是第j阶正交多项式基函数，它们的求取方法相同，以pj(x)为例：

系数α求取如下：

通过方程(5)(6)(7)，我们可以构造任意偏移距的正交多项式，给定α00= N，则P0=1/α00，系数αjk和多项式Pj按照以下的顺序计算：α10，α11，P1，α20，α21，α22，P2，…，αL0，αL1，…，αLL，PL.从上可以看出这个正交多项式的构造完全取决于偏移距的坐标，这就意味着当正交基函数或者基函数的阶数发生变化时，已有低阶正交多项式系数不用重新计算，除非偏移距的坐标发生变化.同时用正交多项式作为基函数计算的各个系数之间彼此是独立的，且正交多项式阶数L的选择并不影响低阶系数的准确度.c(t，0)与平均值有关，c(t，1)与平均梯度有关，c(t，2)表示振幅随偏移距的变化是增大的还是减小的.

我们将公式(4)定义为高阶抛物Radon变换，与抛物Radon变换类似，首先定义高阶抛物Radon变换的反变换，然后利用最小二乘法来求解高阶抛 物Radon变换.高阶抛物Radon反变换离散形式为：

公式(4)与(8)就构成了3D高阶抛物Radon正反变换，对(8)作Fourier变换，写成频率域形式：

将其进一步变形为：

对于地震数据单个频率，可以将公式(10)写成矩阵形式：

其中，L qx=e－iωqxx2·p(x)，L qy=e－iωqyy2·p(y)，M 是f-qx-qy域数据矩阵，D是频率域3D数据矩阵.

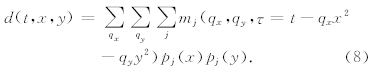
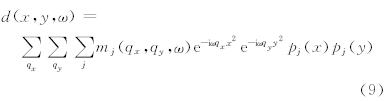
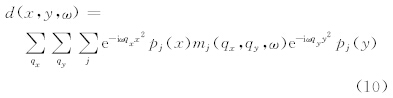
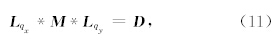
由公式(10)可以看出，M 的规模由qx，qy的采样个数以及正交多项式的阶数决定，因此，与传统Radon变换相比，若正交多项式的阶数为L，则本文方法中 M 的大小是传统方法的L×L倍，相应的计算量会比传统方法大.

3D高阶抛物Radon正变换系数可通过最小二乘方法来求解：

2.2 3D高阶Radon变换保幅性分析

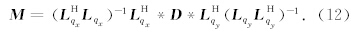
在3D高阶抛物Radon 变换中，mj(τ，qx，qy)表示在τ时刻沿曲率参数为qx，qy的地震数据的分解系数.在本文中只取前三阶分解系数，m0表示同相轴沿着空间方向振幅的叠加信息，我们称之为叠加剖面；m1表示同相轴的平均梯度信息，称之为梯度剖面；m2表示同相轴的曲率信息，称之为曲率剖面.对图 1b的AVO数据分别用传统3D抛物Radon变换和3D高阶抛物Radon 变换进行运算，最小二乘解结果分别如图 2a和图 2b，2c，2d所示.从图 2a可以看出，由于同相轴的振幅沿着偏移距方向是变化的，传统抛物Radon变换缺少描述振幅变化的参数导致m的能量不能够集中；而高阶抛物Radon变换值m0，m1，m2的能量很集中，如图 2b，2c，2d所示.

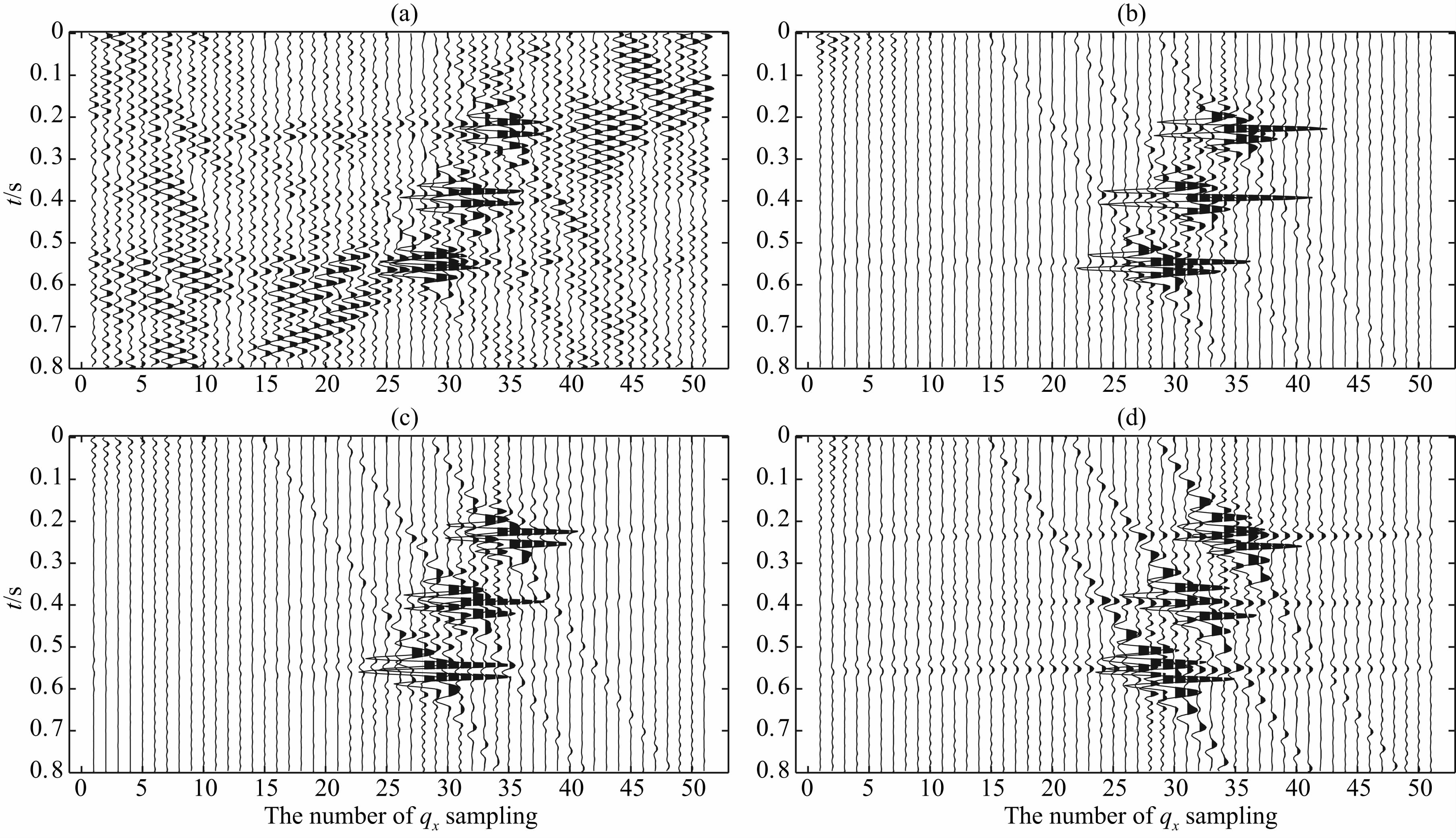图 2 3D PRT和3D HOPRT方法Radon域剖面比较(a)3D PRT法正变换剖面；(b)(c)(d)3D HOPRT法正变换剖面.Fig. 2 Comparison of Radon domain panel for 3D PRT and 3D HOPRT methods(a)For 3D PRT;(b)(c)(d)For 3D HOPRT.

图 3为反变换的结果，图 3a是传统3D抛物Radon变换反变换的结果，图 3b是3D高阶抛物Radon变换反变换的结果，图 3c，3d分别是二者与原始数据的误差剖面.从图中可以明显看出，3D高阶抛物Radon变换的结果要比传统3D抛物Radon变换的结果好.抽出inline=1中偏移距为975 m和1475 m处的两道地震数据，将原始数据和两种变换的结果进行比较，如图 4所示，蓝色是原始数据，绿色是传统3D抛物Radon变换结果，红色是本文方法的结果.从图中可以看出不论是中偏移距还是远偏移距，本文方法的保幅性都比传统3D抛物Radon变换的好，而且产生的噪声小.

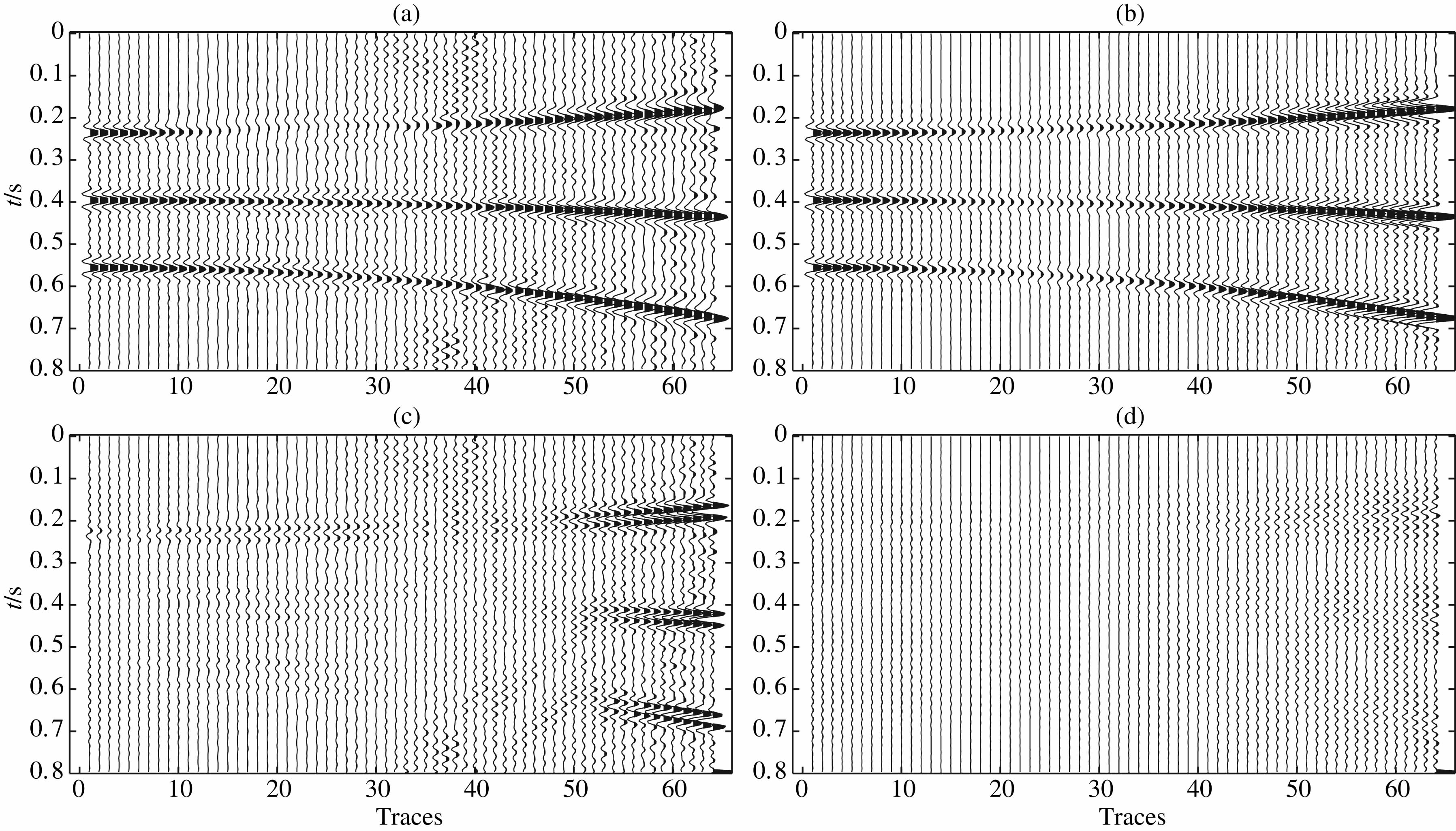图 3 3D PRT和3D HOPRT反变换剖面比较(a)3D PRT反变换剖面;(b)3D HOPRT反变换剖面;(c)3D PRT方法误差剖面;(d)3D HOPRT方法误差剖面.Fig. 3 Comparison of inverse Radon transform for 3D PRT and 3D HOPRT(a)For 3D inverse PRT;(b)For 3D inverse HOPRT;(c)For error of 3D PRT;(d)For error of 3D HOPRT.

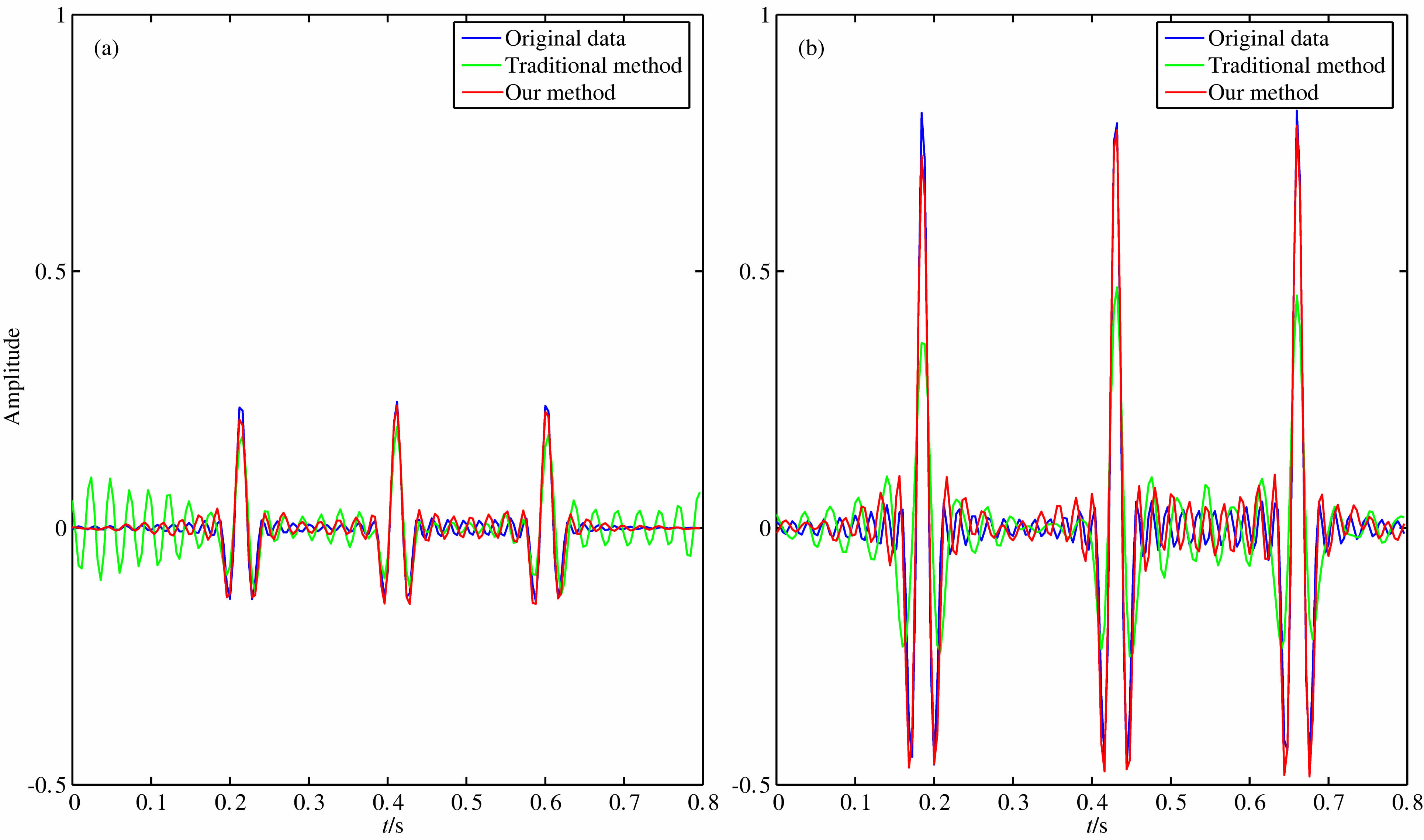图 4 PRT和HOPRT方法保幅性比较(a)中偏移距PRT和HOPRT方法振幅比较;(b)远偏移距PRT和HOPRT方法振幅比较.Fig. 4 Comparison of amplitude preserving for PRT and HOPRT(a)Mid-offset trace;(b)Far-offset trace.
2.3 3D高阶抛物Radon变换地震数据重建

利用Radon变换进行数据重建的原理是当地震数据中有较多的空道时，其抛物Radon正变换上能量分散，反变换后能填补部分空道数据，并可以改善正变换能量分散问题.多次正反抛物Radon变换后可以将缺失的数据重建.本文在重建的过程中引入POCS(凸集投影)方法，重建流程如图 5所示.

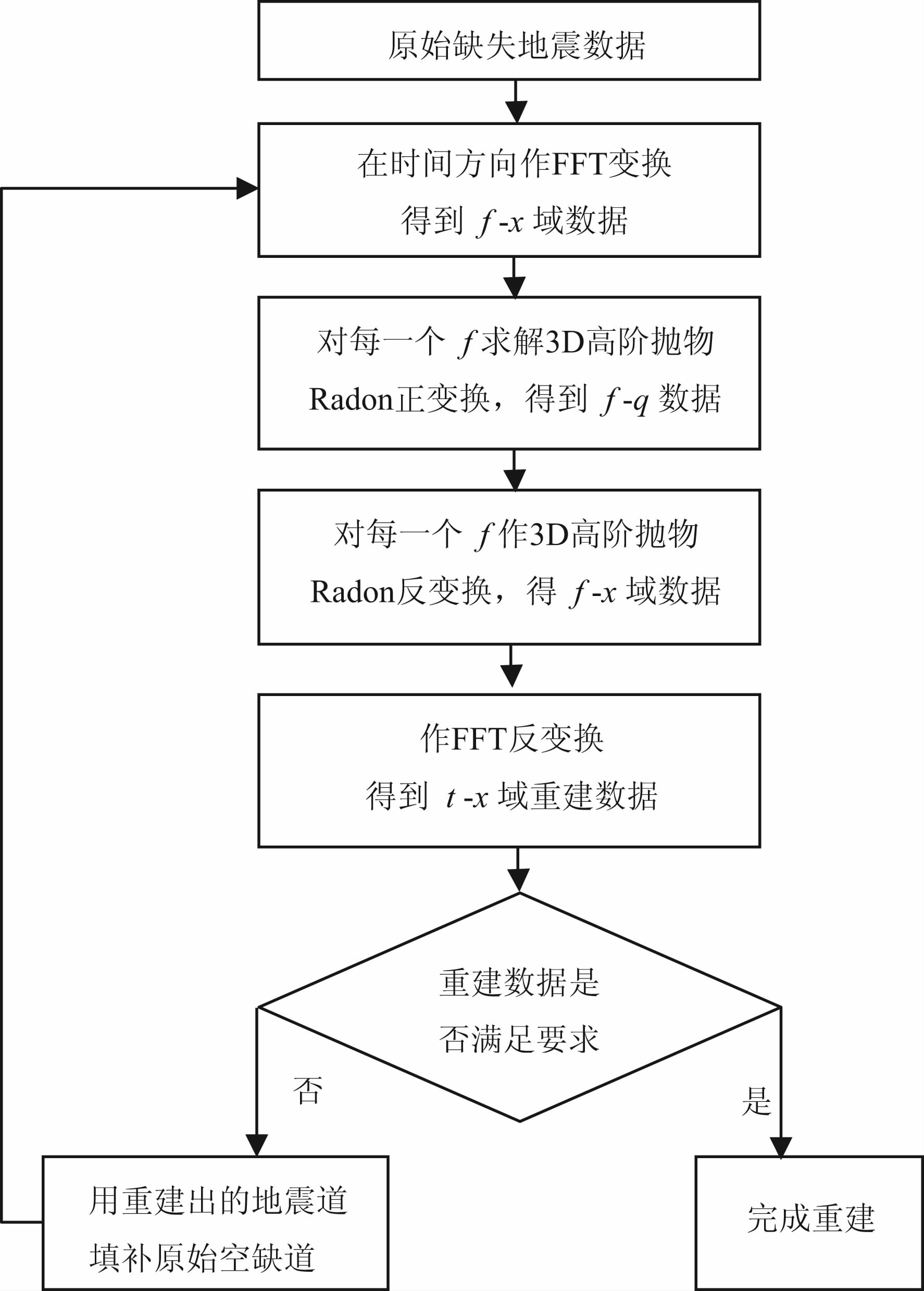图 5 3D HOPRT重建方法流程Fig. 5 Workflow of 3D HOPRT reconstruction method

用本文方法对3D模拟数据重建，模拟数据是将二维剖面沿crossline方向排列了32条(从crossline 1到crossline 32)，每个剖面有64道数据，如图 6a所示为第一条测线剖面，三个同相轴代表三类AVO数据，其中第一个同相轴的振幅随偏移距增大而减小，减小到零极性反转后增大；第二个同相轴的振幅随偏移距的增加而增大；第三个同相轴的振幅随偏移距的增加而减小.图 6b是第1道至第5道缺失的数据，图 6c是用本文方法重建后的数据，图 6d是本文方法(红色曲线)和传统Radon变换方法(绿色曲线)重建后的第1道数据和原始数据(蓝色曲线)的比较.从图 6c和6d可以看出，本文方法的重建数据和原始数据的振幅差异更小，相位也更为准确.

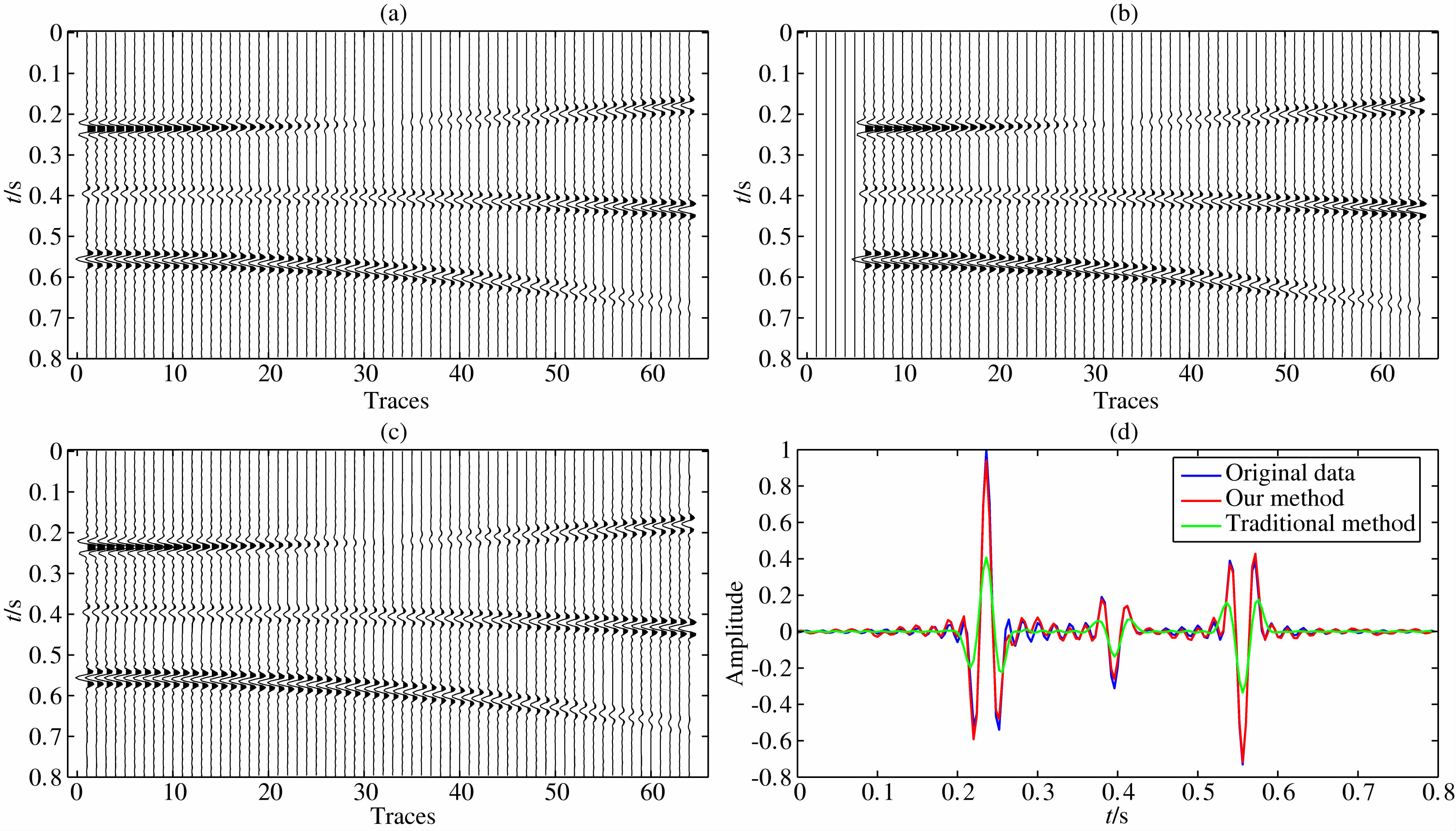图 6 近偏移距连续缺失数据重建(a)第一条测线原始数据;(b)连续缺失数据;(c)3D HOPRT方法重建结果;(d)重建第5道与原道比较.Fig. 6 Reconstruction of missing data within near-offset(a)Original data crossline1;(b)Missing data;(c)Recovery data;(d)Comparison of the 1th trace.

为了检验本文方法的抗噪声能力，在图 6a模型中加了SNR=2的随机噪声，如图 7a所示，重建结果如图 7c，7d所示.可以看出，该方法在重建的同时有效地去除随机噪声，图 7d中蓝色曲线是不加噪声的第一道原始数据，红色曲线是重建后数据，二者振幅一致.

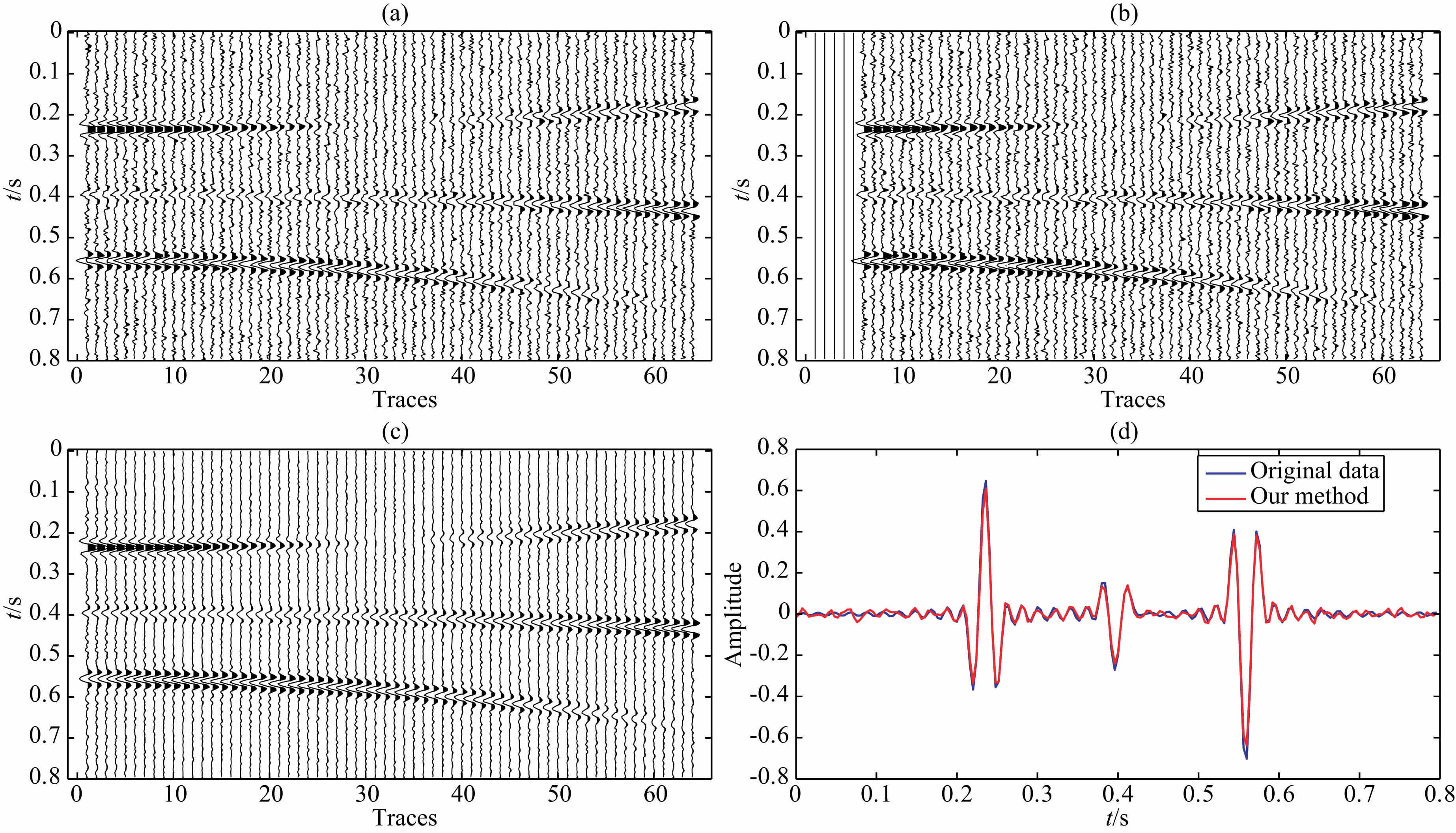图 7 近偏移距连续缺失加噪数据重建(a)第一条测线原始数据;(b)连续缺失数据;(c)3D HOPRT方法重建结果;(d)重建第1道与原道比较.Fig. 7 Reconstruction of containing r and om noise data within near-offset missing(a)Original data crossline1;(b)Missing data;(c)Recovered data;(d)Comparison of the 1st trace.

为了检验本文方法的抗假频能力，设计了规则缺失模型，即将图 6a模型中的偶数道缺失(如图 8a所示).图 8c是本文HOPRT方法重建后的结果，图 8e是原始数据的第二道和重建数据第二道的振幅比较，图 8b，8d，8f分别是规则缺失数据的FK谱，重建数据FK谱以及原始数据FK谱.可以看出，规则缺失数据会产生假频，经本文方法重建后，假频得到有效压制，重建后的数据同相轴连续，并且保幅性很好.

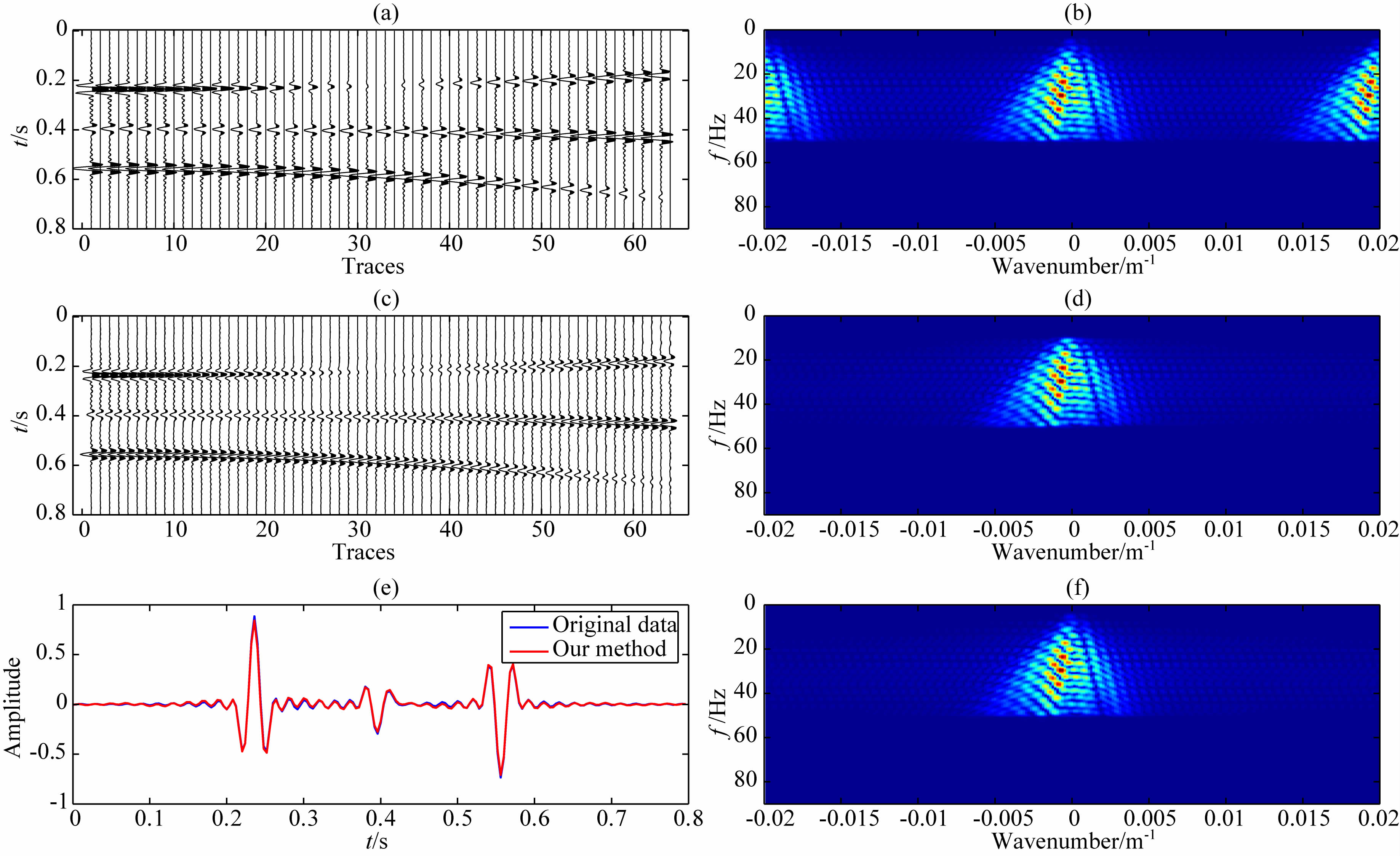图 8 规则缺失数据重建(a)规则缺失数据;(b)图(a)的FK谱;(c)3D HOPRT方法重建结果;(d)图(c)的FK谱;(e)重建第2道与原道比较;(f)原始数据FK谱.Fig. 8 Reconstruction of regular missing data(a)Regular missing data;(b)FK spectrum of(a);(c)Recovery data;(d)FK spectrum of(c);(e)Comparison of the 2nd trace;(f)FK spectrum of original data.

由于inline方向每条测线上第1道至第5道数据缺失从而导致在crossline方向第1到第5条测 线是完全缺失的.图 9a中第1道至32道是crossline 1 的原始数据，第37道至68道是本文方法crossline 1重建的结果.图 9b中第1道至32道是crossline 5 的原始数据，第37道至68道是本文方法crossline 5 重建的结果.从图中可以看出，该方法对crossline方向的数据重建也有很好的效果.

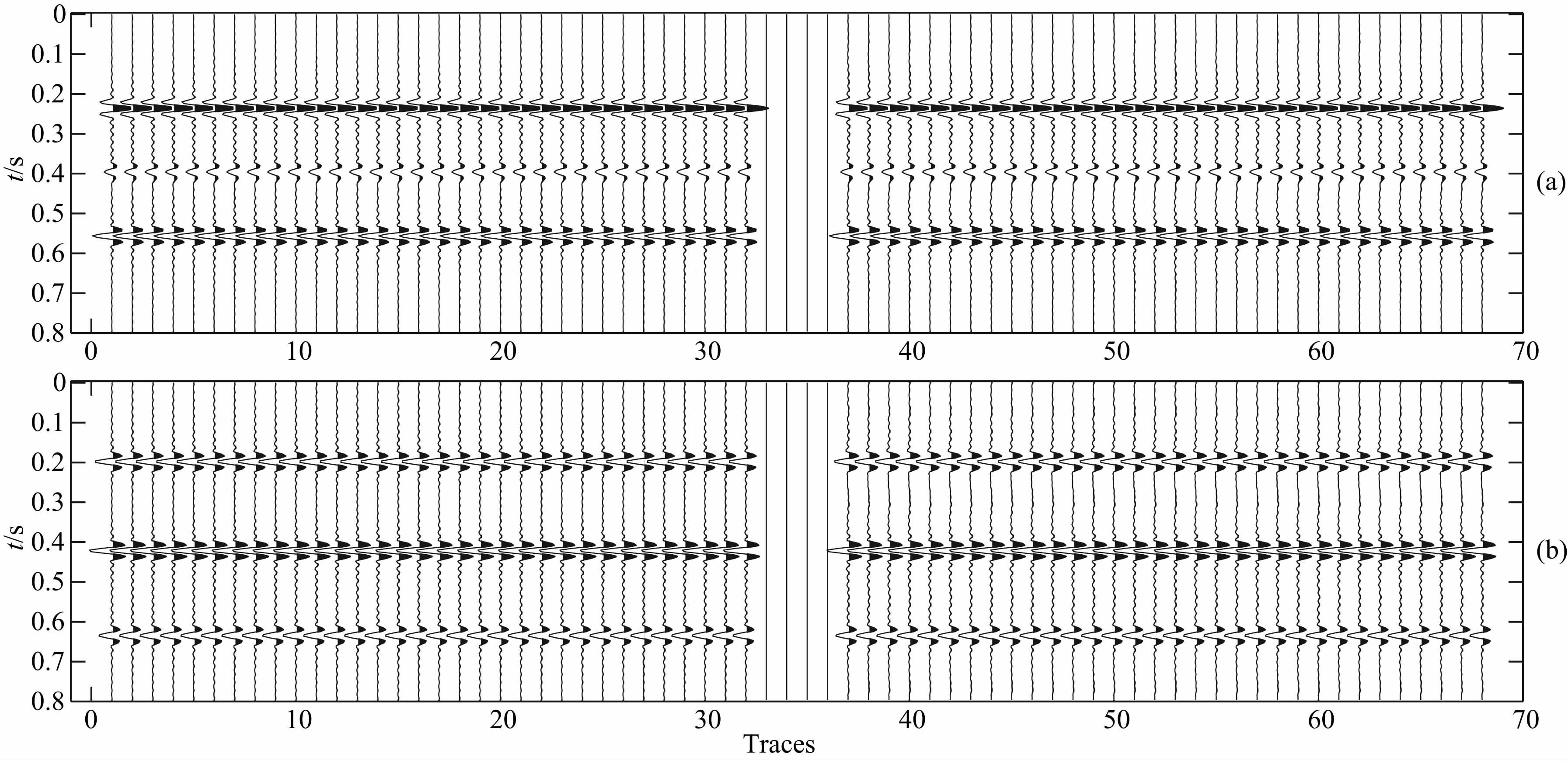图 9 crossline方向重建效果(a)crossline 1原始数据与重建数据;(b)crossline 5原始数据与重建数据.Fig. 9 Reconstruction of crossline(a)Original data and reconstruction data of crossline 1;(b)Original data and reconstruction data of crossline 5.

但是，由于本文HOPRT方法中参数的增加导致计算量的增大，计算效率要低于传统方法.在模型试算中，正交多项式的阶数为3，本文方法在MATLAB中运行时间为265.72 s，传统方法运行时间为28.59 s，与2.1节中的计算效率分析一致.

3 实际资料重建

将3D高阶抛物Radon变换地震数据重建方法应用到某实际资料，以检测其实际应用效果.实际数据是将二维剖面沿crossline方向排列了50条(从crossline 1到crossline 50)，每个剖面有100道数据，如图 10a所示为实际数据第一条测线的部分数据，其中时间采样间隔是4 ms，道间距87.5 m，共 100道；每条测线都随机缺失21道，图 10b是第一条测线随机缺失后的数据；图 10c是用本文方法重建结果，图 10d是本文方法重建第54道结果以及用传统方法重建结果与原始数据的振幅比较.从图中可以看出，缺失的数据得到好的重建效果，同相轴连续性好，和传统方法相比有更好的保幅性.图 10c中 红色椭圆部分由于同相轴密集，本文方法的分辨率不能够完全区分它们，导致同相轴的连续性没有其他部分好.

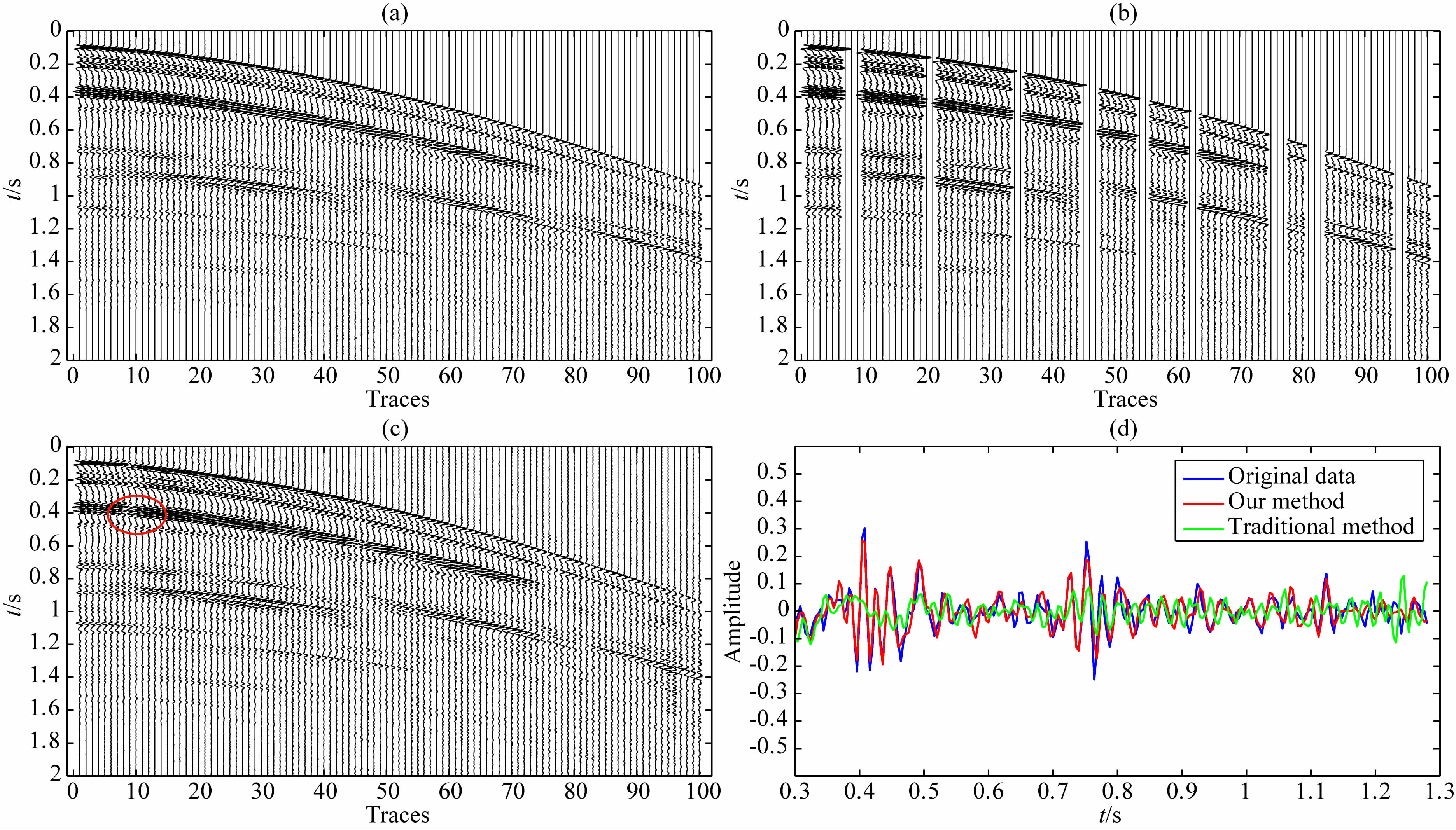图 10 实际数据随机缺失重建(a)第一条测线原始数据;(b)随机缺失数据;(c)3D HOPRT方法重建结果;(d)重建第54道与原道比较.Fig. 10 Reconstruction of r and om missed real data(a)Original data crossline1;(b)Missing data;(c)Recovery data;(d)Comparison of the 54th trace.
4 结论

本文将3D抛物Radon变换与正交多项式变换结合，给出了3D高阶抛物Radon变换地震数据重建方法.该方法在传统3D抛物Radon变换的基础上增加了振幅的梯度及曲率变化参数，从而减小了AVO数据的重建误差，具有很强的保幅特性.在理论数据及实际地震资料中取得了满意的重建结果，振幅损失很小，重建同时能去除随机噪声，而且该方法对含假频数据也能有效地重建.

虽然本文方法中变换参数的增加导致了计算量的增大，但是并行计算的应用以及计算机速度的日益提高，使得该方法在工业生产中的应用具有可行性；在求解高阶抛物Radon正变换系数解时采用了最小二乘方法，解存在一定的拖尾现象，使靠得较近的同相轴不能区分开来，因此如何减小拖尾现象提高解的分辨率是下一步的研究方向.

致谢 感谢薛亚茹老师在本文撰写过程中提出的宝贵意见和建议，对论文评阅人的合理化建议表示感谢.

参考文献
[1] Cary P W. 2011. Aliasing and 5D interpolation with the MWNI algorithm. 73th Ann. Internat. Mtg., Soc. Expi. Geophys. Expanded Abstract, 3080-3084.
[2] Donati M S, Martin N W. 1995. Seismic reconstruction using a 3D tau-p transform. CREWES Research Report, 7: 1-16.
[3] Hampson D. 1986. Inverse velocity stacking for multiple elimination. Journal of the Canadian society of Exploration Geophysicists, 22(1): 44-55.
[4] Huang X Y, Wu L, Niu B H. 2003. Reconstruction of seismic traces by parabolic radon transform. Journal of China University of Mining & Technology (in Chinese), 32(5): 534-539.
[5] Hugonnet P, Boelle J L, Mihoub M. 2008. High Resolution 3D parabolic Radon filtering. Proceedings of the International Water Conference, 5: 2482-2486.
[6] Johansen T A, Bruland L, Lutro J. 1995. Tracking the amplitude versus offset (AVO) by using orthogonal polynomials. Geophysical Prospecting, 43(2): 245-261.
[7] Kabir N, Verschuur J. 1995. Restoration of missing offsets by parabolic Radon Transform. Geophysical Prospecting, 43(3): 347-368.
[8] Kumar R, Aravkin A Y, Mansour H. 2013. Seismic data interpolation and denoising using SVD-free low-rank matrix factorization. 75th EAGE Conference & Exhibition Incorporating SPE EUROPEC 2013.
[9] Larner K, Gibson B, Rothman D. 1981. Trace interpolation and the design of seismic surveys. Geophysics, 46(4): 407-415.
[10] Sacchi M D, Ulrych J. 1995. High-resolution velocity gathers and offset space reconstruction. Geophysics, 60(4): 1169-1177.
[11] Trad D O, Ulrych T J, Sacchi M D. 2002. Accurate interpolation with high-resolution time-variant Radon transforms. Geophysics, 67(2): 644-656.
[12] Trad D. 2009. Five-dimensional interpolation: Recovering from acquisition constraints. Geophysics, 74(6): 123-132.
[13] Wang W H, Pei J Y, Zhang J F. 2007. Prestack seismic data reconstruction using weighted parabolic Radon transform. Chinese J. Geophys. (in Chinese), 50(3): 851-859.
[14] Zhang Y Q, Lu W K, Zhang P. 2013. A new 3D high resolution tau-p transform. 75th EAGE Conference & Exhibition incorporating SPE EUROPEC 2013.
[15] 黄新武, 吴律, 牛滨华. 2003. 基于抛物线拉东变换的地震道重构. 中国矿业大学学报, 32(5): 534-539.
[16] 王维红, 裴江云, 张剑锋. 2007. 加权抛物Radon变换叠前地震数据重建. 地球物理学报, 50(3): 851-859.