1 引言
孔隙介质理论充分考虑了介质骨架的物性与结构、孔隙流体的特殊性质、局部与整体之间的内在联系,能够准确地描述地层性质.Biot理论(Biot,1956;Biot,1962)为含流体多孔隙介质中弹性波传播问题的研究奠定了理论基础,它的建立基于孔隙介质均匀的假设,仅考虑了在波传播方向上,波峰和波谷之间的流体压力梯度所导致的流体全局流动.而实际多孔隙岩石的孔隙结构具有非均匀性,许多研究者考虑到这一重要特点后指出,当波在含流体多孔隙介质中传播时,在刚性孔隙(如:球形孔隙)和柔性孔隙(如:微裂隙、孔隙间吼道、颗粒接触处)之间将产生流体压力梯度,致使流体在波的压缩周期内,从柔性孔隙喷出进入刚性孔隙,而在波膨胀周期内,从刚性孔隙流回柔性孔隙.大量研究表明,对于典型沉积岩石,Squirt流动机制能够对声波和实验室超声波频段的波衰减和频散给出较为合理的解释.Biot流动和Squirt流动是孔隙介质中固-流相互作用的两种重要力学机制,Biot流动具有宏观性,而喷射流动具有局部性.因此,Dvorkin和Nur(1993)认为当波在孔隙介质中传播时Biot流动和Squirt流动应同时存在,它们作为一个耦合过程共同对波的衰减和频散产生影响.他们基于孔隙各向同性一维问题,将这两种固-流相互作用的力学机制有机地结合起来,提出了统一的Biot-Squirt(BISQ)模型,并将BISQ模型的预测结果与实验观测数据进行比较,发现该模型的预测结果更为准确.之后,国内外一些学者对BISQ模型进行了广泛深入地研究(Dai et al., 1995;Carcione,1996;Parra,2000;Yang and Zhang, 2000;Arntsen and Carcione, 2001;Chen et al., 2002;聂建新等,2004;刘财等,2007;Nie et al., 2008;聂建新等,2010;张显文等,2010),形成了较为系统和完整的BISQ理论体系.
数值模拟基于BISQ模型的双相介质中的地震波场是认识含流体孔隙介质中地震波传播规律的重要方法.杨宽德等(2002a,2011)基于BISQ模型先后使用FCT(Flux-Corrected Transport)有限差分法和FCT紧致有限差分法模拟了Biot流动和喷射流动作用下的弹性波传播;杨宽德等(2002b)、李红星等(2007,2009)分别采用低阶交错网格有限差分法和高阶交错网格有限差分法对基于BISQ模型的双相横向各向同性介质中的波场进行了数值模拟;Wang等(2008)研究了基于BISQ机制的三维正交各向异性介质中弹性波的波场数值模拟问题.Carcione和Gurevich(2011)采用时间分裂法和傅立叶伪谱法对基于BISQ模型的双相介质中的波场进行了数值模拟;Du等(2011)应用有限差分技术精确模拟了裂隙多孔介质中的地震波;刘财等(2013)采用伪谱法研究了基于改进BISQ机制的双相HTI介质中地震波的传播问题.
然而,以上波场数值模拟工作都是在时间域进行的.在Biot流动和Squirt流动两种机制耦合作用下,双相各向同性介质中的波动方程中将含有频率相关的复数型参数(Yang et al., 2002).实际地震波是由多个单一频率的简谐波合成的复合波,即不同频率成分具有不同的响应特征,地震波的传播特性与频率有关.因而,若要实现基于BISQ模型的双相介质中弹性波传播的数值模拟,考虑全频带地震波的传播特性,需要采用频率域波场正演模拟的方法.频率域正演模拟方法是按照每个频率对空间网格进行整体求解方程组,计算误差分配到每一个网格点上,并且各个频率片之间是独立计算的,不存在累积误差,是一种特别适合于并行计算的正演方法.采用频率域正演模拟方法进行孔隙介质中的波传播数值模拟相比于时间域方法而言,有较大的优势:频率-空间域方程不存在刚性问题,无需将传播方程分裂为刚性部分和非刚性部分;可以精确地进行全频段的波场数值模拟;易于求解更为复杂的孔隙介质理论的波动方程(例如,基于孔隙黏弹性理论的波动方程).
本文采用Min等(2000)提出的优化25点频率-空间域有限差分算法,在保证精度的前提下,该算法将单个横波波长范围内的网格点数减小到3.3个,正演模拟精度高,压制网格频散效果好.本文将该数值算法用于求解频率-空间域基于BISQ模型的双相各向同性介质的地震波传播方程,从而研究地震频段内基于BISQ模型的双相各向同性介质中的地震波传播规律. 2 基于BISQ模型的双相各向同性介质地震波传播方程
基于BISQ模型的双相孔隙介质中的弹性波传播方程的推导过程见附录A.本文仅考虑双相各向同性孔隙介质二维二分量的情况,波动方程简化为由以下4个方程构成的偏微分方程组(杨宽德等,2002a):
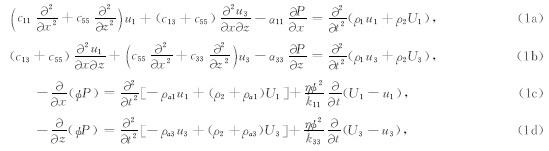
根据Parra(1997)、Yang和Zhang(2002)的研究可知,方程组(1)中的流体压力P为
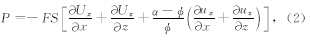

事实上,基于Biot模型的双相介质的波传播方程也可写成(1)式的形式,只是流体压力P的表达 式中不包含喷射流系数,即相当于喷射流系数S(ω)=1,而这恰好是喷射流系数在高频极限(ω→∞)时的取值,换句话讲,Biot模型可以看成BISQ模型中喷射流动处于非松弛状态的情况,而在其它频率,从喷射流系数S(ω)的计算公式可以看出,它是一个与频率相关的复数值.
3 优化的25点频率-空间域有限差分算法 3.1 频率-空间域波动方程将(2)式带入方程组(1)式,并进行傅立叶变换,从而得到BISQ模型的双相各向同性介质的频率-空间域波动方程:
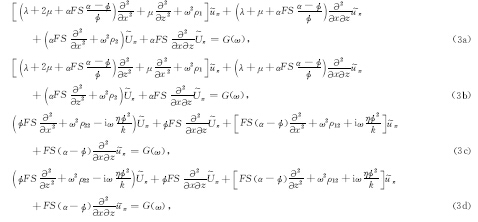
 i和
i和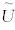 i是频率域固相和流相的位移波场,G(ω)是频率域震源项.
3.2 频率-空间域优化差分算子
i是频率域固相和流相的位移波场,G(ω)是频率域震源项.
3.2 频率-空间域优化差分算子 优化25点差分格式的构造主要包括三个方面:加权平均算子、平均加速度项和优化系数.在频率-空间域波动方程(3)式中,空间二阶微分项:∂2 /∂x2 、 ∂2/∂z2 、 ∂2 /∂x∂z,若以u表示频率域位移波场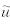 i和
i和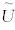 i,相应的加权平均算子可以表示为
i,相应的加权平均算子可以表示为
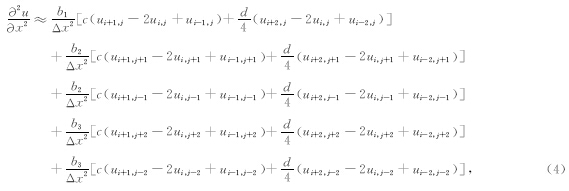
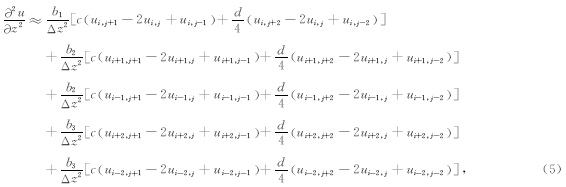
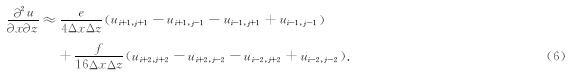
频率-空间域波动方程中还有多个加速度项,为了逼近加速度项要用到25个网格点,25点加速度项的差分算子为
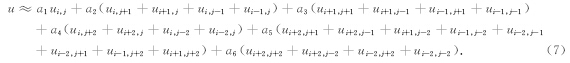
图 1展示了4种25点差分算子网格点的分布情况,网格中心点的坐标为(i,j),更多关于图 1中差分方式以及加权系数的细节描述可参考Min等(2000)文献.
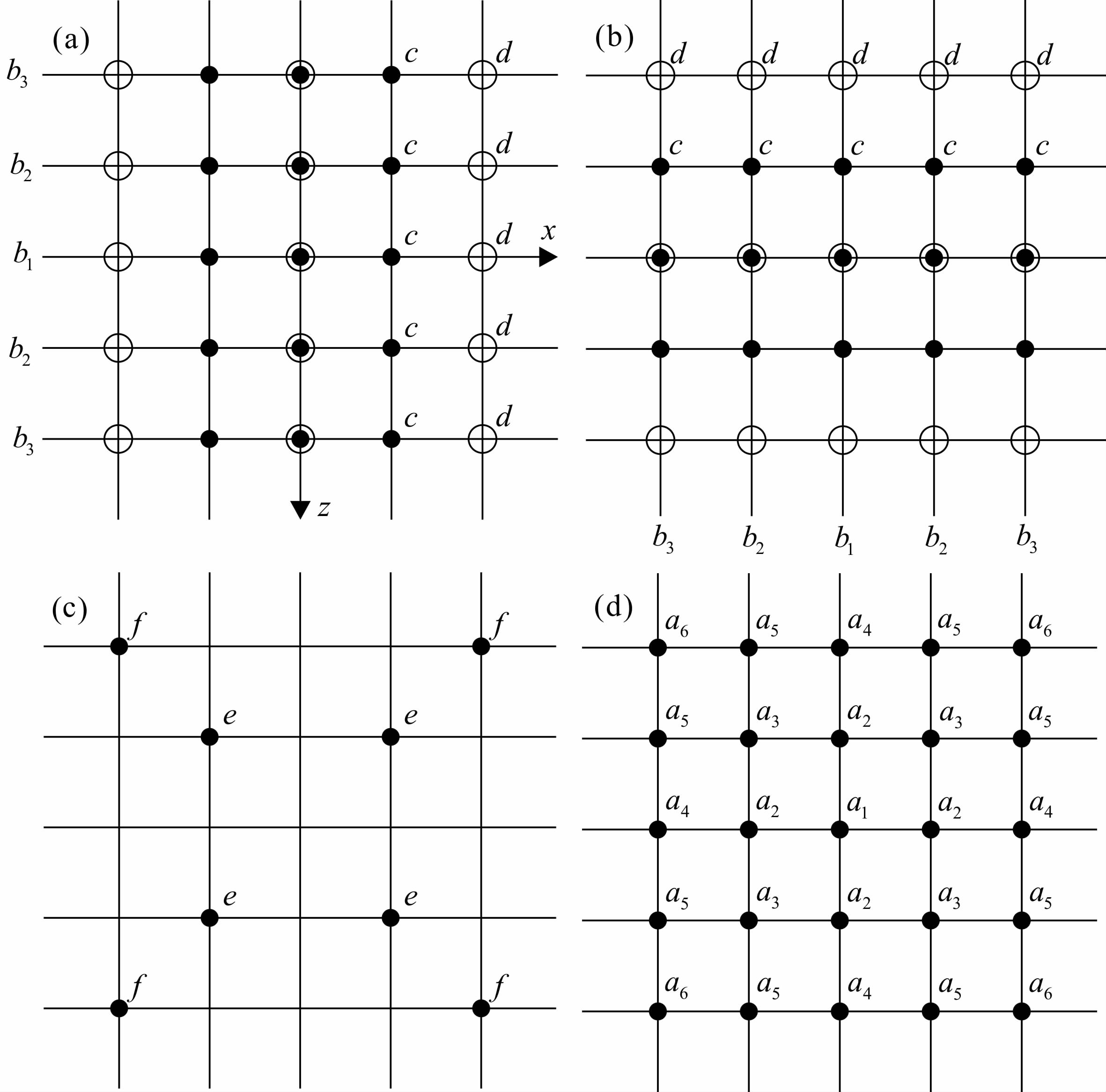 | 图 1 25点有限差分格式的加权系数分布情况 (a)∂2/∂x2;(b)∂2/∂z2;(c)∂2/∂x∂z;(d)加速度项. Fig. 1 Distribution of weighting coefcients in 25-point finite-difference scheme |
差分算子中的ai、bi以及c、d、e、f是25点频率-空间域正演算法的加权系数,Δx和Δz是空间网格步长,为了得到上述差分算子中的优化加权系数,构造其目标函数,使离散模型和连续模型的相速度基本相等.这是一个非线性优化问题,由Gauss-Newton优化方法求解(Min et al., 2000),由此,可以寻找到优化系数使得差分方程相速度与波动方程相速度尽可能地接近,从而得到25点频率-空间域正演算法的最优化加权系数.
将式(4)至(7)式带入频率-空间域波动方程组(3)式,并将式中的其他变量离散化,则可得到离散化的基于BISQ模型双相各向同性介质的频率-空间域波动方程,以(3a)式为例,其离散化方程见附录B.对于每一个计算点,由式(B1)可得到一个线性代数方程,如此对于每一个频率可以得到一个线性方程组,将其表示为矩阵方程的形式,记为
AW = S,
其中 A 是阻抗矩阵,与介质性质、频率等有关,W 是频率域波场,S 是频率域震源项.求解该方程都能够得到单一频率下所有网格点上的波场值,若得到地震频带内足够多的频率域波场,再对其做反傅立叶变换就能得到时间域的地震波场了.
3.3 边界条件本文采用完全匹配层(PML)吸收边界条件(Berenger,1994;吴国忱等,2007;刘璐等,2013),PML边界条件的核心思想是在计算区域四周加上一定厚度的完全匹配层,起到吸收和衰减波能量的作用.我们设定在匹配层中的吸收因子形式为
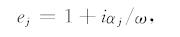
其中,αj=2πa0f0(lj/LPML)2称为衰减系数,a0为常数,f0为子波主频,lj为波在匹配层中的传播距离,LPML为完全匹配层厚度.a0和LPML需因模型不同而变,以吸收效果最佳为准则,本文根据模型实验效果,取a0=1.79,LPML=20.图 2展示了频率-空间域双相各向同性介质的固相垂直位移分量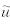 z在不同频率时的单频波场,其波前面呈圆形从震源点向外传播.在PML层内部,可以观察到波前面得到很好地衰减,没有产生明显的反射.
z在不同频率时的单频波场,其波前面呈圆形从震源点向外传播.在PML层内部,可以观察到波前面得到很好地衰减,没有产生明显的反射.
 | 图 2 双相各向同性介质的固相垂直位移分量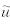 z在不同频率时含PML吸收边界的单频波场
Fig. 2 Frequency maps of the solid vertical displacement z在不同频率时含PML吸收边界的单频波场
Fig. 2 Frequency maps of the solid vertical displacement 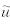 z at 13.69 Hz,25.42 Hz,50.83 Hz in isotropic porous media z at 13.69 Hz,25.42 Hz,50.83 Hz in isotropic porous media
|
为了详细分析地震波在基于BISQ模型的双相各向同性介质中的传播规律,设计一个单层均匀各 向同性双相介质模型,模型大小为2000 m×2000 m,介质物性参数如表 1所示.其他计算参数选择为:空间采样间隔Δx=Δz=10 m,震源子波采用主频为25 Hz的Ricker子波,震源位置(1000 m,1000 m),模拟中震源为固相x方向集中力源.
|
|
表 1 单层模型介质物性参数 Table 1 Physical parameters of the single-layer porous medium |
在本文中我们考虑理想相界(η=0 Pa·s)和黏滞相界(η=0.001 Pa·s)两种情况.为了突出Biot流动和喷射流动耦合作用对地震波传播的影响,我们将基于BISQ模型的波场数值模拟结果与基于Biot模型的波场数值模拟结果进行对比.在前文中我们已经阐述了Biot模型可以看成BISQ模型的高频极限,因而可以直接将基于BISQ模型的双相介质波传播方程中的喷射流系数S(ω)取为1,而其它参数不变,采用同样的求解方式实现基于Biot模型的双相介质中弹性波传播的数值模拟.
在采用25点频率-空间域有限差分法求解基于BISQ模型的双相介质波动方程时,所使用的差分算子的优化加权系数如表 2所示.
|
|
表 2 差分算子中的加权系数 Table 2 Weighting coefficients of finite-difference operator |
首先给出理想相界情况下地震波场数值模拟结果.图 3显示的是基于BISQ模型的双相各向同性介质25Hz频率域单频波场,图 4给出了相应的300ms时时间域波场传播快照,图 5显示的是基于Biot模型的双相各向同性介质25Hz频率域单频波场,图 6是相应的300ms时时间域波场传播快照.
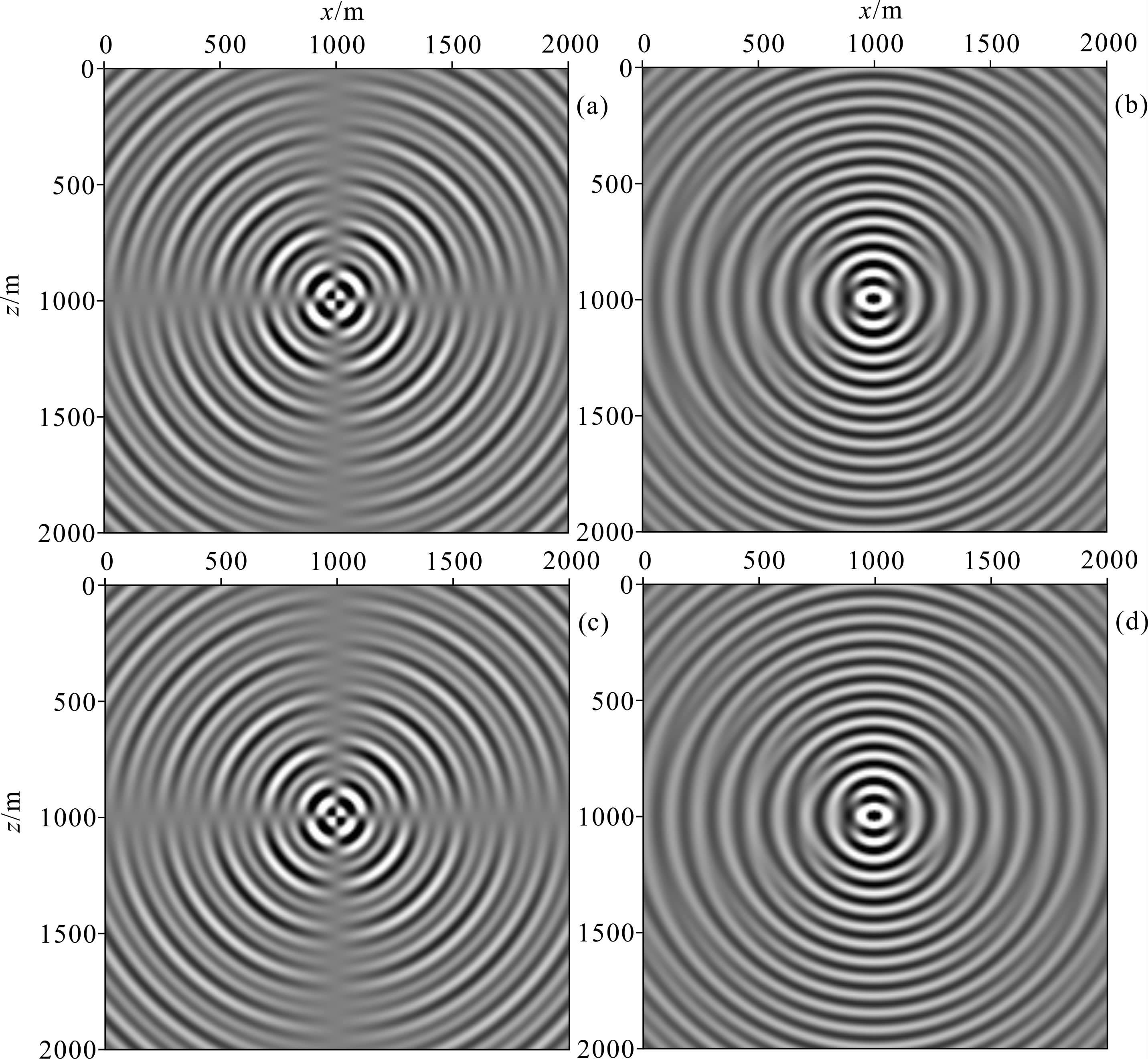 | 图 3 η=0时BISQ模型的固相垂直分量(a)和水平分量(b),流相垂直分量(c)和水平分量(d)的25 Hz单频波场 Fig. 3 Frequency maps at 25 Hz of solid vertical(a) and horizontal(b)components,fluid vertical(c) and horizontal(d)components of BISQ model when η=0 |
 | 图 4 η=0时BISQ模型的固相垂直分量(a)和水平分量(b),流相垂直分量(c)和水平分量(d)的300 ms时波场快照 Fig. 4 Wavefield snapshots at 300 ms of solid vertical(a) and horizontal(b)components,fluid vertical(c) and horizontal(d)components of BISQ model when η=0 |
 | 图 5 η=0时Biot模型的固相垂直分量(a)和水平分量(b),流相垂直分量(c)和水平分量(b)的25Hz单频波场 Fig. 5 Frequency maps at 25 Hz of solid vertical(a) and horizontal(b)components,fluid vertical(c) and horizontal(d)components of Biot model when η=0 |
 | 图 6 η=0时Biot模型的固相垂直分量(a)和水平分量(b),流相垂直分量(c)和水平分量(d)的300ms时波场快照 Fig. 6 Wavefield snapshots at 300 ms of solid vertical(a) and horizontal(b)components,fluid vertical(c) and horizontal(d)components of Biot model when η=0 |
从图 3和图 5中可以看出,单频波场中波前面呈正圆形从震源点向外传播,同时,时间域的波场快照中的波前面也都呈以震源为中心的正圆形,这充分体现了介质的各向同性性质.从图 4中可以观测到快P波和S波,没有观测到慢P波,而在图 6中,除快P波和S波外,还可观测到明显的慢P波,而且慢P波表现出较强的频散,尤其在能量较强的流相分量上.这表明,在理想相界情况下,在Biot流动作用下,慢P波呈传播模式,而在Biot流动和喷射流动耦合作用下,慢P波呈扩散模式,在波场快照中无法观测到,即在两种流体流动机制作用下,慢P波表现出更强的衰减性.同时,通过对比图 4和6,还可以发现,快P波在基于BISQ模型的双相各向同性介质中传播时,其传播速度明显小于在基于Biot模型的双相各向同性介质中传播时的速度,而S波的波速在基于两种模型的双相介质中传播时则无明显差异,这是由于当喷射流动处于非松弛状态时,孔隙介质的胀缩性将变差,但剪切性没有明显变化.这也说明喷射流动对压缩波的影响较大,而对剪切波的影响较小.单独对比图 4和图 6中的固相和流相的波场,固相中的快P波能量都要略强于流相 中的快P波能量,这一点两种模型的情况是一致的.
下面我们考察在黏滞相界情况下,基于BISQ模型和基于Biot模型的双相各向同性介质中地震 波的传播特征.这里取黏滞系数η的值为0.001 Pa·s.
图 7和图 8给出了黏滞相界情况下,基于BISQ模型和基于Biot模型的双相各向同性介质地震波场数值模拟结果,由于在各种状态下频率域单频波场的变化十分微小,所以此处不在展示单频波场.图 7显示的是基于BISQ模型的双相各向同性介质中 固相和流相垂直位移分量和水平位移分量在300 ms 时时间域波场传播快照;而图 8是相应的基于Biot模型的双相各向同性介质中固相和流相垂直位移分量和水平位移分量在300 ms时时间域波场传播快照.为了更直观地对比,在黏滞相界情况下,基于两 种模型的双相各向同性介质中地震波传播的差异性,取(350 m,350 m)处质点的固相x分量振动记录进行分析.图 9给出了基于两种模型的双相各向同性介质中地震波场数值模拟得到的质点(350 m,350 m)处的固相x分量振动记录对比结果.
 | 图 7 η=0.001 Pa·s时BISQ模型的固相垂直分量(a)和水平分量(b),流相垂直分量(c)和水平分量(d)的300ms时波场快照 .7 Wavefield snapshots at 300 ms of solid vertical(a) and horizontal(b)components,fluid vertical(c) and horizontal(d)components of BISQ model when η=0.001 Pa·s |
 | 图 8 η=0.001 Pa·s时Biot模型的固相垂直分量(a)和水平分量(b),流相垂直分量(c)和水平分量(d)的300ms时波场快照 Fig. 8 Wavefield snapshots at 300 ms of solid vertical(a) and horizontal(b)components,fluid vertical(c) and horizontal(d)components of Biot model when η=0.001 Pa·s |
 | 图 9 η=0.001 Pa·s时基于BISQ模型和基于Biot模型的双相各向同性介质中质点(350 m,350 m)处水平分量记录对比图 Fig. 9 Comparison of horizontal component records of the particle(350 m,350 m)in two-phase isotropic media based on BISQ model and Biot model when η=0.001 Pa·s |
从图 7和图 8可以看出,在黏滞相界情况下,基于Biot模型和BISQ模型的双相各向同性介质中的慢P波均由于强衰减作用而无法在波场快照中观测到,波场快照中只能观测到快P波和S波,而且这两种波在基于两种模型的双相介质中传播时的速度差别与理想相界情况下相同,这些特征在图 9中更为直观,而且从图中我们可以看出在基于BISQ模型的双相各向同性介质中传播的快P波的振幅小于基于Biot模型的双相各向同性介质中的快P波,这说明Biot流动和喷射流动两种机制耦合作用造成了更大的快P波衰减.
4.2 双层介质中的地震波传播特征为了研究BISQ模型所描述的双相各向同性介质中地震波在介质分界面处的反射和透射特征,设计一个双层介质模型:模型网格数为200×200,网格大小为10 m×10 m,水平界面位于深度1000 m处,震源点位于(1000 m,900 m).上、下层均为双相各向同性介质,上层介质固体骨架的弹性参数为λ=5.18 GPa,μ=6.12 GPa,下层介质固体骨架弹性参数为λ=22.72 GPa,μ=16.12 GPa.两层介质 中流体黏滞系数η=0.其他介质参数以及震源类型与单层双相各向同性介质波场数值模拟时的情况相同.
图 10、图 11和图 12分别显示的是双层介质模型的25 Hz单频波场、300 ms时的波场快照以及地震记录.从图 11中可以看到入射波、透射波和反射波,入射波和反射波的相互干涉使得反射界面附近波场产生扰动;通过反傅氏变换将频率域波场转换到时间域,得到波场快照和合成地震记录.在图 11和12中,可以观测到:1.直达快P波;2.直达S波; 3.反射快P波;4.快P波与S波之间的反射转换波;5.反射S波;6.透射S波;7.快P波与S波之间的透射转换波;8.透射快P波.可以看出,由于Biot流动和喷射流动两种机制的耦合作用造成慢P波的强衰减,在波场快照和合成地震记录中无法观测到直达慢P波,以及与慢P波相关的反射、透射、转换波类,波场特征类似于单相介质的情况.
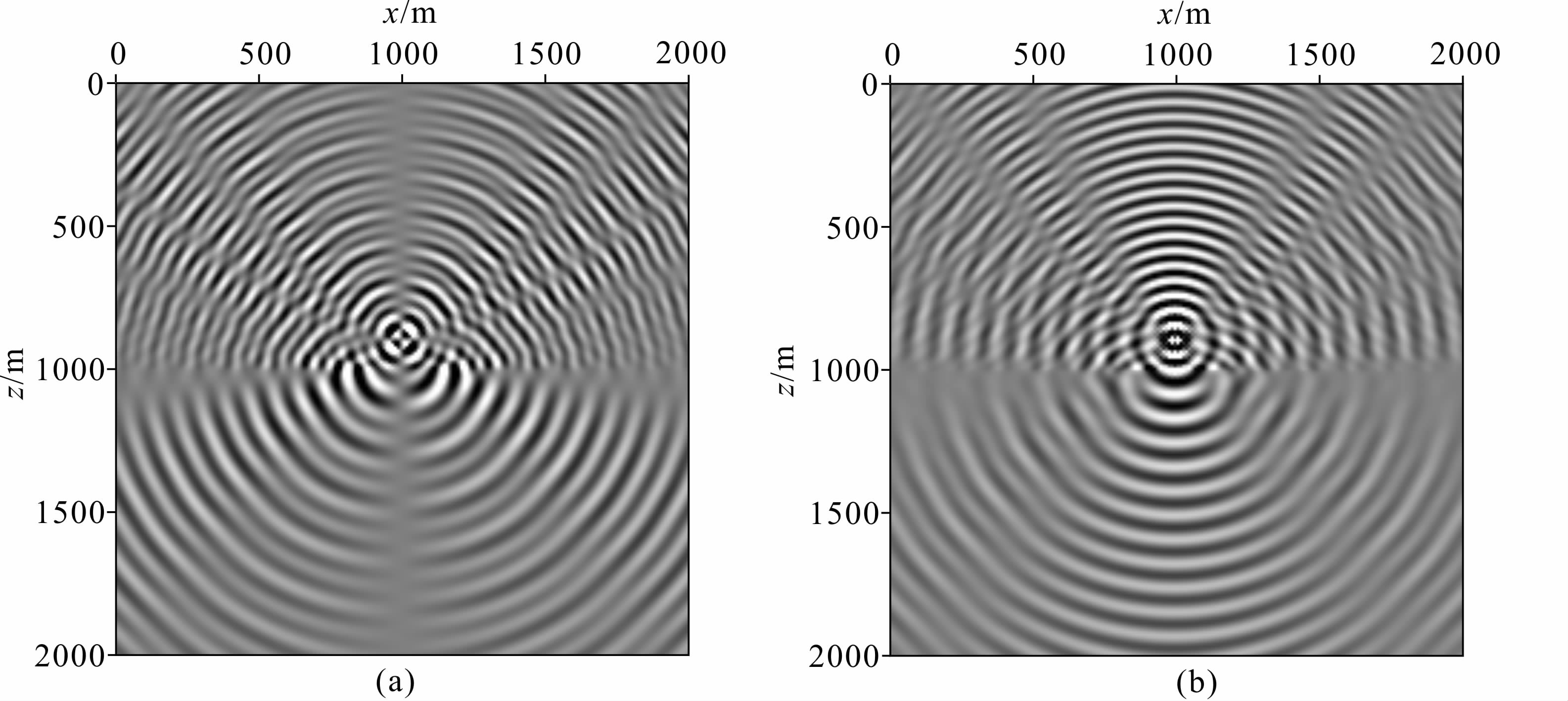 | 图 10 双层双相各向同性介质模型固相垂直分量(a)和水平分量(b)的25Hz单频波场 Fig. 10 Frequency maps at 25 Hz of solid vertical(a) and horizontal(b)components of two-layer two-phase isotropic media |
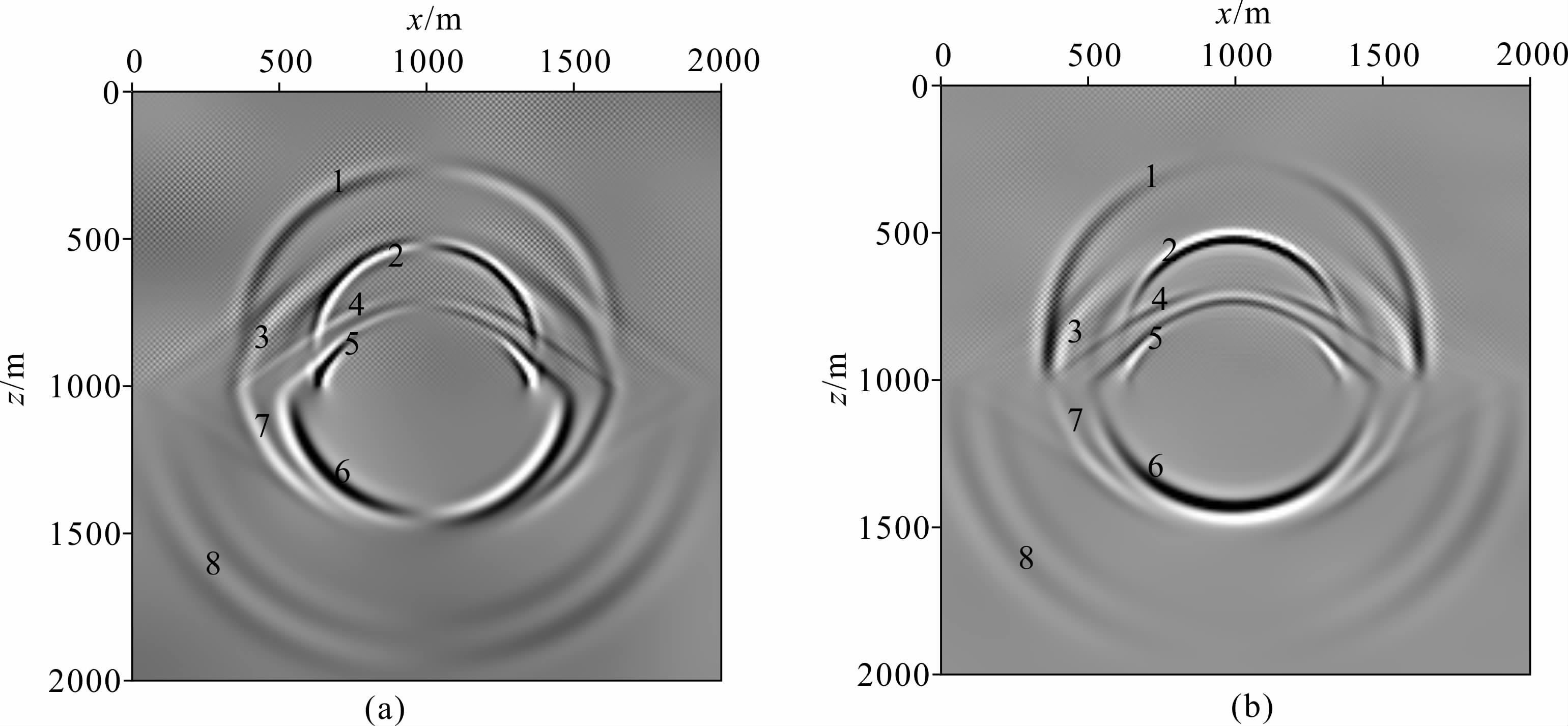 | 图 11 双层双相各向同性介质模型固相垂直分量(a)和水平分量(b)300 ms时的波场快照 Fig. 11 Wavefield snapshots at 300 ms of solid vertical(a) and horizontal(b)components of two-layer two-phase isotropic media |
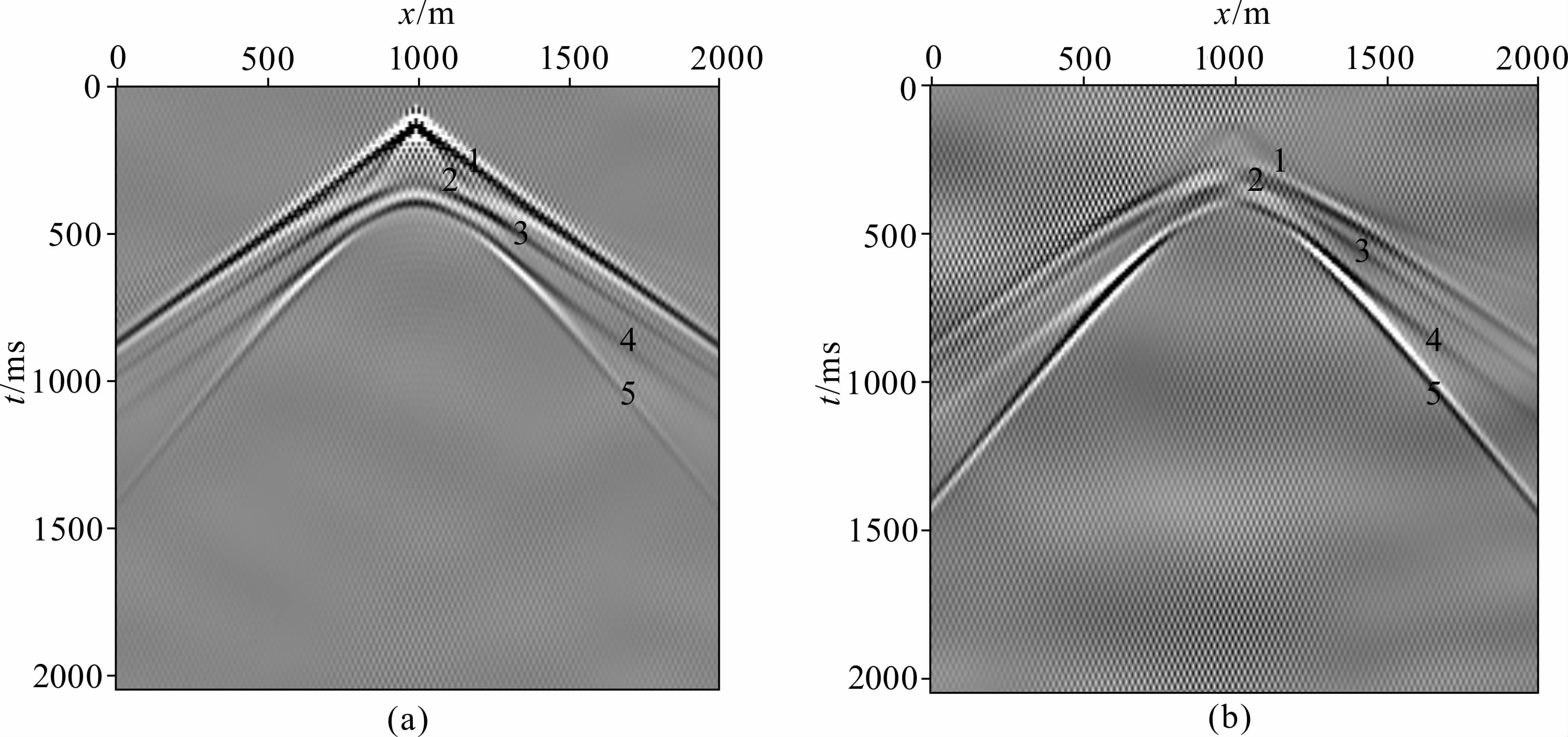 | 图 12 双层双相各向同性介质模型固相垂直分量(a)和水平分量(b)的地震记录 Fig. 12 Seismic synthetic records of solid vertical(a) and horizontal(b)components of two-layer two-phase isotropic media |
本文采用优化的25点频率-空间域有限差分方法模拟研究了基于BISQ模型双相各向同性介质中地震波的传播特性,并与基于Biot模型相同介质中的地震波做了对比,与此同时还模拟研究了地震波在介质界面处的反射与透射特性.通过对以上模拟结果的分析,得出以下结论:
(1)理想相界情况下,基于Biot模型的慢P波呈传播模式,可以在波场快照中观测到,而基于BISQ模型的慢P波呈扩散模式,在波场快照中无法观测到,即在两种流体流动机制作用下,慢P波表现出更强的衰减.
(2)理想相界和黏滞相界两种情况下,基于BISQ模型双相介质中传播的快P波的速度和振幅都小于基于Biot模型双相介质中的快P波,而S波的波速和振幅在基于两种模型的双相介质中传播时则无明显差异.这是由于当喷射流动处于非松弛状态时,孔隙介质的胀缩性将变差,但剪切性没有明显变化,同时也说明喷射流动对P波的影响较大,而对S波的影响较小.
(3)黏滞相界情况下,基于BISQ模型和Biot模型的双相各向同性介质中的慢P波均由于强衰减作用而无法在波场快照中观测到,波场快照中只能观测到快P波和S波.
(4)BISQ模型双层双相各向同性介质的波,由于Biot流动和喷射流动两种机制的耦合作用造成慢P波的强衰减,在波场快照和合成地震记录中无法观测到直达慢P波,以及与慢P波相关的反射、透射、转换波类,波场特征类似于单相介质的情况.
本文建立了基于BISQ机制的双相各向同性介质的频率-空间域波动方程,波场数值模拟结果证实了其合理性和有效性.可以预见,在诸如黏弹性孔隙介质、非饱和孔隙介质、双孔隙度孔隙介质以及裂缝型孔隙介质等更加复杂的孔隙介质中,地震波场都应能在频率-空间域求解,并研究其速度频散、能量衰减等传播特性,从而更进一步为孔隙介质中地震波频率域全波形反演提供帮助.
附录A 本构方程BISQ模型和Biot模型的实际性差别在于所考虑的流体流动机制的不同,这体现在流体压力的表达式中,而二者的应力-应变关系可以写为相同的表达形式.因而,基于BISQ模型的双相介质的应力-应变关系可以表示为
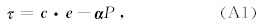
其中,τ 为总应力张量,c 为固体骨架刚度张量,对于一般各向异性介质,c 包含21个独立的排空条件下的孔隙弹性系数,e 为固体骨架应变张量,α 为有效应力之孔隙弹性系数张量,将其写成矢量形式为 α =(α1,α2,α3,α4,α5,α6)T,其分量
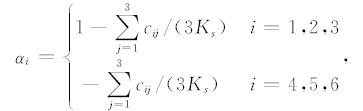
cij为固体骨架刚度张量 c 的元素,Ks是固体颗粒体积模量,P为孔隙流体压力.同时考虑流体全局流动和局部喷射流动的孔隙流体压力P的表达式可写为(Yang and Zhang, 2002):
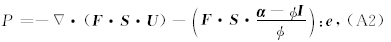
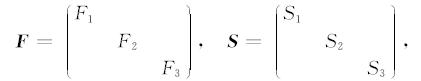
Fj和Sj(j=1,2,3)分别是x、y和z方向的Biot流动系数和喷射流动系数,表达式为
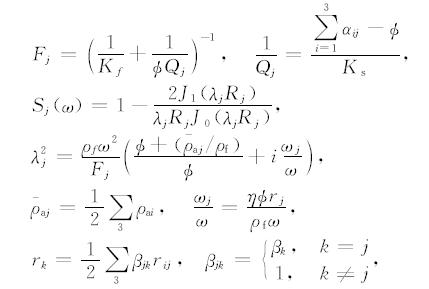
eij为孔隙介质应变张量 e 的分量,其与固体位移 u =(ux,uy,uz)T的分量的关系为
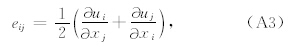
根据Biot理论,在不考虑外力的情况下,描述波在孔隙弹性介质中传播的动力学方程和动力学达西定律可写为(A4)式和(A5)式的形式:
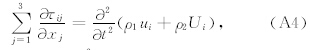

将几何方程(A3)代入本构方程(A1)式,然后再代入到动力学方程(A4)式中,得
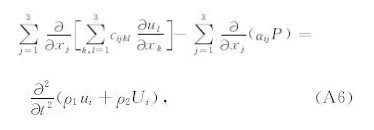
基于BISQ模型双相各向同性介质的频率-空间域波动方程,以(3a)式为例,其离散化方程为:
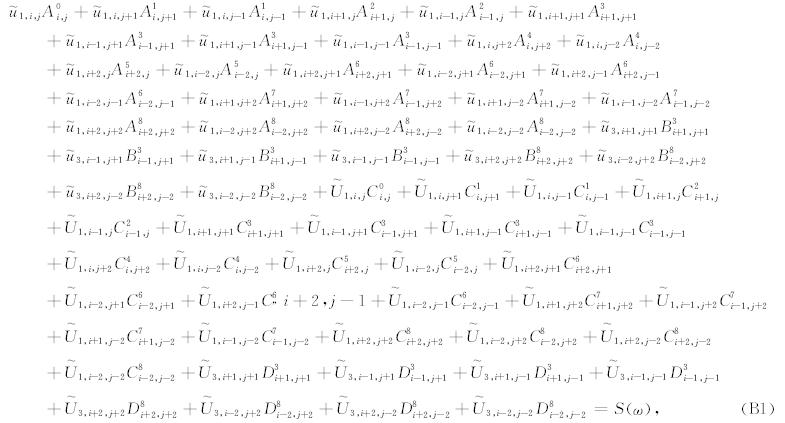
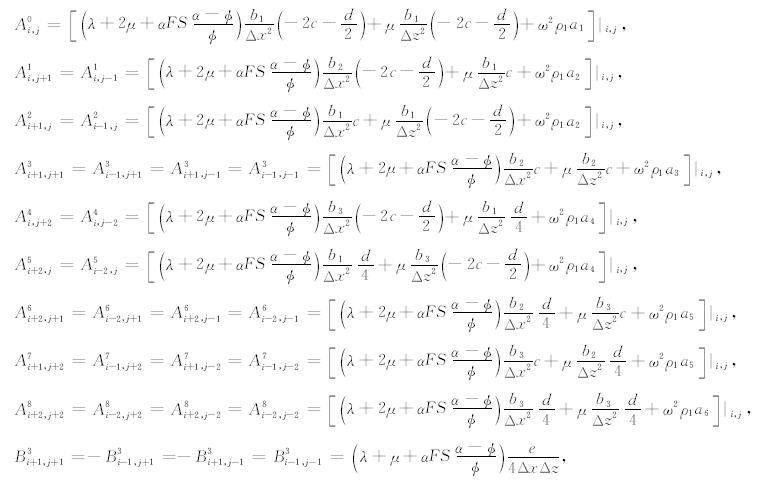
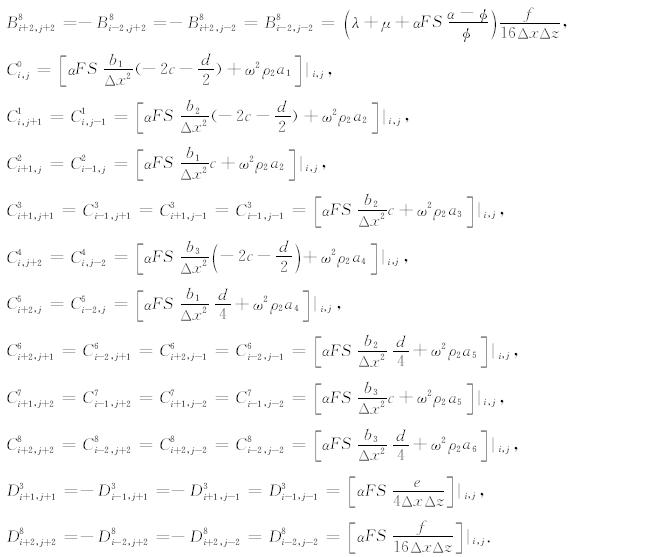
| [1] | Arntsen B, Carcione J M. 2001.Numerical simulation of the Biot slow wave in water-saturated Nivelsteiner Sandstone. Geophysics, 66(3): 890-896. |
| [2] | Berenger J P. 1994. A perfectly matched layer for the absorption of electromagnetic waves.Journal of Computational Physics, 114(2): 185-200. |
| [3] | Biot M A. 1956. Theory of propagation of elastic waves in a fluid-saturated porous solid, PartⅠ: low frequency range. J. Acoust. Soc. Am., 28(2): 168-178. |
| [4] | Biot M A. 1962. Mechanics of deformation and acoustic propagation in porous media. J. Appl. Phys., 33(4): 1482-1498. |
| [5] | Chen Y F, Yang D H, Yang H Z. 2002. Biot/squirt model in viscoelastic porous media. Chinese Physics Letters, 19(3): 445-448. |
| [6] | Carcione J M. 1996. Wave propagation in anisotropic, saturated porous media: Plane-wave theory and numerical simulation. J. Acoust. Soc. Am., 99(5): 2655-2666. |
| [7] | Carcione J M, Gurevich B. 2011. Differential form and numerical implementation of Biot's poroelasticity equations with squirt dissipation. Geophysics, 76(6): N55-N64. |
| [8] | Dai N, Vafidis A, Kanasewich E R. 1995.Wave propagation in heterogeneous, porous media: A velocity-stress, finite-difference method. Geophysics, 60(2): 327-340. |
| [9] | Dvorkin J, Nur A. 1993. Dynamic poroelasticity: A unified model with the squirt and the Biot mechanisms. Geophysics, 58(4): 524-533. |
| [10] | Du Q Z, Wang X M, Ba J, et al. 2011. An equivalent medium model for wave simulation in fractured porous rocks. Geophysical Prospecting, 60(5): 940-956. |
| [11] | Li H X, Liu C, Tao C H. 2007. Elastic wave high-order staggering grid finite-difference numerical simulation based on transversely isotropic BISQ model. Oil Geophysical Prospecting (in Chinese), 42(6): 686-693. |
| [12] | Li H X, Tao C H, Zhou J P, et al. 2009. Analysis on velocity and attenuation feature of wavefield in biphase anisotropic medium. Oil Geophysical Prospecting (in Chinese), 44(4): 457-465. |
| [13] | Liu C, Lan H T, Guo Z Q, et al. 2013. Pseudo-spectral modeling and feature analysis of wave propagation in two-phase HTI medium based on reformulated BISQ mechanism.Chinese J. Geophys. (in Chinese), 56(10): 3461-3473, doi: 10.6038/cjg20131021. |
| [14] | Liu C, Li H X, Tao C H. 2007. Based on BISQ model three-dimensional elastic waves in isotropic porous media staggered-grid high-order finite-difference numerical simulation. Global Geology, 26(4): 501-508. |
| [15] | Liu L, Liu H, Liu H W. 2013. Optimal 15-point finite difference forward modeling in frequency-space domain.Chinese J. Geophys. (in Chinese), 56(2): 644-652, doi: 10.6038/cjg20130228. |
| [16] | Parra J O. 1997. The transversely isotropic poroelastic wave equation including the Biot and the squirt mechanisms: Theory and application. Geophysics, 62(1): 309-318. |
| [17] | Parra J O. 2000.Poroelastic model to relate seismic wave attenuation and dispersion to permeability anisotropy. Geophysics, 65(1): 202-210. |
| [18] | Min D J, Shin C, Kwon B D, et al. 2000. Improved frequency-domain elastic wave modeling using weighted-averaging difference operators. Geophysics, 65(3): 884-895. |
| [19] | Nie J X, Yang D H, Ba J. 2010. Velocity dispersion and attenuation of waves in low-porosity-permeability anisotropic viscoelastic media with clay. Chinese J. Geophys. (in Chinese), 53(2): 385-392, doi: 10.3969/j.issn.0001-5733.2010.02.016. |
| [20] | Nie J X, Yang D H, Yang H Z. 2004. The inversion of reservoir parameters based on the BISQ model in partially saturated porous medium. Chinese J. Geophys. (in Chinese), 47(6): 1101-110. |
| [21] | Nie J X, Yang D H, Yang H Z.2008. A generalized viscoelastic Biot/squirt model for clay-bearing sandstones in a wide range of permeabilities. Applied Geophysics, 5(4): 249-260. |
| [22] | Wang Z J, He Q D, Wang D L. 2008. The numerical simulation for a 3D two-phase anisotropic medium based on BISQ model. Applied Geophysics, 5(1): 24-43. |
| [23] | Wu G C, Luo C M, Liang K. 2007.Frequency-space domain finite difference numerical simulation of elastic wave in TTI media. Journal of Jilin University (Earth Science Edition), 37(5): 1023-1033. |
| [24] | Yang D H, Zhang Z J. 2000. Effects of the Biot and the squirt-flow coupling interaction on anisotropic elastic waves. Chinese Science Bulletin, 45(23): 2130-2138. |
| [25] | Yang D H, Zhang Z J.2002. Poroelastic wave equation including the Biot/squirt mechanism and the solid/fluid coupling anisotropy. Wave Motion, 35(3): 223-245. |
| [26] | Yang K D, Song G J, Li J S. 2011. FCT compact difference simulation of wave propagation based on the Biot and the squirt-flow coupling interaction. Chinese J. Geophys. (in Chinese), 54(5): 1348-1357, doi: 10.3969/j.issn.0001-5733.2011.05.024. |
| [27] | Yang K D, Yang D H, Wang S Q. 2002a. Wavefield simulation based on the Biot/Squirt equation. Chinese J. Geophys. (in Chinese), 45(6): 853-861. |
| [28] | Yang K D, Yang D H, Wang S Q. 2002b. Numerical simulation of elastic wave propagations based on the transversely isotropic BISQ equation. Acta Seismologica Sinica, 24(6): 599-606. |
| [29] | Zhang X W, Wang D L, Wang Z J, et al. 2010. The study on azimuth characteristics of attenuation and dispersion in 3D two-phase orthotropic crack medium based on BISQ mechanism. Chinese J. Geophys. (in Chinese), 53(10): 2452-2459, doi: 10.3969/j.issn.0001-5733.2010.10.019. |
| [30] | 李红星,刘财,陶春辉. 2007. 基于横向各向同性BISQ模型的弹性波高阶交错网格有限差分数值模拟. 石油地球物理勘探, 42(6): 686-693. |
| [31] | 李红星,陶春辉,周建平等. 2009. 双相各向异性介质中波场速度与衰减特征分析.石油地球物理勘探,44(4): 457-465. |
| [32] | 刘财, 李红星, 陶春辉. 2007. 基于BISQ模型的各向同性孔隙介质弹性波三维交错网格高阶有限差分数值模拟. 世界地质, 26(4): 501-508. |
| [33] | 刘财,兰慧田,郭智奇等. 2013. 基于改进BISQ机制的双相HTI介质波传播伪谱法模拟与特征分析. 地球物理学报,56(10): 3461-3473, doi: 10.6038/cjg20131021. |
| [34] | 刘璐,刘洪,刘红伟. 2013. 优化15点频率-空间域有限差分正演模拟. 地球物理学报, 56(2): 644-652, doi: 10.6038/cjg20130228. |
| [35] | 聂建新, 杨顶辉, 杨慧珠. 2004. 基于非饱和多孔隙介质BISQ模型的储层参数反演. 地球物理学报, 47(6): 1101-1105. |
| [36] | 聂建新,杨顶辉,巴晶. 2010. 含泥质低孔渗各向异性黏弹性介质中的波频散和衰减研究. 地球物理学报, 53(2): 385-392, doi: 10.3969/j.issn.0001-5733.2010.02.016. |
| [37] | 吴国忱, 罗彩明, 梁楷. 2007. TTI介质弹性波频率-空间域有限差分数值模拟. 吉林大学学报(地球科学版), 37(5): 1023-1033. |
| [38] | 杨宽德,杨顶辉,王书强. 2002a. 基于Biot-Squirt方程的波场模拟. 地球物理学报, 45(6): 853-861. |
| [39] | 杨宽德,杨顶辉,王书强. 2002b. 基于横向各向同性BISQ方程的弹性波传播数值模拟. 地震学报, 24(6): 599-606. |
| [40] | 杨宽德,宋国杰,李静爽. 2011. Biot流动和喷射流动耦合作用下波传播的FCT紧致差分模拟. 地球物理学报,54(5): 1348-1357, doi: 10.3969/j.issn.0001-5733.2011.05.024. |
| [41] | 张显文,王德利,王者江等. 2010. 基于BISQ机制三维双相正交裂隙各向异性介质衰减及频散方位特性研究. 地球物理学报, [JP3]53(10): 2452-2459, doi: 10.3969/j.issn.0001-5733.2010.10.019. |
 2014, Vol. 57
2014, Vol. 57

