2. 西南交通大学高温高压物理研究所, 成都 610031
2. Laboratory of High Pressure Physics, Southwest Jiaotong University, Chengdu 610031, China
辉长岩主要是长石类矿物和辉石类矿物组成的矿物集合体,其造岩矿物在地壳中普遍存在,因此辉长岩在地壳中普遍发育.不仅在地球,类地行星也可能普遍出现辉长岩.“阿波罗计划”登月带回的月球岩石样品和掉落在地球表面的月球陨石表明,月球表层有着大量的辉长岩.Wood等(1970)建立了以辉长岩为“月幔”的月球模型.
结合地震波的探测数据,确立岩石、矿物热状态方程,可以有效地帮助人们限定地幔的物质组成,进而帮助人们了解、认识地幔的动力学过程.地壳岩石可以俯冲进入地幔,甚至到达核幔边界(CMB)( Vander Hilst et al., 1997;Hutko et al., 2006).在俯冲过程中,岩石经历了高温高压过程.冲击波加载方法可以提供这种“高温高压环境”.通过对样品进行冲击压缩实验,我们可以得到岩石的物态方程以及相变的相关信息,这对于地球深部物质横向不均匀性,地幔对流模型的确定有重大意义.
早年McQueen等(1967)进行了几类常见岩石的冲击波实验,发现与辉长岩成分类似的辉绿岩在大约 30 GPa下表现出相变行为. 进一步,McQueen等又指出9~10 GPa压力下辉绿岩样品也可能发生了相变,但没有指出可能的相变关系.考虑到当时的测量条件,他们得到的实验数据精度不高,而且McQueen等使用天然岩石样品进行测试,这进一步加剧了实验数据的分散性.
长石和辉石是辉长岩的主要造岩矿物.Ahrens、 Jeanloz、McQueen等对斜长石、微斜长石、钙长石、钠长石等矿物进行了冲击压缩实验(McQueen et al., 1967;Ahrens et al., 1969b;Ahrens and Liu, 1973;Jeanloz and Ahrens, 1980).这些实验重点放在了高压相上,从D-u线和压力-密度关系看,不同的长石 矿物在30~40 GPa下完全进入了高压相.Ringwood 等(1967)实验发现,高压下钾长石会变成锰钡矿结构的新相(K-Holl and ite).根据此结果,Ahrens认为不同长石单元在冲击压缩下,其高压相可能都是锰钡矿结构.而随后的一系列静高压实验表明,长石三个单元组分,钾长石、钠长石、钙长石在30~40 GPa下的高压相是不同的.所以在冲击压缩下,混合相区(Mixed Phase Regime)矿物组合也是不同的.长石三个单元组分在较低的压力下都会分解成新矿物+石英,随着压力的升高这种矿物组合又会重新组合成更为稳定的高压相(详见3.3节).McQueen、Trunin、Ahrens、Jeanloz对几种斜方辉石 进行了冲击压缩实验(Trunin et al., 1965;McQueen et al., 1967;Ahrens and Gaffney, 1971;Jeanloz and Ahrens, 1975).相变压力随着铁含量的变化 而变化,大约在20 GPa开始相变,大约在40~50 GPa 完全进入高压相.根据静高压实验结果,这个高压相 可以推断为钙钛矿结构(Perovskite structure).低 于钙钛矿稳定压力之下可存在钛铁矿相(Akimotoite),更低的压力下还可以分解为橄榄石高压相(Wadsleyite、 Ringwoodite)和石英(详见3.3节).
本文在中等压力之下(14~39 GPa)对辉长岩样品进行了冲击压缩实验,避开了高压相,分析了样品中主要的冲击相变关系及状态方程. 2 实验方法与实验结果 2.1 实验样品
实验所用辉长岩样品采集于济南地区,主要成分为斜方辉石和斜长石.为了保证实验样品成分的均匀性,去除大颗粒单晶对实验的影响,我们利用钨钢将天然岩石样品打磨成粉末(200目),最后在真空环境下将粉末热压烧结成型.实验样品加工成直径12 mm,厚度大约为3.5 mm的圆柱体.样品中冲击波速度的确定,受样品平整度影响很大,所以对样品平整度进行了严格的控制,经过抛光后,样品中心与90°圆心角展开的4个边沿点之间的厚度差控制在0.01 mm以下. 2.2 实验装置和方法
通过二级轻气炮产生的高压气体推动飞片高速撞击实验靶(如图 1所示)产生冲击波(Syono and Goto, 1980;王金贵,2001).冲击波通过靶盘进入样品所在的平面.光纤在冲击波作用下被剧烈压缩,温度 随之升高,进而发光.光信号通过高温计(Pyrometer)转化成电信号记录在数字示波器上.通过光纤自身发光来判断冲击波到达时间,测量出样品所在前后界面的时间差,从而计算得出冲击波在样品中的传播速度.由于光纤对光信号非常灵敏,只要有一点杂散光出现,就会影响对冲击波到达时间的判断,因此在光纤所在面贴了一层20 μm厚的铝箔进行挡光处理,从而去除了杂散光的影响.
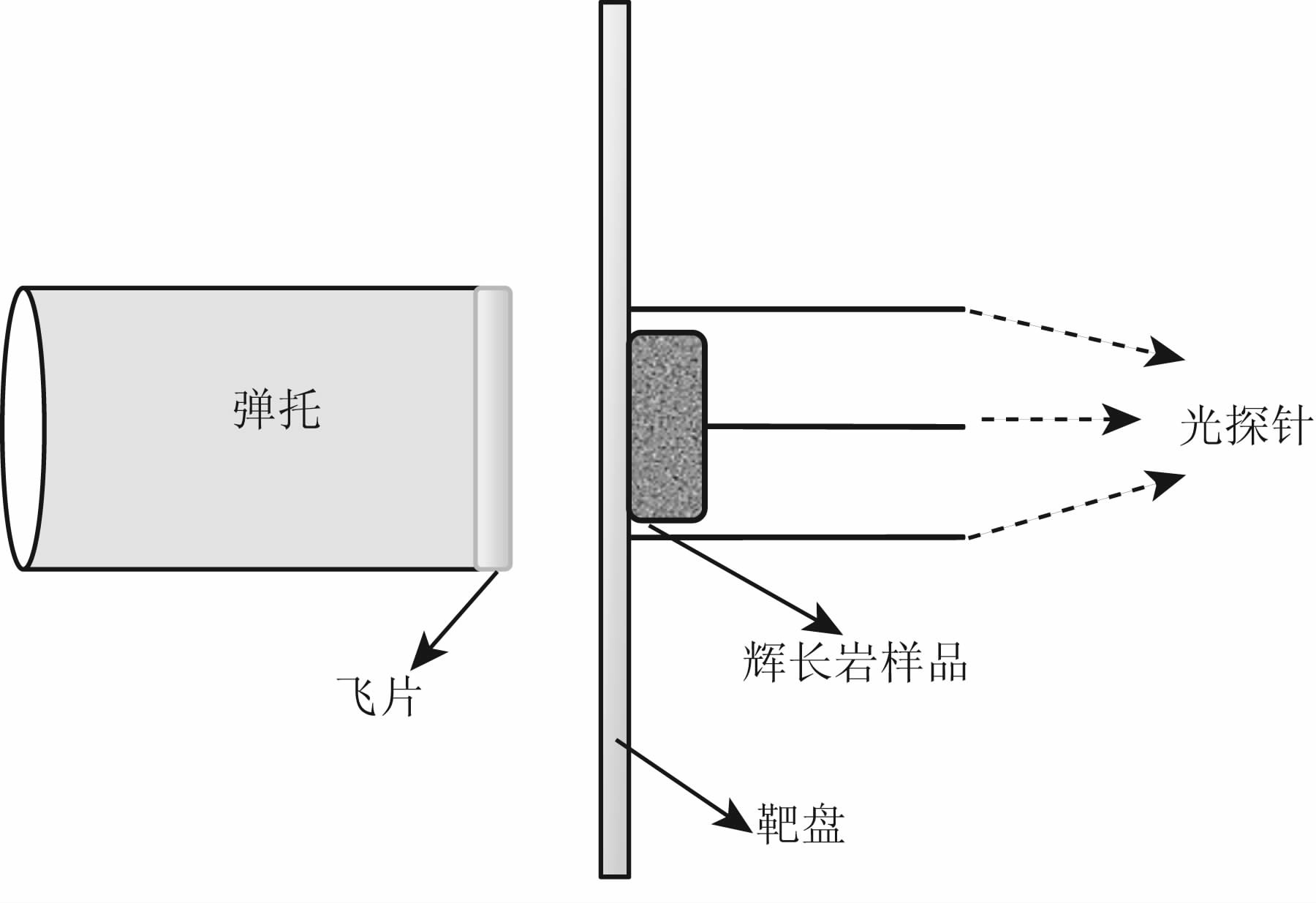 |
图 1 实验装置示意图 Fig. 1 The configuration for shock wave experiments |
飞片由低阻抗的聚碳酸酯和金属片组成.飞片飞离炮口后,依次通过三个磁环(总长150 mm),通过切割磁力线产生电信号,从而确定飞片击靶速度.
金属片和靶盘由冲击阻抗(Dynamic Impedance)已知的铝材料(LY12-硬铝合金)制作,这种利用相同材料碰撞的实验方式称为对称碰撞(Symmetric Impacts),其优点为,后期数据处理较非对称碰撞简单.对称碰撞条件下,冲击波阵面后的粒子速度等于1/2飞片碰撞靶盘的速度.通过阻抗匹配方法,结合平面冲击波基本关系,可以得到粒子速度和压力-密度曲线(如图 2、3所示).
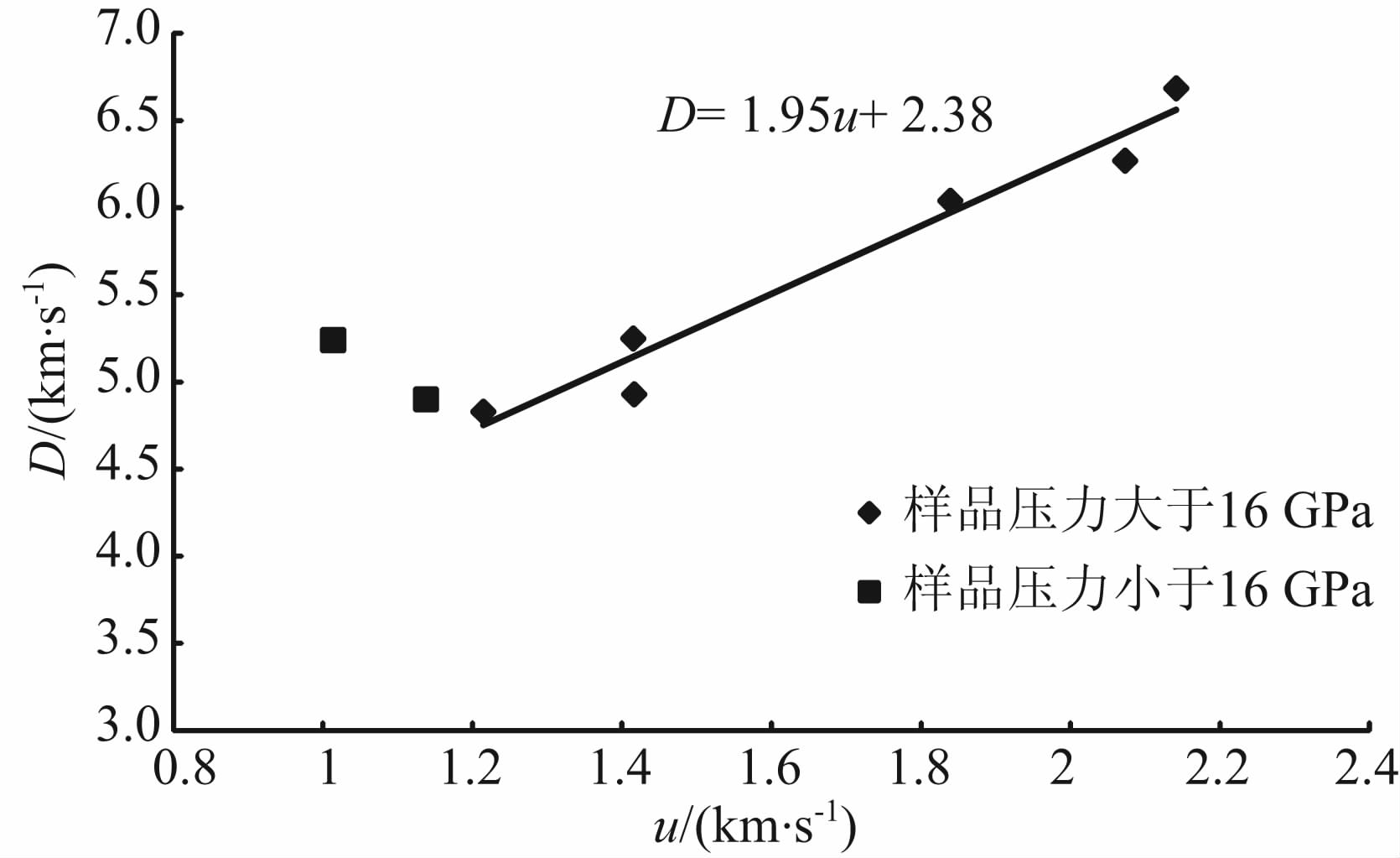 |
图 2 辉长岩样品的冲击波速度与粒子速度关系(D-u关系) Fig. 2 Shock velocity versus particle velocity for gabbro |
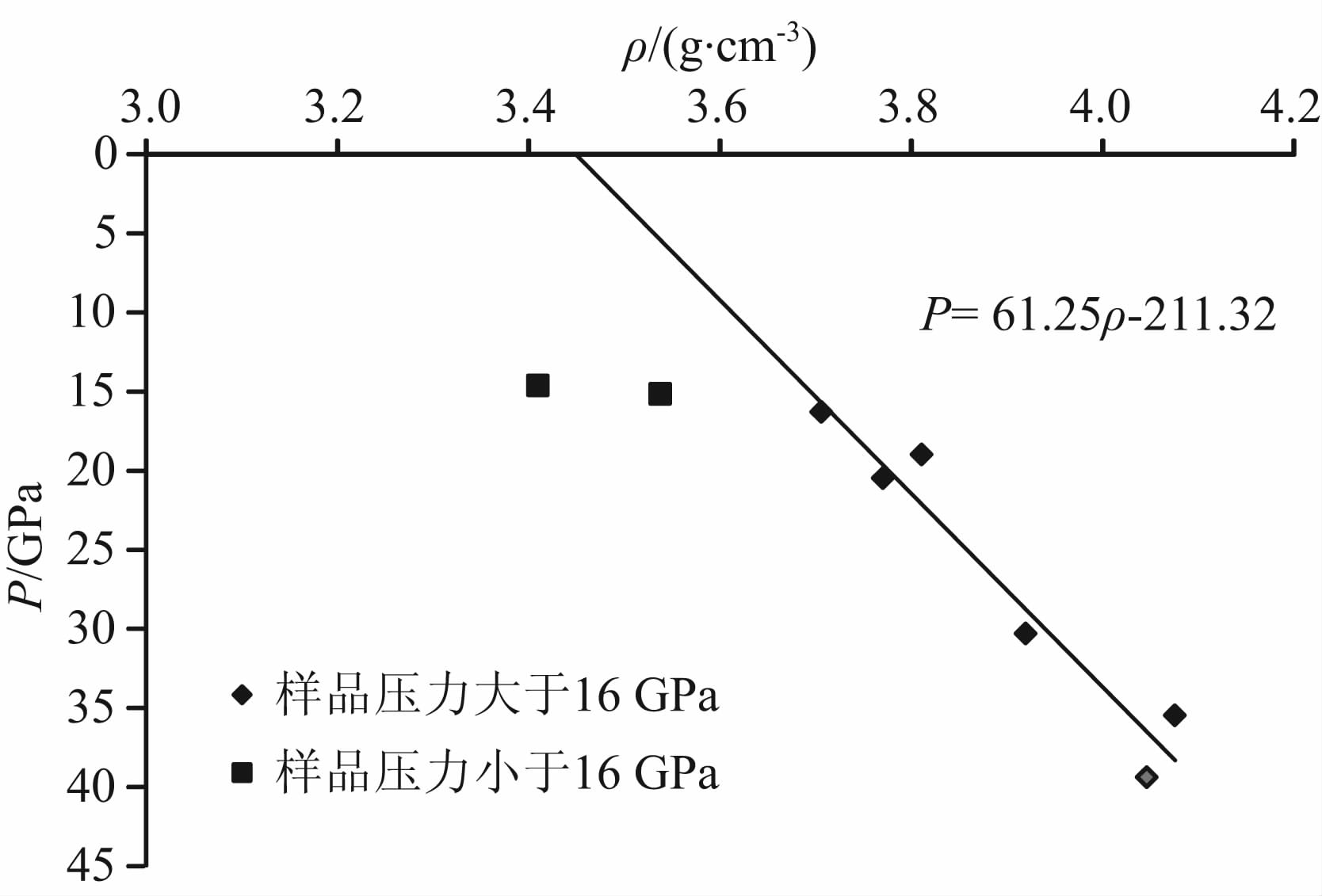 |
图 3 辉长岩样品的冲击密度与冲击压力关系 Fig. 3 Shock density versus shock pressure for gabbro |
飞片撞击样品的过程就是把飞片的动能转化为样品动能和内能的过程.平面冲击波是强间断面,波阵面后物质状态的改变可以看成是瞬间完成的.波阵面前后物质需要满足质量守恒,动量守恒以及能量守恒的关系,根据这三个守恒关系,我们可以得到平面冲击波遵循的基本关系式(经福谦,1999)
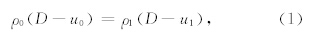
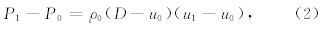

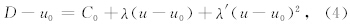

| 表 1 辉长岩样品的冲击压缩数据 Table 1 Shock wave data and calculated shock states |
Grüneisen参数是建立状态方程的重要参数,可根据不同孔隙度物质的Grüneisen物态方程和冲击压缩线确定Grüneisen参数:

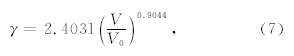
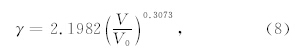


大量的实验研究表明,材料的冲击波速度(D)与粒子速度(u)成线性关系.当D-u线斜率发生变化时,表明材料发生了相变.从图 2辉长岩样品的D-u关系中可以看到明显的斜率变化,这表明从大约16 GPa开始(如图 3所示),辉长岩进入了高压相.高压相的密度是地学当中比较关心的问题.McQueen等最早用冲级压缩线来得到高压相的零压密度.McQueen等通过原始冲击压缩数据得到亚稳相的冲级压缩线(Metastable Hugoniot),从而得到零压密度(McQueen et al., 1967).将原始冲击线的高压部分线性外推可以得到表观零压密度,根据(1)、(2)、(5)式可以得到冲击压力的解析表达式:
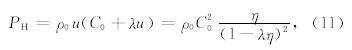
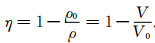 . 利用线性外推无法准确描述(11)式上每个点,所以这种方法只能得到近似的结果,但线性外推结果可以被看做是上限来限定本文的计算结果.将实验数据线性外推,得到高压相的表观零压密度为3.45 g·cm-3(如图 3所示),为了准确获得高压相的零压密度,利用等熵线来确定(Ahrens et al., 1969a).根据热力学关系,冲击压缩过程与等熵过程有如下关系:
. 利用线性外推无法准确描述(11)式上每个点,所以这种方法只能得到近似的结果,但线性外推结果可以被看做是上限来限定本文的计算结果.将实验数据线性外推,得到高压相的表观零压密度为3.45 g·cm-3(如图 3所示),为了准确获得高压相的零压密度,利用等熵线来确定(Ahrens et al., 1969a).根据热力学关系,冲击压缩过程与等熵过程有如下关系:
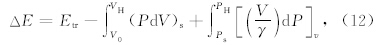
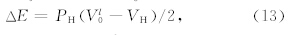


考虑到岩石样品内的主要矿物组成是长石和辉石,因此重点考虑斜长石与斜方辉石的相变问题.斜 长石系列中钠长石(Albite)单元与钙长石(Anorthosite)单元有着不同的高压相变行为.钠长石在较低压力下分解为硬玉(Jadeite)和石英(Quartz)(Ab=Jd+Qz,2~23 GPa)(Birch and Le Comte,1960;Liu,1978),随着压力的升高石英不断相变为高压相,大约在23GPa硬玉进一步分解为铁酸钙结构的CF相和斯石英(Stishovite)(Yagi et al., 1994;Tutti et al., 2000),这两相可以稳定到70 GPa(Ab=CF+St,23~70 GPa),这个过程可以看作是钠长石晶体中不断析出二氧化硅的过程.钙长石在 低压下分解为钙铝榴石(Grossular)、蓝晶石(Kyanite)和石英(Quartz)(An=Gr+Ky+Qz,1~14 GPa)(Boyd and England ,1961;Hariya and Kennedy, 1968),随着压力的升高,钙铝榴石可以与蓝晶石反应生成富铝的CAS相,或者与斯石英反应生成钙钛矿相(Gautron et al., 1996;Liu et al., 2012).除此之外,还有研究表明存在锰钡矿结构(Holl and ite)的长石 高压相(Ringwood et al., 1967;Gautron and Madon, 1994). 目前研究发现只有钾长石单元的高压相(Holl and ite-structure)才是热力学稳定的,斜长石系列只有在金刚石压砧(DAC)和陨石冲击中才发现有锰钡矿结构的高压相.
斜方辉石随着压力的升高,晶胞逐渐变形,从斜方晶系过渡到单斜晶系,压力进一步升高,在较低温度下会分解成橄榄石高压相(β相、γ相)和斯石英.在较为窄的温压条件下,上述产物会重新变成钛铁矿相(Akimotoite),更高的压力下会变成钙钛矿相(Ringwood and Major, 1966;Sawamoto,1987;Anderson,1989).
在本次实验的温压条件下可能会发生以上阐述的各类相变,上述变化大致可以分为“分解生成石英与矿物集合体”和“矿物重新组合为新相”两大类.多相的化学反应需要大量的原子、离子、分子的迁移来完成,除了粉末物质的冲击过程外,一般固体中的冲击波很难完成这种微观粒子的迁移和混合,从而确保化学反应的进行.换言之,冲击加载下发生分解反应和固-固相变的可能性更大(加载条件下材料还没有熔化).结合辉长石在16GPa相变的事实,推断样品中可能的相变关系为斜长石的分解反应和斜方辉石的分解反应.根据这个思路,把石英的冲击波数据与数据进行了对比.融石英的D-u线形态(如图 4所示)与辉长岩样品的D-u形态很类似,其D-u线拐点处的冲击波压力为17 GPa左右,辉长岩样品D-u线拐点处的压力为16 GPa左右.如果把样品成分简化为斜长石与斜方辉石1 ∶ 1(斜方辉石中含铁量较少),考虑钠长石分解为硬玉和石英,由于斯石英的产生(忽略辉石的变化),计算得到的矿物集合体的密度为3.419 g·cm-3.这结果与从等熵线得到的高压相的零压密度一致.用同样的简化模型计算斜方辉石分解产生橄榄石和斯石英得到的零压密度为3.85 g·cm-3,这结果大大超出得到的辉长石高压相的零压密度.另外在陨石坑中也发现了斜长石分解的证据(James,1969),考虑到实验误差的影 响,辉长石样品的冲击相变行为主要由斜长石分解产生的石英的高压相变控制.在冲击压缩中,D-u线较平缓的区域往往代表高压相与低压相共存的区域(Mixed Phase Regime),根据融石英的D-u线,大于17 GPa的冲击压力后石英完全变成斯石英,而富镁斜方辉石分解为橄榄石(β相)和斯石英也在这个压力点附近,很可能是这个反应导致D-u线斜率比常见材料高(大多数金属与无机物D-u线斜率在1.5左右).
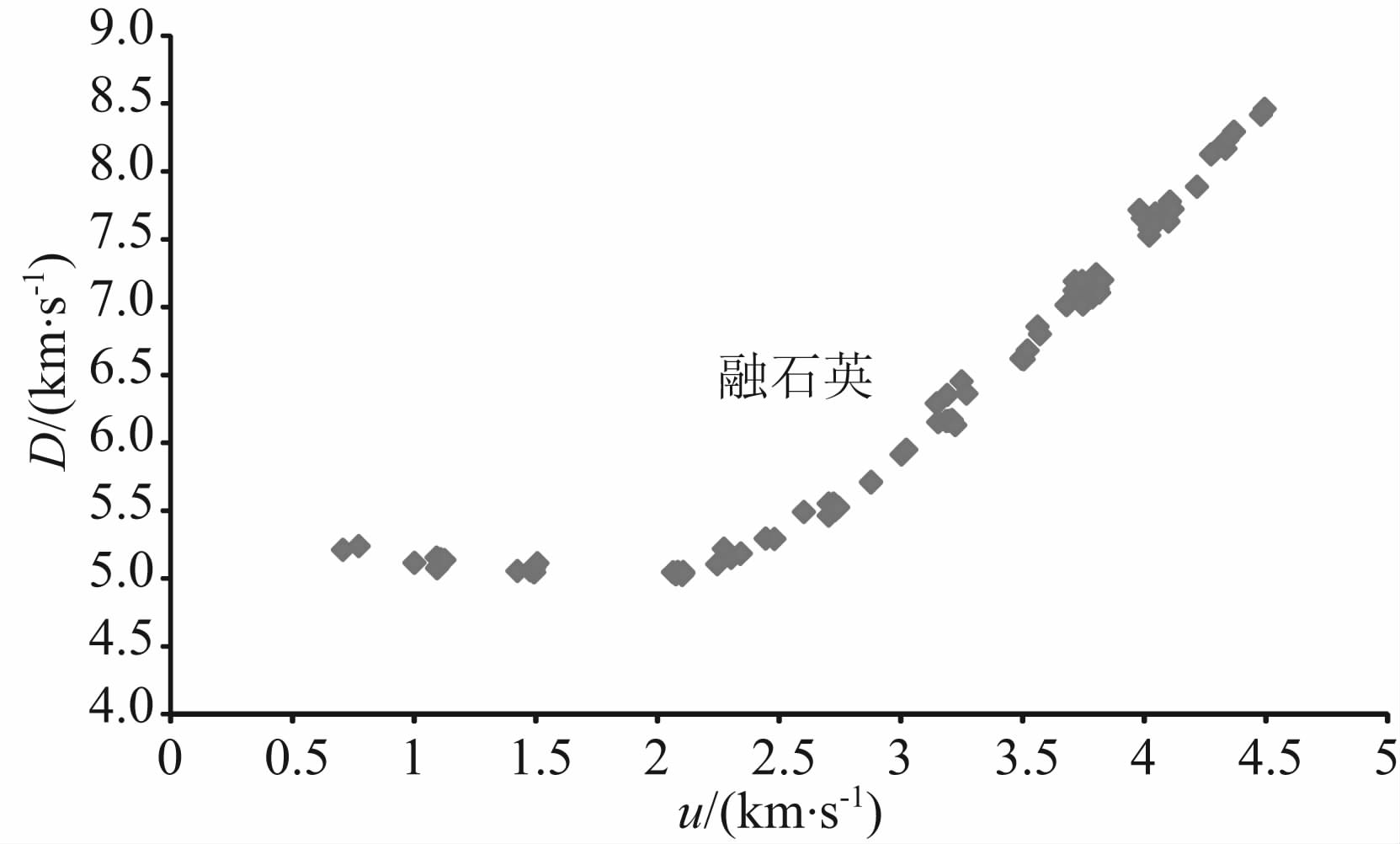 |
图 4 融石英中冲击波速度与粒子速度关系(数据来源于文献Marsh,1980) Fig. 4 Shock velocity versus particle velocity for fused quartz(data from reference Marsh,1980) |
在14~39 GPa压力范围内进行了冲击波加载实验,从D-u线和压力-密度曲线中可以看出相变发生在16 GPa左右.本文使用的样品有大约8%的孔隙度,通过孔隙材料与密实材料的Grüneisen物态方程的关系,计算出了辉长岩的常压Grüneisen系数为2.3.通过等熵途径与冲击压缩途径的关系,计算出了Birch-Murnaghan型的等熵压缩线,高压相的K0、K′ 0分别为150.6 GPa、1.02.根据等熵线确定的高压相的零压密度为3.41 g·cm-3.石英相变为斯石英导致的矿物集合体密度为3.419 g·cm-3,两个结果吻合度很好,说明了相变是由于矿物体系分解生成的石英在高压下的相变所导致的.
致谢 对张明建、薛学东两位老师在实验上的细心指导及博士研究生张宁超、硕士研究生康成在实验过程的帮助表示衷心的感谢.
| [1] | Ahrens T J, Anderson D L, Ringwood A E. 1969a. Equations of state and crystal structures of high-pressure phases of shocked silicates and oxides. Reviews of Geophysics, 7(4): 667-707. |
| [2] | Ahrens T J, Petersen C F, Rosenberg J T. 1969b. Shock compression of feldspars. Journal of Geophysical Research, 74(10): 2727-2746. |
| [3] | Ahrens T J, Gaffney E S. 1971. Dynamic compression of enstatite. Journal of Geophysical Research, 76(23): 5504-5513. |
| [4] | Ahrens T J, Liu H P. 1973. A shock-induced phase change in orthoclase. Journal of Geophysical Research, 78(8): 1274-1278. |
| [5] | Anderson D L. 1967. A Seismic Equation of State. Geophys. J. R. Astr. Soc., 13: 9-30. |
| [6] | Anderson D L. 1989. Theory of the Earth. Boston: Blackwell Scientific Publications. |
| [7] | Birch A F, LeComte P. 1960. Temperature-pressure plane for albite composition. American Journal of Science, 258(3): 209-217. |
| [8] | Birch F. 1961. Composition of the earth's mantle. Geophysical Journal of the Royal Astronomical Society, 4(Supplement 1): 295-311. |
| [9] | Boyd F R, England J L. 1961. Melting of silicates at high pressures. Carnegie Inst. Wash. Year Book, 60: 113. |
| [10] | Cong B L,Ye D N, Zheng X Z,et al.1974. The mean atomic weights of rocks and geological problems. Chinese Journal of Geology (in Chinese),1:43-58. |
| [11] | Gautron L, Madon M. 1994. A study of the stability of anorthite in the PT conditions of Earth's transition zone. Earth and Planetary Science Letters, 125(1): 281-291. |
| [12] | Gautron L, Kesson S E, Hibberson W O. 1996. Phase relations for CaAl2Si2O8 (anorthite composition) in the system CaO-Al2O3-SiO2 at 14 GPa. Physics of the Earth and Planetary Interiors, 97(1): 71-81. |
| [13] | Hariya Y, Kennedy G. 1968. Equilibrium study of anorthite under high pressure and high temperature. American Journal of Science, 266(3): 193-203. |
| [14] | Hutko A R, Lay T, Garnero E J, et al. 2006. Seismic detection of folded, subducted lithosphere at the core-mantle boundary. Nature, 441(7091): 333-336. |
| [15] | James O B. 1969. Jadeite: Shock-induced formation from oligoclase, Ries crater, Germany. Science, 165(3897): 1005-1008. |
| [16] | Jeanloz R, Ahrens T J. 1975. Pyroxenes and olivines: Structural implications of shock-wave data for high pressure phases. California: Inst. of Tech.,Pasadena. Seismological Lab. |
| [17] | Jeanloz R, Ahrens T J. 1980. Anorthite: thermal equation of state to high pressures. Geophysical Journal of the Royal Astronomical Society, 62(3): 529-549. |
| [18] | Jeanloz R. 1989. Shock wave equation of state and finite strain theory. Journal of Geophysical Research: Solid Earth (1978—2012), 94(B5): 5873-5886. |
| [19] | Jing F Q .1999. Introduction to Experimental Equation of State (in Chinese). Beijing : Science Press. |
| [20] | Liu L G. 1978. High-pressure phase transformations of albite, jadeite and nepheline. Earth and Planetary Science Letters, 37(3): 438-444. |
| [21] | Liu X, Ohfuji H, Nishiyama N, et al. 2012. High-P behavior of anorthite composition and some phase relations of the CaO-Al2O3-SiO2 system to the lower mantle of the Earth, and their geophysical implications. Journal of Geophysical Research: Solid Earth (1978—2012), 117(B9). |
| [22] | Marsh S P. 1980. LASL Shock Hugoniot Data. Univ. of California Press. |
| [23] | McQueen R G, Marsh S P, Fritz J N. 1967. Hugoniot equation of state of twelve rocks. Journal of Geophysical Research, 72(20): 4999-5036. |
| [24] | Ringwood A E, Major A. 1966. High-pressure transformations in pyroxenes. Earth and Planetary Science Letters, 1(5): 351-357. |
| [25] | Ringwood A E, Reid A F, Wadsley A D. 1967. High-pressure KAlSi3O8, an aluminosilicate with sixfold coordination. Acta Crystallographica, 23(6): 1093-1095. |
| [26] | Sawamoto H. 1987. Phase diagram of MgSiO3 at pressures up to 24 GPa and temperatures up to 2200°C: Phase stability and properties of tetragonal garnet. Geophysical Monograph Series, 39: 209-219. |
| [27] | Syono Y, Goto T. 1980. A two-stage light gas gun for shock wave research. Science reports of the Research Institutes, Tohoku University. Ser. A, Physics, chemistry and metallurgy, 29: 17-31. |
| [28] | Trunin R F, Gon'Shakova V I, Simakov G V, et al. 1965. A study of rocks under the high pressures and temperatures created by shock compression. Izv. Acad. Sci., USSR, Phys. Solid Earth, 9: 1-12. |
| [29] | Tutti F, Dubrovinsky L S, Saxena S K. 2000. High pressure phase transformation of jadeite and stability of NaAlSiO4 with calcium-ferrite type structure in the lower mantle conditions. Geophysical Research Letters, 27(14): 2025-2028. |
| [30] | Vander Hilst R D, Widiyantoro S, Engdahl E R. 1997. Evidence for deep mantle circulation from global tomography. Nature, 386(6625): 578-584. |
| [31] | Walsh J M, Christian R H. 1955. Equation of state of metals from shock wave measurements. Physical Review, 97: 1544-1556. |
| [32] | Wang J G.2001. Principle and Technology of Gas Gun (in Chinese). Beijing : National Defense Press. |
| [33] | Wood J A, Dickey Jr J S, Marvin U B, et al. 1970. Lunar anorthosites and a geophysical model of the moon. Proceedings of Apollo Lunar Sci Cord, 1: 965-388. |
| [34] | Yagi A, Suzuki T, Akaogi M. 1994. High pressure transitions in the system KAlSi3O8-NaAlSi3O8. Physics and Chemistry of Minerals, 21(1-2): 12-17. |
| [35] | 从柏林, 叶大年, 郑学正等. 1974. 岩石的平均原子量及地质问题. 地质科学, (1): 43-58 . |
| [36] | 经福谦. 1999. 实验物态方程导论. 北京: 科学出版社. |
| [37] | 王金贵. 2001. 气体炮原理与技术, 北京: 国防工业出版社. |
 2014, Vol. 57
2014, Vol. 57


