2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
1 引言
大陆岩石圈在漫长的地史时期乃是一个非均一、非连续,而又具有复杂流变学特性的综合体.它在地球的广阔空间表现出物质结构的变化和构造演化的热历史,而流体和熔融体的相互作用则改变了其流变特征的本构关系.
通道流模型旨在解释一些碰撞造山带共有的腹地变质特征(Godin et al., 2006),并可以以青藏高原为例来表征一些造山带地域,相对于较为刚性的上地壳和岩石圈上地幔,而把处于中间层的中、下地壳视为强度较低的塑性流变层,即具有更强的流动性.因而在高原巨厚地壳的重力差异驱使下或是上地幔的拖曳作用下易于发生流动而形成通道流,且用通道流模型解释了喜马拉雅—青藏高原系统及其它古老造山带动力学演化的有关特征.它使得主中央逆冲断裂与藏南拆沉系断裂具同时代特性与GHS(Greater Himalayan Sequence)顶部的动态反转一致,故导致了喜马拉雅结晶中心从青藏高原腹地向南挤出和剥蚀.不仅如此,还给出了造山尺度范围内倒置的变质岩序列的可能定量的解释,以及构造过程和地表过程的有效耦合.流体动力学中定义的一维基本方程被作为通道流模型的数学理论用于这一模型的研究中(Turcotte and Schubert, 2002),此后有很多研究工作在这一基点上发展了这一方程,以满足特定研究的需要(Grujic,2006).
通道流意指在上、下两个近乎刚性的介质层,即地壳中存在着一层塑性流动强度极高(或发生大规模部分熔融)的岩层,该层的韧性大,其变形犹如“通道”中流动的流体.由于在高原侧向存在静岩压力的梯度变化,这些黏性“流体”可以从高原的内部向其边缘流动(Batchelor,2000;Turcotte and Schubert, 2002).通道流存在的边界条件必须是低黏度的物质被高黏度的物质所包围,形成物理意义上的通道.高级石英长石质岩和复片麻岩最有可能是沿地壳通道挤出的物质,而熔体弱化最有可能是促进通道流的粘度降低机制.通道流模型认为低黏度区域的特异黏滞系数往往是由部分熔融体或含水流体所致,但只靠给定的黏滞系数为约束导出的下地壳流模型是难以令人信服的.很多地质学家在对青藏高原的研究中,是首先认为它具有流变性的,在此前提下设定下地壳的上边界和Moho界面之间为强度极低的塑 性流变层,当必会设定下地壳具有低黏滞系数(Royden et al., 1997; Zhong,1997; Clark and Royden, 2000; Beaumont et al., 2001; Flesch et al., 2001; Shen et al., 2001; Bürgmann and Dreson, 2008).这些认识多为依据浅表层地质过程和GPS观测的推断并给定下地壳特异黏滞系数的数值模拟,却并没有得到深部地球物理探测反演刻划精细壳、幔结构的支持(Flesch et al., 2005; Hilley et al., 2005).针对这些现象,国内学者近年来也开展了一系列的研究工作,如王晓芳和何建坤(2012)根据流体动力学原理,进一步约束了青藏高原不同区位通道流现象发生所需下地壳物质的黏滞系数.我们曾基于青藏高原深部地震所给出的一些规律性结果,针对通道流模型的一些理论或假设基础,对青藏高原下方物质流动所需要的边界条件进行了数值模拟工作(杨辉等,2013),认为青藏高原下地壳与上地幔盖层物质作为坚硬的固态物质相连,不具备下地壳可运动的边界条件,难以在Moho界面的任意地域发生相互运动,即下地壳物质构不成通道流.若深部壳、幔物质中存在可供高速物质运动的边界条件,则只能在局部和特异环境下才能实现.显见,在壳、幔介质中只有以上地壳底部的低速层为上滑移面(低速层与上地壳解耦),以上地幔软流圈顶部为下滑移面(地幔盖层,或称岩石圈地幔与软流圈解耦),才可能在足够强度的力系作用下促使“下地壳+岩石圈盖层”物质发生同步运移.
2 问题的提出Moho面作为地球深部一级间断面,是理解区域构造属性和演化的重要界面——壳-幔边界.Moho界面深度(通常表征地壳厚度)记录了地壳的生长过程,并经历了地球内部物质运动的动力学作用,是人们深化认识地球本体的核心证据之一.
依据高精度人工源地震探测与反演对精细壳、幔结构的刻划,使人们清晰地认识到;青藏高原的壳-幔边界(Moho界面)被一系列规模不一,产状各异的深、大断裂所切割,并分割为喜马拉雅地体、拉萨地体、羌塘地体、巴彦喀拉地体和昆仑地体,而且起伏变化强烈,极为凹凸不平.在常见的通道流模型中,下地壳和上地幔盖层之间通常都为平缓界面,数值模拟工作常简化为平滑的约束界面.但近年的深部地震探测工作揭示出沿Moho边界存在一系列断裂带,其中一些深大断裂甚至从Moho面一直延伸至中地壳(图 1).这一现象的存在,显然是传统的具有平坦Moho界面的通道流数值模拟所欠考虑的(Qiu,2013);另一方面,青藏高原的Moho界面被诸多深大断裂所切割,它不仅不可能构成一个下地壳运移的滑移面,而应是一个阻止下地壳物质沿其界面运动的阻隔面(图 1),若中、下地壳相对于上地壳和地幔盖层强行运动,则必须有足够巨大的力施加于下地壳介质上,而在其强迫运移的过程中则会产生一系列新的物理-力学响应现象,如高强度的摩擦生热效应、同深、一定强度的破裂效应及一系列小地震的发生等.这种效应当必会影响其上、下周边介质产生变形和地震波场及速度的变化,然而尚迄今未见这些现象的产生(滕吉文,2005;滕吉文等,2008).
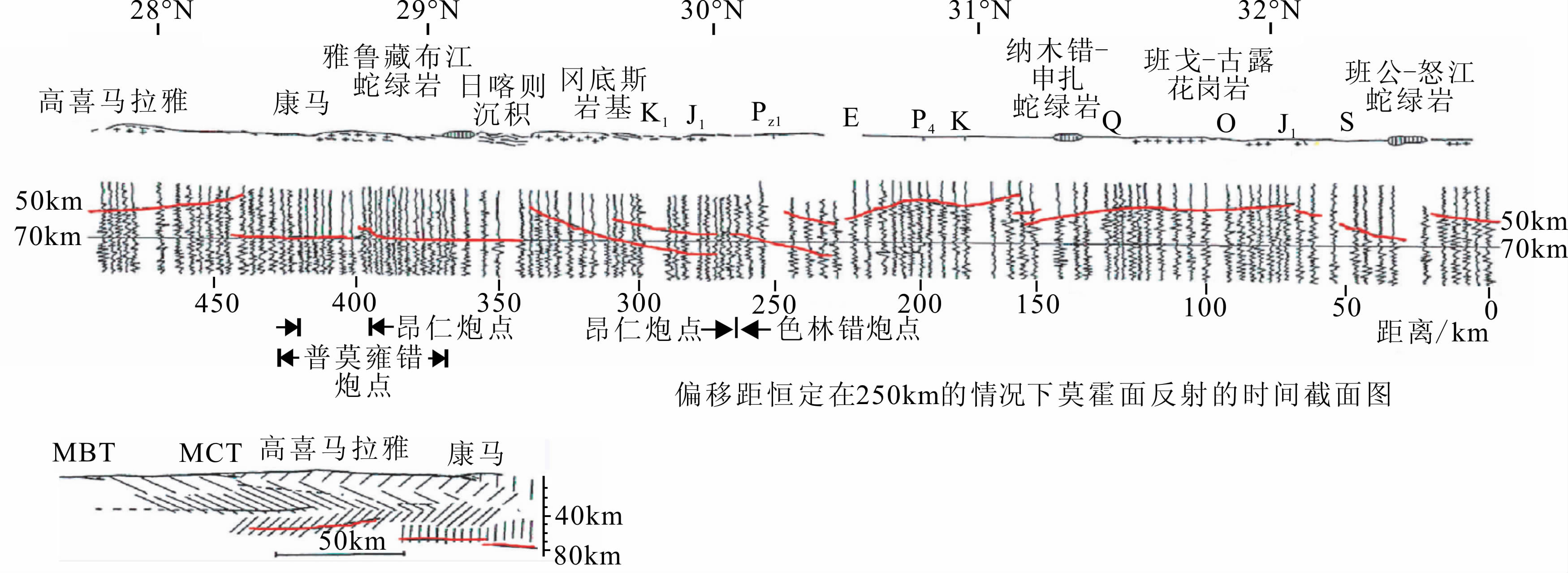 | 图 1 亚东—当雄以西130 km处南北向新吉—塔马—孜松地带扇形地震剖面 与Moho界面起伏(Hirn et al., 1984a,b;滕吉文等,2012) Fig. 1 North-south seismic profile and Moho relief of Xinji-Dama-Zisong area about 130 km west of Yadong-Dangxiong(Hirn et al., 1984a,b; Teng et al., 2012) |
近30年来,一系列高精度的深部地球物理工作研究了青藏高原不同地体之间各种Moho界面深度和主要缝合带下Moho界面的错断(Hirn et al., 1984a,b; Haines et al., 2003; Li et al., 2006; Shi et al., 2009; Tseng et al., 2009; Karplus et al., 2011; Zhang et al., 2011a,b; Gao et al., 2013).青藏高原的Moho界面并不稳定,结构复杂且具有横向的不均匀性,垂直落差可达20 km(Hirn et al., 1984a).Zhang等(2011a)总结了过去35年间(1974—2009)23条宽角反射剖面,得出地壳厚度在青藏高原南部约70~75 km,青藏高原北部、北东和南东均约60~65 km.Gao等(2013)利用深地震反射剖面揭示出了对青藏高原腹地地壳结构和Moho地形的新约束.
至今各国开展的通道流数值模拟工作多是基于Moho界面为平缓的刚性界面,本文将在考虑了青藏高原Moho界面的强烈起伏变化和错断的实际以及前期工作的基础上(杨辉等,2013),即在青藏高原Moho界面起伏情况下,进一步对通道流模型中物质有序运移的影响进行数值模拟,以达深化理解和探讨Moho界面起伏对通道流模型的响应.
3 计算模型的构建基于近40年来青藏高原深部地球物理探测所得到平均模型(滕吉文等,2012),本文采用的青藏高原地壳与上地幔分层结构的基本模型(杨辉等,2013)为:(1)上地壳,厚约20±5 km,P波速度为6.0 km·s-1;(2)下地壳厚度为40±10 km,P波速度为6.7±0.1 km·s-1;(3)上地幔盖层厚度为 30±10 km,P波速度为8.1±0.05 km·s-1;(4)地 壳低速层厚约8±2 km,P波速度为5.7±0.1 km·s-1,软流圈顶部埋藏深度为110±10 km,P波速度为7.4±0.1 km·s-1.设青藏高原岩石圈由三层介质组成,即上地壳、下地壳与岩石圈地幔,岩石圈下方为软流圈.取二维模型,深度为150 km,水平向宽度为300 km,在地质时间尺度下可近似的简化为黏弹性本构关系,即各圈层均采用Maxwell体的黏弹性本构关系以模拟其力学行为.为表征不同深度处圈层结构不同的演化过程,对各圈层介质采用不同的物理-力学参数.在地球动力学数值模拟计算中,对等效黏滞系数进行合理的估计,是能否取得可靠结果的基础.在青藏高原的数值模拟中常选用 “三明治”结构模型,即具有力学性质强的上地壳和岩石圈地幔.软弱层的存在则从力学性质上降低了研究区的等效力学强度,增大了内部位移及应变变形,有利于其间物质的流动.力学性质强的上地壳和岩石圈地幔黏度取1.0×1023Pa·s,以低速层的软弱层作为滑移面,其黏度取为1.0×1019Pa·s.下地壳和软流圈的力学性质要比上地壳和岩石圈地幔弱,比低速层滑移面强,黏度取1.0×1020Pa·s(杨辉等,2013).本文基本模型所采用的力学参数如表 1所示.
|
|
表 1 模型1的力学参数 Table 1 Mechanical parameters of model 1 |
根据青藏高原已开展的人工源深部地震探测数据所刻划的精细结构,或是在天然地震的观测中,不论是地震面波频散与相速度、群速度,地震体波与接收函数,还是地震层析成像所得结果来看,高原内部各块体之间Moho界面埋深的起伏差异为5~10 km不等(滕吉文等,2012;Gao et al., 2013).当Moho界面起伏变化时,对通道流模型是否会产生影响?又会产生何种影响?至今尚缺乏这方面的数值模拟工作.为了便于讨论和明晰起见,分别考虑上地壳和下地壳之间的低速层和软流圈顶面的滑移面存在与否,并构建了两个模型进行比较:
模型1:壳、幔速度结构考虑两个低速层,几何结 构考虑Moho界面的起伏.(a)上地壳厚度为23 km,Vp=5.9±0.1 km·s-1;(b)下方23~30 km深度 处为低速层,Vp=5.7±0.1 km·s-1;(c)30~70 km处为下地壳,Vp=6.7±0.1 km·s-1;(d)岩石圈地幔,即上地幔盖层位于70~97 km深处,Vp=8.1± 0.1 km·s-1;(e)软流圈顶部滑移面,位于深部97~103 km之间,Vp=7.8±0.1 km·s-1;(f)深度103~150 km之间为软流圈,Vp=7.4±0.1 km·s-1.
模型2:与模型1相比,仅考虑Moho界面的起伏,而不考虑两个低速层,即只考虑上地壳、下地壳、 岩石圈地幔和软流圈四层.(a)上地壳厚度为30 km,Vp=5.9±0.1 km·s-1;(b)30~70 km处为下地壳,Vp=6.7±0.1 km·s-1;(c)岩石圈地幔,即上 地幔盖层位于70~100 km深处,Vp=8.1±0.1 km·s-1;(d)100~150 km之间为软流圈,Vp=7.4±0.1 km·s-1.
在两个模型中,Moho界面起伏均呈凹-凸相间形态(如图 2),在距左边界50 km处,深度为70 km的Moho界面向下以45°倾角下陷5 km,即深度变为75 km,再延伸至距左边界85 km处以45°倾角向上抬升5 km,即Moho界面深度恢复为70 km.在距离左边界200 km处以45°倾角向上抬升5 km,即Moho界面深度上升为65 km,然后水平展布至距左边界235 km处向下以45°倾角错断5 km,恢复为70 km深度,其后深度不变,直至右边界.
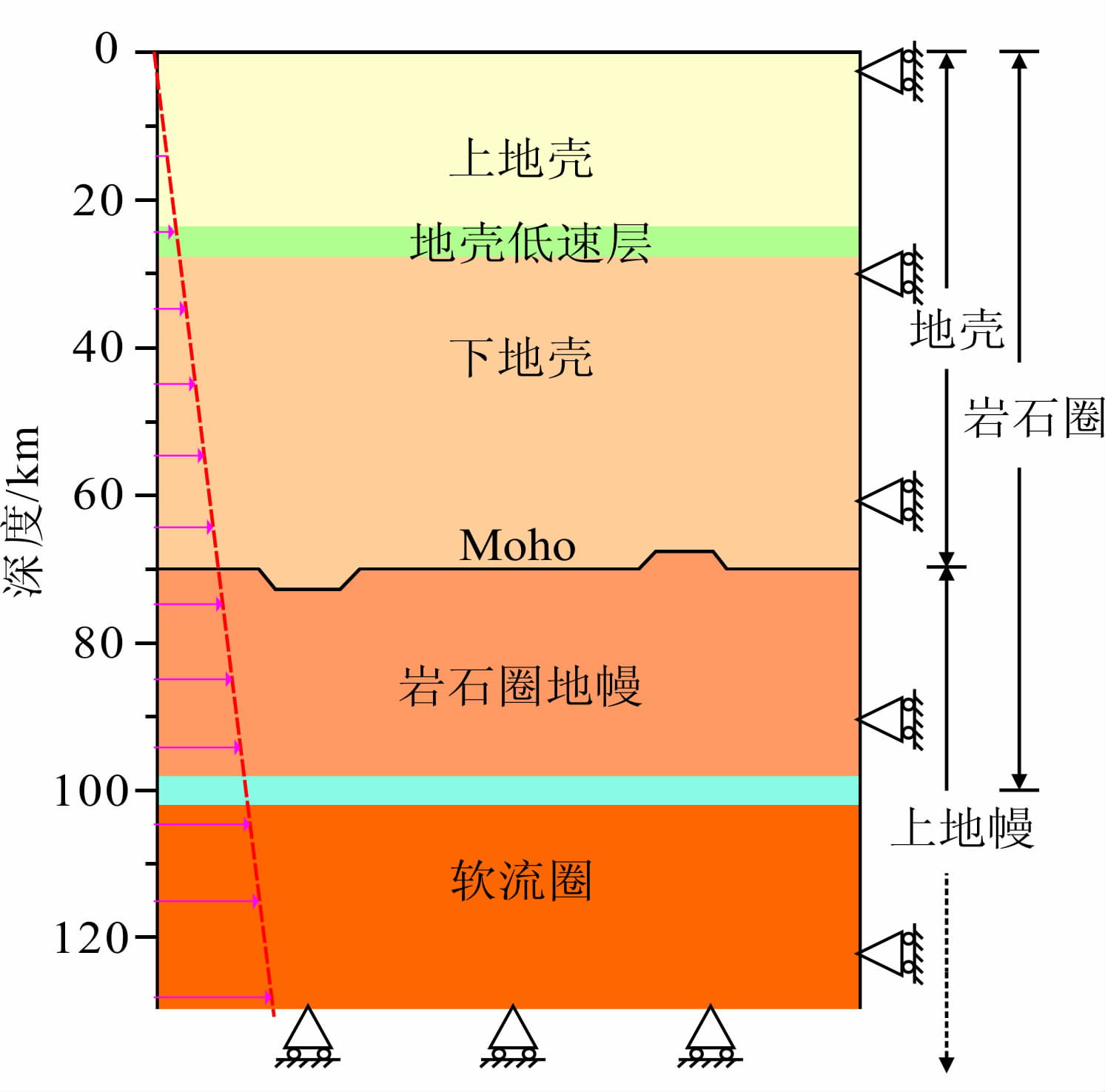 | 图 2 模型1结构示意图 Fig. 2 Sketch of structure of model 1 |
根据Klemperer 等(2006)和张培震(2008)研究 工作认为,在青藏高原东部与南部,更可能是Poiseuille 流而非Couette流的方式.因而,本研究工作的初始边界条件设置为Poiseuille流模式,即在左边界施加由高原重力加载随深度变化的静岩压力,为了减小各层之间由于密度差所带来的影响,抵消重力效应,模型左端除施加静岩压力外(数值上为3倍静水压力值),深部每一圈层均增加与上方所有圈层由于密度差导致随深度变化的压力差值.这样,边界驱动的压力从数值上大为减小了重力对边界力抵消所带来的影响,并确保模型的力源约束属于Poiseuille流方式.在边界条件的选取中,模型底部施加竖直向约束,使其水平向能自由移动.模型的右边界施加水平方向的约束,在竖直方向上自由移动.为便于计算,以上模型的外部边界几何模型均设定为直立或是水平.
基于前述几何模型和以地震波速度结构构建的数值模型,计算处理均在商用有限元计算软件Ansys平台上进行,模型采用8节点Plane183四边形平面单元,增强了单元进行非线性大变形处理的能力.网格密度的划分在上、下地壳之间的低速层及软流圈顶部的滑移面均加密为1.0 km×1.0 km,其余层位均设为2.0 km×2.0 km,模型1的单元数为13364,节点数为13126.其他模型在相同层中的网格密度与之相同,但单元网格数及节点数均有所减少.
模型在计算过程中选择平面应变模式,求解器为软件缺省的稀疏矩阵求解器,计算时以直接消元法为基础,病态矩阵的存在不会引起求解的困难,因而计算过程具有良好的收敛性,但对计算机硬件,尤其是内存及硬盘的配置要求较高.模型总的求解时间均为25 ka,远大于岩石圈和软流圈介质的黏弹性松弛时间(数十至数千年),以达模型最终计算结果均能表征黏性效应.依据收敛情况求解时所选用的时间步取为7800步,运算时间步长小于相应黏度条件下的应力松弛时间.
图 3为两种模型经计算得到的位移场分布图.从两个模型的对比中可以看出,在左边界力源附近位移值最大,向右边界方向逐渐减小.模型1由于中、下地壳间低速层和岩石圈底部滑脱面的存在,使得下地壳与上地壳之间以及岩石圈地幔与软流圈之间均显示出位移解耦的现象,下地壳和软流圈位移 明显大于上地壳和岩石圈地幔,而且越靠近左边界力源差别越显著,其差异向右边界方向逐渐减小.通过与没有低速层和滑移面的模型2相比,仅仅25 ka后,模型1的位移场形态与模型2便有了差异明显的变化,相同位置处位移量比模型2增量超过40%.而且,当没有低速层和滑移面存在时,物质整体运移难以形成下地壳的单独运移.
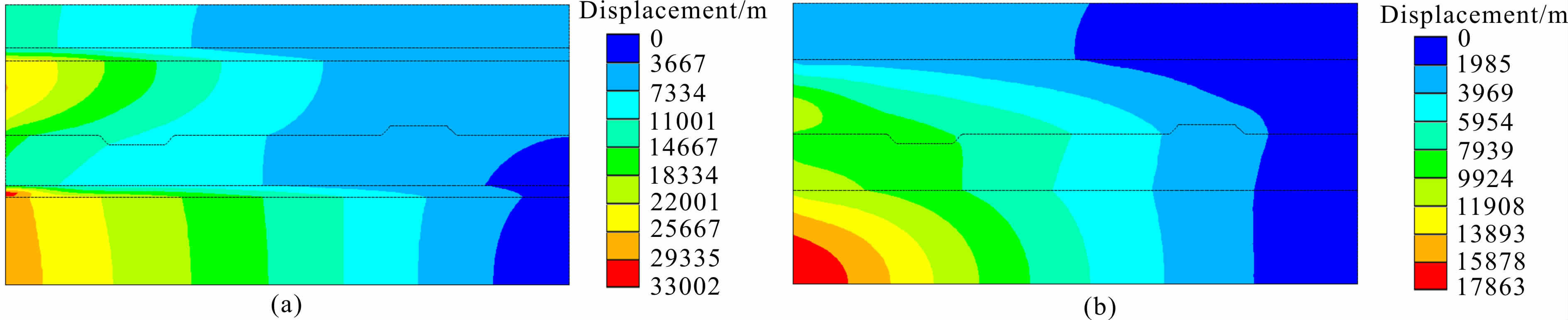 | 图 3(a)模型1位移场分布图;(b)模型2位移场分布图 Fig. 3(a)Displacement field of model 1;(b)Displacement field of model 2 |
同样,与已有的研究工作相比(杨辉等,2013),Moho界面存在锯齿状的变化形态时,使得模型1的下地壳与岩石圈地幔的位移量要比平滑的Moho界面模型有明显增大.显见,并非每个地方都能存在通道流,它需要特异的边界条件,即以上地壳底部的低速层为上滑移面,以上地幔软流圈顶部为下滑移面.Moho界面起伏的存在确实对通道流很有影响,增强了下地壳和岩石圈地幔相对于上、下两层面的快速有序运移,而有低速层存在的模型1更加支持通道流现象的产生.因此,在后面的模型中,本文将基于带有低速层的模型1,进行Moho界面起伏形态对通道流模型影响的探讨.
4 Moho面起伏变化对通道流模型的影响青藏高原已有的深部地球物理探测表明,尽管在局部地区尚存在着部分熔融体,但地震横波能通过岩石圈,说明包括低速层在内的整个岩石圈基本上都是固态.这就表明青藏高原Moho界面处下地壳与上地幔盖层物质之间为固体的“刚性”接触.在漫长的地质时间尺度内,虽然深部物质能够发生蠕变流动,但其本质上依然体现了固体的本性.由于深部Moho界面被诸多条深大断裂所切割,故导致了一系列犬牙交错且不规则的阶面(带)形态.前文的研究结果也表明,Moho面存在起伏时对通道流中物质的运移影响较大,而起伏的状态对于物质运移的影响乃是在进行动力学演化研究中需要探讨的方面.考虑到青藏高原Moho面的错断形态,在进一步的研究中,Moho面的起伏仍设定为5 km,分为距边界50 km处向上错断、距边界50 km处向下错断和边界处开始抬升三种不同的情况.模型其他参数与之前的研究均相同,重新构建了相应的模型3、模型4和模型5(图 4).
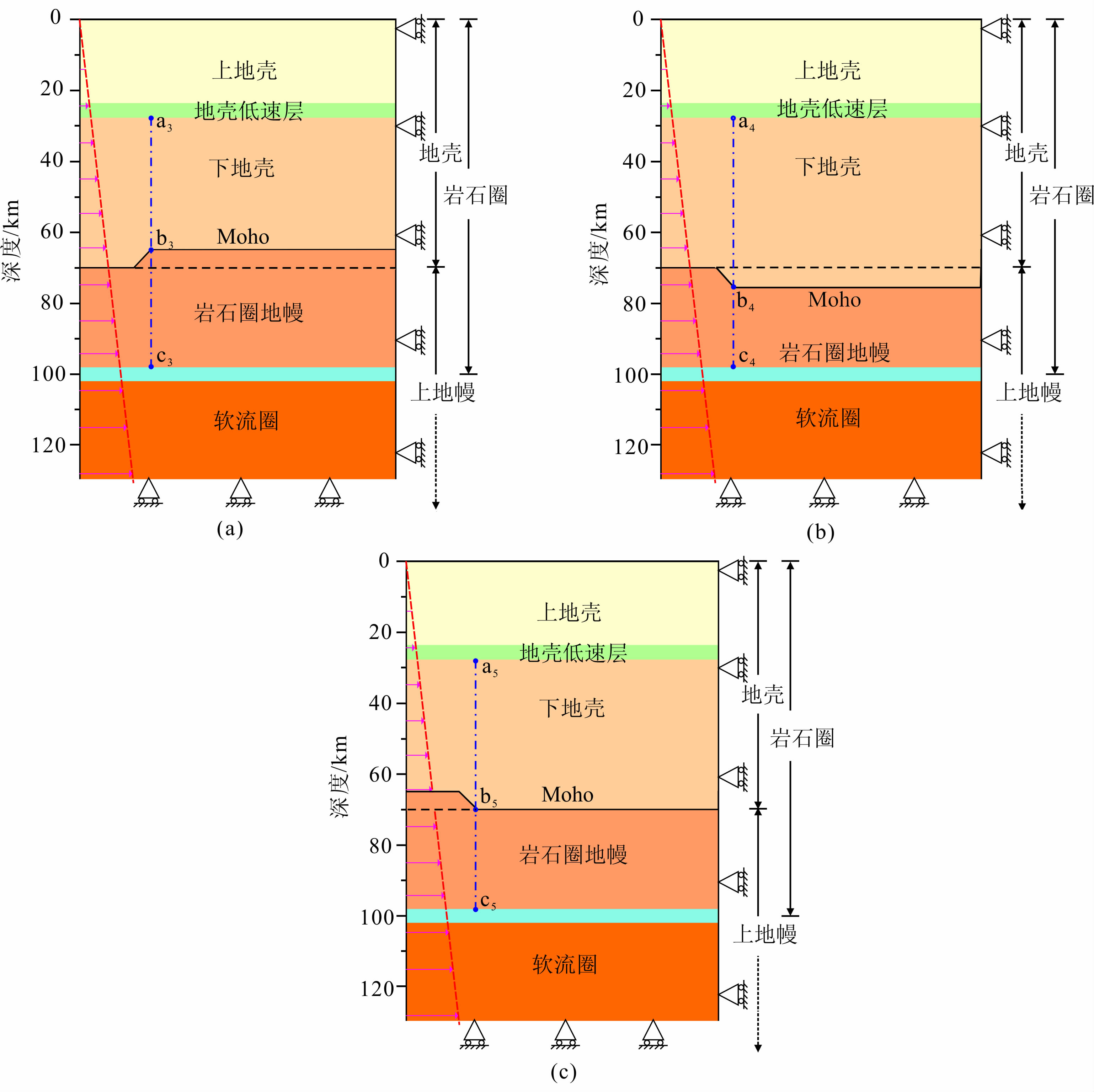 | 图 4(a)模型3;(b)模型4;(c)模型5 Fig. 4(a)Model 3;(b)Model 4;(c)Model 5 |
与模型1相比,模型3的Moho界面在距左边界50 km处向上抬升5 km后平行延伸至右边界;模型4的Moho界面在距左边界50 km处向下错断5 km后平行延伸至右边界;模型5的Moho界面在左边界处开始抬升,平行延伸至50 km处,向下错断5 km,再平行延伸至右边界.在这三个模型中,Moho界面发生变化的地方均采用以45°倾角的方式.
图 5是第二组模型25 ka之后位移场的计算结果.不论Moho面呈何种错断形态,由于地壳间低速层和岩石圈底部滑脱面的存在,使得下地壳与上地壳之间以及岩石圈地幔与软流圈之间均显示出位移解耦的现象.当Moho界面向上抬升时(图 5a),相同位置处的位移量较其他三个模型为最小.当Moho界面向下错断时(图 5b),相同位置处的位移量较其它三个模型为最大,其增量最大可达15%.当Moho界面在边界开始抬升时(图 5c),位移场的分布情况与参考模型(杨辉等,2013中的模型4,下同)的位移场分布情况极为一致.由等效应力场的分布(图 6)可以看出,当Moho界面呈现出错断形态时,错断处均出现了应力集中的现象,而且力学强度较高的岩石圈地幔与上地壳层位表现为应力较大的 区位.特别是当Moho面向下错断的模型4和模型5中(图 6b和图 6c),尽管整体应力场比模型3,即Moho面上升模型(图 6a)为大,但模型3的上地壳应力场的数值却明显偏大.这种应力分布特征,使得Moho界面起伏发生变化的地方呈现出更强的应力集中,亦更容易发生韧性破裂,使得Moho界面的起伏更为破碎,更显凌乱.同时,也必导致地表更容易产生断裂,而深部切穿下地壳的断裂也由于岩石圈地幔的强应力而更显复杂.我们的相关工作也表明,Moho面以不同的方式向下错断时,在不同深度处,主应力场的大小和方向亦各异,故也造成了地表和深部更为复杂的动力学响应.
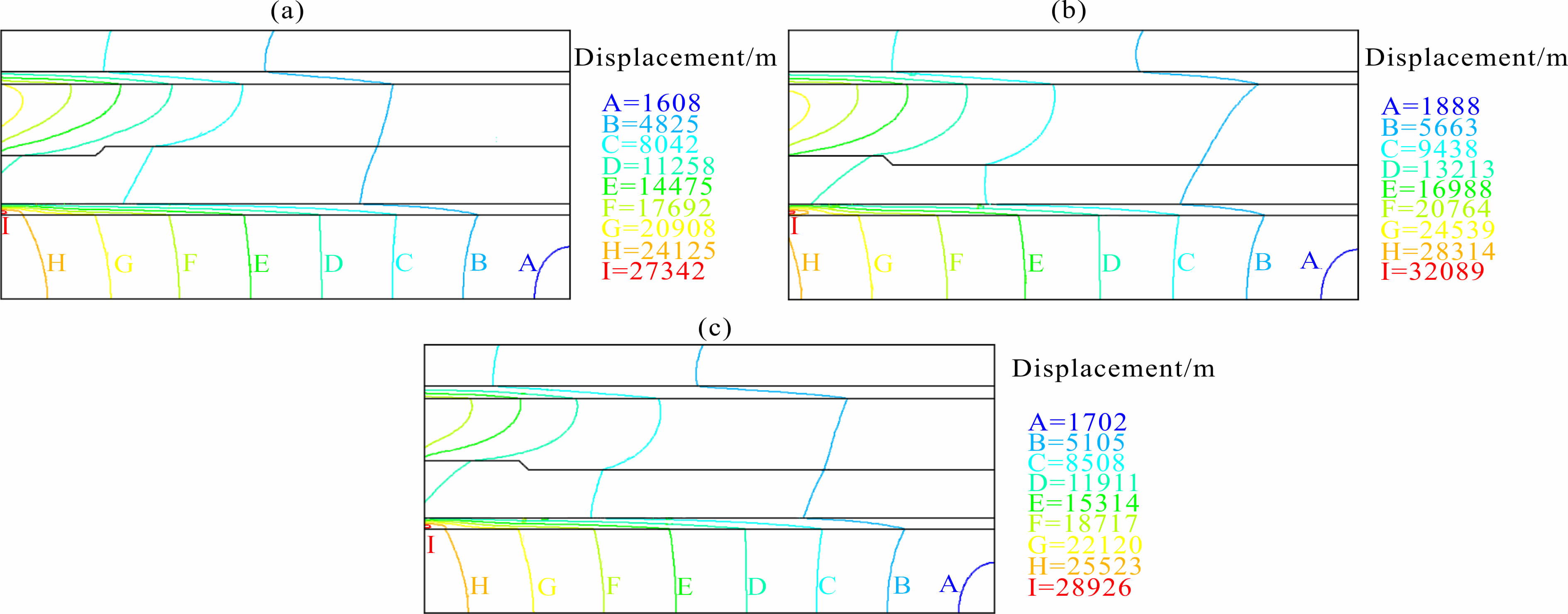 | 图 5(a)模型3位移场计算结果;(b)模型4位移场计算结果;(c)模型5位移场计算结果 Fig. 5(a)Calculated displacement field of model 3;(b)Calculated displacement field of model 4; (c)Calculated displacement field of model 5 |
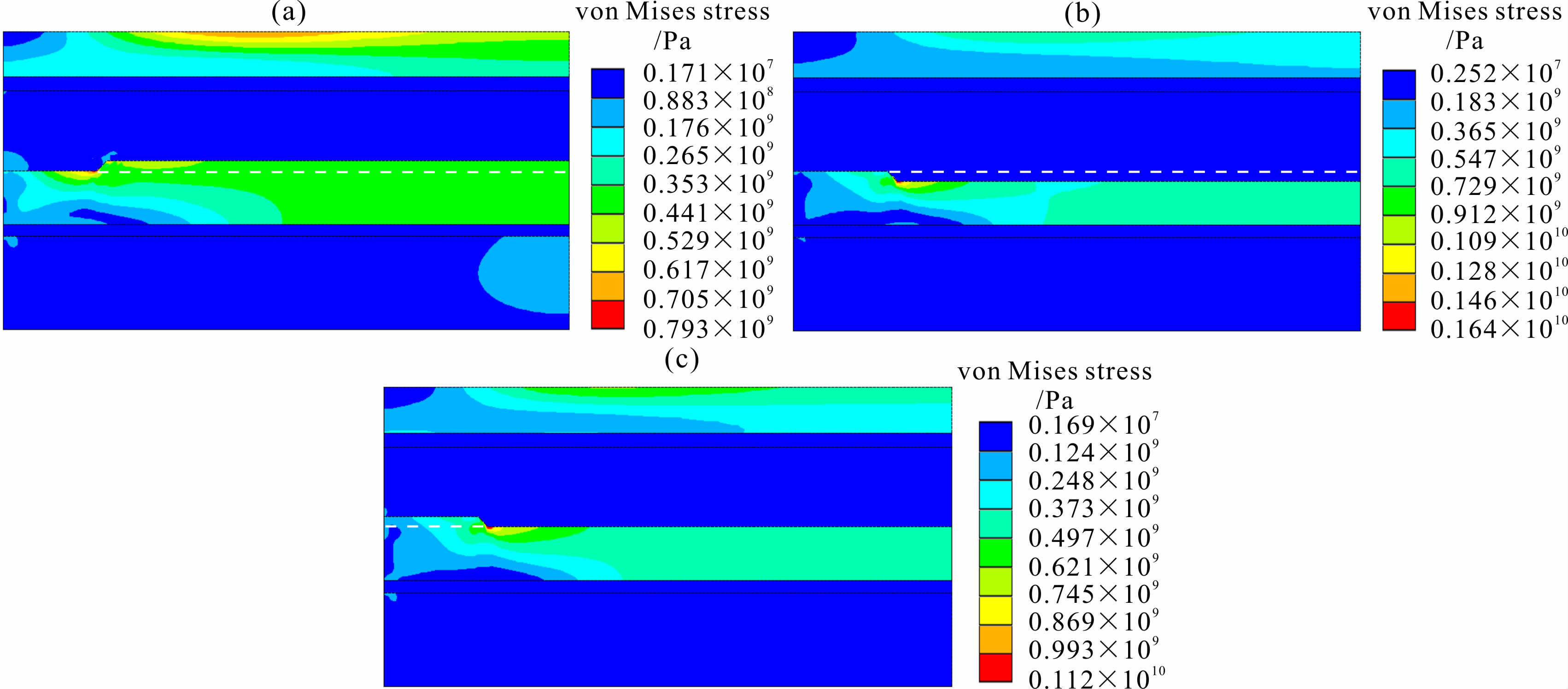 | 图 6(a)模型3等效应力场计算结果;(b)模型4等效应力场计算结果;(c)模型5等效应力场计算结果 Fig. 6(a)Calculated equivalent effctive stress field of model 3;(b)Calculated equivalent effctive stress field of model 4; (c)Calculated equivalent effctive stress field of model 5 |
由此上三个模型中分别截取距离左边界为55km处的地壳低速层与下地壳的交界面、Moho界面与岩石圈地幔的交界面和岩石圈地幔与软流圈交界面的三个单元节点(如图 4中a3,b3,c3,a4,b4,c4,a5,b5,c5),观测它们的水平位移量随时间的变化情况,如图 7所示.
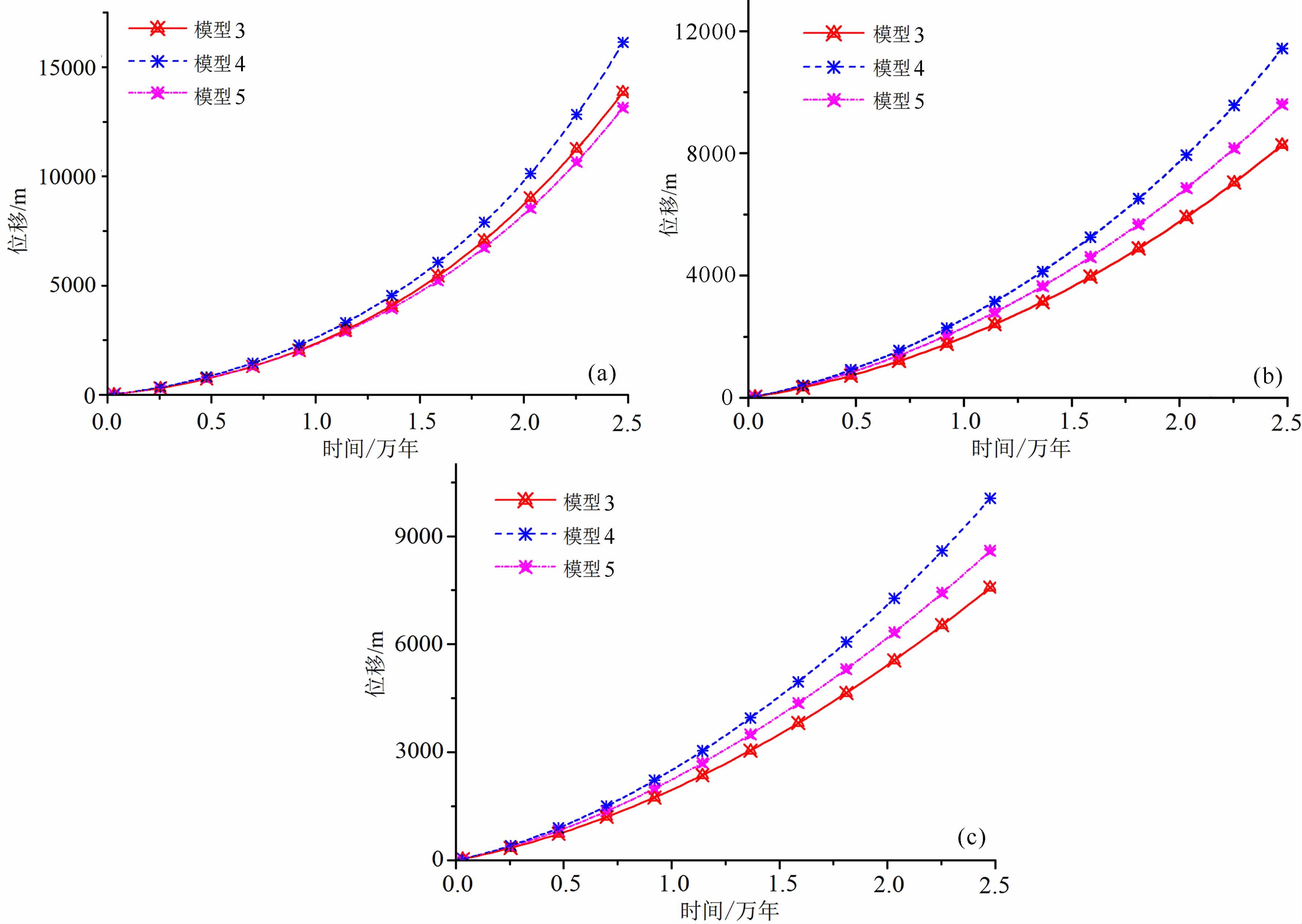 | 图 7(a)上、下地壳间低速层中所选节点处水平位移与时间关系图;(b)Moho界面上所选节点处水平位移与时间关系图; (c)岩石圈地幔与软流圈交界的低速层中所选节点水处平位移与时间关系图 Fig. 7 Relation between the horizontal displacement and the time of the selected nodes.(a)Low-velocity layers between the upper crust and lower crust;(b)Moho interface;(c)Low-velocity interface between the upper mantle and asthenosphere |
三个模型的地壳低速层水平位移量在万年时间尺度后的比较;模型5明显小于模型3和模型4,而模型3和模型5之间地壳低速层变形的差别一直较小.这一组模型的水平位移量是三组比较模型中最大的,这可能是因为地壳低速层强度弱而容易发生变形的原因.Moho界面处的水平位移量;三个模型的差异明显大于其间地壳低速层水平位移的差异量,且依然以模型4的位移量最大,模型5次之,模型3最小.Moho界面向下错断时对通道流中物质流动的影响最大.在岩石圈地幔与软流圈之间的滑 脱层(软流圈顶部)处的水平位移量显示出,三个模型的演变形态与Moho界面处一致,但其水平位移量的数值却是三个模型中最小的,这可能是与岩石圈地幔层速度高和强度较大,较难变形相关.三个模型的竖直向位移量随时间的变化形态均与水平向位移量随时间变化情况一致,在地壳低速层中三个模型的竖直向位移量最大,岩石圈地幔中的最小.当Moho界面向下错断5km时,其竖直向位移量较其它两种Moho界面错断情况相比达最大,在Moho界面边界抬升处次之,Moho界面向上抬升处最小.
5 讨论与结论近年来有关对下地壳通道流的推论和在先验模型下的数值模拟在国内外均为热点(Royden et al., 1997;Clark Royden,2000; Beaumont et al., 2004),并用于对喜马拉雅造山带,乃至青藏高原系统和其它古老造山带地质构造及岩石学特征等地球动力学演化有关的许多现象的解释,通道流模型似乎一时得到广泛应用.但由于很难从实验力学的角度构建逼近真实的物理实验来检验和模拟造山带尺度的地壳介质融化和变形机制,为此,在一定合理黏滞系数约束下的初始模型提取,并用数值模拟来揭示这一演化过程中的一阶动力学特征便不失为一种很好的选择.因此,很多的数值模拟工作可从不同的角度来探讨下地壳通道流模型的不同演化方式和动力学机制,本文的着眼点则为当Moho界面起伏变化时对模型中物质有序运移,即应力、应变及位移场等参数的效应来讨论这一问题,而不去涉及通道流物质的出露等边界现象.
(1)地壳物质的岩石组构对于通道流模型具有重要的影响.由于岩石组构在动力学响应中能最直接的反应或体现在黏滞系数上,因此,Jamieson 等(2011)针对黏滞系数的改变对通道流物质水平或是垂向运移进行了总结,国内学者也对黏滞系数的影响开展了相关的研究工作(王晓芳和何建坤,2012).但黏滞系数的确定更多的是作为一种地球物理观测或是实验室岩石学研究的外推,它不可避免地有着不确定性的缺陷.近年来,随着深部地球物理探测的深入发展和人们对通道流模型更加深化的认识,在大多数情况下,脆性上地壳是孕震的,岩相属干的麻粒岩相;下地壳只有在温度<600 ℃时可能孕震;中地壳是热的、弱的、耐震、部分熔融而且可流动.麻粒岩强下地壳,一般没有含水相和部分熔融,因此下地壳流动是不太可能的.大陆岩石圈通过下地壳干燥、强麻粒岩相而使其保持着它的强度和相对刚度(Searle,2013).地震横波能穿过岩石圈,说明深达核幔边界包括软流圈在内的整个地幔和岩石圈基本上都是固态(尽管强度有一定差别),而固体圈层介质之间基本上均尚属于固体-固体之间的摩擦运动.这就决定了纵使在地质时间尺度下,下地壳也并非如不少地质模型中所说的那般可以像液体一般流动,而更有可能是以上地壳底部的低速层为上滑移面,以下地幔软流圈顶部为下滑移面,在足够强的力系作用下促使“上地壳+岩石圈盖层”物质发生同步运移.
(2)本文的研究结果亦表明,当Moho界面存在起伏变化时,确对通道流产生了影响.图 8和图 9显示了Moho界面起伏形态对地表以及Moho界面水平位移的影响.
图 8显示出模型1、3、4和5随时间演化的地表水平位移.从力学性质看,模型3和模型5的下地壳面积均减小,即力学性质软弱层位的减少,故使得力学模型的刚度有所增加,但对地表水平位移大小而言,却有着不一样的效果.模型3下地壳的面积减少得最多,但与模型1相比,地表位移却没有明显的变化.模型5的水平位移明显比模型1偏小,而且只有模型5的水平位移量大小一直小于没有Moho面起伏的模型(杨辉等,2013中模型4).模型4的下地壳面积有明显增加,这体现在模型的力学性质变软,地表位移相对较大.
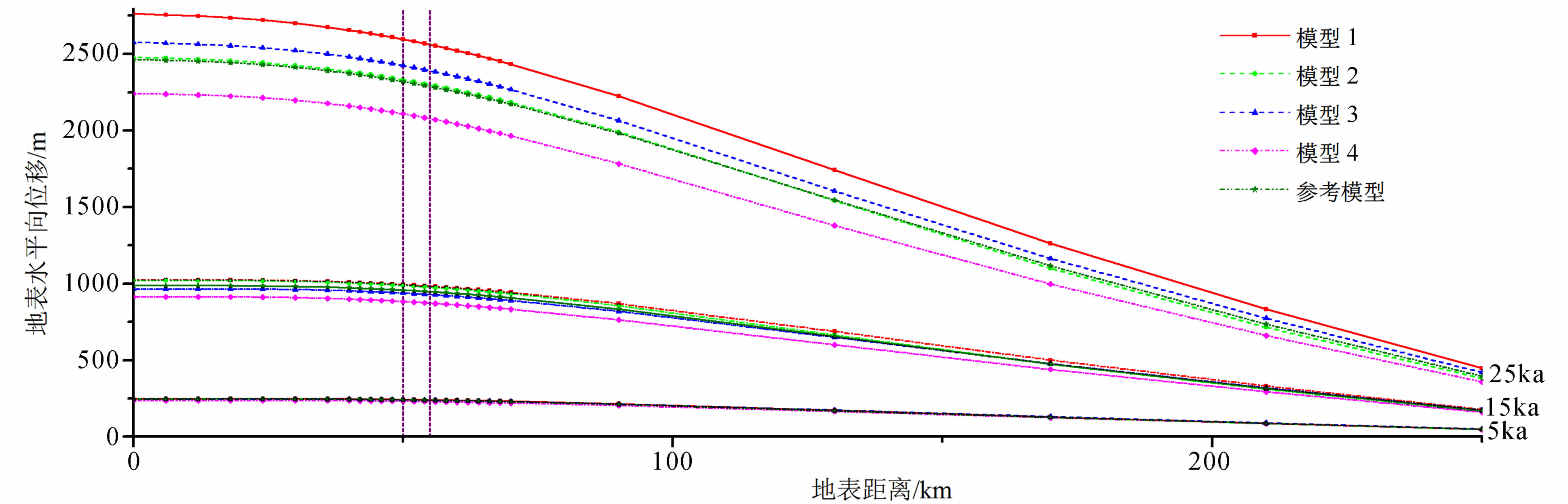 | 图 8 地表水平向位移与时间的关系 Fig. 8 Horizontal displacements on the surface versus time for various models |
由图 8还可以看出,随离受力边界距离的增加,几个模型在地表的水平位移之间的差别也逐渐减小,超过200 km之后基本趋于一致.这便说明,通道流效应的作用有一定的作用区限.从时间效应看,5 ka的时候,尽管已经大于下地壳的特征松弛时间尺度,但几个模型之间尚无明显差别,而到了15 ka时却有了明显的变化.可见,在万年的时间尺度上,地表的水平位移已经受到了通道流效应的影响.从作用区限看,在Moho界面发生错断的地方,体现在地表的便是水平位移开始发生明显加速减小的地方.从作用效果看,模型1和模型4中虽然Moho界面的初始错断形态相同,都是下陷,但是在Moho界面变化相同的区域里,两者的地表水平位移并无明显相似之处.因此,模型深部动力学效应与地表的响应并非局部性的效应,而至少体现出了区域性的响应.
图 9显示的是Moho界面水平位移与水平距离关系的对比关系图,与图 8相比,地表和深部的水平位移对应关系并不耦合,出现了解耦的现象.但是,总的说来,从时间效用看,大致到了15 ka的时候,几个模型之间的Moho界面水平位移量则出现了明显的差别.
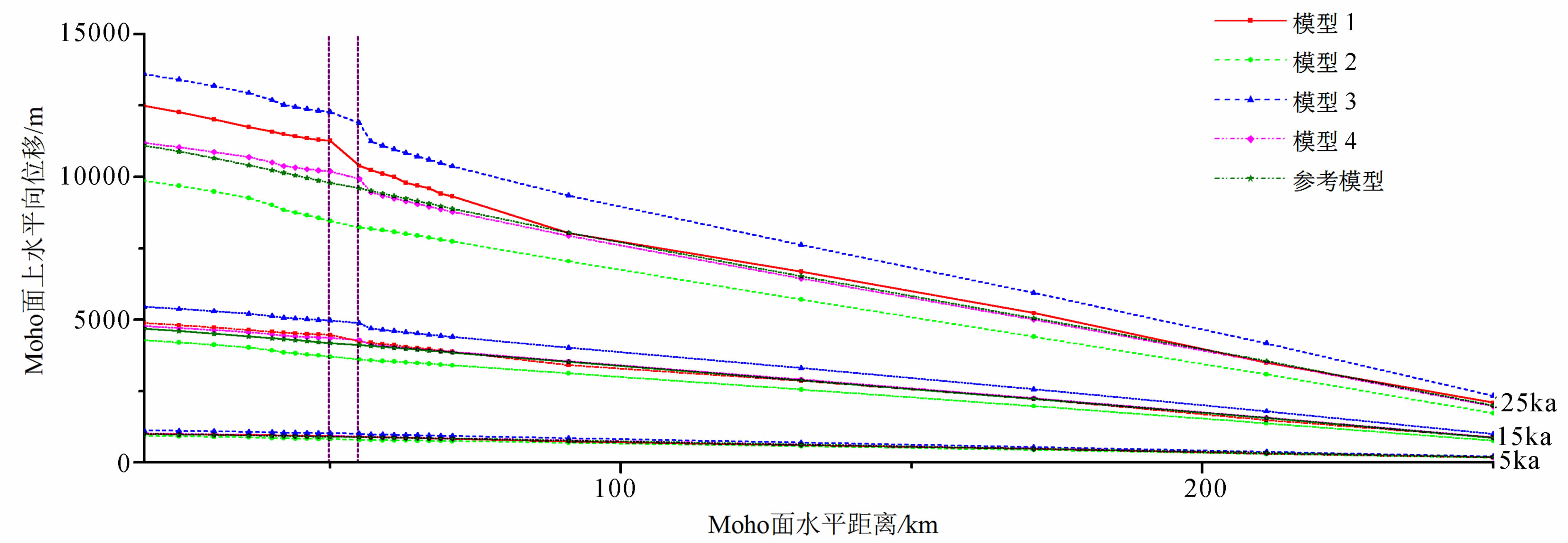 | 图 9 Moho界面上的水平位移与时间关系 Fig. 9 Horizontal displacements on the Moho interface versus time |
Schulmann 等(2008)和Lexa等(2011)的研究表明,通道流模型中物质运移的距离大体在200 km左右.在我们的相关工作中,当将模型的水平尺度加倍,取为600 km或更长时,Moho界面无论是起伏形态与起伏程度均发生变化,但对通道流中物质尾端的运移却没有明显的影响.可见,通道流效应的影响是小区域性的,Moho界面的起伏加强了下地壳和岩石圈地幔的同步运动的效应,而其影响范围亦是局限的.
(3)本文开展的数值模拟工作是基于二维模型,而在实际的深部壳、幔结构中物质运移的流展方式却是三维,而且由于存在应力集中而断层或错断面容易破碎或转化为更为复杂的形态,这不仅对深部物质运动的动力学效应有深远影响,也对地表演化过程及深部岩石垂向运移在地表的表征产生出重要影响.
随着高精度深部地球物理勘探技术的进一步发展,以及实验室对岩石物性测量等研究工作的深入和精度的提高,势必将会为通道流模型的数值模拟和对实际壳、幔物质运移的深层过程逼近提供更为精确的约束,并对大陆动力学响应给出更为科学与合理的解释.
致谢 感谢两位评审专家对本稿提出的宝贵意见和建议,感谢中国南车戚墅堰机车有限公司计算中心陈晓百高工为本工作提供Ansys计算平台.| [1] | Batchelor G K. 2000. Introduction to Fluid Dynamics. New York: Cambridge University Press. |
| [2] | Beaumont C, Jamieson R A, Nguyen M H, et al. 2004. Crustal channel flows: 1. Numerical models with applications to the tectonics of the Himalayan-Tibetan orogen. J. Geophys. Res., 109, B06406, doi: 10.1029/2003JB002809. |
| [3] | Beaumont C, Jamieson R A, Nguyen M H, et al. 2001. Himalayan tectonics explained by extrusion of a low-viscosity crustal channel coupled to focused surface denudation. Nature, 414(6865): 738-742, doi: 10. 1038/414738a. |
| [4] | Bürgmann R, Dreson G. 2008. Rheology of the lower crust and upper mantle: evidence from rock mechanics, geodesy, and field observations. Annu. Rev. Earth Planet. Sci., 36: 531-567, doi: 10.1146/annurev earth. 36. 031207. 124326. |
| [5] | Clark M K, Royden L H. 2000. Topographic ooze: building the eastern margin of Tibet by lower crustal flow. Geology, 28(8): 703-706, doi: 10. 1130/0091-7613(2000)28. |
| [6] | Flesch L M, Haines A J, Holt W E. 2001. Dynamics of the India-Eurasia collision zone. J. Geophys. Res., 106(B8): 16435-16460, doi: 10.1029/2001JB000208. |
| [7] | Flesch L M, Holt W E, Silver P G, et al. 2005. Constraining the extent of crust-mantle coupling in central Asia using GPS, geologic, and shear wave splitting data. Earth Planet. Sci. Lett., 238(1-2): 248-268, doi: 10.1016/j. epsl. 2005.06. 023. |
| [8] | Gao R, Chen C, Lu Z W, et al. 2013. New constraints on crustal structure and Moho topography in central Tibet revealed by SinoProbe deep seismic reflection profiling. Tectonophysics, 606: 160-170, doi: 10.1016/j. tecto. 2013. 08. 006. |
| [9] | Godin L, Grujic D, Law R D, et al. 2006. Channel flow, ductile extrusion and exhumation in continental collision zones: an introduction.//Law R D, Searle P, Godin L. Channel flow, ductile extrusion and exhumation in continental collision zones, Geological Society, London, Special Publications, 268: 1-23. |
| [10] | Grujic D. 2006. Channel flow and continental collision tectonics: an overview.//Law R D, Searle P, Godin L. Channel flow, ductile extrusion and exhumation in continental collision zones, Geological Society, London, Special Publications, 268: 25-37. |
| [11] | Haines S S, Klemperer S L, Brown L, et al. 2003. INDEPTH III seismic data: from surface observations to deep crustal pro-cesses in Tibet. Tectonics, 22(1): 1-18, doi: 10.1029/2001TC001305. |
| [12] | Hilley G E, Bürgmann R, Zhang P Z, et al. 2005. Bayesian inference of plastosphere viscosities near the Kunlun Fault, northern Tibet. Geophysical Research Letters, 32, L01302, doi: 10. 1029/2004GL021658. |
| [13] | Hirn A, Nercessian A, Sapin M, et al. 1984a. Lhasa block and bordering sutures—a continuation of a 500 km Moho traverse through Tibet. Nature, 307: 25-27, doi: 10. 1038/307025a0. |
| [14] | Hirn A, Lepine J C, Jobert G, et al. 1984b. Crustal structure and variability of the Himalayan border of Tibet. Nature, 307: 23-25, doi: 10. 1038/307023a0. |
| [15] | Jamieson R A, Unsworth M J, Harris N B W, et al. 2011. Crustal melting and the flow of mountains. Elements, 7(4): 253-260, doi: 10.2113/gselements.7.4. 253. |
| [16] | Karplus M S, Zhao W, Klemperer S L, et al. 2011. Injection of Tibetan crust beneath the south Qaidam basin: evidence from INDEPTH IV wide-angle seismic data. J. Geophys. Res., 116, B07301, doi: 10. 1029/2010JB007911. |
| [17] | Klemperer S L. 2006. Crustal flow in Tibet: geophysical evidence for the physical state of Tibetan lithosphere, and inferred patterns of active flow.//Law R D, Searle P, Godin L. Channel flow, ductile extrusion and exhumation in continental collision zones, Geological Society, London, Special Publications, 268: 39-70. |
| [18] | Lexa O, Schulmann K, Janousek V, et al. 2011. Heat sources and trigger mechanisms of exhumation of HP granulites in Variscan orogenic root. Journal of Metamorphic Geology, 29(1): 79-102, doi: 10.1111/j.1525-1314. 2010. 00906. x. |
| [19] | Li Y H, Wu Q J, Tian X B, et al. 2006. Crustal structure beneath Qiangtang and Lhasa terrane from receiver function. Acta Seismol. Sin. , 19(6): 633-642, doi: 1000-9116(2006)06-0633-10. |
| [20] | Qiu J. 2013. China's exquisite look at earth's rocky husk wins raves. Science, News & Analysis, 341(6141): 20. |
| [21] | Royden L H, Burchfiel B C, King R W, et al. 1997. Surface deformation and lower crustal flow in eastern Tibet. Science, 276(5313): 788-790, doi: 10. 1126/science.276.5313. 788. |
| [22] | Schulmann K, Lexa O, Štípská P, et al. 2008. Vertical extrusion and horizontal channel flow of orogenic lower crust: key exhumation mechanisms in large hot orogens? Journal of Metamorphic Geology, 26(2): 273-297, doi:10.1111/j.1525-1314.2007 00755.x. |
| [23] | Searle M. 2013. Crustal melting, ductile flow, and deformation in mountain belts: Cause and effect relationships. Lithosphere, 5(6): 547-554. doi: 10.1130/RF. L006. 1., |
| [24] | Shen F, Royden L H, Burchfiel B C. 2001. Large-scale crustal deformation of the Tibetan Plateau. J. Geophys. Res., 106(B4): 6793-6816, doi: 10.1029/2000JB900389. |
| [25] | Shi D N, Shen Y, Zhao W J, et al. 2009. Seismic evidence for a Moho offset and south-directed thrust at the easternmost Qaidam-Kunlun boundary in the Northeast Tibetan plateau. Earth Planet. Sci. Lett., 288: 329-334, doi: 10. 1016/j. epsl. 2009. 09. 036. |
| [26] | Teng J W, Ruan X M, Zhang Y Q, et al. 2012. The stratificational velocity structure of crust and covering strata of upper mantle and the orbit of deep interaquifer substance locus of movement for Tibetan Plateau. Acta Petrologica Sinica (in Chinese), 28(12): 4077-4100. |
| [27] | Teng J W. 2005. The Exchange of Substance and Energy and Dynamic Process in the Earth Interior.//The 100 crossing-subject problems in 21st century (in Chinese). Beijing: Science Press, 327-338. |
| [28] | Teng J W, Bai D H, Yang H, et al. 2008. Deep processes and dynamic responses associated with the Wenchuan Ms8.0 earthquake of 2008. Chinese J. Geophys. (in Chinese), 51(5): 1385-1402. |
| [29] | Tseng T, Cheng W, Nowack R L. 2009. Northward thinning of Tibetan crust revealed by virtual seismic profiles. Geophys. Res. Lett., 36, L24304, doi: 10. 1029/2009GL040457,2009. |
| [30] | Turcotte D L, Schubert G. 2002. Geodynamics. New York: Cambridge University Press. |
| [31] | Wang X F, He J K. 2012. Channel flow of the lower crust and its relation to large-scale tectonic geomorphology of the eastern Tibetan Plateau. Science in China (Series D), 55(8): 1383-1390. |
| [32] | Yang H, Teng J W, Pi J L. 2013. Numerical simulation on the study of the geodynamical condition about the channel flow model in Tibetan plateau. Chinese J. Geophys. (in Chinese), 56(8): 2625-2635,doi: 10.6038/cjg20130812. |
| [33] | Zhang P Z. 2008. The present day's deformation, strain distribution and deep dynamic process on the Western Sichuan, Eastern Tibetan Plateau. Science in China (Series D) (in Chinese), 38(9): 1041-1056. |
| [34] | Zhang Z J, Deng Y F, Teng J W, et al. 2011a. An overview of the crustal structure of the Tibetan plateau after 35 years of deep seismic soundings. Journal of Asian Earth Sciences, 40(4): 977-989, doi: 10. 1016/j. jseaes. 2010.03. 010. |
| [35] | Zhang Z J, Klemperer S L, Bai Z M, et al. 2011b. Crustal structure of the Paleozoic Kunlun orogeny from an active-source seismic profile between Moba and Guide in East Tibet, China. Gondwana, 19(4): 994-1007, doi: 10.1016/j. gr. 2010. 09. 008. |
| [36] | Zhong S J. 1997. Dynamics of crustal compensation and its influence on crustal isostasy. Journal of Geophysical Research, 102(15): 15287-15299, doi: 10.1029/97JB00956. |
| [37] | 滕吉文. 2005. 地球内部物质与能量交换和动力过程. //21世纪100个交叉科学难题. 北京: 科学出版社, 327-338. |
| [38] | 滕吉文, 白登海, 杨辉等. 2008. 2008汶川Ms8.0地震发生的深层过程和动力学响应. 地球物理学报, 51(5): 1385-1402. |
| [39] | 滕吉文, 阮小敏, 张永谦, 等. 2012. 青藏高原地壳与上地幔成层速度结构与深部层间物质的运移轨迹. 岩石学报, 28(12): 4077-4100. |
| [40] | 王晓芳, 何建坤. 2012. 下地壳管道流动与青藏高原东缘大尺度构造地貌. 中国科学(D辑), 42(4): 505-512. |
| [41] | 杨辉, 滕吉文, 皮娇龙. 2013. 青藏高原通道流模型动力环境的数值模拟. 地球物理学报, 56(8): 2625-2635,doi: 10. 6038/cjg20130812. |
| [42] | 张培震. 2008. 青藏高原东缘川西地区的现今构造变形、应变分配与深部动力过程. 中国科学(D辑), 38(9): 1041-1056. |
 2014, Vol. 57
2014, Vol. 57


