1 引言

船载声呐测量作为一种传统的水下测绘手段，仅能获得少量的高精度海底地形数据；航空航天的光学和多光谱手段也可以实现海洋测绘，但仅适宜于几十米深的浅海.20世纪70年代出现的海洋卫星雷达测高技术，使全球海洋大地水准面测量成为可能，在此基础上得到的高精度重力异常能够用于反演海底地形，由于其在空间和时间上的巨大优越性使得该地形反演技术得到了飞速发展.

南海作为西太平洋的一部分，是重要的地区.为深入了解该海域地理特征与地壳结构，国内外的地球科学家们发表了一系列研究论文(Briais et al., 1993; 方迎尧等，2001；王虎彪等，2009；陈洁等，2012; 张亮和栾锡武，2012)，通过对该海域的重力异常、重力梯度、地磁异常等进行分析后发现，受印度板块和欧亚板块碰撞所产生的“海岭跳跃”和2700万年前的海底扩张等因素影响，南海海底地形起伏和地壳密度的变化非常强烈.针对南海海底地形的反演研究在早期的国内外研究论文中鲜有出现，但美国地球物理中心(NGDC)、海军研究实验室(NRL)等组织很早就通过测高反演技术建立了包括ETOPO、DBDB2等在内的多个全球地形模型.国内学者针对该技术的研究始于2000年以后，南海海域由于其地质形态的多样化特征，成为了研究热点.Hwang(1999)综合利用卫星测高重力异常、船测水深、ETOPO5模型和GMT海岸线数据，采用向下延拓、回归分析和数据融合手段建立了南海海底地形模型，其相对精度达到7.0%，与实测水深差异结果的标准差为250 m；罗佳(2000)、王勇等(2001)、方剑和张赤军(2003)、李大炜等(2009)等基于位场理论反演了南海海底地形，经与ETOPO5模型比较，分辨率大大提高，但位场理论存在自身局限，响应函数难以与局部海域严格符合；黄谟涛和翟国君(2002)基于最小二乘配置理论，提出了统计算法的改进模型，在南海海域进行的实际反演计算相对精度为10%；吴云孙等(2009)利用测高数据计算得到南海海域重力梯度异常垂直分量，采用FFT求解法，反演了南海海域的海底地形，但效果并不理想.

重力地质法(GGM)作为一类地形反演技术，最初被应用于沉积物下的基岩高度测量(Ibrahim and Hinze， 1972；Adams，1990; Chandler et al., 2000)，但由于地下物质的密度变化，该方法在陆地区域的使用受到了限制.海底洋壳和海水之间密度差异变化较小，这使得重力地质法十分适宜于利用卫星测高重力异常反演海底地形的研究.现如今，该方法已经被成功地应用于东日本海、皇帝海山、格陵兰岛南部以及阿拉斯加南部附近海域的地形反演(Silva et al., 2006;Kim et al., 2010;Hsiao et al., 2010;胡敏章等，2012)，在对格陵兰岛南部海域的海底地形反演计算中，将实测水深和反演水深进行比较，两者差异的标准差甚至达到了35.8 m.

采用重力地质法反演局部海底地形时，不宜使用全球海底洋壳平均密度和海水平均密度的差异常数，需要精确估计局部海域的密度差异常数.向下延拓技术是最常用的密度差异常数推估方法，Hwang(1999)利用向下延拓技术和高斯滤波分离出参考场和残差场，利用残余水深和残余异常之比确定差异常数；Kim等(2010)采用向下延拓技术计算延拓异常，利用延拓异常和原始异常之比确定差异常数，推估出的密度差异常数为9.0 g/cm³，远高于理论值1.67 g/cm³，这种情况在Hsiao等(2010)、Kim等(2011)的研究论文中同样存在，究其原因，Nagarajan(1994)认为重力地质法本质上是通过单个密度差异常数去推估真实密度差异存在微弱变化的海底洋壳界面，其物理意义已经被削弱，可以将该常数视为一个经验参数，目的是为了取得一个平衡，使短波重力异常和海深之间具有线性关系.向下延拓技术的缺点在于计算的比值结果存在噪声，影响计算精度，且涉及滤波等频域计算，过程较为复杂，有学者建议为获得更好的反演精度，可以通过船测检核点水深迭代计算的办法精确判定密度差异常数(Kim et al., 2010; Hsiao et al., 2010; 胡敏章等，2012).

鉴于本文反演海域拥有船测水深，因而首先采用船测检核点水深迭代计算的办法判定密度差异常数，基于此常数，采用重力地质法，联合南海海域卫星测高自由空间重力异常和稀疏船测水深反演得到南海1′×1′的海深模型，模型精度优于5.0%.前人采用重力地质法在不同海域业已成功实现了海底地形反演，然而对于该方法在精度和可行性等方面的研究尚缺乏详尽分析，本文通过剖析不同海域和不同船测航迹的反演精度，对反演海深的重力地质法进行了详细的精度评定和可行性分析，并结合ETOPO1模型优势，生成了综合模型.文章使用的自由空间重力异常模型来自丹麦科技大学空间中心，经与实测重力异常值比较，两者差异的均值为 0.39 mGal，标准差为3.82 mGal，最大值为36.89 mGal，船测水深控制点的重力异常数据通过对该模型插值得到.船测水深数据来自NGDC，NGDC拥有自上世纪50年代以来，不同时期的海洋深度测绘数据.

自由空间重力异常和海水深度之间的关系是非线性的，在大地测量计算中，非线性问题一般通过定 义合适的“参考场”和“残差场”进行线性化(Hwang，1999)，因此可以将重力异常划分为长波参考场和短波残差场，其中长波部分由深层次的质量变化产生，短波部分由计算点周围海底地形变化产生.将短波和长波合并，就得到观测的自由空间重力异常(g_观)，公式如下：

图 1

Fig. 1

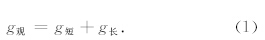
图 1 GGM原理图 Fig. 1 Principle of the GGM

使用控制点j_n的水深计算重力异常短波分量，公式如下：

由公式(1)，将船测水深控制点观测重力异常减去其短波部分得到控制点长波重力异常，通过适当的插值方法可以得到未经测量海域内任意一点i的长波重力异常，再利用如下两式就得到i点的短波重力异常和水深：

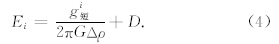
GGM原理建立在垂直方向上海水密度不发生变化的假设条件之上，海水和海底洋壳密度差异常数(即Δρ)的确定是该方法的关键(Strykowski et al., 2005).

研究范围位于南海112°E—119°E，12°N—20°N之间，该海域船测水深分布如图 2所示，由于部分船测水深存在粗差(如在上千米的深海海域其数值仅为数百米)，因此必须首先对其进行人工删除.经过处理后的船测点共计73708个，将图 2中红色的点作为水深控制点，共计63179个，黄色点作为检核点，共计10529个，控制点和检核点不重复，且在海域内均匀分布.图 2背景为ETOPO1海深模型；该海域测高自由空间重力异常如图 3所示，船测控制点的观测重力异常g_观通过对其内插得到.

图 2

Fig. 2

图 2 船测航迹分布 Fig. 2 Distribution of shipborne tracks

图 3

Fig. 3

图 3 测高自由空间重力异常 Fig. 3 Altimetry-derived gravity anomalies

密度差异常数的确定是为了使重力异常和水深保持良好的线性关系，如果常数过小，GGM模型的预测海深值就会偏大，反之，若常数过大，预测海深就会接近参考海深D(Kim et al., 2011; Wild-Pfeiffer.，2008).由文献可知，检核点预测水深和实测水深的相关系数越大，两者比较结果的标准差(STD)就越小(胡敏章等，2012)，因此，当STD最小且相关系数最大时的密度差异常数即为最优.根据GGM原理，利用船测水深控制点计算出不同密度差异常数下的水深模型，再通过双线性插值方法计算出检核点预测水深，将检核点实测水深和预测水深进行比较，得到不同密度差异常数下两者的相关 系数和较差结果的STD，图 4示出了较差结果的STD和相关系数的变化趋势，经比较，该海域密度差异常数的最优值为1.32 g·cm^－3.

图 4

Fig. 4

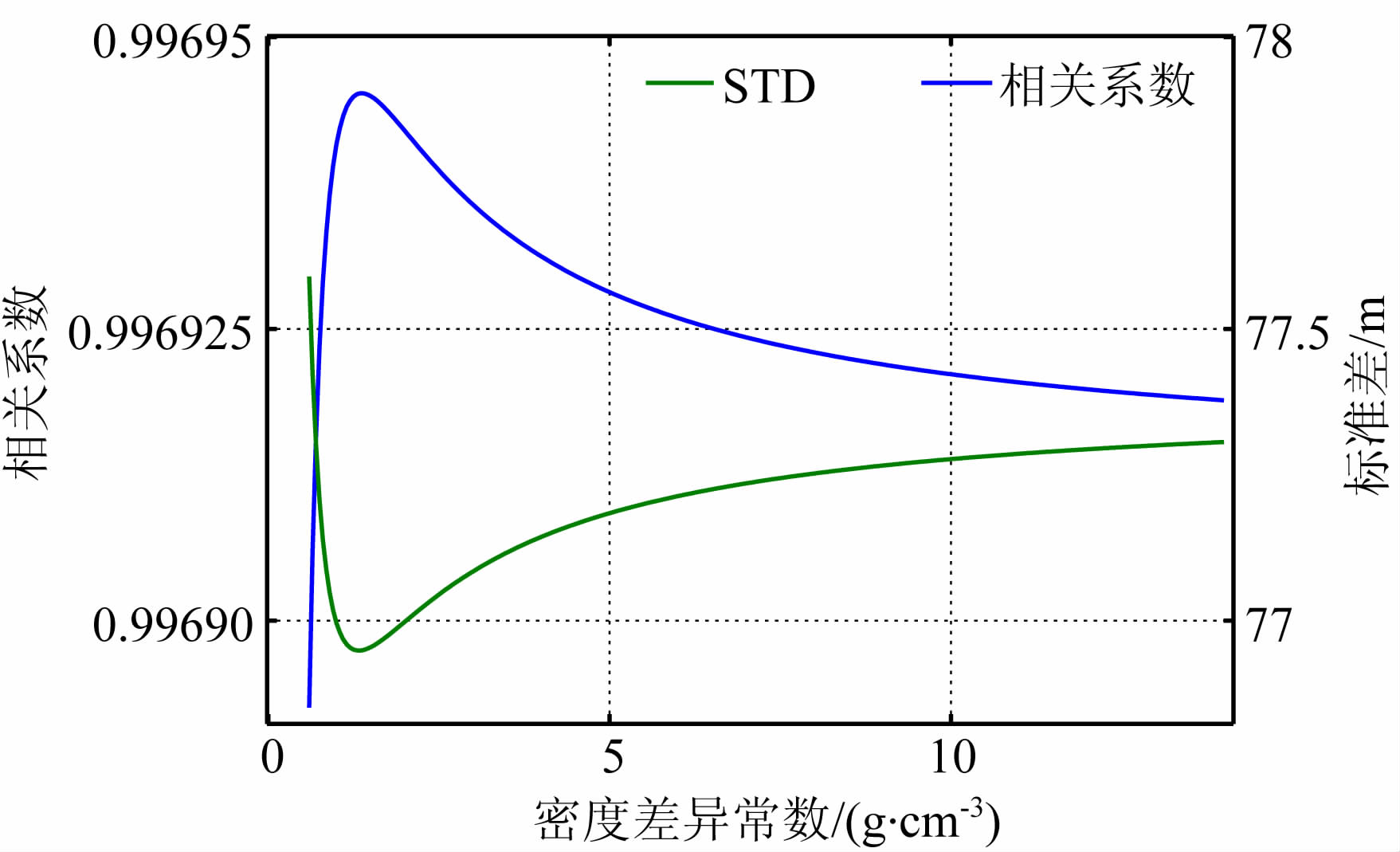图 4 GGM模型插值水深与检核点实测水深相关系数和较差的STD Fig. 4 Correlation coefficient between interpolation depths of GGM model and ship datum of check points， and the STD of the difference of this two

利用卫星测高重力异常通过插值方法得到所有船测水深控制点的自由空间重力异常gjn观，利用公式(2)，由控制点水深和密度差异常数计算出短波重力异常分量gjn短，进而得到长波重力异常gjn长.将长波异常值格网化生成1′×1′长波重力异常格网(如图 5所示)，利用海域内1′×1′测高重力异常格网减去该长波异常格网，得到短波异常格网，按公式(4)即可生成1′×1′的南海GGM海底地形模型，如图 6a所示.

图 5

Fig. 5

图 5 长波重力异常格网 Fig. 5 Long-wavelength gravity anomalies grid

图 6

Fig. 6

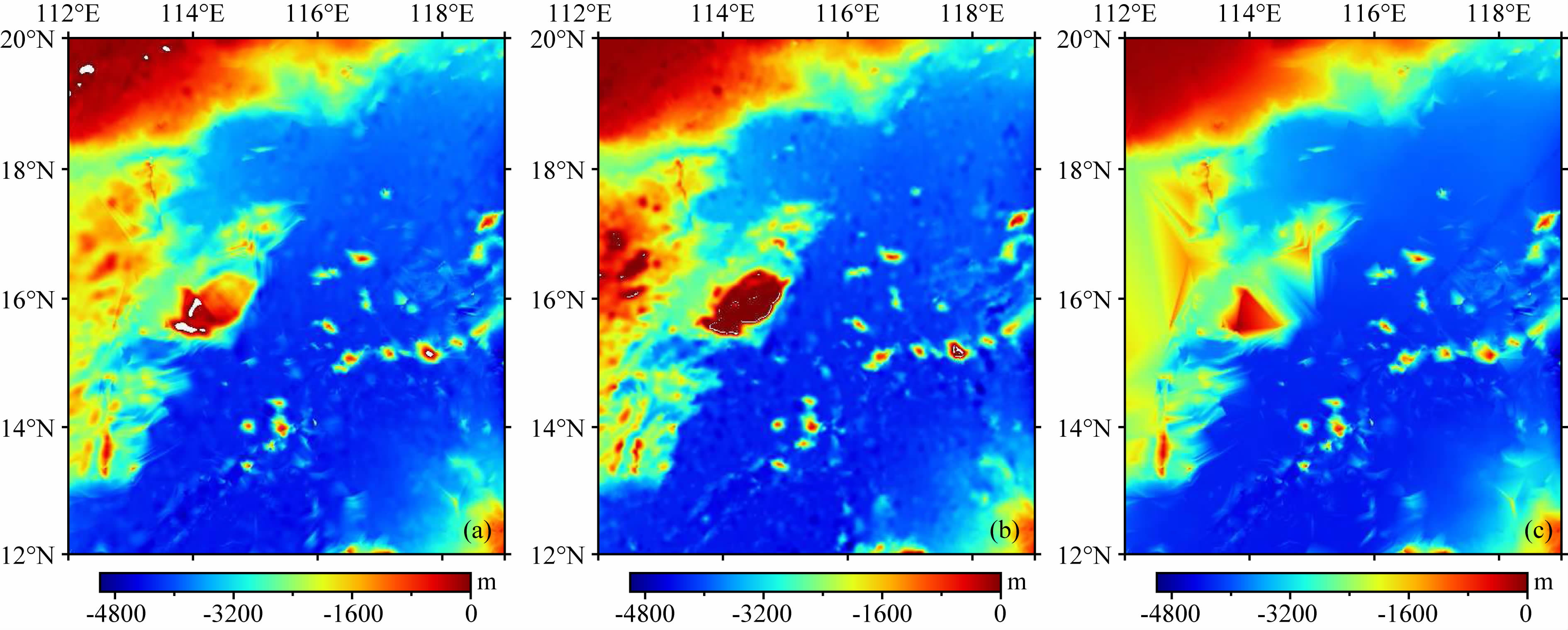图 6 南海海底地形模型 (a)GGM模型；(b)ETOPO1模型；(c)格网化船测水深模型. Fig. 6 Bathymetry model in the South Sea (a)GGM model；(b)ETOPO1 model；(c)Ship data grided model.

为了评价精度，本文使用NGDC于2008年发布的1′分辨率的全球地形数据(ETOPO1)模 型，其中的海洋深度数据来源于日本海洋地理数据 中心(JOC)、NGDC、里海环境计划(CEP)和地中海 科学委员会(CIESM)等组织，各组织的数据提供情况见表 1(Amante et al., 2009)，将这些数据提供给NGDC，NGDC根据需要对其统一编辑和评价.EOTPO1模型能够清晰地描绘出大陆架、海山、海沟和海盆等地形地貌，但对于短波段的部分特征如暗礁、浅滩、海岛等还需精化，经与检核点比较，该模型在南海地区的精度统计如表 2所示.

表 1(Table 1)

表 1 ETOPO1模型中使用的海深数据 Table 1 Bathymetric data sets used in compiling ETOPO1 来源 年份 数据类型 分辨率 坐标系 JODC 水道测量数据的格网化结果 0.5 km WGS 84 NGDC 2006 多波束侧扫声呐数据的格网化结果 7 弧秒 WGS 84 CEP 1999 等深模型数字化 1 弧分 WGS 84 CIESM 2005 多波束侧扫声呐数据的格网化结果 0.5 km WGS 84

表 1 ETOPO1模型中使用的海深数据 Table 1 Bathymetric data sets used in compiling ETOPO1

表 2(Table 2)

表 2 GGM模型、ETOPO1模型与实测水深统计及其比较(单位：m) Table 2 Statistic comparisons between the GGM model， ETOPO1 model and shipborne depths(Unit：m) 数据 Min Max Mean STD RMS GGM模型 -4999.12 529.73 -3221.73 1170.55 3427.79 GGM-ETOPO1 -3271.85 2691.43 20.93 263.36 264.19 GGM 模型插值- 检核水深 -1758.28 2069.28 -1.64 76.95 76.96 ETOPO1模型 插值-检核水深 -1358.49 2157.76 8.85 179.47 179.68

表 2 GGM模型、ETOPO1模型与实测水深统计及其比较(单位：m) Table 2 Statistic comparisons between the GGM model， ETOPO1 model and shipborne depths(Unit：m)

与此同时，需要利用到检核点实测水深进行精度评价.图 6(b、c)示出了ETOPO1模型和利用所有船测水深值的格网模型，可以看出GGM模型比船测水深格网化模型更加精细，能够有效填补无船测海域的海底地形.对GGM模型和ETOPO1模型分别内插得到检核点插值水深，表 2给出了模型、模型插值水深与检核点实测水深的统计信息及比较结果.从表 2可见，GGM模型能够获得比ETOPO1模型更高的精度，但受船测控制点分布的影响，这种精度上的优势是相对的.从图 2可以看出，不同海域的船测点分布差别很大，在112°E、16°N附近几乎没有船测点作为控制，图 7示出了GGM模型和ETOPO1模型的格网点差值分布，显然，在中沙群岛和西沙群岛等船测控制点过于分散的海域和海山附近两模型的差异明显增大，究其原因，一方面在于船测水深控制点的匮乏，另一方面则反映了两模型在多海山地区的精度差别.

图 7

Fig. 7

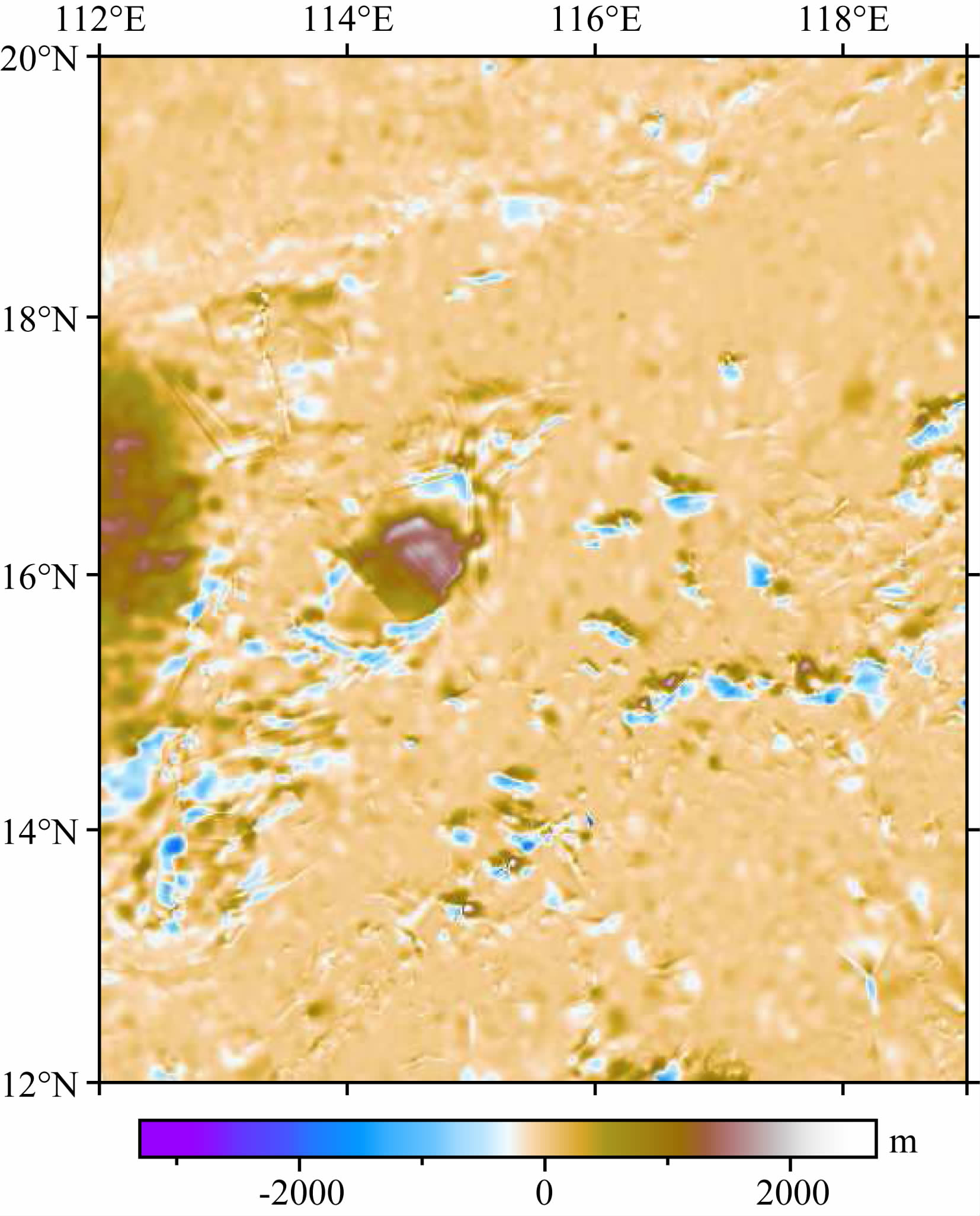图 7 GGM模型-ETOPO1模型/m Fig. 7 GGM model-ETOPO1 model/m

为了更好地对GGM模型精度进行评价，本文划定了南海三个不同海域进行比较，如图 8中A、B、C区域.A海域有半数区域位于深海，船测点密集，但分布不均；B海域大部分位于浅海，船测点数量稀少，但分布匀称；C海域存在海山，测点数量众多.对三个海域的模型、模型插值水深与实测水深的统计及比较结果见表 3，从表中可知，测点数量的多少并不能决定预测模型的好坏，与此相反，测点分布对模型精度会产生很大影响，控制点分布均匀海域的GGM模型预测精度明显好于分布情况较差的海域；GGM模型精度受海水深浅影响较小，但在海山地区呈现明显的下降趋势.

图 8

Fig. 8

图 8 实验海域和检核航迹 Fig. 8 Text areas and check ship cruises

表 3(Table 3)

表 3 不同海域的GGM模型，ETOPO1模型与检核点水深统计及比较(单位:m) Table 3 Statistic comparison between the GGM model，ETOPO1 model and shipborne depths in different areas(Unit：m) 海域及点数 类型 Min Max Mean STD RMS #A 2389个 GGM-ETOPO1 -2252.93 2642.38 -19.52 224.60 225.45 GGM 插值-检核水深 -1758.28 719.56 -1.34 69.03 69.03 GGM模型 -4745.79 -331.44 -3716.43 869.53 3816.80 #B 1112个 GGM-ETOPO1 -2019.28 710.68 -31.93 104.02 108.81 GGM 插值-检核水深 -254.31 253.00 -0.75 30.11 30.11 GGM模型 -4119.02 -188.35 -2910.59 1023.93 3085.44 #C 2814个 GGM-ETOPO1 -2431.15 2066.32 -10.53 231.88 232.12 GGM 插值-检核水深 -1513.18 2069.28 -4.02 98.67 98.74 GGM模型 -4999.11 363.38 -3926.10 539.45 3962.99

表 3 不同海域的GGM模型，ETOPO1模型与检核点水深统计及比较(单位:m) Table 3 Statistic comparison between the GGM model，ETOPO1 model and shipborne depths in different areas(Unit：m)

海底地形变化复杂，仅利用检核点较差结果进行精度评价是不够的，因而，将较差结果与实测水深之比定义为相对精度，作为评价指标.图 9示出了采用GGM模型计算的检核点相对精度的绝对值大 小，大部分检核点的相对精度十分微小，在113.5°E、 18°N和116°E、15°N附近的部分点位相对精度较大，这些海域多存在海沟、海山等复杂的海底地形地貌特征；图 10示出了采用GGM模型和ETOPO1模型计算的检核点相对精度统计直方图，表 4为各 自的相对精度统计信息，可以看出，GGM模型相比ETOPO1海深模型反演出了更加详细的海底特征.

图 9

Fig. 9

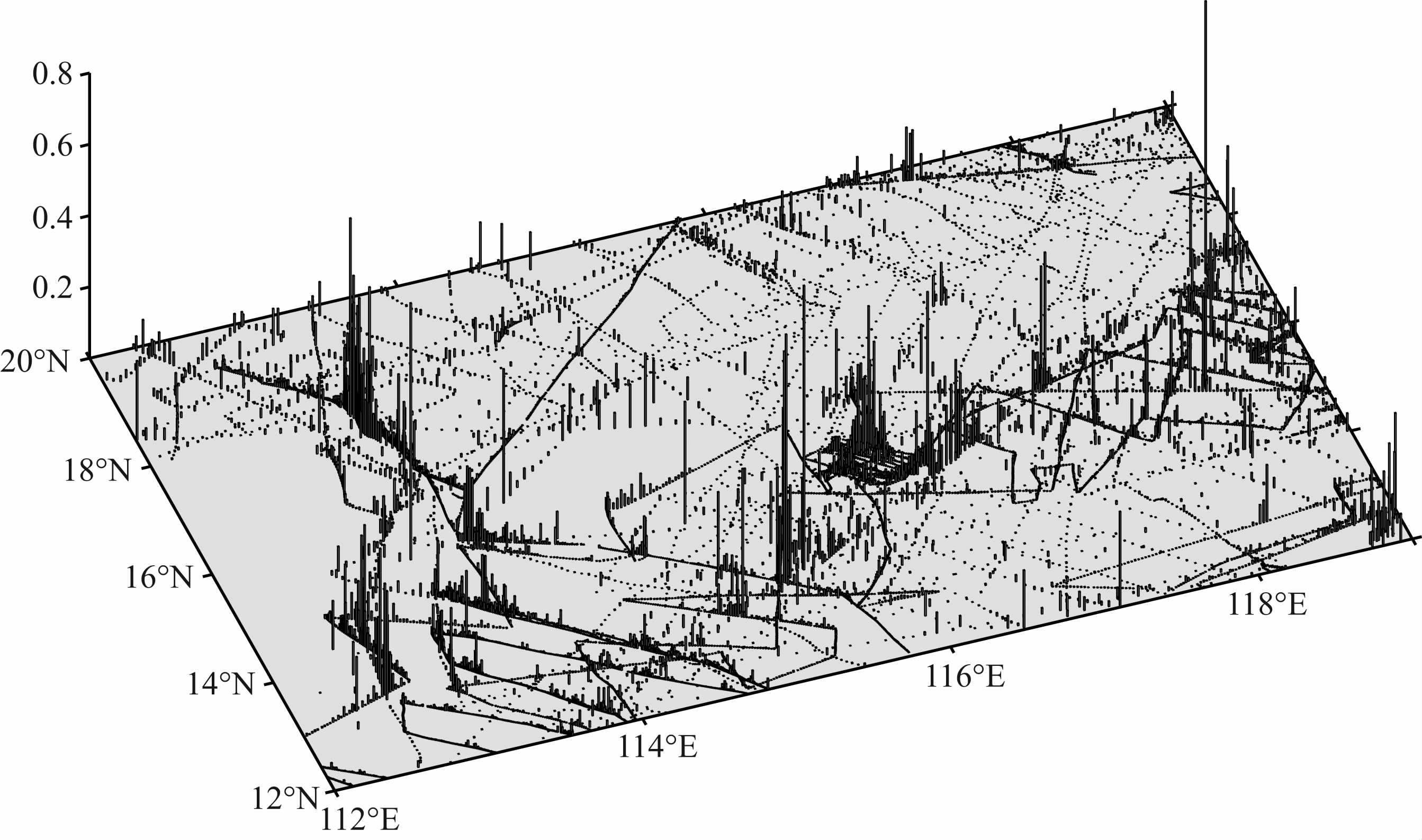图 9 GGM模型插值检核点水深的相对精度绝对值 Fig. 9 The absolutely bathymetry differences between GGM model and shipborne depths of check points

图 10

Fig. 10

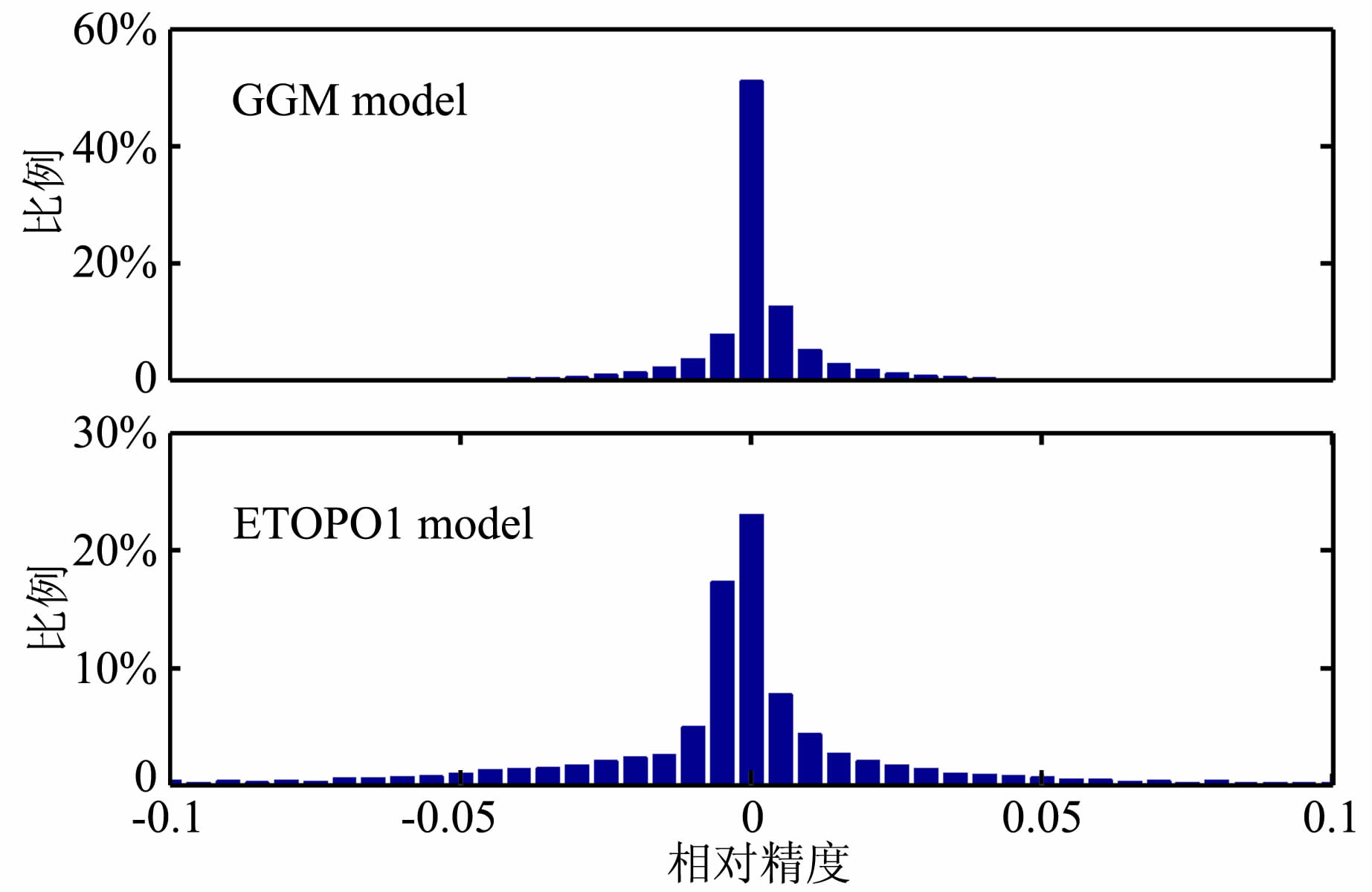图 10 不同模型插值计算的检核点较差结果相对精度统计直方图 Fig. 10 Histogram of relative precision of differences in check points

表 4(Table 4)

表 4 相对精度统计 Table 4 Statistic of relative precision 数据 Min Max Mean STD RMS GGM 模型插值 -检核水深 -0.9763 1.9006 -0.00077 0.0406 0.0406 ETOPO1模型插 值-检核水深 -1.4695 0.6810 -0.0084 0.0827 0.0832

表 4 相对精度统计 Table 4 Statistic of relative precision

上文中GGM模型计算的检核点较差结果和相对精度中仍然有较大数值存在，最大值达到2000 m左右，因而有必要探讨其成因.图 11示出了精度较大的检核点位置分布图，将较差结果中绝对值大于400 m的点显示为黄色，共计54个，约占总数的0.5%；相对精度中绝对值大于8%的点显示为粉 色，共计218个，约占总数的2%，这些点分布范围较广，且在部分海域相对集中.究其原因，一方面在于还存留有少量船测海深质量较差的点尚未剔除，这些点同数据准备阶段剔除的粗差不同，未有明显特征，尚未有好的办法加以辨别，它们可能隐藏在控制点中对反演的局部海域水深造成影响，也可能隐藏在检核点中将正确的水深结果造成错误的假象.另一方面原因在于海底地形的剧烈变化导致了反演精度的下降，这可以从图 11检核点的分布情况中推断出来，这些点多分布于海山、海沟等存在较大地形落差和突变的海域附近.总而言之，第一方面的原因是起次要作用的，第二方面的原因是起主要作用的.

图 11

Fig. 11

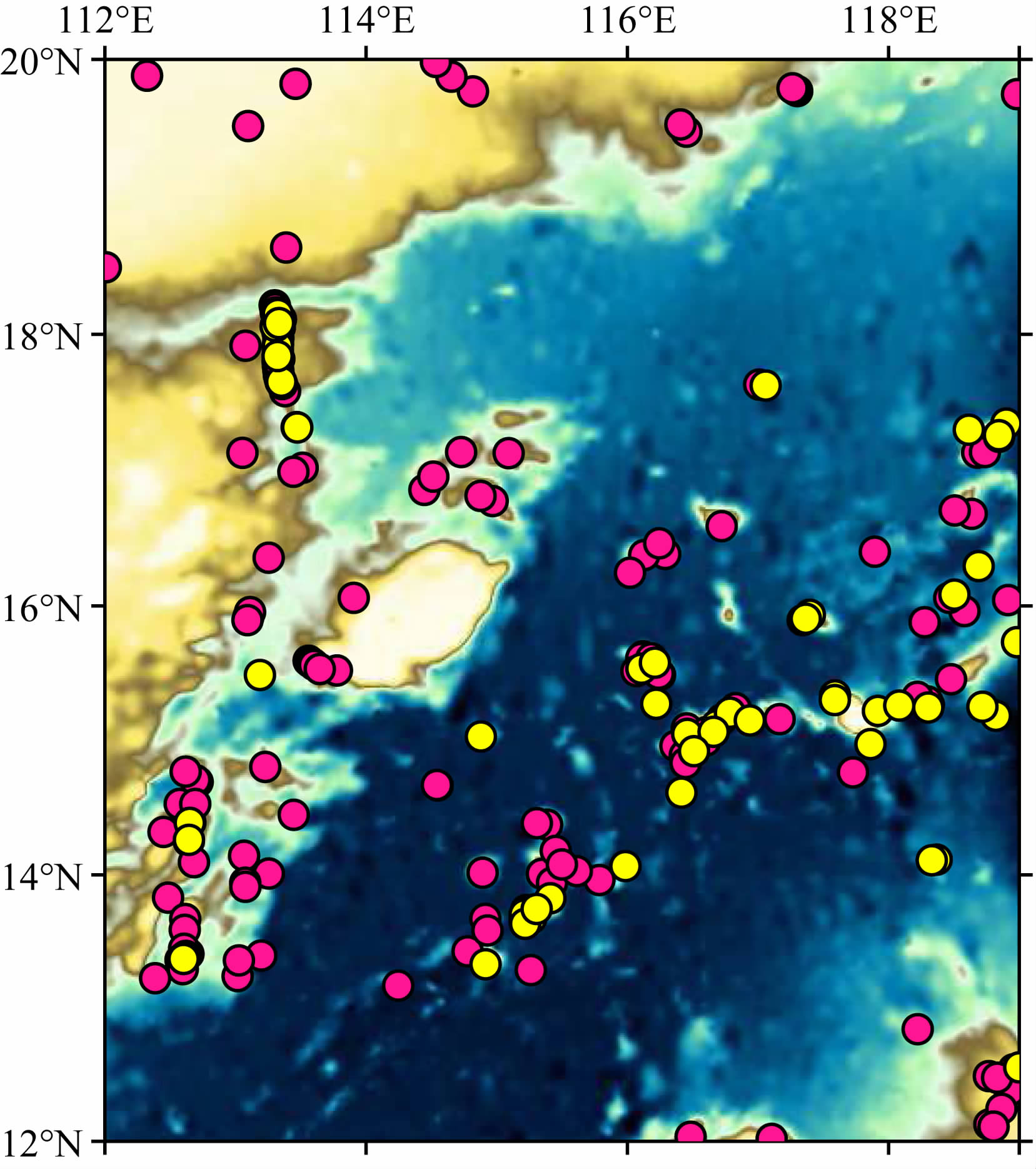图 11 精度较差点的位置分布图 Fig. 11 Distribution of check points with worse precision

为进一步证实该结论，本文同时选定了两条船测航迹进行分析，即图 8中的Cruise_01、Cruise_02航迹，并分析了所有检核点的较差结果、相对精度与水深和重力异常的关系. 图 12为Cruise_01和Cruise_02航迹测深剖面，绿色线条示出了航迹剖面上实测水深和GGM模型插值水深的比较结果，差异较大部分大多出现在地形剖面变化复杂的海域，在地形坡度变化平缓的海域两者符合较好.

图 12

Fig. 12

图 12 Cruise_01和Cruise_02航迹比较 Fig. 12 Comparisons for bathymetry along the Cruise_01 and Cruise _02

图 13示出了采用GGM模型计算的检核点水深的较差结果、相对精度与水深和重力异常的关系，可以看出，较差结果在深海地区普遍偏大，但这种情况在相对精度上有所改善，浅海地区相对精度较高的点明显多于3000 m以上的深海地区；相比水深而言，在与重力异常的关系图中，较差结果、相对精度的分布更加集中，其较大值出现在高异常值区间的概率大于低异常值区间.但总体而言，检核点较差结果、相对精度与水深和重力异常的相关性不强.

图 13

Fig. 13

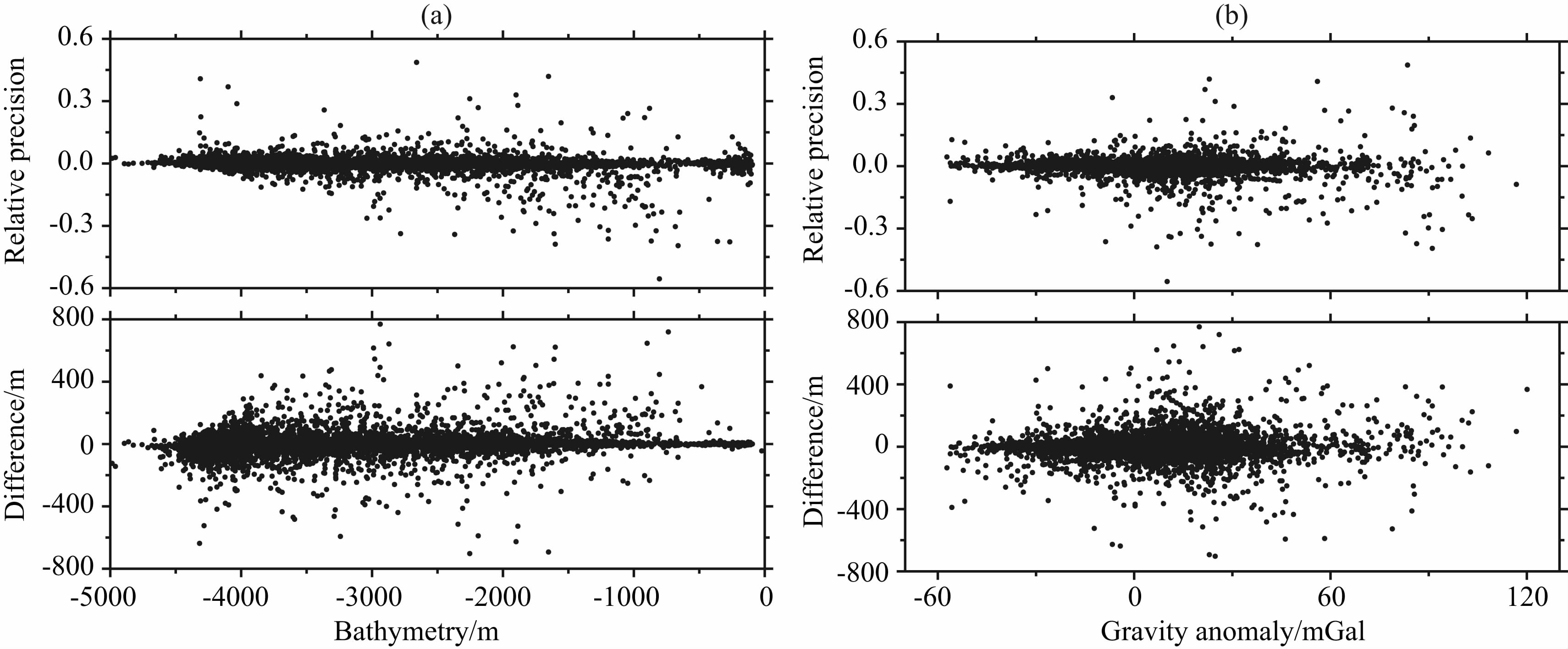图 13 检核点较差结果、相对精度与水深和重力异常的关系 (a)较差结果、相对精度与水深的关系；(b)较差结果、相对精度与重力异常的关系. Fig. 13 The relationship between the difference and relative precision of check points and bathymetry and gravity anomaly (a)The relationship between the difference，relative precision of check points and bathymetry； (b)The relationship between the difference，relative precision of check points and gravity anomalies.

前文论述了GGM模型的建立，并评价了其精度.鉴于GGM模型在海域的良好精度和ETOPO1模型在陆地和海洋的数据完备性，因而有必要结合两者优势生成综合的南海海深预测模型.考虑到测 量船的吃水深度和船测水深范围限制，对大于-30 m 深的浅海和岛屿部分采用ETOPO1模型进行填补，其余部分利用重力地质法进行反演，采用该方法时将海域内所有船测点作为控制，密度差异常数定为1.32 g·cm^－3，生成的综合模型见图 14a.图 14b示出了综合模型与GGM模型(图 6a)的差异，除去中沙群岛和西沙群岛，综合模型和GGM模型差别不大，两者相关系数为0.9971.值得注意的是，综合模型是两模型的优势互补，在两模型接边处不可避免地会产生跳跃，这与实际海底地形不符，如何更好地融合两者模型数据有待进一步研究.

图 14

Fig. 14

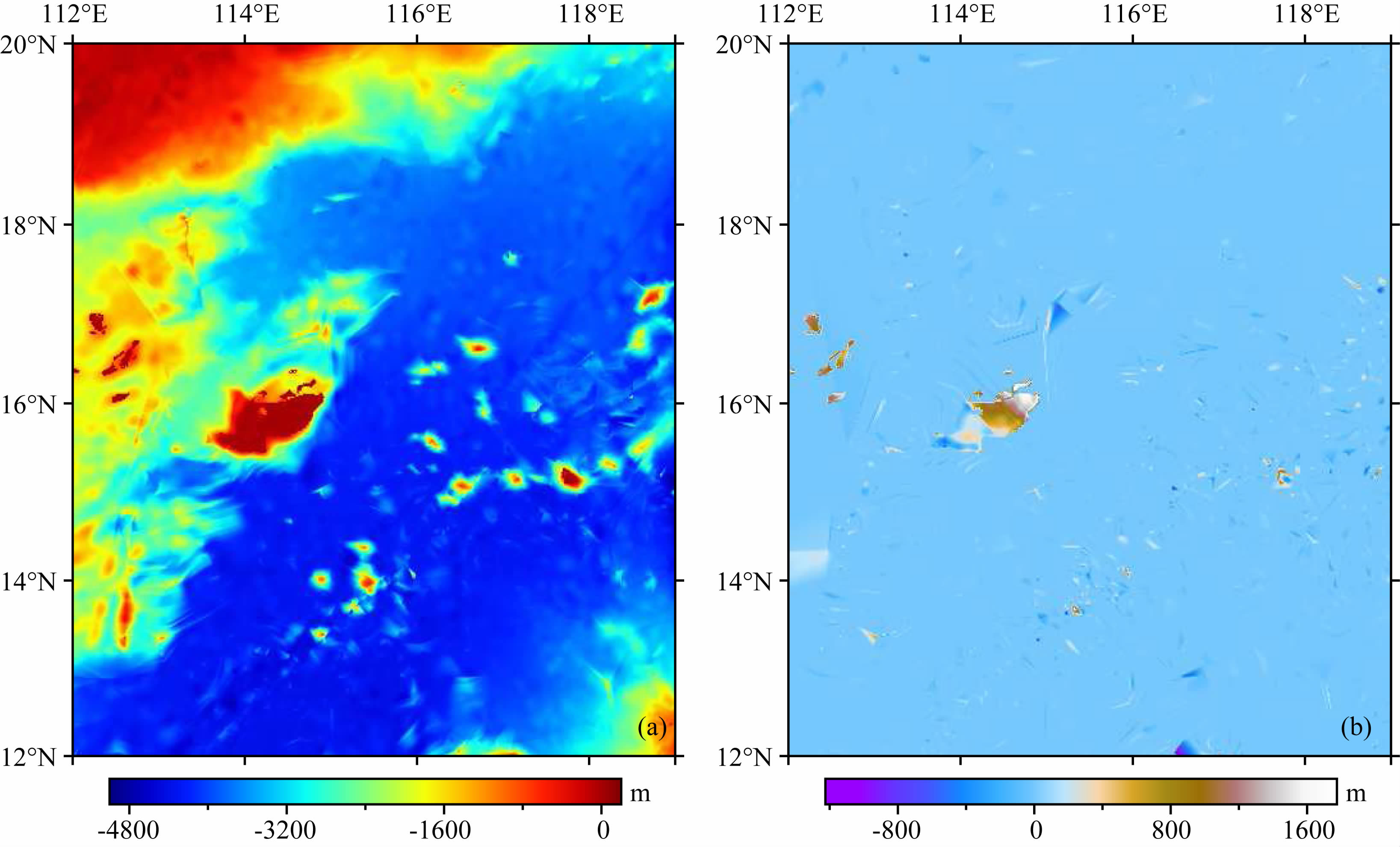图 14 综合模型及其与GGM模型的比较 (a)综合模型；(b)综合模型-GGM模型. Fig. 14 Enhanced bathymetry model and differenced GGM bathymetry model (a)Enhance bathymety model；(b)Enhance bathymety model-GGM model.

重力地质法的主要优点在于能够满足大面积水域的地形反演要求，但前提是需要事先确定海水和海底洋壳的密度差.本文采用检核点实测水深确定密度差异常数，以南海为例对重力地质法反演海底地形的精度进行了评价，并生成了综合模型，通过分析，得到以下初步结论：

(1)采用重力地质法计算海底地形模型结果可靠，方法简便，能够有效填补船测稀疏海域水深测量的不足，不涉及复杂的地球物理参数求取，在船测水深控制点分布均匀的海域，GGM模型精度优于ETOPO1模型，在控制点过于分散的海域其精度有所下降，但好于船测水深的直接格网化结果.

(2)GGM模型精度受船测控制点数量影响较小，受控制点分布影响较大，受水深和重力异常的相关性影响较小，受海底地形复杂程度影响较大，地形坡度变化平缓海域的预测精度明显高于海山地区.

(3)重力地质法中海水和海底洋壳的密度差异常数确定十分关键，该常数的目的是为了让残余重力异常和海深之间保持良好的线性关系，在有船测水深的海域可以利用检核点水深的迭代方法进行计 算，在无船测水深的海域可以采用向下延拓的频率域方法进行计算，两者的一致性有待进一步研究.