地球物理学报  2014, Vol. 57 Issue (8): 2732-2742   PDF    
引用本文
王瑞甲, 乔文孝. 2014. 非对称圆弧片状声源在井旁地层中产生的声场. 地球物理学报, 57(8): 2732-2742, doi: 10.6038/cjg20140831   
WANG Rui-Jia, QIAO Wen-Xiao. 2014. Study of acoustic field in the near-borehole formation generated by an asymmetric arcuate acoustic source. Chinese J. Geophysics, 57(8): 2732-2742, doi: 10.6038/cjg20140831   
非对称圆弧片状声源在井旁地层中产生的声场
王瑞甲1,2, 乔文孝1,2    
1. 中国石油大学油气资源与探测国家重点实验室, 北京 102249;
2. 北京市地球探测与信息技术重点实验室, 北京 102249
投稿时间:2013-10-9    最后修改时间: 2014-5-13 .
基金项目：国家自然科学基金项目（11204380、11374371、11134011和61102102）、国家油气重大科技专项（2011ZX05020-009）、中国石油科技创新基金（2013D-5006-0304）和中国石油天然气集团公司项目（2011A-3903、2011B-4001）资助.
作者简介：王瑞甲，男，山东无棣人，汉族，博士，主要从事地球物理测井方法、检测声学等方面的研究工作.E-mail：wruijia@foxmail.com
通讯作者：乔文孝，男，山东禹城人，博士、博士生导师；中国声学学会理事.研究方向：声波测井、检测声学.E-mail：qiaowx@cup.edu.cn
摘要：提出了一种可用于随钻三维反射声波成像测井的圆弧片状声源，推导了该声源声学性质在波数-频率域内的数学描述，并利用实轴积分的方法对该声源在井旁地层中产生的声场进行求解，考察了声源的线度、频率等因素对该声源向地层中辐射的声场的影响.研究结果表明，特定尺寸和特定频率下的圆弧片状声源产生的纵波场的水平和垂直指向性图中仅具有一个明显的主瓣，且主瓣三分贝角宽较窄，方位分辨率较高，指向性良好，适用于随钻三维反射成像测井；SV波场和SH波场的指向性图中存在两个或者多个角瓣，SV波场在垂直于井轴方向上辐射的能量为0，另外在井中发射和接收的反射SH波场和SV波场会相互干扰，所以难以利用SV波场和SH波场进行三维反射声波成像；声源的线度和频率等因素对其辐射声场影响较大，考虑到激励效率和方位分辨率等因素，对于本文描述的井孔模型，选择圆周角在75°和90°之间， 主频为12 kHz左右的声源是合适的.
关键词： 随钻声波测井     声波反射成像     非对称声源     圆弧片状声源    
Study of acoustic field in the near-borehole formation generated by an asymmetric arcuate acoustic source
WANG Rui-Jia1,2, QIAO Wen-Xiao1,2    
1. State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum, Beijing 102249, China;
2. Key Laboratory of Earth Prospecting and Information Technology, Beijing 102249, China
Abstract: We propose an asymmetric arcuate acoustic source to develop a three-dimension acoustic reflection LWD method, and deduce the mathematical description of the source in wavenumber-frequency domain. The acoustic field in the formation produced by the source is obtained by the real axis integration method, and the influences of the dimension and frequency of the source on the compressional wave field, SH wave field and SV wave field are investigated. The results indicate that only one main lobe is observed in the horizontal and vertical directivity of the compressional wave field produced by the arcuate source with specific size and frequency. The 3dB angular width of the main lope is narrow. Hence compressional wave field excited by the source is of high azimuthal resolution and suitable for the three-dimension acoustic reflection LWD. Two or more lobes exist in the directivity of SV field and SH field, and the radiant energy of the SV field at the direction perpendicular to the borehole axis is 0. Additionally, the reflected SH waves and SV waves may interfere with each other because of similar ray path and velocity. Therefore, it is difficult to image the geological structure in three-dimension by the SV field and SH field. The dimension and frequency of the source greatly impact the radiated wave field, and in consideration of the excitation efficiency and azimuthal resolution, for the borehole model described in this paper, the source with azimuthal width between 75° and 90°, and main frequency around 12 kHz is an appropriate choice.
Key words: Acoustic LWD     Acoustic reflection image     Asymmetric source     Arcuate source    
1 引言

在声波测井中，声源的革新往往带动井孔声学测量方式的革新(乔文孝等， 2011a，2011b).近些年，国内外学者在新声源的研究上做了许多有益的工作，极大地推动了声波测井技术的进步.唐晓明(2012)提出采用四极子声源进行慢速地层随钻横波速度测量，现场测量结果已证实了他的结论(Tang and Cheng， 2004).乔文孝等提出了采用组合相控圆弧阵声源在井内进行声学测量的方法，并分别从理论、数值模拟、物理模拟及现场实验等多个方面证实了组合相控圆弧阵声源在非均质各向异性地层评价方面的可靠性(乔文孝等，2002; 车小花和乔文孝，2004; 乔文孝等，2006;陈雪莲，2006;乔文孝等，2008; 卢俊强等，2011).Market和Deady(2008)等数值研究了偏心点声源在充液井孔及含钻铤充液井孔中激发的声场，并给出了实例分析.他们的研究结果表明，声波测井仪器不仅对横波速度的方位各向异性敏感，对纵波的方位特性同样敏感.Wang 等(2011)研究了偏心点声源在慢地层井孔中激发的声场，并将其与偶极子和四极子仪器的模拟结果进行了对比，认为偏心点声源可以近似等效为单极子声源、偶极子声源的叠加或者单极子声源、偶极子声源和四极子声源的叠加.王兵等(2012)实验研究了偏心的非对称点声源在含钻铤充液井孔中激发的多极子声场，证明可以通过非对称点声源得到有效的地层单极子、偶极子和四极子模式波信号.在随钻反射成像测井方面，陈雪莲和魏周拓(2012)采用有限差分方法研究了单极子声源在随钻反射成像方面的应用，他们的研究结果表明，在随钻环境下，当井旁存在地层界面时，井周八个方位接收到的反射纵波信息具有明显差别，通过对不同方位上接收的信号做矢量计算，可以得到来自井旁地层界面的反射纵波信息.

上述的研究大多集中在电缆测井方面，部分涉及到随钻声波测井的文献仅分析了单极子声源或者偏心点声源的情况，未考虑声源的形状、线度和频率等因素对向地层中辐射的声场的影响.在随钻条件下，钻铤占据了井孔内的大部分空间，从而使得随钻声波测井和电缆声波测井有很大不同(Tang and Cheng， 2004).对于反射声波测井而言，钻铤对声信号的屏蔽作用可能会使得位于钻铤一侧的声源向另外一侧辐射的能量降低.基于此，本文提出一种应用于随钻三维反射声波成像测井的非对称圆弧片状声源，通过对该声源在井附近地层中激发的声场的计算和分析，研究了该声源在不同频率、不同几何尺寸条件下的声场辐射特征，并进一步论证利用其进行随钻三维反射成像测井的可行性.

2 理论 2.1 数值计算模型

图 1a为随钻声波测井模型井孔截面示意图.该模型为典型的柱状径向分层声学模型.模型由内向外各介质依次为水眼(水)、钻铤、井孔(水)和地层，各层介质的外径分别为r0、r1、r2和无穷大.井孔内充满液体.井孔外地层为无限大地层.钻铤位于井孔中央，钻铤水眼内也充满液体.圆弧片状声源加载在钻铤外表面，其半径为rs，高度为h，圆周角为φ，如图 1中红色粗线部分所示.对于实际的测井仪器，往往采用隔声材料将钻铤和声源进行声隔离，本文在声源和钻铤之间加了一层厚度为0.005 m的水层，使得声源与钻铤未直接接触.根据圆弧片状压电振子的有限元模拟分析结果，将该声源看作由圆弧上无数个振幅相同偶极子声源组成.实际计算中，采用的偶极子声源的极距为0.0001 m，其声轴方向与r轴平行.与未发表的实验数据的对比结果表明，这种处理方式和实际情况是一致的.

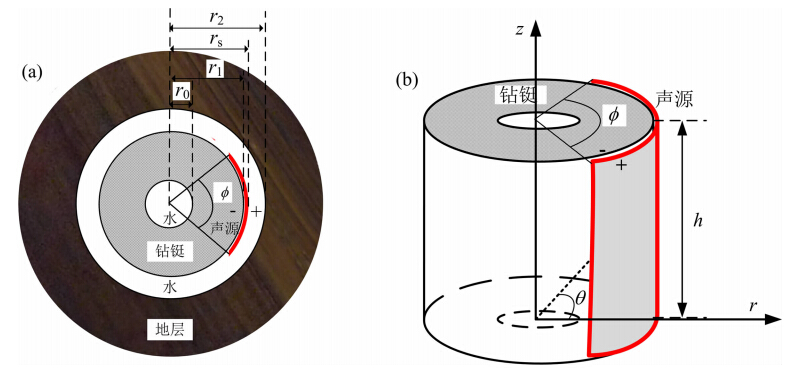图 1 随钻声波测井声学模型示意图，包括(a)模型横截面和(b)声源的三维示意图Fig. 1 Schematic diagram of acoustic LWD model，including(a)cross-section and (b)arcuate source
2.2 声源的数学描述

势函数法是计算各向同性固体和液体介质中的声场的常用方法.在柱坐标系下，位置(r′，θ′，z′)处的点声源可以展开为多极子声场叠加的形式(Tang and Cheng， 2004)：

其中，Φ为纵波位移势；kz和f分别为液体内纵波的轴向和径向波数；In和Kn为n阶修正的贝塞尔函数，分别代表向内和向外传播的波动；εn为权重系数，当n=0时，εn=1，当n≥1，εn=2.首先推导由点声源组成的圆弧片状声源产生的声场的数学表达式. 不考虑声源的径向厚度，假定声源中心位置对应的坐标为(rs，0，0)， 那么该声源在液体中辐射声场的位移势为

上述的积分可写做

其中，

其中，H表示单位阶跃函数.最终得到波数-频率域内该声源产生声场的位移势的数学表达式:

由偶极子声源组成的圆弧片状声源可以看作由振幅相同、极性相反的两排点声源组成，假设内排声源阵列的半径为rs1，外排声源阵列的半径为rs2，那么该声源产生声场的位移势为

其中，

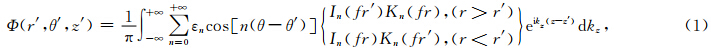
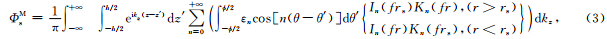
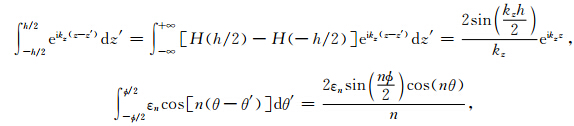
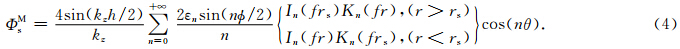
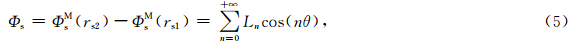
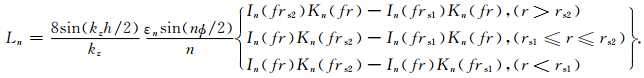
由式(5)可以看出，圆弧片状声源激发的声场可以看作无穷多种方位阶数的多极子声场的叠加.在实际计算中，由于方位阶数较高的多极子声场的幅度较小，可忽略不计.声源在均匀液体内的任意位置产生的径向位移和声压可以通过式(6)得到(Tang and Cheng， 2004)：

2.3 井孔内外声场的解

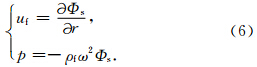
文献(Tang and Cheng， 2004;张海澜等，2004; 崔志文，2004; 王瑞甲，2012)均介绍了各向同性固体介质中多极子声场的通解.固体中的多极子声场可以采用位移的势函数表示：

其中Φ表示纵波位移势，χ表示SH波位移势，Γ表示SV波位移势，qp、qsh和qsv分别表示地层内纵波、SH横波和SV横波的径向波数.对于液体而言，仅存在纵波位移势Φ.假设水眼内代表沿径向向内传播的纵波的势函数的系数为A(wh)n，钻铤内代表向内和向外传播的纵波和两种横波的势函数的系数分别为A(co)n、B(co)n、C(co)n、D(co)n、E(co)n和F(co)n，井孔中表示向内和向外传播的纵波的势函数的系数分别为A(bh)n、B(bh)n，地层中表示向外传播的纵波和两种横波的势函数的系数分别为B(fo)n、D(fo)n、F(fo)n，缩写“co”、“wh”、“bh”、“fo”分别表示钻铤、水眼、井孔和地层.根据水眼-钻铤、钻铤-井孔和井孔-地层处的边界条件(Tang and Cheng， 2004;崔志文，2004; 王瑞甲，2012)，得到

式(8)—(10)分别代表水眼-钻铤、钻铤-井孔和井孔-地层边界.联立式(8)—(10)得到

其中，

其中，X 表示位移势函数的系数向量，其中各元素的上标代表介质类型，下表n代表多极子的方位阶数. S 表示声源项，ud，nf，co和ud，nf，bh分别为声源在钻铤壁和井壁上产生的方位阶数为n的多极子声场的位移，τd，nf，co和τd，nf，bh表示声源在钻铤壁和井壁上产生的方位阶数为n的多极子声场的正应力，可由式(6)得到.为描述方便，在矩阵 M 12×12和声源项 S 中省略公共因子cos(nθ)exp(ikzz).矩阵 M 中各元素的详细表达式参见文献(崔志文，2004; 王瑞甲，2012).

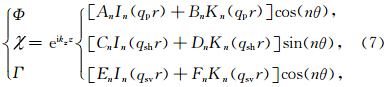
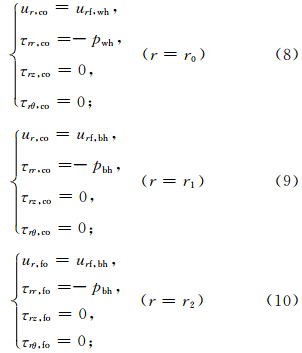
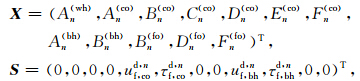
通过对式(11)的求解，求得描述井孔内外声场的势函数的系数:

计算不同方位阶数n的声场(本文计算时，取n的上限为20)，通过积分可得到地层中坐标(r，θ，z)位置处纵波、SV波场和SH波场以位移势形式表示的激发谱：

根据声场的位移势可获得水眼、井孔，钻铤和地层中各位移分量、应力分量的值.其中，地层中声场的径向位移u为

其中M(9，10)、M(9，11)和M(9，12)代表式(11)中矩阵 M 的元素，下标表示矩阵元素的位置.

2.4 声源在无限大液体中激发的声场的解

将钻铤和圆弧片状声源置于无限大液体中，此时仅需考虑水眼-钻铤、钻铤-井孔流体两个边界条件，即联立式(7)—(8)，得到

其中，

矩阵 M′ 中各元素与矩阵 M 类似.通过求解系数矩阵 X′ 即可得到波场的解.其中该声源在液体中激发的纵波场以位移势形式表示的激发谱为

其中，式(16)右侧被积函数中第一项BnKn(fr)表示钻铤向无限大液体中散射的声场，第二项Ln表示声源辐射的直达波声场.忽略钻铤散射声场项，即可得到在不含钻铤的情况下，声源向液体中辐射的声场的位移势.

3 数值计算结果 3.1 模型参数

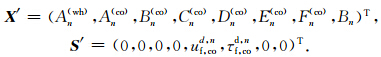
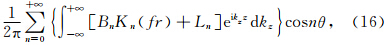
钻铤内半径r0、外半径r1分别为0.027和0.090 m. 井孔半径r2为0.12 m.考虑了两种地层模型，分别是快速地层、慢速地层.模型中各种介质的弹性参数分别如表 1所示.

表 1 各种介质的弹性参数Table 1 Elastic parameters of the material
3.2 辐射声场的能量分布

水平指向性是指声源所辐射声场在z为常数的平面内的分布，垂直指向性是指声源所辐射声场在θ为常数的平面内的分布.如图 2中的接收器阵列RA-1所示，固定接收器的坐标r和z，利用式(13)或(16)计算方位角θ不同的接收器记录的声场激发谱，取激发谱的模，并对其做归一化处理，即可得到该声源激发声场的水平指向性曲线.引入任意方向与井轴的夹角φ=arctan(r/z)，如图 2中接收器阵列RA-2所示，固定接收器的坐标(r2+z2)1/2和θ，计算不同φ对应位置的声场，并对其做归一化处理，可得到该声源激发的声场的垂直指向性曲线.

图 2 接收器位置示意图Fig. 2 Schematic diagram of the receiver locations

首先采用式(16)计算了将声源置于无限大液体中时，该声源产生的纵波场.图 3为该声源辐射的纵波场位移势的归一化幅度图，其中实线表示钻铤存在的情况，虚线表示不含钻铤的情况.声源频率为 12 kHz，圆周角为85°，高度为0.08 m(如无特殊说明，下同).对于图 3a所示的水平指向性图，各个 接收器的坐标r为4 m，z为0 m，θ=0~360°;对于图 3b所示的垂直指向性图，接收器坐标(r2+z2)1/2 为4 m，θ为0°，φ=0~360°.从图 3可见，钻铤阻挡了声源向钻铤后方(θ=180°)辐射的声信号，使得声源仅向换能器正对的方向(θ=0°)辐射能量.在钻铤存在的情况下，声源的指向性图中仅存在一个主瓣，幅度最大处为换能器正对的方位(θ=0°)，主瓣角宽较窄，旁瓣级低，有较好的方位分辨率，适合三维反射声波成像方法.另外，在垂直指向性图中可观察到指向性曲线的剧烈抖动，这是由钻铤模式波向液体 中泄露的纵波与声源辐射的纵波的干涉叠加形成的.

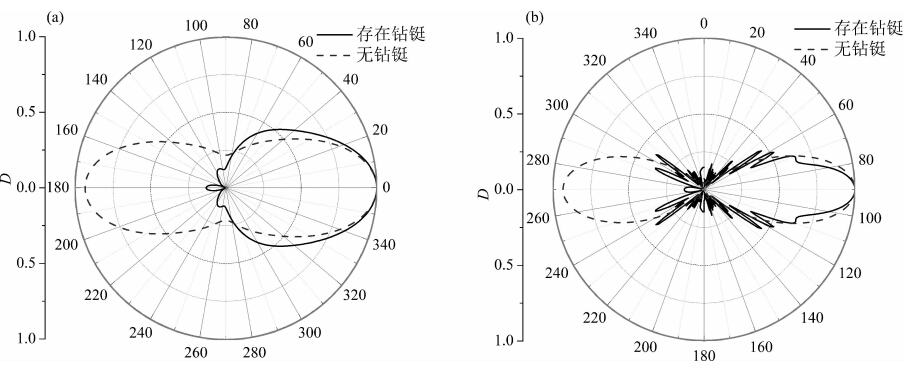图 3 圆弧片状声源在无限大液体中产生的纵波场的水平指向性(a)和垂直指向性(b)图(圆周边的数字单位为°，下同)Fig. 3 Horizontal(a) and vertical(b)directivity of the compressional wave field in the infinity liquid produced by the arcuate acoustic source

进一步探讨充液井孔中的圆弧片状声源向地层中辐射声场的特征.图 4是数值计算得到的圆弧片状声源在地层中产生的纵波场、SH波场和SV波场的指向性图，其中(a)和(b)为慢速地层结果，(c)和(d)为快速地层结果.声源参数与图 3相同，接收器距离声源的圆弧圆心的距离为4 m.图 4a和4c为水平指向性图，其中纵波和SH波指向性曲线所采用的接收器的坐标z为0 m，SV波接收器坐标z为2.0 m.图 4b和4d为垂直指向性图，纵波场和SV波场指向性曲线所采用的接收器的方位角θ为0°，SH波接收器采用的方位角θ为45°.之所以采用这 样的接收器布置方式，是因为该声源在z=0 m的 水平面内辐射的SV波场能量为0，在方位角θ=0°垂直平面内辐射的SH波场能量为0.由图 4a和4c可知，纵波场指向性良好，仅存在一个主瓣，主瓣三分贝角宽较窄，分别为90.6°(慢速地层)和88.5°(快速地层)，方位分辨率较高，主瓣的能量最大处为换能器正对的方位，θ=180°时能量很弱；SH波场的指向性图呈现多个辐射角瓣，沿周向辐射能量分布较复杂；在慢速地层情况下，SV波场θ=180°附近存在较大幅度的旁瓣.从垂直指向性图可见，该声源辐射的纵波场在水平方向辐射的能量最强，随着角度增加或者减小，辐射能量逐渐减弱，三分贝角宽分别为50.1°(慢速地层)和63.3°(快速地层)；由于纵波垂直入射到井壁时不发生模式转换，该声源无法激励沿水平方向传播的SV波，所以在φ=0°时，SV波场能量为0；SH波场的指向性图较复杂.综上所述，圆弧片状声源产生的纵波场水平指向性和垂直指向性特征良好，适用于三维反射声波成像，而SH波场和SV波场的归一化幅度图中存在多个辐射旁瓣，在部分角度的辐射能量接近0，不适用于三维反射声波成像.

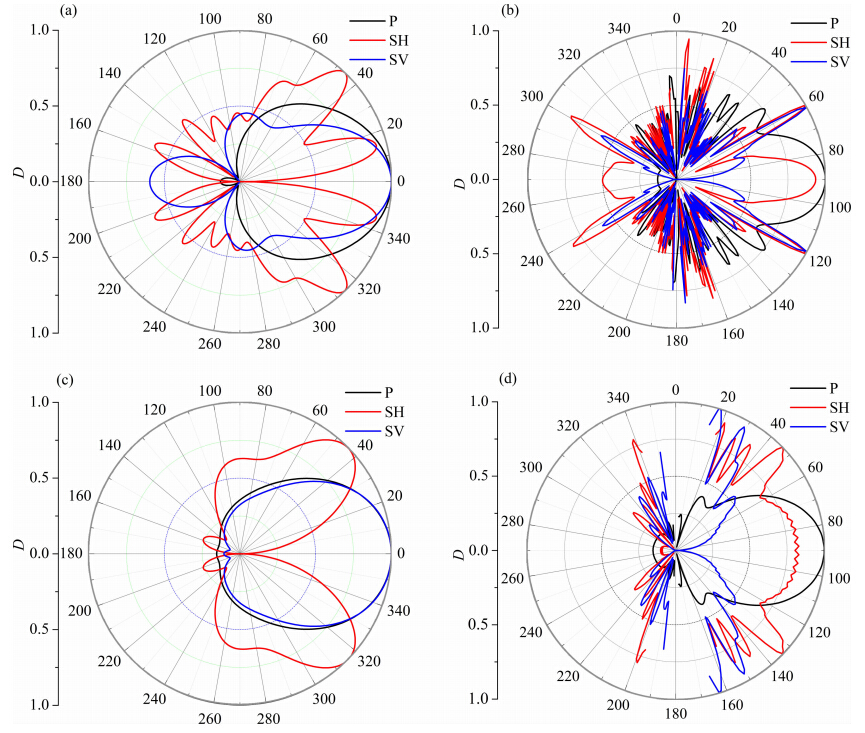图 4 圆弧片状声源在地层中辐射的纵波、SV和SH波场的水平指向性和垂直指向性图(a)和(b)为慢速地层结果，(c)和(d)为快速地层结果；(a)和(c)为水平指向性图，(b)和(d)为垂直指向性图.Fig. 4 Horizontal and vertical directivity of the compressional，SV and SH wave field in the formations produced by the arcuate acoustic sourceWhere(a) and (b)representthe results of the slow formation，(c) and (d)represent the results of the fast formation，respectively.
3.3 声源频率对声场的影响

计算了不同频率下的圆弧片状声源向慢速地层和快速地层中辐射的纵波场的水平指向性，如图 5所示.声源的频率取3~14 kHz，其他参数与图 3 相同.计算结果表明，在声源频率为3 kHz和6 kHz时，在90°<θ<270°范围内存在较强能量的波场，方位分辨能力较差；而当声源频率为12~14 kHz时，其辐射主瓣角宽较小，旁瓣级低，方位特征良好，适用于三维反射声波成像技术.

图 6是不同频率的圆弧片状声源在z=0 m，r=4 m，θ=0°位置处产生纵波场的激发谱，由式(13)计算得到.为了忽略声源本身性质对激发谱的影响，图 6中显示物理量为Φ/ω，并采用显示频率 范围内慢速地层幅值的极大值将计算结果归一化.由图 6可见，纵波场的激发谱存在多个峰值和谷值.峰值频率约为8.7 kHz和15.8 kHz，谷值频率约为 4.0 kHz和9.7 kHz.对于本文所关心的频率段10~15 kHz，激发谱随频率的变化相对较为缓和.

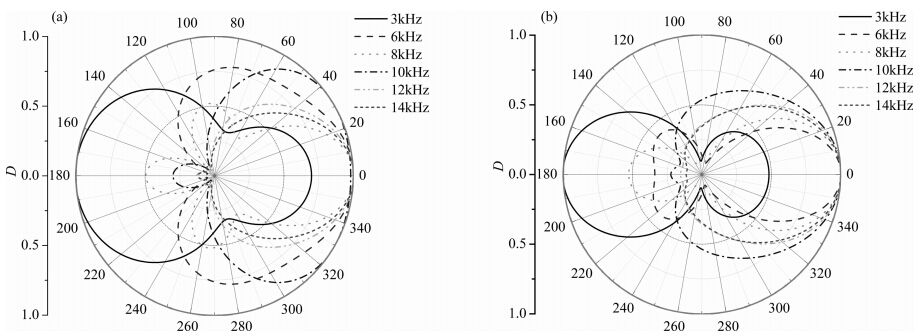图 5 不同频率的圆弧片状声源在地层中产生的纵波场的水平指向性图
(a)、(b)分别为慢度地层和快速地层情况.Fig. 5 The horizontal directivity of compressional wave field in the formation produced by the arcuate acoustic source with different frequencies
Where(a) and (b)represent the slow formation and the fast formation，respectively.

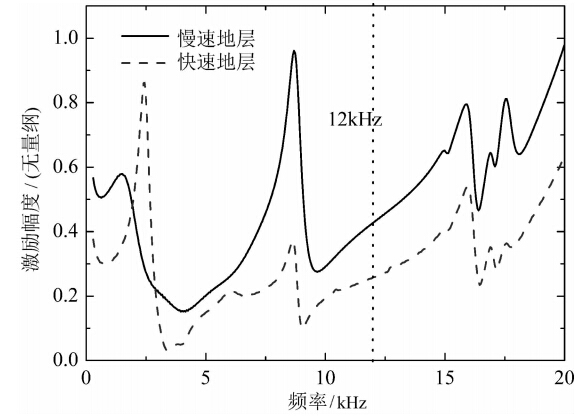图 6 圆弧片状声源在井旁地层中产生的纵波场的激发谱Fig. 6 Normalizedexcitation spectra of the compressional wave field in the formation near borehole produced by the arcuate source
3.4 声源线度对声场的影响

图 7为不同圆周角的声源在井孔中产生的纵波场的水平指向性图，其中(a)和(b)分别对应慢速和快速地层.圆周角取值30°~180°，其他参数与图 3相同.如图 7所示，当φ≤60°时，对于慢速地层情况，其辐射主瓣的角宽较大，方位分辨率较低；当φ≥120°，主瓣的角宽较大，方位特征较差；当75°≤φ≤90°时，快速地层和慢速地层中纵波场的指向性图方位特征均良好.

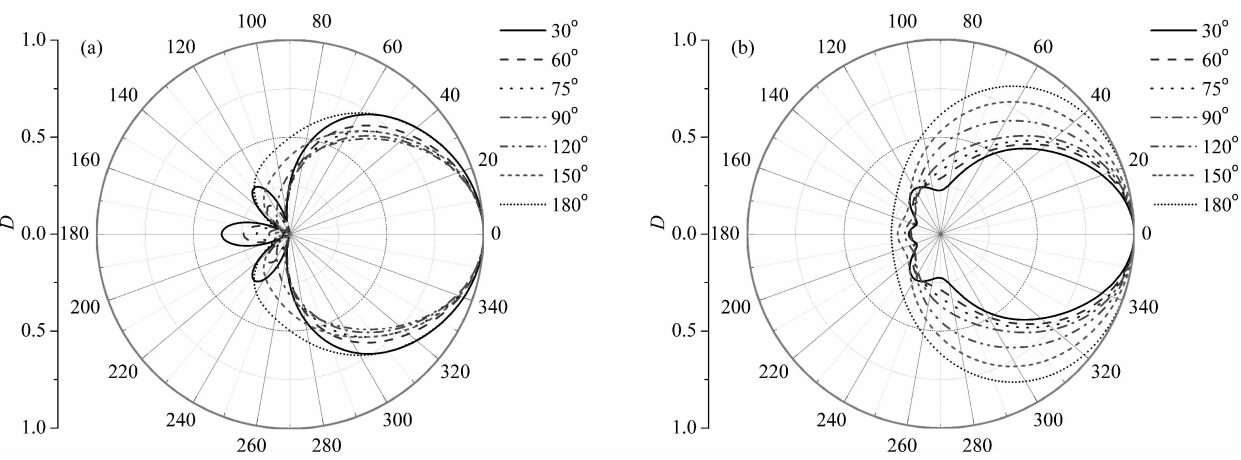图 7 充液井孔中声源的圆周角对纵波场水平辐射指向性的影响
(a)和(b)分别对应慢速和快速地层.Fig. 7 Influence of source angular width on the horizontal directivity of compressional wave field
Where(a) and (b)represent the slow formation and the fast formation，respectively.
计算了不同高度的声源向慢速和快速地层中辐射的纵波场的垂直指向性图，分别如图 8a和8b所示.声源高度取值0.04~0.64 m，其他参数与图 3相同.由图 8可见，随着声源高度的增加，主瓣角宽逐渐变窄，在h=0.04 m时，三分贝角宽为85.4°(慢速地层)和66.5°(快速地层)，在h=0.64 m时，其三分贝角宽为11.5°(慢速地层)和17.6°(快速地层).向钻铤后侧地层辐射的纵波场幅度始终远小于主瓣的声场幅度，声源的高度变化对其影响不大.

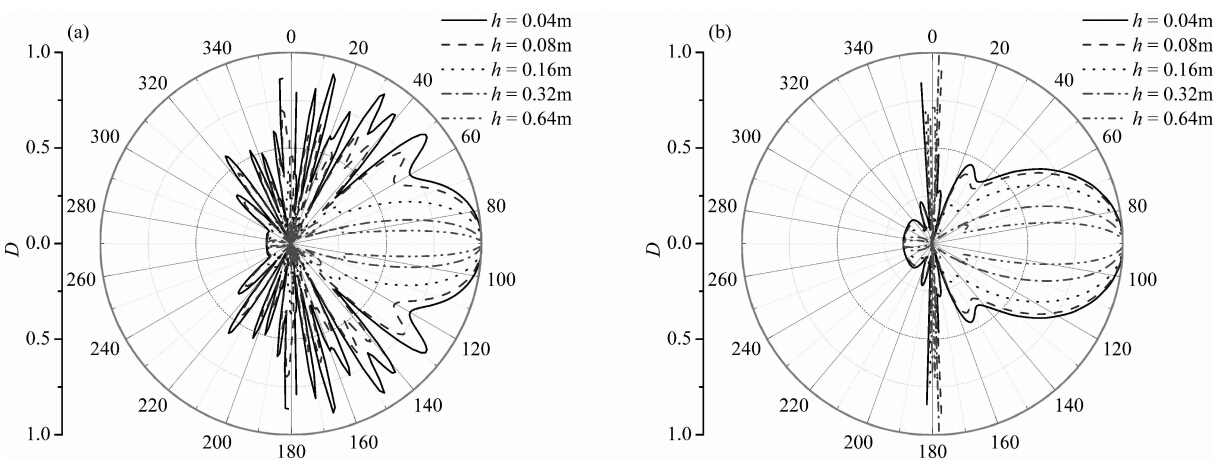图 8 声源的高度对纵波场垂直辐射指向性的影响
(a)和(b)分别对应于慢速和快速地层.Fig. 8 Influence of source height on the vertical directivity of compressional wave field
Where(a) and (b)represent the slow formation and the fast formation，respectively.
3.5 合成阵列波形分析

在z=0 m和2.0 m的水平面内分别布置多个接收器，接收器的布置方式如图 2中的RA-1所示.通过计算接收器记录到的阵列波形来分析圆弧片状声源在地层中辐射的声场的分布特征.假设接收器采集的为径向位移u，利用式(14)计算即可得到该接收器接收到的波形信号.采用的声源的圆周角为85°，高度为0.08 m.声源信号函数如式(17)所示.采用的声源信号的主频为12 kHz，系数b为3000.

图 9是慢速地层情况下的计算结果，其中(a)对应的接收器位置为r=4 m，θ=0~360°，z=0 m，(b)为r=3.46 m，θ=0~360°，z=2.0 m.由图 9a可 见，在z=0 m的水平面内，仅观察到了纵波场，未观察到明显的横波场；θ=0°的接收器接收到的纵波的幅度最大，而θ=180°的接收器接收到的波形幅度 较弱，约为θ=0°时幅度值的1/6；纵波信号的幅度 随着θ变化而均匀变化.由图 9b可见，在z=2.0 m平面内，接收器可接收到纵波和横波信号.纵波信号到时较早，其幅度随着角度的变化与图 9a类似；横波信号中的主要成分为SV波，在θ=0°和θ=180°位置均可接收到较强幅度的横波信号，其方位特征较差.由于SH波的偏振方向垂直于r方向，在图 9中幅度较小，不易观察到.图 10是快速地层情况下，坐标r=4 m，θ=0~360°，z=0 m和坐标r=3.46 m，θ=0~360°，z=2.0 m处的接收器记录的径向位移u.由图 10可见，与慢速地层类似，在θ=0°时，记录的纵波波形幅度较大，在θ=180°时，幅度较低.

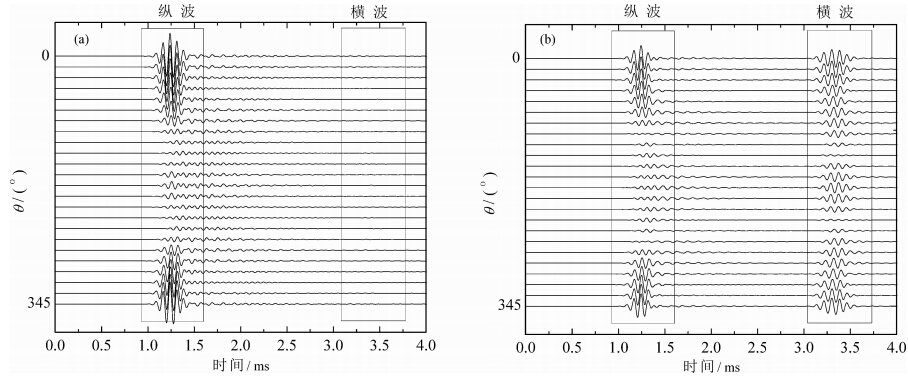图 9 在慢速地层情况下，不同方位角下的地层中的接收器接收到的波形
(a)中接收器的坐标位置为r=4 m，θ= 0~360°，z=0 m；(b)为r=3.46 m，θ=0~360°，z=2.0 m.Fig. 9 The waveforms received by the receivers with different azimuths in the slow formation
Where(a)r=4 m，θ=0~360°，z=0 m，(b)r=3.46 m，θ=0~360°，z=2.0 m.

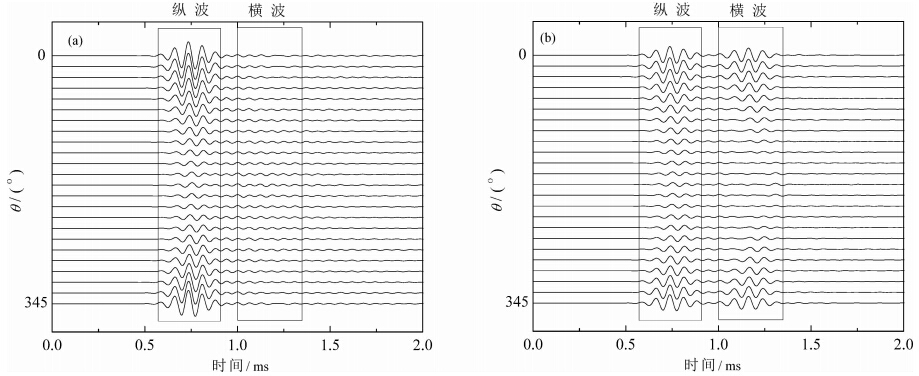图 10 在快速地层情况下，不同方位角下的地层中的接收器接收到的波形
(a)中接收器的坐标位置为r=4 m，θ=0~360°，z=0 m；(b)为r=3.46 m，θ=0~360°，z=2.0 m.Fig. 10 The waveforms received by the receivers with different azimuths in the fast formation
Where(a)r=4 m，θ=0~360°，z=0 m，(b)r=3.46 m，θ=0~360°，z=2.0 m
4 讨论

随钻三维反射成像涉及到许多复杂的问题，包括声源设计、隔声体设计、信号处理和偏移成像等方面.本文主要就非对称圆弧片状声源激发的声场方面展开了数值模拟研究.

由于钻铤的屏蔽作用，使得声源在周向上具有方位分辨特征，本文的研究结果也证实了这一点.实际应用中，声源是置于井孔中的，因此有必要研究井内外声场分布，进一步分析该声源在地层中产生的各类声场的辐射特征.

本文的研究表明，无论水平面内还是垂直面内，纵波场的指向性图主瓣清晰，角宽较窄，旁瓣幅度很小，适用于三维反射成像；而SV波场和SH波场存在多个辐射旁瓣，且由于SV波和SH波的传播速 度相同(各向同性地层)或者相当(各向异性地层)，二者相互影响，无法采用波场分离的方法将其分开，难以利用该声源激励的SV波场和SH波场进行三维反射声波成像.一种可能的方法是利用正交偶极子声源进行SV波场和SH波场的反射成像，该方法在电缆测井情况下的应用已见诸报道(唐晓明和魏周拓，2012)，而在随钻条件下的应用仍需进一步的研究和分析.

声源的频率和线度决定着声源辐射声场的指向性.考虑辐射效率和传播过程中的衰减，在保证方位分辨率的前提下，声源频率越低，探测深度越大.笔者认为，对于本文研究的井孔模型，采用主频为12 kHz左右的声源是合适的.声源的圆周角与辐射声场的指向性关系密切，圆周角太大或者太小时均有可能导致其方位分辨率变差，或者辐射能量降低.对于本文的模型，采用圆周角在75°和90°之间的声源是合适的.对于实际的仪器设计，需要结合换能器的激发效率和频率等众多因素，选择合适的声源.另外，可采用该角度下的圆弧片状换能器片设计出复合的换能器，使得仪器兼具有多极子声场发射和接收的功能，从而节约成本，并提高测量的效率.

为了提高声源在某个特定角度的辐射效率，可以借鉴电缆测井中声源研究的经验(乔文孝等，2002;车小花和乔文孝，2004;乔文孝等，2006;陈雪莲，2006; 乔文孝等，2008)，采用多个圆弧片状声源组成线阵或者组合圆弧阵的形式.通过各阵元的激励延迟控制改变声源辐射能量的方向和角宽，达到提高辐射能量和方位分辨率的目的.另外，根据声学发射和接收的对称性原理，本文的结论同样适用于非对称的圆弧片状接收器.

三维随钻反射声波成像测井还涉及到复杂的声信号处理问题.由于非对称圆弧片状声源为偏心的声源，在井孔中激发了多种方位阶数的声场，井中接收器接收到的波形中存在多种沿井孔传播的导波(崔志文，2004).另外，接收到的阵列波形中除了反射纵波以外还含有SV反射波、SH反射波、泥浆循环噪声、以及钻铤钻进过程中噪声信号.如何对这些信号进行滤除和压制需要进一步的研究和分析.

5 总结

推导了圆弧片状声源的辐射声场在频率-波数域的数学表达式，并采用实轴积分的方法研究了该声源在井旁地层中激发的声场，进一步分析了利用该声源进行三维随钻反射声波成像测井的可行性，主要得到以下结论：

(1)无论是水平面内还是垂直面内，特定频率和特定尺寸下的圆弧片状声源在地层中激励纵波场的指向性图主瓣清晰，角宽较窄，旁瓣级低，适用于三维反射声波成像；

(2)SV波场和SH波场存在多个辐射角瓣，且由于SV波和SH波的传播速度相同(各向同性地层)或者相当(各向异性地层)，二者相互影响，无法通过波场分离方法得到单纯的SV波场和SH波场，难以利用该声源产生的SV波场和SH波场进行三维反射声波成像.

(3)声源的频率和线度决定着声源辐射声场的指向性.对于本文研究的井孔模型，采用主频为12 kHz左右、圆周角在75°和90°之间的圆弧片状声源是合适的.

(4)合成的阵列波形验证了上述结论.

致谢  石油大学吴金平博士和德州大学奥斯汀分校黄山博士对本文提供了一些帮助，并提出了很多好的建议，在此表示衷心感谢.

参考文献
[1] Che X H, Qiao W X. 2004. Acoustic field in formation generated by linear phased array transmitters in fluid-filled boreholes. Chinese J. Geophys. (in Chinese), 47(4): 731-736.
[2] Chen X L. 2006. Study on the foundation of three-dimension acoustic logging (in Chinese). Dongying: China University of Petroleum.
[3] Chen X L, Wei Z T. 2012. Numerical simulation of monopole acoustic reflection imaging logging in the logging-while-drilling condition. Acta Petrolei Sinica (in Chinese), 33(5): 835-840.
[4] Cui Z W. 2004. Theoretical and numerical study of modified Biot's models, acoustoelectric well logging and acoustic logging while drilling excited by multipole acoustic sources (in Chinese). Changchun: Jilin University.
[5] Lu J Q, Ju X D, Qiao W X, et al. 2011. Electronic system design of azimuthally acoustic bond tool. Well Logging Technology, 35(3): 284-287.
[6] Market J, Deady R. 2008. Azimuthal sonic measurements: New Methods in theory and Practice. SPWLA 49th annual Logging symposium, May 25-28.
[7] Qiao W X, Du G S, Chen X L. 2002. Feasibility of application of phased array in acoustic well-logging. Chinese J. Geophys. (in Chinese), 45(5): 714-722.
[8] Qiao W X, Ju X D, Che X H, et al. 2006. Multipole acoustic logging transmitter structurized by annular array. Journal of China University of Petroleum (in Chinese), 30(5): 33-36.
[9] Qiao W X, Che X H, Ju X D, et al. 2008. Acoustic logging phased arc array and its radiation directivity. Chinese J. Geophys. (in Chinese), 51(3): 939-946.
[10] Qiao W X, Ju X D, Che X H, et al. 2011. Progress in acoustic well logging technology. Well Logging Technology (in Chinese), 35(1): 14-19.
[11] Qiao W X, Ju X D, Che X H, et al. 2011. Transducer's and acoustic well logging technology. Physics (in Chinese), 40(2): 99-106.
[12] Tang X M, Cheng C H. 2004. Quantitative Borehole Acoustic Methods. San Diego: Elsevier Science Publishing Co. Inc..
[13] Tang X M, Wei Z T. 2012. Single-well acoustic reflection imaging using far-field radiation characteristics of a borehole dipole source. Chinese J. Geophys. (in Chinese), 55(8): 2798-2807.
[14] Wang B, Tao G, Chen T R, et al. 2012. Experimental study of acoustic logging while drilling measurements using an asymmetric source. Chinese J. Geophys. (in Chinese), 55(1): 327-332.
[15] Wang R J. 2012. Simulation research on acoustic logging in fluid-filled borehole surrounded by anisotropic formations [Ph. D. thesis](in Chinese). Beijing: China University of Petroleum.
[16] Wang T, Dawber M, Boonen P, et al. 2011. Theory of unipole acoustic logging tools and their relevance to dipole and Quadrupole Tools for slow formation. SPE Annual Technical conference and exhibition held in Denver, Colorado, USA.
[17] Zhang H L, Wang X M, Zhang B X. 2004. Acoustic Filed and Waves in Borehole (in Chinese). Beijing: Science Press.
[18] 车小花, 乔文孝. 2004. 充液井孔中的相控线阵声波辐射器在地层中产生的声场. 地球物理学报, 47(4): 731-736.
[19] 陈雪莲. 2006. 井附近地层三维声波测井基础方法研究[博士学位论文]. 东营: 中国石油大学, 714-722.
[20] 陈雪莲, 魏周拓. 2012. 随钻单极子声反射测井数值模拟. 石油学报, 33(5): 835-840.
[21] 崔志文. 2004. 多孔介质声学模型与多极源声电效应测井和多极随钻声测井的理论与数值研究[博士学位论文]. 长春: 吉林大学.
[22] 卢俊强, 鞠晓东, 乔文孝等. 2011. 方位声波测井仪电子系统设计. 测井技术, 35(3): 284-287.
[23] 乔文孝, 杜光升, 陈雪莲. 2002. 相控线阵声波辐射器在声波测井中应用的可行性分析. 地球物理学报, 45(5): 714-722.
[24] 乔文孝, 鞠晓东, 车小花, 等. 2006. 基于圆弧阵的多极子声波测井辐射器. 中国石油大学学报(自然科学版), 30(5): 33-36.
[25] 乔文孝, 车小花, 鞠晓东等. 2008. 声波测井相控圆弧阵及其辐射指向性. 地球物理学报, 51(3): 939-946.
[26] 乔文孝, 鞠晓东, 车小花等. 2011a. 从换能器技术的变化看声波测井技术的发展. 物理, 40(2): 99-106.
[27] 乔文孝, 鞠晓东, 车小花等. 2011b. 声波测井技术研究进展. 测井技术, 35(1): 14-19.
[28] 唐晓明, 魏周拓. 2012. 利用井中偶极声源远场辐射特性的远探测测井. 地球物理学报, 55(8): 2798-2807.
[29] 王兵, 陶果, 陈天润等. 2012. 非对称声源多极子随钻声波测井实验室测量研究. 地球物理学报, 55(1): 327-332.
[30] 王瑞甲. 2012. 各向异性地层声波测井模拟研究[博士学位论文]. 北京: 中国石油大学.
[31] 张海澜, 王秀明, 张碧星. 2004. 井孔中的声场与波. 北京: 科学出版社.