2. 吉林大学地球探测科学与技术学院, 长春 130061
2. College of Geo-Exploration Science and Technology, Jilin University, Changchun 130061, China
微动是地球表层时刻存在的微弱振动,主要由自然因素和人类活动等随机源引起.微动勘探无需人工激振、无破坏,适合于地下有空洞、积水的不良地质环境和人口密集的城镇区.微动探测技术是利用微动信号中携带的面波频散特性,通过数据处理与分析手段提取面波的频散曲线来反演获得地下横波速度构造(Xu et al., 2012).由于面波频散曲线反演的大部分时间都用在正演模拟计算上,因此面波频散曲线的提取是反演的前提和瓶颈,成为提高反演精度的关键因素之一.
大量理论研究和实际应用表明,对于非均匀半空间层状介质,其弹性波场较为复杂,可能会出现多个导波模式,如果忽略高阶模式瑞雷波的频散特性,会影响反演精度,将不能准确推断地质构造(Xia et al., 2003).需要充分利用高阶模式瑞雷波的另外一个原因是在某些情况下,高阶模式相对于基阶模式瑞雷波在高频带具有更高的能量和更大的穿透深度,而且高阶模式瑞雷波对地层参数变化的敏感性较基阶模式瑞雷波更强,这就意味着高阶模式瑞雷波能够在某些基阶模式失效的情况下发挥作用(Xia et al., 1999; Song and Li, 2011).然而,在实际应用中一般只能从微动信号中得到基阶模式的频散曲线,如何从微动信号反演得出所有模式的多条频散曲线是对微动探测技术研究的一个焦点和难点(Lu et al., 2001).因此,为了提高微动面波技术的反演精度,提取高阶模式瑞雷波频散曲线的方法研究变得尤为必要.
目前,从微动中提取面波频散曲线的方法主要有空间自相关法(SPAC:spatial autocorrelation)(Aki,1957)、频率-波数法(F-K:frequency-wavenumber)(Capon,1969)、扩展的空间自相关法(ESAC:extensible spatial autocorrelation)(Okada,2003)、圆台阵法(CCA:centerless circular array)(Cho et al., 2006)、 多模式台阵空间自相关法(MMSPAC:multi-mode SPAC)(Asten,2006)和近期被提出的地震波干涉法(SI:seismic interferometry)(Yokoi,2010).现有基于微动的面波技术中,高阶模式面波的提取存在一定困难,实际应用中常假设面波以基阶模式为主(如SPAC法、ESAC法和CCA法),反演均基于基阶模式的面波.本文提出了一种从微动面波中提取高阶模式面波频散曲线的方法,该方法从微动信号入手,采用映射式方法从微动信号中提取出多模式瑞雷波频散曲线.文中首先给出映射式提取技术的实现方法,然后建立并优化实现从多半径台阵相关系数曲线到多模式瑞雷波频散曲线的映射模型,最后为检验所提出方法的正确性,分别对三种常见的典型地质结构(递增模型、含低速软夹层模型和含高速硬夹层模型)中的微动信号进行数值模拟,采用映射方法提取各模型的多模式瑞雷波频散曲线,并对比分析不同地质结构的提取效果. 2 映射式提取方法
映射式提取方法的实现思路为:首先通过多半径的单点观测台阵在同一测区获得不同组实测数据,采用相关法提取台阵的多条相关系数曲线,然后建立从多条相关系数曲线到多模式瑞雷波频散曲线的映射模型,最后采用分区拟合准则优化实现模型结构,求得多模式瑞雷波频散曲线.由此确定的映射式提取方法实现路线如图 1所示.
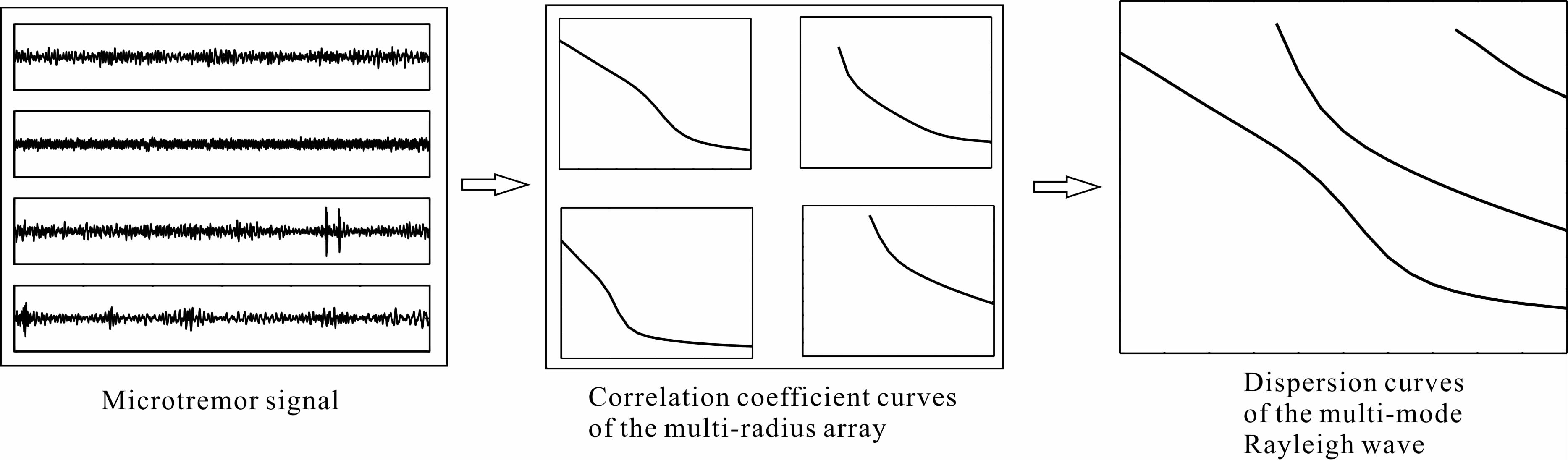 | 图 1 映射方法的实现路线 Fig. 1 Sketch showing implementation processes of the mapping method |
考虑到微动信号的特征,采用空间自相关法提 取多半径单点观测台阵的相关系数曲线.空间自相关法是采用圆形台阵观测微动数据,然后估算出空间自相关系数,通过拟合空间自相关系数推导出瑞雷波的相速度,由此获得瑞雷波的频散曲线.
基阶模式瑞雷波占主导的空间自相关系数可以表示为
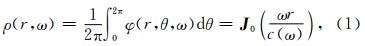
由于公式(1)是对单个模式(基阶或某高阶模式)成立,通常假设基阶模式瑞雷波占主导地位,得不到高阶模式信息,所以不能通过该公式直接提取多模式瑞雷波频散曲线,但它对高阶单个模式仍然成立.为了获取多模式瑞雷波频散曲线,本文设置单点台阵的多个不同圆周半径rM取得多个空间自相关系数ρM,采用公式(2)得到在同一观测点的多条相关系数曲线(ω~ρ(ω)),将多条相关系数曲线(ω~ρ(ω))映射求解得到多模式瑞雷波的频散曲线(ω~c(ω)).公式(2)可表示为
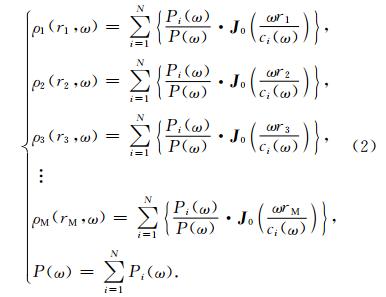
公式(2)中第i阶模式瑞雷波相对能量Pi需要借助地质构造求取,由于Pi是地层结构的特征函数,一旦地层结构给定,Pi则唯一确定.式(2)中∑ N i=0 Pi(ω)P(ω)和ci(ω)分别作为未知数,通过优化实现公式(2)来得到多模式瑞雷波的频散曲线(ω~ci(ω)).例如,要提取基阶和第一高阶模式瑞雷波的频散曲线,则需要3个不同半径的台阵,求解公式可表示为
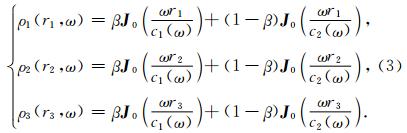
为实现从多条相关系数曲线到多模式瑞雷波频散曲线的映射并提高运算效率,对映射模型进行结构优化.首先分析获得多模式瑞雷波频散曲线的阶数和形态,然后按照高阶模式瑞雷波的截止频率判断各阶模式瑞雷波存在的频率范围,最后通过分区拟合准则优化实现映射模型.具体实现方法如下:
步骤1:确定各阶模式瑞雷波存在的频率范围.各阶模式的截止频率可以根据实际情况采用地质模型来估算(Kennett,2001)或者通过分析微动信号来获得(Asten,2003;Luo et al., 2008).
步骤2:根据步骤1获得的各阶模式瑞雷波存在的频率范围进行映射模型的结构优化.由各阶模式瑞雷波存在的频率范围,确定多模式瑞雷波的阶数,对公式(3)的形式进行优化确定.
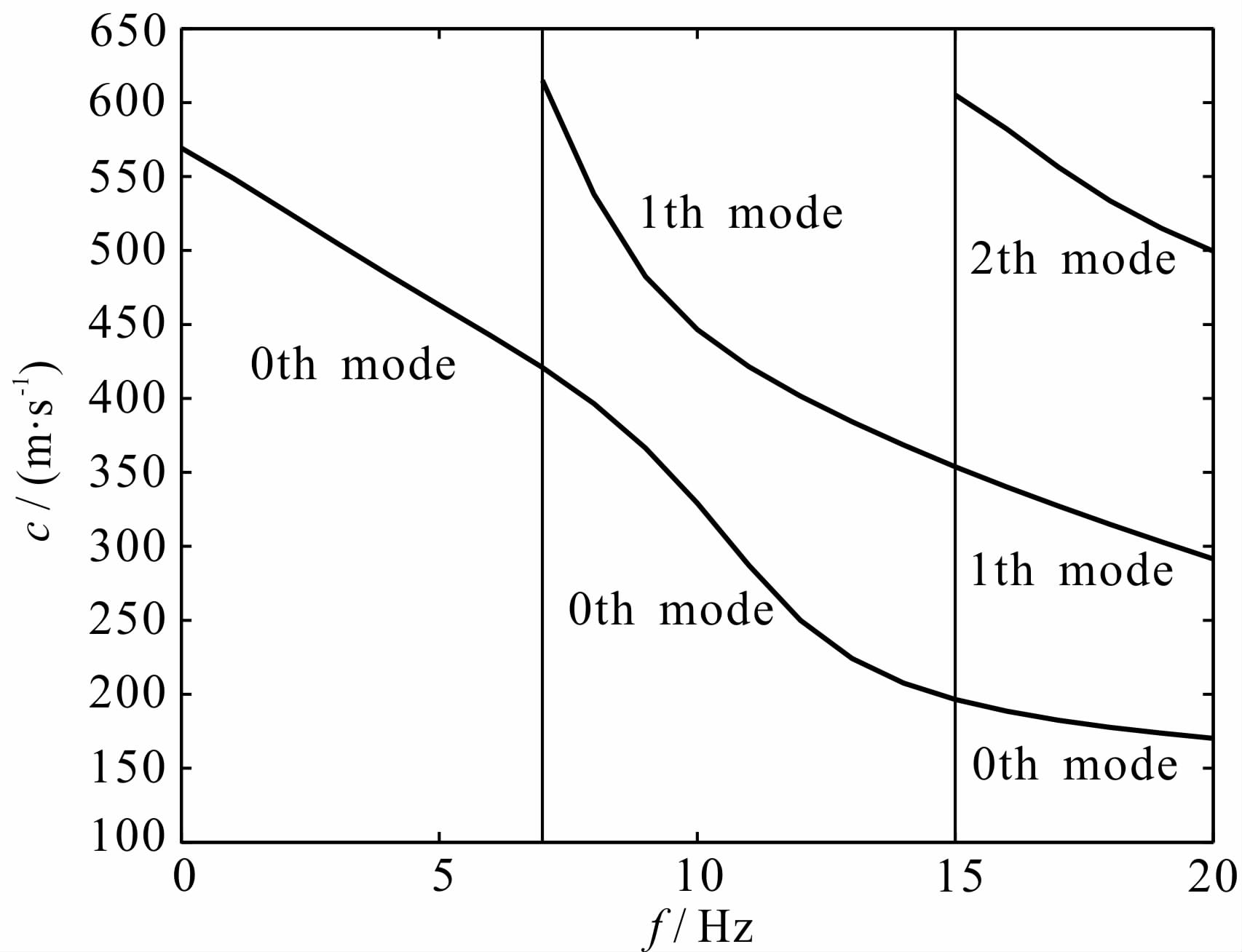 | 图 2 三阶模式瑞雷波频散曲线的分区拟合示意图 Fig. 2 Sketch of zonal fitting for dispersion curves of three-mode Rayleigh waves |
步骤3:分区拟合准则实现多条相关系数曲线到多模式瑞雷波 频散曲线的映射,在拟合求解模型中的参数时,采用目标函数及约束条件来提高运算效率.
步骤4:整合步骤3得到各频率段满足精度条件的最优解,即为整个频率范围的多模式瑞雷波的频散曲线.
以提取三阶模式瑞雷波(基阶(0th mode)、第一高阶(1th mode)、第二高阶(2th mode))为例说明映射模型的建立与实现.假设通过地质模型估算确定了第一高阶和第二高阶模式瑞雷波的截止频率分别为f1和f2,整个分析频率范围可 划分为如图 2所示的[0,f1)、[f1,f2)和[f2,f]区域.
三个区域的截止频率范围内模式个数及映射方程组确定为:[0,f1)区域存在1个模式,采用基阶模式瑞雷波占主导的公式(1)提取基阶模式瑞雷波 频散曲线;[f1,f2)区域存在2个模式,采用基阶、 第一高阶模式瑞雷波共存的公式(3)提取2个模式的频散曲线;[f2,f] 区域存在3个模式,采用基阶、第一高阶和第二高阶模式瑞雷波共存的公式(4)提取3个模式瑞雷波的频散曲线.其中公式(4)可表示为
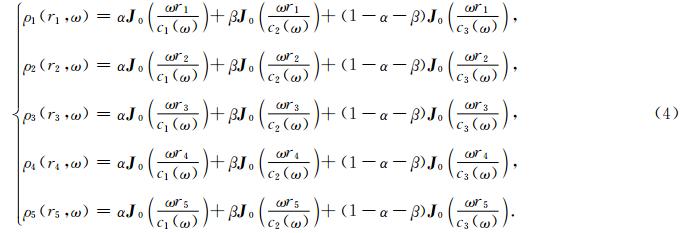
在分别拟合求解三个区域确定的模型中的对应参数时,目标函数和约束条件的确定方法如下:
目标函数的确定 :考虑到各模式瑞雷波对不同半径的台阵布设方案的敏感性不尽相同,在拟合求解模型中的参数时,目标函数采用拟合差函数,可表示为公式(5),参数同前述.
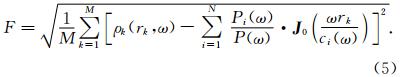
为了说明映射方法提取微动信号中多模式面波频散曲线的有效性,首先采用交错网格有限差分方法数值计算地质结构的微动记录,然后采用映射方法提取多模式瑞雷波频散曲线,最后将提取结果和理论频散曲线进行对比分析. 3.1 地质结构设计
地质结构采用实际近表面应用中三种常见的典型地质结构(递增模型、含低速软夹层模型和含高速硬夹层模型),表 1给出了各地质模型的参数.递增 模型的横波速度随深度的增加而逐渐增大,含低速软夹层模型在第一层和第三层之间含有一个150 m·s-1 的低速软弱夹层,含高速硬夹层模型在第一层和第三层之间含有一个400 m·s-1的高速硬夹层.
|
|
表 1 水平层状介质地层模型 Table 1 Layered earth models |
针对微动产生机理和微动信号中多模式瑞雷波频散曲线提取方法的需要(本文以提取三阶模式频散曲线为例),以测区圆心为中心布设同一规格不同检波器构成的圆形观测台阵,台阵包含的观测点数G为16,组成5个不同半径的同心圆,半径R分别 为2、4、8、16 m和32 m.在场地方圆500 m和1000 m 环形范围内随机分布100个强度不同的随机震源,震源子波采用主频为8 Hz的雷克子波.如图 3所示为随机震源和信号采集阵列的空间分布.
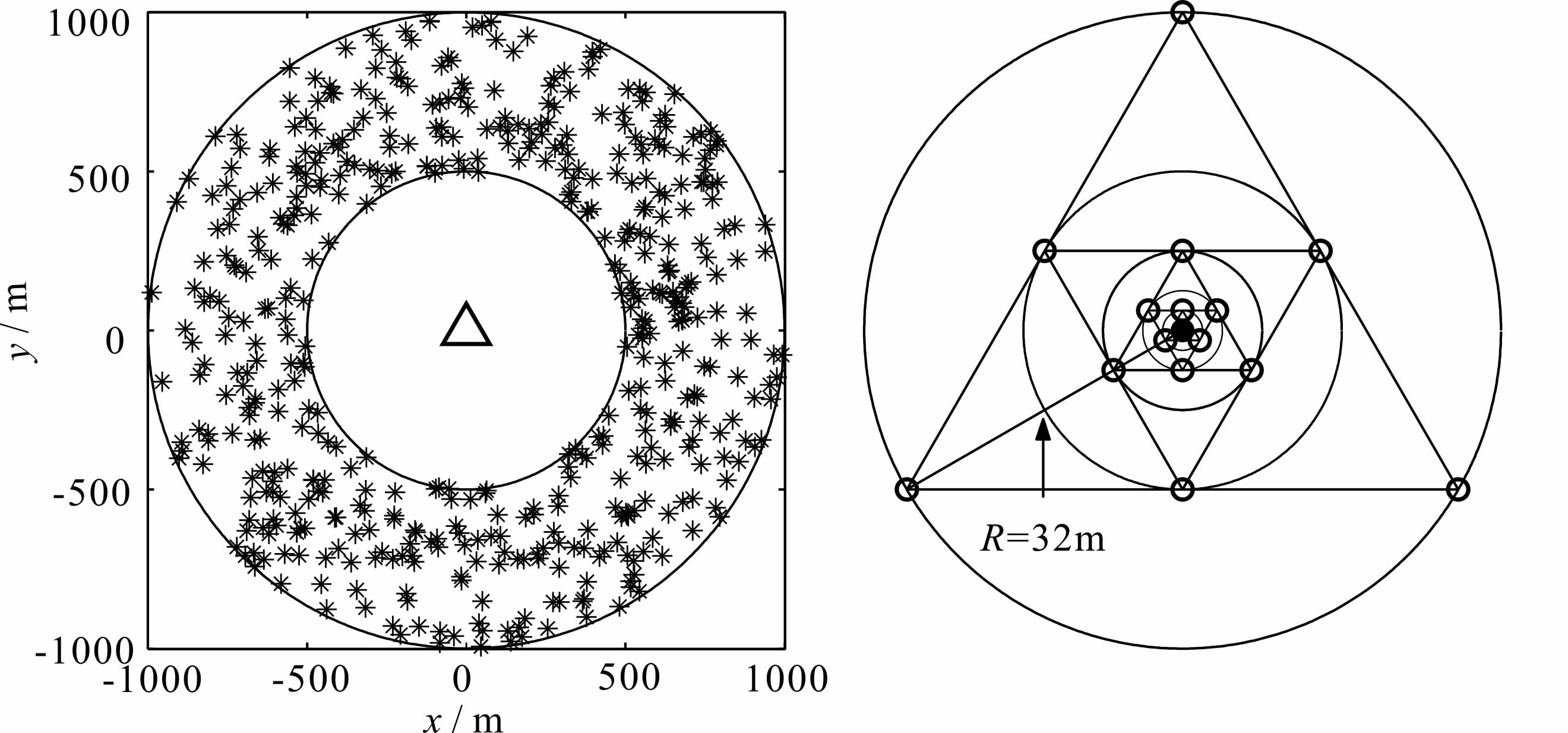 | 图 3 随机震源和观测台阵的空间分布 Fig. 3 Spatial distribution of r and om seismic sources and the array |
采用交错网格有限差分法和完全匹配层 PML(Perferct Matching Layer)吸收边界条件对三种常见典型地质结构模型进行全波场正演计算(Gao et al., 2012),这三组数据的台阵形状、半径和观测点坐标均相同,仅合成所用的地质结构模型和震源的分布不同.如图 4所示为其中一种地质结构模型合成所得的一段微动记录.
从图 4可以看出,由于震源随机分布且强度不同,微动记录呈现为随机噪声.为了提高多模式频散曲线提取结果的准确性和稳定性,在提取瑞雷波的多模式频散曲线之前进行相关的数据预处理.首先将不同半径台阵的记录按相同起止时刻依次截取长度为40.96 s的分段记录,其中相邻的记录段间重叠20.48 s;然后进行窄带滤波,并计算每段记录的 空间自相关系数,再将各段记录平均值作为该半径的最终空间自相关系数;最后综合观测场地不同半径台阵的空间自相关系数,采用分区拟合准则优化实现映射模型结构,求得该场地的多模式瑞雷波频散曲线.
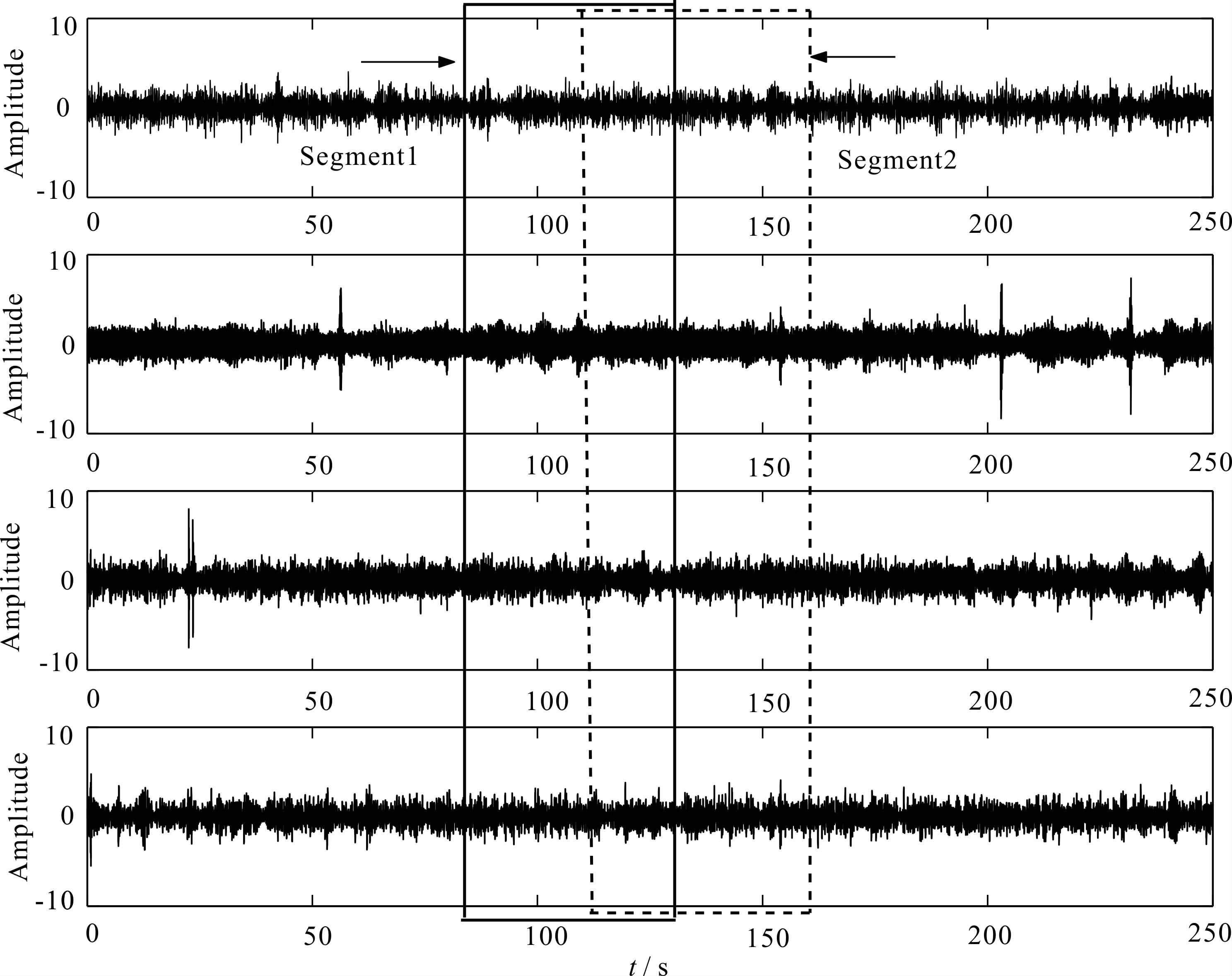 | 图 4 检波器记录的一段微动信号 Fig. 4 Microtremor signals recorded by sensors |
采用映射式方法从三种常见的典型地质结构对应的微动记录中提取多模式瑞雷波的频散曲线,将提取结果与根据场地模型结构数值计算的理论频散曲线进行比较来评价本文方法提取多模式瑞雷波频散曲线的能力.
按照前述映射式方法的实现步骤,首先确定截止频率的范围,然后确定这一范围内的模式个数,最后选取合适的映射方程组进行映射.由于本部分采用数值算例以重点分析映射式方法的有效性,为了避免由于截止频率的选取产生较大误差,所以分区频率选取真实模型的截止频率.由于微动信号存在于较低频区域,所以讨论三种地质结构对应[0,20]频域内的微动记录.需分析的截止频率范围内模式个数及映射方程组确定为:对于递增模型,[0,4)区域存在1个模式,采用公式(1)提取基阶模式瑞雷波频散曲线,约束参数为c1(ω)≤600;[4,8)区域存在2个模式,采用公式(3)提取基阶、第一高阶模式的频散曲线,约束参数为c1(ω)≤c2(ω);[8,20]区域存在3个模式,采用公式(4)提取基阶、第一高阶和第二高阶模式的频散曲线,约束参数为c1(ω)≤c2(ω)≤c3(ω)和100≤c1(ω)≤200.对于含低速软 夹层模型,[0,3)区域存在1个模式,采用公式(1)提取基阶模式瑞雷波频散曲线,约束参数为c1(ω)≤600;[3,8)区域存在2个模式,采用公式(3)提取基阶、第一高阶模式的频散曲线,约束参数为c1(ω)≤c2(ω);[8,20]区域存在3个模式,采用公式(4)提取基阶、第一高阶和第二高阶模式瑞雷波的频散曲线,约束参数为c1(ω)≤c2(ω)≤c3(ω)和150≤c1(ω)≤250.对于含高速硬夹层模型,[0,5)区域存在1个模式,采用公式(1)提取基阶模式瑞雷波频散曲线,约束参数为c1(ω)≤600;[5,16)区域存在2个模式,采用公式(3)提取基阶、第一高阶模式的频散曲线,约束参数为c1(ω)≤c2(ω);[16,20]区域存在3个模式,采用公式(4)提取基阶、第一高阶和第二高阶模式的频散曲线,约束参数为c1(ω)≤c2(ω)≤c3(ω)和100≤c1(ω)≤200.
为了求取公式(4)中的参数ρ1、ρ2、ρ3、ρ4和ρ5,设置5个不同半径(2 m,4 m,8 m,16 m和32 m)的同圆心观测台阵在同一测区获得5组微动信号(采用前述的微动信号合成方法:三种地质模型的空间采样间隔选为2 m,时间采样间隔选为1 ms,模拟的时间长度为 10 min),经过方位平均求取ρ1、ρ2、ρ3、ρ4和ρ5,即获得5条相关系数曲线,通过已建立的映射模型进行优化实现,求得多模式瑞雷波频散曲线.
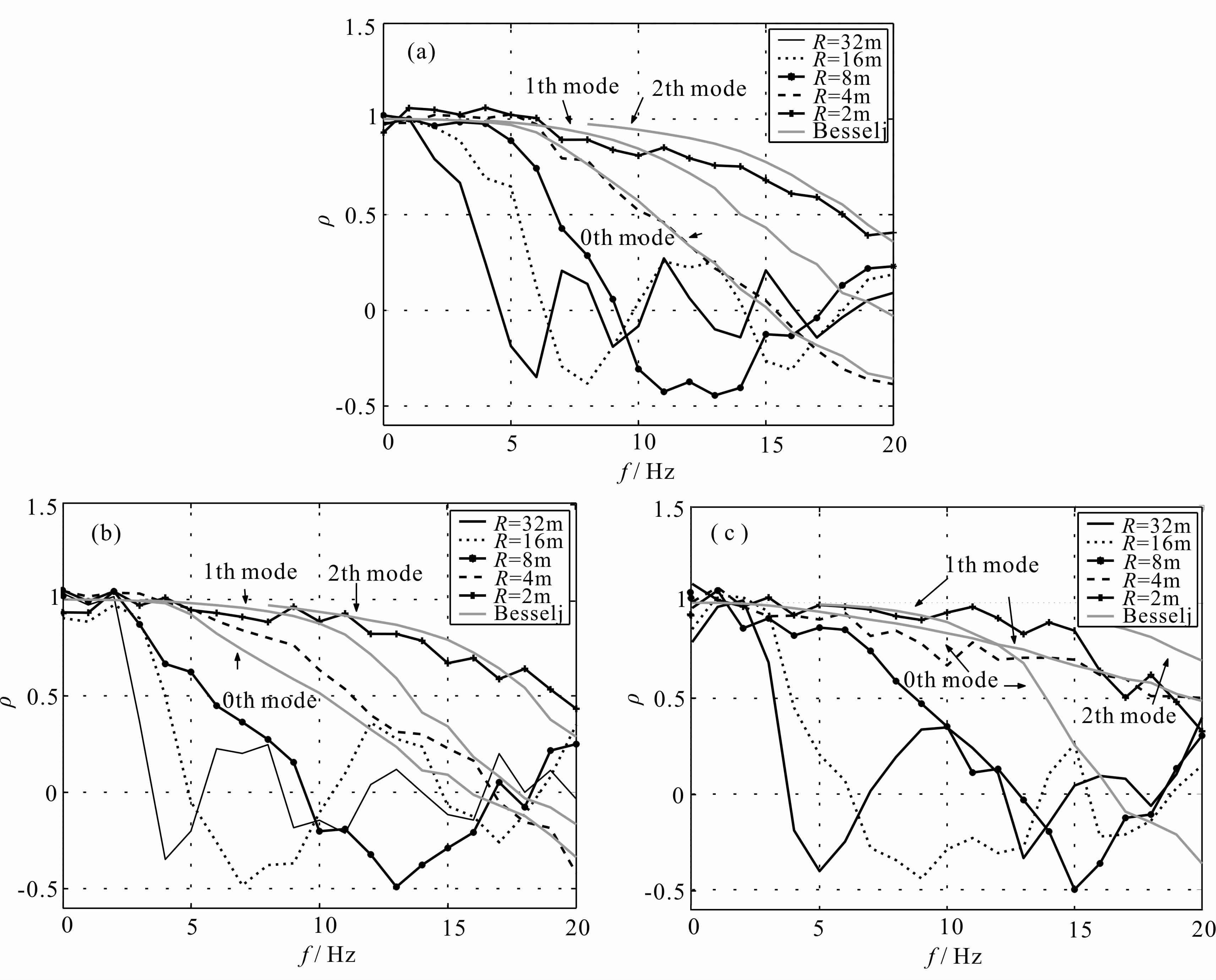 | 图 5 不同地质模型的空间自相关系数 (a)递增模型;(b)夹低速模型;(c)夹高速模型. Fig. 5 Space auto-correlation coefficients of different layered earth models (a)Stiffness increasing model;(b)Soft layer mixed model;(c)Stiff layer mixed model. |
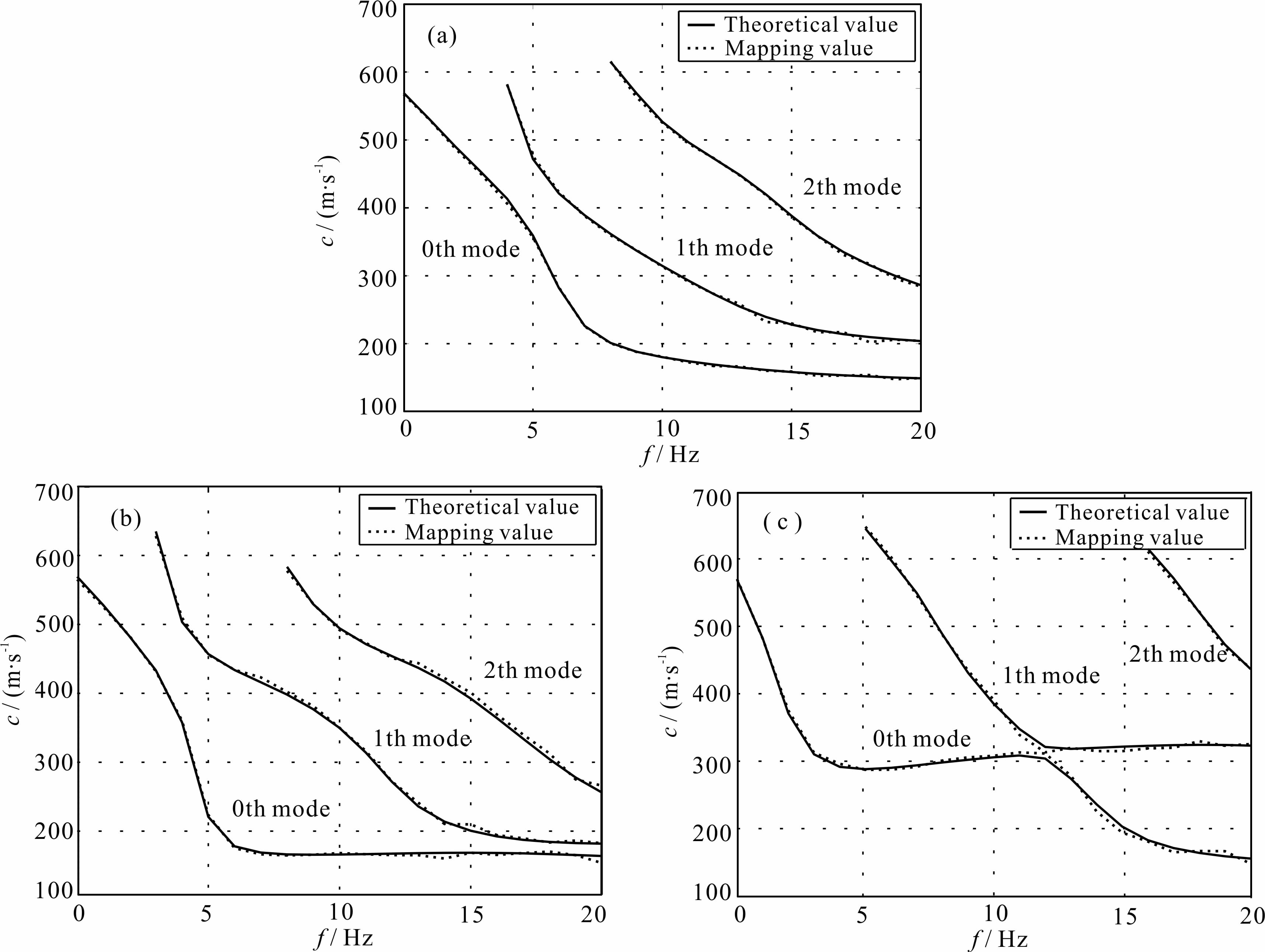 | 图 6 不同地质模型的频散曲线 (a)递增模型;(b)夹低速模型;(c)夹高速模型. Fig. 6 Dispersion curves of different layered earth models (a)Stiffness increasing model;(b)Soft layer mixed model;(c)Stiff layer mixed model. |
图 5为通过不同地质结构的微动信号记录计算分析得到的空间自相关系数曲线.图 6为采用分区拟合准则将图 5所得的空间自相关系数曲线映射分析获得的三阶模式频散曲线及根据场地模型结构计算得到的三阶模式频散曲线.为了便于分析比较,取得3个模式瑞雷波的频散曲线后,将各模式表示的贝塞尔函数曲线(Besselj)显示在图 5中.为避免较多曲线难以比较,只给出了观测台阵半径为4 m时各模式表示的贝塞尔函数曲线.
从图 6可以看出,映射方法分析得到的多模式频散曲线与理论结果整体上基本一致,尤其基阶频散曲线吻合得较好.对于递增型的地质结构,各阶模式的频散曲线与另两种模型相比,更接近理论结果;对于含低速软弱夹层的地质结构,在较低频和较高频时略有偏离;对于含高速硬夹层的地质结构,在11~13 Hz范围内基阶和第一高阶模式频散曲线的分辨力不足,从图 5所示的空间自相关系数曲线上也可以看到在这一频段范围不同半径台阵的空间自相关系数有不规则的波动现象,这是由于在某些地质分层,某些阶次模式的频散曲线在某一频率范围内可能接近甚至相同.
为了探讨映射方法的稳定性,以相同的场地模型结构和信号模拟方法合成不同观测台阵的微动信号.台阵包含的观测点数G仍然为16,考察5个不同半径减小到1、2、4、8 m和16 m以及增加到3 m、6、12、24 m和48 m时频散曲线的提取情况;考察观测台阵半径不变,即为2、4、8、16 m和32 m,增加观测点数到21个和61个的频散曲线提取情况;考察同时增大台阵半径增加观测点数,即半径为3、6 m、12、24 m和48 m,观测点数为61个的频散曲线提取情况.以夹低速模型地质结构为例,频散曲线的提取结果如图 7所示.
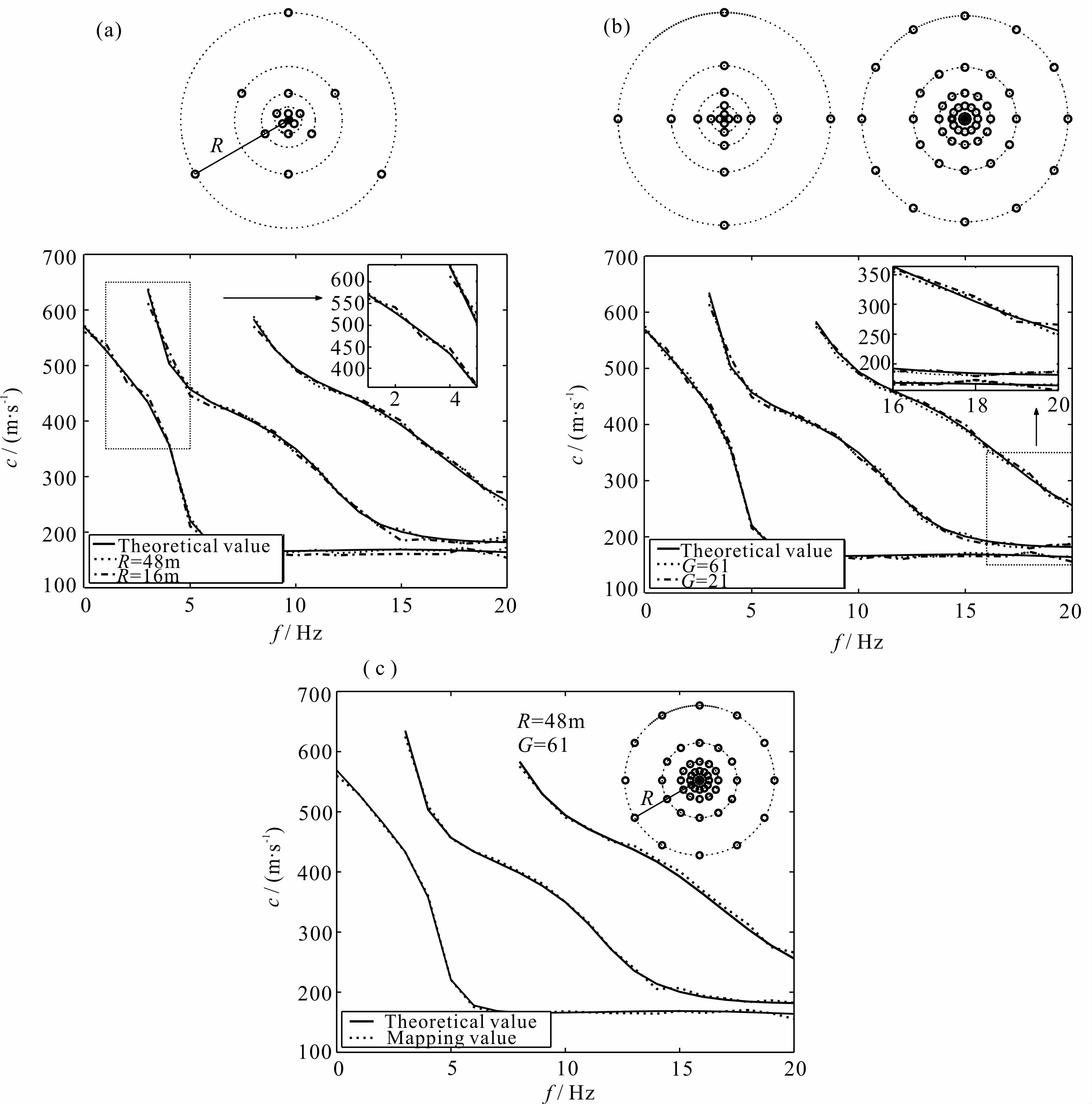 | 图 7 不同观测台阵下夹低速模型的频散曲线 (a)台阵最大半径为16 m和48 m;(b)观测点数为21和61;(c)台阵最大半径为48 m,观测点数为61. Fig. 7 Dispersion curves of the soft layer mixed model with different arrays (a)R=16 m,R=48 m;(b)G=21,G=61;(c)R=48 m,G=61. |
对比图 6b和图 7中频散曲线的提取结果,从图 7a可以看出,增大台阵的尺寸,低频区的频散曲线波动有所减小;从图 7b可以看出,增加观测点个数,低频区和高频区的频散曲线波动都有所减小;从图 7c可以看出,同时增大台阵的尺寸和增加观测点个 数,可以改善频散曲线的提取效果.在实际应用中, 可以针对不同场地,采用不同尺寸的台阵进行观测,将不同结果进行分析对比,综合平均各结果来作为最后结论以增加计算的可靠性. 3.4 多模式瑞雷波频散曲线提取误差分析
为了探讨映射式方法的可行性,对多模式瑞雷波频散曲线的提取误差进行定量分析.首先采用公式(6)和(7)分别计算各阶模式频散曲线中相速度的平均相对误差,然后采用公式(8)计算各阶模式频散曲线中不同频率对应相速度的相对误差,最后分析截止频率及噪声源的不均匀性对各阶模式频散曲线的影响.
第m阶模式频散曲线中相速度的平均相对误差Rave可表示为
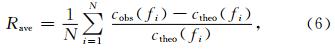
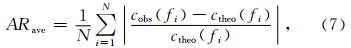
第m阶模式频散曲线中不同频率fi对应相速度的相对误差Ri可表示为

图 8为对三种地质结构模型各阶模式频散曲线误差的估算结果,可以看出映射方法对三种地质结构计算得到的多模式频散曲线能满足地质结构反演的需要.
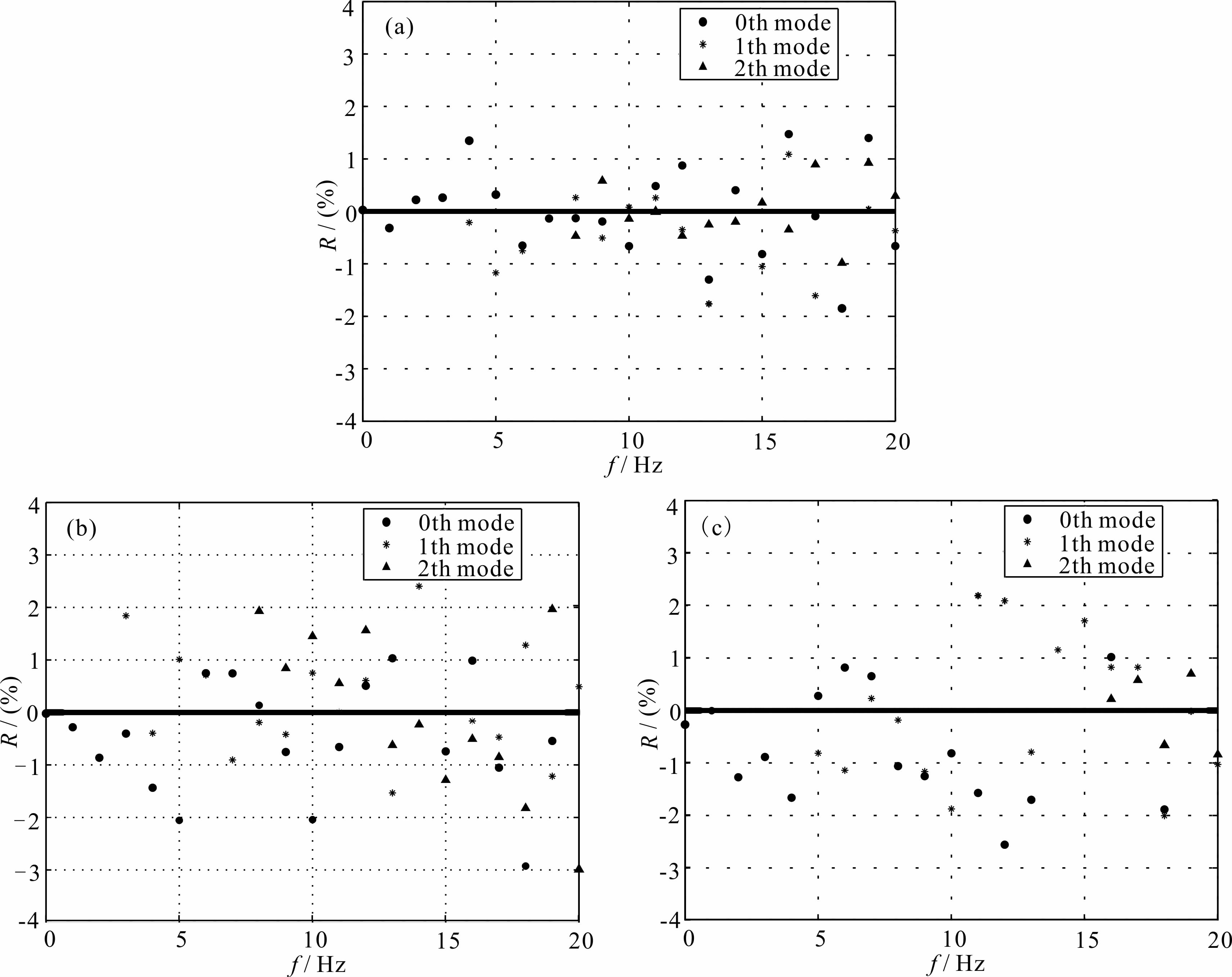 | 图 8 不同地质模型相速度的相对误差 (a)递增模型;(b)夹低速模型;(c)夹高速模型. Fig. 8 Relative phase velocity deviations of different layered earth models (a)Stiffness increasing model;(b)Soft layer mixed model;(c)Stiff layer mixed model. |
在实际应用中截止频率的选取是产生误差的主要原因之一,这是因为在映射式方法实现过程中,要先确定截止频率的范围,然后确定这一范围内的个数,选取合适的映射方程组进行映射,其中截止频率的选取非常关键,否则无法确定某个频率范围有几个模式,映射方程组也无法确定的,这会造成较大误差.为了分析截止频率在未知或者和实际模型 不符时对多模式频散曲线提取结果的影响,仍然以提取三 阶模式瑞雷波频散曲线为例,假设图 2中[f1,f2) 区域的第一高阶和第二高阶模式瑞雷波的截止频率f1和f2分别变化20%,分析数值算例中三种地质结构模型的各阶模式频散曲线的绝对平均相对误差如图 9所示.
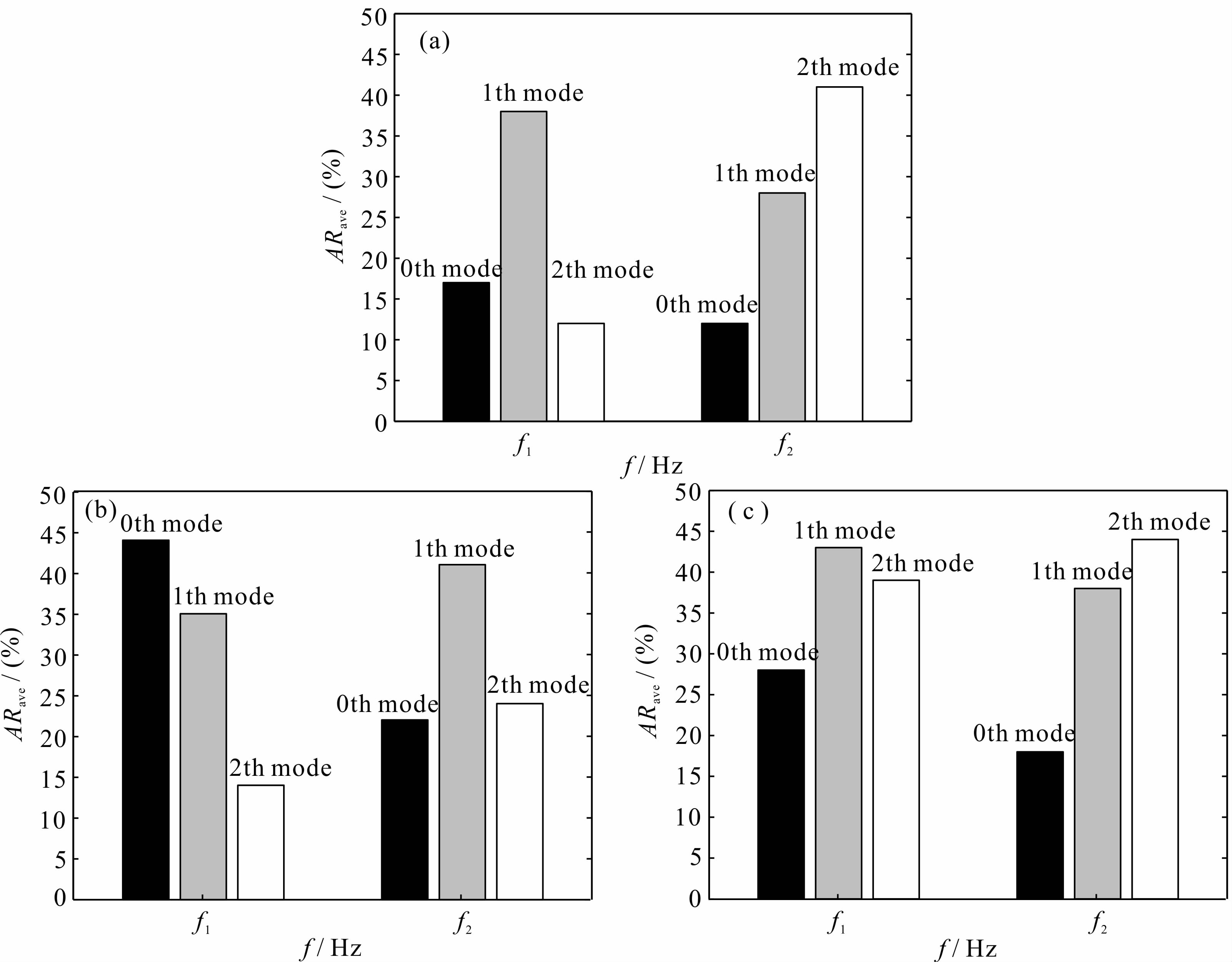 | 图 9 不同地质模型各阶模式频散曲线的绝对平均相对误差 (a)递增模型;(b)夹低速模型;(c)夹高速模型. Fig. 9 Absolute average relative deviations of different modes dispersion curves in different layered earth models (a)Stiffness increasing model;(b)Soft layer mixed model;(c)Stiff layer mixed model. |
从图 9可以看出,当[f1,f2)区域的第二高阶模式瑞雷波截止频率f2确定,第一高阶模式瑞雷波截止频率f1变化20%时,对基阶和第二高阶模式瑞雷波的提取结果影响相对较小,对第一高阶模式瑞雷波的提取结果影响较大;当[f1,f2)区域的第一高阶模式瑞雷波截止频率f1确定,第二高阶模式瑞雷波截止频率f2变化20%时,对基阶和第一高阶模式瑞雷波的提取结果影响相对较小,对第二高阶模式瑞雷波的提取结果影响较大.从整体来看,截止频率的变化对于各模式的提取结果都有不同程度的影响.
另外,研究对象为合成微动信号时,虽然微动记录是随机噪声,但噪声的方位分布近似均匀,实际中尤其是短期观测时,噪声源的分布可能并非理想均匀,甚至有很强的方向性.因此,噪声源分布的不均匀性是产生误差的又一主要原因.为了进一步考察噪声源分布不均匀情况下映射方法提取多模式瑞雷波频散曲线的性能,利用合成的微动信号,设定噪声源数的50%在全方位内分布作为背景波场,另外50%的噪声源以2倍振幅集中在方位角Φ为30°或60°范围内,噪声源空间分布如图 10所示.
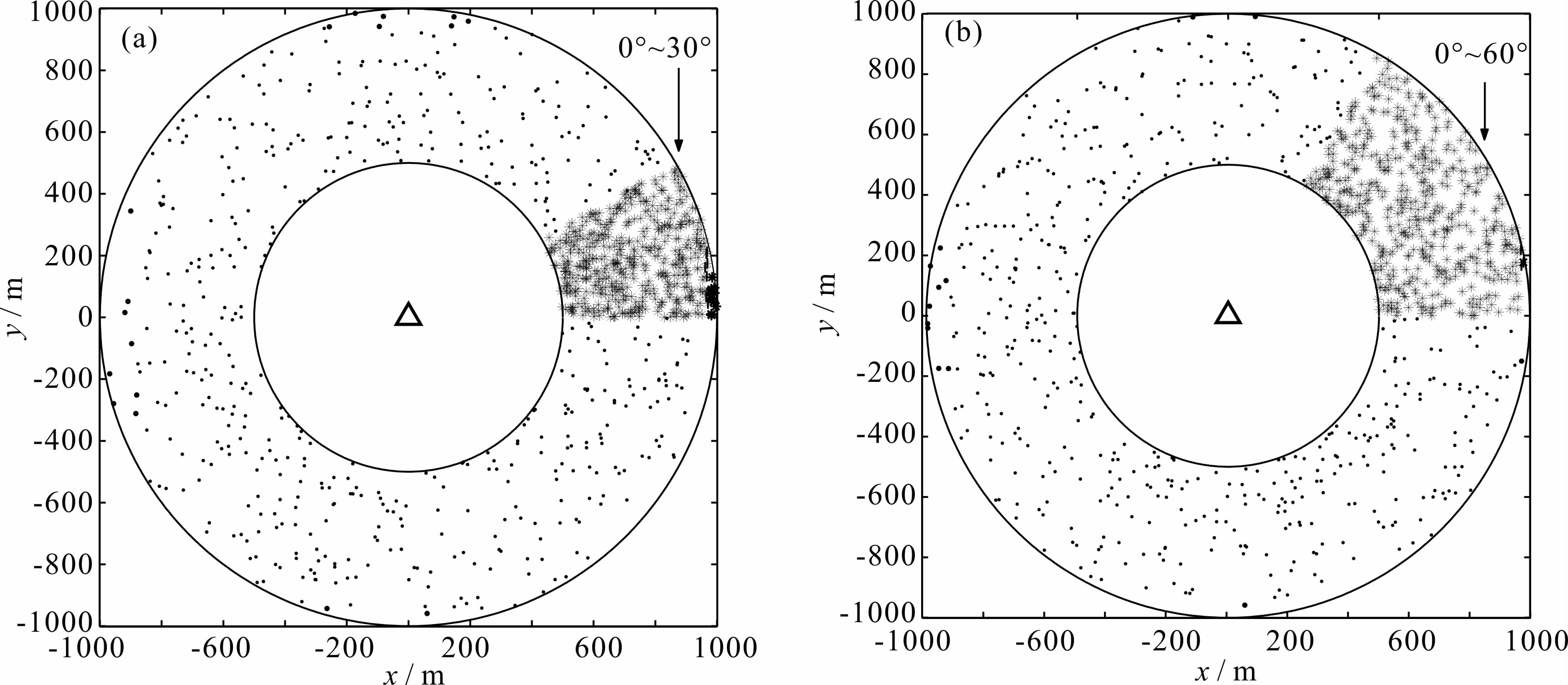 | 图 10 集中在不同方位噪声源的空间分布 (a)0°~30°;(b)0°~60°. Fig. 10 Spatial distribution of r and om sources in different azimuthal directions (a)0°~30°;(b)0°~60°. |
当50%的噪声源集中在0°~30°方位范围时,对三种场地模型计算得到的三阶模式瑞雷波频散曲线如图 11所示.以含低速软夹层地质结构为例,分析50%的噪声源集中在30°和60°不同方位范围内各阶模式相速度的绝对平均相对误差如图 12所示.
从图 11可以看出,当噪声源主能量部分集中在0°~30°方位范围内时,对三种地质结构的各阶频散曲线都有不同程度的影响,而且对高频域的影响比对低频域的影响大,其中对含低速软弱夹层和含高速硬夹层的地质结构比递增型地质结构的影响大.从图 12可以看出,噪声源主能量部分集中在30°方位范围内比60°方位范围内的误差大,对第一高阶和第二高阶模式比基阶模式的误差大.在实际应用中可以采用不同形状的台阵进行观测,同时可以结合主动源法提高瑞雷波的高频段频散特征的提取,以利于对多模式瑞雷波的正确识别.
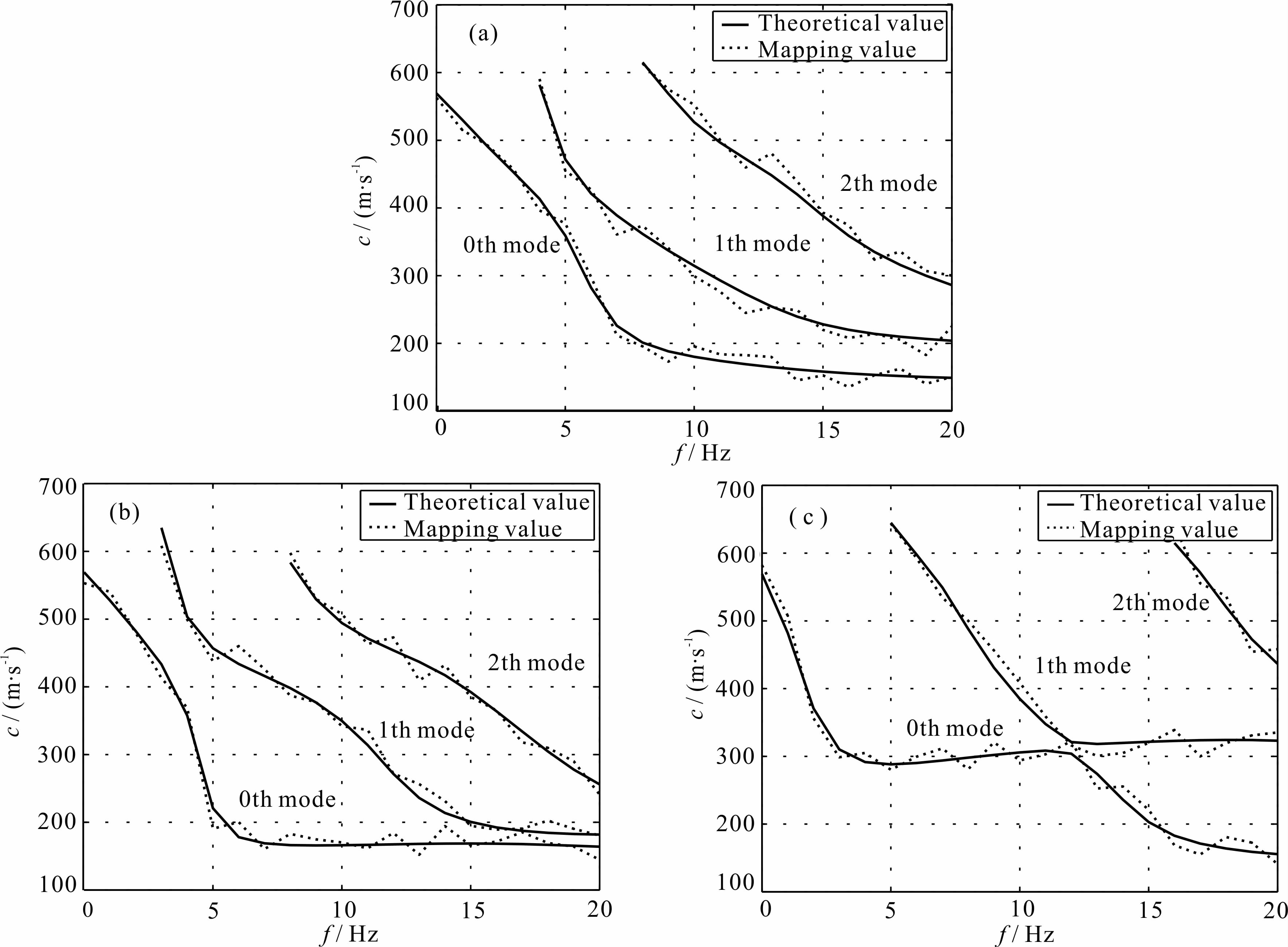 | 图 11 在50%噪声源集中分布在0°~30°方向情况下不同地质模型的频散曲线 (a)递增模型;(b)夹低速模型;(c)夹高速模型. Fig. 11 Dispersion curves of different layered earth models with half r and om sources in 0°~30°azimuthal directions (a)Stiffness increasing model;(b)Soft layer mixed model;(c)Stiff layer mixed model. |
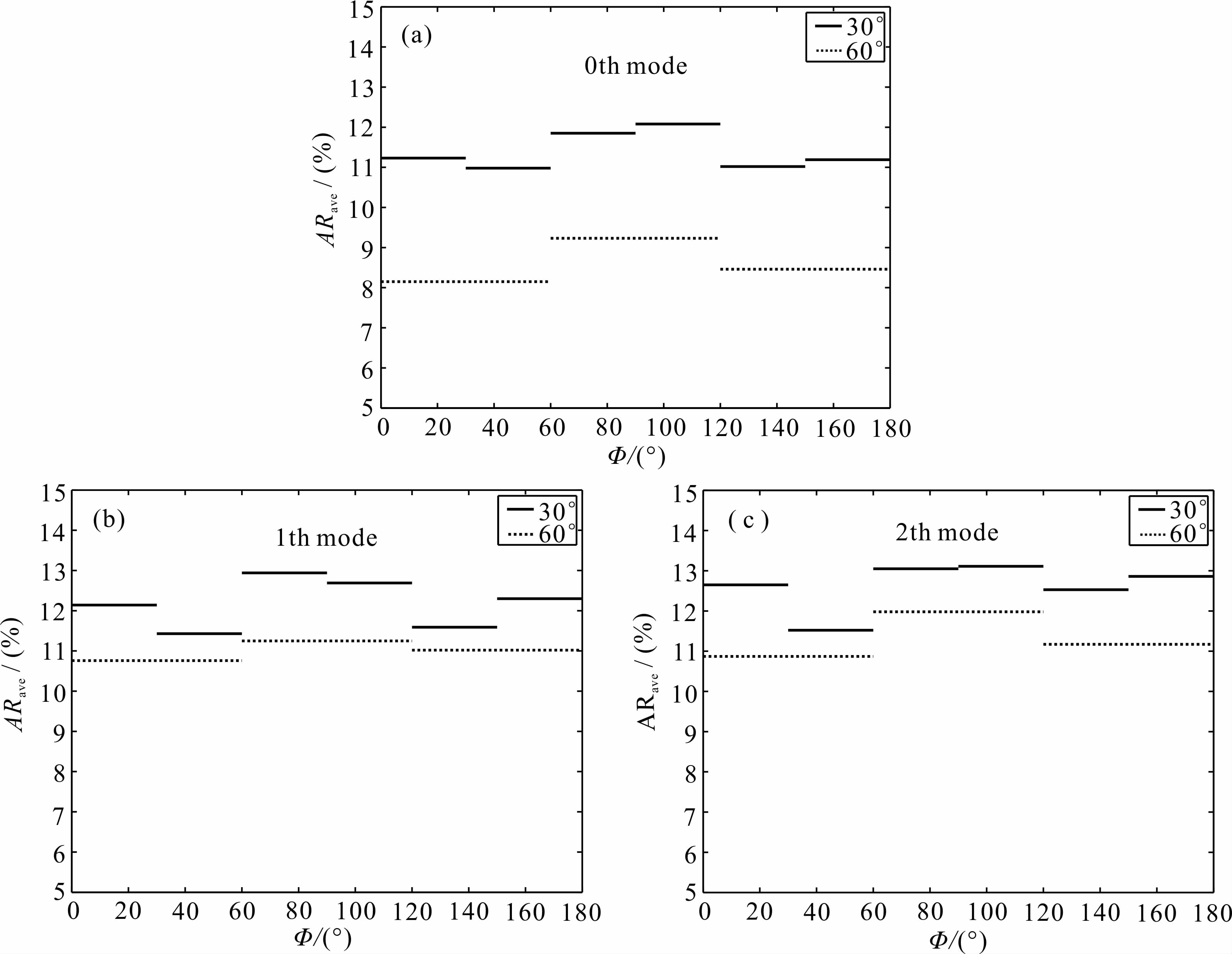 | 图 12 在含低速软夹层地质结构中50%噪声源集中分布在30°和60°方向范围内不同阶模式频散曲线的绝对平均相对误差 (a)基阶模式;(b)第一高阶模式;(c)第二高阶模式. Fig. 12 Absolute average relative deviations of different modes dispersion curves with half r and om sources in 30° and 60°azimuthal directions for soft layer mixed model (a)0th mode;(b)1th mode;(c)2th mode. |
本文提出采用映射式方法提取微动信号中多模式瑞雷波的频散曲线,研究了该方法在三种常见典型地质结构(递增型、含低速软夹层模型和含高速硬夹层模型)中的应用情况,数值计算结果表明映射方法可以从微动信号中计算得到不同阶模式的瑞雷波频散曲线,其中截止频率的选取、分区频段内模式数量的确定及噪声源的不均匀分布对多模式瑞雷波频散曲线的提取结果均有影响.在应用中可以先借助地质模型来确定截止频率,然后根据高阶模式瑞雷波只能大于某个频率出现来确定模式个数,最后采用相应的映射方程组求解不同阶模式的瑞雷波频散曲线.
在处理实际观测数据时,由于浅层速度结构的横向不均匀性、噪声源的分布不均匀性及观测系统的限制等因素的影响,可能会存在不同阶模式瑞雷波频散曲线分辨力不足、在较低频和较高频处有偏离等现象.在实际应用中,可以在同一测区,采用不同尺寸、不同形状的台阵进行观测,综合平均各结果以提高计算精度,同时可以结合主动源法来提高瑞雷波高频段频散特征的提取精度,以满足反演速度结构的要求,为开展基阶和高阶模式瑞雷波联合反演地质构造的研究提供技术支撑.
| [1] | Aki K. 1957. Space and time spectra of stationary stochastic waves with special reference to microtremors. Bull. Earthq. Res. Inst. , 35: 415-456. |
| [2] | Asten M W. 2003. Comment on "Microtremor observations of deep sediment resonance in metropolitan Memphis, Tennessee" by Paul Bodin, Kevin Smith, Steve Horton, and Howard Hwang. Engineering Geology, 72(3-4): 343-349. |
| [3] | Asten M W. 2006. On bias and noise in passive seismic data from finite circular array data processed using SPAC methods. Geophysics, 71(6): 153-162. |
| [4] | Capon J. 1969. Applications of detection and estimation theory to large array seismology. Proc. IEEE, 58(5): 760-770, doi:10.1109/PROC.1970. 7730. |
| [5] | Cho I, Tada T, Shinozaki Y. 2006. Centerless circular array method: Inferring phase velocities of Rayleigh waves in broad wavelength ranges using microtremor records. J. Geophy. Res., 111(B9), doi: 10. 1029/2005JB004235. |
| [6] | Gao J H, He Y Y, Ma Y C. 2012. Comparison of the Rayleigh wave in elastic and viscoelastic media. Chinese J. Geophys. (in Chinese), 55(1): 207-218, doi:10.6038/j.issn.0001-5733.2012.01.020. |
| [7] | Kennett B L N. 2001. The Seismic Wavefield: Volume 1, Introduction and Theoretical Development. Cambridge: Cambridge University Press. |
| [8] | Lu L Y, Wang W, Zhang B X, et al. 2001. Guided modes in stratified half-space and Rayleigh wave exploration. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 23(3): 215-221, doi: 10.3969/j.issn.1001-1749.2001.03.005. |
| [9] | Luo Y H, Xia J H, Liu J P, et al. 2008. Joint inversion of fundamental and higher mode Rayleigh waves. Chinese J. Geophys. (in Chinese), 51(1): 242-249, doi:10.3321/j.issn:0001-5733.2008.01.030. |
| [10] | Okada H. 2003. The Microtremor Survey Method. Society of Exploration Geophysicists. |
| [11] | Song X H, Li G. 2011. Study on field characteristics of multimode Rayleigh waves and energy distribution. Yangtze River (in Chinese), 42(7): 11-14, doi:10.3969/j.issn.1001-4179.2011.07. 003. |
| [12] | Xia J H, Miller R D, Park C B. 1999. Estimation of near-surface shear wave velocity by inversion of Rayleigh wave. Geophysics, 64(3): 691-700. |
| [13] | Xia J H, Miller R D, Park C B, et al. 2003. Inversion of high frequency surface waves with fundamental and higher modes. Journal of Applied Geophysics, 52(1): 45-57. |
| [14] | Xu P F, Shi W, Ling S Q, et al. 2012. Mapping spherically weathered "Boulders" using 2D microtremor profiling method: A case study along subway line 7 in Shenzhen. Chinese J. Geophys. (in Chinese), 55(6): 2120-2128, doi: 10.6038/j.issn.0001-5733.2012.06.034. |
| [15] | Yokoi T. 2010. New formulas derived from seismic interferometry to simulate phase velocity estimates from correlation methods using microtremor. Society of Exploration Geophysicists, 75(4): SA71-SA83. |
| [16] | 高静怀, 何洋洋, 马逸尘. 2012. 黏弹性与弹性介质中Rayleigh面波特性对比研究. 地球物理学报, 55(1): 207-218,doi:10.6038/j.issn.0001-5733.2012.01. 020. |
| [17] | 鲁来玉, 王文, 张碧星等. 2001. 层状半空间中的多模问题和瑞利波勘探. 物探化探计算技术, 23(3): 215-221. |
| [18] | 罗银河, 夏江海, 刘江平等. 2008. 基阶与高阶瑞利波联合反演研究. 地球物理学报, 51(1): 242-249. |
| [19] | 宋先海, 李刚. 2011. 多模式瑞雷波波场特征及能量分布特性研究. 人民长江, 42(7): 11-14. |
| [20] | 徐佩芬, 侍文, 凌甦群等. 2012. 二维微动剖面探测“孤石”:以深圳地铁7号线为例. 地球物理学报, 55(6): 2120-2128,doi:10.6038/j.issn.0001-5733.2012.06. 034. |
 2014, Vol. 57
2014, Vol. 57

