2. 武汉大学测绘遥感信息工程国家重点实验室, 武汉 430079
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
金星(Venus)是太阳系的八大行星之一,也是离地球最近的一颗类地行星.因此,在人类探索太阳系及宇宙的过程中,金星和月球、火星一样,也是人类优先探索的重要目标.而高精度重力场的获取,一直是行星探测的重要组成部分.一方面,高精度重力场模型能确保探测器精密导航定位.另一方面,与地震、磁场等其他地球物理数据的空间分布局限性相比,重力场信息可以实现全球覆盖.此外,结合高精度地形模型,可以加深对行星内部构造特征和热演化等过程的理解.
行星重力场主要通过探测器的轨道跟踪数据获得,但随着探测器轨道高度的增加,重力信息迅速衰减,这极大限制了重力场模型的空间分辨率.基于1978年发射的Pioneer Venus Orbiter(PVO)卫星的重力数据和雷达测高数据,使得人们首次获得了金星的重力和地形信息.而之后于1989年发射的Magellan卫星则大大提高了精度和覆盖率.目前,最新的金星重力场模型MGNP180U空间分辨率仅有赤道区域约100 km(Konopliv et al., 1999),而通过雷达测距得出的金星地形在赤道区域的分辨率却可以达到约5 km(Rappaport et al., 1999),大大高于现有重力场的精度.由于地形信息被认为是地球、月球及其他类地行星重力场短波成分的主要来源(Forsberg and Tscherning, 1981; Wieczorek,2007),通过合理的假设和建模,金星的地形数据可以用于改进和精化重力场短波部分.其中一个重要方法就是利用实际地形和球谐截断地形的差值建立残差地形模型(RTM),并以此作为影响重力场短波成分的主要因素.Forsberg(1984)提出将残差地形部分划分为矩形晶格(Rectangular Prisms),通过数值积分逐晶格近似计算地形对重力场短波部分、密度异常等地球物理参数的影响,以此得到三维的重力场相关参数.Nagy等(2000)推导了通过矩形晶格方法估算重力位及其一至三阶导数的解析表达形式并进一步分析了该方法的应用.Hirt等(2010,2012),Hirt和Featherstone(2012)通过地形数据结合矩形晶格法改进地球、月球和火星的重力场,取得了很好的效果.
但该方法用于金星重力场精化需面对新的问题,一是金星地形的缺陷,金星的地形数据尚不能达到完全覆盖,需要对地形进行预处理;二是过去通过矩形晶格算法精化行星重力场的研究均没有考虑均衡补偿效应,但这在金星上不可忽略(Kucinskas and Turcotte, 1994; Kucinskas et al., 1996; Grimm and Hess, 1997). 本文采用地形数据结合矩形晶格 法改进了金星的重力场的同时,加入了均衡改正,得到分辨率为0.1°的精化的金星表面重力模型VGM2013(Venus Gravity Model 2013).此外,本文还在引入均衡改正的过程中进一步得出了关于全球补偿深度和壳密度的重要结论. 2 数据介绍 2.1 地形数据
金星表面覆盖着浓密的酸性大气层,故为了获得表面的观测数据,必须使用能够穿透大气的波段.金星的地形数据是通过Venera 15、16,Pioneer Venus Orbiter(PVO)和Magellan的星载雷达测高计获得的,其中Magellan探测器起了最重要的作用.Magellan任务发射于1989年3月4日,于1990 年8月10日抵达金星.在前八个月的探测中(cycle 1),Magellan收集了火星表面84%的雷达影像,分辨率是前苏联Venera 15和16号的10倍.在其扩展任 务中,Magellan又进一步测量了两个周期(cycle 2,3),生成了覆盖金星98%的地图(Solomon and Head, 1991).Magellan于1990年9月开始测量时,人们对金星的重力场信息还知之甚少,仅有的了 解源于大偏心率轨道的PVO探测器,这导致Magellan 的轨道星历误差极大,从而直接影响了地形测量精 度(Wieczorek,2007).随后,由于JPL(Jet Propulsion Laboratory)导航小组的McNamee等(1992)改进了金星重力场,轨道误差也随之减小.Konopliv 等提 出的120阶的重力模型MGNP120PSAAP(Konopliv et al., 1996)和180阶模型MGNP180U(Konopliv et al., 1999)大大提高了探测器的导航精度,这些改进了的轨道星历被Rappaport等(1999)用于重新处理测高数据并提出了一个改进后的360阶地形模型. 最终的地形数据以4096×8192大小的格网形式保存在了行星数据系统(PDS)的地球科学节点(ftp://voir. mit.edu/pub/mg_3003/),文件名为Global Topographic Data Record(GTDR),文件编号GTDR.3;2.
最新的金星地形球谐模型是Wieczorek 计算的 719阶模型VenusTopo719(http://www.ipgp.fr/~wieczor/SH/SH.html). 该模型主要基于Magellan的GTDR3;2数据,2%的空白区域则先后利用PVO以及Venera15和16的数据进行填补,并通过GMT软件进行一定的内插和平滑处理,得到0.125°×0.125°的格网数据,最后通过 Driscoll和Heally(1994)的算法将格网数据转化为球谐系数形式. 本文采用的地形模型即为GTDR3;2和Venus Topo719. 2.2 重力数据
由于测量手段的限制,对金星重力场的解算均基于不同时期不同探测器大量的轨道跟踪数据,通过对轨道跟踪数据进行最优权重分配,结合轨道动力学理论进行探测器精密定轨及重力场模型位系数计算.金星重力场模型已通过对PVO和Magellan探测器的轨道跟踪数据分析得以建立,后者因其大 大提高的数据覆盖率对重力场起了主要作用(Sjogren et al., 1997).
最新的金星重力场模型是Konopliv等(1999)的180阶模型MGNP180U,亦即本文采用的重力场模型.由于当时的计算限制,该模型通过三个步骤建立.首先一步解算出前120阶系数,即为之前的120阶模型MGNP120PSAAP(Konopliv et al., 1996),然后在第一步的基础上使用相同的空间约束进一步解得116到155阶系数,最后加入Kaula约束解出154~180阶系数.由于第一二步中都采用了空间约束,模型不同表面位置的空间分辨率差异非常大,接近180阶的频谱分辨率可以被认为是接近赤道地区的,其他区域的分辨率有的低至40阶(Konopliv et al., 1999). 3 基本原理
本文提出的金星重力场模型VGM2013是由以下三部分组成的:(1)金星表面的正常重力γ;(2)重力扰动的中长波部分δgMGNP;(3)重力扰动短波部分δgVRTM和δgAH. 3.1 表面正常重力和中长波重力扰动
金星的表面正常重力可近似表达为:

|
|
表 1 本文所用的金星基本参数 Table 1 Basic parameters used in this paper |
中长波重力扰动部分δgMGNP可以通过重力扰动位的径向偏导数直接得到(Torge,2001):
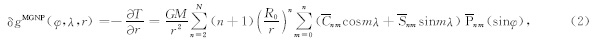
普遍认为,类地行星重力场的短波部分主要由地形引起的,去掉了中低频地形信号得到的残差地形(RTM)相当于一个高通滤波器,其中包含了大量的高频重力信息.另一方面,精确的数值积分需要知道各点的密度值,这在目前的观测条件下是不可能的,考虑到金星壳的主要成分为玄武岩,密度估计在2700到2900 kg·m-3之间(Konopliv et al., 1999; Banerdt,1986),由于该范围的密度取值对整个短波部分的重力扰动影响不超过7.4%,本文取值为2700 kg·m-3.于是,本文先在金星浅层壳密度为均值、非补偿的假设下,通过残差地形模型(RTM)结合矩形晶格求积估计重力场的短波成分δgVRTM.
任一格网点的地形残差zRTM(φ,λ)通过实际地形与截断的球谐函数计算的参考地形之差获得:
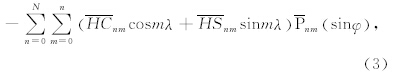
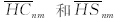 为完全正规化的地形球谐系数.
为完全正规化的地形球谐系数.采用Forsberg(1984)和Nagy等(2000)的方法,将每个格网点看作一个晶格(prism),见图 1,对任一所求的格网点P,附近的残差地形对该点的短波重力扰动影响可利用牛顿万有引力定律,通过数值积分逐晶格近似计算,每个晶格Q的高度为z<sup>RTMQ(φ,λ),即z1=0,z2=z<sup>RTMQ(φ,λ),长宽范围分别为x1到x2,y1到y2,则所有晶格引起的重力扰动之和δg<sup>VRTM可表示为:
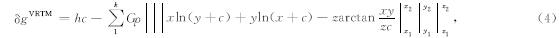
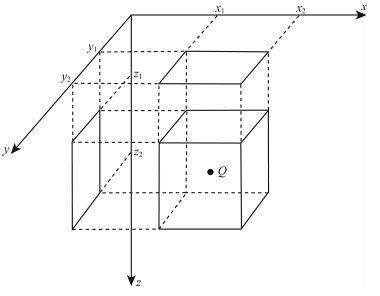 | 图 1 矩形晶格示意图 Fig. 1 Sketch of rectangular crystal lattice |
其中,ρ为晶格密度,c为点P和点Q间的距离,k为所有对P点有影响的晶格数目,参考Hirt和Featherstone(2012)在月球和Hirt等(2012)火星计算中的取值,这里的积分半径选为400 km,同时,通过对金星的试算可以发现,400 km以外的晶格对计算点的重力扰动的影响远小于本文的计算量级,可忽略不计.当点P位于参考面之下时,需要加入层间改正项hc,即
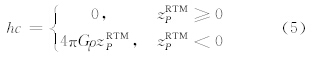
以往通过矩形晶格精化重力场的研究均没有考虑均衡补偿的影响(Forsberg,1984; Nagy et al., 2000; Hirt et al., 2010,2012;Hirt and Featherstone, 2012),因为对地球、月球和火星,10~100 km尺度的地形载荷被认为主要由岩石圈支撑而非均衡补偿(Banerdt,1986),更小尺度的地形载荷更是如此,因此,小尺度的地形可以认为处于非均衡补偿状态.与此不同的是,通过对金星导纳等其他相关研究表明金星处于高度均衡、充分补偿状态(Kucinskas and Turcotte, 1994; Kucinskas et al., 1996; Grimm and Hess, 1997).故本文认为非均衡地形假设在金星不成立,即使对于短波地形,均衡改正也是必须的.
目前的研究认为,考虑到岩性相变的因素,理想的Pratt-Hayford均衡模型不适用于金星(James et al., 2013),而对于Airy-Heiskanen补偿,其补偿深度普遍认为在30~50 km范围(Kucinskas and Turcotte, 1994; Kucinskas et al., 1996; Grimm and Hess, 1997),故本文采用全球性的Airy-Heiskanen补偿假设,通过计算比较分析后,补偿深度选为30 km,具体选取过程见5.2节.
Airy-Heiskanen补偿引起的重力改正可通过完全规格化的重力位系数表示为(Rummel et al., 1988):
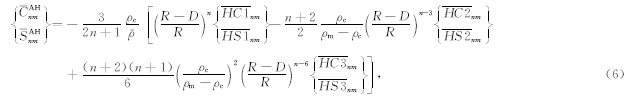
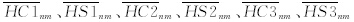 为完全规格化的球谐函数系数:
为完全规格化的球谐函数系数:
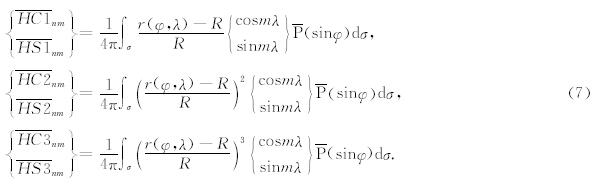
于是对于短波重力δgVRTM,其对应的均衡改正为:
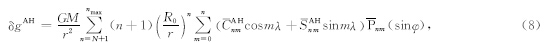
综合以上所述三部分重力信息,本文获得的最终计算结果为金星表面重力加速度gVGM及重力扰动δgVGM:
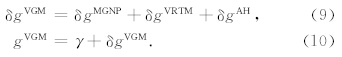
为了将重力信号的中长波成分和短波成分分开,以便用地形数据改进重力的短波成分,我们需要选取合适的重力场和地形模型截断阶次N.相关系数是常用的判断指标.重力g和地形f的相关系数γ l 可通过重力和地形球谐模型的系数计算得到,表示为(Wieczorek,2007):
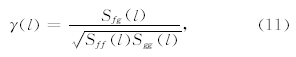
其中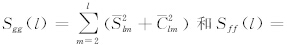
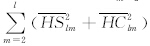 分别为重力和地形在频率域内的能量,即自功率谱,
分别为重力和地形在频率域内的能量,即自功率谱,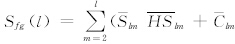
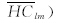 为重力和地形的互功率谱,2~180阶金星重力与地形相关性如图 2所示.
为重力和地形的互功率谱,2~180阶金星重力与地形相关性如图 2所示.
图 2中可以看出,120阶以后的重力与地形球谐系数相关性小于0.4,同时参考MGNP180U重力模型的阶方差曲线(见图 11a),120阶以后的重力信号迅速衰减,综合两者可以认为,120阶之前的重力信号基本有效,其位系数代表了重力场的中长波成分,而120阶以后的剧烈衰减可以认为是由不精确的重力场短波成分造成的.因此,本文选取N=120阶作为重力场和地形的截断阶次.
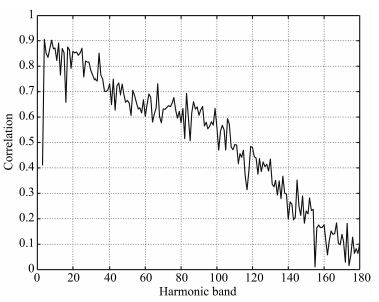 | 图 2 金星重力与地形的相关性 Fig. 2 Correlation of gravity and topography on Venus |
本文选取GTDR.3;2的正弦投影地形数据作为真实地形见图 3,分辨率为0.0439°.由图 3中可明显看出,GTDR.3;2地形数据在金星表面有多处狭长形轨道未覆盖区域,部分区域还有呈散点状的轨道误差,见红框区域所示.对于GTDR.3;2没有数据覆盖的区域,本文先使用VenusTopo719模型的计算值来填补,并以一定的平滑处理来减少散点状的轨道误差,最终通过二次插值转化为0.1°格网数据.填补和平滑的效果见图 4.
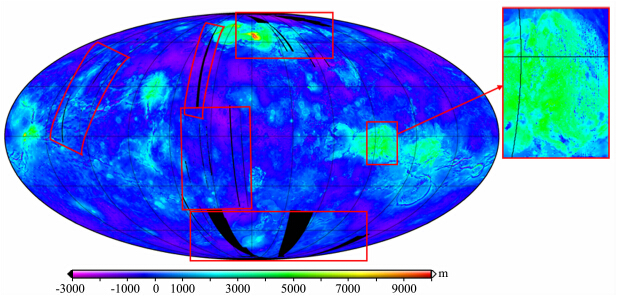 | 图 3 GTDR.3;2地形图,参考半径为6051877 m Fig. 3 Topography map of GTDR 3;2 with referenced radius of 6051877 m |
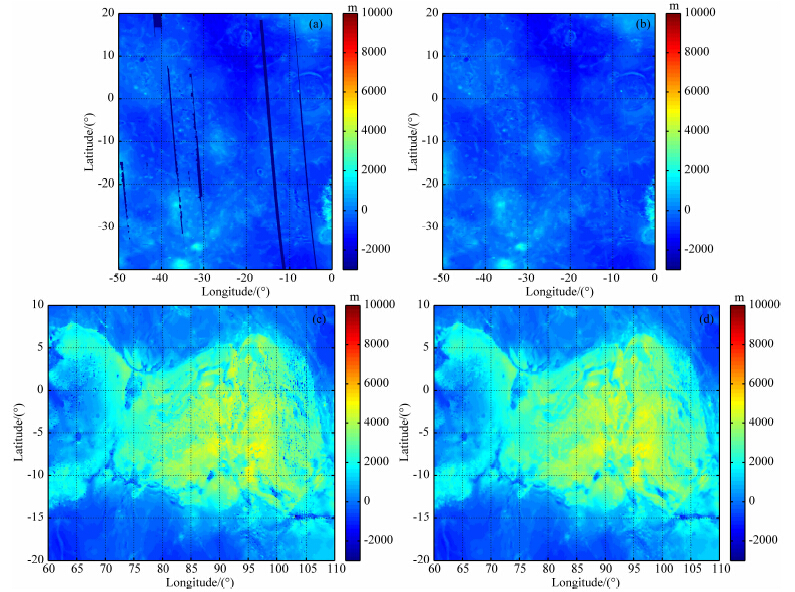 | 图 4 地形数据预处理示意图 (a)原始地形图;(b)空白区域以VenusTopo719模型填补后的地形图;(c)平滑前;(d)平滑后. Fig. 4 Topographic data preprocessing (a)Original topography;(b)After gap filling by VenusTopo719 model;(c)Before smoothing;(d)After smoothing. |
本文使用的实际地形见图 5a,残差地形(RTM)见图 5b.需要注意图 3中红框位置对应的区域实际并未达到本文计算的分辨率,其值本身也不准确.图 3、图 5(a,b)均为Mollweide投影,投影中心为0°经线.
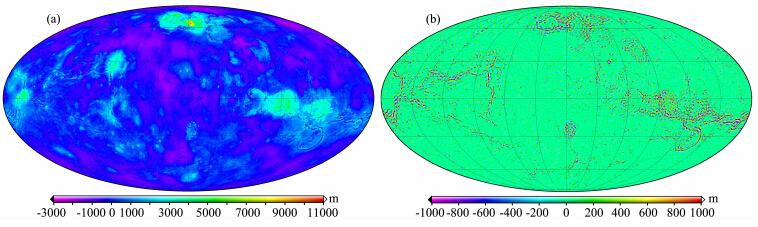 | 图 5 本文所用的输入地形 (a)本文使用的地形,参考半径为6051877 m;(b)金星残差地形图(RTM). Fig. 5 Input topography used in this paper (a)Topography in this paper referenced to a radius of 6051877 m;(b)RTM of Venus. |
图 6a为3.2节计算的中长波重力扰动部分,图 6b为3.3节计算的短波重力扰动部分,两部分之和即为金星表面的重力扰动,见图 6c.金星表面重力扰动结合3.1节的表面正常重力,可得到金星表 面的重力加速度,见图 6d.图 6(a—d)均为Mollweide 投影,投影中心为0°经线.
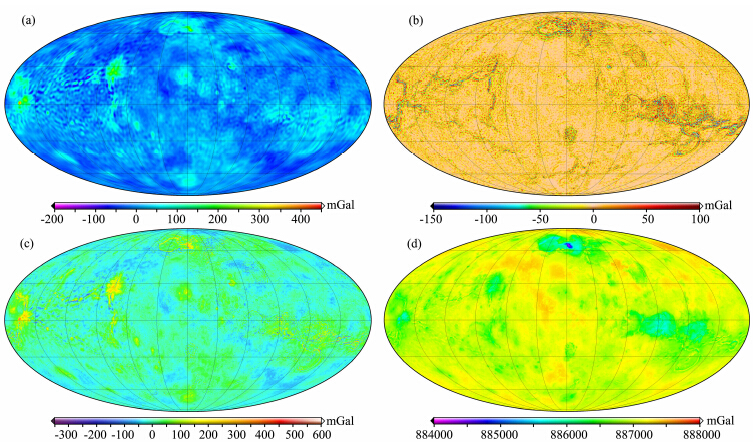 | 图 6 VGM2013模型结果 (a)中长波重力扰动;(b)短波重力扰动;(c)VGM2013金星表面重力扰动;(d)VGM2013金星表面重力加速度. Fig. 6 Results of VGM2013 model (a)Gravity disturbances of middle-long wavelength;(b)Gravity disturbances of short wavelength; (c)VGM20013 surface gravity disturbances;(d)VGM20013 surface gravity acceleration. |
为了更直观清晰地显示不同阶次的重力成分对 最终重力扰动的影响,图 7和图 8分别选取因其有着和地球相似的火山地貌而一直是研究热点的Beta Regio(10°~40°,-65°~-90°)和Atla Regio(-20°~25°,-155°~-180°)区域进行分析.Beta Regio位于中北纬地区,是金星上最早被识别的地貌之一.主要地貌特征为岩石圈抬升和火山作用下隆起的南部Beta高地被南北向的裂谷Devana Chasma所截断(Basilevsky and Head, 2007).Atla Regio位于赤道一带,周围有着为数众多相互覆盖的熔岩流,主要地貌特征有位于东南的Ozza Mons,位于西南的Maat Mons和西北的Sapas Mons三大火山,以及 Ganis Chasma、Dali Chasma和Parga Chasma三大裂谷(Senske and Head, 1992).图中可以明显看出,中长波部分的重力扰动主要反映了火山隆起抬升等大尺度的重力场信息,而短波部分的重力扰动主要反映了裂谷、脊状带等小尺度的重力场信息,通过对小尺度重力场的改进,可以得到分辨率更高的重力场.
 | 图 7 Beta Regio区域不同波段重力扰动示意图,单位为mGal (a)中长波部分;(b)短波部分;(c)最终结果,(a)和(b)的叠加. Fig. 7 Gravity disturbances of different wavelength at Beta Regio(in mGal) (a)Middle-long wavelength part;(b)Short wavelength part;(c)Summation of(a) and (b). |
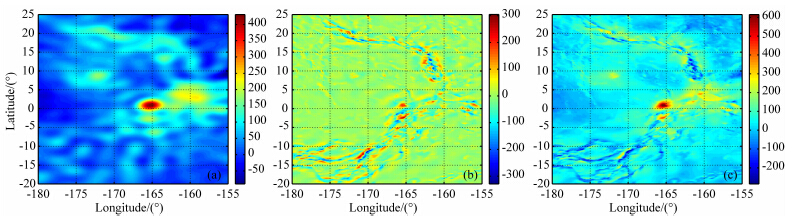 | 图 8 Atla Regio区域不同波段重力扰动示意图,单位为mGal (a)中长波部分;(b)短波部分;(c)最终结果,(a)和(b)的叠加. Fig. 8 Gravity disturbances of different wavelengths at Atla Regio(in mGal) (a)Middle-long wavelength part;(b)Short wavelength part;(c)Summation of(a) and (b). |
总体看来,由于金星表面相对平坦,地形最高处和最低处相差不超过14000 m(Solomon and Head, 1991),故除了部分特征区域外,金星的表面重力扰动总体较小,MGNP180U模型的金星表面重力扰动约在-200到500 mGal范围内(Konopliv et al., 1999),而本文的VGM2013模型由于用地形残差改进了短波重力成分,对平坦区域影响不大,但对高地和低地的重力扰动影响很大,这使得金星表面重力异常范围明显增大,图 6c也可以看出,只有 在高地和低地,短波地形才会引起明显的重力扰动.表 2给出了VGM2013模型的基本统计信息,VGM2013表面重力加速度的最小值为8.84177 m·s-2,位于Maxwell地区,和MGNP180模型的表面重力加速度最小值位置相同.
|
|
表 2 VGM2013模型基本统计信息(单位mGal) Table 2 Basic statistical information of VGM2013 model(in mGal) |
表 3对比了本文提出的金星表面重力模型VGM2013和之前四个金星重力模型在金星12个 特征区域的表面重力扰动最大值.MGNP120PSAAP、MGNP180U分别为Konopliv等(1996,1999)通过轨道跟踪数据获得的120、180阶重力模型.可以看出,相对于最新的MGNP180U模型,本文的VGM2013模型对其中大部分区域的重力扰动峰值有很大改进,对Sapas、Atalanta和Mead区域的改进较小,表明该处的短波结构较少.金星表面重力异常的最大值与MGNP120PSAAP和MGNP180U模型一致,位于Atla Regio的Maat Mons区域.
|
|
表 3 VGM2013和之前的重力模型在金星12个特征区域的表面重力扰动峰值(单位mGal) Table 3 Gravity disturbance peaks at the surface of Venusian features of interest for three gravity models(in mGal) |
图 9和图 10对比了本文提出的VGM2013与之前MGNP180U模型在Beta Regio和Atla Regio区域的表面重力扰动,可以看到,VGM2013模型的重力扰动不仅在整体趋势上和MGNP180U模型一致,还可以体现裂谷、脊状带等更多小尺度的重力细节,分辨率远高于MGNP180U.
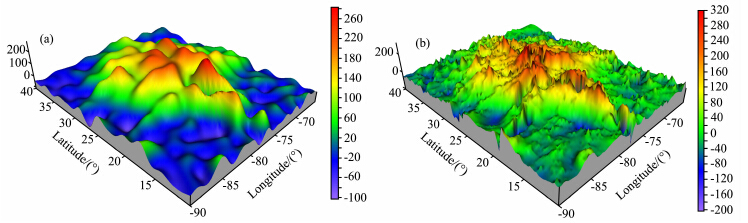 | 图 9 Beta Regio区域的重力扰动,单位为mGal (a)MGNP180U;(b)VGM2013. Fig. 9 Gravity disturbances at Beta Regio(in mGal) |
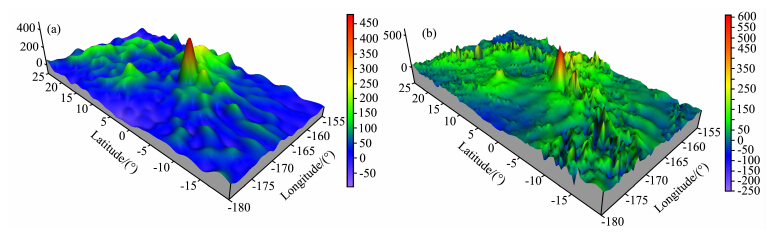 | 图 10 Atla Regio区域的重力扰动,单位为mGal (a)MGNP180U;(b)VGM2013. Fig. 10 Gravity disturbances at Atla Regio(in mGal) |
相似的方法在地球、月球和火星(Hirt et al., 2010,2012; Hirt and Featherstone, 2012)重力场的计算上得到了很好的结果,可以间接证明该模型用于金星的可行性,但由于金星尚没有表面实测重力值,直接的验证目前还没有可能.为了分析VGM2013模型的频谱特征,本文以格网重力加速度数据为基础进行试验,将重力加速度通过空间改正向上延拓到金星外固定半径的参考球面上,并将此0.1°的二维重力加速度格网数据通过Wieczorek的SHTOOLS软件(http://shtools.ipgp.fr/)转化为899阶重力球谐系数.图 11a为MGNP180U模型和本文的VGM2013模型的位系数阶方差对 比,Kaula约束取1.5×10-5/n2.可以看出,MGNP180U 模型在约120阶以后的阶方差明显降低,而本文的VGM2013模型在120阶以后依然有很强的重力信息,可见VGM2013模型对金星重力场的高阶部分有了很好的改善.
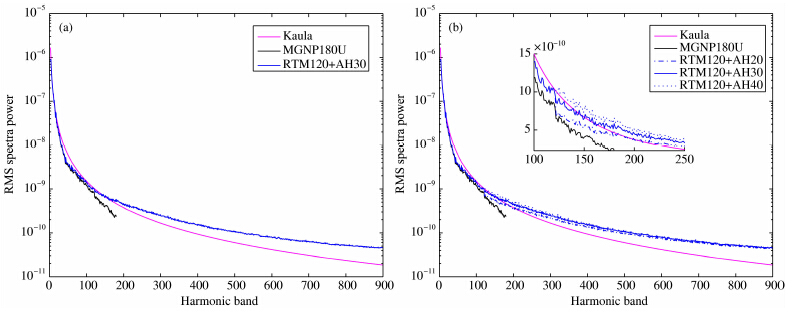 | 图 11 MGNP180U和VGM2013模型的重力位系数阶方差 Fig. 11 Gravity RMS spectra power of MGNP180U and VGM2013 |
过去研究对于金星处于高度均衡、充分补偿状态以及30~50 km的平均补偿深度的结论通常是 根据其重力和地形的导纳或GTR(Geoid/Topography Ratio)等相关方法获得的(Kucinskas and Turcotte, 1994; Kucinskas et al., 1996; Grimm and Hess, 1997).而在本文的计算中,如图 11b,若不能引入合理的均衡补偿模型,则精化的金星重力场的位系数 阶方差不能平稳衔接,而会在截断阶数附近有极 大的跳跃,这和Hirt等(2010,2012),Hirt和Featherstone(2012)计算的月球和火星重力场精化结果的阶方差情况差别很大,从另一角度证明了金星的补偿情况与月球和火星确有很大不同,且在本文计算的尺度下不可忽略.图 11b对比了20 km、30 km和40 km补偿深度下的阶方差.可以看出,VGM2013模型30 km补偿深度的曲线在120阶前后衔接光滑,而偏大或偏小的补偿深度不能消除阶方差的跳跃,从侧面可以证明30 km的补偿深度假设是合理的.另一方面,该模型的阶方差在高频部分相较于Kaula曲线有着更高的能量,在短波重力的计算过程中,均衡改正虽然对120阶以上的重力有影响,但在更小的尺度(400阶以上)对重力的影响几乎可以忽略,故在本文提出的模型中,对于更高的阶次,能够影响重力阶方差的因素唯有过高的平均壳密度取值.目前对金星壳的玄武岩成分以及平均密度的估计,主要是基于对登陆金星的探测器获取岩石样本的化学成分分析(Grimm and Hess, 1997).但由于采样数目稀少,且采样的岩石来自风化层而不是真正的岩床,并不能反映金星壳的真实情况,部分区域如Venera13和14着陆点的表层物质为高孔隙度低密度的成分,其 密度低达1150~1500 kg·m-3(Zolotov and Volkov, 1992). 基于以上情况,本文认为,金星壳的平均密度很有可能小于本文采用的2700 kg·m-3.
需要注意的是,VGM2013模型最终结果是格网形式的金星表面重力加速度和重力扰动,可为将来的金星探测器定轨和着陆提供参考,可作为重力计算的先验模型,也可用于地球物理分析,但并不用于球谐模型的频率域分析,因为空间改正和均值壳密度等宏观假设都会损失一定的重力信息,使得反算的球谐系数不精确.此处的球谐分析只是作为模型验证之用. 6 结论
本文参考利用地形精化地球、月球、火星重力场的理论和方法,通过合理的建模和假设,提出了一个新的金星重力模型VGM2013.同时基于该模型的计算过程及结果分析,从侧面验证了金星的补偿深度约为30 km的合理性,并得出了金星壳的实际平 均密度很有可能小于目前认为的2700~2900 kg·m-3 的结论.该模型分辨率达10 km量级,大大高于现有的金星重力场.VGM2013模型的最终结果是格 网形式的金星表面重力加速度和重力扰动.该模型基 于金星浅层壳为均值、30 km深度的Airy-Heiskanen 均衡补偿的假设,故计算结果在地壳密度及补偿机制与假设符合的地方符合较好,而在密度异常较大、补偿机制不同的区域差异较大,若将来能够得到更精确的密度变化和补偿模型,相信可以得到更好的结果.VGM2013模型的结果可为将来的金星探测器定轨和着陆提供参考,作为重力计算的先验模型,但由于该模型没有包含120阶以后的短波重力观测信息,不建议直接用于更小尺度的地质和地球物理解释.
致谢 本文所用的重力场球谐系数取自美国NASA PDS Geoscience Node Data中心,地形球谐系数取自Wieczorek个人网站,球谐分析使用了SHTOOLS 2.8,球面投影采用了Generic Mapping Tools(GMT)软件,三维图像绘制使用了Surfer 10软件.| [1] | Banerdt W B. 1986. Support of long-wavelength loads on Venus and implications for internal structure. Journal of Geophysical Research, 91(B1): 403-419. |
| [2] | Basilevsky A T, Head J W. 2007. Beta Regio, Venus: Evidence for uplift, rifting, and volcanism due to a mantle plume. Icarus, 192(1): 167-186. |
| [3] | Driscoll J R, Healy D M. 1994. Computing Fourier transforms and convolutions on the 2-sphere. Advances in Applied Mathematics, 15(2): 202-250. |
| [4] | Forsberg R, Tscherning C C. 1981. The use of height data in gravity field approximation by collocation. Journal of Geophysical Research, 86(B9): 7843-7854. |
| [5] | Forsberg R. 1984. A study of terrain reductions, density anomalies and geophysical inversion methods in gravity field modelling (No.OSU/DGSS-355). Department of Geodetic Science and Surveying, Ohio State University, Columbus. |
| [6] | Grimm R E, Hess P C. 1997. The Crust of Venus.//Venus II. Tucson: Univ. of Arizona Press. |
| [7] | Hirt C. 2010. Prediction of vertical deflections from high-degree spherical harmonic synthesis and residual terrain model data. Journal of Geodesy, 84(3): 179-190. |
| [8] | Hirt C, Featherstone W E. 2012. A 1.5 km-resolution gravity field model of the Moon. Earth and Planetary Science Letters, 329-330: 22-30. |
| [9] | Hirt C, Claessens S J, Kuhn M, et al. 2012. Kilometer-resolution gravity field of Mars: MGM2011. Planetary and Space Science, 67(1): 147-154. |
| [10] | James P B, Zuber M T, Phillips R J. 2013. Crustal thickness and support of topography on Venus. Journal of Geophysical Research: Planets, 118(4): 859-875. |
| [11] | Konopliv A S, Sjogren W L, Yoder C F, et al. 1996. Venus 120th degree and order gravity field.//1996 AGU Fall Meeting, San Francisco, CA. |
| [12] | Konopliv A S, Banerdt W B, Sjogren W L. 1999. Venus gravity: 180th degree and order model. Icarus, 139(1): 3-18. |
| [13] | Kucinskas A B, Turcotte D L. 1994. Isostatic compensation of equatorial highlands on Venus. Icarus, 112(1): 104-116. |
| [14] | Kucinskas A B, Turcotte D L, Arkani-Hamed J. 1996. Isostatic compensation of Ishtar Terra, Venus. Journal of Geophysical Research, 101(E2): 4725-4736. |
| [15] | McNamee J B, Kronschnabl G R, Wong S K, et al. 1992. A gravity field to support Magellan navigation and science at Venus. J. Astron. Sci., 40(1): 107-134. |
| [16] | Nagy D, Papp G, Benedek J. 2000. The gravitational potential and its derivatives for the prism. Journal of Geodesy, 74(7-8): 552-560. |
| [17] | Rappaport N J, Konopliv A S, Kucinskas A B, et al. 1999. An improved 360 degree and order model of Venus topography. Icarus, 139(1): 19-31. |
| [18] | Rummel R, Rapp R H, Sunkel H, et al. 1988. Comparisons of global topographic/isostatic models to the Earth's observed gravity field. Geod. Sci., Ohio State Univ., Columbus. |
| [19] | Senske D A, Head J W. 1992. Atla Regio, Venus: Geology and origin of a major equatorial volcanic rise. Proceedings of Lunar and Planetary Science, 789: 107-109. |
| [20] | Sjogren W L, Banerdt W B, Chodas P W, et al. 1997. The Venus gravity field and other geodetic parameters.//Venus II. Tucson: Univ. of Arizona Press, 1125-1161. |
| [21] | Solomon S C, Head J W. 1991. Fundamental issues in the geology and geophysics of Venus. Science, 252(5003): 252-260. |
| [22] | Torge W. 2001. Geodesy, 3rd ed. Berlin: Gruyter. |
| [23] | Wieczorek M A. 2007. 10.05-Gravity and topography of the terrestrial planets.//Treatise on Geophysics. Oxford: Elsevier-Pergamon. |
| [24] | Zolotov M Y, Volkov V P. 1992. Chemical processes on the planetary surface.//Venus Geology, Geochemistry and Geophysics: Research Results from the Soviet Union. Tucson: Univ. of Arizona Press. |
 2014, Vol. 57
2014, Vol. 57


