2. 河南理工大学测绘与国土信息工程学院, 焦作 454000;
3. 中国科学院大地测量与地球动力学国家重点实验室, 武汉 430077
2. School of Surveying and Land Information Engineering, Henan Polytechnic University, Jiaozuo 454000, China;
3. State Key Laboratory of Geodesy and Earth's Dynamics, Chinese Academy of Sciences, Wuhan 430077, China
电离层层析成像技术是计算机层析成像技术在电离层监测中的一种新的应用(Kersley,2005; 刘裔文等,2013; Mitchell and Spencer, 2003),该技术借助于卫星观测信息,通过对电离层进行分层研究,不仅克服了传统的薄层假设电离层模型的局限性,而且特别适合于监测大尺度电离层电子密度的垂直分布及其在太阳活动异常状态下的扰动特性(Yao et al., 2013; Pokhotelov et al., 2011; Jin et al., 2008; Rius A et al., 1997; Yizengaw et al., 2006).然而,在实际的电离层电子密度重构中,由于电离层层析系统本身所具有的局限性,如接收机空间分布的不均匀性和数量的有限性以及观测视角的有限性,所有这些因素的存在导致了电离层电子密度层析反演的不适定性(Garcia and Crespon, 2008; Yao et al., 2013; Wen et al., 2012; Zhao et al., 2013).
电离层电子密度层析重构中常用的经典代数重构算法通过给每个像素附加先验信息来克服反演过程中不适定问题引起的解不唯一或不稳定问题(Wen et al., 2010).该类方法通常对迭代初值的精度要求较高,对于那些没有任何观测信息的像素来说,迭代收敛后的结果与其初值则完全相同.实际反演过程中,这些初值通常是由精度不高的经验电离层模型(如IRI2007)给出.然而,经验电离层模型反映的是电离层电子密度的月平均效应.因此,对于没有任何射线通过的像素,利用经验模型给出的初值作为最终的迭代结果与实际情况存在一定的差异.在电离层活动异常的情况下,这种差异显得尤为突出,从而导致重构的电离层电子密度图像存在一定程度的失真现象.针对上述问题,本文将选权拟合法(欧吉坤,2004)应用到电离层电子密度层析重构中,该方法利用水平方向相邻像素之间的电子密度变化的连续性以及垂直方向上相邻像素电子密度之间的平滑性,通过施加水平方向平滑约束和垂直约束,来克服那些没有观测信息的像素对经验电离层模式给出初值的依赖,得到了符合客观实际的重构结果. 2 电离层层析重构的选取拟合法 2.1 层析模型和算法
电离层斜总电子含量(Total Electron Content,简称为TEC)为电离层电子密度沿信号传播路径的线积分,一般表示为:

由式(1)可以看出,电离层电子密度与电离层TEC之间是一种积分关系.在实际反演过程中,为了简化计算,通常利用离散反演方法将待反演的电离层空间离散化,为此,事先需要选取合适的基函数bj,模型化待反演的电离层电子密度,于是有:
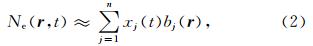

假如以Aij代表(3)式中的积分项,则有:
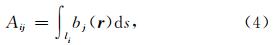
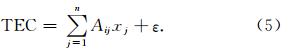

将(6)式代入(4)式后有:

将(5)式以矩阵的形式表示,则有:

如前所述,由于观测数据的不足和地面GNSS观测站的分布不均匀性等因素的影响,电离层电子密度层析反演呈现出不适定性.针对上述问题,为了使(8)式有稳定而唯一的解,根据Tikhonov正则化(Tikhonov and Arsenin, 1997)方法,构造如下准则函数:
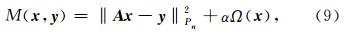
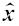 即为所求的解.其中Pn=P,P为电离层层析表达式的权阵,Ω(x)称为稳定范函,它的作用是将原来的不适定问题转化为适定问题,α为正则化参数.稳定泛函Ω(x)可根据具体的应用而采用不同形式,根据欧吉坤(2004)提出的选权拟合法的思想,在电离层电子密度层析反演中,取为如下形式:
即为所求的解.其中Pn=P,P为电离层层析表达式的权阵,Ω(x)称为稳定范函,它的作用是将原来的不适定问题转化为适定问题,α为正则化参数.稳定泛函Ω(x)可根据具体的应用而采用不同形式,根据欧吉坤(2004)提出的选权拟合法的思想,在电离层电子密度层析反演中,取为如下形式:
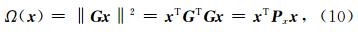
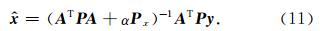
选权拟合法不同于一般正则化方法,它强调辨证地选择稳定范函,即根据具体的研究对象选择合适的约束条件.这里的约束条件不再局限于已知的统计信息,也包括对某一领域规律性的认识,即根据具体的应用建立起参数之间的相关关系.这种约束是依据具体问题中较可靠的先验信息,因而具有明确的物理意义.由于补充了这些有用信息,原来的不适定问题转化为适定问题,使得反演结果更加符合客观实际. 2.2 参数权矩阵的构造
利用选权拟合法反演电离层电子密度时,问题的关键是如何构造待估参数的约束阵.在构造(8)式时,假定待研究的电离层空间在经度、纬度和高度方向上分别被离散化成i、j、k个像素,于是待反演的电离层空间被划分成ijk个像素.像素编号按照经度方向由左至右,纬度方向由前至后,高度方向由下至上的方式进行,具体的划分和编号方式如图 1所示.
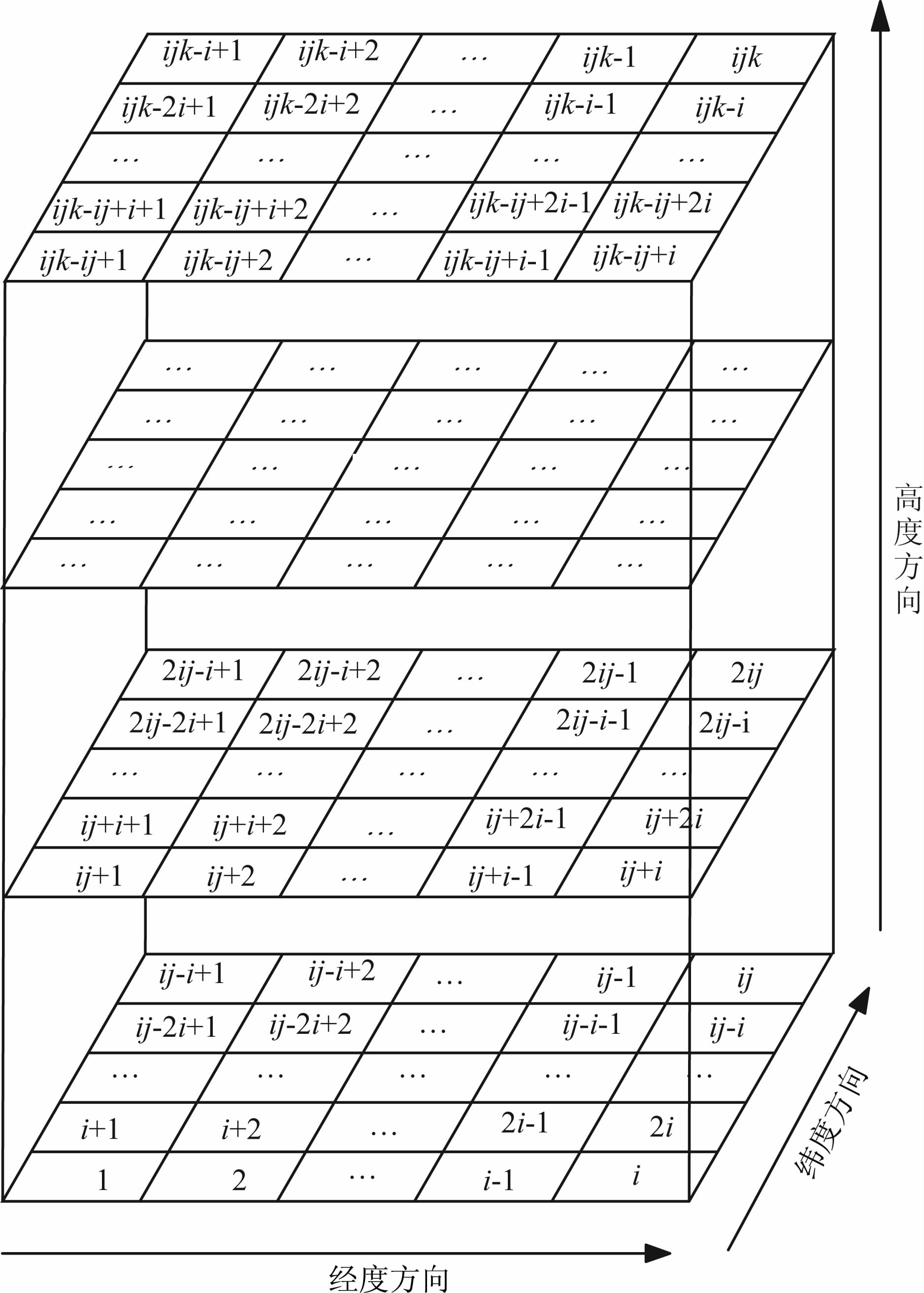 | 图 1 像素划分和编号示意图 Fig. 1 Sketch of pixel division and numbering |
根据离散像素的编号法则,顾及相邻像素之间电离层电子密度和电子密度差变化的平滑性,可构造约束矩阵 G,进而确定选权拟合法中的权矩阵 P x,具体的约束阵构成方式如下:
首先,对于一个含有ijk个像素的电离层空间,根据同一层内沿经度方向排列的各相邻像素电子密度变化连续性的原则,可以构造出水平约束阵 G 1(矩阵顶部与右部分别表示矩阵 G 1的列号和行号):
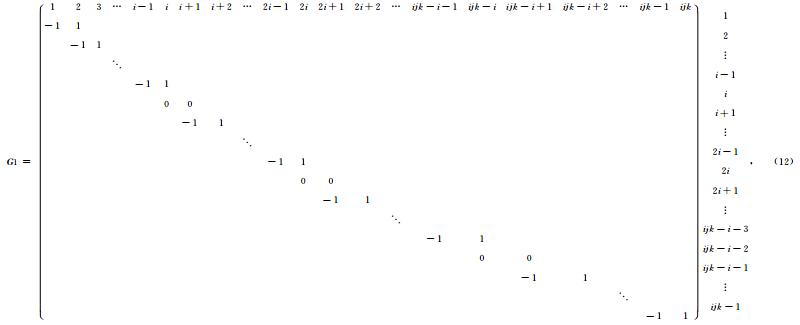

其次,根据同一层内经度方向上排列的各相邻像素之间的电子密度差变化的连续性,可以构造出如下二阶差分矩阵 G 3:


在电离层电子密度的反演过程中,为了确定合理的电离层垂直剖面,Flore(1999)等人借助探空资料提供的剖面信息建立垂直方向上的约束方程.考虑到探空资料的时空分辨率比较低和获取该数据的困难性,本文采用IRI2007模型给出的电离层垂直剖面信息构造垂直约束阵,该信息提供了垂直剖面上相邻像素内电离层电子密度之间的近似比值关系,以此关系来设计构造垂直方向上的约束矩阵 G 5,具体形式如下:

联合水平和垂直方向上的约束条件,可得到统一的约束公式:

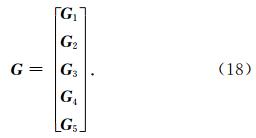
为了验证选权拟合法在电离层电子密度反演过程中的有效性和稳定性,首先进行模拟实验,模拟选定的时段为地磁平静的2013年5月11日10 ∶ 30—11 ∶ 00.模拟过程中,利用湖北省CORS(Continuous Operational Reference System的简称)网36个GNSS观测站的实际坐标构造系数矩阵 A,所选择的36个观测站均匀分布在29°N—32°N和113°E—116°E范围内.因此,实际模拟的地理经纬度范围与所选择测站的覆盖范围保持一致,高度范围则选择在100~1000 km之间.经纬度和高度方向上的分辨率分别为0.25°、0.25°和10 km.详细的模拟步骤如下:
(1)模拟电子密度真值:利用IRI2007模型模拟待反演时刻各个像素内的电离层电子密度,并以此作为反演的真值 x 真;
(2)构造系数阵:利用重构区域内布设的36台GPS接收机观测数据中卫星和地面接收机的坐标,计算出某一反演时段内GPS信号传播路径在其所经过像素内的截距,构造系数矩阵 A ;
(3)模拟电子密度反演所需要的电离层斜距TEC的真值:联合步骤(2)构造出来的系数阵,计算各条射线传播路径上的电离层斜距TEC值 y 真;

(4)构造带误差的TEC观测值:顾及实际观测中噪声和离散误差的存在,在模拟计算中,需要向模拟电离层斜距TEC真值中加入一定量的随机误差 e,于是有:

(5)反演计算:设定迭代计算初值向量 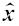 (0),该初值向量为步骤(1)中给定真值的0.6倍.令
(0),该初值向量为步骤(1)中给定真值的0.6倍.令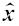 (k)=
(k)= 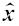 (0),由密度初值 x (k)计算 y (k),y (k)= Ax (k),然后计算 y和y (k)之差Δ y (k),
(0),由密度初值 x (k)计算 y (k),y (k)= Ax (k),然后计算 y和y (k)之差Δ y (k),
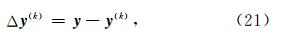
将Δ y (k)代入(11)式中计算Δ x (k+1);
(6)判断迭代是否收敛:计算电离层电子密度估值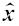 (k+1),
(k+1),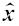 (k+1)=
(k+1)=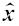 (k)+Δx(k+1),并求出
(k)+Δx(k+1),并求出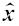 (k+1)与步 骤(6)中 x (k)之间的差值,找出该差值绝对值的最大值,即 Δxj max= x<sup>(k+1)j-x<sup>(k)j max(k=0,1,2,…),当 Δxj max≤τ,迭代终止.否则,用
(k+1)与步 骤(6)中 x (k)之间的差值,找出该差值绝对值的最大值,即 Δxj max= x<sup>(k+1)j-x<sup>(k)j max(k=0,1,2,…),当 Δxj max≤τ,迭代终止.否则,用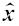 (k+1)替代步骤(5)中的
(k+1)替代步骤(5)中的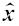 (k),即
(k),即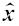 (k)=
(k)=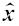 (k+1),重复步骤(5)和步骤(6)的计算过程,直到迭代收敛为止,此时所得到的结果即为最终的电离层电子密度值.
(k+1),重复步骤(5)和步骤(6)的计算过程,直到迭代收敛为止,此时所得到的结果即为最终的电离层电子密度值.
为了分析选权拟合法中约束矩阵对电离层电子密度反演结果的影响,首先对电离层层析方程不施加任何约束,通过奇异值分解后,其最大奇异值为5678.390,最小奇异值约为1.23×10-4,法矩阵的条件数约为4.62×107.在附加上水平方向上的平滑约束后,没有观测信息的像素可以通过同一层内相邻像素的相关性获得其内部电子密度的估计值,进行奇异值分解后,最大奇异值为4907.183,最小奇异值为0.126,法矩阵的条件数为4.91×104,相对于没有施加平滑约束的情况,法矩阵的条件数得到一定程度的改善.
在实际的电离层电子密度层析反演中,为了减少多路径效应等引起的观测噪声的影响,GPS观测射线的截至高度角选为10°.由于GPS观测射线的高度角较大,有些近乎于垂直方向,使得电离层电子密度重构图像的垂直分辨率较低,因此,对选权拟合法模拟验算时考虑施加上垂直约束.如果不考虑水 平约束,仅施加垂直约束,其法矩阵条件数约为5.07×105,条件数虽然得到改善,但层析反演问题仍然病 态.附加水平和垂直约束后,法矩阵的条件数为1.7×102,相对于没有施加任何约束条件时的条件数,施加了水平和垂直约束后,电离层层析系统法矩阵的条件数得到了明显改善,电离层层析系统呈现出良态,电子密度反演过程中出现的不适定问题得到有效解决.
图 2给出了施加不同约束时电离层电子密度重构结果与真值差值示意图.从图 2a可以看出,在没有施加任何约束的情况下,电离层电子密度层析反演结果与真值差异较大,最大密度差值的绝对值达到8×1010el/m3,重构误差小的像素占总像素的比 重较小.图 2b显示施加水平方向约束后,最大密度差值的绝对值约为3.2×1010 el/m3,重构误差较小的像素数明显增多,电离层电子密度层析反演精度得到一定程度的提高.图 2c给出了施加水平和垂直平滑约束后选权拟合法反演的结果与真值的差值,通过比较可以看出,施加水平和垂直约束后,电离层电子密度与真值的差值范围缩小,重构误差较小的像素数所占的比重显著增加,反演精度得到了明显的提高,从而证实了选权拟合法在电离层电子密度层析反演过程中的有效性和可行性.
 | 图 2 不同约束条件下层析反演的电离层电子密度值与真值的差值 (a)无约束条件下;(b)施加水平约束后;(c)施加水平和垂直约束后. Fig. 2 Differences between inversion results and real values of ionospheric electron density for different constraints on the tomographic system (a)No constraint;(b)Horizontal constraint is imposed;(c)Horizontal and vertical constraints are imposed. |
考虑到2003年8月16日地磁条件较为平静,顾及GPS观测视角的有限性,反演过程中,为了弥 补有限视角条件下水平射线缺失给反演结果带来的不利影响,本文利用CHAMP掩星数据和中国区域 的地基GPS观测站的原始导航文件和观测数据文件对当天的电离层电子 密度进行反演.原始导航文件主要是用来计算GPS卫星的瞬时坐标,然后根据卫星的瞬时坐标和地面接收机坐标计算每一信号传播路径与重构区域内相应像素的交叉距离,构造反 演所需的系数矩阵 A,观测数据文件主要用来计算满足反 演条件的每条射线传播路径上的电离层斜距TEC.
图 3显示了选权拟合法重构的114°E经度链上区域性电离层电子密度的时空分布的周日变化情况.从图 3可以看出,在05 ∶ 00UT(北京时间13时)之前,电离层电子密度随着时间的推移逐渐增加,在05 ∶ 00UT,电离层电子密度达到最大值,其值约为1.77×1012 el/m3.随后,电离层电子密度值逐渐减小,到21 ∶ 00UT(北京时间凌晨5时),电离层电子密度达到最小,其值约为2.48×1011 el/m3,这与地球自转中国区域的昼夜交替现象一致.图 3也显示出南方与北方的电离层电子密度变化差异,南方电离层电子密度值总体上高于北方,反映出电离层活动与纬度有较大关系.
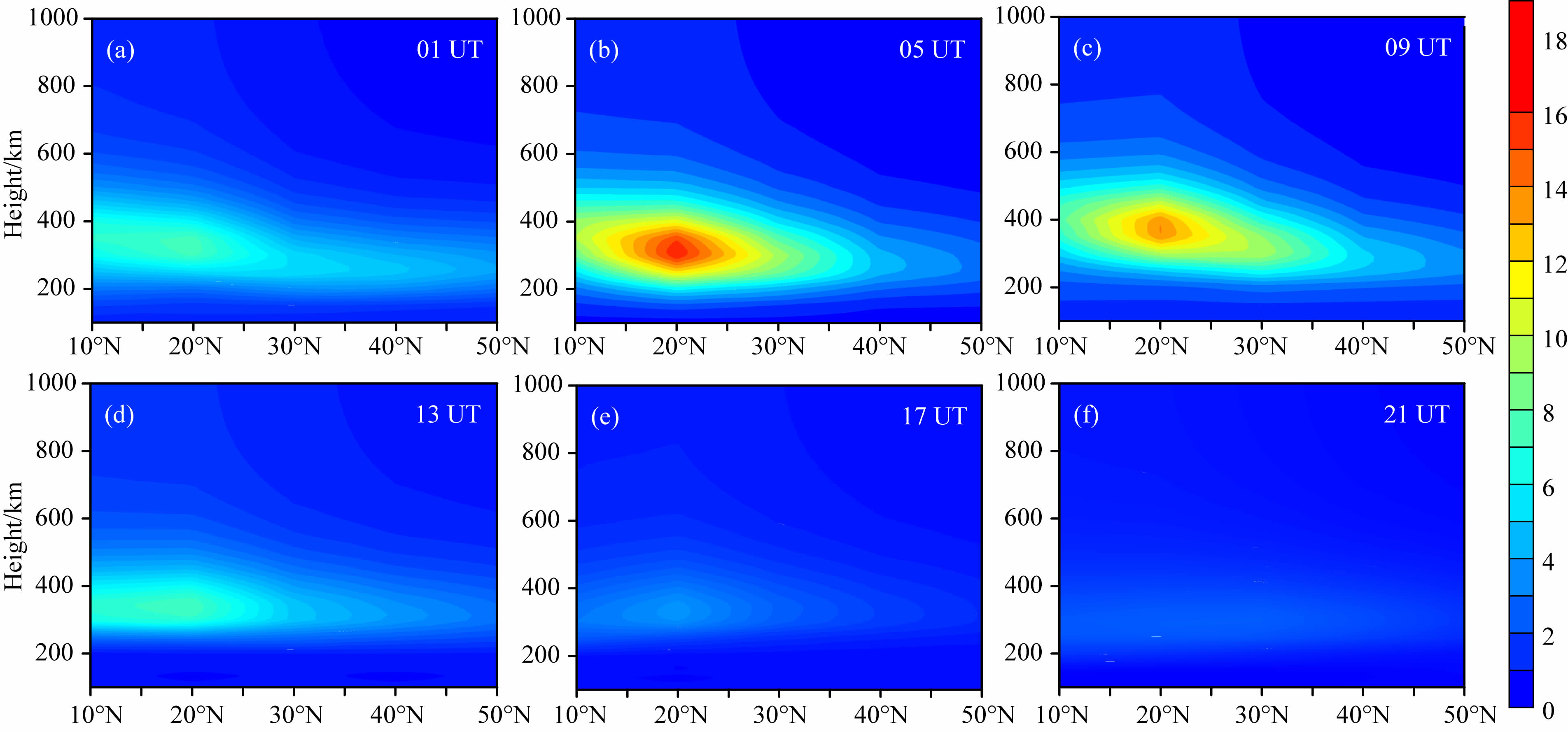 | 图 3 选权拟合法重构的2003年8月16日区域性电子密度分布(电离层电子密度单位为1011 el/m3) Fig. 3 Distribution of ionospheric electron density on August 16,2003 by reconstruction. The unit of electron density is 1011 el/m3 Each snapshot represents the corresponding electron density reconstructed at different universal time,which is labeled at the right-top corner of the snapshot. |
图 4给出了代数重构法和选权拟合法在01 ∶ 00UT和09 ∶ 00UT重构的电离层电子密度剖面与武汉站电离层测高仪观测结果的比较.其中,图 4a表示 01 ∶ 00UT三种不同剖面的比较,图 4b显示的是09 ∶ 00UT三种不同剖面的比较.从图 4的比较结果可以看出,选权拟合法重构的两个不同时刻的电离层剖面与电离层测高仪观测结果吻合的比较好,相对于选权拟合法重构的剖面,代数重构法重构的电子密度剖面与电离层测高仪的观测结果差异比较大,这种较大的差异在峰值高度附近尤其明显.上述比较显示出选权拟合法能够较好地重构电离层电子密度剖面,从而证实了选权拟合法的可靠性和其相对于经典代数重构法的优越性.
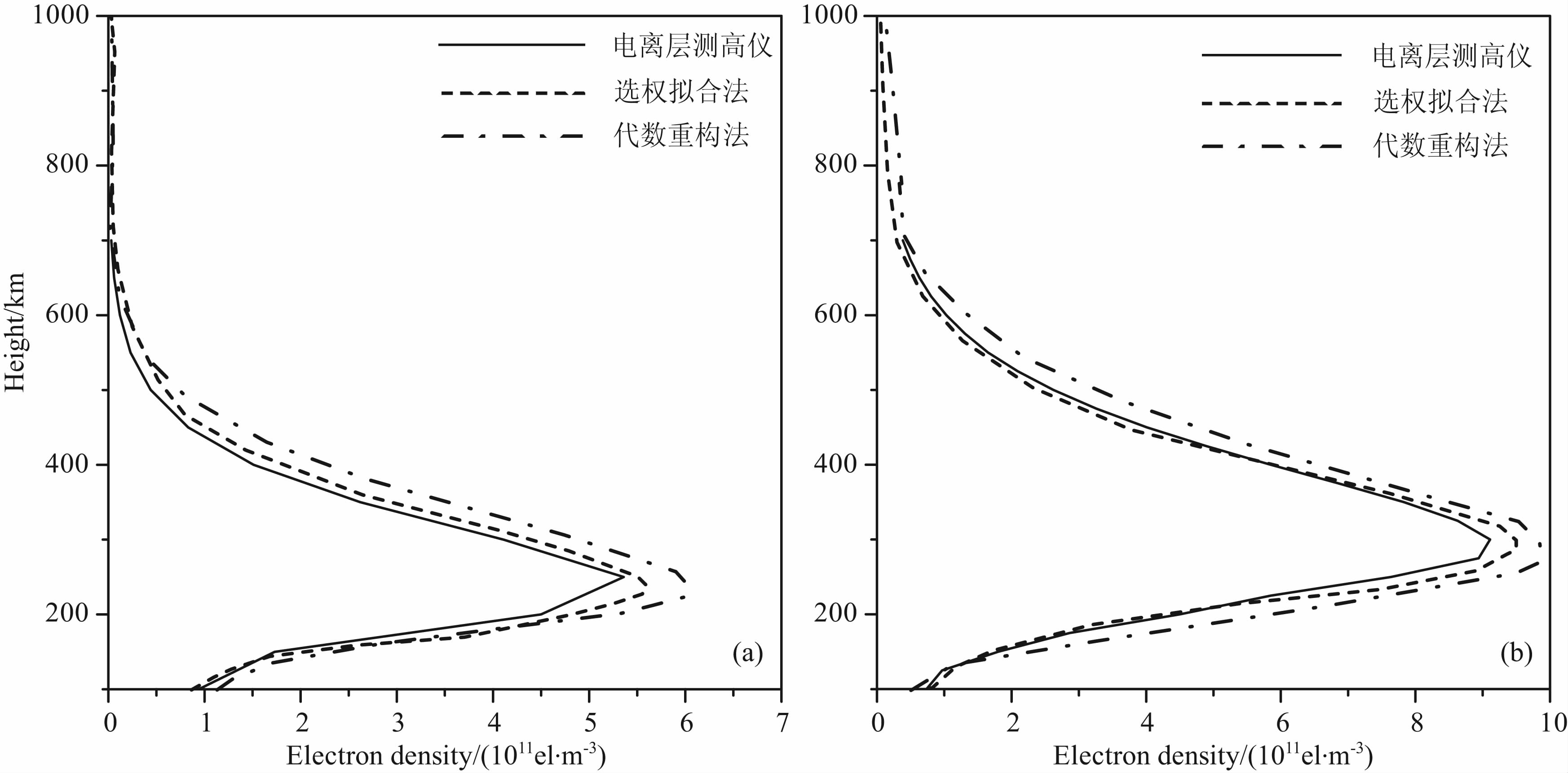 | 图 4 选权拟合法和代数重构算法重构的电离层电子密度剖面与武汉站电离层测高仪所得剖面的比较(a)01 ∶ 00UT;(b)09 ∶ 00UT. Fig. 4 Comparisons of electron density profiles reconstructed from FMSPW,ART and those obtained from the data of ionosonde station located at Wuhan |
本文将选权拟合法拓展应用到电离层电子密度层析反演中,该方法根据相邻像素间电子密度平滑变化的原则,构造约束权阵.不同于现有算法,新方法有明确的物理意义,为解决观测数据不充足和地面接收机分布不均匀等因素引起的不适定问题提供了一种新的途径,可以克服没有观测信息的像素在电离层电子密度反演过程中对初值的过度依赖,提高了反演结果的精度.
构造约束矩阵后,通过数值模拟实验对选权拟合算法进行了验证,证实了该算法在电离层电子密度反演过程中的有效性和可行性.实测数据反演结果表明,利用选权拟合法重构的电离层电子密度时空分布图,能够较好地反映电离层电子密度的周日 变化特性和垂直结构变化规律,重构剖面的比较结 果证实了选权拟合法的可靠性和其相对于经典代数重构算法的优越性.
本文的研究结果是基于离散静态假设的三维层析模型得到的,实际上,在选择的反演时段内,电离层电子密度在三维空间中是动态变化的.今后,随着人们对电离层内部结构和变化规律认识的进一步深入,在顾及电子密度随时间动态变化关系后,本文研究的选权拟合法可以进一步拓展到四维层析模型的应用.另外,本文研究结果是基于地磁平静条件下进行的,在电离层天气异常情况下,如何构造选权拟合法的约束矩阵,是今后重点研究的一个内容.
致谢 感谢地壳运动观测网络提供的地基GNSS观测资料,感谢GFZ提供的CHAMP掩星资料,感谢中国科学院地质与地球物理研究所刘立波研究员提供的电离层测高仪资料.
| [1] | Flores A J. 1999. Atmospheric tomography using satellite radio signals[Ph.D.thesis]. Barcelona: Universitat Politècnica de Catalunya. |
| [2] | Garcia R, Crespon F. 2008. Radio tomography of the ionosphere: Analysis of an underdetermined, ill-posed inverse problem, and regional application. Radio Sci., 43(2): doi:10. 1029/2007RS003714. |
| [3] | Jin S G, Luo O F, Park P. 2008. GPS observations of the ionospheric F2-layer behavior during the 20th November 2003 geomagnetic storm over South Korea. J. Geod. , 82(12): 883-892. |
| [4] | Kersley L. 2005. Ionospheric tomography and its applications in radio science and geophysical investigations. Ann. Geophys. , 48(3): 535-548. |
| [5] | Liu Y W, Xu J S, Xu L, et al. 2013. Electron density distribution in the upper ionosphere and plasmasphere-CT imaging based on GRACE GPS data. Chinese J. Geophys. (in Chinese), 56(9): 2885-2891. |
| [6] | Mitchell C N, Spencer P S J. 2003. A three-dimensional time-dependent algorithm for ionospheric imaging using GPS. Ann. Geophys. , 46(4): 687-696. |
| [7] | Ou J K. 2004. Uniform expression of solutions of ill-posed problem in surveying adjustment and the fitting method by selection of the parameter weights. Acta Geod. Cart. Sin. (in Chinese), 33(4): 283-288. |
| [8] | Pokhotelov D, Jayachandran P T, Mitchell C N, et al. 2011. GPS tomography in the polar cap: comparison with ionosondes and in situ spacecraft data. GPS Solut. , 15(1): 79-87. |
| [9] | Rius A, Ruffini G, Cucurull L. 1997. Improving the vertical resolution of ionospheric tomography with GPS occultations. Geophys. Res. Lett. , 24(18): 2291-2294. |
| [10] | Tikhonov A N, Arsenin V Y. 1997. Solutions of Ill-Posed Problems. New York: John Wiley. |
| [11] | Wen D B, Liu S Z, Tang P Y. 2010. Tomographic reconstruction of ionospheric electron density based on constrained algebraic reconstruction technique. GPS Solut. , 14(4): 375-380. |
| [12] | Wen D B, Wang Y, Norman R. 2012. A new two-step algorithm for ionospheric tomography solution. GPS Solut. , 16(1): 89-94. |
| [13] | Yao Y B, Chen P, Zhang S, et al. 2013. Temporal and Spatial variations in ionospheric electron density profiles over South Africa during strong magnetic storms. Nat. Hazard. Earth Sys. , 13(2): 375-384. |
| [14] | Yao Y B, Tang J, Chen P, et al. 2013. An improved iterative algorithm for 3-D ionospheric tomographic reconstruction. IEEE Trans. Geosci. Remote Sens., 52(8): 4696-4706, doi: 10.1109/TGRS.2013. 2283763. |
| [15] | Yizengaw E, Moldwin M B, Dson P L, et al. 2006. First tomographic image of ionospheric outflows. Geophys. Res. Lett., 33(20): L20102, doi: 10. 1029/2006GL027698. |
| [16] | Zhao H S, Xu Z W, Wu Z S, et al. 2013. A stable and fast method of ionospheric tomography by using diverse data sources. J. Atmos. Sol-Terr. Phys. , 97: 99-105. |
| [17] | 刘裔文, 徐继生, 徐良等. 2013. 顶部电离层和等离子体层电子密度分布——基于GRACE星载GPS信标测量的CT反演. 地球物理学报, 56(9): 2885-2891. |
| [18] | 欧吉坤. 2004. 测量平差中不适定问题解的统一表达与选权拟合法. 测绘学报, 33(4): 283-288. |
 2014, Vol. 57
2014, Vol. 57

