2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
全波形反演的研究早在几十年前就已开始,最先由Tarantola(1984)提出时间域全波形反演,为全波形反演的研究开启了先河;随后提出的频率域全 波形反演(Pratt, 1990a,1990b; Pratt and Wothington, 1990)又为全波形反演的研究开辟了新的道路.但全波形反演需要巨大的计算量和存储量,而且它需要大偏移距的数据才能得到好的反演效果,而早期的计算机技术和地震数据采集技术都很难达到相应的要求,这些困难成为全波形反演实际应用的瓶颈,所以在早期其并非勘探地震领域的主流研究方向.随着勘探地震技术(如地震数据采集技术和多分量检波器)的日趋成熟和计算机计算能力的大大提升(如高性能计算等),为全波形反演的进一步发展和实际应用提供了坚实的硬件基础,所以近几年勘探地震领域掀起了一股全波形反演研究的热潮,几乎遍及了国内外所有大大小小勘探地震相关的研究机构.
目前全波形反演的研究正处于非常活跃的时期,人们取得了一系列的研究成果,但还是有许多极具挑战性的问题没有很好解决.如实际的地震数据往往缺失低频成分或者低频成分被噪音污染而变得不可用,不使用低频数据如何得到好的反演效果?用什么方法去得到初始模型,走时层析成像,抑或是Shin和Cha(2008,2009),Shin等(2010)提出的Laplace域和Laplace-Fourier域反演?地震数据的采集要达到什么要求?利用3-D全方位角数据的全波反演是不是代价太大?等等.本文主要针对初始模型问题.
全波形反演是个高度非线性问题,对初始模型的依赖性强,如果初始模型选在了离目标函数全局最小值很远的地方,那么反演过程中目标函数就很容易陷入局部最小点.使用低频数据可以降低反演的非线性性,它的目标函数相对光滑,能够比较容易收敛到全局最小点,它对初始模型的依赖程度相对低很多.所以如果在反演的初始阶段利用较低频数据得到比较准确的光滑背景速度和大尺度的结构,在此基础上再利用高频数据去刻画精细结构,能提高反演的稳定性,使目标函数逐步收敛到全局最小值附近,比较容易就能得到好的反演结果,这就是所谓的多尺度反演.无论在时间域还是在频率域,都可以实现多尺度反演,这也是如今全波形反演普遍采用的一种策略.低频数据的重要性不言而喻,使用合成数据反演时可以轻轻松松就利用低频数据,如果实际数据中也包含有效低频成分是很幸运的,但毕竟这种情况很少.缺少低频数据,我们需要为反演提供相对准确的初始模型,因为高频数据对初始模型的依赖性很大.本文研究复频率+频率的方式进行反演,在整个反演过程中相当于复频率反演阶段的中间结果为频率反演阶段提供了初始模型.并将此方式的反演结果跟直接进行频率域反演的结果进行对比,可以看出前者对反演效果的改善,以此验证此方法的有效性.此外,还对复频率的不同组合方式对反演结果的影响进行研究. 2 频率域全波形反演回顾
频率域全波形反演经过二十几年的研究发展,衍生出了很多不同的变种,这里只简单回顾传统的并被广泛采用的基于L2范数目标函数和高斯牛顿反演方法的反演理论.
基于L2范数的反演目标函数为
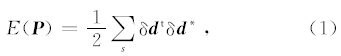
目标函数梯度的表达式为
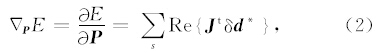
具体计算时,第i个参数点的梯度方向为
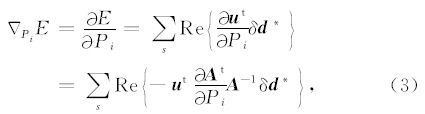
梯度的预处理使用近似Hessian矩阵 H a的对角元素diag H a,H a表达式为
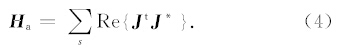
虽然快速求取梯度方向时避免了求取雅克比矩阵的繁琐过程,但从上式可看出在求 H a时回避不了这个问题,第i个参数点处对角线元素Ha(i,i)表达式为
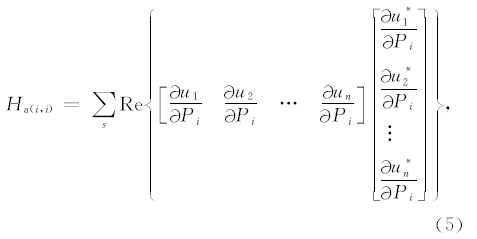
具体第k个检波点处uk对Pi的偏导数的求取计算式为
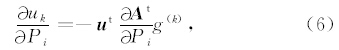
第i个模型参数点的更新:
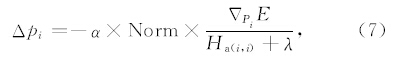
复频率并不是个陌生的名词,它的主要作用就是衰减,尤其是衰减到达时刻较晚的波,可用于去除周期混叠现象、减小数据孔径等.Mallick和Frazer(1987)、Sirgue和Pratt(2004)、Operto等(2007)、以及Shin和Min(2006)都曾用复频率进行过正演和反演,但只用一个或少数几个较小的阻尼因子作为复频率的虚部.本文中的复频率和Shin等提出的拉普拉斯频率域的反演所用复频率组成方式类似,由一组阻尼因子和一个或少数几个超低频率组成.
复频率的推导基于时间域的阻尼波场.如果u(t)是衰减前的波场,其傅里叶变换:
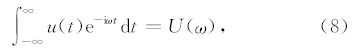
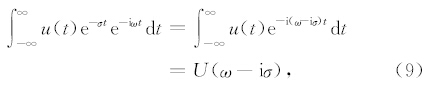
图 1(a、b)分别给出了主频为10Hz的雷克子波及其频谱;图 1(c、e)分别给出了阻尼因子σ为2和10时的衰减震源子波,图 1(d、f)分别对应了两个衰减震源子波的频谱.从图中可以看出,σ为2时,子波有轻微衰减,波形变化不大,也很难分辨其频谱变化;但σ为10时,可以看出子波衰减剧烈,波形不再对称,频谱中的零频明显有了不为零的振幅.可以想象如果放大零频附近的地方,同样能看出原来零频附近的超低频也由振幅几乎为零变为有了明显的振幅,这就是对波场进行衰减的目的,衰减会对频谱产生改造,使频谱中出现一些原来不存在的频率成分,同时使得原来能量非常小的频率成分振幅得到增强.至于对波场衰减为什么会产生这样的效果,Shin和Cha(2009)在文章中有详细验证,通过实验结果,他把这种对超低频成分的恢复解释为像海市蜃楼的出现.其实单纯从傅里叶变换的原理去分析也可以得到较合理解释:如果对每个时刻的波场做相同衰减,傅里叶变换后频谱不会变化;这里对每个时刻波场做时间相关的不同程度衰减,傅里叶变换后频谱肯定会改变,促使0频附近出现明显振幅;至于其他频率处振幅的改变无需关心;可以把这种基于实验和经验的做法看成一种数学手段.
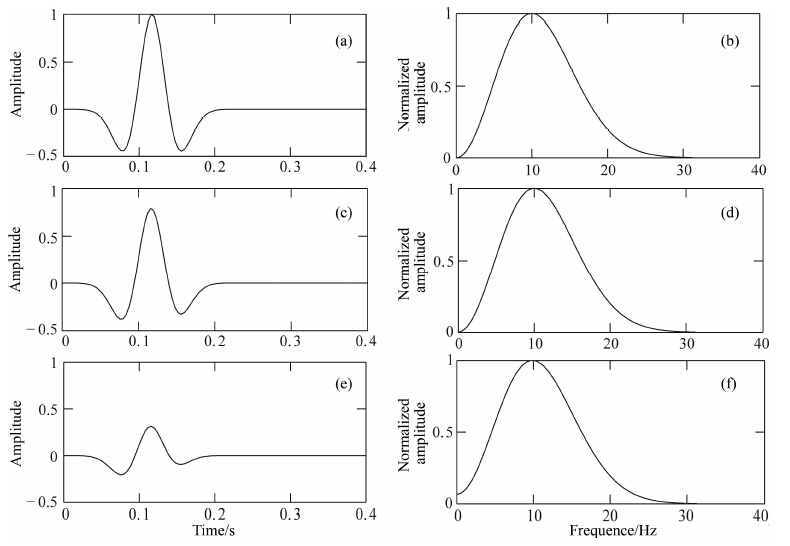 |
图 1 雷克子波频谱及其衰减后子波频谱 (a)雷克子波;(b)雷克子波频谱;(c)σ=2,衰减后子波;(d)对应(c)的频谱;(e)σ=10,衰减后子波;(f)对应(e)的频谱. Fig. 1 Spectrum of Ricker wavelet and its damped wavelets (a)Ricker wavelet;(b)Spectrum of(a);(c)σ=2,damped wavelet;(d)Spectrum of(c);(e)σ=10,damped wavelet;(f)Spectrum of(e). |
虽然本文和Laplace-Fourier域中复频率组成方式类似,但二者的反演实现方式有很大不同,后者反演的目标函数使用对数波场,本文直接使用常规波场;后者梯度预处理时使用伪Hessian矩阵(Shin and Min, 2006)的对角元素,本文直接使用传统高斯牛顿法中近似Hessian矩阵的对角元素;另外在步长的选取、迭代次数的限定等方面都不相同.而本文复频率反演的实现和频率域反演实现基本相同,所以不在这里做重复的理论推导,只是在确定好复频率之后,首先要对观测波场进行衰减,然后对衰减后波场做傅里叶变换(相当于将原始观测波场变换到复频率域),当然后续计算中,ω要用ωc代替.由于反演原理和实现流程基本相同,复频率反演和频率域反演可以糅合在一个程序中实现:即设置反演频率时,把复频率和频率依次组合在一起,同样,反 演数据也依次用复频率数据和频率域数据,也就是上文提到的复频率+频率反演. 4 模型计算 4.1 简单模型
这里选用一透镜体模型(如图 2a所示)作为真 实模型.模型中间透镜体处速度大小为3500 m·s-1,周围速度均为3000 m·s-1.模型网格大小nz×nx=201×201,采样间隔dz和dx都为25 m.炮点放在模型的上边界和左边界,各50炮,炮点间距为100 m;上边界和左边界炮点分别对应下边界和右边界接收点,两边接收点同样都为50个,间距为100 m.反演的初始模型为线性增加模型(如图 2b所示),线性增加模型垂直方向速度随深度线性增加(v=v0+kz,v0=2500 m·s-1,k=7.5).正演时的差分格式采用二阶最优9点格式(Jo et al., 1996),也可以采用四阶差分格式(曹书红和陈景波,2012).
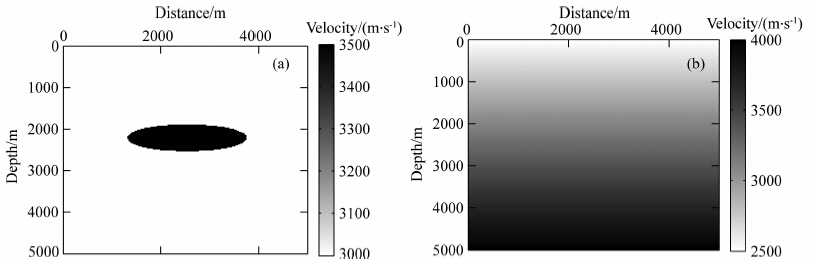 |
图 2 透镜体模型和线性增加模型 (a)透镜体模型;(b)线性增加模型. Fig. 2 Lens model and linearly increasing velocity model (a)Lens model;(b)Linearly increasing velocity model. |
首先看直接进行频率域反演的情况.反演所用 频率分为四组(每组7个频率),第一组为1.89,3.54,4.76,7.2,9.64,13.3,16.97 Hz,第二组为3.54,4.76,7.2,9.64,13.3,16.97,20.63Hz,第三组为5.1,7.2,9.64,13.3,16.97,20.63,24.29 Hz,第四 组为7.2,9.64,13.3,16.97,20.63,24.29,30.4 Hz,在下文中直接称这四组频率为频率组1、频率组2、频率组3和频率组4.各组每个频率的迭代次数限定不超过12,各组反演结果如图 3(a—d)所示.可以看出频率组1和频率组2都得到了很好的反演结果,而频率组3和频率组4反演结果完全脱离了真实情况,因为缺乏低频反演过程不能收敛.图 4(a—d)分别为抽取的图 3(a—d)中x方向2500 m处的深度方向速度(红线代表真实速度,蓝线代表反演速度),可以 看出,前两组频率反演速度值在此处很好地逼近了真 实模型,后两组频率反演速度值跟真实模型相差很大.
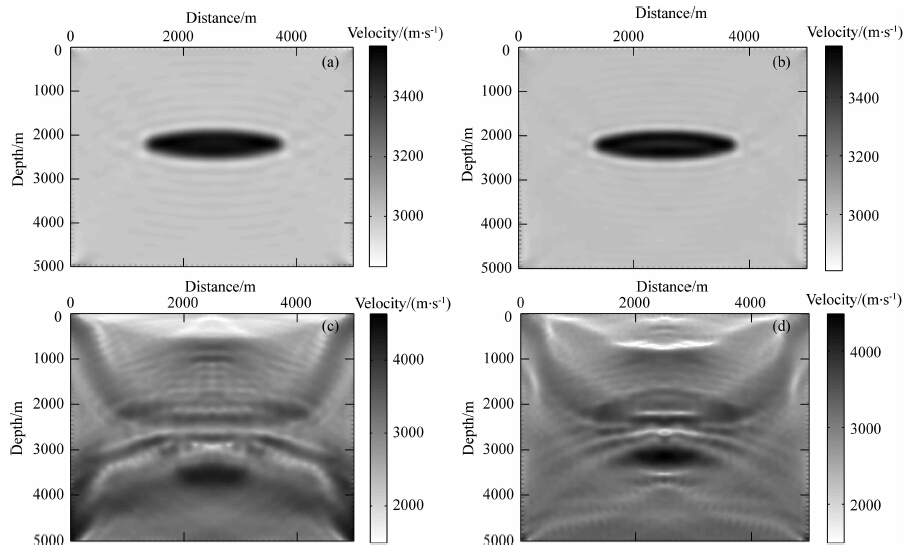 |
图 3 各组频率对透镜体模型的频率域反演结果 (a)频率组1;(b)频率组2;(c)频率组3;(d)频率组4. Fig. 3 Frequency domain inversion results of lens model with different frequency groups (a)Frequency group 1;(b)Frequency group 2;(c)Frequency group 3;(d)Frequency group 4. |
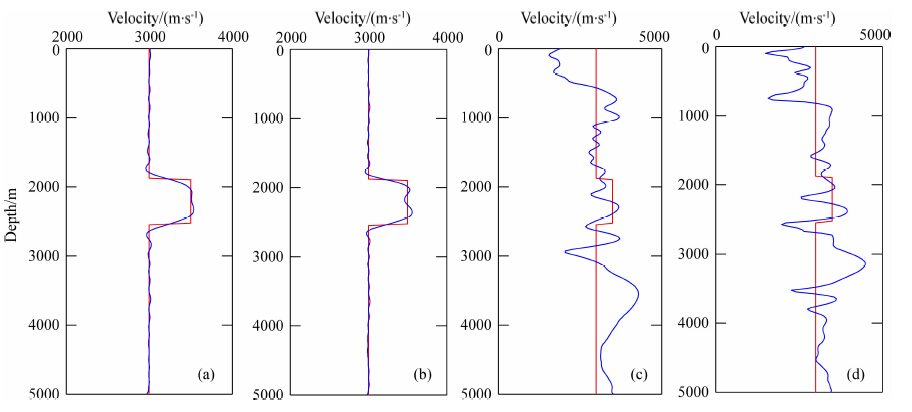 |
图 4 距离为2500 m处,图 3中各反演结果与真实速度对比 (a)频率组1;(b)频率组2;(c)频率组3;(d)频率组4. Fig. 4 Comparison of inverted velocity in Fig. 3 and true velocity at a distance of 2500 m (a)Frequency group 1;(b)Frequency group 2;(c)Frequency group 3;(d)Frequency group 4. |
接下来看复频率+频率反演的情况.这里的复频率一共21个,用7个阻尼因子和3个超低频组成,σ分别为1,3,5,7,9,11,13,ω分别为0.01,0.15,0.3Hz.ωc的组合方式可以是频率优先,即前7个复频率由第一个频率和7个阻尼因子组成,后面依此类推;也可以是阻尼因子优先,即前3个复频率由第一个阻尼因子和3个频率组成,后面依此类推;下文中将两种组合方式分别称为组合方式1和组合方式2.这21个复频率和之前的各个频率组结合起来进行复频率+频率反演.图 5a和6a分别为组合方式1和组合方式2时的复频率反演阶段的中间结果,可以看出两种组合方式的结果类似,说明两种组合方式都可选,而且从两图中都已经可以看到真实模型的雏形,中间的透镜体已经隐约可见.后续各组频率的反演过程视图 5a和6a中的中间结果为初始模型,最终的复频率+频率反演结果分别如图 5(b—e)和图 6(b—e)所示.可以看出各组频率都很好地反演出了真实模型,而且频率越高的频率组反演的结果更加干净清晰,因为这里已经提供了一个很好的初始模型,高频频率组在此基础上能很好发挥精细刻画结构的作用.同样抽取图 5(b—e)和图 6(b—e)中x方向2500 m处的深度方向速度,如图 7(b—e)(红线代表真实速度,蓝线代表组合方式1,绿线代表组合方式2)所示,图中蓝线和绿线重合度 比较大,不易区分,可见两种复频率组合方式反演结果为初始模型时,频率域反演结果接近.这里各频率组反演速度值都能很好逼近真实速度,而且高频频率组反演的速度值更加精确.
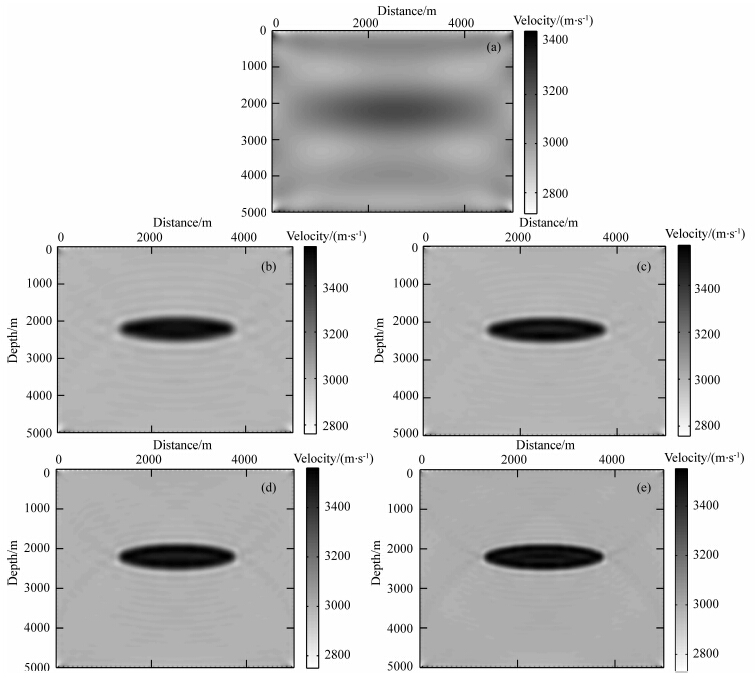 |
图 5 复频率组合方式1+各组频率对透镜体模型的反演结果 (a)复频率反演阶段中间结果;(b)频率组1;(c)频率组2;(d)频率组3;(e)频率组4. Fig. 5 Inversion results of lens model under complex-frequency-combination-scheme 1+different frequency groups (a)The intermediate inversion result in complex-frequency inversion stage;(b)Frequency group 1; (c)Frequency group 2;(d)Frequency group 3;(e)Frequency group 4. |
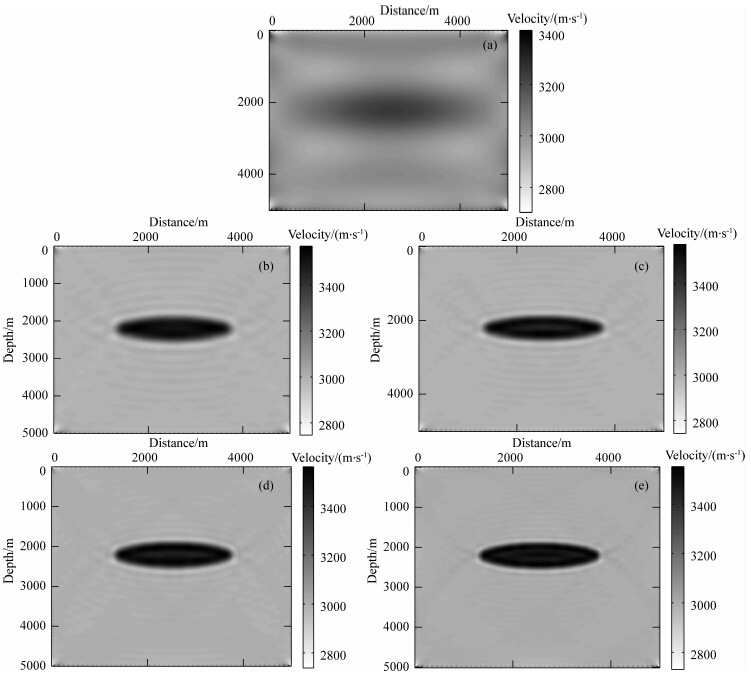 |
图 6 复频率组合方式2+各组频率对透镜体模型的反演结果 (a)复频率反演阶段中间结果;(b)频率组1;(c)频率组2;(d)频率组3;(e)频率组4. Fig. 6 Inversion results of lens model under complex-frequency-combination-scheme 2+different frequency groups (a)The intermediate inversion result in complex-frequency inversion stage;(b)Frequency group 1; (c)Frequency group 2;(d)Frequency group 3;(e)Frequency group 4. |
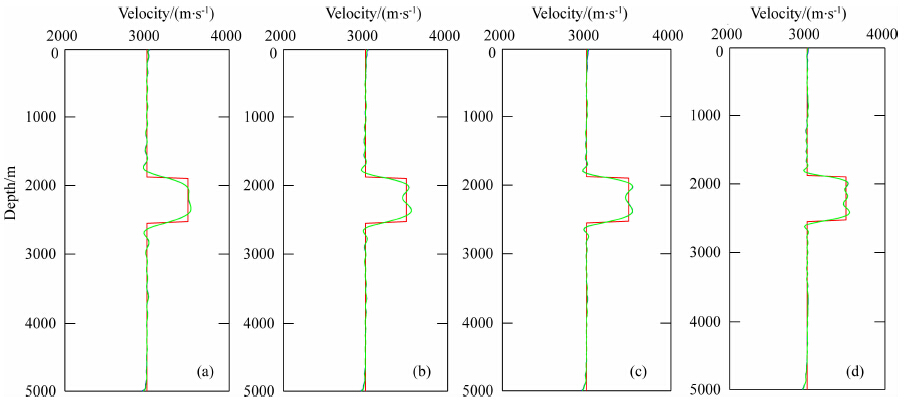 |
图 7 距离为2500 m处,图 5和图 6中各反演结果与真实速度对比 (a)频率组1;(b)频率组2;(c)频率组3;(d)频率组4. Fig. 7 Comparison of inverted velocity in Fig. 5,Fig. 6 and true velocity at a distance of 2500 m (a)Frequency group 1;(b)Frequency group 2;(c)Frequency group 3;(d)Frequency group 4. |
这里所用的真实模型是从Marmousi模型中截取的一部分(如图 8),初始模型同样为线性增加模型(v=v0+kz,v0=1975 m·s-1,k=8.375).网格大小nz×nx=201×201,z方向采样间隔dz和x方向采样间隔dx分别为4 m和12.5 m(保留真实Marmousi模型的采样间隔),由于两方向采样间隔不相等,正演时不能用传统的差分格式,这里采用平均导数优化格式(Chen J B, 2012,2013).炮点放在模型网格第2层,共49炮,炮点间距为100 m;检波点放在第1层,共50个,检波点间距也为100 m.
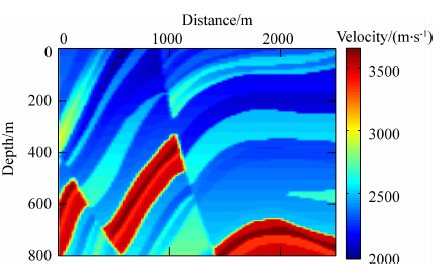 | 图 8 局部Marmousi模型 Fig. 8 Part Marmousi velocity model |
同样首先看直接进行频率域反演的情况.反演用的是跟简单模型中相同的四组频率,各频率反演迭代次数不超过12,各组反演结果如图 9(a—d)所示.前两组由于包含低频成分,反演出的结构相对清晰些,更接近真实模型;后两组分别去掉了5 Hz和7 Hz以下的频率,反演出的结构更加模糊,尤其是模型的底部.再进一步比较各组频率反演出的速度值与真实速度值的差别,抽取x方向位置为1250 m的深度方向速度,如图 10(a—d)(红线代表真实速度,蓝线代表反演速度)所示.可以看出前两组从浅部到深部反演效果差别不是很大,反演速度值和真实速度值总体上比较吻合;后两组浅部反演速度值比较准确,但深部的误差非常大,总体效果明显比前两组差.这些都体现了低频描绘总体背景速度分布的重要性,它可以改善整体反演效果.
 |
图 9 各组频率对局部Marmousi模型的频率域反演结果 (a)频率组1;(b)频率组2;(c)频率组3;(d)频率组4. Fig. 9 Frequency domain inversion results of part Marmousi model with different frequency groups (a)Frequency group 1;(b)Frequency group 2;(c)Frequency group 3;(d)Frequency group 4. |
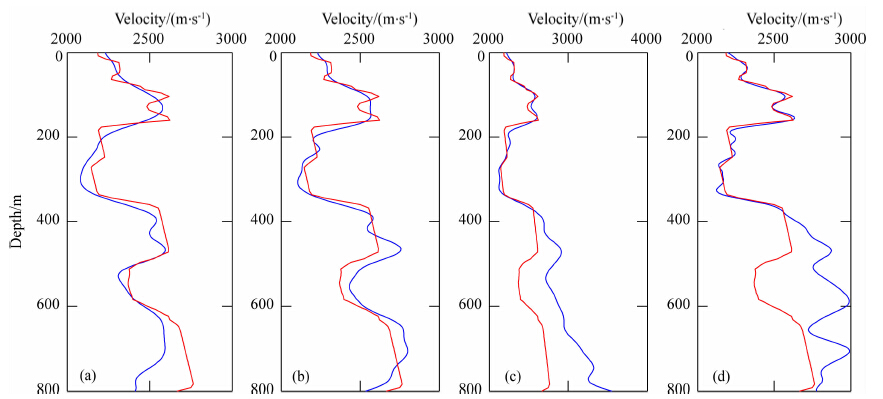 |
图 10 距离为1250 m处,图 9中各反演结果与真实速度对比 (a)频率组1;(b)频率组2;(c)频率组3;(d)频率组4. Fig. 10 Comparison of inverted velocity in Fig. 9 and true velocity at a distance of 1250 m (a)Frequency group 1;(b)Frequency group 2;(c)Frequency group 3;(d)Frequency group 4. |
然后看复频率+频率反演的情况.所用复频率跟简单模型中相同.采用组合方式1和组合方式2时复频率反演阶段的中间结果如图 11a和12a所示.后续各组频率的反演过程视图 11a和12a中的中间结果为初始模型,最终的复频率+频率反演结果分别如图 11(b—e)和图 12(b—e)所示.图 11a和12a看上去相似程度不是很高,而且从上两图中都并不容易看出其反映了真实速度背景,这跟简单模型的情形有所不同;但从复频率+频率反演的最终结果(图 11(b—e)、12(b—e))与单纯频率域反演结果(图 9(a—d))的比较中都可看出,前者各组频率反演结果中速度结构都更加清晰了,尤其对缺乏低频的后两组频率反演效果改善更明显;而且还可以看出两种复频率组合方式下,最终的复频率+频率反演结果在总体速度结构上很相似,所以说两种方式都是可取的.图 13(a—d)同样为抽取图 11(b—e)和图 12(b—e)中x方向1250 m处的深度方向速度(红线代表真实速度,蓝线代表组合方式1,绿线代表组合方式2),从单道速度比较来看,并不能明显看出比图 9(a—d)使用线性增加初始速度模型的反演效果好多少,但整体的速度结构确实更加清晰了,从统计的角度思考大部分位置肯定是更准确的,这里选取单道位置的时候并没有特意挑选,而是直接取了中间的位置.为了更好地评估,这里挑选频率组4,以光滑速度模型(真实速度模型经过平滑之后)的频率域反演结果为参考,进一步比较线性增加模型为初始模型时单纯频率域反演和两种组合方式下的复频率+频率反演的效果,分别如图 14(b—e).图 14a为光滑速度模型.图 14b(光滑模型为初始模型时频率域反演结果)明显效果最好,图 14c(线性增加模型为初始模型时频率域反演结果)效果 最差,图 14d、14e(线性增加模型为初始模型时复频率+频率反演结果)效果介于二者之间.在实际反演过程中,通过平滑真实速度模型来获得初始模型肯定不可能,初始模型只能通过其他方法去计算,这样计算得到的初始模型自然很难达到光滑速度模型的效果,但在实际中只能这么做,从图 14d和14e达到的效果来看,这种将复频率反演阶段的中间结果作为后续频率域反演的初始模型的复频率+频率反演方式不失为一个可行的方法,当然这种方法还有很多地方需要研究改进才能达到更好的效果,这是下一步的研究工作.
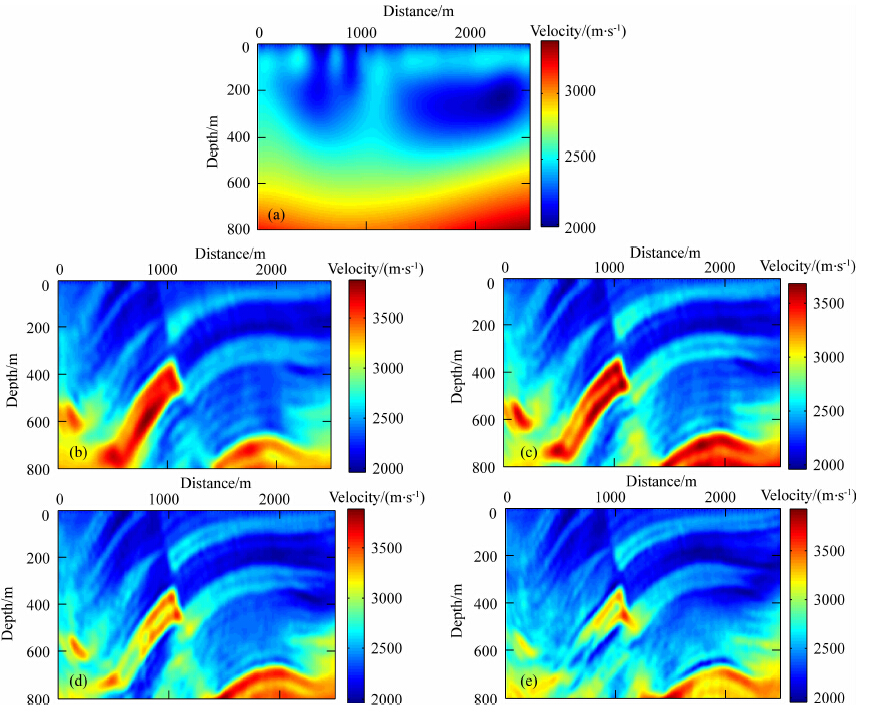 |
图 11 复频率组合方式1+各组频率对局部Marmousi模型反演结果 (a)复频率反演阶段中间结果;(b)频率组1;(c)频率组2;(d)频率组3;(e)频率组4. Fig. 11 Inversion results of part Marmousi model under complex-frequency-combination-scheme 1+different frequency groups (a)The intermediate inversion result in complex-frequency inversion stage;(b)Frequency group 1; (c)Frequency group 2;(d)Frequency group 3;(e)Frequency group 4. |
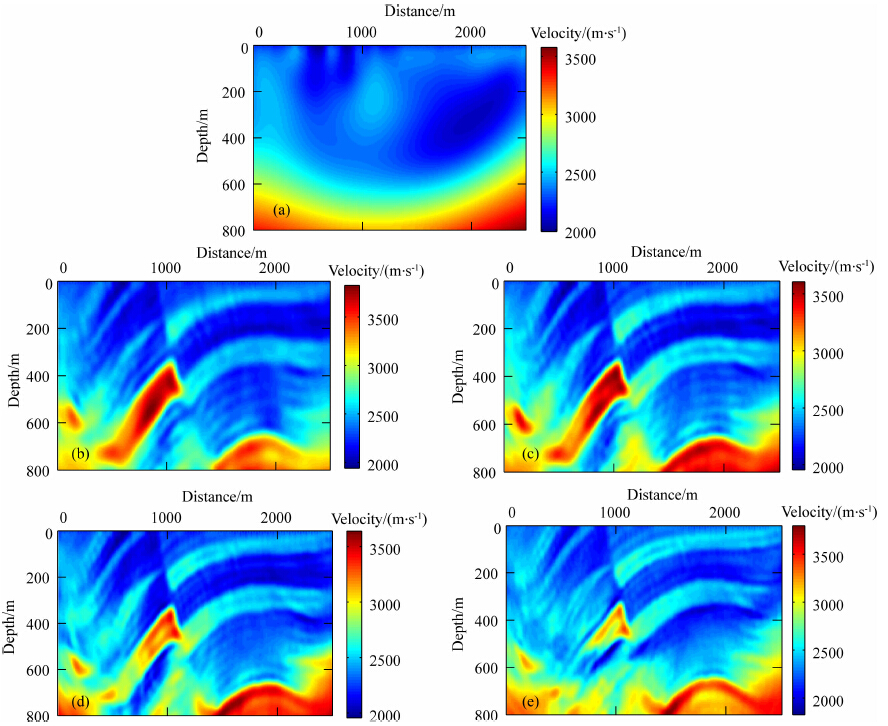 |
图 12 复频率组合方式2+各组频率对局部Marmousi模型反演结果 (a)复频率反演阶段中间结果;(b)频率组1;(c)频率组2;(d)频率组3;(e)频率组4. Fig. 12 Inversion results of part Marmousi model under complex-frequency-combination-scheme 2+different frequency groups (a)The intermediate inversion result in complex-frequency inversion stage;(b)Frequency group 1; (c)Frequency group 2;(d)Frequency group 3;(e)Frequency group 4. |
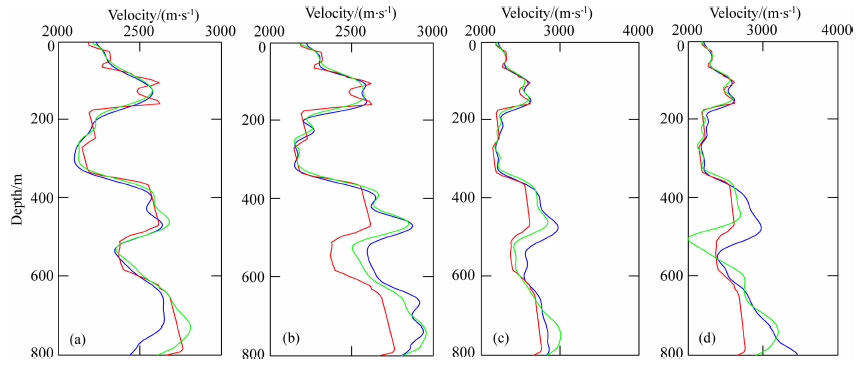 |
图 13 距离为1250 m处,图 11和图 12中各反演结果与真实速度对比 (a)频率组1;(b)频率组2;(c)频率组3;(d)频率组4. Fig. 13 Comparison of inverted velocity in Fig. 11,Fig. 12 and true velocity at a distance of 2500 m (a)Frequency group 1;(b)Frequency group 2;(c)Frequency group 3;(d)Frequency group 4. |
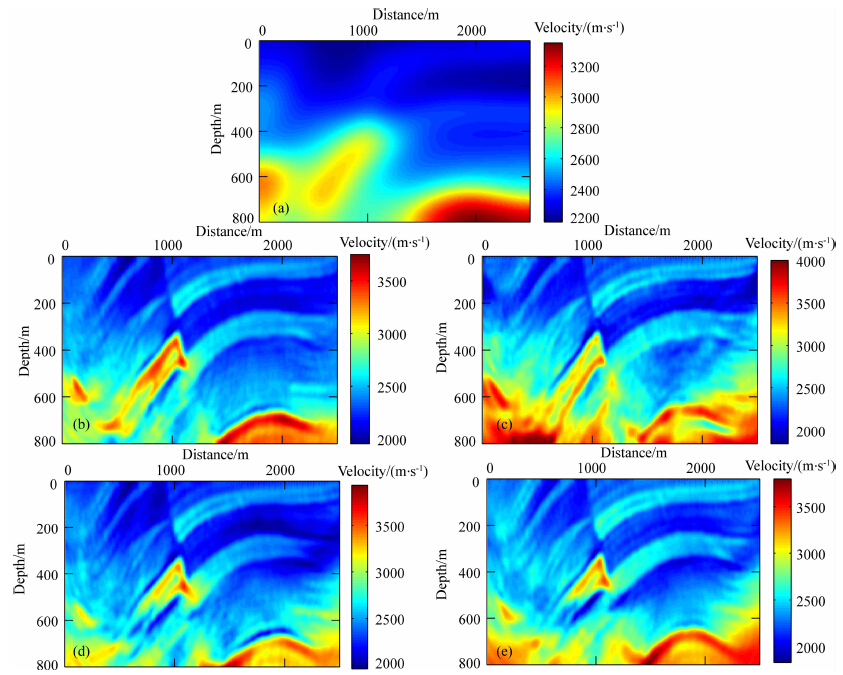 |
图 14 频率组4频率域反演结果与复频率+频率反演结果对比 (a)光滑模型;(b)光滑模型为初始模型时频率组4的频率域反演结果;(c)线性增加模型为初始模型时频率组4的频率域反演结果;(d)线性 增加模型为初始模型时复频率组合方式1+频率组4的反演结果;(e)线性增加模型为初始模型时复频率组合方式2+频率组4的反演结果. Fig. 14 Comparison of frequency domain inversion results and complex-frequency-plus-frequency inversion results of frequency group 4 (a)Smoothed velocity model;(b)Frequency domain inversion result of frequency group 4 with smoothed velocity model as initial mode;(c)Frequency domain inversion result of frequency group 4 with linearly increasing velocity model as initial model;(d)Inversion result of complex-frequency-combination-scheme 1+frequency group 4 with linearly increasing velocity model as initial model;(e)inversion result of complex-frequency-combination-scheme 2+frequency group 4 with linearly increasing velocity model as initial model. |
本文推导了复频率的组成,介绍了复频率反演理论,对比研究了不同频率组直接进行频率域反演和进行复频率+频率反演的效果.首先用线性增加模型作为初始模型对比存在和不存在低频时频率域反演的效果,可看出有低频数据存在时反演对初始模型的依赖性相对较小,即使初始模型不准确,也能反演出比较满意的结果,而把低频数据去掉后反演效果就会明显变差,甚至不收敛.再比较结合复频率之后各个频率组的反演效果,从简单模型和复杂模型的测试中都可以看出这种复频率+频率反演的方式对反演效果有明显改善,对缺乏低频成分的频率组改善效果更加明显.并且比较了复频率的不同组合方式对反演效果的影响,数值实验表明两种组合方式下反演效果相近,因此都可取.
总体来说,复频率+频率域反演不失为实际反演的一种可行办法.本文结果还没有达到非常理想的效果,在未来的工作中将重点研究如何改进复频率 反演,包括复频率中阻尼因子的范围、频率的选择等.
| [1] | Cao S H, Chen J B. 2012. A 17-point scheme and its numerical implementation for high-accuracy modeling of frequency-domain acoustic equation. Chinese J. Geophys. (in Chinese), 55(10): 3440-3449. |
| [2] | Chen J B. 2012. An average-derivative optimal scheme for frequency-domain scalar wave equation. Geophysics, 77(6): T201-T210. |
| [3] | Chen J B. 2013. A generalized optimal 9-point scheme for frequency-domain scalar wave equation. Journal of Applied Geophysics, 92: 1-7. |
| [4] | Jo C H, Shin C, Suh J H. 1996. An optimal nine-point, finite-difference, frequency-space, 2-D scalar wave extrapolator. Geophysics, 61(2): 529-537. |
| [5] | Mallick S, Frazer L N. 1987. Practical aspects of reflectivity modeling. Geophysics, 52(10): 1355-1364. |
| [6] | Operto S, Virieux J, Sourbier. 2007. Documentation of FWT2D program (verison 4.8), Frequecy domain full-waveform modeling/inversion of wide-aperture seismic data for imaging 2D acoustic media: Technical report N 007-SESMICCOPE project. |
| [7] | Pratt R G, Wothington M H. 1990. Inverse theory applied to multi-source cross-hole tomography, Part 1: Acoustic wave equation method. Geophysical Prospecting, 38(3): 287-310. |
| [8] | Pratt R G. 1990a. Frequency-domain elastic wave modeling by finite differences: A tool for cross-hole seismic imaging. Geophysics, 55(5): 626-632. |
| [9] | Pratt R G. 1990b. Inverse theory applied to multi-source cross-hole tomography, Part 2: Elastic wave-equation method. Geophysical Prospecting, 38(3): 311-329. |
| [10] | Shin C, Min D J. 2006. Waveform inversion using a logarithmic wavefield. Geophysics, 71(3): R31-R42. |
| [11] | Shin C, Cha Y H. 2008. Waveform inversion in the Laplace domain. Geophys. J. Int., 173(3): 922-931. |
| [12] | Shin C, Cha Y H. 2009. Waveform inversion in the Laplace-Fourier domain. Geophys. J. Int., 177(3): 1067-1079. |
| [13] | Shin C, Koo N H, Cha Y H, et al. 2010. Sequentially ordered single-frequency 2-D acoustic waveform inversion in the Laplace-Fourier domain. Geophys. J. Int., 181(2): 935-950. |
| [14] | Sirgue L, Pratt R G. 2004. Efficient waveform inversion and imaging: a strategy for selecting temporal frequencies. Geophysics, 69(1): 231-248. |
| [15] | Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation. Geophysics, 49(8): 1259-1266. |
| [16] | 曹书红, 陈景波. 2012. 声波方程频率域高精度正演的17点格式及数值实现. 地球物理学报, 55(10): 3440-3449. |
 2014, Vol. 57
2014, Vol. 57

