2. 中国石油勘探开发研究院, 北京 100083
2. Research Institute of Petroleum Exploration & Development, PetroChina, Beijing 100083, China
高斯束(Gaussian beam)已经被广泛应用于偏移成像中(Hill, 1990,2001;Hale,1992;Gray,2005;Popov et al., 2010;岳玉波,2011),观测波场在频率域被分解成波束并用高斯束描述上行波实现高斯束偏移.高斯波包传播算子(Babich and Ulin, 1981;Ralston,1983;Klimeš,1989a,2004)是一种在时空域描述波束传播的方法,其理论与我们熟知的高斯束(Červený et al., 1982;Popov,1982)类似,不同的是后者在频率域描述波束传播.高斯波包算子的特点是能描述时空域局部波场,适用于起伏地表,但要求传播介质光滑.相应地,高斯波包叠前深度偏移(Gaussian packet pre-stack depth Migration,GPM)有如下特点:应用灵活,可实现面向目标成像,起伏 地表成像,并能自然地提取角度域成像道集(ADCIG). 积分法高斯束成像(Hill, 1990,2001;Hale,1992;Gray,2005;岳玉波,2011)难以确定波传播过程中的振幅及波形变化,而顾及到振幅及波形变化的高斯束偏移(Popov et al., 2010)的计算量非常大,GPM利用互相关成像条件,考虑了波场传播时的振幅和波形变化,同时体现出了高斯波包在时间方向上的局部性.
GPM中,炮点波场的正传和检波点波场的反传均利用高斯波包传播算子实现.炮点波场可利用高斯波包的积分计算(李辉等,2012).计算检波点波场时先对炮道集做Gabor分解(也称为高斯波包分解)(Sondergaard et al., 2007),每个高斯波包框架函数逆时传播的局部波场线性叠加实现完整炮道集的反传,这一点不同于Žáček K(2003,2004,2005)及Bucha(2008)在频率域实现GPM的方法.Žáček K(2003)的高斯波包分解方法是相干态变换(coherent-state transform),该方法试图构造完备的Gabor框架函数,由于Gabor框架函数的冗余度高(Sondergaard et al., 2007),Žáček K的方法需要巨大数量的高斯波包函数来描述观测波场.Geng等(2011)忽略了一些不重要的参数,压缩了重构观测波场的高斯波包泛函空间,从而减少框架函数的数目,但其应用于偏移中计算量仍然很大.鉴于上述方法的不足,我们把控制束偏移(Vinje et al., 2008)的思想引入GPM中,通过局部τ-p变换提取出观测波场的时空和方向特征,在Gabor域利用这些特征实现波场的稀疏化表达,大大减少了高斯波包框架函数的数量,提高了高斯波包反传观测波场的效率.由于分解观测数据时引入了波场的τ-p特征,我们称上述波场分解为特征高斯波包(CGP)分解,相应的成像方法为特征高斯波包偏移(CGPM).文中给出了CGP分解的具体策略,通过一个水平层模型详细解释了实现过程,并对比了CGP反传波场与有限差分反传波场.数值实验部分通过对比CGPM与逆时偏移(RTM)的剖面,验证了本文方法的有效性.本文把CGPM定位为偏移速度分析(MVA)的引擎,所以生成共成像点道集是CGPM的主要目的之一.文中给出了CGPM提取ADCIG的过程,展示了CGPM方法产生的ADCIG.此外,我们讨论了CGPM实现面向目标偏移的策略,并分析了相应的模型实验.
本文中理论推导及数值实验在二维常密度标量波的假设下实现,由于三维及弹性波高斯波包的基础理论已经成熟(Červený,1983,Klimeš,1989a),相应的CGPM可自然地拓展得到. 2 高斯波包传播算子
高斯波包传播算子在射线中心坐标系中进行构造.射线中心坐标系(s,q)(Červený et al., 1982;Popov,1982)是沿射线路径变化的局部正交坐标 系,如图 1所示,坐标s大小为射线长度,方向与局部射线 相切,q与局部射线垂直,沿射线路径与s坐标始终组成右手(或左手)系,坐标值q是点到射线的距离.
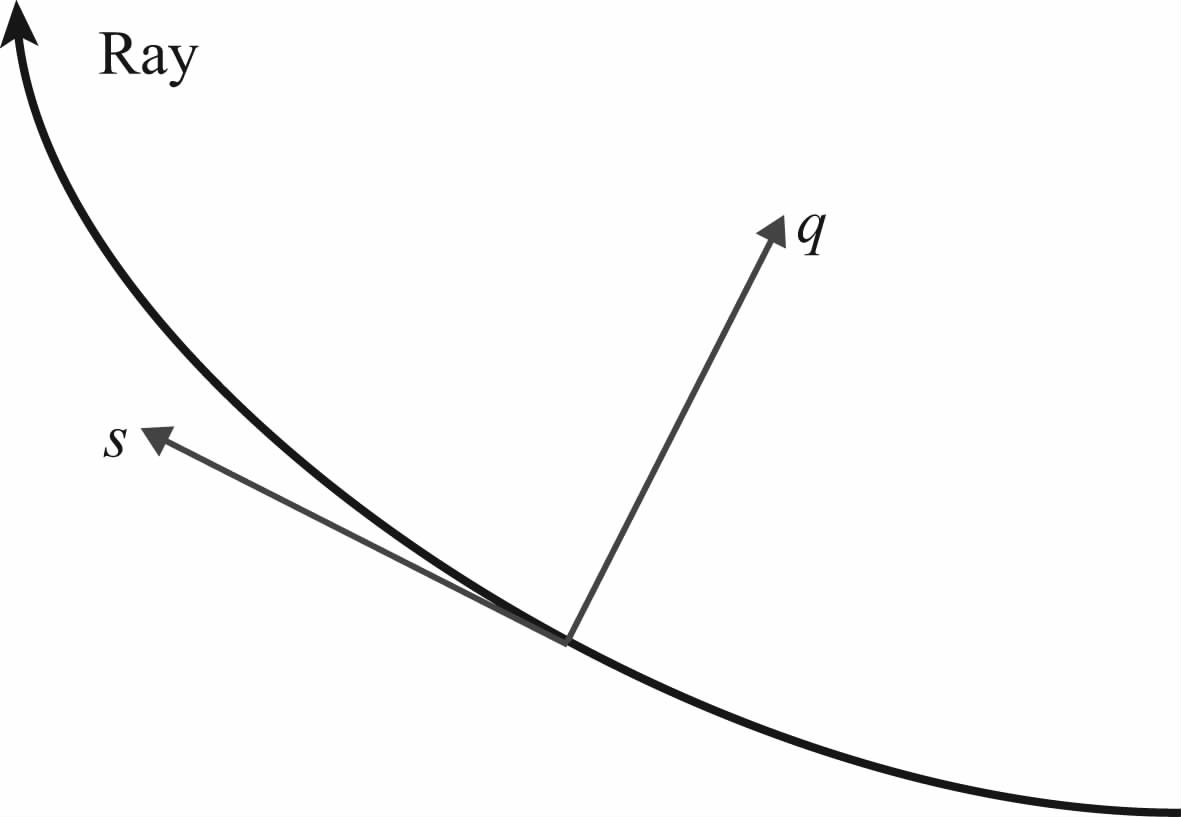 | 图 1 射线中心坐标系 Fig. 1 The ray centered coordinate system |
高斯波包传播算子是波动方程的高频渐进解,高斯波包空间波场可以写成零阶WKBJ近似的形式(Ralston,1983;Klimeš,1989a,2004)
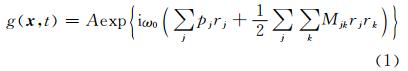
本文中运动学射线追踪通过求解经典汉密尔顿(Hamilton)力学系统下的射线方程(Červený et al., 1977;Červený,2001)实现
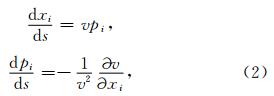
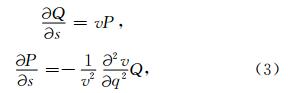

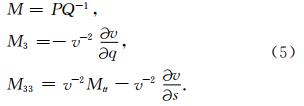
高斯波包振幅的计算公式为(Babich and Ulin, 1981;Klimeš,2004)
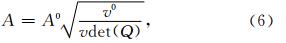
至此可以利用公式(1)计算高斯波包波场.高斯波包反传和正传的方法相同,不同的是运动学及动力学射线追踪的条件,正传已知初始点信息,反传已知终点信息.
图 2展示了高斯波包在一个光滑速度模型中的形态,图 2a为某时刻三条射线对应的高斯波包,红、绿、蓝三条曲线为射线路径.图 2b是这三个高斯波包沿射线路径方向的一维波形,三条曲线所示的一维波场分别对应图 2a中相应颜色的射线.分析高斯波包表达式(1)及图 2可知,振幅随距离中心点的大小呈高斯型衰减,这也是高斯波包名称的来由.
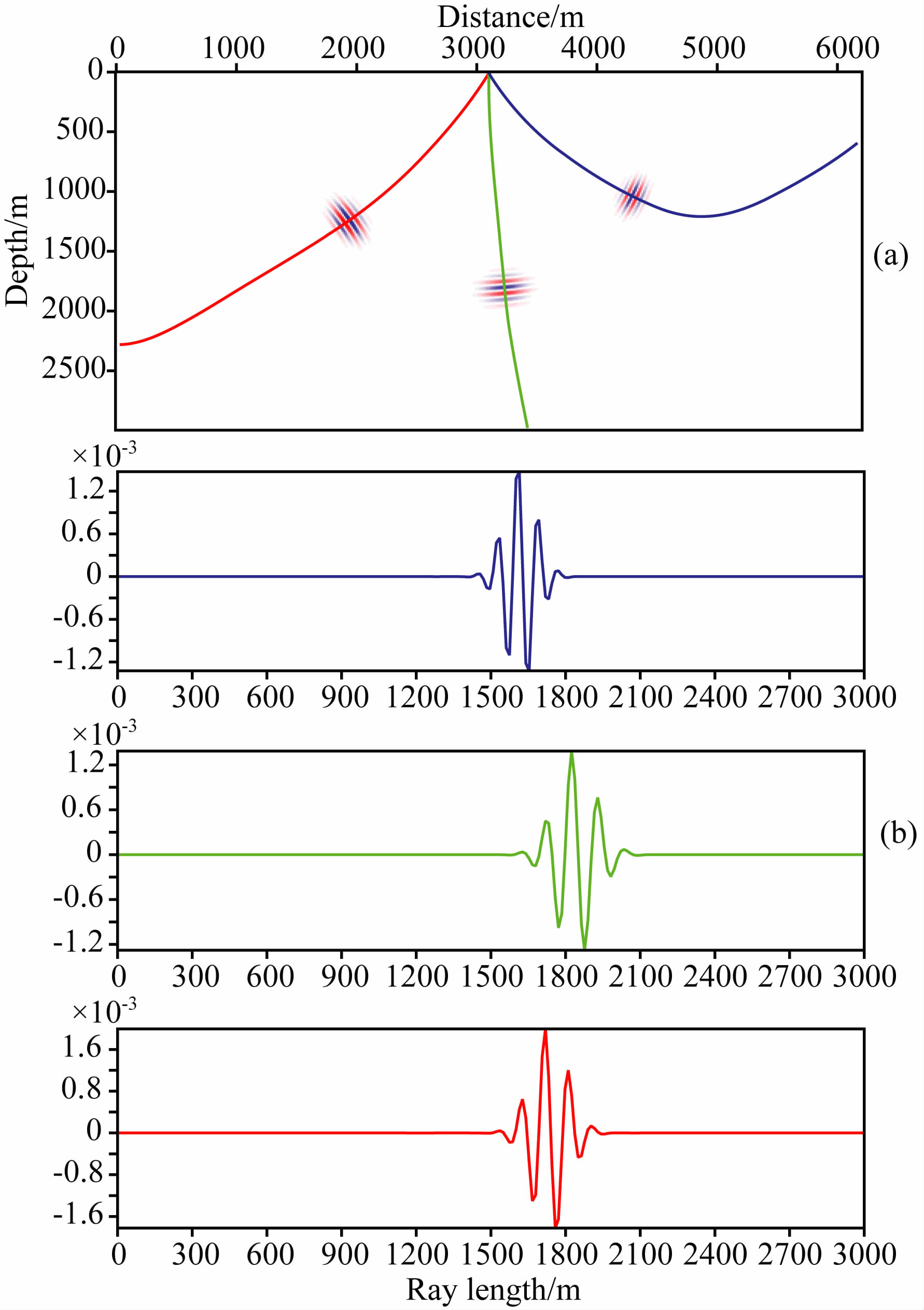 | 图 2(a)三条射线对应的高斯波包空间分布,彩色曲线为 射线追踪的射线路径;(b)高斯波包沿射线路径的一维空 间分布,红、绿、蓝色曲线对应图 2a中相应颜色的射线 Fig. 2(a)The patterns of 3 Gaussian packets correspond with three center rays,the curves are ray paths;(b)The form of 3 Gaussian packets along traced rays which are correspond with the patterns shown in(a) |
本文CGPM使用互相关成像条件(Claerbout,1971)
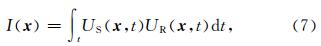
李辉等(2012)证明了不同角度中心射线的高斯波包积分等价于Gabor函数作为震源的点源波场.本文令偏移中正传波场的震源函数为Gabor函数,则正传波场可利用高斯波包的角度积分计算

观测波场的反传播是偏移的主要环节之一,也是本文的着眼点.
炮道集的高斯波包分解是高斯波包反传波场的基础.信号的精确分解需要数量巨大的框架函数,由于观测数据中含有大量对偏移没有贡献的波现象甚至噪声,所以我们不再精确重构完整的观测数据,而是用少数的特征高斯波包(CGP)框架函数描述观测数据的特征成分,以实现观测波场的快速反传(王华忠等,2013).
一个如图 3a所示的上行波波前到达观测面时,在观测点附近可认为是一个局部平面波,图 3b用红、蓝、绿、黑四种颜色示意了四个局部波包,图 3b中所有波包叠加后可得到图 3a中的上行波.每一个局部波包可由若干高斯波包函数描述,则观测波场可利用这些高斯波包函数在Gabor域表达.观测数据的CGP分解思想,实现了观测数据的稀疏描述,减小数据量的同时亦可以用高斯波包实现波场的快速传播.
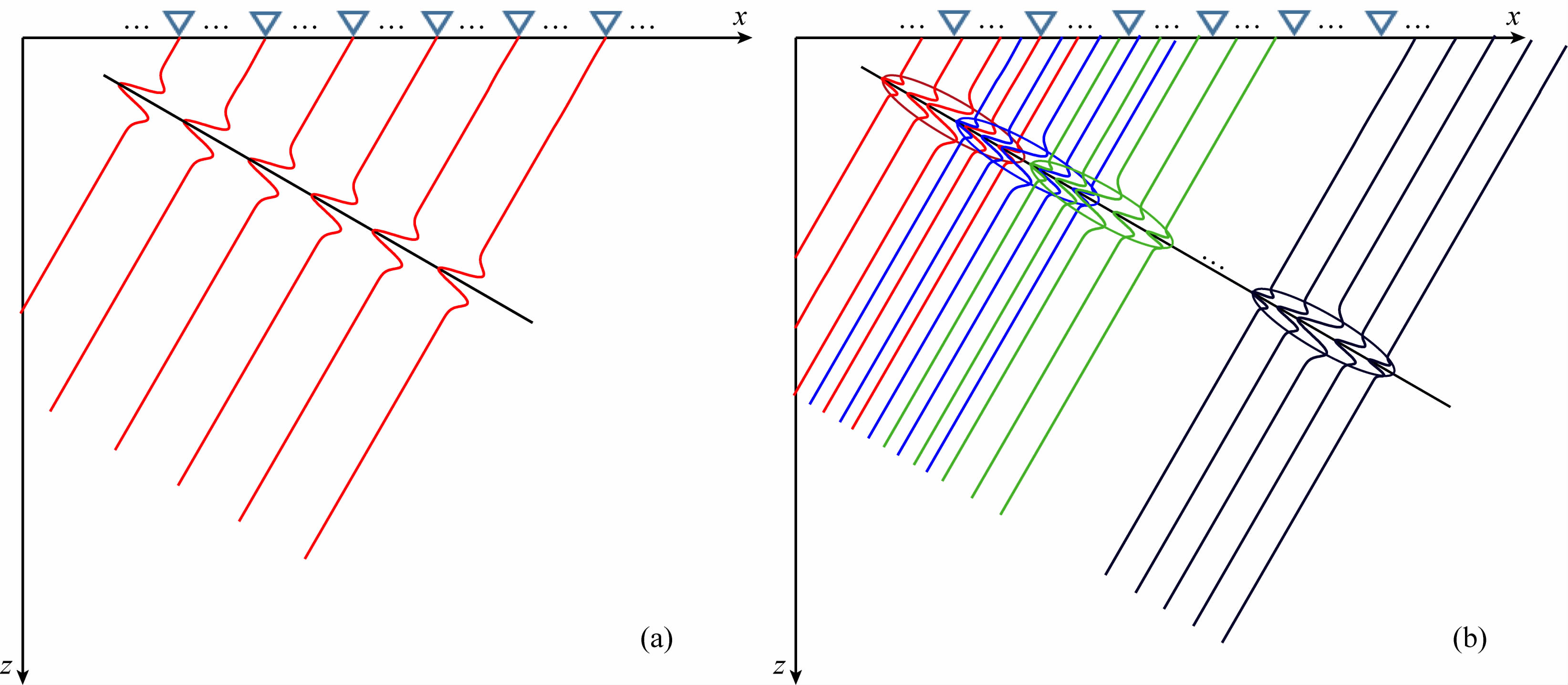 | 图 3(a)上行波到达地表附近的形态示意图;(b)一个上行波波前可以由 多个局部波包叠加表达,红、蓝、绿、黑四种颜色示意了四个波包 Fig. 3(a)An up-going wave-front arriving receiver surface;(b)Composition of several wave packets can express the wave-front shown in(a),four wave packets are sketched |
以上述分析为指导思想,CGP分解波场首先寻找有炮道集数据特征的高斯波包函数,选择高斯波包参数的原则是令高斯波包和上行局部波包相似.高斯波包参数主要包括时空域中心点(x0,t0)、慢度向量 p 、主频ω和走时时空方向二阶导数M及Mtt.高斯波包中心点x0为检波点的位置,t0为上行波到达时,上行波到达检波点的方向由 p 的x方向分量px决定,t0和px 可在τ-p谱中拾取得到.走时空间二阶导数M控制高斯波包的宽度,利用高斯束的宽度优化方法(Klime and Psencik, 1989b;Žáček K,2006)计算.令高斯波包的波形与炮道集波形相似可计算ω和Mtt,具体公式为
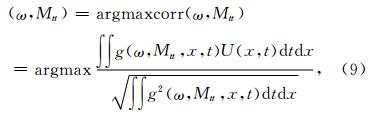
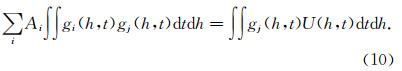
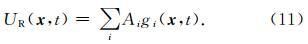
Ⅰ)对炮道集的包络信号做局部τ-p变换,并优化变换后的τ-p谱;
Ⅱ)在优化的τ-p谱中拾取局部平面波的方向及到达时,得到高斯波包在观测面处的传播方向和到达时;
Ⅲ)利用(9)式计算高斯波包参数ω和Mtt;
Ⅳ)利用(10)式计算高斯波包的初始振幅;
Ⅴ)每一个高斯波包独立传播;
Ⅵ)所有高斯波包框架反传的结果以振幅为系数线性叠加得到单炮数据的反传波场.
 | 图 4 单反射界面模型和单炮的炮检点位置 Fig. 4 The single interface model and the locations of source and receivers |
从上述流程中可看出,挑选CGP的关键点是如何提高τ-p谱的分辨率(优化τ-p谱)以及如何挑选出既稀疏又符合物理意义的τ-p特征点.Wang X和Wang H(2014)根据τ-p谱的对称性提出了一种优化策略,我们利用此方法提高τ-p谱的分辨率,以增加拾取的精度.图 5b和5c对比了优化前和优化后的τ-p谱,从中可看出优化后τ-p谱的分辨率远大于原始τ-p谱.在谱中拾取极值点的工作被广泛应用于地震勘探中,如速度分析、偏移及反射层析等.人工拾取可以保证拾取结果稀疏且符合物理意义,但需要大量的人工工作;如何自动拾取符合 物理意义的点一直是一个研究热点(Simpson,1967; Zamorouev,1999; Almarzoug and Ahmed, 2012;刘鹏等,2013),但至今没有能取代人工拾取的方法.本 文实验中我们采取自动加人工的拾取策略,首先检测出τ-p谱中梯度为零的点作为自动拾取结果,之后人工调整拾取点的数量,得到最终的τ-p谱特征点.
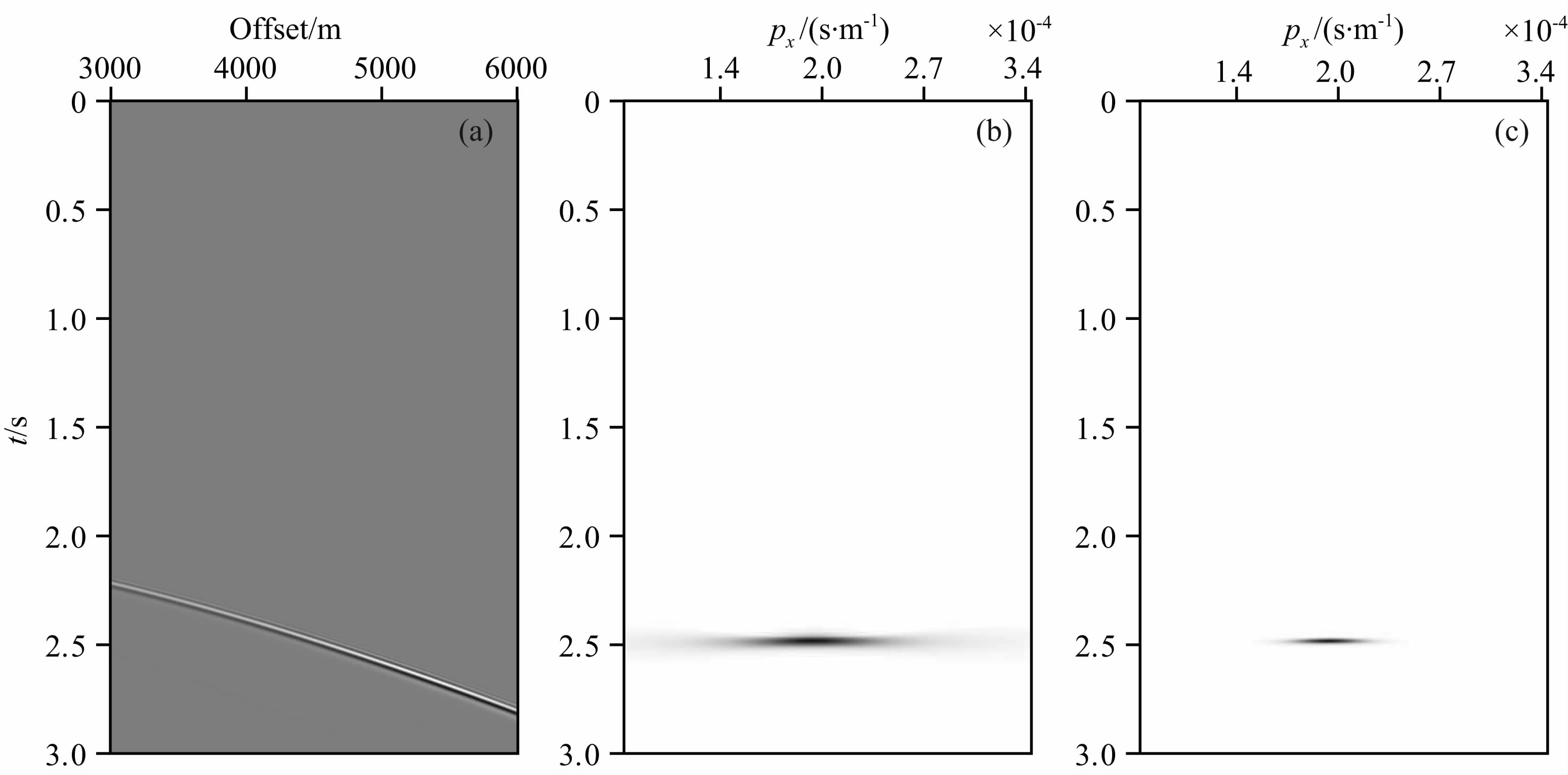 | 图 5(a)切除直达波的单炮道集;(b)炮道集包络信号的τ-p谱;(c)优化后的τ-p特征谱 Fig. 5(a)The single shot gather without direct wave;(b)The τ-p spectrum of shot gather′s envelope;(c)The modified τ-p spectrum |
下面通过一个单层模型测试CGP反传单炮地震数据的方法.速度模型及炮检点位置如图 4所示,炮点位于2000 m处,301个观测点等间隔地从5000 m 排列至8000 m.切除直达波的单炮道集如图 5a所示,图 5b和5c是偏移距4000 m处局部τ-p特征谱和优化谱,从中选出的极值点位置(p0,t0)即为局部平面波的到达时和慢度水平分量,取以该点为中心的若干坐标作为高斯波包到达观测面的时刻和慢度水平分量.计算出参数ω、Mtt和振幅后可确定高斯波包的初始值.图 6中位于6000 m处的一个高斯波包在光滑模型中从2.1 s反传至0.6 s,所有高斯波包叠加得到完整的反传波场.图 7对比了利用CGP和有限差分(FD)计算的单炮反传波场快照,从中可看出两者的波前及波形特征都非常相似,此外,高斯波包反传出的波场没有出现FD由于观测孔径有限而引入的假象.
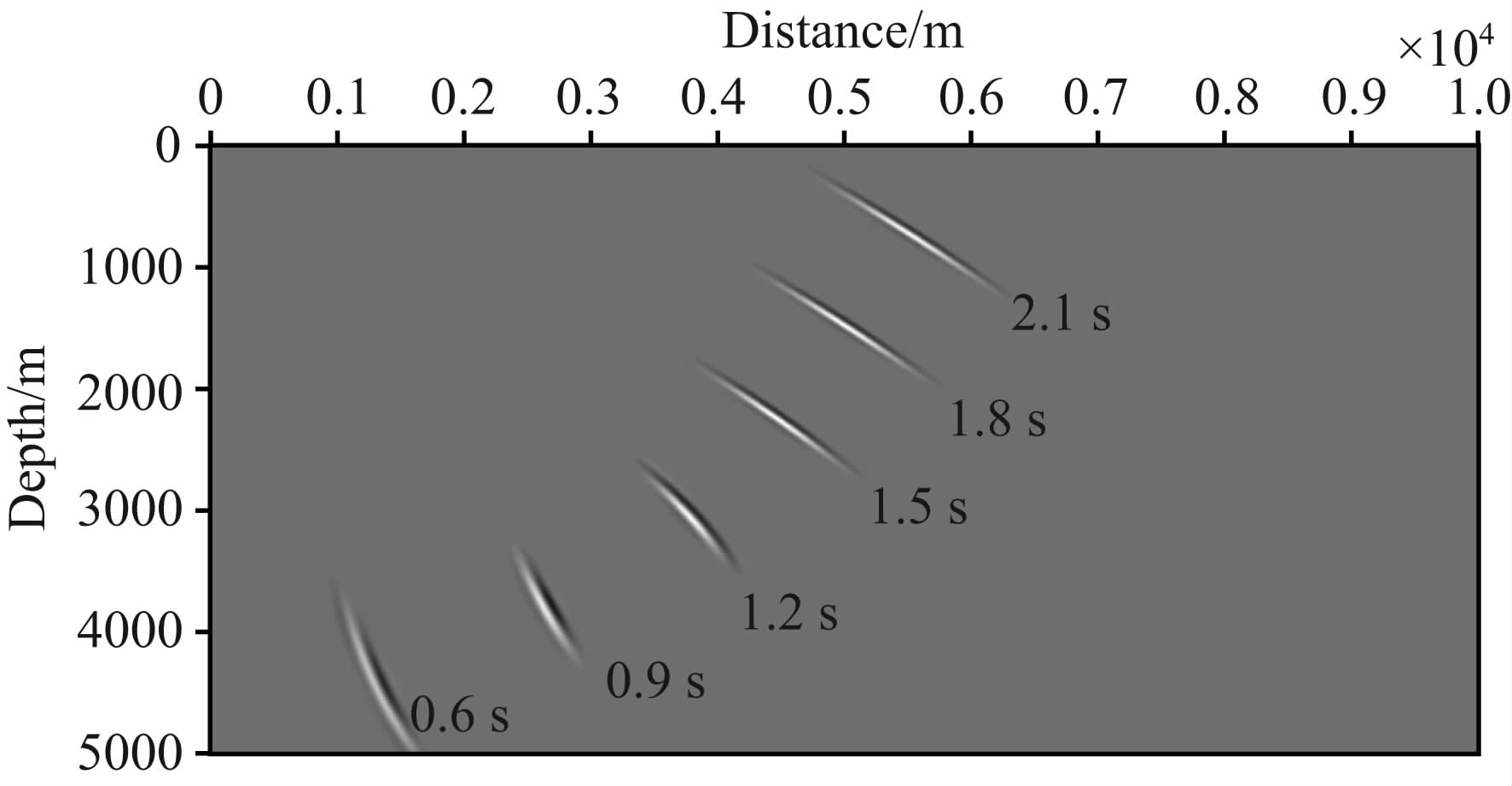 | 图 6 单个高斯波包不同时刻的反传波场快照 Fig. 6 The snapshots of single backward Gaussian packet |
 | 图 7 单炮数据不同时刻的反传波场快照:(a)高斯波包计算结果,(b)有限差分计算结果 Fig. 7 The snapshots of backward wave-fields calculated with Gaussian packet(a) and FD(b) |
CGPM应用在偏移速度分析(MVA)中,为MVA提供所需数据——共成像点道集(CIG).相对于偏移距域成像道集(ODCIG),角度域成像道集(ADCIG)中的MVA更有优势.首先,ADCIG中层析MVA的正演是初值射线追踪而ODCIG中需要费时且不稳定的两点射线追踪,更重要的是ADCIG可以更清楚地反映出不同路径的波对应的成像结果,而ODCIG中可能出现多路径等问题(Stolk and Symes, 2004).CGPM提取ADCIG时,把炮点波场(8)及检波点波场(11)代入成像公式(7),有
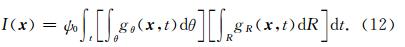
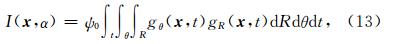

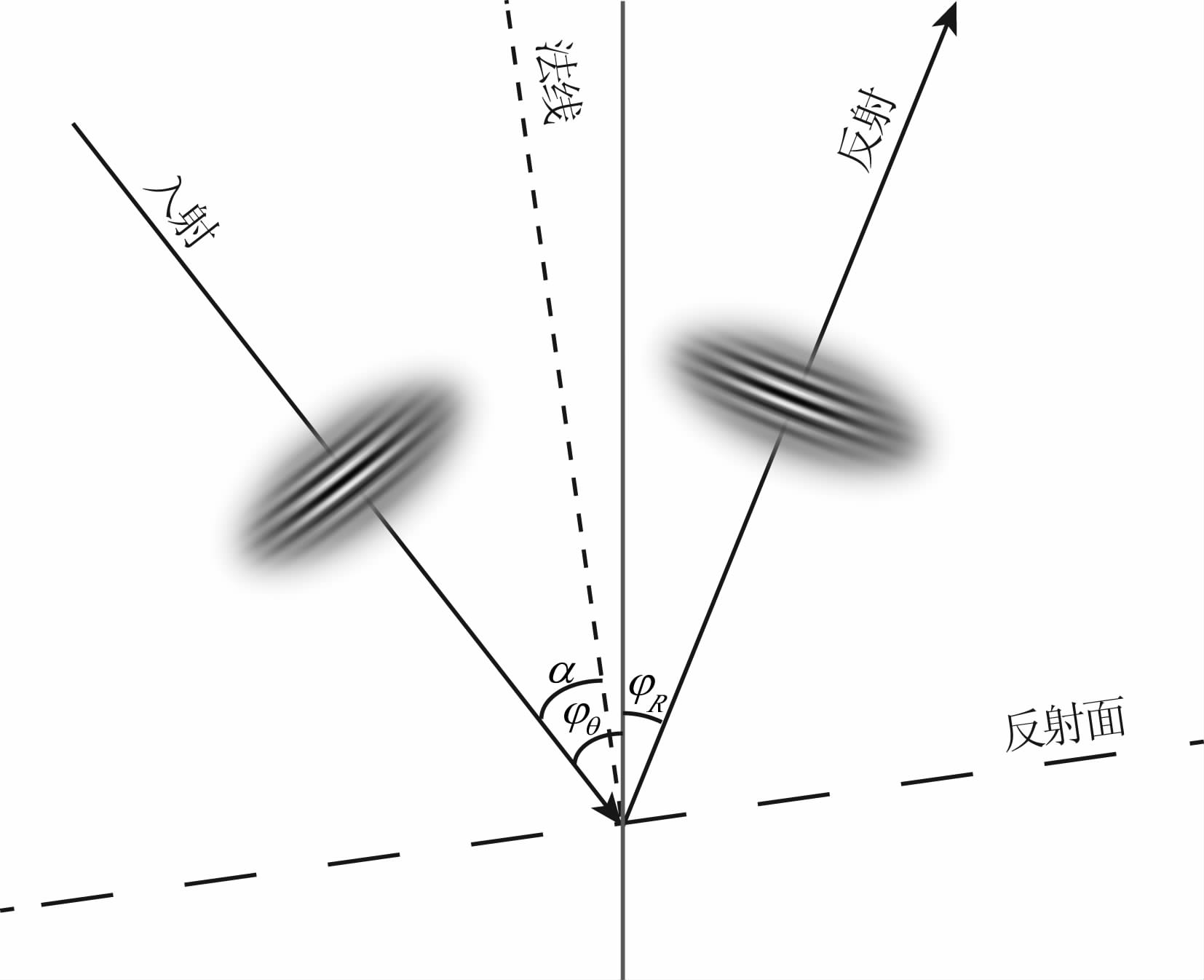 | 图 8 CGPM成像时角度计算示意图 Fig. 8 The schematic diagram for calculating reflecting angle in CGPM |
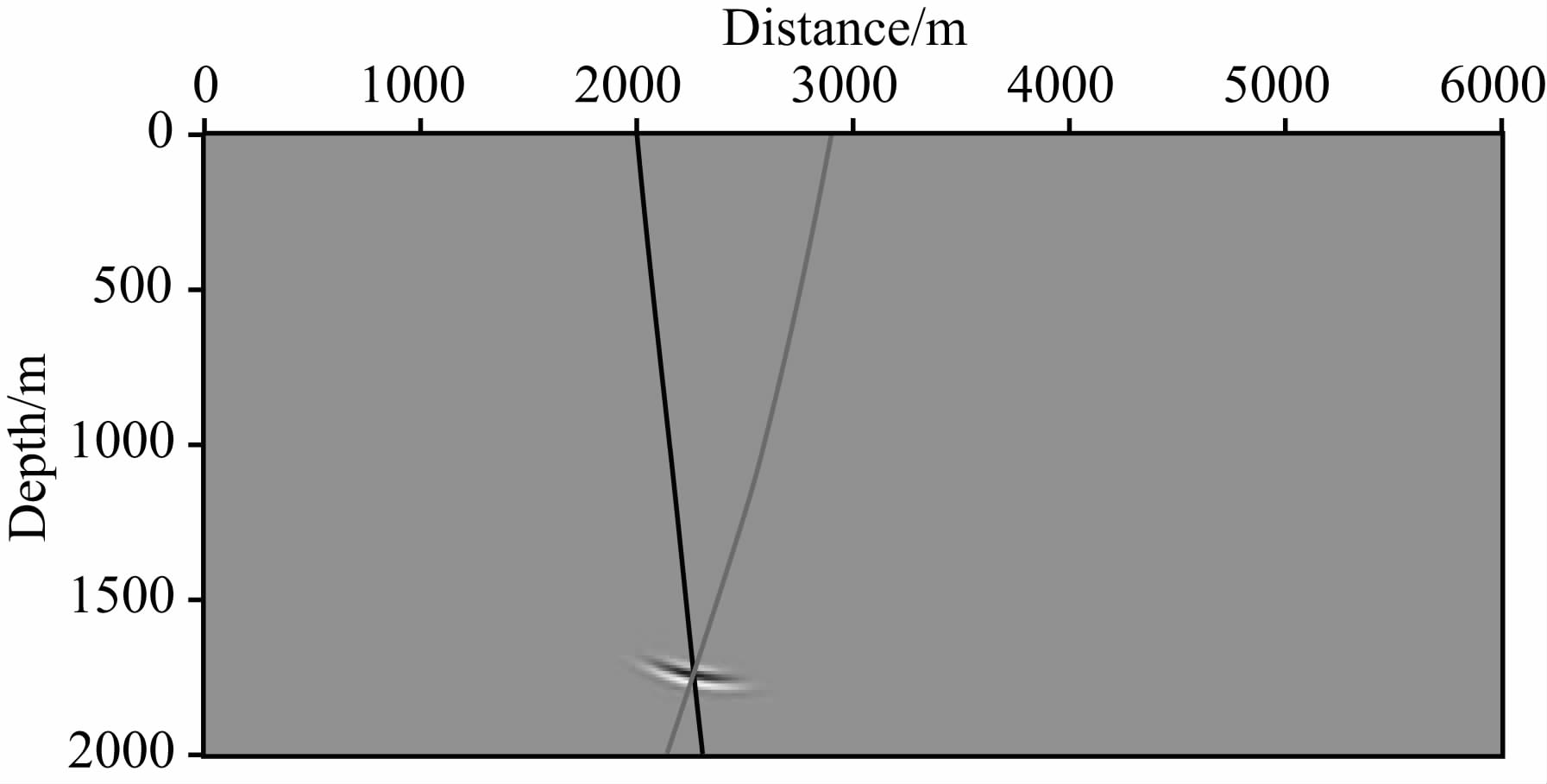 | 图 9 一对正、反传高斯波包的成像结果,深色和浅色曲线分别是正、反传高斯波包的中心射线 Fig. 9 The image migrated with a pair of Gaussian packets,the dark and tint curves are the centered rays of forward and backward Gaussian packets respectively |
实际应用中,我们可能只对部分构造感兴趣,此时可针对区域或局部构造体进行偏移,分别称之为目标区域偏移和目标体偏移,统称为面向目标偏移.面向目标偏移的一个实用之处是降低MVA流程中的偏移时间,面向目标MVA与面向目标成像联合应用,可显著提高MVA的效率.本文成像方法受益于高斯波包时空域局部化的特点,易于实现面向目标偏移,这也是CGPM的优势之一.
高斯波包描述了局部相空间的波场传播,计算波传播(包括正传和反传)时可以自然地考察高斯波包与指定区域的空间关系,目标区域成像时仅仅令经过目标区域的正传与反传高斯波包两两成像即可.图 10示意了两个射线对应的四个高斯波包的空间位置,图 10中黑色椭圆表示目标区域,深色曲线(左)是高斯波包g1(t1)和g1(t2)的中心射线,浅色曲线(右)是高斯波包g2(t3)和g2(t4)的中心射线,高斯波包g1(t1)位于目标区域内,高斯波包g1(t2)对应的中心射线虽然经过目标区域,但在t2时刻高斯波包g1(t2)不在目标区域内,g2(t3)和g2(t4)对应的射线距离目标区域较远,射线上的高斯波包均不经过目标区域.
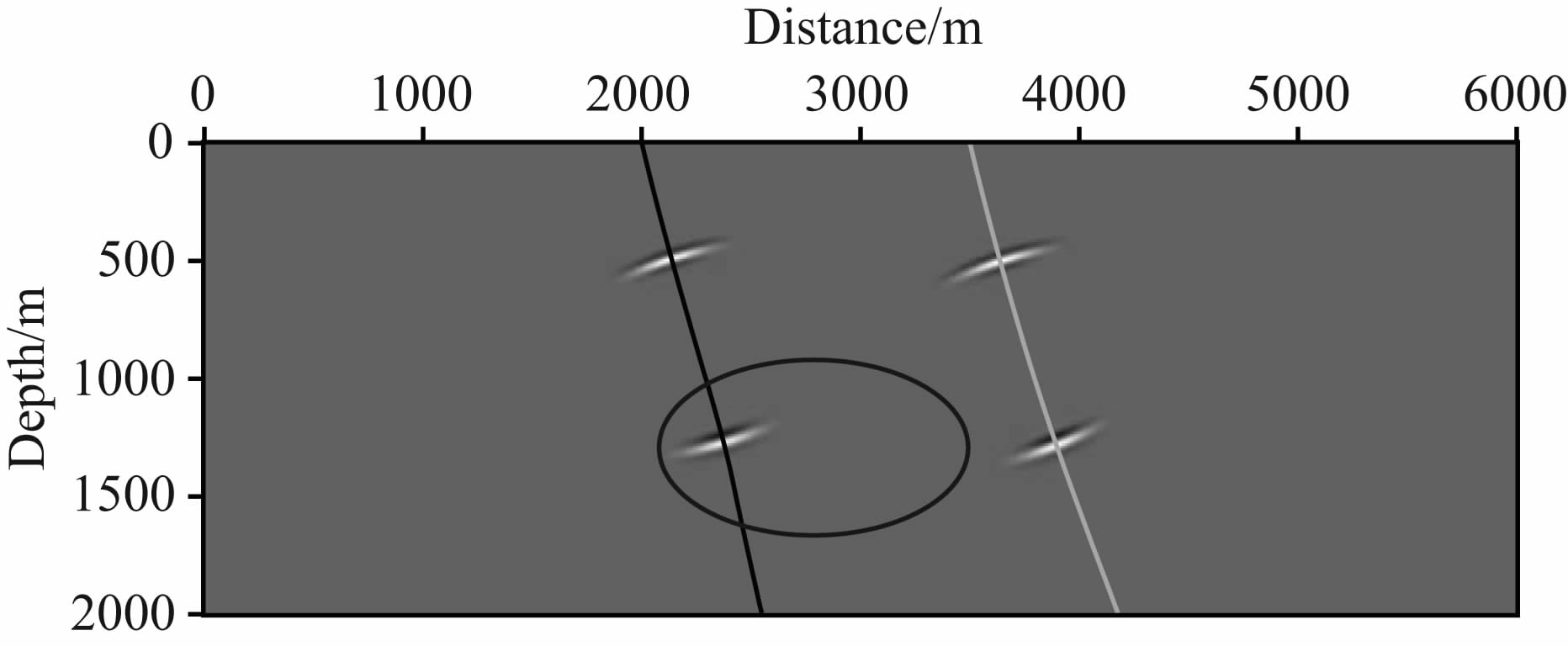 | 图 10 高斯波包、射线与目标区域几何关系示意图 Fig. 10 The schematic relationship of Gaussian packets,rays, and the target zone |
目标体偏移应用于MVA时,每次更新速度模型后均需重新成像.首先在成像剖面上识别出目标体区域,之后做一次完整的CGPM,在此过程中记录对目标体区域有贡献的反传高斯波包并计算出地表处相应的特征高斯波包,这样就在Gabor域挑选出了描述目标构造体反射(或散射,下同)的特征高斯波包.在目标体偏移中,只反传挑选出的特征高斯波包即可. 4 数值实验
我们利用图 11a所示的理论模型检验CGPM.模型及观测系统参数如表 1所示.偏移速度场在理论模型的基础上稍做光滑,如图 11b所示.
 | 图 11 理论模型速度场(a)和用于偏移的光滑速度场(b) Fig. 11 The velocity model(a) and the smoothed one for migration(b) |
根据第3节中CGPM的方法描述,我们设计了如下数值实现过程.
|
|
表 1 模型和观测系统参数 Table 1 The parameters of model and geometry |
Ⅰ对共炮道集的包络信号做局部τ-p变换,并优化变换结果;
Ⅱ利用半自动策略,在优化后的τ-p谱中分选出局部平面波的方向及到达时;
Ⅲ对每个特征点,计算参数M33和ω,对参数做平滑及野值剔除处理;
Ⅳ计算高斯波包在观测面上的振幅;
Ⅴ计算不同起射角度的高斯波包正传波场;
Ⅵ计算反传高斯波包;
Ⅶ所有正传和反传高斯波包两两相关成像,同时计算反射角,得到ADCIG和成像剖面.
CGPM应用在MVA中时速度更新之后均需重新偏移,而上述流程中步骤Ⅰ—Ⅳ只需执行一次,之后每次偏移时仅实现Ⅴ—Ⅶ即可.
CGPM成像剖面如图 12a所示,图 12b是逆时偏移(RTM)成像剖面,CGPM和RTM的成像结果均没有任何修饰.通过对比可看出CGPM剖面和RTM剖面基本相同,没有满覆盖部分CGPM的像甚至优于RTM,因为有限差分反传波场时的精度受制于观测孔径.由于高斯波包描述了零阶WKBJ近似下波传播的所有特征,如波前扩散和透射效应引起的振幅、子波相位变化等,所以CGPM偏移剖面中的子波也和RTM相当,两种剖面的抽道对比图 12c和12d证明了这一点.
把CGPM产生的ADCIG每10个CDP显示一个,并按CDP号排列在图 13a中.图 13b和13c展示了x坐标为2100 m和3000 m的两个ADCIG,ADCIG在正确速度场中同相轴水平.图 13b和13c 中局部放大以波形显示为图 13d和13e,可见同一反射层子波相位随角度连续变化,这点在MVA中非常重要,因为MVA中利用不同角度成像深度的差异来更新速度,ADCIG中成像深度自动拾取利用的信息即为同一反射层相邻角度的子波相位一致.
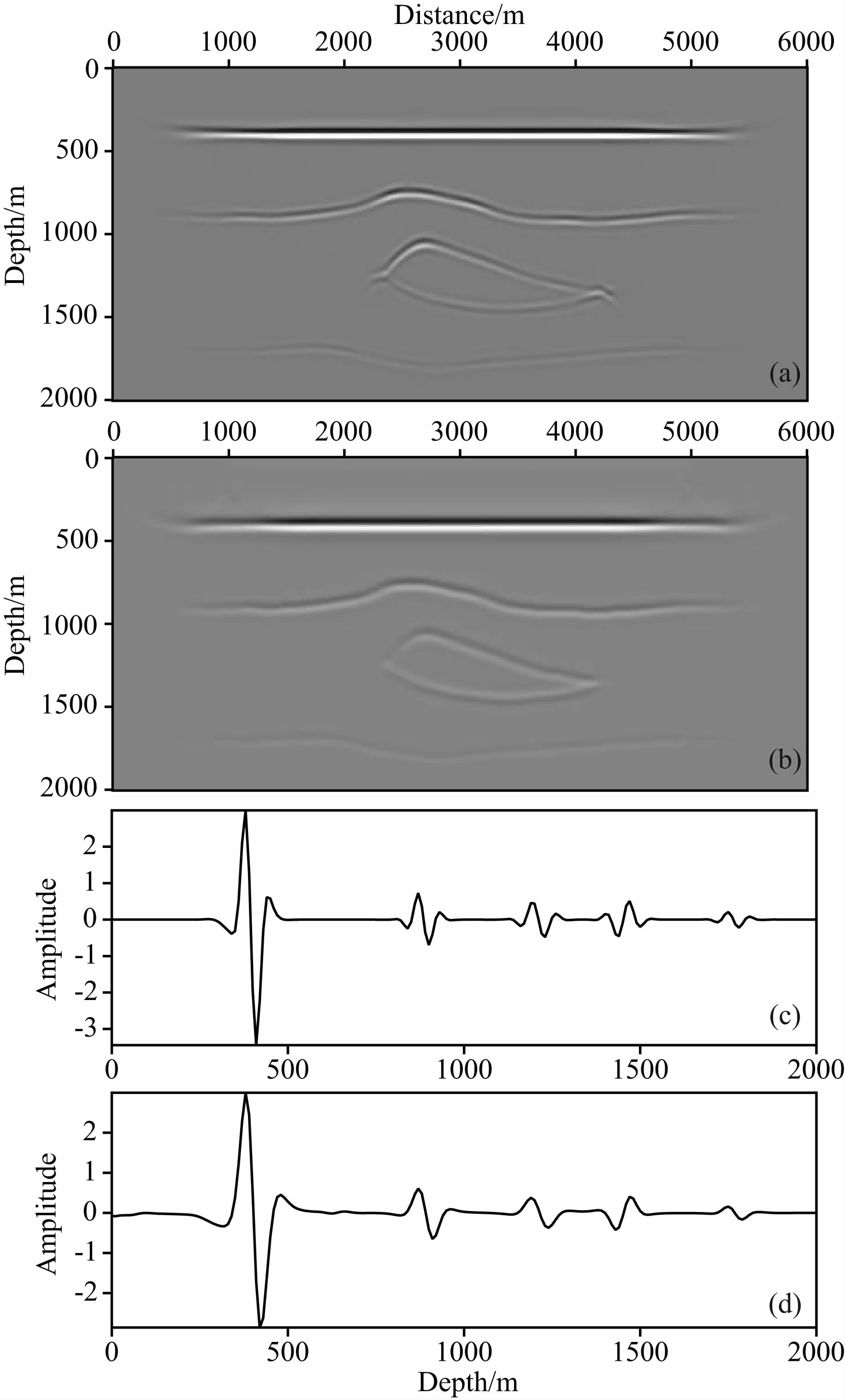 | 图 12 CGPM成像剖面(a)和RTM成像剖面(b),(a)和(b)中横向位置3400 m处抽出一道,以波形显示为(c)和(d) Fig. 12 The images migrated with CGPM(a) and RTM(b),two traces extracted from(a) and (b)that located at x=3400 m form as(c) and (d) |
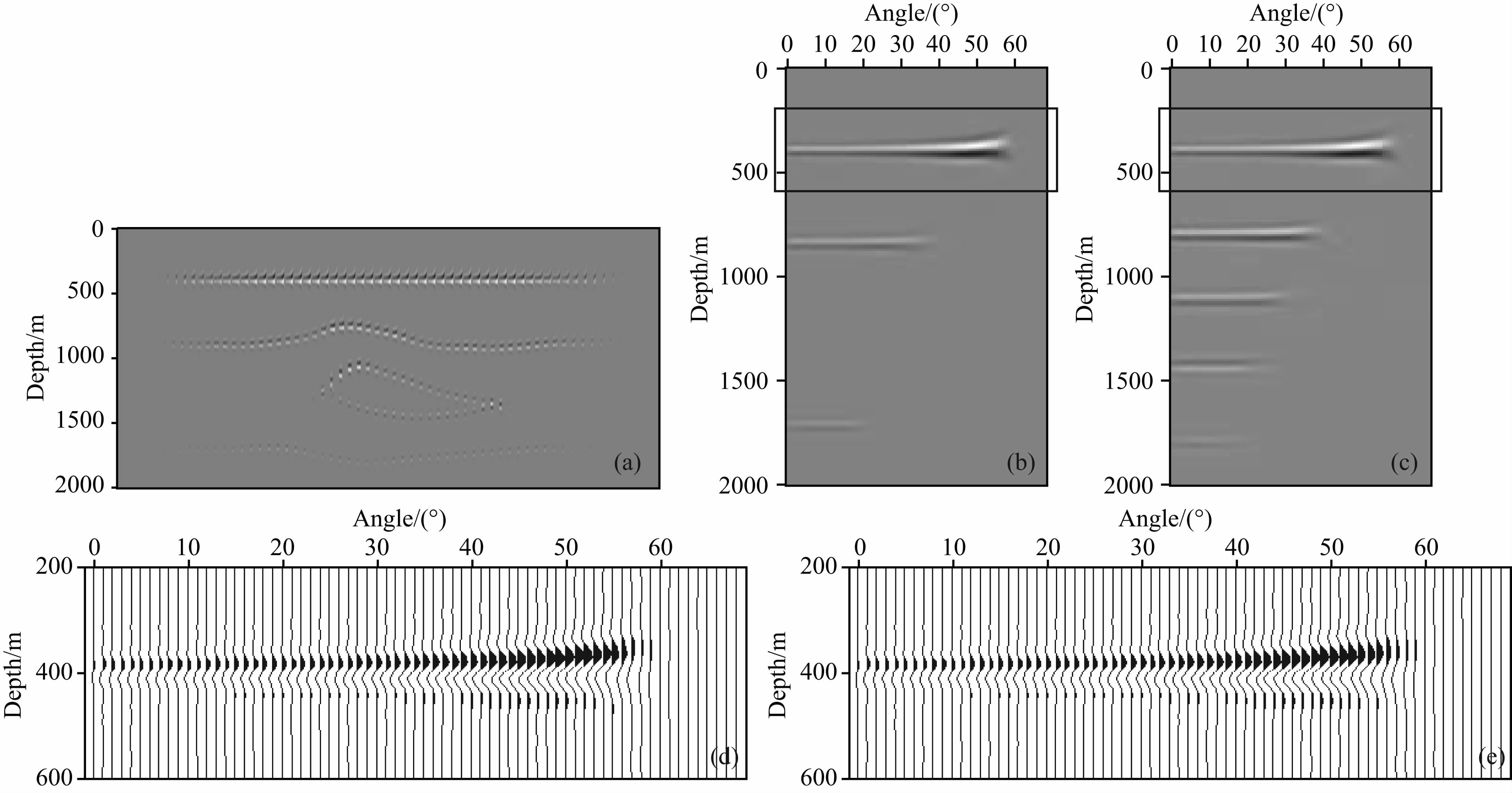 | 图 13 ADCIG按CDP号排列(a),水平位置2100 m和3000 m处的ADCIG(b) 和(c),(b)和(c)中标记的局部区域放大以波形显示为(d)和(e) Fig. 13 The ADCIGs arranged with CDP numbers(a),the ADCIGs of traces that x coordinates equal 2100 m(b) and 3000 m(c),the zoomed region in(b) and (c)displayed with wiggle form as(d) and (e) |
针对目标区域进行叠前深度偏移时,4.1节偏移步骤Ⅴ和Ⅵ中只保留经过目标区域的高斯波包,其他不变,目标区域偏移流程如下:
……
Ⅴ计算不同起射角度的高斯波包正传波场,判断高斯波包是否在目标区域内,是则应用于成像,否则计算上一时刻的高斯波包;
Ⅵ计算反传高斯波包,判断高斯波包是否在目标区域内,是则应用于成像,否则计算上一时刻的反传高斯波包;
……
图 14a是对图 11a中模型进行目标区域成像的剖面,目标区域是图中曲线示意的闭合区域.目标区域成像计算的ADCIG只有目标范围内的部分,图 14b把ADCIG按照CDP号排列显示,图 14c是横向位置在3000 m处的一个ADCIG.
3.4节中已经详细描述了挑选目标体特征高斯波包的策略,此策略取代4.1节所示偏移步骤的第Ⅱ步.并在第Ⅵ步反传时判断高斯波包空间位置与目标体的关系再次筛选反传高斯波包,当其位于目标体指定范围内时方与正传高斯波包成像.目标体CGPM的流程修改如下:
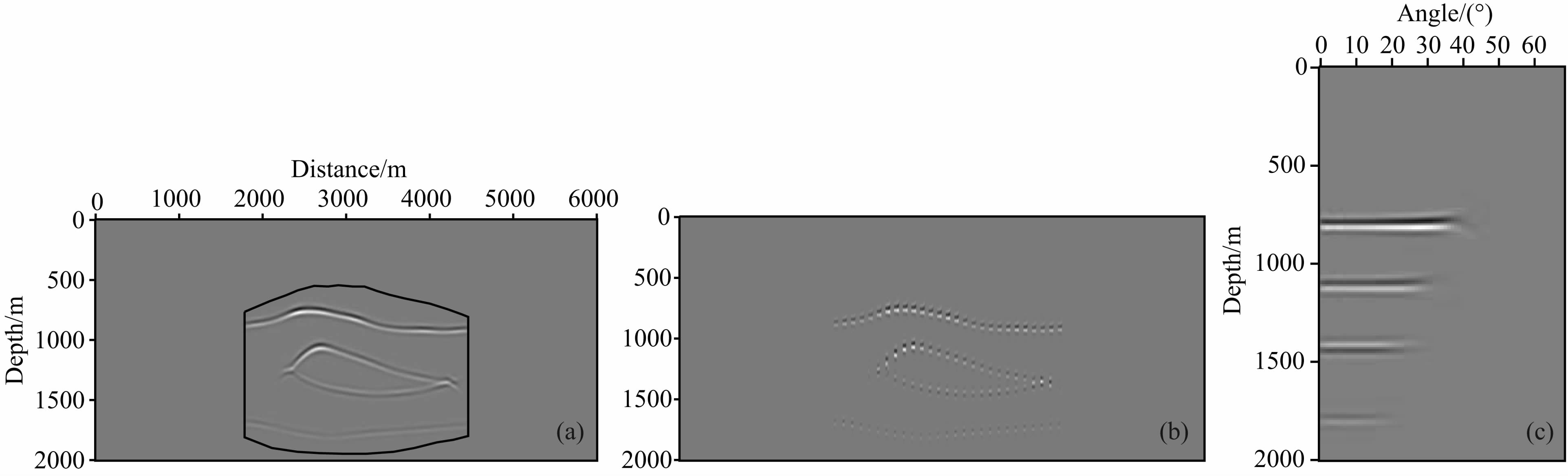 | 图 14 目标区域成像剖面(a),曲线所示的闭合区域是目标区域,ADCIG的排列显示(b),横向位置3000 m处的ADCIG(c) .14 The image of target zone migrated with target-zone-CGPM(a),the closed region with black curve is the target zone,the ADCIGs of different CDPs(b), and the ADCIG located at x=3000m(c) |
II挑选对目标体有贡献的特征高斯波包;
……
VI计算反传高斯波包.判断反传高斯波包与目 标体空间的距离,小于一定阈值则成像,否则不成像;
……
图 15是图 11a模型中盐丘目标体的成像剖面.图 15b是不同CDP点的ADCIG排列显示,图 15c为横向位置3000 m处的一个ADCIG,针对盐丘的目标体成像只对盐丘边界做了刻画.在层析MVA的实际应用中,若只有目标构造体之下的部分模型需要更新,如盐丘下方,则可以用盐丘的下界面约束反演过程,使得反演时只更新盐丘之下的模型,目标体成像为获取目标体界面(如解释盐丘边界)提供了一个简洁的剖面,同时可以提高偏移效率.
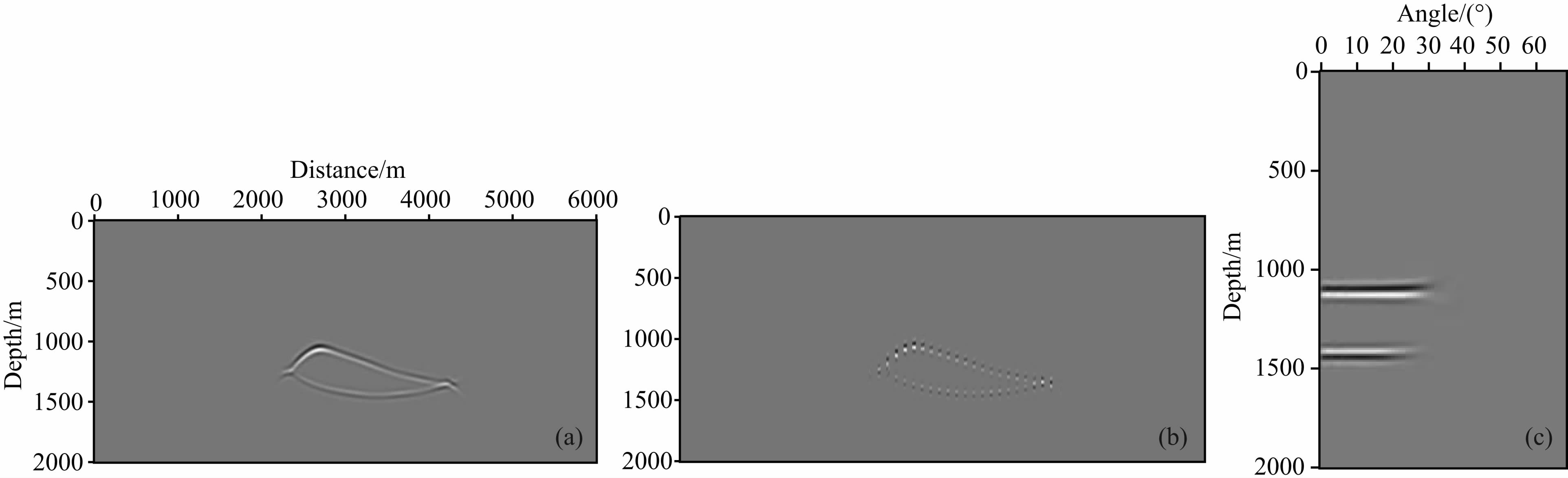 | 图 15 针对盐丘的目标体成像剖面(a),不同CDP的ADCIG(b),横向位置为3000 m处的ADCIG(c) Fig. 15 The salt image migrated with target-struct-CGPM(a),the ADCIGs of different CDPs(b), and the ADCIG located at x=3000 m(c) |
本文通过局部τ-p变换提取出上行波到达观测点时的方向和到达时特征,据此特征在Gabor变换域选择高斯波包函数描述观测点附近的局部平面波,称之为观测数据的特征高斯波包(CGP)分解.选取特征高斯波包时,函数的所有参数均定量计算,使得高斯波包函数尽可能精确地描述观测数据.以CGP为初始条件,利用高斯波包传播算子模拟出所有高斯波包框架函数表达的局部平面波反传波场,最终合成了单炮数据的反传波场,即CGP反传.CGP分解的框架函数数量相对常规高斯波包分解大大减少,从而大大提高了CGP反传的效率.Gabor点震源产生的正传波场可利用高斯波包的角度积分模拟,采用互相关成像条件即可实现特征高斯波包偏移(CGPM).
CGPM过程中根据高斯波包中心射线提供的方向信息,容易计算出高斯波包两两成像的反射角,据此输出ADCIG.ADCIG是偏移速度分析(MVA)的基础数据,这也是本文方法的定位——为MVA提供高效的偏移引擎.利用高斯波包的时空域局部化特点,能方便地实现面向目标CGPM,这也是本文方法的优势之一.
我们设计了一个CGPM的工作流程,并以此为基础设计了面向目标的CGPM流程.文中给出了理论模型的数值实验,常规CGPM和面向目标CGPM的测试结果证明了方法是有效可行的.
CGPM的难点是如何从炮道集的τ-p特征谱中提取稀疏的、有物理意义的特征数据,人工拾取特征谱需要巨大的工作量,自动拾取又难以保证特征数据稀疏且有物理意义.本文使用的方法是自动识别特征数据,再通过人工调整得到最终的结果.但这并不足以保证上述特征数据的两个特点——稀疏性与物理意义,所以特征数据的拾取策略仍需继续研究.
致谢 感谢中国石化集团公司科技部、中国石化石油物探技术研究院(南京)及中国石油勘探开发研究院对WPI研究组及本项研究的支持.| [1] | Almarzoug A M, Ahmed F Y. 2012. Automatic seismic velocity picking. 82nd Annual International Meeting, SEG, Expanded Abstracts: 1-5. |
| [2] | Babich V M, Ulin V V. 1981. Complex space-time ray method and "quasiphotons". Journal of Soviet Mathematics, 24(3): 269-273. |
| [3] | Bucha V. 2008. Gaussian packet prestack depth migration. Part 2: Optimized Gaussian packets. SW3D report 18, Charles University: 129-138. |
| [4] | Červený V, Vaněk R J. 1976. Ray amplitudes in a three-dimensional inhomogeneous medium. Studia Geophysica et Geodaetica, 20(4): 401-404. |
| [5] | Červený V, Molotkov I A, Molotkov I A, et al. 1977. Ray Method in Seismology. Praha: Univerzita Karlova. |
| [6] | Červený V, Popov M M, Psencik I. 1982. Computation of wave fields in inhomogeneous media-Gaussian beam approach. Geophysical Journal of the Royal Astronomical Society, 70(1): 109-128. |
| [7] | Červený V. 1983. Synthetic body wave seismograms for laterally varying layered structures by the Gaussian beam method. Geophysical Journal International, 73(2): 389-426. |
| [8] | Červený V. 2001. Seismic Ray Theory. Cambridge: Cambridge University Press. |
| [9] | Claerbout J F. 1971. Toward a unified theory of reflector mapping. Geophysics, 36(3): 467-481. |
| [10] | Geng Y, Wu R S, Gao J. 2011. Efficient Gaussian packets representation and seismic imaging. 81st Annual International Meeting, SEG, Expanded Abstracts: 3398-3403. |
| [11] | Gray S H. 2005. Gaussian beam migration of common-shot records. Geophysics, 70(4): S71-S77. |
| [12] | Hale D. 1992. Migration by the Kirchhoff, slant stack, and Gaussian beam methods. CWD-121, Center for Wave Phenomena, Colarado School of Mines, Golden, CO. |
| [13] | Hill N R. 1990. Gaussian beam migration. Geophysics, 55(11): 1416-1428. |
| [14] | Hill N R. 2001. Prestack Gaussian beam depth migration. Geophysics, 66(4): 1240-1250. |
| [15] | Klimeš L. 1989a. Gaussian packets in the computation of seismic wavefields. Geophysical Journal International, 99(2): 421-433. |
| [16] | Klimeš L, Psencik I. 1989b. Optimization of the shape of Gaussian beams of a fixed length. Studia Geophysica et Geodaetica, 33(2): 146-163. |
| [17] | Klimeš L. 2004. Gaussian packets in smooth isotropic media. SW3D report 14, Charles University: 43-54. |
| [18] | Klimeš L. 2008. Stochastic wavefield inversion using the sensitivity Gaussian packets. SW3D Structures, Report 18: 71-85. |
| [19] | Li H, Feng B, Wang H Z. 2012. A new wave field modeling method by using Gaussian Packets. Geophysical Prospecting for Petroleum (in Chinese), 51(4): 327-337. |
| [20] | Liu P, Wang Y F, Yang M M, et al. 2013. Seismic data decomposition using sparse Gaussian beams. Chinese Journal of Geophysics (in Chinese), 56(11): 3887-3895. |
| [21] | Popov M M. 1982. A new method of computation of wave fields using Gaussian beams. Wave Motion, 4(1): 85-97. |
| [22] | Popov M M, Semtchenok N M, Popov P M, et al. 2010. Depth migration by the Gaussian beam summation method. Geophysics, 75(2): S81-S93. |
| [23] | Ralston J. 1983. Gaussian beams and the propagation of singularities.//Littman W, Caffarelli L A eds. Studies in Partial Differential Equations. MAA Studies in Mathematics, 23(1): 206-248. |
| [24] | Simpson S M. 1967. Traveling signal-to-noise ratio and signal power estimates. Geophysics, 32(3): 485-493. |
| [25] | Sondergaard P L, Hansen P C, Christensen O. 2007. Finite discrete Gabor analysis. Copenhagen,Denmark: Technical University of Denmark. |
| [26] | Stolk C C, Symes W W. 2004. Kinematic artifacts in prestack depth migration. Geophysics, 69(2): 562-575. |
| [27] | Vinje V, Roberts G, Taylor R. 2008. Controlled beam migration: a versatile structural imaging tool. First Break, 26: 109-113. |
| [28] | Wang H Z, Feng B, Liu S Y, et al. 2013. Sparse expression of seismic data in characteristic and inversion imaging (in Chinese). WPI Annual Report, Tongji University, 3: 177-182. |
| [29] | Wang X, Wang H. 2014. High-resolution linear radon transformation with L0-norm constraint. CPS/SEG Conference, Expanded Abstracts: 284-287. |
| [30] | Yue Y B. 2011. Study on Gaussian beam migration methods in complex medium (in Chinese). Qingdao: China University of Petroleum. |
| [31] | Žáček K. 2003. Decomposition of the wave field into optimized Gaussian packets. 73rd Annual International Meeting, SEG, Expanded Abstract: 1869-1872. |
| [32] | Žáček K. 2004. Gaussian packet prestack depth migration. 74th Annual International Meeting, SEG, Expanded Abstracts: 957-960. |
| [33] | Žáček K. 2005. Gaussian packet prestack depth migration of the Marmousi data set. 75th Annual International Meeting, SEG, Expanded Abstracts: 1822-1925. |
| [34] | Žáček K. 2006. Optimization of the shape of Gaussian beams. Studia Geophysica et Geodaetica, 50(3): 349-366. |
| [35] | Zamorouev A. 1999. Automatic picking of seismic events. 69th Annual International Meeting, SEG, Expanded Abstracts: 1158-1161. |
| [36] | 李辉, 冯波, 王华忠. 2012. 波场模拟的高斯波包叠加方法. 石油物探, 51(4): 327-337. |
| [37] | 刘鹏, 王彦飞, 杨明名等. 2013. 地震数据的稀疏高斯束分解方法. 地球物理学报, 56(11): 3887-3895. |
| [38] | 王华忠, 冯波, 刘少勇等. 2013. 特征域数据稀疏表达及反演成像. WPI年度研究报告, 同济大学, 3: 177-182. |
| [39] | 岳玉波. 2011. 复杂介质高斯束偏移成像方法研究[博士论文]. 青岛: 中国石油大学. |
 2014, Vol. 57
2014, Vol. 57

