地球物理学报  2014, Vol. 57 Issue (7): 2190-2196   PDF    
引用本文
郝世峰, 杨诗芳, 楼茂园. 2014. 半拉格朗日模式风的半解析解及与差分解的比较试验. 地球物理学报, 57(7): 2190-2196, doi: 10.6038/cjg20140714   
HAO Shi-Feng, YANG Shi-Fang, LOU Mao-Yuan. 2014. The semi-analytical solutions of the wind for semi-Lagrangian model and the comparative experiments with the finite difference solutions. Chinese J. Geophysics, 57(7): 2190-2196, doi: 10.6038/cjg20140714   
半拉格朗日模式风的半解析解及与差分解的比较试验
郝世峰, 杨诗芳, 楼茂园    
浙江省气象台, 杭州 310017
投稿时间:2013-7-24    最后修改时间: 2014-5-15 .
基金项目：公益性行业专项（GYHY201306010）、国家重点基础研究发展计划项目（2009CB421505）、国家自然科学基金面上项目（41175056）、中国科学院重点部署项目课题（KZZD-EW-05-01）、国家自然科学基金海峡两岸合作研究项目（40921160379）联合资助.
作者简介：郝世峰，男，1973年生，汉族，硕士，正研级高工，从事数值天气预报研究.E-mail：shifenghao@aliyun.com
摘要：质点的轨迹计算是半拉格朗日模式的重要基础，传统的数值计算方法由于采用时间差分代替微分，只能得到质点运动轨迹终点的速度，因此质点的移动轨迹（位移）只能靠风速外推的方法计算，导致了模式计算不稳定等问题.借鉴精细积分法中使用半解析解的思路，利用正压原始方程研究了用运动方程的半解析解构建数值模式的可能性.求解了运动方程的一阶和二阶微分方程组的半解析解，通过时间积分半解析解计算质点运动轨迹.数值试验表明，一阶微分方程组的半解析解比差分解略有优势.二阶微分方程组的半解析解在时间步长增大时优势非常明显，而且在保证计算精度的前提下，节省计算时间，这对提高模式性能有重要作用.
关键词： 半解析解     半拉格朗日     运动方程     精细积分法    
The semi-analytical solutions of the wind for semi-Lagrangian model and the comparative experiments with the finite difference solutions
HAO Shi-Feng, YANG Shi-Fang, LOU Mao-Yuan    
Zhejiang Meteorology Observatory, Hangzhou 310017, China
Abstract: The algorithm for calculating parcel trajectory is very important in semi-Lagrangian weather prediction models, in which the traditional method is finite difference scheme. Since only the velocity at the end point of the parcel trajectory can be calculated, the displacement is obtained by wind speed extrapolation method. By referring to the semi-analytical solution (SAS) used in the precise integration method, the possibility of constructing a numerical weather prediction model by using the SAS method is raised. For this purpose, the SAS of the first and second order differential kinematics equations are obtained, then the displacement of air parcel can be obtained by integrating the SAS. The numerical experiments show that the result of the SAS of the first order kinematics equations is a little better than that of the finite difference scheme, and the SAS of the second order kinematics equations can get more accurate result and save the computing time by using a long integration time step.
Key words: Semi-analytical solution     Semi-Lagrangian     Kinematics equations     Precise integration method    

1 引言

对于半拉格朗日模式来说，拉格朗日轨迹计算是整个模式动力框架的基础，它关系到平流过程计算的合理性和正确性.由于数值模式在空间和时间上均采用差分代替微分，因此采用半拉格朗日方法构建的模式只能计算出质点运动轨迹终点时刻的速度，而不能直接得到质点的运动轨迹，因此只能进行估算.最早Robert(1982)采用三时间层方案，通过外推轨迹中点的速度计算质点的轨迹.McDonald(1986)提出了两时间层的计算方案，减少了计算量. Hortal(2002)提出了SETTLS(Stable Extrapolation Two Time Level Scheme)方案，并采用线性稳定性分析证明了计算方案的稳定性.以上都采用了风速外推的方法，White(2003)指出，轨迹计算时应该考虑动力平衡关系，并证明了用起点与终点的平均速度计算轨迹是无条件稳定的，Staniforth等(2003)，Staniforth和Wood(2008)对该方案开展了计算精度和稳定性的试验，并在非静力的天气、长期和气候一体化模式中应用.Wood等(2010)将该方案发展到深层大气的球坐标系模式中.

在国内，关于质点轨迹计算方法的研究开展得不多.中国气象科学研究院研制的Grapes全球中期数值预报模式采用了风速外推法，利用半时间步长时的风速计算轨迹(陈德辉等，2008).陈起英等(2007)在T319模式中应用SETTLS方案把模式积分时间步长从900 s提高到1200 s.通过分析以上这些研究成果，尽管White(2003)提出的方案取得了比较好的效果，但对于质点的运动轨迹依然无法给出一个较为准确的数学表达式，而且在理论上并不完善.除此之外，半拉格朗日模式采用质点在轨迹起点与终点处所受外力的线性权重平均作为平均作用力，也给轨迹计算精度带来很大影响.如果源汇项是高度非线性，甚至是不连续的，那么常用的采用首尾两点平均的计算方法将导致严重的误差，大时间步长会将误差进一步放大(胡志晋和史月琴，2006).

导致质点轨迹计算困难的根源是运动方程的时间坐标采用了差分法，那么积分数值模式时是否一定要采用时间差分方案呢?对于这一问题，我国著名学者钟万勰早在1993年就提出了精细积分法，即采用半解析解的时程积分方法.精细积分法在空间上采用差分格式，时间坐标采用微分，求得微分方程的半解析解(近似解析解)，再采用时间分段求解半解析解的方法得到微分方程的数值解.钟万勰(1996)，钟万勰和朱建平(1995)利用精细积分法研究了“对流-扩散”方程的数值积分问题，证明了该方法不但计算精度高，而且计算无条件稳定.在钟万勰的研究成果基础上，强士中等(1999)提出了任意差分精细积分法，适用于不规则边界和不规则的空间离散点.采用半解析解的精细积分法在很多领域得到了广泛的应用和不断的改进.Fan 等(2006)基于精细积分法提出了非线性动力方程的数值求解方法；谭述君等(2010)研究了非线性方程的Duhamel项的精细积分方法；王润秋等(2010)采用三维任意差分精细积分法实现了塔里木地震波的正演模拟；Duan等(2013)基于精细积分法开展了三维弹性波的数值模拟.

精细积分法的基础是利用微分方程的半解析解，目前这一方法在数值天气预报模式领域的应用还未见报道.采用时间差分方案的计算方法是不可能给出质点运动轨迹的数学表达式，因此造成了质点轨迹计算的困难，计算误差给模式稳定性等方面带来了很多问题.微分方程的半解析解恰恰可以解决这一问题，因此研究半解析解在半拉格朗日天气预报模式中的应用具有一定的意义.

2 正压原始方程组的差分格式和半解析解格式

直角坐标系下的正压原始方程组为：

其中函数φ=φ(x，y，t)，f为科氏参数.将时间轴划 分为等Δt间隔的时间层.以下方程中符号的上标均表示时间层.首先给出方程(1)的两时间层隐式差分格式.

由方程(2)和(3)联合求解得风矢量的差分解，写成矩阵形式为：

第二步，给出运动方程的半解析解格式.将(1)式的梯度力项采用时间隐式离散化得：

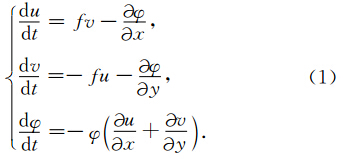
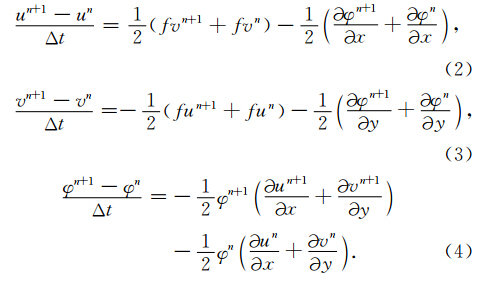
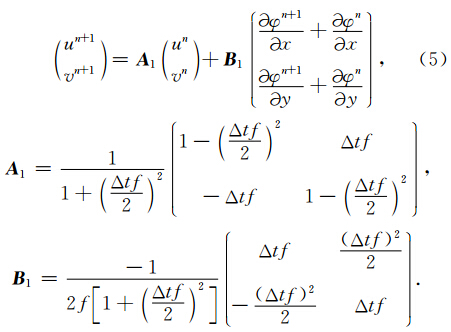
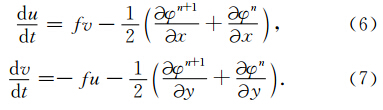
将(6)与(7)式联合解微分方程组，写成矩阵形式为：

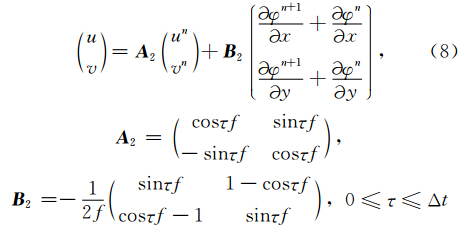
方程(8)为运动方程的半解析解，并且和(5)式非常相似，分为两项，第一项与n时间层的速度有关，第二项与梯度力有关.如果不考虑梯度力的作用，(8)式实际上就是真解，而且 A 2是辛矩阵，说明无外力作用下系统是保守系统.显然(5)式为近似解， A 1不是辛矩阵，但具有平方守恒的性质.相比而言，(8)式可能更合理，而且和(5)式一样具有Δt的二阶计算精度.

采用差分格式的半拉格朗日数值模式的求解方法通常是将(5)式求散度后代入(4)式消掉n+1时次的散度项，得到φn+1的方程，通过迭代法求得φn+1， 再代入(5)式求解风速.我国自主研发的Grapes模式也是采用这一方案(薛纪善和陈徳辉，2008). 因此不妨检验采用(8)式是否也容易得到类似的关于φ

其中：

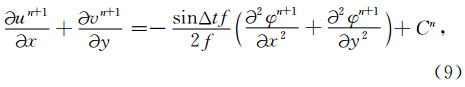
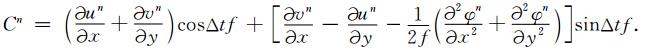
将(9)式代入(4)式消去散度项得φn+1的方程，如下：

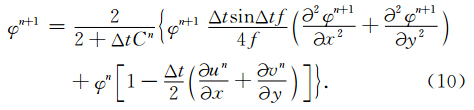
不难看出，(10)式可采用直接迭代法求解，或化为Helmholtz型方程求解.以上结论说明，采用半解析解构建数值天气预报模型是可能的.本文在此不进一步讨论如何求解φn+1及数值模型的守恒性等复杂问题，因为“半解析解”的风速和轨迹(位移)计算是否比“差分解”更准确才是是否有必要开展这项研究工作的前提.

3 二阶运动方程的半解析解

半拉格朗日隐式差分方案通常将梯度力项用首尾平均法表示成平均作用力，如(2)和(3)式，因φ是非线性项，在用大时间步长积分时必然给计算精度带来很大影响，而且求解φ时必须计算φ的二阶空间微分，如(10)式，说明φ的二阶微分是不可忽略 的，因此很有必要研究二阶微分运动方程的半解析解.

将方程组(1)的运动方程求时间微分得：

给定已知条件：

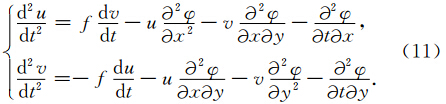
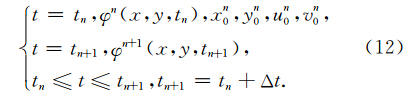
方程(11)为非线性微分方程组，难以求解，需采用线性化近似.设质点在第n个时间层位置为(xn0，yn0)，起始速度为un0，vn0.为书写和表达简洁，以下符号中下标为x、y和ζ时均表示偏微分.

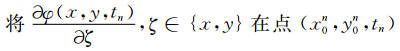处Taylor展开，并取一阶近似得：

在第n时间层，气压梯度力时间倾向场为

设质点在第n+1时间层移动至位置(xn+10，yn+10)，将质点移动轨迹上的气压梯度力时间倾向表示为仅为时间t的线性函数.

容易验证，用(15)式计算，在第n和n+1时间 层满足轨迹起点与终点处的气压梯度力.将(15)式代入(13)式，再将(13)式代入(11)式得线性化微分方程：

方程(16)与(2)、(3)及(6)、(7)的重要区别在于用Taylor级数近似来描述非线性项φζ的时空变化，并满足质点运动轨迹首尾处梯度力的边界条件，而不是用简单的线性平均法求得的平均梯度力代替.

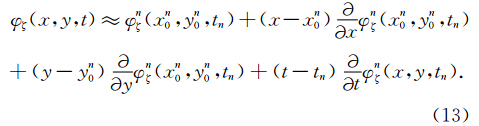
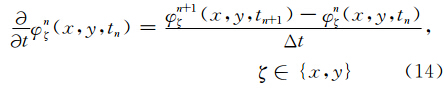
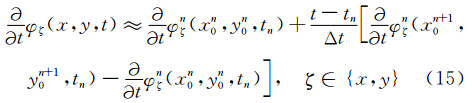
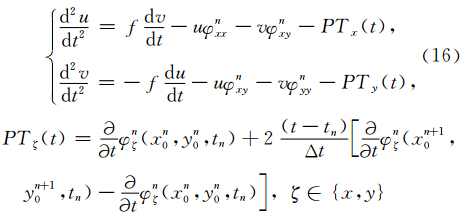
令 du dt =u ·，dv dt =v ·，将方程(16)降阶求解.

其中

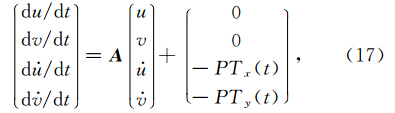
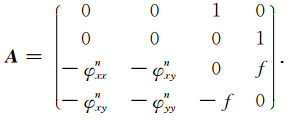
利用给定初值条件得方程组解为：

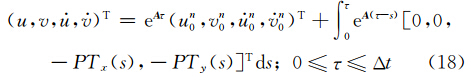
矩阵 A 的特征根完全由环境力场决定(气压梯度力场和科氏参数构成)，将其表示成复数形式为Rk=ak+bki，k∈{1，2，3，4}.特征根决定了矩阵指数eAτ的形式，它由四个线性无关的波动解组成，波动的频率由特征根的虚部决定，特征根的实部决定波动振幅的变化，当特征根是重根时对应的是新生的波动.因方程(18)为简单的方程，限于篇幅不详细介绍解的具体形式，可参考有关教材(焦宝聪等，2008).大气运动的复杂性和多样性取决于环境力场形态的复杂性和多样性，方程(18)采用近似的方法考虑了这一因素，对深入理解大气运动的物理过程具有一定的意义.

4 运动方程的差分解和半解析解的比较试验 4.1 试验设计

试验原理和目的是，在给定相同气压梯度力场的条件下比较差分解和半解析解计算风速和位移的精度与时间步长Δt的关系，Δt最大取为50 min.

首先设φn(x，y，tn)为已知，给定质点的初始速度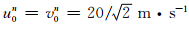，；取45°N处的科氏参数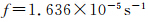，；设起始点为原点，并考虑非地转平衡条件，取


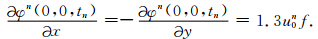
设第n时间层原点附近气压梯度力场为：


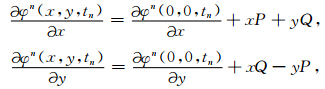
其中：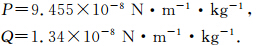

假定n+1时间层的气压梯度力也已求得，并由(14)式得气压梯度力的时间倾向函数：

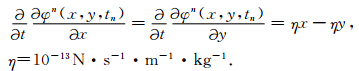
方案1为差分法，计算方法为(5)式，位移采用White提出的方案，用第n和n+1时间层的平均速度计算，并利用迭代法确定终点位置.

方案2为一阶微分方程组的半解析解，计算方法为(8)式，位移采用时间积分(8)式，并利用迭代法确定终点位置.

方案3为二阶微分方程的半解析解，计算方法为(18)式，位移采用时间积分(18)式，并利用迭代法确定终点位置.由初值条件求得矩阵 A 的特征根为两实根和两个纯虚根：

二阶微分方程组的u和v的半解析解如下

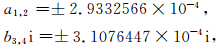
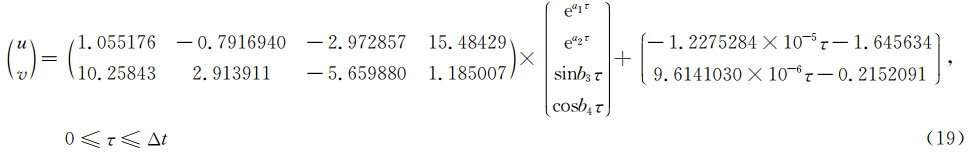
方案4，由于无法得到真解，因此方案4采用数值解代替.既然(5)式是在模式中实际使用的方法，并得到了检验，因此采用小时间步长通过直接积分(5)式作为最接近真解的解，时间步长取为Δt=1 s，其他参数同方案1.

4.2 风速和位移误差分析

以上四种方案计算位移时最多经过5次迭代即可确定终点位置.首先给出风速计算结果对比.图 1所示，在Δt<20 min时，四条曲线几乎都是重合的，在此之后开始分岔并逐渐加大，方案1和2接近重合，最大差距约0.1 m·s-1.既然方案1是在实际业务中使用的方法，这一结果说明使用半解析解方法的方案2可能也是可行的.方案1、2和方案4比较，Δt=50 min时u误差约2.6 m·s-1，v误差约3.2 m·s-1.对比方案3和4的计算结果，在Δt>30 min后误差逐渐加大，Δt=50 min时u和v的误差值分别为1.6 m·s-1和1.4 m·s-1.表 1给出了详细的计算结果对比.

虽然前三种方案和方案4比较在轨迹终点时刻的风速计算结果均具有很高的精度，但并不代表计算的轨迹也是相近的.图 2给出了方案1、2、3以方案4为参照标准的轨迹终点的位移绝对误差和相对误差.方案1、2的位移误差随Δt近似呈指数变化趋势，并且二者误差非常接近，但方案2略好.在Δt=20 min时误差分别为0.31 km和0.27 km. 在Δt= 30 min时绝对误差接近1 km，相对误差约为3％，以后迅速增大，在Δt=50 min时绝对误差分别达到6.9 km和6.4 km，相对误差分别为11.5%和10.6%.对比方案3的计算结果，在Δt<5 min时三种方案的误差相近，在此之后方案3的误差始终要比方案1、2低一个量级，在Δt等于20 min和30 min时误差分别为0.03 km和0.07 km，即使在Δt=50 min时绝对误差也仅为0.8 km，相对误差为1.4%.三种方案对比，方案3的误差最小，取Δt>10 min时具有非常明显的优势.

在方案3中将气压梯度力时间倾向进行了线性近似，必然会给计算结果带来误差.因此很有必要检验在定常大气下，即的条件下半解析解的精度，图 3给出了风速的对比结果.无论u还是v，方案3和4在整个时间段内曲线均几 乎是重合的，最大误差为0.02 m·s-1.方案1和2的结果非常接近，在Δt>20 min以后开始和方案4分岔，并逐渐加大.对比位移计算误差结果表明，方案3的误差明显最小，最大误差为0.26 km(图略).由此可见，方案3计算误差的主要根源是气压梯度力时间倾向的线性近似.

表 1 方案3和4的u、v 计算结果对比(单位:m·s-1) Table 1 Comparison of the calculation result of Scheme 3 and Scheme 4(unit: m·s-1)

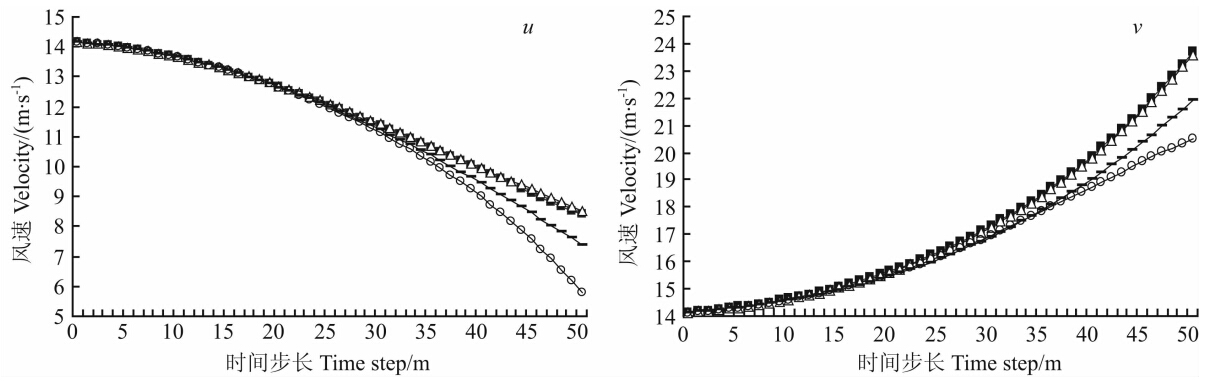图 1 四种方案风速的计算结果对比 ■方案1;Δ方案2；方案3；○方案4.Fig. 1 Comparison of the results of wind speed from four computing schemes ■ Scheme 1； Δ Scheme 2；Scheme 3；○ Scheme 4.

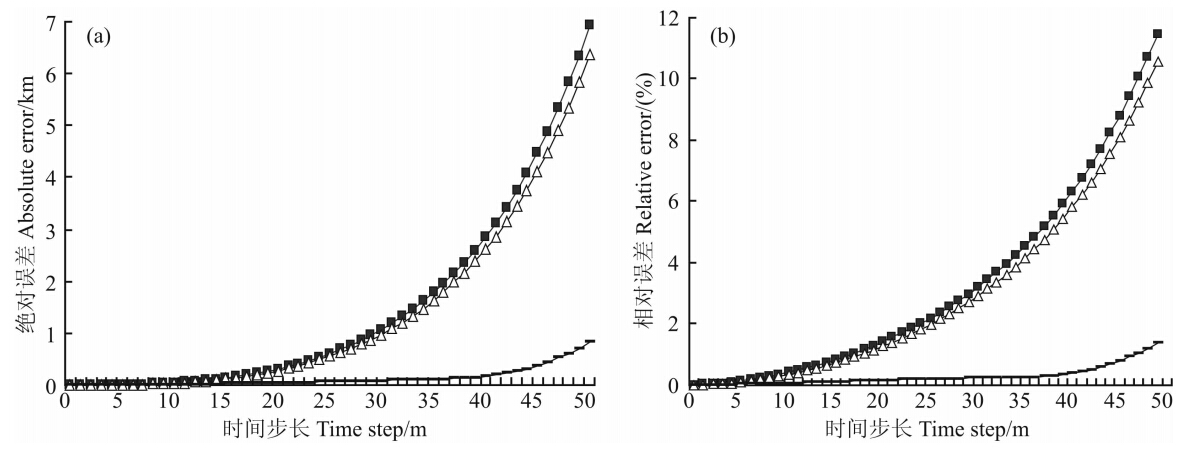图 2 三种方案相对于方案4的位移计算绝对误差(a)和相对误差(b) ■ 方案1; Δ 方案2; 方案3Fig. 2 The absolute error(a) and relative error(b)of the displacement for the scheme 1，2， and 3 ■ Scheme 1； Δ Scheme 2；Scheme 3.

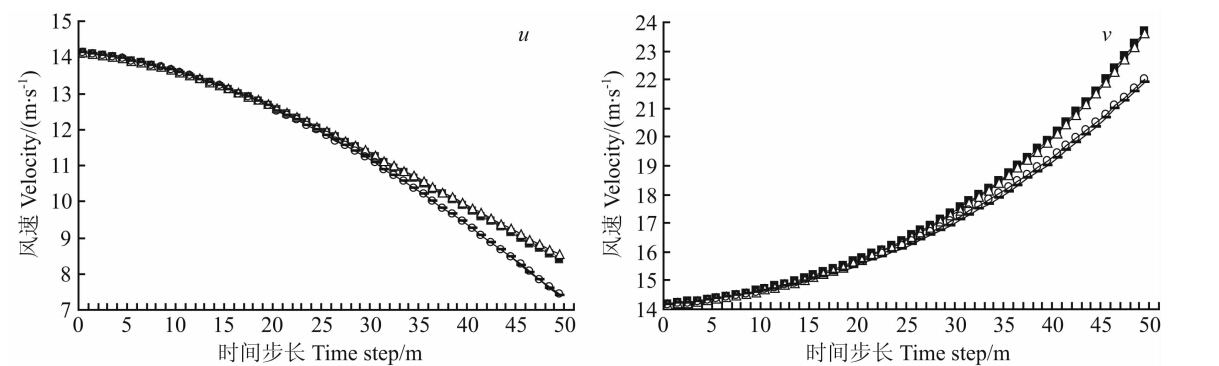图 3 同图 1，但为定常大气下四种方案的风速计算结果对比Fig. 3 Same as Fig. 1，but for stationary atmosphere

分析以上试验结果，环境场外力不仅是时空的函数，而且与质点本身的运动速度有关，难以用线性函数表示，只有在短时间步长内，首尾平均法才近似成立.使用大时间步长必然会给方案1和2的计算结果造成较大的误差.方案2虽然只是略优于方案1，但位移计算合理，这对保证模式的长时间积分稳定性及计算精度方面可能会有很大改进.

从消耗的计算时间来看，方案3是半解析解，消耗机时与Δt的长短无关，而要达到和方案3接近的计算结果，方案1、2必须采用小时间步长经过多次时间积分.如方案3选取Δt=20 min，方案1需采用Δt=10 min 积分2次，二者计算结果位移相差50 m.测试计算十万个格点，方案3消耗的机时为方案1、2的64%.可见，大气运动二阶微分方程的半解析解，不仅具有很高的计算精度，而且节省计算时间，可以使用更大的时间步长，这对提高模式性能有重要作用.

5 结论及展望

采用差分方程代替微分方程很难满足微分方程的诸多属性，针对采用时间差分方案的半拉格朗日模式轨迹计算存在的问题，本文以正压大气原始方程组为例，讨论了运动方程的半解析解，结论如下：

(1)在积分时间步长内，采用隐式格式离散气压梯度力，求得了一阶运动方程组的半解析解.利用Talyor级数展开法将气压梯度力项线性近似，得到常系数非齐次大气运动二阶微分方程组，并给出方程组的半解析解，半解析解描述了环境力场的复杂变化，对深入理解大气运动的物理过程，深入研究拉格朗日轨迹计算方法具有一定的意义.

(2)通过直接积分半解析解计算质点轨迹(位移)，从理论上更合理，对保持模式计算稳定性方面具有重要作用.数值试验表明，一阶微分方程组的半解析解比差分解略有优势，二阶微分方程组的半解析解在时间步长增大时优势非常明显，在保证计算精度的前提下，可以使用更大的时间步长，并且节省计算时间，这对提高模式性能有重要作用.

(3)采用质点运动轨迹上的首尾权重平均法将环境场外力线性化是导致差分法(方案1)和一阶微分方程组半解析解(方案2)计算误差的主要根源，采用大时间步长求解位移时误差较大.

(4)将气压梯度力时间倾向线性化近似是导致二阶大气运动微分方程半解析解误差的主要根源，还需进一步的研究和改进.

(5)进一步研究半解析解方法在斜压数值天气模式中的应用是更具有科学意义的工作.

参考文献
[1] Chen D H, Xue J S, Yang X S, et al. 2008. Total design and research on the new generation globe and regional multiscale Grapes numerical model. Chinese Science Bulletin (in Chinese), 53(20): 2396-2407.
[2] Chen Q Y, Guan C G, Yao M M, et al. 2007. Development of key techniques and experiments in globe model upgrading. Acta Meteorologica Sinica (in Chinese), 65(4): 478-492.
[3] Duan Y T, Hu T Y, Yao F C, et al. 2013. 3D elastic wave equation forward modeling based on the precise integration method.   Applied Geophysics, 10(1): 71-78.
[4] Fan J P, Huang T, Tang C Y, et al. 2006. A predict-correct numerical integration scheme for solving nonlinear dynamic equations. Acta Mechanica Solida Sinica, 9(4): 289-296.
[5] Hu Z J, Shi Y Q. 2006. On the time step of semi-Lagrangian semi-implicit atmospheric model. Chinese Journal of Atmospheric Sciences (in Chinese), 30(1): 1-10.
[6] Hortal M. 2002. The development and testing of a new two-time-level semi-Lagrangian scheme (SETTLS) in the ECMWF forecast model. Quart. J. Roy. Meteor. Soc.  , 128(583): 1671-1687.
[7] Jiao B C, Wang Z H, Shi H T. 2008. Ordinary Differential Equations (in Chinese). Beijing: Tsinghua University Press.
[8] McDonald A. 1986. A semi-Lagrangian and semi-implicit two time-level integration scheme. Mon. Wea. Rev.  , 114: 824-830.
[9] Qiang S Z, Wang X G, Tang M L, et al. 1999. On the arbitrary difference precise integration method and its numerical stability. Applied Mathematics and Mechanics (in Chinese), 20(3): 256-262.
[10] Robert A. 1982. A semi-Lagrangian and semi-implicit numerical integration scheme for the primitive meteorological equations. J. Met. Soc. Japan, 60(1): 319-325.
[11] Staniforth A, White A, Wood N. 2003. Analysis of semi-Lagrangian trajectory computations. Quart. J. Roy. Meteor. Soc.  , 129: 2065-2085.
[12] Staniforth A, Wood N. 2008. Aspects of dynamical core of a nonhydrostatic, deep-atmosphere unified weather and climate-prediction model.   Journal of Computational Physics, 227(7): 3445-3464.
[13] Tan S J, Gao Q, Zhong W X. 2010. Applications of Duhamel term's precise integration method in solving nonlinear differential equations. Chinese Journal Computational Mechanics (in Chinese), 27(5): 752-758.
[14] White A A. 2003. Dynamical equivalence and the departure-point equation in semi-Lagrangian numerical models. Quart. J. Roy. Meteor. Soc.  , 129(589): 1317-1324.
[15] Wood N, White A A, Staniforth A. 2010. Treatment of vector equations in deep-atmosphere, semi-Lagrangian models. II: kinematic equation. Quart. J. Roy. Meteor. Soc., 136(647): 507-516.
[16] Wang R Q, Li L L, Li H J. 2010. Forward modeling research for seismic exploration of Tarim Area. Chinese Journal of Geophysics (in Chinese), 53(8): 1875-1882.
[17] Xue J S, Chen D H. 2008. The Scientific Design and Application of the Numerical model Grapes System (in Chinese). Beijing: Science Press, 109-113.
[18] Zhong W X, Zhu J P. 1995. Rethinking to finite difference time-step integrations. Applied Mathematics and Mechanics (in Chinese), 16(8): 663-668.
[19] Zhong W X. 1996. Single point subdomain precise integration and finite difference. Acta Mechanics Sinica (in Chinese), 28(2): 159-163.
[20] 陈德辉, 薛纪善, 杨学胜等. 2008. GRAPE新一代全球/区域多尺度统一数值预报模式总体设计研究.   科学通报, 53(20): 2396-2407. 
[21] 陈起英, 管成功, 姚明明等. 2007. 全球中期模式升级关键技术研发和预报试验.   气象学报, 65(4): 478-492. 
[22] 胡志晋, 史月琴. 2006. 关于半拉格朗日半隐式大气模式的时步问题.   大气科学, 30(1): 1-10. 
[23] 焦宝聪, 王在洪, 时红廷. 2008. 常微分方程. 北京: 清华大学出版社.
[24] 强士中, 王孝国, 唐茂林等. 1999. 任意差分精细积分法及数值稳定性分析.   应用数学和力学, 20(3): 256-262. 
[25] 谭述君, 高强, 钟万勰. 2010. Duhamel项的精细积分方法在非线性微分方程数值求解中的应用.   计算力学学报, 27(5): 752-758. 
[26] 王润秋, 李兰兰, 李会俭. 2010. 塔里木地区勘探地震正演模拟研究.   地球物理学报, 53(8): 1875-1882. 
[27] 薛纪善, 陈徳辉. 2008. 数值预报系统GRAPES的科学设计与应用. 北京: 科学出版社, 109-113. 
[28] 钟万勰, 朱建平. 1995. 对差分法时程积分的反思.   应用数学和力学, 16(8): 663-668. 
[29] 钟万勰. 1996. 单点子域积分与差分.   力学学报, 28(2): 159-163.