1 引言
20世纪70年代末,Silverman(1979)首次在陆地勘探中提出使用可控震源同时激发采集的思想.2008年,Berkhout(2008)在此基础上发展并提出了混合激发的概念,使得混合采集技术得到了迅速发展.由于混合采集中单炮之间的激发间隔远小于常规采集的情况,因此得到的炮集记录中会不可避免地采集到其它炮激发的信号,这些不属于待研究的其他炮激发的信号,即混合噪声.混合噪声在很大程度上降低了地震记录的信噪比,因此,做进一步处理之前,最重要的就是对混合噪声的压制,实现混合炮的单炮分离.
混合噪声的压制可以看作滤波处理:将共炮域的混叠数据转入共检波点域或其他域(共偏移距域,共中心点域)中,此时混合噪声以脉冲的形式随机分布,进而,混合噪声的压制过程就近似成随机噪声的压制问题.基于这样的理论基础,2009年,Huo等(2009)在共中心点域使用矢量中值滤波器移除混合噪声.Kim等(2009)设计了新的思路:基于地下速度模型和波动方程建立一个噪声模型,然后在共偏移距域中自适应地减去混合噪声.Doulgeris等(2010)和Mahdad等(2011)相继在2010年和2011年优化设计了迭代算法,在共检波点域中压制混合噪声.
如上的滤波方法仅在一些情况下应用效果良好.混合噪声属于有效信号的一部分,它和有效信号具有相同的能量分布特征,所以利用滤波原理消除混合噪声的过程会对有效信号产生潜在的不良影响.因此,一些学者提出了新的思路:将压制混合噪声的问题视作反演问题处理.同基于滤波压制混合噪声的方法相比,基于反演的混合噪声压制方法能够更好地保持有效信号的基本特征,并且更适合于振幅分析和延时处理(Akerberg et al., 2008; Moore et al., 2008; Lin and Herrmann, 2009; Herrmann et al., 2009; Abma et al., 2010; Ayeni et al., 2011; Doulgeris et al., 2012).
之前的学者在处理混合震源数据时,仅仅对信噪分离本身进行了研究,未能进一步考虑含有随机噪音和地震道缺失等情形.本文将含有混合噪声、随机噪音以及缺失道集的地震记录转入稀疏域,进而利用稀疏约束反演将这些采集过程中遇到的实际问题在统一的框架内解决,不仅提高了地震资料的处理效率,也提高了地震资料的信噪比.文章首先介绍该方法的原理,其次论述了实现流程,然后分别利用模拟数据和实际数据对本方法进行了验证,并和常规方法在分离方面做了对比,最后得出结论.
2 方法原理一个基本的线性问题可以写成

具体来讲,在炮分离过程中,式(1)中 A 即代表混合算子矩阵,x 代表原始单炮记录,b 代表混合炮数据;在压制随机噪音过程中,A 代表产生随机噪音的算子矩阵,x 是不含随机噪音的数据,b 是伴随随机噪音的地震记录;在插值的情况下,A 代表使记录缺失道集的算子矩阵,x 是完整的炮集数据,b 是缺失道集的地震记录.在以上三种情况下,c 都是未知的噪音数据.将以上情况汇总为表 1.
|
|
表 1 式(1)中 A和b 的物理意义 Table 1 The physical significance of A and b in equation(1) |
一般地,由于采集信息不足以及噪声(本文中涉及的混合噪声和随机噪声)的影响,会使得线性问题求解存在多解性,为降低多解性,需要引入正则化方法(Scales and Gersztenkorn, 1988)对求解进行约束.稀疏约束反演(Malioutov et al., 2005; Beck and Teboulle, 2009; Han et al., 2012)就是随着压缩感知技术的兴起而迅速发展起来的一种正则化反演方法,并已被应用于地震数据去噪、插值等方面.
本文将数据变换到稀疏域,将式(1)转化为下式,即只需使目标函数 J 最小,便可求得待求解:
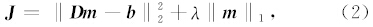
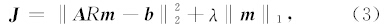
本文采用FISTA(Fast Iterative Shrinkage- Thresholding Algorithm)(Beck and Teboulle, 2009)求 解式(2).FISTA基于ISTA(Iterative Shrinkage-Thresholding Algorithm)(Daubechies et al., 2004; Figueiredo and Nowak, 2003)改进而来.ISTA作为一种有效的解决线性反演问题的算法,其最大的优点是实现简单,但在一些情况下,ISTA的收敛速度非常慢,严重影响了计算效率.为了弥补这个缺点,很多学者提出了优化的算法,FISTA即是其中一种,它可以以很少的迭代次数得到理想的预期效果.
ISTA定义了一种软阈值的迭代公式求取式(2)中的 m :
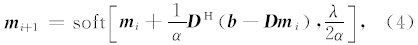

FISTA通过改变式(4)中的 m i提高收敛速度,新建一个和m i与 m i-1相关的参量 l i+1,
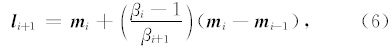
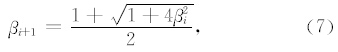
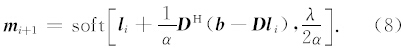
FISTA在保留了ISTA算法实现简单的基础上,同时也提高了算法的收敛速度,并且将复数的运算也包括在运算范畴内,扩大了使用范围.
3 实现流程文章分别采用模拟数据和实际地震记录进行方法验证.首先,进行模拟混合采集数据的伪分离;其次,在共偏移距域中进行普通小时窗的中值滤波;最后,将数据转换入共中心点域采用稀疏约束反演,一步完成混合噪声和随机噪音的去除,以及缺失道集的插值.
3.1 混合炮数据的伪分离混合炮数据的伪分离可以在频率域和时间域中进行.本文采用的是时间域.
混合炮人工拟合的示例如图 1所示.如图,左上角的炮集即是由其他4张单炮记录模拟合成的混合炮记录,图中的箭头指示了每张单炮记录在混合炮集中所处的位置.
 | 图 1 混合炮在时间域的合成图 Fig. 1 The composite diagram of blending shot in time domain |
本文的混合算子采用相位编码.混合炮的伪分离处理过程如下:假设一个混合炮中包含N个单炮,首先将混合炮复制N次,然后每个单炮按照混合编码中相应的延时反向移回初始位置即可.之所以称之为伪分离,是因为每个单炮只是按混合编码反向移回初始位置,每个单炮记录中仍旧含有其他炮集记录的数据,并没有进行实质性的炮分离处理.
3.2 小时窗中值滤波预处理如果直接把数据转入稀疏域,噪声尤其是混合噪声在稀疏域的稀疏系数可能接近甚至大于有效信号,将会严重影响后续的反演结果,所以在稀疏约束反演之前,需要首先进行中值滤波.图 2是共偏移距域中混合数据的分布,其中呈规则分布的是有效信号,呈随机分布的则是混合噪声.本文采用的小时窗滤波可以使有效信号的损失降低到最小.
 | 图 2 共偏移距中混合数据的信号和噪声分布图 Fig. 2 The distribution diagram of signal and noise in blending data in common offset domain |
信号的中值滤波(Stork,2003)原理:中值滤波是基于排序统计理论的一种能有效抑制噪声的非线性信号处理技术.其中式(9)是二维中值滤波的数学表达式:
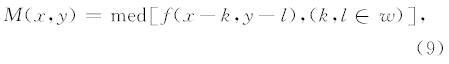
其中,f(x,y)为待处理数据,w是二维窗口,med的响应是选择窗口内待处理的所有数据,然后将其排序,取出中间的值代替窗口中心的值,M(x,y)是处理后的数据.
3.3 采用稀疏反演压制混合噪声和随机噪音,并对缺失道进行插值将中值预处理后的数据转入共中心点域进行稀疏约束反演.在该域中,有效信号呈抛物线状,而噪声则呈随机分布.在程序中输入含有缺失道集以及随机噪音的伪分离数据.然后调节正则化参数λ,选择合适的迭代次数,观测对比最后的输出值,最终得 到去除了随机噪音和混合噪声,以及插值补空后完整的地震数据.
4 算例文章分别用模拟数据和实际数据进行模拟混合采集,对本文提出的方法进行验证.
4.1 模拟数据模拟采集参数:地表布置 90个检波器,道间距12 m.第1个震源位于测线起始端,第2个与其相隔18个道间距,以此等距方式类推直到第5个震源.5个震源近乎同时(每2个震源激发间隔在0~2 s内随机选取)激发之后,集体沿测线向前移动一个道间距,直至第5个震源在最后一个检波器上激发完成.最后得到的混合地震记录中,每个混合炮中包含5个单炮.
图 3是模拟数据的分步处理结果,选用第35炮作为示例.图 3a是未混合的原始单炮数据;图 3b是模拟混合采集之后,在混合数据中加入20%的高斯白噪,并随机将20%的地震道充零的数据;图 3c是仅做了小时窗中值滤波的结果,如图 3c所示,在仅经过普通小时窗中值滤波之后,混合记录中的混合噪声得到部分压制,这和一般炮分离方法的原理和结果类似,但是其对缺失道集的插值和随机噪音的衰减处理效果不理想(在下文展示的实际数据的例子中表现的更明显).图 3d是在图 3c的基础上在Radon域采用本文提出的稀疏约束反演处理的结果.由图 3d和图 3c对比可得,应用了本文提出的方法后,不仅混合噪声得到了进一步压制,而且同时完成了缺失道集的插值和随机噪音的衰减.
 | 图 3(a)未混合的原始数据,选90炮中的第35炮作为示例;(b)含信噪比为20%的高斯白噪、 有20%的缺失道集的伪分离数据;(c)经过小时窗中值滤波的数据;(d)反演后的最终结果 Fig. 3(a)Shows the original data that is not blended. We choose the 35th shot record among 90 shots.(b)is the pseudodeblending result of the shot that is added with white Gaussian noise(SNR=20%) and has 20% missing traces.(c)shows the shot record filtered by the small window median filtering in common offset domain.(d)is the final outcome that is processed by inversion in common mid-point domain after median filtering |
应用某一海域的实测地震资料进一步验证本方法的可行性和有效性.模拟混合观测系统参数:第1个震源位于首个检波器处,第2个震源和第1个相隔20个道间距,位于第21个检波点处,以此类推直至第71个检波点处的第5个震源.5个震源近乎同时(每2个震源激发间隔在0~2 s内随机选取)激发后,同时向前移动一个道间距,直至覆盖完所有的检波器为止.得到的混合炮记录中,每个混合炮中含有5个单炮记录.图 4是分步处理结果图,为了便于对比,采用的时窗相同:横轴为100个检波器,纵轴为4 s采集时间.
 | 图 4(a)未混合的原始数据,选了100炮中的第50炮作为示例;(b)含信噪比为20%的高斯白噪、 有20%的缺失道集的伪分离数据;(c)经过小时窗中值滤波的数据;(d)反演后的最终结果 Fig. 4(a)Shows the original data that is not blended. We choose the 50th shot record among 100 shots.(b)is the pseudodeblending result of the shot that is added with white Gaussian noise(SNR=20%) and has 20% missing traces.(c)shows the shot record filtered by the small window median filtering in common offset domain.(d)is the final outcome that is processed by inversion in common mid-point domain after median filtering |
图中选用第50炮作为示例.过程分析与图 3类似:图 4a是未混合的单炮记录;图 4b是模拟混合采集之后,在混合记录中加入20%的高斯白噪,并随机充零20%的地震道的记录;图 4c是仅做完小时窗中值滤波的预处理结果,由图 4c所示,仅有部分混合噪声得到压制,而缺失的道集和随机噪音没有得到理想的处理结果;而由图 4d可得,在共中心点域应用本文提出的方法后,同时去除了这三种影响混合地震采集质量的因素,得到了满意的结果.
为了从微观上展示本方法的实际能力,选用理论数据(图 4a)和结果数据(图 4d)中的任意两道做了波形对比,如图 5所示.图 5a是第10道的波形对比,图 5b是第70道的波形对比,其中,黑色线代表理论数据,红色线代表结果数据(为了清晰展示,选取的时窗是800~2400 ms).从波形对比可以看出,理论数据和结果数据的吻合度较高,再一次论证了本方法的可行性和有效性.
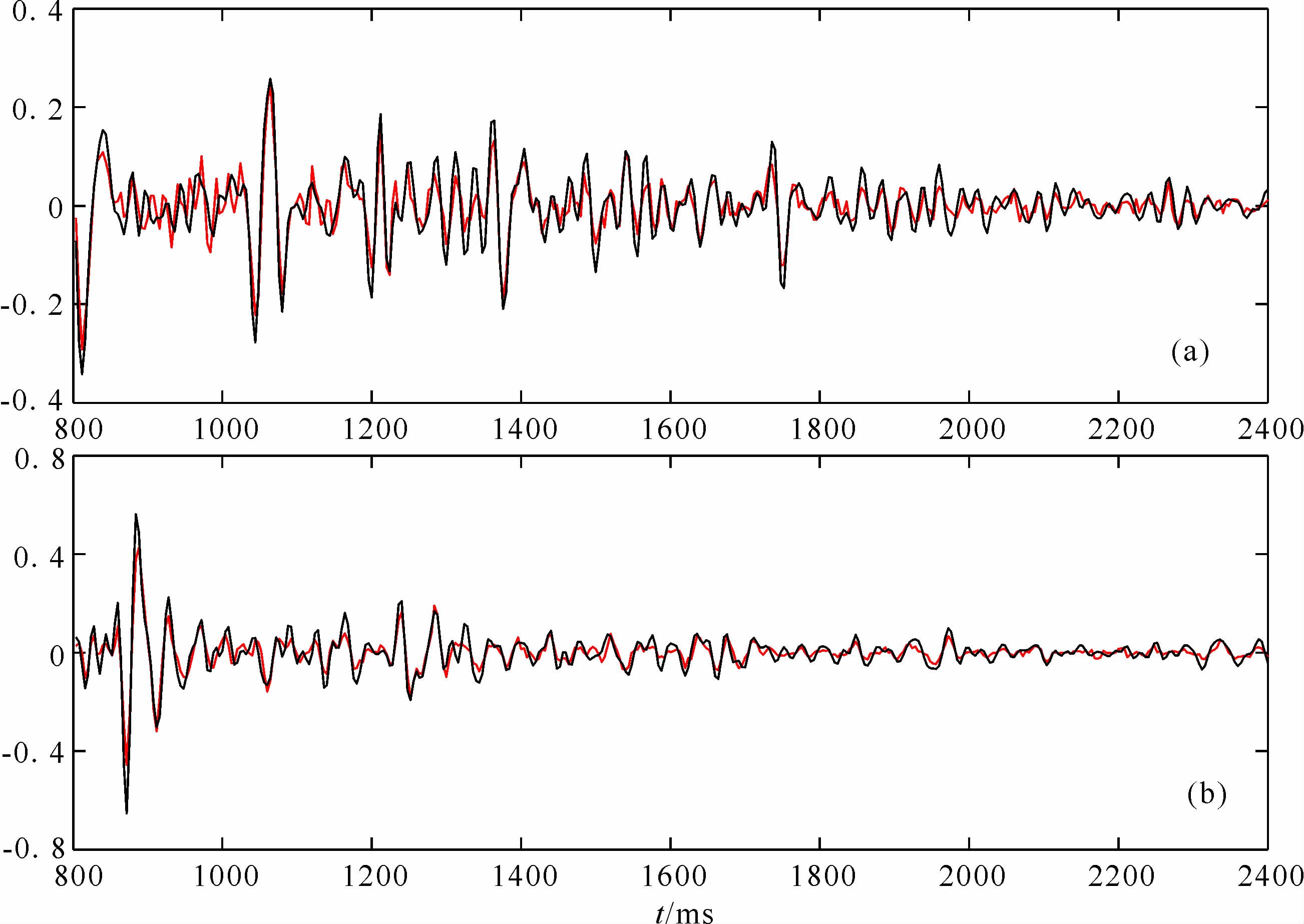 | 图 5 理论数据(黑色线)和结果数据(红色线)的波形对比图,其中,图a是第10道的数据,图b是第70道的数据,纵坐标为振幅,无量钢 Fig. 5 The waveform comparison of theoretical data(black line) and result data(red line): (a)is the data of the 10th trace,(b)is the data of the 70th trace |
目前国际上还没有正式规定判定混合炮分离质量的通用标准,大多数学者采用下式计算分离结果的质量:

按照式(10)的判定标准,从近几年提出的方法中挑出典型的5类与本方法进行对比,结果如下:第一类,混合炮的单炮个数是2,在共偏移距采用频率-波数(f-k)滤波(Doulgeris et al., 2011; Mahdad et al., 2012)进行15次迭代后的分离信噪比是9.79;第二类,混合炮的单炮个数是2,结合一维中值滤波和频率-波数(f-k)滤波(Mahdad et al., 2012)迭代15次后的分离信噪比是12.54;第三类,混合炮的单炮个数是2,应用频率-检波器方向波数-炮点方向波数(f-kr-ks)滤波(Doulgeris et al., 2011; Mahdad et al., 2012)15次迭代后的分离信噪比是14.37;第四类,混合炮的单炮个数是2,采用线性Radon(τ-p)滤波(Doulgeris et al., 2011; Mahdad et al., 2012)进行15次迭代后的分离信噪比是18.11;第五类,混合炮的单炮个数是3,利用频率-波数(f-k)滤波(Mahdad et al., 2011)进行44次迭代后的分离信噪比是12.
采用本文方法对实际资料的处理中,混合的单炮数为5炮,迭代次数50次,分离信噪比为13.62.可以看出,本方法在提高地震资料处理效率的同时,不仅炮分离个数的制约程度要小于上文提及的方法,而且保证了分离信噪比不受损失.
6 结论混采数据中包含的混合噪声不同于一般意义上 的随机噪声,虽然它在非炮域显示了随机分布的特点,其能量大小却与随机噪声大相径庭,尤其值得注意的是,一些混合噪声的能量甚至大于有效信号;混合采集中,每个检波器携带的地震信号较常规采集更多,所以缺失道集产生的影响更大,因此插值对混合采集更为重要;由于采集环境的干扰而引入的随机噪音对地震记录的影响也不容忽视.
本文将混合噪声的去除,缺失道集的插值以及随机噪音的衰减描述为同类反演问题,利用FISTA(Fast Iterative Shrinkage-Thresholding Algorithm)算法,将这三类反演问题同时带入反演迭代算法中,输出的数据不仅完成了混合噪声的去除,实现了混合 炮中单炮的分离,而且去除了随机噪音并补充了缺失道集的地震数据.模拟数据和实际数据的算例均表明,本方法在很大程度上提高了工作效率,并且得到了信噪比较高的预期效果.
| [1] | Abma R L, Manning T, Yu J, et al. 2010. Sparse inversion of simultaneous sources. 72nd Annual International Meeting, EAGE, Extend Abstracts, B06. |
| [2] | Akerberg P, Hampson G, Rickett J, et al. 2008. Simultaneous source separation by sparse radon transform. 78th Annual International Meeting, SEG, Expanded Abstracts, 2801-2805. |
| [3] | Ayeni G, Almomin A, Nichols D. 2011. On the separation of simultaneous-source data by inversion. 81st Annual International Meeting, SEG, Expanded Abstracts, 20-25. |
| [4] | Beck A, Teboulle M. 2009. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Img. Sci. , 2(1):183-202. |
| [5] | Berkhout A J. 2008. Changing the mindset in seismic data acquisition. The Leading Edge, 27(7), 924-938. |
| [6] | Daubechies I, Defrise M, Mol C D. 2004. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Mathe. , 57(11):1413-1541. |
| [7] | Doulgeris P, Mahdad A, Blacquière G. 2010. Separation of blended data by iterative estimation and subtraction of interference noise. 80th Annual International Meeting, SEG, Expanded Abstracts, 3514-3518. |
| [8] | Doulgeris P, Mahdad A, Blacquière G. 2011. Iterative separation of blended marine data: discussion on the coherence-pass filter. 81st Annual International Meeting, SEG, Expanded Abstracts, 26-31. |
| [9] | Doulgeris P, Verschuur D J, Blacquière G. 2012. Separation of blended data by sparse inversion utilizing surface-related multiples. 74th Annual International Meeting, EAGE, Extend Abstracts, A041. |
| [10] | Figueiredo M A T, Nowak R D. 2003. An EM algorithm for wavelet-based image restoration. IEEE Trans. Image Process, 12(8): 906-916. |
| [11] | Han L, Han L G. 2012. Seismic spectral decomposition and denoising with in-crowd algorithm. 82nd Annual International Meeting, SEG, Expanded Abstracts, 31:1-5. |
| [12] | Herrmann F J, Erlangga Y A, Lin T T Y. 2009. Compressive simultaneous full-waveform simulation. Geophysics, 74:35-40. |
| [13] | Huo S D, Luo Y, Kelamis P. 2009. Simultaneous sources separation via multi-directional vector-median filter. 79th Annual International Meeting, SEG, Expanded Abstracts, 31-35. |
| [14] | Kim Y, Gruzinov I, Guo M H, et al. 2009. Source separation of simultaneous source OBC data. 79th Annual International Meeting, SEG, Expanded Abstracts, 51-55. |
| [15] | Lin T T Y, Herrmann F J. 2009. Designing simultaneous acquisitions with compressive sensing. 71st Annual International Meeting, EAGE, Extend Abstracts, S006. |
| [16] | Mahdad A, Doulgeris P, Blacquière G. 2011. Separation of blended data by iterative estimation and subtraction of blending interference noise. Geophysics, 76:9-17. |
| [17] | Mahdad A, Doulgeris P, Blacquière G. 2012. Iterative method for the separation of blended seismic data: discussion on the algorithmic aspects. Geophysical Prospecting, 60(4): 782-801 |
| [18] | Malioutov D M, Cetin M, Willsky A S. 2005. Homotopy continuation for sparse signal representation: Proc. IEEE Int. Conf. Acoustics Speech Signal Process (ICASSP), 5. |
| [19] | Moore I, Dragoset W B, Ommundsen T, et al. 2008. Simultaneous source separation using dithered sources. 78th Annual International Meeting, SEG, Expanded Abstracts, 2806-2809. |
| [20] | Scales J A, Gersztenkorn A. 1988. Robust methods in inverse theory: Inverse Problems, 4(4):1071-1091. |
| [21] | Silverman D. 1979. Method of three dimensional seismic prospecting. US Patent, 4, 159, 463. |
| [22] | Stork M. 2003. Median filters theory and applications. Third International Conference on Electrical and Electronics Engineering Papers, 3:1-5. |
 2014, Vol. 57
2014, Vol. 57


