精密动态PPP定位技术仅用一台GPS接收机就能提供精确的位置信息,在精密卫星定轨、大地测量、航空摄影测量、海洋勘探、地球物理、军事等方面具有广阔的应用前景.同时,产生的电离层、对流层等副产品信息为构建高精度高分辨率空间大气模型提供重要的数据源(Zhang et al., 2010;张宝成,2012).但是,动态PPP精确定位的前提是模糊度准确初始化后必须保持连续,即准确修复周跳,否则严重影响PPP定位的精度,甚至使PPP定位发散,大大限制其应用.由于动态环境下GPS信号失锁比较频繁,周跳的处理相比静态PPP要困难和复杂得多,探索更有效的周跳探测与处理方法是动态PPP的关键.
近年来,许多学者对动态PPP周跳探测问题进行了深入探讨,大致分为基于观测域的周跳探测法和基于估计域的周跳探测法.基于观测域的周跳探测法是利用原始载波相位、码、多普勒观测或由此形成的具有优良特性的组合观测来探测周跳,如被广泛采用的无几何距离组合(GF组合或 L4 组合)历元间差分法(Xu et al., 2003; 徐绍铨等,2003;Zhen,2012;Cai et al., 2013;王敬和赵军祥,2011;朱绍攀等,2012).该组合消除了与频率无关的项,只与电离层延迟误差和模糊度有关,因此也称为电离层残差法.如果忽略历元间电离层延迟误差变化,L4 组合历元间差分仅与周跳有关.该方法只利用相位观测组合,精度比较高,对小周跳比较敏感.但是 该方法也存在不足:不能探测特殊的周跳,如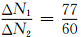 及满足某些条件的周跳(易重海等,2011);仅利用该组合只能判断观测值中是否存在周跳,但是不能定位哪个频率的观测发生了周跳;对残余电离层误差比较敏感,适合电离层平静状态下周跳探测(朱绍攀等,2012).Blewitt提出的利用Melbourne-Wubbena(MW)组合和电离层残差(GF)法相结合的周跳探测法(王敬和赵军祥,2011).MW组合需要利用码观测,因为我们所用的接收机一般不能获取高精度P码信息,因此受C/A码观测噪声、残余电离层误差、多路径误差影响,该方法探测小周跳比较困难;MW组合不能探测 ΔN1=ΔN2 的周跳.赖育网提出将CUSUM算法引入到星载GPS小周跳探测中,思想是将检测历元及以前历元的MW组合量相加,以放大小周跳的影响.该方法只能把周跳发生位置定位在一个区间内,不能准确定位哪个历元的观测发生了周跳(赖育网等,2011).刘志赵提出利用电离层TEC变化率及MW组合来探测周跳,即TECR法(Liu,2011).该方法与其他方法不同之处在于恰恰利用电离层延迟误差在历元间变化比较平稳的特点来探测周跳,而不是忽略电离层变化.实际上,该方法的思想与电离层残差法是一致的.张小红提出利用 L5-L3-LX 分级周跳探测法(Zhang and Li, 2012),其步骤为:首先利用LAMBDA和TRIM电离层模型得到的电离层信息固定宽巷周跳;再利用LAMBDA方法和解算的宽巷模糊度及 L3 组合固定窄巷周跳;最后利用 L5组合和L1、L2或L4 任一观测来解算 L1和L2 周跳,直至周跳被完全修复.由于doppler观测精度比较高,且不存在模糊度问题,在周跳探测中一般用doppler积分代替伪距观测历元间求差(Zhen,2012;丁文武,2012),但是doppler观测噪声一般在cm/s到dm/s量级,因此doppler辅助适合探测采样率比较高且大于3周的周跳.随着GPS现代化及北斗、Galileo等导航系统的建设和逐步完善,一些学者研究了基于多频数据的周跳探测方法,但是目前普通用户获取第三频数据还比较困难,双频GNSS数据质量控制仍是主要任务(Maria,2012).
及满足某些条件的周跳(易重海等,2011);仅利用该组合只能判断观测值中是否存在周跳,但是不能定位哪个频率的观测发生了周跳;对残余电离层误差比较敏感,适合电离层平静状态下周跳探测(朱绍攀等,2012).Blewitt提出的利用Melbourne-Wubbena(MW)组合和电离层残差(GF)法相结合的周跳探测法(王敬和赵军祥,2011).MW组合需要利用码观测,因为我们所用的接收机一般不能获取高精度P码信息,因此受C/A码观测噪声、残余电离层误差、多路径误差影响,该方法探测小周跳比较困难;MW组合不能探测 ΔN1=ΔN2 的周跳.赖育网提出将CUSUM算法引入到星载GPS小周跳探测中,思想是将检测历元及以前历元的MW组合量相加,以放大小周跳的影响.该方法只能把周跳发生位置定位在一个区间内,不能准确定位哪个历元的观测发生了周跳(赖育网等,2011).刘志赵提出利用电离层TEC变化率及MW组合来探测周跳,即TECR法(Liu,2011).该方法与其他方法不同之处在于恰恰利用电离层延迟误差在历元间变化比较平稳的特点来探测周跳,而不是忽略电离层变化.实际上,该方法的思想与电离层残差法是一致的.张小红提出利用 L5-L3-LX 分级周跳探测法(Zhang and Li, 2012),其步骤为:首先利用LAMBDA和TRIM电离层模型得到的电离层信息固定宽巷周跳;再利用LAMBDA方法和解算的宽巷模糊度及 L3 组合固定窄巷周跳;最后利用 L5组合和L1、L2或L4 任一观测来解算 L1和L2 周跳,直至周跳被完全修复.由于doppler观测精度比较高,且不存在模糊度问题,在周跳探测中一般用doppler积分代替伪距观测历元间求差(Zhen,2012;丁文武,2012),但是doppler观测噪声一般在cm/s到dm/s量级,因此doppler辅助适合探测采样率比较高且大于3周的周跳.随着GPS现代化及北斗、Galileo等导航系统的建设和逐步完善,一些学者研究了基于多频数据的周跳探测方法,但是目前普通用户获取第三频数据还比较困难,双频GNSS数据质量控制仍是主要任务(Maria,2012).
基于估计域的周跳探测法是利用线性化观测模型,在定位解算中利用残差信息对周跳进行探测并修复,比较有代表性的有DIA法、拟准检定法、假设检验法等(Teunissen,1998;2012;Chai et al., 2005;孔巧丽等,2005).这类方法是基于统计检验量来探测周跳,而统计检验量的可靠性是建立在大样本基础上的,这类方法比较适合静态GPS数据的质量控制.
以往周跳定位后多采用LAMBDA搜索法或直接归整确定其整数值大小并进行修复(Zhen,2012;Cai et al., 2013;王敬和赵军祥,2011;Zhu et al., 2012;Zhang and Li, 2012;张小红等,2012;郭金运等,2009),但是确定整周数需要充分的信息(张玉册和梁开龙,2002),由于受多种残余误差的影响及动态观测条件下多余观测信息比较少的限制,周跳的固定比较困难.由于动态PPP定位中没有参考基准来评定定位精度,因此周跳修复错误会直接影响动态定位的精度.
基于以上对多种动态PPP周跳探测与修复方法的分析,本文提出采用doppler观测联合 L1、L2、L4和L5 观测对周跳进行自动探测,然后对判断发生周跳的卫星作为新升起的卫星进行模糊度的重新解算,对没有发生周跳的卫星,直接采用前一历元解算的模糊度及其协方差阵进行预报和滤波的处理策略.
2 联合 L1、L2、L4、L5 历元间差分和doppler积分进行动态GPS周跳探测动态GPS周跳探测常用的检验量主要有 L1、L2和由此形成的 L4、L5 组合观测历元间差分.下面基于GPS载波相位,伪距和doppler原始观测方程,对这几种重要的检验量及能探测的最小周跳进行分析.
2.1 GPS基本观测模型载波相位、伪距和doppler观测方程:
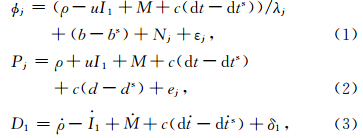
L4 组合模型为
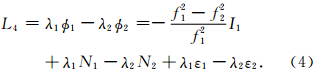

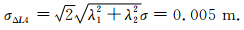 但是受组合观测残余电离层延迟误差和多路径误差等的影响,一般取 σΔL4=0.02m.
但是受组合观测残余电离层延迟误差和多路径误差等的影响,一般取 σΔL4=0.02m. 周跳判断准则为
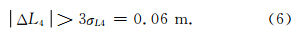
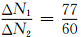 或同时发生相同的小周跳(小于2周)(Yi et al., 2011),因此仅利用该条件探测周跳存在周跳漏检的风险.
2.3 L5 组合检验量
或同时发生相同的小周跳(小于2周)(Yi et al., 2011),因此仅利用该条件探测周跳存在周跳漏检的风险.
2.3 L5 组合检验量 L5 组合表示形式为
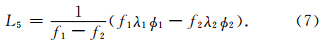
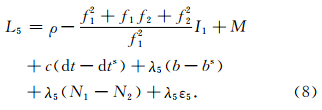
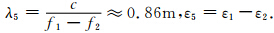 . 由式(8)可知,相位宽巷组合与单个频率的相位观测方程类似,只是波长变长,电离层延迟参数的系数发生了变化,因此 L5 比较适合周跳探测.忽略历元间残余大气延迟误差,并顾及相位偏差的稳定性,对 L5 进行历元间差分得
. 由式(8)可知,相位宽巷组合与单个频率的相位观测方程类似,只是波长变长,电离层延迟参数的系数发生了变化,因此 L5 比较适合周跳探测.忽略历元间残余大气延迟误差,并顾及相位偏差的稳定性,对 L5 进行历元间差分得
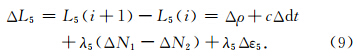
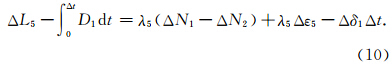
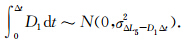 由误差传播律得:σΔL5-D1Δt=
由误差传播律得:σΔL5-D1Δt= 如果采样间隔为1 s,σΔL5-D1Δt≈0.2m,当采样间隔达到5 s时,σΔL5-D1Δt≈0.7m,因此doppler辅助一般适合采样间隔小于5 s的周跳探测.当采样间隔为1 s时,周跳判断准则为
如果采样间隔为1 s,σΔL5-D1Δt≈0.2m,当采样间隔达到5 s时,σΔL5-D1Δt≈0.7m,因此doppler辅助一般适合采样间隔小于5 s的周跳探测.当采样间隔为1 s时,周跳判断准则为
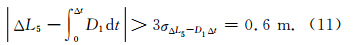
综合以上分析可知,如果检验量符合条件(6)式或(11)式,可以判定相位观测中发生了周跳,但是需要进一步确定周跳发生在哪个频率的观测上.反之,需要检验两个频率的相位观测是否同时发生相同的小周跳(小于2周),本文提出再结合 L1、L2 观测信息来定位和探测小周跳.
2.4 联合 L1、L2 历元间差分和doppler积分定位周跳L1、L2 观测历元间差分和doppler积分求差形成检验量为
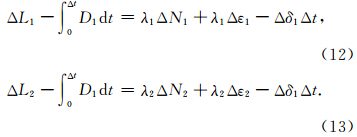
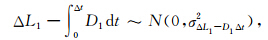
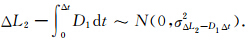 当采样间隔为1 s 时,由误差传播律可得: σΔL1-D1Δt=σΔL2-D1Δt≈0.1m.
当采样间隔为1 s 时,由误差传播律可得: σΔL1-D1Δt=σΔL2-D1Δt≈0.1m.
判断准则:
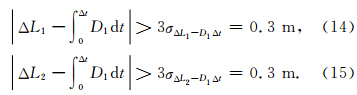
通过分析周跳探测的检验量(6)、(11)、(14)式和(15)式,制定如下周跳自动探测和定位步骤:
(一)如果检验量满足条件(6)式(或(11)式)和(14)式,判定 L1 发生周跳;
(二)如果检验量满足条件(6)式(或(11)式)和(15)式,判定 L2 发生周跳;
(三)如果检验量满足条件(6)式(或(11)式)和(14)式、(15)式,判定 L1和L2 都发生周跳.
3.2 动态PPP定位模型动态PPP定位采用扩展 Kalman滤波模型为(Zhang et al., 2010)

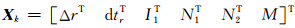 为状态参数,假设k时刻观测到m颗卫星,状态参数共有3m+5个,则各分量为 Δr 为接收机3维位置改正量、dtr 为接收机钟差、 I1 为 f1 频率上m维站星斜向电离层延迟误差、 N1,N2 为L1、L2的m维模糊度、 M 为1维天顶对流层延迟误差.Φk,k-1=
为状态参数,假设k时刻观测到m颗卫星,状态参数共有3m+5个,则各分量为 Δr 为接收机3维位置改正量、dtr 为接收机钟差、 I1 为 f1 频率上m维站星斜向电离层延迟误差、 N1,N2 为L1、L2的m维模糊度、 M 为1维天顶对流层延迟误差.Φk,k-1=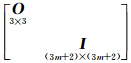 为状态转移矩阵,O 3×3 为3阶零矩阵,
为状态转移矩阵,O 3×3 为3阶零矩阵,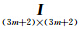 为(3m+2)阶单位阵. Lk 为经过超过厘米量级的系统误差改正后的码和相位观测值减去由接收机近似坐标和卫星精密坐标计算的近似距 离形成的观测量.动态PPP中,接收机近似坐标 由伪距定位实时计算. Hk 为线性化系数阵. ωk-1~N(0,Qk-1)、wk~N(0,Rk)分别为服从正态分布的状态噪声和观测噪声.
3.3 动态PPP周跳处理策略
为(3m+2)阶单位阵. Lk 为经过超过厘米量级的系统误差改正后的码和相位观测值减去由接收机近似坐标和卫星精密坐标计算的近似距 离形成的观测量.动态PPP中,接收机近似坐标 由伪距定位实时计算. Hk 为线性化系数阵. ωk-1~N(0,Qk-1)、wk~N(0,Rk)分别为服从正态分布的状态噪声和观测噪声.
3.3 动态PPP周跳处理策略 模糊度参数:如果根据3.1节判定某颗卫星发生了周跳,将该卫星作为新升起的卫星,在滤波模型中重新初始化该卫星的模糊度参数及其方差阵,即利用伪距减相位观测值重新计算该卫星的模糊度初值,方差重新配置为102m2.对于连续跟踪的卫星,模糊度参数作为时不变参数,利用前一历元估计的模糊度参数及其方差协方差阵直接代入当前历元的滤波方程中.
其他参数的处理与常用的动态PPP处理一致:位置参数作为时变参数处理,每个历元利用码定位结果进行初始化,方差重新配置为1002m2;接收机钟差参数由于稳定性比较差,用白噪声模型来描述,每个历元进行估计;斜向电离层延迟误差参数根据纬度不同采用不同的模型,对于中高纬地区,用高斯-马尔科夫模型或随机游走模型来描述,对于低纬地区,电离层变化比较剧烈,用白噪声模型来描述.本文数据采集于深圳,纬度比较低,因此本文采用白噪声模型描述电离层参数.天顶对流层参数采用分段线性模型描述,动态定位时采用每2 min进行一次更新,静态PPP一般15 min进行一次更新.
这一处理策略的优势是:只要有不少于4颗的卫星连续跟踪,就能保证动态PPP定位精度的稳定,同时,精确的位置信息也可使发生周跳的卫星的模糊度快速收敛,避免周跳修复不准影响整个动态PPP定位精度.
4 实验结果分析 4.1 实验数据为了验证新方案周跳探测及处理的效果,利用一套船载双天线GPS实测数据进行检验,其中一台是Trimble接收机,另一台是NovAtel接收机,天线位置如图 1.数据采集于深圳海域2012-07-10 UTC 时间1 ∶ 53 ∶ 50—7 ∶ 15 ∶ 10,采样率1 Hz.开始时,海面比较平静,3 h后海面有4~5 m的海浪.
 |
图 1 接收机天线位置图 Fig. 1 The locations of the GPS receivers on the ship |
首先利用本文提出的周跳探测及处理策略分别对两台GPS接收机数据进行动态PPP定位,然后将PPP定位结果做差求基线长度,并和双差基线结果进行比较,来验证新方案的效果.船的运动轨迹及高程变化如图 2.
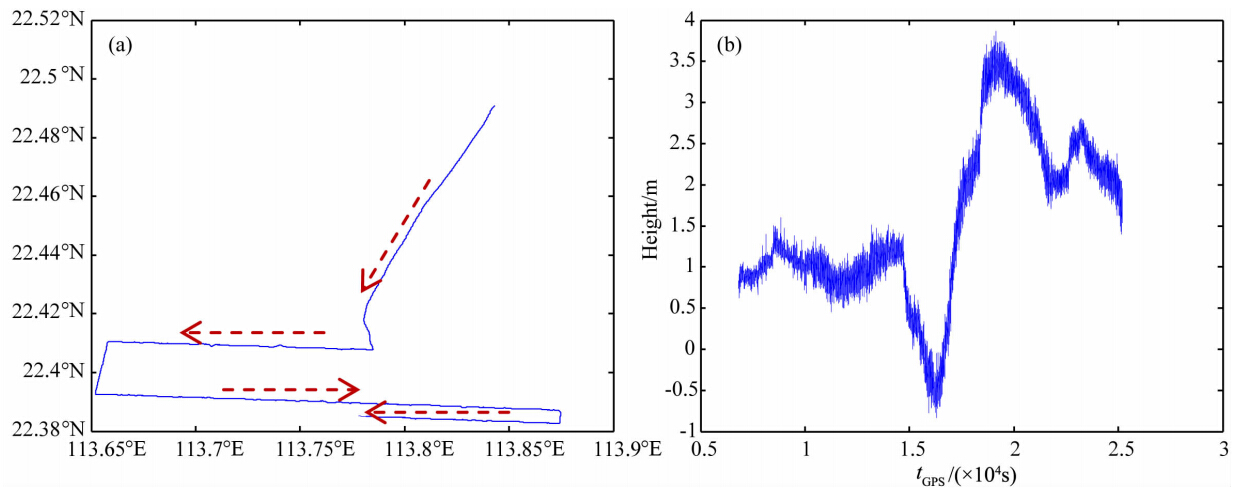 |
图 2 船运动轨迹及高程变化 Fig. 2 The trajectory and height of the ship |
利用新方案探测到NovAtel接收机6、7、11、19、20号和30号卫星发生周跳.下面给出这些卫星周跳探测结果,如图 3,其中 dL1-D1、dL2-D1、dL5-D1 分别表示 L1、L2、L5 历元间差分与doppler积分之差,dL4 表示 L4 历元间差分.
从图 3各卫星检验量随时间变化可知:6、7、19号卫星周跳发生比较少,而11、20和30号卫星周跳 发生比较频繁,尤其是20号卫星.这主要是由于 NovAtel天线安装的位置距离船甲板比较近,船上 的栏杆等对其遮挡造成的.以6号卫星发生周跳的 7860时刻为例,分析如何根据各量的变化判定周跳.首先根据该时刻检验量:
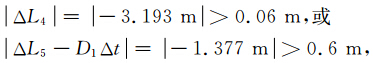
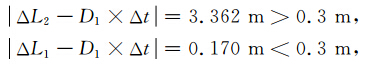
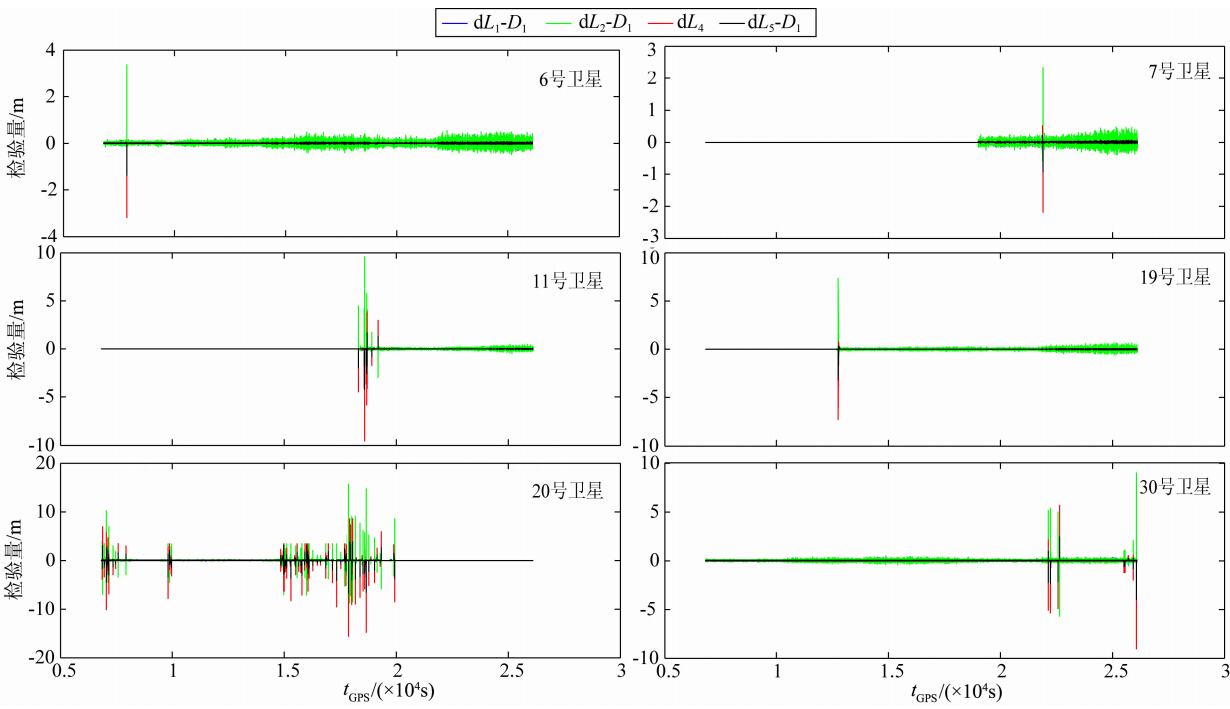 |
图 3 探测到发生周跳的卫星4种检测量变化序列 Fig. 3 Time series of the satellites for cycle-slips detection |
如果探测到卫星在某时刻发生周跳,将其在该时刻作为新升起的卫星,重新计算模糊度初值及方差.但是,对于20号卫星,由于受干扰非常严重,如果在发生周跳的时刻将其做新星处理,需要不断重新计算模糊度,不仅大大增加了计算负担,而且20号卫星一直处于未收敛情况,对动态PPP定位贡献不大,因此在处理中直接将该卫星的观测删除.为了检验新处理策略的效果,分别利用新方案和周跳探测与修复方案,对两台船载GPS接收机数据分别进行动态PPP定位结果再求差,计算两个接收机形成的基线长度,并以双差解算的基线长度为参考,计算两种方案的基线误差,结果如图 4.由于基线比较短且长度固定,双差计算结果为:基线均值12.045 m,标准差0.0066 m.
由图 4可知,(1)对探测到发生周跳的观测采用周跳修复方案,由于某些历元模糊度固定错误,导致该历元PPP定位存在比较大的误差;(2)PPP定位误差开始时约0.5 m,收敛后平静状态下在0.1 m以内,2~3 m海浪状况下,定位误差在0.2 m以内,这与目前动态PPP定位精度相当,说明本文提出的周跳探测及处理策略是可行的.
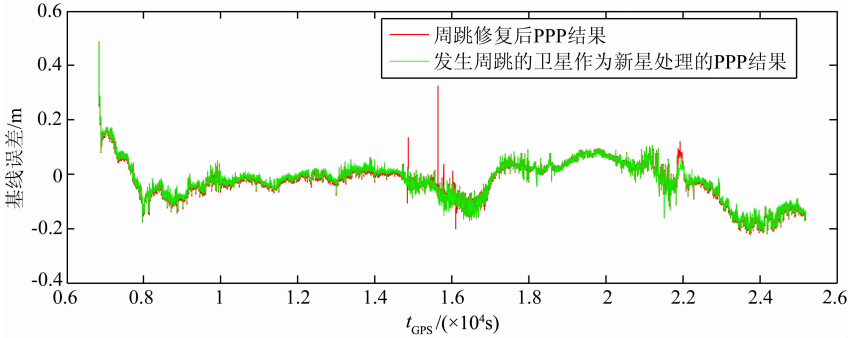 |
图 4 两种方案计算的基线误差 Fig. 4 Baseline errors of the new program and the previous program |
另外,利用该方案对GPS/GLONASS/BD多导航系统的观测数据进行了处理,周跳探测效果比较好,由于篇幅限制,将在另文中介绍.
5 讨论本文提出的周跳探测与处理策略具有如下优点:
(1)利用 L1、L2、L5、L4 历元间差分,联合doppler 积分综合探测动态PPP观测中的周跳不仅能探测特殊的周跳,而且能准确定位周跳;
(2)采用将发生周跳的卫星作为新星处理,不仅减少了周跳固定的计算负担,而且避免了由于观测信息不足导致周跳固定错误,影响动态PPP定位精度.
当然,动态GNSS数据受多种环境因素影响,预处理工作非常复杂和棘手,新算法还需要通过大
量的动态GNSS数据进行测试,以便进一步完善新方法.
致谢本文船载多天线GPS数据采集得到国家海洋局第二海洋研究所罗孝文博士后的大力支持,在此表示感谢.
| [1] | Cai C S, Liu Z Z, Xia P F, et al. 2013. Cycle slip detection and repair for undifferenced GPS observations under high ionospheric activity. GPS Solut. , 17(2): 247-260. |
| [2] | Chai Y J, Ou J K, Ren C. 2005. Method for detecting and repairing cycle slips in GPS navigation. Transactions of Nanjing University of Aeronautics & Astronautics, 22(2): 119-123. |
| [3] | Ding W W. 2012. Research on key technologies of real time precise point positioning system[Doctor's thesis](in Chinese). Beijing: University of Chinese Academy of Sciences.. |
| [4] | Guo J Y, Sun J L, Ju X L, et al. 2009. Solution of ambiguity and cycle slip for satellite-borne GPS phase data with wide-lane/ narrow-lane method. Science of Surveying and Mapping (in Chinese), 34(6): 89-91. |
| [5] | Kong Q L, Ou J K, Chai Y J. 2005. Detection and repair for gross errors and cycle slips in LEO based on GPS data on zero level. Journal of Geodesy and Geodynamics (in Chinese), 25(4): 105-109. |
| [6] | Lai Y W, Zhang Y S, Cheng H W, et al. 2011. Satellite-borne dual frequency GPS cycle-slip detection based on CUSUM algorithm. Science of Surveying and Mapping (in Chinese), 36(1): 42-44. |
| [7] | Liu Z Z. 2011. A new automated cycle slip detection and repair method for a single dual-frequency GPS receiver. J. Geod. , 85(3): 171-183. |
| [8] | Lacy M C D, Reguzzoni M, Sanso F. 2012. Real-time cycle slip detection in triple-frequency GNSS. GPS Solut. , 16(3): 353-362. |
| [9] | Teunissen P J G, Bakker P F. 2012. Next Generation GNSS Single Receiver Cycle Slip Reliability. VⅡ Hotine-Marussi Symposium on Mathematical Geodesy. Berlin Heidelberg: Springer-Verlag, 159-164. |
| [10] | Teunissen P J G. 1998. Quality Control and GPS. GPS for Geodesy. Berlin Heidelberg: Springer-Verlag. |
| [11] | Wang J, Zhao J X. 2011. An improvement of Blewitt cycle slip detection. Journal of Spacecraft TT&C Technology (in Chinese), 30(2): 80-83. |
| [12] | Xu G C. 2003. GPS Theory, Algorithms and Applications. Berlin Heidelberg, New York: Springer-Verlag. |
| [13] | Xu S Q, Zhang H H, Yang Z Q, et al. 2003. GPS Measurement Principle & Application (The second Edition) (in Chinese). Wuhan: Wuhan University Press. |
| [14] | Yi C H, Zhu J J, Chen Y Q, et al. 2011. Cycle-Slip detection and correction algorithm for real-time PPP. Geomatics and Information Science of Wuhan University (in Chinese), 36(11): 1314-1319. |
| [15] | Zhang B C, Ou J K, Yuan Y B, et al. 2010. Yaw attitude of eclipsing GPS satellites and its impact on solutions from precise point positioning. Chinese Science Bulletin, 55(32): 3687-3693. |
| [16] | Zhang B C, Teunissen J G P, Odijk D, et al. 2012. Rapid integer ambiguity-fixing in precise point positioning. Chinese J. Geophy. (in Chinese), 55(7): 2203-2211. |
| [17] | Zhang X H, Li X X. 2012. Instantaneous re-initialization in real-time kinematic PPP with cycle slip fixing. GPS Solut. , 16(3): 315-327. |
| [18] | Zhang X H, Guo F, Li P, et al. 2012. Real-time quality control procedure for GNSS precise point positioning. Geomatics and Information Science of Wuhan University (in Chinese), 37(8): 940-944. |
| [19] | Zhang Y C, Liang K L. 2002. Automated cycle-slip correction of dual-frequency kinematic GPS data. Bulletin of Surveying and Mapping (in Chinese), (7): 3-4. |
| [20] | Zhen D. 2012. MATLAB software for GPS cycle-slip processing. GPS Solut. , 16(2): 267-272. |
| [21] | Zhu S P, Sun X R, Zhang S B. 2012. Research on mixed-method algorithm forcycle slips detection and correction. Geotechnical Investigation & Surveying (in Chinese), 40(5): 68-72 |
| [22] | 丁文武. 2012. 实时精密单点定位系统的若干关键技术研究[博士论文]. 北京: 中国科学院大学. |
| [23] | 郭金运, 孙佳龙, 鞠晓蕾等. 2009. 基于宽巷/窄巷法的星载GPS相位数 据的模糊度解算和周跳探测. 测绘科学, 34(6): 89-91. |
| [24] | 孔巧丽, 欧吉坤, 柴艳菊. 2005. 星载GPS相位非差观测粗差和周跳的探测与修复. 大地测量与地球动力学, 25(4): 105-109. |
| [25] | 赖育网, 张寅生, 程洪玮等. 2011. CUSUM算法的星载双频GPS周跳探测研究. 测绘科学, 36(1): 42-44. |
| [26] | 王敬, 赵军祥. 2011. Blewitt周跳探测方法的改进. 飞行器测控学报, 30(2): 80-83. |
| [27] | 徐绍铨, 张华海, 杨志强等. 2003.GPS测量原理及应用(第二版). 武汉: 武汉大学出版社. |
| [28] | 易重海, 朱建军, 陈永奇等. 2011. 实时精密单点定位中周跳探测与修复的算法研究. 武汉大学学报: 信息科学版, 36(11): 1314-1319. |
| [29] | 张宝成, Teunissen J G P, Odijk D等. 2012. 精密单点定位整周模糊度快速固定. 地球物理学报, 55(7): 2203-2211. |
| [30] | 张小红, 郭斐, 李盼等. 2012. GNSS精密单点定位中的实时质量控制. 武汉大学学报(信息科学版), 37(8): 940-944. |
| [31] | 张玉册, 梁开龙. 2002. 双频动态GPS观测数据周跳的自动改正. 测绘通报, (7): 3-4. |
| [32] | 朱绍攀, 孙小荣, 张书毕. 2012. 多方法混合周跳探测与修复算法研究. 工程勘察, 40(5): 68-72. |
 2014, Vol. 57
2014, Vol. 57

