2. 武汉科技大学理学院, 武汉 430081
2. College of Science, Wuhan University of Science and Technology, Wuhan 430081, China
21世纪是利用卫星跟踪卫星技术(SST)和卫 星重力梯度技术(SGG)提升对“数字地球”认知能 力的新纪元. 重力卫星CHAMP(CHAllenging Minisatellite Payload)、GRACE(Gravity Recovery and Climate Experiment)和GOCE(Gravity field and steady-state Ocean Circulation Explorer)的成功升空以及GRACE Follow-On的即将发射昭示着人类将迎来一个前所未有的卫星重力探测时代. CHAMP、GRACE和GOCE卫星各有所长,它们的相继发射不是相互竞争而是互相补充. CHAMP是卫星重力测量计划成功实施的先行者,GRACE的优越性体现于可高精度探测地球重力场的中长波信号及时变(2≤L≤120阶),而GOCE擅长于感测地球中短波静态重力场(120<L≤250阶)(郑伟等,2011a),因此联合求解GRACE和GOCE的卫星观测数据有利于反演高精度、高空间分辨率和全频段的地球重力场. 基于GRACE卫星重力测量计划高精度探测地球中长波静态和长波时变重力场的巨大贡献(Jekeli,1999; Reigber et al., 2005; 张捍卫等,2004; 沈云中等,2005; Tapley et al., 2005; Zheng et al., 2005,2011,2012a,2012b; 程芦颖和许厚泽,2006; 郑伟等, 2006,2008,2009a,2009b,2009c; 周旭华等,2006; Xu,2008),美国宇航局(NASA)提出了下一代专用于地球中短波静态和中长波时变重力场精密探测的GRACE Follow-On卫星重力测量计划. GRACE Follow-On双星预期采用近圆、近极和超低轨道设计,利用激光干涉测距系统高精度测量星间距离和星间速度,利用高轨GPS(Global Positioning System)卫星对低轨双星精密跟踪定位,利用非保守力补偿系统(DFACS)高精度消除双星受到的非保守力,利用恒星敏感器精密测量卫星和载荷的空间三维姿态. 由于激光具有超短波长和极好的波长稳定性,因此利用GRACE Follow-On星载激光干涉测距系统获得的星间距离和星间速度精度至少比GRACE星载K波段测距系统精度高1个数量级.
目前国内外科研机构均基于卫星跟踪卫星高低/低低(SST-HL/LL)观测原理开展了GRACE Follow-On地球重力场的需求论证和反演研究(Stephens et al., 2006; Flechtner et al., 2009; Loomis, 2009,2012; Zheng et al., 2009; 郑伟等, 2010,2012). 由于GRACE Follow-On双星系统相当于基线长为星间距离50 km的一维水平重力梯度仪,因此利用GRACE Follow-On卫星观测数据能否获得更高精度的地球中高频重力场信息是当前卫星重力反演领域的研究热点之一. Rummel等(1993)利用扭称原理测量了GRACE重力梯度仪的精度;Keller和Heβ(1998)开展了GRACE卫星重力梯度测量的原理研究;Keller和Sharifi(2005)围绕GRACE双星加速度差的线性近似、三次方近似、改进的线性近似、以及线性和三次方混合近似等方法开展了GRACE卫星重力梯度反演的论证研究,但在建立的卫星观测方程中直接将卫星受到的合外力等效为地球引力,而未考虑保守力(日月引力,地球固体潮、海潮、大气潮、极潮汐力,以及相对论效应等)和非保守力(大气阻力、太阳光压、地球辐射压、轨道高度和姿态控制力等)对GRACE卫星系统的实质性影响. 不同于前人已有研究,本文首次将地球引力加速度差按照泰勒展开进而获得地球引力位的二阶张量,并在卫星重力梯度观测方程中加入保守力和非保守力的综合影响,进而精确和快速反演了120阶GRACE Follow-On卫星重力梯度地球重力场.
GRACE Follow-On卫星重力梯度反演法的优点如下:由于SST-HL/LL模式主要感测地球重力场的中长波信号,SGG模式敏感于地球重力场的中短波信号,因此,其旨在联合SST-HL/LL和SGG模式的优点,有利于进一步提高全频段地球重力场的反演精度;缺点如下:由于GRACE Follow-On双星仅相当于基线长为星间距离的一维水平重力梯度仪(Vxx),无法同时获得垂向和径向(Vyy和Vzz)的重力梯度信息,因此其对地球重力场中高频信号的灵敏度低于当前GOCE重力梯度卫星. 综上所述,由于下一代GRACE Follow-On卫星重力计划仍采用SST-HL/LL模式,因此GRACE Follow-On卫星重力梯度反演法有利于适当弥补SST-HL/LL模式的缺陷,有望成为下一代高精度、高空间分辨率和全频段地球重力场模型建立的优选方法. 2 方法 2.1 卫星重力梯度观测方程建立
如图 1所示,地心惯性坐标系OI-XIYIZI的原点OI位于地球的质心,XI轴的正方向指向历元的平春分点,ZI轴的正方向指向地球的北极,YI轴和XI、ZI轴成右手螺旋法则关系. 星体坐标系OS1(2)-XS1(2)YS1(2)ZS1(2)的原点OS1(2)分别位于双星各自的质心;XS1(2)(翻滚轴)的正方向分别由坐标原点指向激光干涉测距系统的相位中心,XS1和XS2的正方向反向共线;ZS1(2)(偏航轴)垂直于XS1(2)轴且位于同一轨道平面内;YS1(2)(倾斜轴)垂直于轨道平面且与XS1(2)、ZS1(2)轴成右手螺旋法则关系.
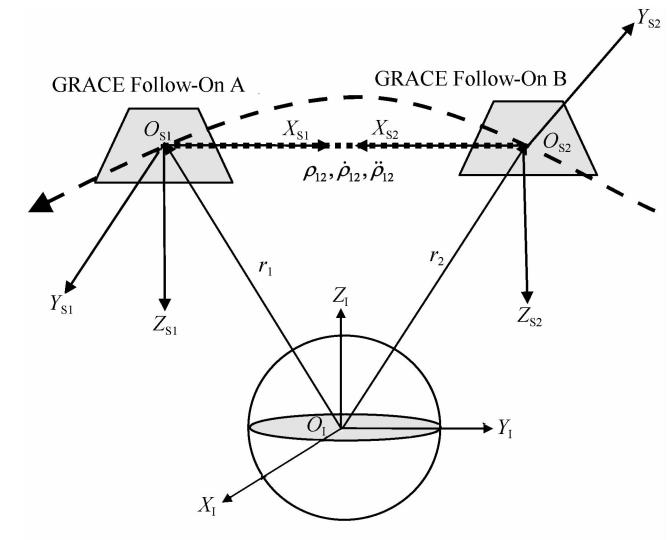 |
图 1 GRACE Follow-On双星系统的星间距离ρ12、
星间速度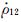 和星间加速度 和星间加速度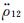 的测量原理
Fig. 1 Measurement principles of intersatellite range ρ12,intersatellite range-rate 的测量原理
Fig. 1 Measurement principles of intersatellite range ρ12,intersatellite range-rate 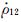 and intersatellite range- acceleration and intersatellite range- acceleration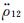 from the twin GRACE Follow-On satellites from the twin GRACE Follow-On satellites |
在地心惯性系OI-XIYIZI中,GRACE Follow-On-A/B系统的星间距离ρ12表示如下:

其中,
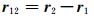 表示GRACE Follow-On-A/B双星的轨道位置矢量差,r 1和r2表示双星各自的轨道位置矢量;e12= r 12/r12表示由GRACE Follow-On-B卫星指向GRACE Follow-On-A卫星的单位矢量.
表示GRACE Follow-On-A/B双星的轨道位置矢量差,r 1和r2表示双星各自的轨道位置矢量;e12= r 12/r12表示由GRACE Follow-On-B卫星指向GRACE Follow-On-A卫星的单位矢量.
在(1)式两边同时对时间t求一阶导数,可得GRACE Follow-On-A/B系统的星间速度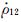
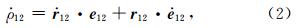
其中,
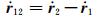 表示GRACE Follow-On-A/B双星的轨道速度矢量差,
表示GRACE Follow-On-A/B双星的轨道速度矢量差,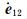 表示垂直于GRACE Follow-On-A/B双星连线方向的单位矢量
表示垂直于GRACE Follow-On-A/B双星连线方向的单位矢量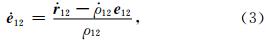
由于
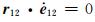 ,所以(2)式可简化为
,所以(2)式可简化为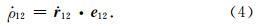
在(4)式两边同时对时间t求一阶导数,可得GRACE Follow-On-A/B系统的星间加速度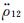
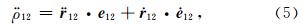
其中,
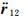 表示GRACE Follow-On-A/B双星的轨道加速度矢量差.
表示GRACE Follow-On-A/B双星的轨道加速度矢量差.
在(5)式中,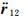 的具体形式表示如下:
的具体形式表示如下:
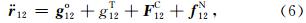
其中,
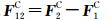 表示除地球引力之外的作用于GRACE Follow-On-A/B双星的所有保守力差(包括日月引力,地球固体潮、海潮、大气潮和极潮摄动力,广义相对论效应摄动力等),
表示除地球引力之外的作用于GRACE Follow-On-A/B双星的所有保守力差(包括日月引力,地球固体潮、海潮、大气潮和极潮摄动力,广义相对论效应摄动力等),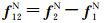 表示作用于GRACE Follow-On-A/B双星的所有非保守力差(包括大气阻力、太阳光压、地球辐射压、卫星轨道高度及姿态控制力、经验摄动力等),
表示作用于GRACE Follow-On-A/B双星的所有非保守力差(包括大气阻力、太阳光压、地球辐射压、卫星轨道高度及姿态控制力、经验摄动力等),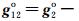
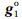 表示作用于GRACE Follow-On-A/B双星的地球中心引力差
表示作用于GRACE Follow-On-A/B双星的地球中心引力差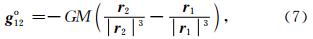
其中,GM表示地球质量M和万有引力常数G之积,
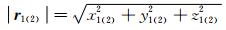 表示GRACE Follow-On-A/B 双星各自的地心半径,x1(2),y1(2),z1(2)表示双星各自位置矢量r 1(2)的三个分量.
表示GRACE Follow-On-A/B 双星各自的地心半径,x1(2),y1(2),z1(2)表示双星各自位置矢量r 1(2)的三个分量.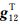 表示作用 于GRACE Follow-On-A/B双星的地球扰动引力差
表示作用 于GRACE Follow-On-A/B双星的地球扰动引力差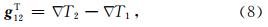
其中,ΔT1和ΔT2分别表示GRACE Follow-On-A/B双星的地球扰动位梯度. 在GRACE Follow-On-A卫星质心处将GRACE Follow-On-B卫星的扰动位梯度ΔT2按泰勒展开(取零阶和一阶项)
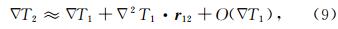
其中,Δ2T1表示GRACE Follow-On-A卫星的地球扰动位二阶梯度.O(ΔT1)表示ΔT2按泰勒展开的二阶项以上的高阶小量. 数值计算结果表明:由于O(ΔT1)的误差量级小于10-14 m·s-2,较关键载荷(如加速度计精度10-11 ~ 10-13 m·s-2)测量误差至少小1/10,因此对下一代GRACE Follow-On地球重力场反演精度的影响可忽略.
将(9)式代入(8)式可得
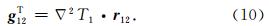
联合(1)、(3)、(5)、(6)、(7)和(10)式,GRACE Follow-On卫星重力梯度观测方程表示如下:
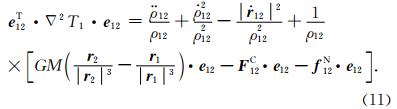
本文基于预处理共轭梯度迭代法(郑伟等,2011b)精确和快速求解了GRACE Follow-On卫星重力梯度观测方程(11). 预处理共轭梯度迭代法是目前求解大规模线性超定方程组最有效的迭代方法之一. 另外,据数值模拟计算可知:由于本文反演地球重力场的阶数截断至120阶,正规方阵病态性对 地球重力场精度影响较小,因此本文在解算GRACE Follow-On 卫星重力梯度观测方程(11)时未采用正则化方法(如Kaula、Tikhonov等)抑制地球重力场高频误差. 2.2 地球扰动位的一阶梯度
在球坐标系中,地球扰动位T(r,θ,λ)表示如下:
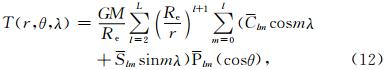
其中,r,θ和λ分别表示卫星的地心半径、地心余纬度和地心经度,Re表示地球平均半径;plm(cosθ)表示规格化的Legendre函数,l表示阶数,m表示次数;Clm和Slm表示待求的规格化地球引力位系数.
地球扰动位梯度Δ T在球坐标系(r,θ,λ)和直角坐标系(x,y,z)中的转换关系表示如下:
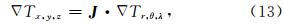
其中,Δ Tr,θ,λ表示T对(r,θ,λ)的偏导数
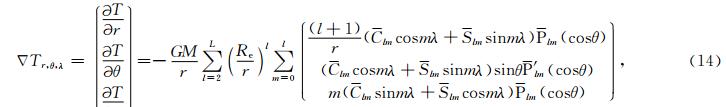
其中,Legendre函数plm(cosθ)表示如下(Koop,1993):
初值表示如下:
系数表示如下:
Legendre函数的一阶导数 ′ lm(cosθ)表示如下:
初值表示如下:
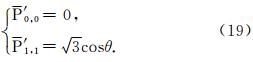
J表示由Δ Tr,θ,λ到Δ Tx,y,z的转换矩阵,
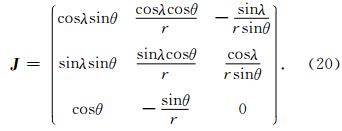
2.3 地球扰动位的二阶梯度
地球扰动位的二阶梯度表示如下:
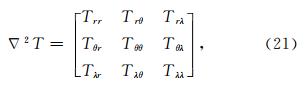
其中,
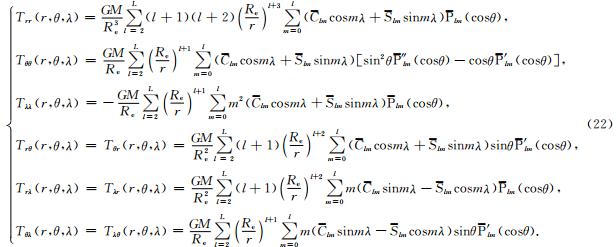
Legendre函数的二阶导数 ″ lm(cosθ)表示如下:
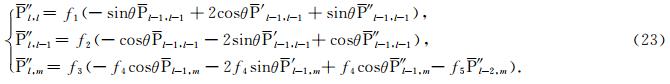
初值表示如下

(21)式可改写为:
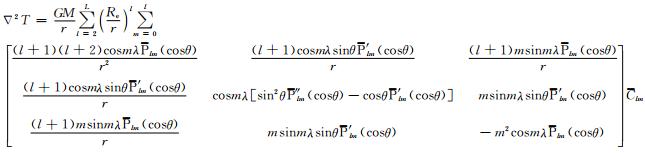
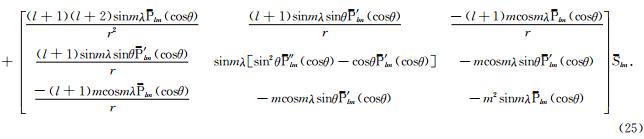
基于Newton-Gregory插值模型,星间距离ρ12的泰勒展开表示如下:
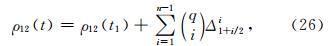
其中,
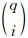 表示二项式系数,
表示二项式系数,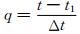 ,t1表示初始时间,t表示插值点时间,Δt表示采样间隔;
,t1表示初始时间,t表示插值点时间,Δt表示采样间隔;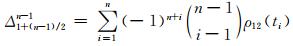 表示差分算子,n表示插值点数.
表示差分算子,n表示插值点数.
在(26)式两边同时对时间t求二阶导数可得星间加速度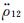 展开公式
展开公式
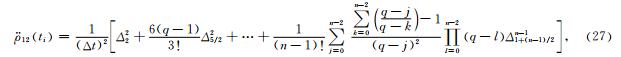
其中,9点Newton-Gregory插值公式表示如下:
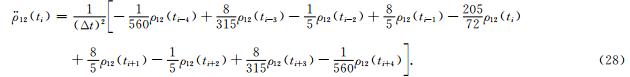
3 结果 3.1 卫星轨道模拟
在卫星重力梯度观测方程(11)建立之后,本文首先利用9阶Runge-Kutta线性单步法结合12阶Adams-Cowell线性多步法数值积分公式分别模拟了当前GRACE-A/B和下一代GRACE Follow-On-A/B双星的轨道位置和轨道速度,轨道模拟参数如表 1所示. 图 2表示GRACE Follow-On-A卫星在地心惯性坐标系OI-XIYIZI(图 1)中XIYI平面内的轨迹投影.
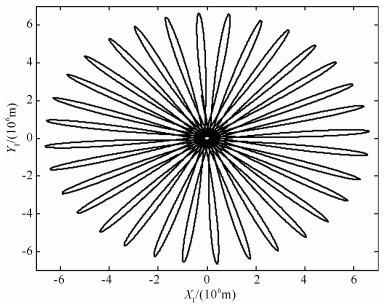 |
图 2 GRACE Follow-On-A卫星在XIYI平面内的轨迹图(1天) Fig. 2 One-day tracks of the GRACE Follow-On-A satellite in the XIYI-plane |
如图 3所示,十字线表示德国波兹坦地学研究中心(GFZ)公布的120阶EIGEN-GRACE02S地球重力场模型的实测精度,在120阶处累计大地水准面精度为1.893×10-1 m;虚线和实线分别表示基于GRACE和GRACE Follow-On卫星重力梯度法,利用卫星轨道参数(表 1)和关键载荷精度指标(表 2),反演地球重力场的模拟精度,在120阶处累计大地水准面精度分别为1.708×10-1 m和9.331×10-4 m;在各阶处的累计大地水准面精度统计结果如表 3所示. 研究结果表明:
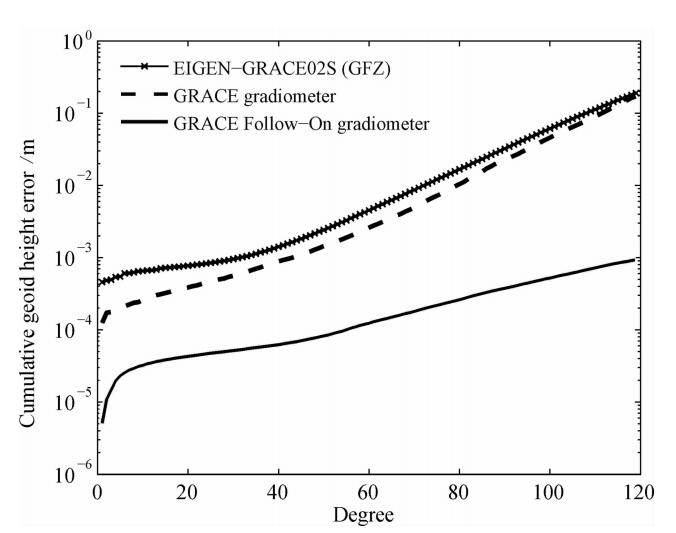 |
图 3 基于GRACE和GRACE Follow-On卫星重力梯度法反演累计大地水准面精度对比 Fig. 3 A comparison of cumulative geoid height errorsbased on the GRACE and GRACE Follow-On satellitegravity gradiometry method |
| 表 1 GRACE和GRACE Follow-On卫星轨道模拟参数 Table 1 Simulation parameters of the GRACE and GRACE Follow-On satellite orbits |
| 表 2 当前GRACE和下一代GRACE Follow-On卫星关键载荷精度指标 Table 2 Statistics of the measurement accuracies of key payloads from the current GRACE and next-generation GRACE Follow-On satellites |
| 表 3 GRACE和GRACE Follow-On累计大地水准面精度统计 Table 3 Statistics of cumulative geoid height errors from GRACE and GRACE Follow-On |
第一,据图 3中十字线和虚线对比可知,在120阶内,通过GRACE卫星重力梯度法反演地球重力 场精度较EIGEN-GRACE02S模型精度平均提高 72%.主要原因分析如下:由于当前的动力法、能量法、加速度法等均基于SST观测模式解算GRACE地球重力场,而GRACE卫星重力梯度法通过联合SST和SGG观测模式的优点反演地球重力场,因此有利于进一步提高地球重力场的解算精度.
第二,据图 3中十字线和实线对比可知,基于下一代GRACE Follow-On卫星重力计划解算地球重力场精度较当前GRACE计划平均提高61倍,因此GRACE Follow-On卫星重力梯度法是建立下一代高精度和高空间分辨率地球重力场模型的有效途径. 主要原因分析如下:(1)GRACE Follow-On(200~300 km)卫星轨道高度低于GRACE(400~500 km). GRACE卫星采用加速度计实时测量非保守力,在数据后处理中再扣除非保守力. 由于非保守力随着卫星轨道高度降低而急剧增加,因此GRACE卫星无法采用超低轨道设计. GRACE Follow-On卫星将采用非保守力补偿系统精确屏蔽作用于卫星的非保守力,因此可实质性降低卫星轨道高度,进而有效抑制地球重力场信号随轨道高度的衰减.(2)GRACE Follow-On卫星关键载荷测量 精度高于GRACE. GRACE卫星采用K波段测距系统测量星间距离(10 μm)和星间速度(1 μm/s),利用加速度计测量卫星受到的非保守力(10-10 m·s-2). GRACE Follow-On卫星基于激光干涉测距系统高精度测量星间距离(10~1000 nm)和星间速度(1~100 nm/s),通过非保守力补偿系统消除作用于卫星的非保守力(10-11~10-13 m·s-2)效应.(3)GRACE Follow-On星间距离短于GRACE. 适当增加星间距离有利于提高地球长波重力场的精度,适当缩短星间距离有利于提高地球短波重力场的精 度. GRACE Follow-On(50~100 km)卫星较GRACE(220 km)缩短了星间距离,进一步提高了地球中高频重力场的感测精度. 4 结论
基于当前GRACE卫星重力测量计划对相关学科(大地测量学、地球物理学、海洋学、水文学、冰川学等)的卓越贡献和固有局限性(轨道高度无法降低、载荷精度无法提高等),国内外众多学者正在积极寻求下一代更高时空分辨率的卫星重力测量计划. 基于以上原因,本文通过联合星间距离、星间速度、星间加速度、以及地球引力位二阶张量数据精确和快速反演了120阶GRACE Follow-On地球重力场. 研究结果显示:基于将来GRACE Follow-On卫星反演地球重力场精度较当前GRACE卫星至少提高10倍,因此GRACE Follow-On卫星重力梯度反演法有利于建立下一代高精度和高空间分辨率的地球重力场模型.
致谢感谢匿名评审专家和编辑对本文的帮助. 感谢美国宇航局(NASA)提供了GRACE Follow-On卫星的相关资料.
| [1] | Cheng L Y, Xu H Z. 2006. The rotation of the gravity potential on the Earth's gravity field recovery. Chinese J. Geophys. (in Chinese), 49(1): 93-98. |
| [2] | Flechtner F, Neumayer K H, Doll B, et al. 2009. GRAF-A GRACE follow-on mission feasibility study. Geophysical Research Abstracts, Vol. 11, EGU2009-8516. |
| [3] | Jekeli C. 1999. The determination of gravitational potential differences from satellite-to-satellite tracking. Celestial Mechanics and Dynamical Astronomy, 75(2): 85-101. |
| [4] | Keller W, Heβ D. 1998. Gradiometrie mit GRACE. Z Vermess, 124: 137-144. |
| [5] | Keller W, Sharifi M A. 2005. Satellite gradiometry using a satellite pair. Journal of Geodesy, 78(9): 544-557. |
| [6] | Koop P. 1993. Global gravity field modeling using satellite gravity gradiometry. Netherlands Geodetic Commission, Publ. Geod. Series No. 38, Delft. |
| [7] | Loomis B. 2009. Simulation study of a follow-on gravity mission to GRACE. Boulder: University of Colorado, 1-193. |
| [8] | Loomis B D, Nerem R S, Luthcke S B. 2012. Simulation study of a follow-on gravity mission to GRACE. Journal of Geodesy, 86(5): 319-335. |
| [9] | Reigber C, Schmidt R, Flechtner F. 2005. An Earth gravity field model complete to degree and order 150 from GRACE: EIGEN-GRACE02S. Journal of Geodynamics, 39(1): 1-10. |
| [10] | Rummel R, Van Gelderen M, Koop R, et al. 1993. Spherical harmonic analysis of satellite gradiometry. Rep New Series 39, Netherlands Geodetic Commission, Delft. |
| [11] | Shen Y Z, Xu H Z, Wu B. 2005. Simulation of recovery of the geopotential model based on intersatellite acceleration data in the low-low satellite to satellite tracking gravity mission. Chinese J. Geophys. (in Chinese), 48(4): 807-811. |
| [12] | Stephens M, Craig R, Leitch J, et al. 2006. Demonstration of an interferometric laser ranging system for a follow-on gravity mission to GRACE.// Proceedings of IEEE International Conference on Geoscience and Remote Sensing Symposium. Denver, CO: IEEE, 1115-1118. |
| [13] | Tapley B, Ries J, Bettadpur S, et al. 2005. GGM02—An improved Earth gravity field model from GRACE. Journal of Geodesy, 79(8): 467-478. |
| [14] | Xu P L. 2008. Position and velocity perturbations for the determination of geopotential from space geodetic measurements. Celestial Mechanics and Dynamical Astronomy, 100(3): 231-249. |
| [15] | Zhang H W, Xu H Z, Liu X Q. 2004. Basic theory and numerical result of the love number of solid Earth tide. Progress in Geophysics (in Chinese), 19(2): 372-378. |
| [16] | Zheng W, Lu X L, Xu H Z, et al. 2005. Simulation of the Earth's gravitational field recovery from GRACE using the energy balance approach. Progress in Natural Science, 15(7): 596-601. |
| [17] | Zheng W, Shao C G, Luo J, et al. 2006. Numerical simulation of Earth's gravitational field recovery from SST based on the energy conservation principle. Chinese J. Geophys. (in Chinese), 49(3): 712-717. |
| [18] | Zheng W, Xu H Z, Zhong M, et al. 2008. Efficient and rapid estimation of the accuracy of GRACE global gravitational field using the semi-analytical method. Chinese J. Geophys. (in Chinese), 51(6): 1704-1710. |
| [19] | Zheng W, Xu H Z, Zhong M, et al. 2009. Accurate and rapid error estimation on global gravitational field from current GRACE and future GRACE Follow-On missions. Chinese Physics B, 18(8): 3597-3604. |
| [20] | Zheng W, Xu H Z, Zhong M, et al. 2009a. Influence of the adjusted accuracy of center of mass between GRACE satellite and Superstar accelerometer on the accuracy of Earth's gravitational field. Chinese J. Geophys. (in Chinese), 52(6): 1465-1473. |
| [21] | Zheng W, Xu H Z, Zhong M, et al. 2009b. Effective processing of measured data from GRACE key payloads and accurate determination of Earth's gravitational field. Chinese J. Geophys. (in Chinese), 52(8): 1966-1975. |
| [22] | Zheng W, Xu H Z, Zhong M, et al. 2009c. Demonstration on the optimal design of resolution indexes of high and low sensitive axes from space-borne accelerometer in the satellite-to-satellite tracking model. Chinese J. Geophys. (in Chinese), 52(11): 2712-2720. |
| [23] | Zheng W, Xu H Z, Zhong M, et al. 2010. Efficient and rapid estimation of the accuracy of future GRACE Follow-On Earth's gravitational field using the analytic method. Chinese J. Geophys. (in Chinese), 53(4): 796-806. |
| [24] | Zheng W, Xu H Z, Zhong M, et al. 2011. Efficient calibration of the non-conservative force data from the space-borne accelerometers of the twin GRACE satellites. Transactions of the Japan Society for Aeronautical and Space Sciences, 54(184): 106-110. |
| [25] | Zheng W, Xu H Z, Zhong M, et al. 2011a. Accurate and rapid determination of GOCE Earth's gravitational field using time-space-wise-approach associated with Kaula regularization. Chinese J. Geophys. (in Chinese), 54(1): 14-21. |
| [26] | Zheng W, Xu H Z, Zhong M, et al. 2011b. Accurate and rapid determination of the GRACE Earth's gravitational field using improved pre-conditioned conjugate-gradient approach and three-dimensional interpolation method. Progress in Geophysics (in Chinese), 26(3): 805-812. |
| [27] | Zheng W, Xu H Z, Zhong M, et al. 2012. Impacts of interpolation formula, correlation coefficient and sampling interval on the accuracy of GRACE Follow-On intersatellite range-acceleration. Chinese J. Geophys. (in Chinese), 55(3): 822-832. |
| [28] | Zheng W, Xu H Z, Zhong M, et al. 2012a. Efficient accuracy improvement of GRACE global gravitational field recovery using a new inter-satellite range interpolation method. Journal of Geodynamics, 53: 1-7. |
| [29] | Zheng W, Xu H Z, Zhong M, et al. 2012b. Precise recovery of the Earth's gravitational field with GRACE: Intersatellite range-rate interpolation approach. IEEE Geoscience and Remote Sensing Letters, 9(3): 422-426. |
| [30] | Zhou X H, Xu H Z, Wu B, et al. 2006. Earth's gravity field derived from GRACE satellite tracking data. Chinese J. Geophys. (in Chinese), 49(3): 718-723. |
| [31] | 程芦颖,许厚泽.2006.地球重力场恢复中的位旋转效应. 地球物理学报,49(1):93-98. |
| [32] | 沈云中,许厚泽,吴斌.2005.星间加速度解算模式的模拟与分析. 地球物理学报,48(4):807-811. |
| [33] | 张捍卫,许厚泽,刘学谦.2004.固体潮Love数的基本理论和数值结果. 地球物理学进展,19(2):372-378. |
| [34] | 郑伟,邵成刚,罗俊等.2006. 基于卫-卫跟踪观测技术利用能量守恒法恢复地球重力场的数值模拟研究.地球物理学报,49(3): |
| [35] | 郑伟,许厚泽,钟敏等.2008.基于半解析法有效和快速估计GRACE全球重力场的精度. 地球物理学报,51(6):1704-1710. |
| [36] | 郑伟,许厚泽,钟敏等.2009a.GRACE星体和SuperSTAR加速度计的质心调整精度对地球重力场精度的影响. 地球物理学报, 52(6):1465-1473. |
| [37] | 郑伟,许厚泽,钟敏等.2009b.GRACE卫星关键载荷实测数据的有效处理和地球重力场的精确解算. 地球物理学报,52(8): 1966-1975. |
| [38] | 郑伟,许厚泽,钟敏等.2009c.卫星跟踪卫星测量模式中星载加速度计高低灵敏轴分辨率指标优化设计论证. 地球物理学报,52 (11):2712-2720. |
| [39] | 郑伟,许厚泽,钟敏等.2010.利用解析法有效快速估计将来GRACEFollow-On地球重力场的精度. 地球物理学报,53(4): 796-806. |
| [40] | 郑伟,许厚泽,钟敏等.2011a.基于时空域混合法利用Kaula正则化精确和快速解算GOCE地球重力场. 地球物理学报,54(1): 14-21. |
| [41] | 郑伟,许厚泽,钟敏等.2011b.基于改进的预处理共轭梯度法和三维插值法精确和快速解算GRACE地球重力场. 地球物理学进展,26(3):805-812. |
| [42] | 郑伟,许厚泽,钟敏等.2012.插值公式、相关系数和采样间隔对GRACEFollow-On星间加速度精度的影响. 地球物理学报,55 (3):822-832. |
| [43] | 周旭华,许厚泽,吴斌等.2006.用GRACE卫星跟踪数据反演地球重力场. 地球物理学报,49(3):718-723. |
 2014, Vol. 57
2014, Vol. 57

