重磁异常解释的主要任务之一是确定异常体的空间赋存状态.局部波数法是近几年应用较为广泛的一种自动解释方法,该方法利用局部波数可快速地完成场源体的反演(Thurston and Smith, 1997),但该方法在进行场源体深度反演时需要已知场源体的构造指数,但未知地区场源体的构造指数往往是未知的,构造指数的错误选取会为反演结果带来较大的误差.后来人们对该方法进行改进,使其能够同时完成深度及构造指数的反演(Smith et al., 1998; Salem and Smith, 2005),然而改进后方法需要计算异常的三阶甚至更高阶导数,对数据精度要求较高,且当测量点距较大时,高阶导数的计算是非常不稳定的.Salem等(2005)利用原始局部波数和相位转换后局部波数进行异常体的反演,并于2008年(Salem et al., 2008)试验了该方法在三维情况下的应用效果.Keating(2009)利用局部波数及其垂直导数对异常体的深度及构造指数进行反演,但是该方法会增大噪声的干扰.Ma(2013)利用不同水平位置与不同高度局部波数曲线的组合进行异常的解释,获得了良好的效果.归一化总梯度法是一种利用高精度重力异常来确定异常源分布的方法,该方法不需要附加条件,计算简便,并能半定量地确定地质体的位置而被广泛用于研究含油气构造或检测油气(肖一鸣和张林详,1984;沈庆夏等,2010),但该方法的结果由展开式的项次来决定,为异常的解释工作带来了不确定性(孟平等,2003),为此提出采用Fourier变换和Hilbert变换来完成归一化总梯度的计算,避免了展开项次的约束(曾华霖等,1999;肖鹏飞等,2006).
本文提出归一化局部波数法进行重磁异常的解释,并提出多种不同的归一化函数.通过理论模型和实际数据验证方法的可行性和有效性,并给出了不同归一化方式的应用效果.
2 归一化局部波数法对于异常T而言,局部波数kx被定义为局部相位θ的水平方向的导数:

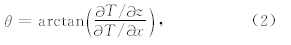

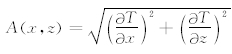 为异常T的解析信号.
为异常T的解析信号.Salem等(2005)定义相位转换后局部波数kz的表达式
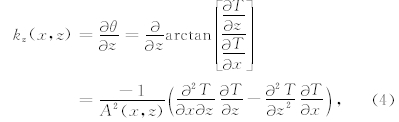
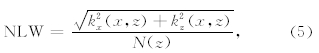

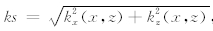 ,M是深度z上的总测点数.三维情况下归一化局部波数法的表达式为:
,M是深度z上的总测点数.三维情况下归一化局部波数法的表达式为:
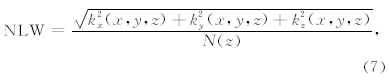
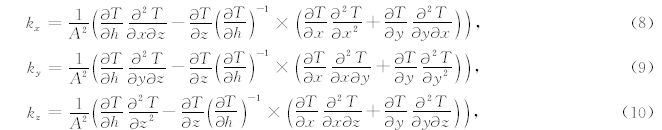
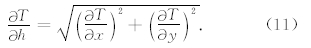
局部波数为异常的二阶导数,因此归一化局部波数法相对归一化总梯度法受背景异常干扰更小.为了降低下延过程的不稳定性及噪声的干扰,采用ISVD(Integrated Second Vertical Derivative)法来完成局部波数的延拓工作( Fedi and Florio, 2002; Rapolla et al., 2002),具体表达式为:
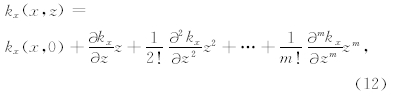
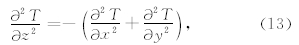
 | 图 1 不同阶垂直导数的计算方法Fig. 1 Computation method of vertical derivatives with different orders |
垂直导数的计算采用两个水平导数之和来完成,水平导数采用空间域方法来计算,具有受噪声干 扰小和计算稳定的优势,因此该方法能稳定地完成异常的延拓工作.由于导数随埋深衰减速度更快,因此足够多的阶数参与计算就会得到准确的结果,一般展开到7~10阶就可以满足精度要求.
3 理论模型试验水平位置为100 m,埋深为20 m,半径为5 m,与围岩密度差为1 g·cm-3的圆柱体所引起的重力异常如图 2a所示.分别利用Fourier变换法和ISVD法将异常向下延拓4 m,ISVD法计算时阶数m为7.
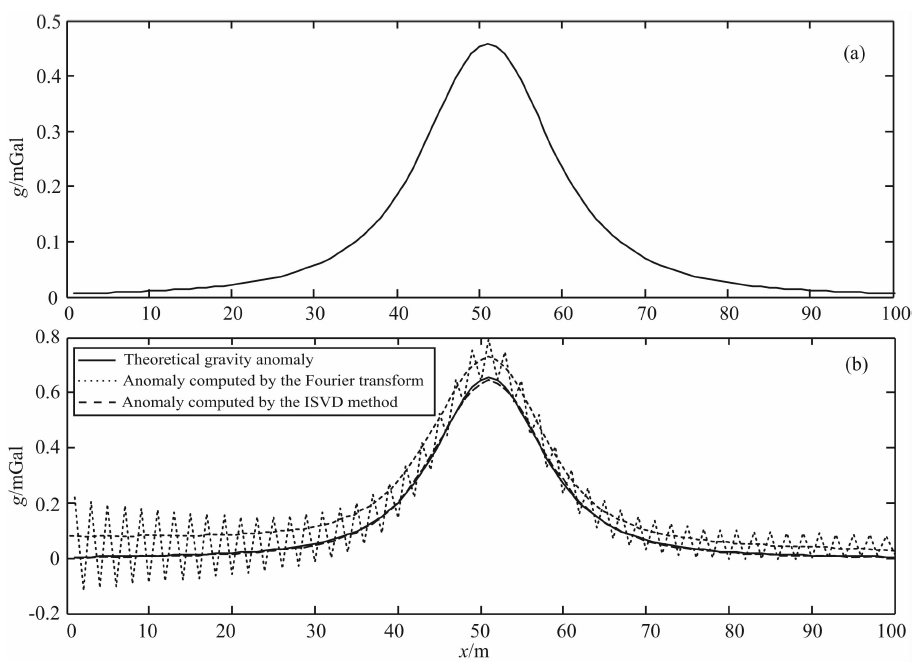 | 图 2(a)圆柱体重力异常;(b)下延4 m后重力异常Fig. 2(a)Synthetic gravity anomalies of a horizontal cylinder; (b)Gravity anomalies after downward continuation by 4 m |
从图 2b中可以看出,ISVD方法能较稳定地完成异常的下延工作,且与理论异常之间的差距较小.Fourier变换计算结果稳定性较差,异常出现不规则地波动,为此需对数据进行低通滤波处理,滤波后数据较圆滑,但与原始数据的差距较大.
利用归一化局部波数法对该异常进行反演(图 3).
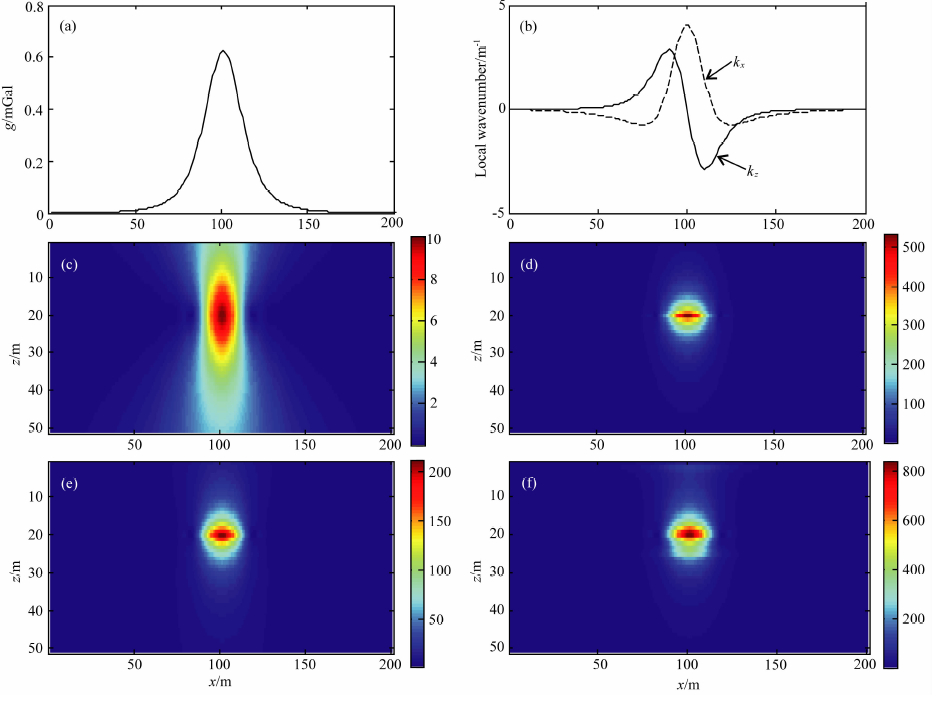 | 图 3(a)单个圆柱体产生的重力异常;(b)异常的局部波数;(c)算术平均归一化局部波数;(d)中值归一化局部波数; (e)几何平均归一化局部波数;(f)调和平均归一化局部波数Fig. 3(a)Gravity anomaly generated by a horizontal cylinder;(b)Local wavenumber of the data in Fig. 3a;(c)Normalized local wavenumber based on arithmetic mean;(d)Normalized local wavenumber based on median value;(e)Normalized local wavenumber based on geometric mean;(f)Normalized local wavenumber based on harmonic mean |
从图 3中可以看出,归一化局部波数法能准确地获得地质体的位置与深度信息,且中值、几何平均和调和平均归一化局部波数相对算术平均归一化局 部波数具有更高的分辨率,反演得到的结果更加收敛.
先给出归一化局部波数法对于多个地质体产生异常的应用效果.地下水平位置50、100和150 m存在埋深均为10 m的垂直薄板状体,其宽度为3 m,磁化强度为20 A/m,在磁倾角为70°时板状体引起的磁异常如图 4a所示,利用归一化局部波数法对磁异常进行反演.
从图 4中可以看出,归一化局部波数法对于磁异常也有较好的应用效果,其归一化局部波数的最大值处埋深为9.8 m,与异常体的实际深度相一致,具有不受磁化方向干扰的优势.
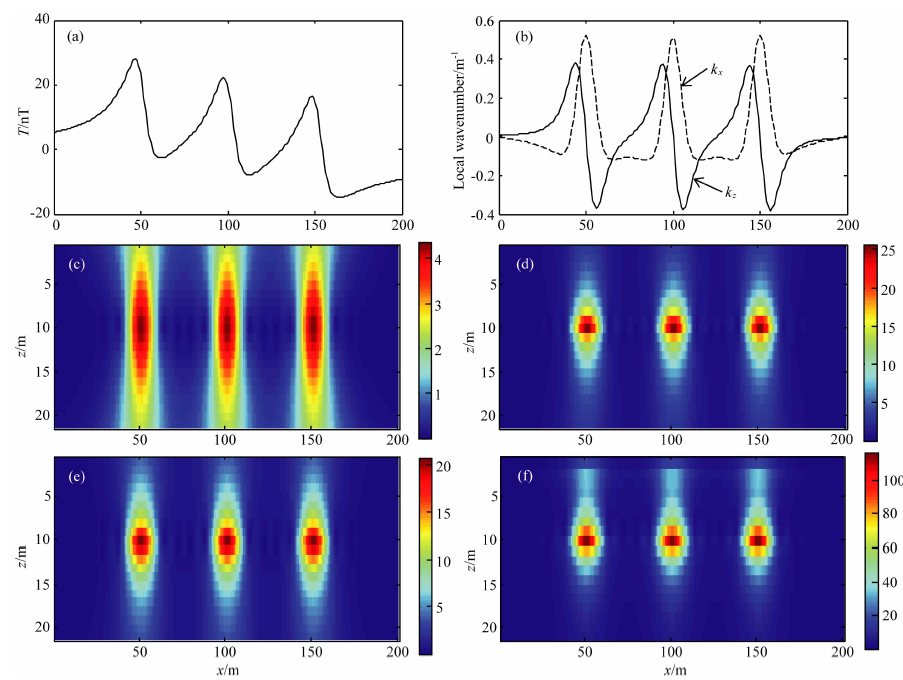 | 图 4(a)三个板状体产生的磁异常;(b)磁异常局部波数;(c)算术平均归一化局部波数;(d)中值归一化局部波数; (e)几何平均归一化局部波数;(f)调和平均归一化局部波数Fig. 4(a)Original magnetic anomaly generated by three dikes;(b)Local wavenumber of the data;(c)Normalized local wavenumber based on arithmetic mean;(d)Normalized local wavenumber based on median value;(e)Normalized local wavenumber based on geometric mean;(f)Normalized local wavenumber based on harmonic mean |
在实际数据解释中噪声和区域场的干扰是不可避免的.为了验证方法的稳定性,在图 4模型中部加入一埋深为20 m,半径为3 m的圆柱体,磁化强度为20 A/m,并加入均值为0,方差为1 nT的随机噪声,磁异常如图 5a所示.采用图 1所示方法计算得到的局部波数如图 5b所示,可以看出局部波数能很好地消除区域异常的影响.利用归一化局部波数法进行含噪磁异常的解释(图 5c-5f).从反演结果中可以看出,本文方法受噪声和区域场的干扰小,能有效地完成异常的解释工作.
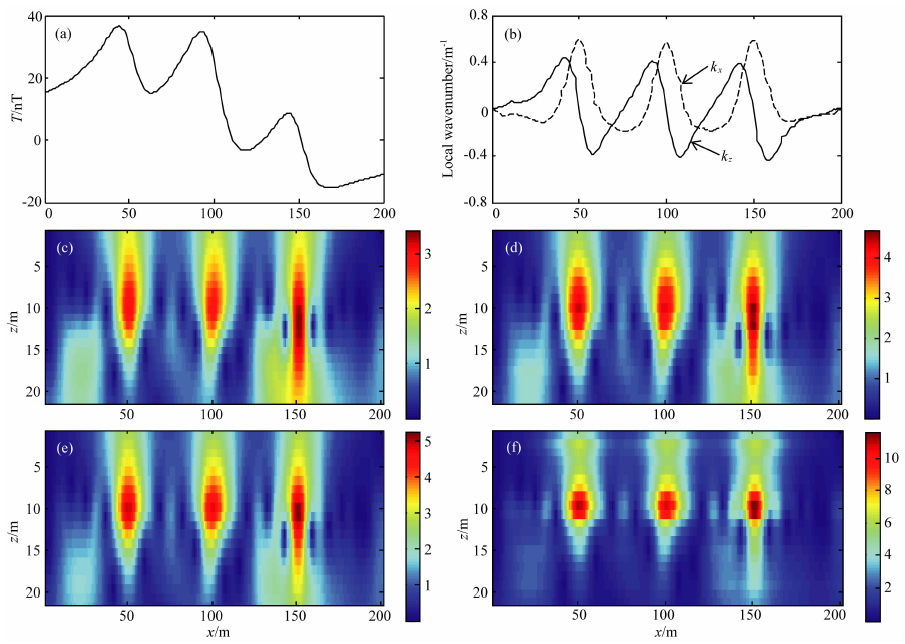 | 图 5(a)含噪磁异常;(b)磁异常局部波数;(c)算术平均归一化局部波数;(d)中值归一化局部波数; (e)几何平均归一化局部波数;(f)调和平均归一化局部波数Fig. 5(a)Noise-bearing magnetic anomalies;(b)Local wavenumber of the data;(c)Normalized local wavenumber based on arithmetic mean;(d)Normalized local wavenumber based on median value;(e)Normalized local wavenumber based on geometric mean;(f)Normalized local wavenumber based on harmonic mean |
下面给出归一化局部波数法在较为复杂情况下 的应用效果.地下水平位置40 m、80 m、120 m、160 m和220 m存在埋深分别为7 m、9 m、12 m、15 m和15 m的垂直薄板状体,其宽度为1 m,磁化强度均 为20 A/m,磁倾角为70°时产生的磁异常如图 6a所示.
反演结果得到异常体的水平位置分别为40 m、80 m、120 m、 160 m和220 m,根据结果最大值判断 出地质体的埋深分别为6.9 m、8.8 m、11.5 m、13.3 m和14.4 m.可以看出当异常体之间距离与异常体埋深的比值较小时,受其他邻近异常体的干扰,反演结果的准确性较低.当异常体之间的水平距离较大时,埋深较大的异常体也可以得到准确的结果,所以反演结果的准确性依赖于异常体埋深与异常体之间水平距离的比值.
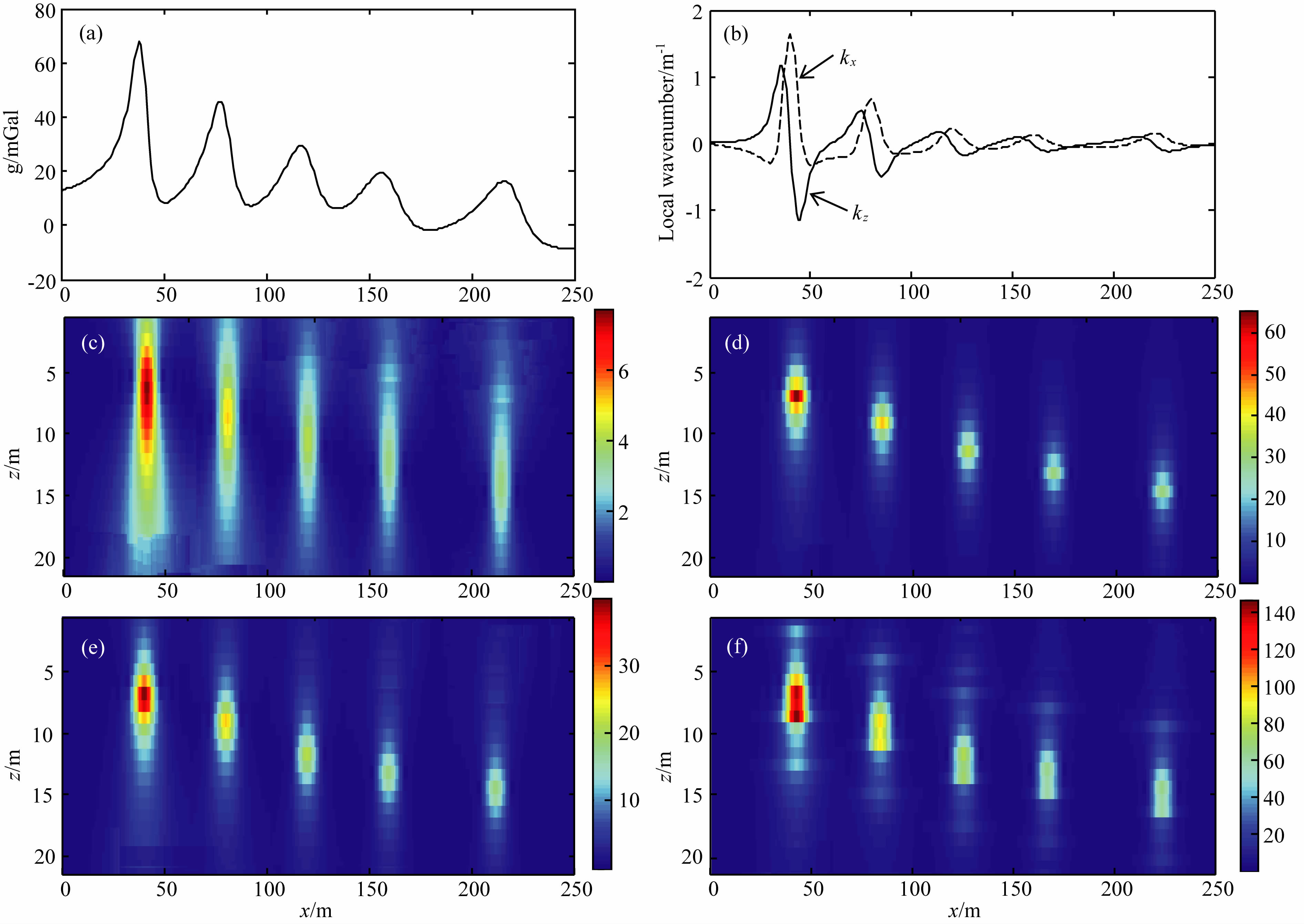 | 图6(a)原始磁力异常;(b)磁异常局部波数;(c)算术平均归一化局部波数;(d)中值归一化局部波数; (e)几何平均归一化局部波数;(f)调和平均归一化局部波数Fig.6(a) Synthetic magnetic anomalies generated by multiple sources; (b) Local wavenumber of the data; (c) Normalized local wavenumber based on arithmetic mean; (d) Normalized local wavenumber based on median value; (e)Normalized local wavenumber based on geometric mean; (f) Normalized local wavenumber based on harmonic mean |
将本文提出的归一化局部波数法应用于实 际数据的解释.图 7a为埃及红海西部边缘Hamrawien 地区一条实测磁异常剖面(Salem et al., 1999),点距为10 m.现已验证地下存在两个板状体,其埋深分别为555.7 m和441.2 m.图 7b为磁异常的局部波数.图 7c—7f为不同方法获得的归一化局部波数,反演结果显示地质体中心的水平位置分别为4530 m和14860 m,其埋深分别为546 m和447 m,归一化局部波数法的反演结果与实际埋深相接近,说明该方法具有良好的实际应用效果.
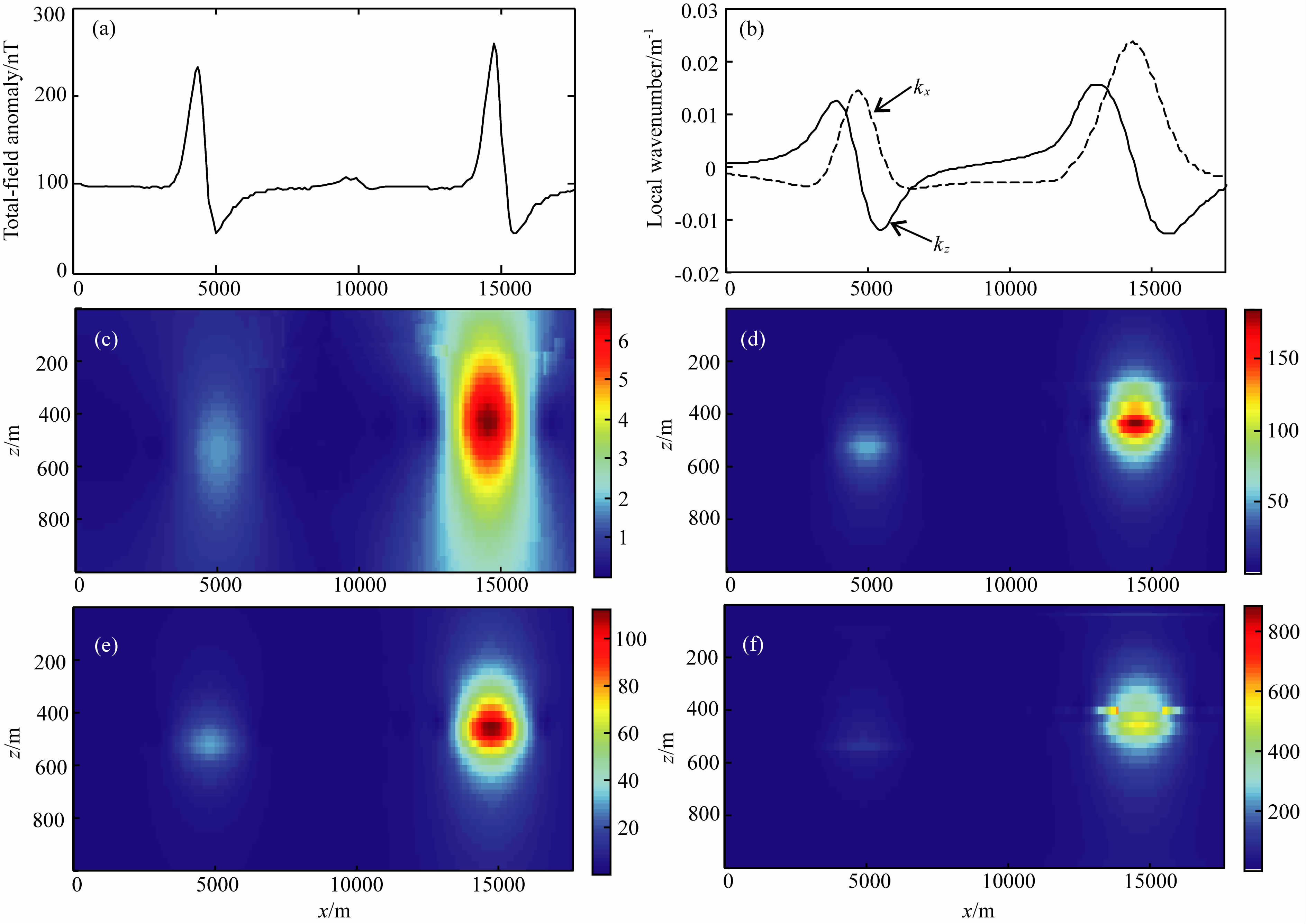 | 图7(a) 加拿大安大略省北部实测磁异常;(b)磁异常局部波数;(c)算术平均归一化局部波数; (d)中值归一化局部波数;(e)几何平均归一化局部波数;(f)调和平均归一化局部波数Fig.7(a) Measured magnetic anomaly; (b) Local wavenumber of the data; (c) Normalized local wavenumber based on arithmetic mean; (d) Normalized local wavenumber based on median value; (e) Normalized local wavenumber based on geometric mean; (f) Normalized local wavenumber based on harmonic mean |
从反演结果中可以看出较深地质体的归一化局部波数幅值相对较小,反映不是很清晰. 为了清晰地获得不同埋藏深度地质体的位置,对归一化函数进行简单的变形,采用分段函数来表示:
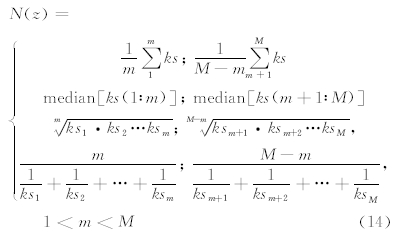
不同的地质体采用异常体范围内的归一化值,可有效地凸显出不同深度异常体的效应,能更清晰地显示异常体的分布,因此在应用本文方法进行复杂异常解释时具有一定的局限性.利用改进的归一化局部波数法对异常进行反演(图 8).
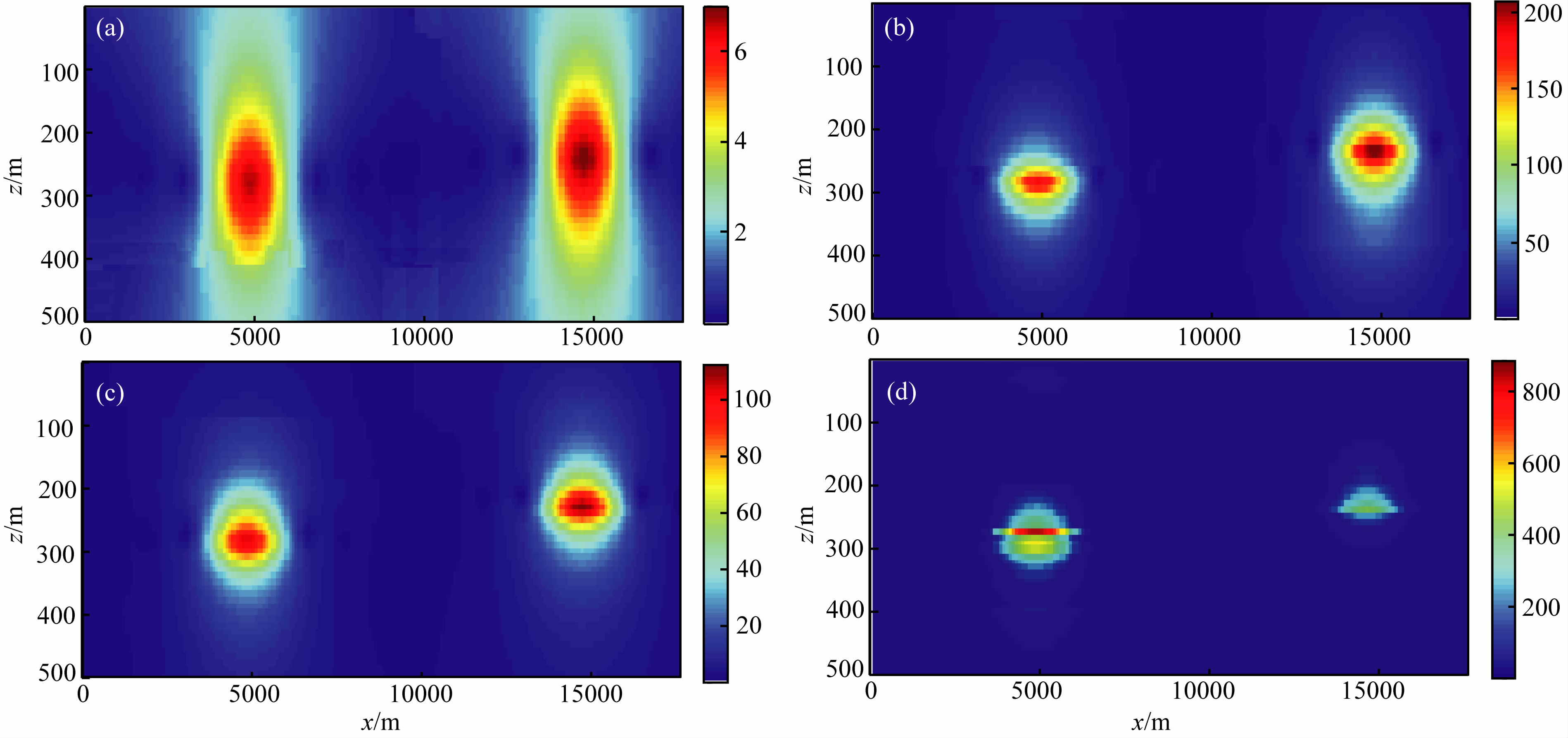 | 图8(a)算术平均归一化局部波数;(b)中值归一化局部波数;(c)几何平均归一化局部波数;(d)调和平均归一化局部波数Fig.8(a) Normalized local wavenumber based on arithmetic mean; (b) Normalized local wavenumber based on median value; (c) Normalized local wavenumber based on geometric mean; (d) Normalized local wavenumber based on harmonic mean |
从图 8中可以看出,通过分段归一化函数可以使改进的局部波数法能更清晰地反映地下地质体的分布,能更好地完成异常的解释工作.
利用归一化局部波数法对朱日和地区磁异常进行解释,其原始磁异常如图 9所示.
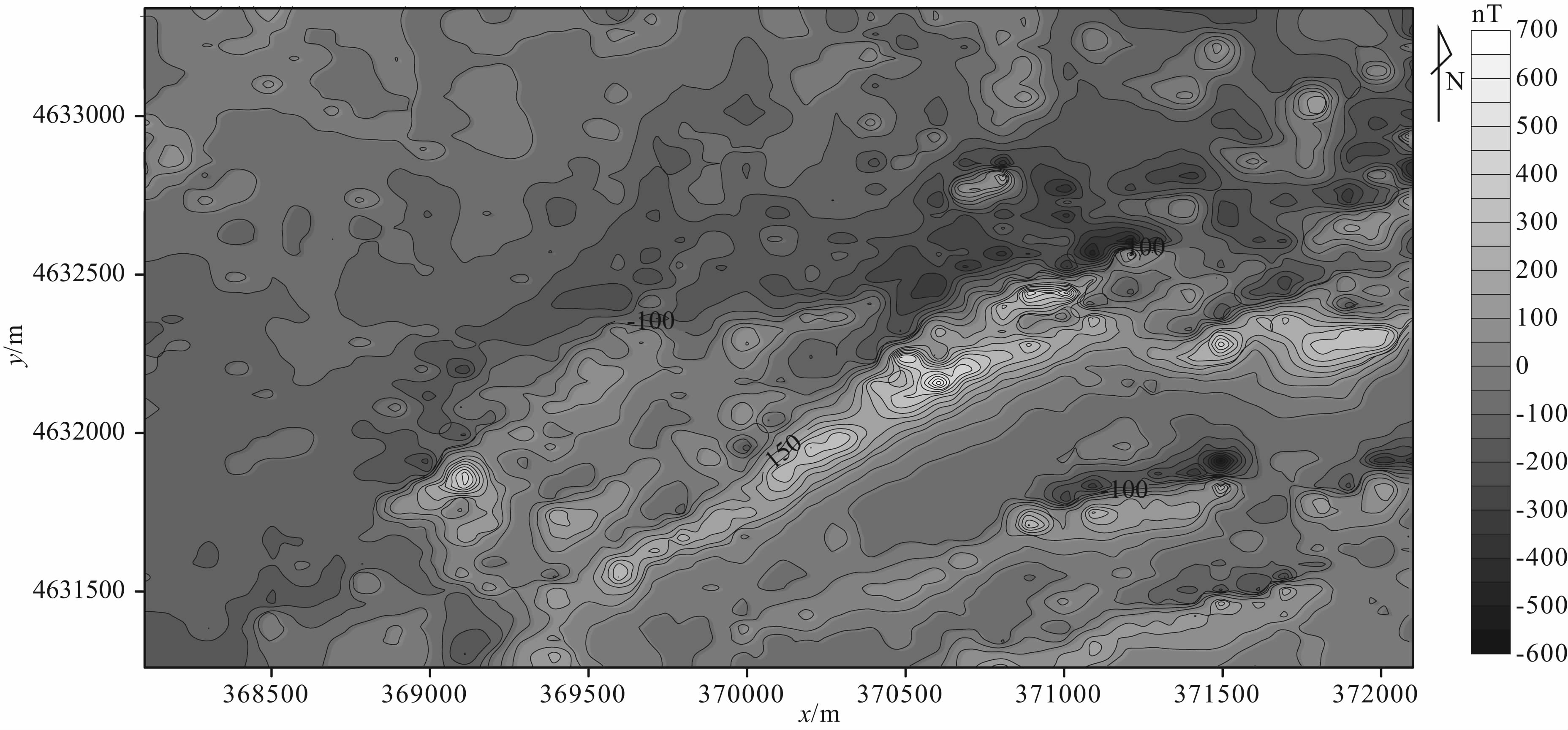 | 图9实测磁异常Fig.9Measured magnetic anomaly of Zhurihe area |
计算不同深度(0 m,10 m,30 m,50 m,100 m,150 m)磁异常的几何平均归一化局部波数(图 10).
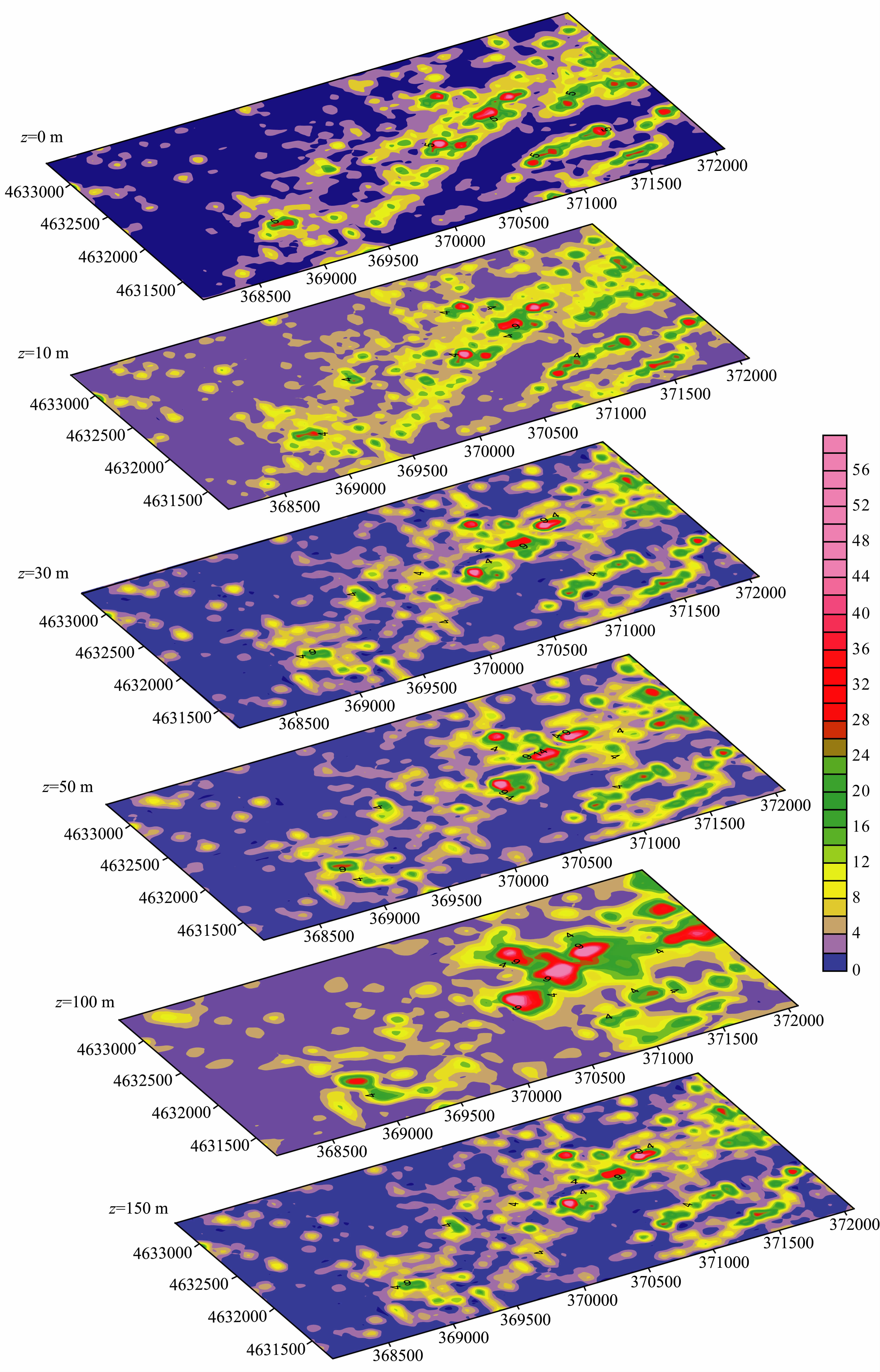 | 图10不同深度归一化局部波数Fig.10Normalized local wavenumber of different depths |
根据图 10所示不同深度归一化局部波数可以看出,大部分矿体埋藏深度在50~150 m范围内,且异常有向东延伸的趋势.
5 结论本文提出归一化局部波数法进行重磁异常的解释工作,并提出了多种不同的归一化方式.通过理论模型试验证明本文方法能有效地完成异常的反演工作,且通过对比发现算术平均归一化局部波数所获得结果的分辨率较低.将该方法应用于实际数据的解释,获得了地下地质体的深度,与已知深度相一致,并针对不能清晰地反映较深地质体的缺点采用 分段归一化的方式来使异常体得到更加清晰地显示.
| [1] | Fedi M, Florio G. 2002. A stable downward continuation by using the ISVD method. Geophysical Journal International, 151(1): 146-156, doi: 10.1046/j.1365-246X.2002.01767.x. |
| [2] | Keating P. 2009. Improved use of the local wavenumber in potential-field interpretation. Geophysics, 74(6): L75-L85, doi: 10.1190/1.3242270. |
| [3] | Ma G Q. 2013. Improved local wavenumber methods in the interpretation of potential field data. Pure and Applied Geophysics, 170(4): 633-643, doi: 10.1007/s00024-012-0551-z. |
| [4] | Meng P, Qin T, Wu Y H. 2003. Study of nonuniqueness of the solution to normalized total gradient method. Geophysical Prospecting for Petroleum (in Chinese), 42(2): 252-253. |
| [5] | Rapolla A, Cella F, Fedi M, et al. 2002. Improved techniques in data analysis and interpretation of potential fields: examples of application in volcanic and seismically active areas. Annals of Geophysics, 45(6): 733-751, doi: 10.4401/ag-3541. |
| [6] | Salem A, Elsirafi A, Ushijima K. 1999. Design and application of high-resolution aeromagnetic survey over Gebel Duwi area and its offshore extension. Egypt: Memoirs of the Faculty of Engineering. Kyushu University, 59(3): 201-213. |
| [7] | Salem A, Smith R S. 2005. Depth and structural index from normalized local wavenumber of 2D magnetic anomalies. Geophysical Prospecting, 53(1): 83-89, doi: 10.1111/j.1365-2478.2005.00435.x. |
| [8] | Salem A, Ravat D, Smith R, et al. 2005. Interpretation of magnetic data using an enhanced local wavenumber (ELW) method. Geophysics, 70(2): L7-L12, doi: 10.1190/1.1884828. |
| [9] | Salem A, Williams S, Fairhead D, et al. 2008. Interpretation of magnetic data using tilt-angle derivatives. Geophysics, 73(1): L1-L10, doi: 10.1190/1.2799992. |
| [10] | Shen Q X, Wang Z Q, Li R. 2010. Simple analysis of the normalized full gradient of gravity anomaly in the exploration of shallow reservoir. Contributions to Geology and Mineral Resources Research (in Chinese), 25(1):72-75. |
| [11] | Smith R S, Thurston J B, Dai T, et al. 1998. iSPI—The improved source parameter imaging method. Geophysical Prospecting, 46(2): 141-151, doi: 10.1046/j.1365-2478.1998.00084.x. |
| [12] | Thurston J B, Smith R S. 1997. Automatic conversion of magnetic data to depth, dip, and susceptibility contrast using the SPI method. Geophysics, 62(3): 807-813, doi: 10.1190/1.1444190. |
| [13] | Xiao P F, Li M, Xu S Z, et al. 2006. Stable solution of normalized total gravity gradient. Oil Geophysical prospecting (in Chinese), 41(5):596-598. |
| [14] | Xiao Y M, Zhang L X. 1984. The application of normalized gravity gradient in hydrocarbon exploration. Oil Geophysical Prospecting (in Chinese), (3): 247-254. |
| [15] | Zeng H L, Li X M, Yao C L, et al. 1999. The modified normalized full gradient of gravity anomalies and its application to Shengli oil field, East China. Petroleum Exploration and Development (in Chinese), 26(6): 1-6. |
| [16] | 孟平, 秦瞳, 吴云海. 2003. 关于归一化总梯度异常多解性问题的研究. 石油物探, 42(2): 252-253 . |
| [17] | 沈庆夏,王志强,李瑞. 2010. 重力归一化总梯度法勘探浅层油气藏浅析. 地质找矿论丛,25(1):72-75. |
| [18] | 肖鹏飞, 李明, 徐世浙等. 2006. 重力归一化的稳定解法. 石油地球物理勘探, 41(5): 596-598. |
| [19] | 肖一鸣, 张林详. 1984. 重力归一化总梯度法在寻找油气中的应用. 石油地球物理勘探, (3): 247-254 . |
| [20] | 曾华霖, 李小孟, 姚长利等. 1999. 改进的重力归一化总梯度法及其在胜利油区油气藏探测中的应用效果. 石油勘探与开发, 26(6): 1-6. |
 2014, Vol. 57
2014, Vol. 57


