2. 中国石化石油物探技术研究院, 南京 211103;
3. 中国科学院海洋研究所, 青岛 266071
2. Sinopec Geophysical Research Institute, Nanjing 211103, China;
3. Institute of Oceanology Chinese Academy of Sciences, Qingdao 266071, China
地震波成像的目标就是将地表接收到的反射波反向归位至产生它的反射点上,并由此得到地下构造特征.多数地震偏移成像算法是基于所有散射能量在地下界面仅反射一次的假设,而实际上,声波在向地表返回过程中会有部分发生二次或多次反射,形成多次波.由于海水面存在着强的波阻抗差异,所以多次波在海洋地震资料中尤为严重.多次波的出现经常使地震剖面上主要目的层反射难以解释,特别是沿潜在油气储层的微小变化将被多次波严重干扰,所以,长期以来多次波一直被视为噪音并从地震数据中去除(郭科等,2010;石颖和邢小林,2011;陈小宏和刘华锋,2012; 石颖等,2012;赵昌垒等,2013),以免在之后的地震资料解释中造成误解.
事实上,多次波也是众多地震信号中的一种,像一次波一样,多次波也包含了地下界面信息.在复杂地下构造的情况下,有的区域一次反射波难以照明,而多次波却可以通过多次反射而照明,包含了一次波所没有的地下信息,所以,近些年来,国内外许多专家学者都在利用多次波方面做了一系列的研究.
将多次波转变为一次波再按照传统偏移方法进行成像是多次波成像方法之一,Shan等(2003)提出了将含有多次波的数据进行互相关变换为准一次波,基于双平方根方程,在炮点-检波点域进行多次波叠前深度偏移.Shan和Guitton(2004)等通过一次波与多次波的互相关得到准一次波,在炮集实现了多次波叠前深度偏移,并应用Sigsbee2B模型进行了测试,取得了一定的效果.He 等(2007)提出了地震干涉成像法对自由表面多次波进行成像,并在VSP数据中得到了较好的应用.Jiang(2006)利用层间多次波对VSP资料进行成像,前提是需要有较强产生层间多次波的界面才能够较好的对层间多次波进行识别和成像.Vasconcelos 等(2008)也利用地震干涉法对墨西哥湾盐下构造进行VSP数据的目标成像,成像结果与传统地面地震成像结果一致.Berkhout和Verschuur(2006)提出了可以先通过SRME预测出地表相关多次波,再将多次波转变为 一次波,然后再进行多次波成像.(Muijs and Holliger 2005,Muijs et al., 2007)首先将波场分解为上行波场与下行波场,然后再进行基于单程波的下行波场和上行波场延拓,最后通过多维成像得到成像结果,这种方法的缺点是在前期需要进行波场分离.Brown和Guitton(2005)提出了一种多次波和一次波联合成像的方法,称为多次波和一次波最小二乘法联合成像,这种方法利用模型正则化算子将一次波与多次波分离,结合一次波与多次波的信息来提高信号的保真度.
近年来,随着计算机硬件的发展,逆时偏移得到了一定程度的应用,Liu等(2011)将逆时偏移震源波场用地震记录来替代、记录波场用预测出的多次波来替代实现了基于逆时偏移的多次波成像,取得了较好的效果,然而由于逆时偏移本身的特点,这种 计算方法也是比较耗时的.Zhang和Schuster(2014)提出了基于最小二乘的多次波逆时偏移方法,通过多次迭代运算,改善了逆时多次波偏移方法的成像质量,在照明均衡和纵向成像分辨率方面都有了明显的提高.Wang 等(2014)提出了一种不需要预先预测多次波的方法,以脉冲震源与原始记录为下行延拓初始波场,以原始记录为初始上行波场,避免了多次波预测所增加的误差.郭书娟等(2011,2012)提出了基于广义的炮偏移方法实现地表多次波和一次波的联合成像,该方法是将包含有震源的记录波场做为下行波场,多次波为上行波场来实现一次波与多次波的联合成像,由于震源子波包含在记录波场中,如果子波能量太小,一次波成像比重就较小,如果子波能量太强,多次波成像比重就掩盖了一次波成像,所以在确定震源子波能量上存在一定的困难.
在前人研究的基础上,本文系统阐述了多次波在基于单程波叠前深度偏移中的影响,并提出了基于单程波偏移算子的多次波成像方法.该方法在输入数据上采取了多次波逆时偏移类似的做法,将输入的下行波场用包含多次波的记录来替代,输入的上行波场用预测的表层相关多次波来替代,采用基于波动方程的单程波偏移算子来实现多次波成像,具有较高的计算效率.为了应用多次波成像结果来弥补一次波成像的不足,通过基于二范式的能量匹配原则将多次波与一次波成像结果匹配叠加,实现一次波与多次波的联合成像,避免了广义炮偏移联合成像中子波能量难以确定的缺点的同时也具有较高的计算效率.简单模型验证了多次波成像方法的正确性,Sigsbee2B模型进行的一次波与多次波联合成像结果取得了明显的改善,尤其是多次波发育的盐丘边界构造成像质量得到了明显提高.
2 多次波在单程波叠前深度偏移中的影响在密度恒定的各向同性完全弹性介质中,假设 地震波震源是t=0时刻激发的脉冲,则地震波的传播可以用如下时间-空间域的二维标量声波方程表示为
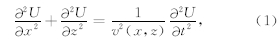
基于拟微分算子理论,假设光滑介质中层间多次反射非常弱,或者认为多次波被视为噪声已经提前滤除,不考虑地震波的反射和透射得到解耦的单程波方程在频率域表示为(张关泉,1993;Zhang et al., 2005)
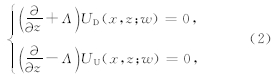
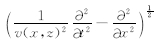 ,称为拟微分算子,从(2)式就可以推导出分步傅里叶与傅里叶有限差分等经典 的单程波的波场延拓算子(Stoffa et al., 1990;Ristow and Rūhl,1994).
,称为拟微分算子,从(2)式就可以推导出分步傅里叶与傅里叶有限差分等经典 的单程波的波场延拓算子(Stoffa et al., 1990;Ristow and Rūhl,1994). 图 1是多次波传播的路径图,其中US是震源波场,在地下R处发生第一次反射,UP是接收到的一次反射波场,一次反射波场在地表被接收后又被反射回地下,在R1处产生二次反射波,返回地表形成一阶多次波UM1,类似地产生一系列多次波,最大阶为N阶多次波UMN.在常规叠前深度偏移中,输入下行波场是震源子波,输入的上行波场是地表接收到的地震记录,一般认为多次波已经在前期预处理中被衰减掉,按照Claerbout教授的入射波的初 至与反射波的产生时间相同的成像原则(Claerbout,1971),当不存在多次波时,单程波偏移方法成像条件可写为
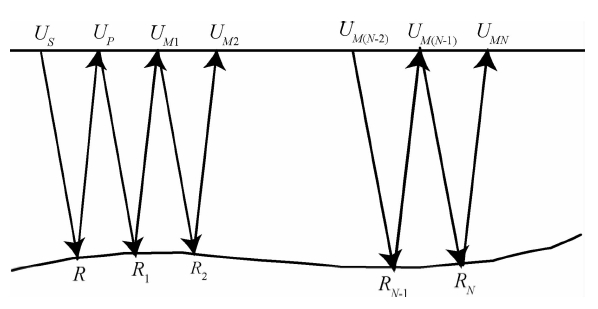 | 图 1 多次反射波传播路径Fig. 1 Propagation paths of reflective multiples |
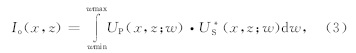
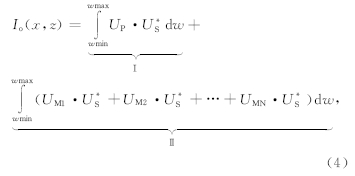
基于波动方程的单程波叠前深度偏移方法相对于射线类的Kirchhoff积分法偏移可以适应速度场的强横向变化,相对于全波逆时偏移具有较高的计算效率和较低的速度依赖性.本文采取类似于Liu (2011)提出的逆时偏移多次波成像方法的边界条件,首先采用地表相关多次波预测的方法,预测出地表相关多次波;其次用含有多次波的地震记录作为单程波偏移中的输入下行波场UD,用预测出的地表相关多次波作为单程波偏移中的输入上行波场UU;最后用式(5)互相关成像条件成像,公式为

在时间域相关的两个信号,在频率域是一个信号与另一个信号复共轭的标量积.式(5)中的复共轭项代表了下行波场的正向外推,非复共轭项代表了上行波场的反向外推.整个多次波成像由三部分构成,第一部分Ⅲ项是多次波真实构造成像部分,认为地表接收到的第N-1阶多次波UM(N-1)为震源波场,经地层界面RN反射后,在地表接收到的第N阶多次波为该源产生的记录波场UMN,上、下行波场通过互相关成像得到RN位置的成像值,根据第Ⅲ项,依次可以得到R1,R2…,RN-1位置处的成像;第二部分Ⅳ项是多次波偏移中产生的噪音,成像条件中的UM(N-2)和UMN分别是下行波场与上行波场,虽然能够成像,但是所成的像是偏移假象或噪音,因为在UM(N-2)与UMN之间还有一次波场的往返,而单程波叠前深度偏移并没有考虑到这种往返,还是按照单程波场延拓的方式来延拓波场,在比实际反射层更深的地层处相关成像,产生偏移假象或噪音;第三部分Ⅴ是不能够产生成像值的,以UMN·U<sub>MN为例,因为下行波场UMN的正向延拓意味着波前面时间在变长,而上行波场UMN的反向延拓意味着波前面时间在变小,两者随着波场延拓是不可能相遇并相关成像的,由于没有偏移噪音产生,这部分对偏移成像影响不大.
4 最小二范式一次波与多次波成像匹配叠加对于构造成像来说,应该是最大限度的利用地下信息来获取真实构造特征.广义一次波与多次波联合成像方法(郭书娟等,2011)将同时含有表层多次波的炮记录与脉冲震源之和作为下行延拓波场,但是,脉冲震源的能量与炮记录存在能量差,如果脉冲震源能量太强,联合成像结果主要表现为一次波对成像的贡献;如果脉冲震源能量太弱,那么联合成像的结果主要表现为多次波对成像的贡献,需要权衡脉冲子波的能量是该方法的一个缺陷.本节采取的思路是先分别得到一次波成像结果Io(x,z)与多次波成像结果Im(x,z),然后再基于最小二乘能量匹配原则,求取匹配因子,进行匹配叠加,一次波与多次波成像结果的优势得到互补,实现联合成像.这样做既利用多次波成像结果补充了一次波对一些构造照明的不足,又避免了广义一次波多次波联合成像方法中震源子波在输入波场中能量难以确定的缺点.最小误差能量匹配叠加的关键因素在于匹配因子的求取,本文采取基于最小二范式的匹配滤波方法来求取匹配因子,使得多次波成像结果与一次波成像结果数量级一致,联合成像结果Iom(x,z)可以表示为
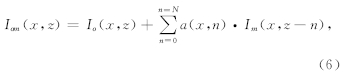
其中,a(x,n)是匹配因子,N是信号的长度,匹配因子由式(7)的Toeplitz矩阵决定,可以通过Levinson快速递推算法求解为
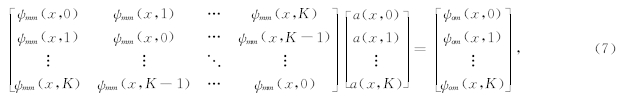
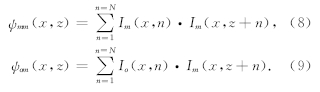
为了验证本文方法的有效性,本文首先对三层模型进行了基于波动方程的一次波叠前深度偏移试处理和多次波成像,最后对Sigsbee2b模型进行了 一次波与多次波联合成像试处理,取得了一定的效果.
5.1 三层简单模型试算该三层模型的速度场如图 3a所示,第一层、第 二层和第三层速度分别是1500 m·s-1、2500 m·s-1和3500 m·s-1.图 2是正演模拟单炮记录,中间放炮,151道接收,道间距20 m,记录时间3 s,采样率4 ms.其中图 2a是含有多次波的单炮记录,D1是直达波,R1和R2分别是第一层和第二层的一次反射波,能量较弱的I1反射同相轴是第一层与第二层间的一阶层间多次波,M11和M21分别是第一层界面和第二层界面对应的地表相关一阶多次波,P1是微屈多次波,M11和M21分别是第一层界面和第二层界面对应的地表相关二阶多次波.去除出多次波后得到包含直达波的一次反射波记录如图 2b所示,预测出的地表相关多次波如图 2c所示.
 | 图 2 三层模型正演记录 (a)包含多次波的单炮记录;(b)一次波记录;(c)多次波记录.Fig. 2 Forward shot gathers of a three-Layer velocity model (a)Single shot gather with multiples;(b)Primaries;(c)Multiples. |
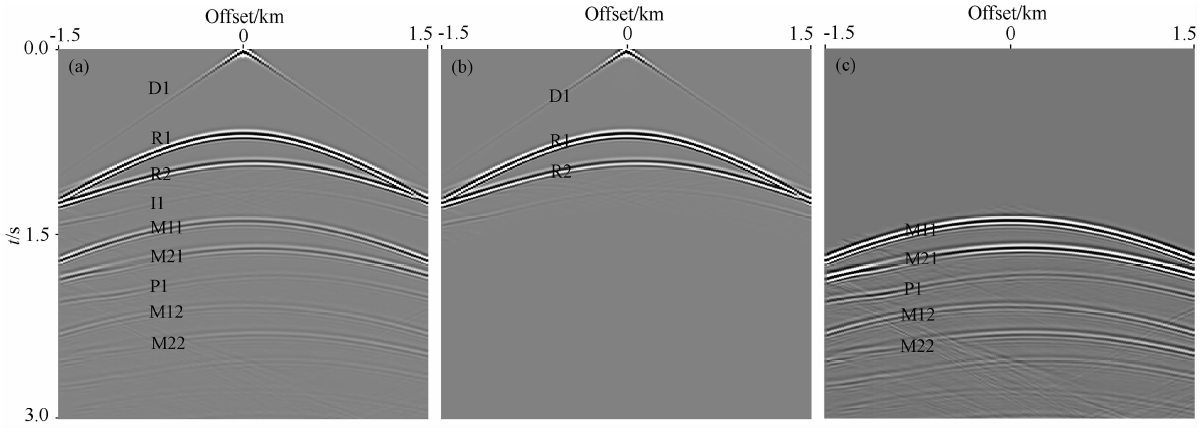
 | 图 3 简单模型和偏移结果 (a)简单模型速度场;(b)一次波叠前深度偏移;(c)包含多次波的记录叠前深度偏移;(d)多次波成像.Fig. 3 Simple velocity model and migration (a)Simple velocity model;(b)Migration of primaries;(c)Migration with records including primaries and multiples;(d)Imaging with multiples. |
图 3b是应用去除多次波后的记录(图 2b)做的单程波叠前深度偏移,第一反射层界面L1与第二个反射层界面L2都得到了正确的成像,而且偏移噪音很小.应用包含多次波炮集数据进行单程波叠前深度偏移的结果如图 3c所示,虽然可以正确成像L1与L2层界面,但是,由于多次波的存在产生了严重的偏移假象,其中,I是由震源子波延拓的下行波场与层间多次波延拓的上行波场I1产生的偏移假象;M1与M2分别是震源延拓的下行波场与第一层界面和第二层界面对应的地表相关一阶多次波M11和M12延拓的上行波场产生的偏移假象.图 3d是应用本文方法得到的多次波成像结果,其中,N1是层间多次波I1与第一个反射层的一阶地表相关多次波M11得到的偏移假象;N2是第二层的反射波R2与第一反射层的一阶地表相关多次波M11得到的偏移假象;L1是实际反射层的成像,它的成像贡献来自多个上、下行延拓波场的相关叠加,包括第一层的反射波R1与第一层的一阶地表相关多次波M11的相关成像、第二层的反射波R2与第二层 的一阶地表相关多次波M21的相关成像、第一层的一阶地表相关多次波与第一层的二阶地表相关多次波的相关成像、第二层的一阶地表相关多次波与第二层的二阶地表相关多次波的相关成像等,也就是式(5)中的第Ⅲ部分.类似地,L2层的成像由第二层的一次反射R2与第二层的一阶多次波、第二层的一阶多次波与第二层的二阶多次波等相关成像得到,这就是为什么多次波相对于一次波具有很广照明范围的原因,明显的表现就是图 3d中L1层成像范围大广于一次波对L1层成像(图 3c)的原因.N3、 N4和N5都是偏移假象,如式(5)中的第Ⅳ部分所示.
5.2 Sigsbee2B模型试算为了测试本方法对复杂模型的适用性,下面对国际上通用的多次波数据处理测试模型,Sigsbee2B进行试算.该模型的主要特点是存在起伏的海底和高陡盐丘构造(图 4a),图 4b是含有多次波的记录,图 4c是不含有地表相关多次波的记录,图 4d是地表相关多次波记录,共3495炮,每炮348道,记录长度12 s.图 5a是对炮集数据基于单程波偏移算子传 统叠前深度偏移结果,整体构造得到了较好的成像,但是在盐下及盐丘边界处由于初至反射波照明不足以及盐丘的遮挡屏蔽作用,使得成像质量差,成像能量弱.图 5b是基于本文的方法得到的多次波成像结果,由于地表相关多次波主要发育在具有强速度差的地方,也就是盐丘构造存在的地方,所以多次波成像的主要贡献就是在盐丘边界处,多次波成像使得盐丘边界得到了较好的刻画.对于不存在盐丘的地方(图 4a左边部分),不存在强速度差,地表相关多次波不发育,所以多次波成像能量非常弱(图 5b左边部分),这也说明了只有在多次波发育的地方,多次波对构造成像的贡献才比较大.为了利用多次波对盐下构造成像的优势,通过匹配叠加的方式,进行一次波与多次波联合成像.图 6是该匹配滤波因子,匹配因子的长度是49,匹配叠加后的结果如图 5c所示.图 7b、图 7c和图 7d分别是传统单程波偏移、多次波成像和联合成像结果在盐下高陡构造处的局部放大,箭头所指地方结果多次波成像后得到了明显改善和提高.
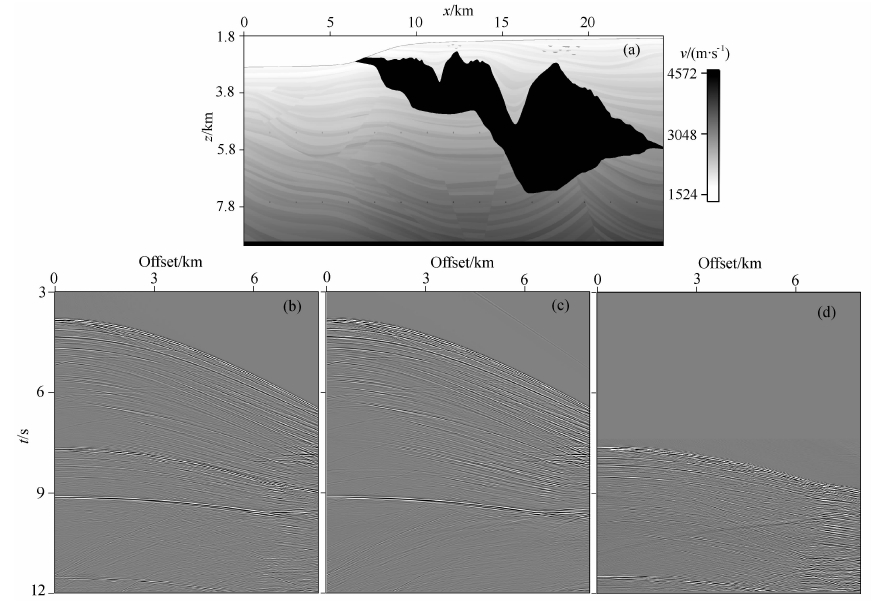 | 图 4 Sigsbee2B模型速度场与单炮记录(a)速度-深度模型;(b)包含多次波的单炮记录;(c)去除地表相关多次波后的单炮记录;(d)地表相关多次波.Fig. 4 Sigsbee2B velocity model and single shot record(a)Velocity-depth model;(b)Single shot record including multiples;(c)Single shot record after multiples elimination;(d)Surface-related multiples. |
 | 图 5 Sigsbee2B模型叠前深度偏移结果吧(a)一次波叠前深度偏移;(b)多次波叠前深度偏移;(c)一次波与多次波成像结果匹配叠加.Fig. 5 Pre-stack depth migration results of Sigsbee2B model(a)Pre-stack depth migration with primaries;(b)Pre-stack depth migration with multiples;(c)Matched stack of pre-stack depth migration of primaries and multiples. |
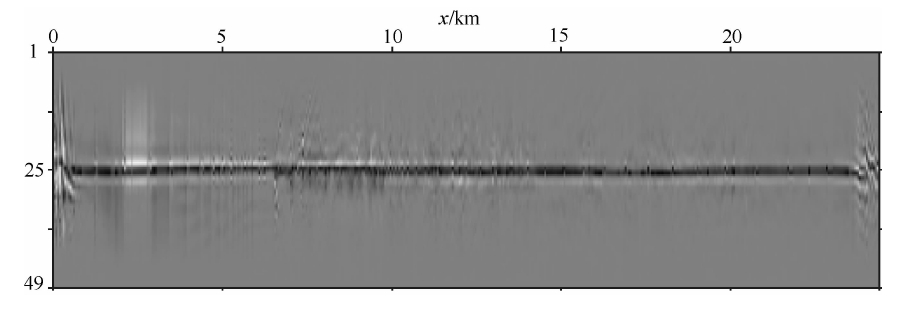 | 图 6 匹配滤波因子Fig. 6 Filter operator for matching |
 | 图 7 Sigsbee2B模型盐丘边界处叠前深度偏移 (a)速度模型;(b)一次波叠前深度偏移;(c)多次波叠前深度偏移;(d)一次波与多次波成像结果匹配叠加.Fig. 7 Salt boundary pre-stack depth migration of Sigsbee2B model (a)Velocity model;(b)Pre-stack depth migration of primaries;(c)Pre-stack depth migration of multiples; (d)Matched stack of pre-stack depth migration of primaries and multiples. |
基于单程波偏移算子的叠前深度偏移方法可以适应速度场强横向变化的同时具有较高的计算效率,本文对多次波在叠前深度偏移中的影响做了详细的分析,修改了单程波叠前深度偏移的初始条件,地震记录替代震源子波,预测得到的地表相关多次作为上行波场而实现了基于单程波偏移算子的地表相关多次波成像,发挥了多次波能够对地下构造多次照明的优势.使用了基于最小二范式一次波与多次波成像匹配叠加的方法,使得多次波的成像结果较好的弥补一次波成像的不足,尤其是高陡盐下构造边界这些一次波照明不足的地方成像效果得到了显著的改善.该项技术研究使我们意识到多次波这类“噪音”也是携带地下构造信息的信号,地球物理工作者可充分发挥其对地下构造多次照明的优势,最大限度的提取地下信息.
| [1] | Berkhout A J, Verschuur D J. 2006. Imaging of multiple reflections. Geophysics, 71(4): SI209-SI220, doi:10.1190/1. 2215359. |
| [2] | Brown M P, Guitton A. 2005. Least-squares joint imaging of multiples and primaries. Geophysics, 70(5): S79-S89, doi: 10. 1190/1. 2052471. |
| [3] | Chen X H, Liu H F. 2012. Comparison between inverse scattering series method and SRME method in free surface related multiple prediction. Progress in Geophysics (in Chinese), 27(3): 1040-1050, doi: 10. 6038/j. issn. 1004-2903. 2012. 03. 026. |
| [4] | Claerbout J F. 1971. Toward a unified theory of reflector mapping. Geophysics, 36(3): 467-481. |
| [5] | Guo K, Guo S, He G Z, et al. 2010. A method of multiple blind separation based on ICA. Progress in Geophysics (in Chinese), 25(3): 1075-1080, 10. 3969/j. issn. 1004-2903. 2010. 03. 048. |
| [6] | Guo S J, Li Z C, Tong Z Q, et al. 2011. Joint imaging of primaries and surface-related multiples based on generalized shot-profile migration. Chinese J. Geophys. (in Chinese), 54(4): 1098-1105. doi: 10. 3969/ j. issn. 0001-5733. 2011. 04025. |
| [7] | Guo S J, Li Z C, Tong Z Q, et al. 2012. Method and technique for imaging of surface-related multiples. Progress in Geophysics (in Chinese), 27(6): 2570-2576, doi:10. 6038/ j. issn. 1004-2903. 2012. 06. 034. |
| [8] | He R Q, Hornby B, Schuster G. 2007. 3D wave-equation interferometric migration of VSP free-surface multiples. Geophysics, 72(5): S195-S203, doi: 10. 1190/1. 2743375. |
| [9] | Jiang Z Y. 2006. Migration of interbed multiple reflections. //76th Ann. Internat. Mtg., Soc. Expl. Geophys. Expanded Abstracts, 3501-3505. |
| [10] | Liu Y K, Chang X. 2011. Reverse time migration of multiples. //81st Ann. Internat. Mtg., Soc. Expl. Geophys. Expanded Abstracts, 3326-3331. |
| [11] | Liu Y K, Chang X, Jin D G, et al. 2011. Reverse time migration of multiples for subsalt imaging. Geophysics, 76(5): WB209-WB216, doi: 10. 1190/GEO2010-0312. 1. |
| [12] | Muijs R, Holliger K. 2005. Prestack depth migration of primary and surface-related multiple reflections. //75th Ann. Internat. Mtg., Soc. Expl. Geophys. Expanded Abstracts, 2107-2110. |
| [13] | Muijs R, Robertsson J O, Holliger K. 2007. Prestack depth migration of primary and surface-related multiple reflections: Part I-Imaging. Geophysics, 72(2): S59-S69, doi: 10. 1190/1. 2422796. |
| [14] | Ristow D, Rūhl T. 1994. Fourier finite-difference migration. Geophysics, 59(12): 1882-1893. |
| [15] | Shan G J, Guitton A. 2004. Migration of surface-related multiples: tests on the Sigsbee2B dataset. //74th Ann. Internat. Mtg., Soc. Expl. Geophys. Expanded Abstracts, 1285-1288. |
| [16] | Shan G. 2003. Source-receiver migration of multiple reflections. //73rd Ann. Internat. Mtg., Soc. Expl. Geophys. Expanded Abstracts, 1008-1011. |
| [17] | Shi Y, Jing H L, Li Y. 2012. Surface-related multiple suppression effect analysis by feedback iteration approach. Progress in Geophysics (in Chinese), 27(4): 1493-1500, doi: 10. 6038/j. issn. 1004-2903. 2012. 04. 024. |
| [18] | Shi Y, Xing X L. 2011. Investigation progress on surface-related multiple suppression: review and outlook. Progress in Geophysics (in Chinese), 26(6): 2046-2054, doi: 10. 3969/j. issn. 1004-2903. 2011. 06. 020. |
| [19] | Stoffa P L, Fokkema J T, De Luna Freire R M, et al. 1990. Split-step Fourier migration. Geophysics, 55(4): 410-421. |
| [20] | Vasconcelos I, Snieder R, Hornby B. 2008. Imaging internal multiples from subsalt VSP data-examples of target-oriented interferometry. Geophysics, 73(4): S157-S168, doi: 10. 1190/1. 2944168. |
| [21] | Wang Y B, Chang X, Hu H. 2014. Simultaneous reverse time migration of primaries and free-surface related multiples without multiple prediction. Geophysics, 79(1): S1-S9, doi: 10. 1190/GEO2012-0450. 1. |
| [22] | Zhang D L, Schuster G T. 2014. Least-squares reverse time migration of multiples. Geophysics, 79(1): S11-S21, doi: 10. 1190/GEO2013-0156. 1. |
| [23] | Zhang G Q. 1993. System of coupled equations for upcoming and downgoing waves. Acta Mathematicae Applicatae Sinica (in Chinese), 16(2): 251-263. |
| [24] | Zhang Y, Zhang G Q, Bleistein N. 2005. Theory of true-amplitude one-way wave equations and true-amplitude common-shot migration. Geophysics, 70(4): E1-E10, doi: 10. 1190/1. 1988182. |
| [25] | Zhao C L, Ye Y M, Yao G S, et al. 2013. Prediction deconvolution in linear radon domain on the application of ocean multiples attenuation. Progress in Geophysics (in Chinese), 28(2):1026- 1032, doi: 10. 6038/pg20130256. |
| [26] | 陈小宏, 刘华锋. 2012. 预测多次波的逆散射级数方法与SRME方法及比较. 地球物理学进展, 27(3): 1040-1050. |
| [27] | 郭科, 郭思, 何国柱等. 2010. 基于独立分量分析的多次波盲分离方法研究. 地球物理学进展, 25(3): 1075-1080. |
| [28] | 郭书娟, 李振春, 仝兆岐等. 2011. 基于广义的炮偏移方法实现地表多次波和一次波联合成像. 地球物理学报, 54(4): 1098-1105. |
| [29] | 郭书娟, 李振春, 仝兆岐等. 2012. 表层多次波成像方法技术研究. 地球物理学进展, 27(6): 2570-2576. |
| [30] | 石颖, 井洪亮, 李莹. 2012. 反馈迭代法压制表面多次波效果分析. 地球物理学进展, 27(4): 1493-1500. |
| [31] | 石颖, 邢小林. 2011. 表面多次波压制的研究进展: 回顾与展望. 地球物理学进展, 26(6): 2046-2054. |
| [32] | 张关泉. 1993. 波动方程的上行波和下行波的耦合方程组. 应用数学学报, 16(2): 251-263. |
| [33] | 赵昌垒, 叶月明, 姚根顺等. 2013. 线性拉东域预测反褶积在海洋多次波去除中的应用. 地球物理学进展, 28(2): 1026-1032. |
 2014, Vol. 57
2014, Vol. 57

