1 引言
随着人类对矿产资源需求的不断增加,地表和浅层的金属矿产资源越来越少,寻找深部隐伏金属矿产已成为拓展新的找矿空间的必由之路.在勘探深度和精度方面都有明显优势且在油气勘探领域取得广泛成功的地震勘探方法有希望在寻找深部隐伏金属矿产方面发挥作用.由于金属矿多产出在造山带,因而通常表现为起伏地表的复杂特征.不仅如此,金属矿区往往经历强烈的构造变动和岩浆活动,矿体形状复杂,在空间尺度上要远远小于油气藏.因而金属矿地震勘探具有地表起伏地下地质体复杂的显著特征,其地震波传播规律要比水平地表和层状介质情形复杂得多.采用地震数值模拟技术是揭示起伏地表复杂地质体情形下地震波传播规律的有效手段.
地震波方程求解的数值方法主要有有限元法(杨顶辉,2002)、边界元法(Fu and Wu, 2000)和有限差分法(王德利等,2005;郑海山和张中杰,2005).有限元法可有效处理复杂边界,边界点与内点具有相同的离散处理手段,但采用有限元法求解与时间变量有关的发展方程,每个时间层都要求解一个大型线性代数方程组,计算速度很慢.边界元法比有限元法计算量小,处理复杂外边界比较有效,但是当内边界较多时,该方法计算效率明显降低.常规的矩形网格有限差分法具有计算速度快的显著特点,但该方法处理复杂边界比较困难.
在复杂边界地震波方程数值模拟方面,国内外许多学者开展了大量富有探索性的研究工作.薛东川等(2007)采用有限元法对起伏地表复杂介质波动方程进行正演模拟,Ge和Chen(2008)采用边界元方法就复杂地下分界面情形进行地震波场数值模拟,李绪宣等(2011)采用边界元方法分析复杂海底的地震散射特征.采用矩形网格有限差分方法进行复杂边界地震波数值模拟仍然是国内外研究的一个主流方向,Jih等(1988)对自由表面为折线边界情形区分六种情况给出了边界点处理的一种局部旋转坐标方法,Pérez-Ruiz等(2005)在自由表面之上引入了虚介质的概念并区分13种情形对边界点进行处理,Appel和Petersson(2009)采用曲线坐标系到直角坐标系映射方法处理复杂自由边界,Lan和Zhang(2011)就三维情形利用坐标映射方法处理非规则自由表面,裴正林(2004)采用零速度法和广义虚像法相结合的办法处理自由边界,董良国等(2007)将自由边界上的点划分为22类并分别采用不同的差分格式处理边界点.为了克服单一数值方法的局限性,又相继出现了几种组合方法.黄自萍等(2004)采用有限元与有限差分耦合的区域分裂法,克服了单纯用有限差分法对区域的依赖性.马德堂和朱光明(2004)采用有限元与伪谱法混合求解方法,并采用过渡区域解决了两种算法的衔接问题.管西竹等(2011)采用边界元和体积元结合的方法在频域求解含有面积分和体积分的积分方程.此外,由于三角网差分如同有限元一样可适应复杂边界,褚春雷和王修田(2005)采用三角网有限差分法求解复杂边界地震波方程,孙小东等(2012)研究了基于三角网有限差分法的叠前逆时偏移技术.在这些方法中,组合方法与三角网差分也都存在计算效率低的弱点.鉴于矩形网有限差分法在计算效率上具有突出的优点,而一般的二维地球物理模型边界都可由分段光滑曲线来逼近,本文研究二维分段光滑曲线边界地震波方程矩形网格有限差分的有效算法和数值模拟技术.
2 方法原理
采用矩形网格有限差分法求解地震波传播的波动方程数学模型,有两类边界条件最难处理,其一是地表Γ上的自由边界条件
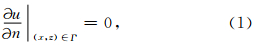
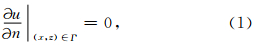
矩形网格有限差分法处理复杂边界问题的关键有两点,其一是对复杂边界进行合理的网格化形成网格边界点,其二是利用网格边界点附近的波场值计算自由边界条件(1)式和衔接条件(2)式中的方向导数.
2.1 边界网格化
如果边界Γ是封闭曲线,可将Γ分解成多支依次连接的曲线,每支曲线都可由单值函数来表示.不妨假定边界Γ可由单值函数z=φ(x),(xl≤x≤xr)来表示,其中xl和xr分别为边界Γ左右端点的x坐标.按如下的就近迁移原则将实际边界点迁移到最近的网格点形成网格边界点:
(1)选定包含计算区域R在内的一个矩形区域[0,X]×[0,Z],其中X和Z分别为矩形区域的长度和高度,取定x和z方向的空间步长分别为Δx,Δz,设X/Δx=M,Z/Δz=N,则网格点坐标为
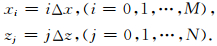
(2)设函数nint表示取整数运算,计算Γ左右端点x坐标对应的水平网格点的序号为
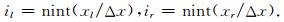
(3)计算
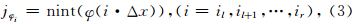
如果|jφi+1-jφi|≤1(对应横向变化平缓的边界),则节点(i,jφi),(i=il,il+1,…,ir)就构成了网格边界点,也就是说(i,jφi)是距离实际边界点(xi,φ(xi)) 最近的网格节点.
如果|jφi+1-jφi|=L(L>1)(对应横向变化剧烈的边界,比如陡倾角边界),这时在jφi与jφi+1之间要插入L-1个点,才能使离散化之后的网格边界是按网格点“连续”变化的.插值方法是:取jzk=jφi±k,(k=1,…,L-1).其中±号的选择取决于 曲线沿z轴方向是上升还是下降.然后由反函数计算 ixk=nint(φ-1(jzk·Δz)),则(ixk,jzk),(k=1,…,L-1)便是在(i,jφi)与(i+1,jφi+1)之间插入的网格边界点.
如果没有特殊需要,通常情况下都采用Δx=Δz的正方形网格,本文计算过程中采用的就是正方形网格. 2.2 法线方向上波场值的插值计算
对于自由表面边界条件来说,计算方向导数需要自由面以下介质内部沿边界法线方向上的波场值;对于内边界衔接条件而言,计算方向导数需要内部边界两侧沿边界法线方向上的波场值.一般情况下,法线与网格节点并不相交,因而法线上的波场值通常是未知的.本文给出了一种插值方法来计算法线方向上的波场值.
该插值方法在正方形网格条件下要求将角度区间 [0°,180°]以45°为间隔分四种情况来讨论,这里我们仅以[0°,45°]情况为例进行论述.
首先假设边界Γ是光滑曲线z=φ(x),曲线在(xi,φ(xi))处的切线L与ox轴夹角为α,0≤α≤45°.将边界点(xi,φ(xi))就近迁移到网格边界点(i,j),过点(i,j)做平行于切线L的直线 AB,则直线 AB 可作为网格边界点(i,j)处的切线.为叙述方便,不妨假定边界Γ上的点(xi,φ(xi))恰好位于网格边界点(i,j)处,直线 AB 恰为点(xi,φ(xi))处的切线,对应的法线为PQ,AB 与ox轴的夹角为α(如图 1).
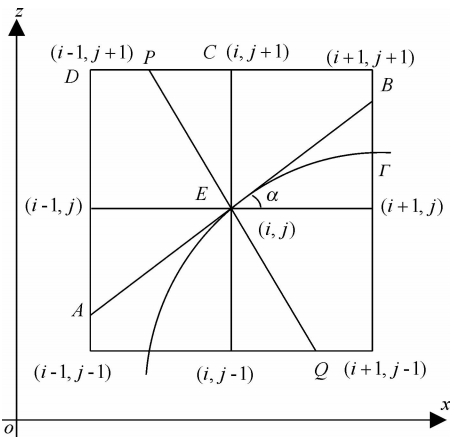 | 图 1 插值计算示意图Fig. 1 Sketch of interpolation calculation |
设点(i-1,j+1),(i,j+1)分别为D和C(如图 1),则线段PC和PD 可分别写成
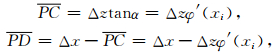
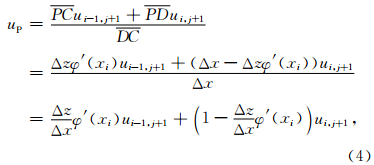
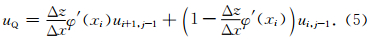
在正方形网格条件下,由于Δz=Δx,于是有
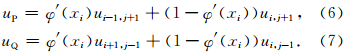
2.3 方向导数与边界条件计算
在图 1中记(i,j)点为E,首先假设Γ是内边界.当Γ作为上部介质的边界时,边界Γ上点E处的外法线方向导数可按下式计算
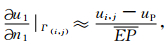
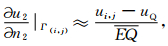
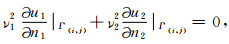
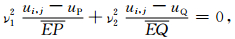
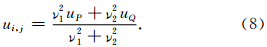
如果假设图 1中Γ为自由面,且Γ下部为地球介质,则自由面边界条件为
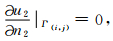
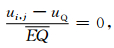

在上述公式(6)—(9)中,φ′(xi)仅仅是空间变量x的函数,与时间变量无关,在差分法的波场时间递推计算之前,可一次性计算出φ′(xi).因此,这种算法明显具有复杂度低与计算量小的特点.
2.4 正则导数定义
在前面的讨论中,公式(4)—(7)的计算要求φ′(xi)处处存在,也就是要求边界Γ处处光滑,而实际地层中常出现断层、尖灭等非光滑边界情形,讨论分段光滑边界更具普遍意义.由于分段光滑边界尖点处的导数不存在,要想使前述算法仍然可用,就必须给出尖点处的某种广义导数.
首先考虑分段光滑曲线边界的特例——折线边界,在折线边界的尖点处我们引入一种正则导数,具体定义如下:
在图 2的xoz坐标系下,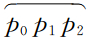 构成了一条折线,p1是尖点.p0,p1,p2的坐标分别记为(x0,z0),(x1,z1),(x2,z2).构造向量为
构成了一条折线,p1是尖点.p0,p1,p2的坐标分别记为(x0,z0),(x1,z1),(x2,z2).构造向量为
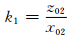
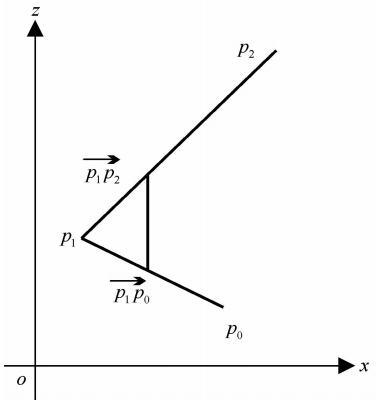 | 图 2 尖点正则导数定义Fig. 2 Definition of regular derivative for a cusp |
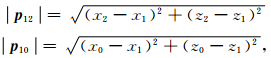

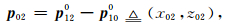
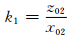 为尖点p1处的正则导数,而正则法向导数
为尖点p1处的正则导数,而正则法向导数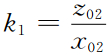 所决定的法向量恰在∠p0p1p2的角平分线上.
所决定的法向量恰在∠p0p1p2的角平分线上.对于一般的分段光滑曲线,可根据尖点两侧的常规左右导数的变化趋势做出两条在尖点相交的切线,设交点为p1,在两条切线上分别取点p0和p2,与折线尖点正则导数类似可定义分段光滑曲线尖点处的正则导数.
3 正演模拟计算与波场特征分析 3.1 正演模拟计算
构造图 3所示的地球介质模型I.地表Γ0为曲线自由边界.区域内部边界Γ1为斜线边界,内部边界Γ2为封闭折线边界,Pk(k=1,2,…,7)为折线上的尖点,区域内部边界都采用衔接条件.左边界x=0、右边界x=1000 m和下边界z=1000 m为人工截断边界,处理为吸收边界.图中v1是上层介质的波速,v2是Γ1以下Γ2外部介质的波速,v3是Γ2所围区域内部介质的波速.
依据以上边界条件建立如下的二维地震纵波数学模型为
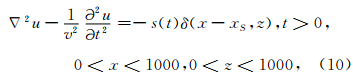
 | 图 3 地球介质模型I Fig. 3 Earth medium model I |
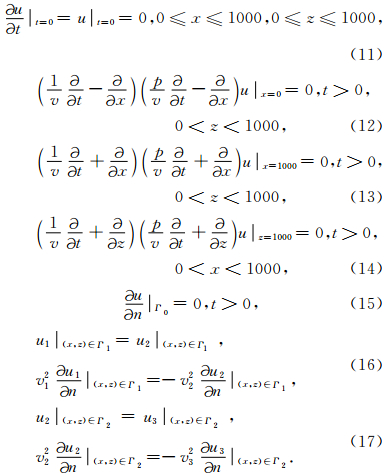
在由(10)—(17)式给出的数学模型中,(10)式是内点的泛定方程,时间和空间的二阶偏导数均采用二阶中心差商进行离散;(12)—(14)式分别是左边界、右边界和底边界上的吸收边界条件,由于吸收边界是与坐标轴平行的直线边界,可用常规差分法直接离散;(15)式是地表Γ0上的自由边界条件,(16)—(17)式分别是内边界Γ1和Γ2上的衔接条件,(15)—(17)式中的方向导数采用本文给出的插值法计算.
采用矩形网有限差分法对上述模型进行地震正演数值模拟.震源子波采用主频为62.5 Hz的雷克子波,炮点坐标为(500,5),地面接收排列的起点为x=100,道间距为10 m,设置80道,计算中取空间 步长为Δz=Δx=1.25 m,时间步长为Δt=0.25 ms,记录长度为0.9 s,模拟得到的波场系列快照和地震记录见图 4和图 5.
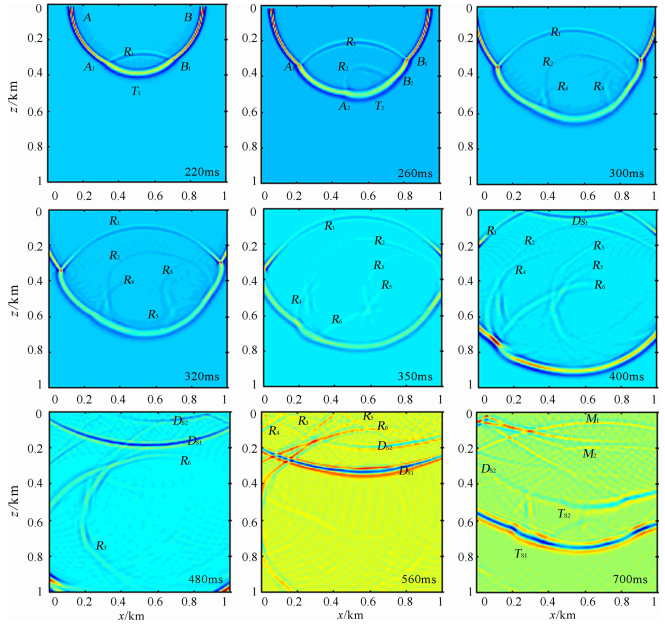 | 图 4 波场系列快照 Fig. 4 Snapshots of wave fields |
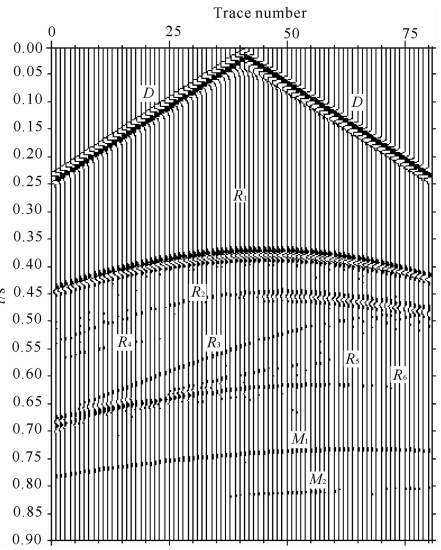 | 图 5 正演模拟的地震记录Fig. 5 Seismic record by forward simulation |
3.2 波场特征分析
在图 4中的220 ms波场快照中,T1是地震波经过界面Γ1向下方介质透射的波前,R1是对应的反射波前,A1、B1位于内边界Γ1上.A、B两点在曲线地表Γ0上,地表检波器接收到的A、B两点的波场是直达波,在图 5的地震记录中对应的是直达波同相轴D.在260 ms波场快照中,弧 与
与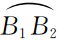 是介质V2中的入射波前,T2是透射到介质V3中的透射波前,R2是对应的反射波前,A2位于内边界Γ2的线段
是介质V2中的入射波前,T2是透射到介质V3中的透射波前,R2是对应的反射波前,A2位于内边界Γ2的线段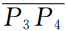 上,B2位于内边界Γ2的线段
上,B2位于内边界Γ2的线段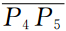 上.
上.
3 00 ms波场快照中新出现的波前R3是Γ2上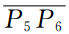 段产生的反射,R4是Γ2上
段产生的反射,R4是Γ2上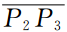 段产生的反射,R4与R2形成的“蝴蝶结”是凹陷
段产生的反射,R4与R2形成的“蝴蝶结”是凹陷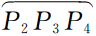 反射的结果.320 ms波场快照中新出现的波前R5是Γ2上
反射的结果.320 ms波场快照中新出现的波前R5是Γ2上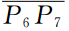 段产生的反射,从该快照中还可看出,当反射波前R2向上透过Γ1时,波前的形状、曲率以及能量分布的均匀性都发生了改变.350 ms波场快照中新出现的波前R6是Γ2上
段产生的反射,从该快照中还可看出,当反射波前R2向上透过Γ1时,波前的形状、曲率以及能量分布的均匀性都发生了改变.350 ms波场快照中新出现的波前R6是Γ2上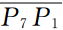 段产生的反射,而反射波R1即将到达地表Γ0并将被地表检波器所接收,在图 5的地震记录中在350 ms以后将开始出现反射波同相轴R1.
段产生的反射,而反射波R1即将到达地表Γ0并将被地表检波器所接收,在图 5的地震记录中在350 ms以后将开始出现反射波同相轴R1.
在400 ms以后的波场快照中,除了反射波之外还将讨论自由表面引起的多次波(包括二次入射波、二次反射波和二次透射波).400 ms波场快照中反射波R1经过自由表面反射后产生了二次入射波DS1.在480 ms和560 ms的波场快照中,DS2是反射波R2经过自由表面反射后生成的二次入射波.而且在此期间反射波前R2完整经过了地表的检波器排列,在图 5的地震记录中出现了对应的反射波同相轴R2;反射波前R3按道号由大到小的规律也被地表检波器依次接收,在图 5中出现了对应的反射波同相轴R3,并将继续向小道号方向扩展;反射波前R4只有波震面的一小部分被少量小道号地表检波器所接收,在图 5中对应的是同相轴R4,对应时间是在550 ms到600 ms之间.在700 ms的波场快照中,TS1是二次入射波DS1 经过介质分界面产生的下行透射波前(这里可包含多次下行透射),M1是DS1入射到界面Γ1产生的二次反射波前;TS2是二次 入射波DS2 经过介质分界面产生的下行透射波前,M2是DS2入射到界面Γ1产生的二次反射波前.在600 ms与700 ms期间反射波前R5、R6也依次到达地表检波器排列,在图 5的反射记录中,反射波R5、R6表现为交叉“蝴蝶结”状同相轴.而二次反射波前M1和M2将在720 ms至850 ms期间先后到达地表检波器排列,在图 5的地震记录上对应两个二次波同相轴M1和M2.
3.3 边界条件处理对比计算
我们研究的法向导数插值计算方法,自由表面外边界处理只是内边界处理的一个简单特例.为此我们选择了另一种处理内边界的方法进行比较,就是内边界不给定衔接条件(也就不涉及方向导数的计算),只用介质参数(这里是波速)的不同分区来表征内边界.图 6是参数分区表征边界情形模拟的地震记录.
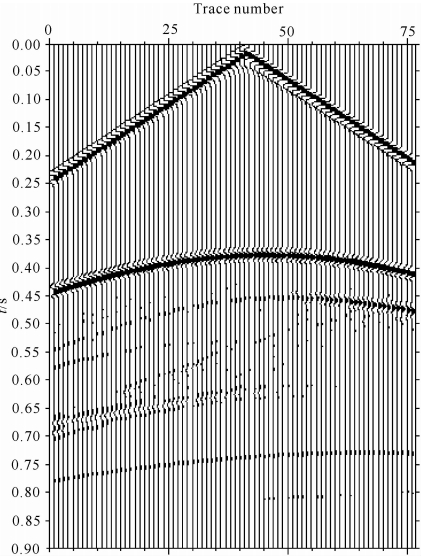 | 图 6 参数分区表征边界情形模拟的地震记录 Fig. 6 Seismic record at boundary condition characterized by parameter partition |
粗略地看,图 5与图 6给出的两种计算结果似乎没有太大差别.但仔细观察就会发现,给定衔接条件计算法向导数的情形下,反射波的相位与入射波(或直达波)的相位是相反的,符合真实的物理规律;而在不给定衔接条件的情形下,反射波的相位与入射波(或直达波)的相位是相同的,这与真实的物理规律是相悖的.通过图 7给出的波场快照可以更明显地看出两种情形反射波相位的差别.
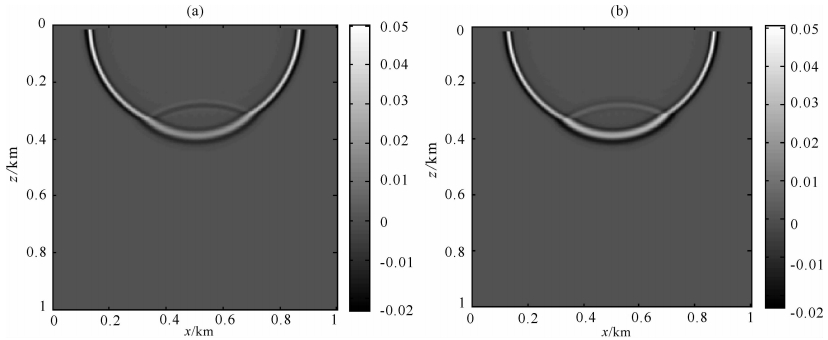 | 图 7 220 ms波场快照(a)衔接边界情形;(b)参数分区表征边界情形. Fig. 7 Wave field snapshots at 220 ms(a)The case at join condition boundary;(b)The case at boundary of parameter partition characterization. |
为了衡量插值算法的计算效率,我们采用节3.1 给出的计算参数,在双核处理器为AMD Athlon(t)II×2250的普通微机上进行对比计算,衔接条件边界情形的计算时间为16.5 min,无衔接条件的参数分区表征边界情形的计算时间为15.9 min,二者的时间差就是处理内部衔接条件边界Γ1和Γ2所耗费的机时,这表明对本文给定的模型而言,其内部衔接条件边界插值处理的计算量只占全部模拟过程所用 计算量的3.6%,因此插值处理衔接边界条件的计 算效率是可以接受的.当然对于不同模型不同总长度的内边界,其计算效率是不同的.
3.4 尖点导数对波场绕射特征的影响
在尖点正则导数的定义下,我们实现了对地球介质模型I的数值模拟计算.为了研究尖点导数对波场特征的影响,就要给出另一种尖点导数,通过对比两种不同的尖点导数对应的波场及波场差,揭示不同的尖点导数处理技术对波场特征的影响规律.为此,我们又研究了另一种尖点导数.对分段光滑曲线而言,尖点两侧以尖点为中心的去心邻域内曲线上的导数存在而且连续,在曲线上由尖点一侧的导数向尖点处取单侧极限,将尖点处的这个极限值作为尖点的一种广义导数,我们称之为单侧连续导数.
由于模型I过于复杂,掩盖了尖点绕射的微弱特征,我们建立了模型II(图 8)用来讨论尖点问题,除了介质模型结构不同之外,其余的计算参数与模型I相同.分别采用正则导数和单侧连续导数两种定义对模型II进行数值计算,图 9a是采用正则导数计算得到的160、200 ms和230 ms的波场快照,图 9b是采用单侧连续导数计算得到的对应波场快照,图 9c是二者的波场差.图 9a中的C1、C2和C3分别是尖点P2、P3和P4产生的绕射波.绕射波前在均匀介质中都是以尖点为圆心的圆周,与反射波相比 绕射波能量相对较弱.由图 9a和b可见,两种方法 的模拟效果在宏观上几乎看不出差别.然而由图 9c的波场差可见,两者存在着微小差别,这种差别产生的原因仅仅是两种方法在尖点导数的处理技术上有所不同,而这种不同并没有引起传播规律的改变,改变的只是尖点对绕射波能量大小的贡献略有不同.
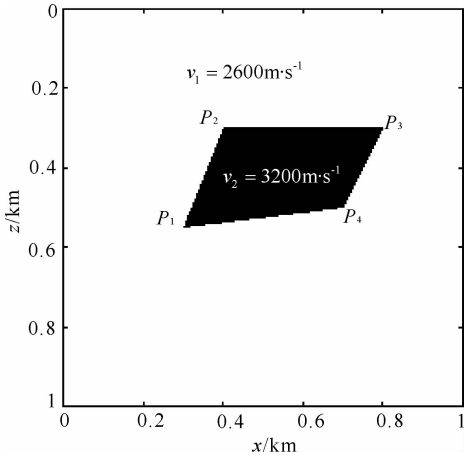 | 图 8 地球介质模型Ⅱ Fig. 8 Earth medium model Ⅱ |
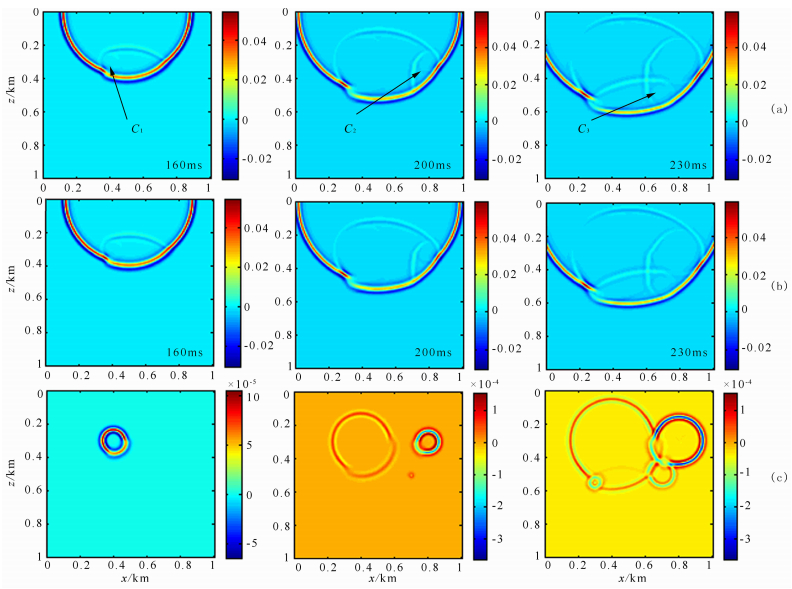 | 图 9 模型Ⅱ波场快照(a)正则导数法;(b)单侧连续导数法;(c)(a)与(b)波场差. Fig. 9 Wave field snapshots for model Ⅱ a)Wavefields of regular derivative method;(b)Wavefields of unilateral continuous derivative method;(c)Wavefields difference between(a) and (b). |
3.5 稳定性与数值频散问题讨论
泛定方程(10)所对应的齐次方程的二阶显式差分格式为
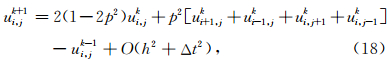
差分格式(18)的稳定性条件为(Alford et al., 1974)
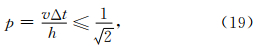
利用有限差分法数值求解波动方程仅靠稳定性条件限制是不能有效解决数值频散问题的.为了有效消除数值频散误差,通常要求在一个地震波长范围内涵盖足够多的空间网格点.本文正演模拟计算中取空间步长h=1.25 m,对给定的震源子波使得在一个最小地震波长内涵盖了23个空间网格点,有效地消除了数值频散现象.通过减小空间步长的办法虽然可以减弱数值频散误差,但同时也大大增加了计算量.近年来,(Ma et al., 2011;Yang et al., 2012a,2012b; Tong et al., 2013)研究了几种具有弱数值频散特性的数值方法,可以放宽空间步长的限制,并有效压制数值频散误差.
4 结论
给出的边界网格化方法可方便地处理横向变化剧烈的内外边界.提出的法向导数插值算法具有复杂度低和计算量小的显著特点.通过补充定义分段光滑曲线在尖点处的广义导数(正则导数或单侧连续导数),可将法向导数插值算法拓展到分段光滑曲线边界情形.该算法弥补了矩形网格有限差分法处理复杂边界问题的缺陷.模型试算结果验证了该算法的有效性.
根据波场快照中各个波前到达检波器排列位置所对应的快照时间,可以准确地分析与识别地震记录中的各个同相轴.利用波场系列快照技术,可揭示地震波场在复杂边界(包括地表自由边界和内部边界)控制下的传播规律.
| [1] | Alford R M, Kelly K R, Boore D M. 1974. Accuracy of finite-difference modeling of the acoustic wave equation. Geophysics, 39(6): 834-842. |
| [2] | Appel D, Petersson N A. 2009. A stable Finite difference method for the elastic wave equation on complex geometries with free surfaces. Commun. Comput. Phys., 5(1): 84-107. |
| [3] | Chu C L, Wang X T. 2005. Seismic Modeling with a Finite-Difference Method on Irregular Triangular Grids. Periodical of Ocean University of China (in Chinese), 35(1): 43-48. |
| [4] | Dong L G, Guo X L, Wu X F, et al. 2007. Finite difference numerical simulation for the elastic wave propagation in rugged topography. Natural Gas Industry (in Chinese), 27(10): 38-41. |
| [5] | Fu L Y, Wu R S. 2000. Infinite boundary element absorbing boundary for wave propagation simulations. Geophysics, 65(2): 596-602. |
| [6] | Ge Z X, Chen X F. 2008. An efficient approach for simulating wave propagation with the boundary element method in multilayered media with irregular interfaces. Bulletin of the Seismological Society of America, 98(6): 3007-3016. |
| [7] | Guan X Z, Fu L Y, Tao Y, et al. 2011. Boundary-volume Integral equation numerical modeling for complex near surface. Chinese J. Geophys. (in Chinese), 54(9): 2357-2367. |
| [8] | Huang Z P, Zhang M, Wu W Q, et al. 2004. A domain decomposition method for numerical simulation of the elastic wave propagation. Chinese J. Geophys. (in Chinese), 47( 6): 1094-1100. |
| [9] | Jih R S, Mclaughlin K L, Der Z A. 1988. Free-boundary conditions of arbitrary polygonal topography in a two-dimensional explicit elastic finite-difference scheme. Geophysics, 53(8): 1045- 1055. |
| [10] | Lan H Q, Zhang Z J. 2011. Three-dimensional wave-field simulation in heterogeneous transversely isotropic medium with irregular free surface. Bulletin of the Seismological Society of America, 101(3): 1354-1370. |
| [11] | Li X X, Yu G X, Fu L Y, et al. 2011. Analysing seismic scattering characteristics of complex seabed by using the boundary-element simulation method. China Offshore Oil and Gas (in Chinese), 23(6): 357-361, 368. |
| [12] | Ma D T, Zhu G M. 2004. Hybrid method combining finite difference and pseudospectral method for solving the elastic wave equation. Journal of Earth Sciences and Environment (in Chinese), 26(1): 61-64. |
| [13] | Ma X, Yang D H, and Liu F Q. 2011. A nearly analytic symplectically partitioned Runge-Kutta method for 2-D elastic wave equations. Geophysical Journal International, 187(1): 480-496. |
| [14] | Pei Z L. 2004. Numerical modeling using staggered-grid high-order finite-difference of elastic wave equation on arbitrary relief surface. Oil Geophysical Prospecting (in Chinese), 39(6): 629-634. |
| [15] | Pérez-Ruiz J A, Luzón F, García-Jerez A. 2005. Simulation of an irregular free surface with a displacement finite-difference scheme. Bulletin of the Seismological Society of America, 95(6): 2216-2231. |
| [16] | Sun X D, Li Z C, Wang X L. 2012. Pre-stack reverse-time migration using a finite difference method based on triangular grids. Progress in Geophysics (in Chinese), 27(5): 2077-2083. |
| [17] | Tong P, Yang D H, Hua B L, et al. 2013. A high-order stereo-modeling method for solving wave equations. Bulletin of the Seismological Society of America, 103(2A): 811-833. |
| [18] | Wang D L, He Q D, Han L G. 2005. Multi-azimuth three-component surface seismic modeling for cracked monoclinic media. Chinese J. Geophys. (in Chinese), 48(2): 386-393. |
| [19] | Xue D C, Wang S X, Jiao S J. 2007. Wave equation finite-element modeling including rugged topography and complicated medium. Progress in Geophysics (in Chinese), 22(2): 522-529. |
| [20] | Yang D H. 2002. Finite element method of the elastic wave equation and wavefield simulation in two-phase anisotropic media. Chinese J. Geophys. (in Chinese), 45(4): 575-583. |
| [21] | Yang D H, Tong P, Deng X Y. 2012a. A central difference method with low numerical dispersion for solving the scalar wave equation. Geophysical Prospecting, 60(5): 885-905. |
| [22] | Yang D H, Wang N, Liu F Q. 2012b. A strong stability-preserving predictor-corrector method for the simulation of elastic wave propagation in anisotropic media. Communications in Computational Physics, 12(4): 1006-1032. |
| [23] | Zheng H S, Zhang Z J. 2005. Synthetic seismograms of nonlinear seismic waves in anisotropic (VTI) media. Chinese J. Geophys. (in Chinese), 48(3): 660-671. |
| [24] | 褚春雷, 王修田. 2005. 非规则三角网格有限差分法地震正演模拟. 中国海洋大学学报, 35(1): 43-48. |
| [25] | 董良国, 郭晓玲, 吴晓丰等. 2007. 起伏地表弹性波传播有限差分法数值模拟. 天然气工业, 27(10): 38-41. |
| [26] | 管西竹, 符力耘, 陶毅等. 2011. 复杂地表边界元-体积元波动方程数值模拟. 地球物理学报, 54(9): 2357-2367. |
| [27] | 黄自萍, 张铭, 吴文青等. 2004. 弹性波传播数值模拟的区域分裂法. 地球物理学报, 47(6): 1094-1100. |
| [28] | 李绪宣, 于更新, 符力耘等. 2011. 应用边界元模拟方法分析复杂海底地震散射特征. 中国海上油气, 23(6): 357-361, 368. |
| [29] | 马德堂, 朱光明. 2004. 有限元法与伪谱法混合求解弹性波动方程. 地球科学与环境学报, 26(1): 61-64. |
| [30] | 裴正林. 2004. 任意起伏地表弹性波方程交错网格高阶有限差分法数值模拟. 石油地球物理勘探, 39(6): 629-634. |
| [31] | 孙小东, 李振春, 王小六. 2012. 三角网格有限差分法叠前逆时偏移方法研究. 地球物理学进展, 27(5): 2077-2083. |
| [32] | 王德利, 何樵登, 韩立国. 2005. 裂隙型单斜介质中多方位地面三分量记录模拟. 地球物理学报, 48(2): 386-393. |
| [33] | 薛东川, 王尚旭, 焦淑静. 2007. 起伏地表复杂介质波动方程有限元数值模拟方法. 地球物理学进展, 22(2): 522-529. |
| [34] | 杨顶辉. 2002. 双相各向异性介质中弹性波方程的有限元解法及波场模拟. 地球物理学报, 45(4): 575-583. |
| [35] | 郑海山, 张中杰. 2005. 横向各向同性(VTI)介质中非线性地震波场模拟. 地球物理学报, 48(3): 660-671. |
 2014, Vol. 57
2014, Vol. 57

