2. 中国海洋石油集团公司研究总院, 北京 100027
2. CNOOC Research Institute, CNOOC Plaza, Beijing 100027, China
偏移,特别是叠前偏移是目前地震资料处理的一个重要环节.当前实现偏移成像的途径大致分为两类,即基于射线理论的Kirchhoff积分法偏移和基于波动方程的偏移.Kirchhoff积分法偏移是目前工业界广泛使用的方法,它的基本理论几何意义明确,这类偏移方法具有较灵活的目标处理能力和较高的计算效率,还可以适应不规则观测系统.但是,Kirchhoff积分类偏移方法的基础是射线追踪,在复杂介质条件下,射线追踪存在多路径、焦散等问题,因为这些问题,积分类偏移方法有时得不到令人满意的成像结果(Han,1998;金胜汶等,2002;刘喜武和刘洪,2002).波动方程相对于射线追踪技术,能更准确地描述波在复杂介质中的传播以及波场能量的变化情况,这使得基于波动方程的偏移方法更受青睐.波动方程偏移方法又可以进一步分为基于单程波方程的偏移方法和基于双程波方程的偏移方法.精确的单程波方程只能在频率-波数域表示,如相移法(Gazdag,1978).但是相移法无法适应速度的横向变化,因此一些学者在相移法的基础上相继提出了一些改进措施以适应速度的横向变化(Gazdag and Sguazzero, 1984;Stoffa et al., 1990;Ristow and Rühl,1994;Biondi,2002).另外一种途径是直接获得在空间域表述的单程波方程,采用有限差分法进行数值计算,从而隐式地适应速度的任意变化.最早的时空域单程波方程由Claerbout(1976)提出,它是基于对双程波方程频散关系近似得到的.然而,在空间域表述的单程波方程有明显的倾角限制,无法对高陡构造准确成像.为了进一步扩大单程波的传播角度以满足大倾角地层成像的要求,一些学者采用了不同的高阶近似方法,获得了一系列高阶单程波方程(马在田,1983;Bamberger et al., 1988;Collins and Westwood, 1991).但这些方程往往包含高阶偏导数项(二阶以上),使得数值计算成为令人头疼的问题.
基于双程波的逆时偏移能有效地克服单程波成像倾角的限制,并且在保幅方面具有优势.逆时偏移(Baysal et al., 1983)包含波场的正向外推和逆时外推,其成像过程需要存储各个时刻的波场,非常耗时.即便采取一些措施避免波场存储的问题(Clapp,2009),但也是以计算换存储的策略,会额外增加计算量.此外,适用于波动方程偏移的互相关成像条件最初是针对单程波方程提出的,将其直接用于逆时偏移,会产生低频噪音干扰(Fletcher et al., 2006).不可否认,逆时偏移是波动方程偏移方法的发展趋势,但三维逆时偏移的计算量和对速度模型的高要 求使得它在目前工业界的应用效果并不是十分理想.
本文的研究对象是Guddati(2006)提出的任意广角波动方程(AWWE),它是一种在空间域表述的高精度单程波方程.AWWE的优点是精度高,要提高AWWE的成像倾角,只需增加参考速度的个数即可.AWWE的形式简单,只包含二阶偏导数项,数值计算非常方便.因为这些优点,AWWE已成功用于偏移成像(Guddati and Heidari, 2005;何兵寿等,2008a;何兵寿等,2008b;孙歧峰和杜启振,2011;Zhou et al., 2012).Chen等(2013)将完美匹配层(PML)用于AWWE,有效地解决了AWWE数值计算中的吸收边界问题.尽管AWWE具有高精度的特点,但是其计算过程包含重复的矩阵求逆和矩阵相乘,使得其计算代价比其他单程波方程高出许 多,特别是增加参考速度个数时,其计算量显著增加.
AWWE与其他单程波方程都存在的一个问题是倏逝波干扰,这是由单程波方程近似的本质造成的.推导单程波方程的过程实际上是用一个有理函数近似平方根算子,当波数较大,平方根算子出现复数值时,近似的有理函数却仍然是一个实数,这样的误差造成了倏逝波干扰.抑制倏逝波干扰有两种途 径,一种是采用复有理函数近似平方根算子(Milinazzo et al., 1997),这种方法已在傅里叶有限差分偏移方法中得到应用,但该方法会因参数选择不当产生不稳定的问题(Amazonas et al., 2009).另一种途径是在倏逝波产生后进行压制,如频率-波数(f-k)滤波.Kosloff和Baysal(1983)在进行波场深度延拓时,逐层采用f-k滤波抑制倏逝波干扰.用f-k滤波方法抑制倏逝波的关键在于合理选取滤波所需要的视速度.Kosloff和Baysal(1983)采用延拓所在层的最大速度作为滤波器的门槛,会损失一部分高角度波场信息,从而降低对高陡构造的成像能力,这已被S and berg和Beylkin(2009)证实.此外,逐层进行滤波也会增加额外的计算量.
本文的研究内容针对上述两个问题,即AWWE计算量大和存在明显的倏逝波干扰.首先,本文改进现有的有限差分计算方案,包括内部区域和PML吸收边界区域,使其计算效率大幅度提高.其次,采用一种有效的方法,能在f-k域比较准确地区分倏逝波和非倏逝波,从而获得一个合理的视速度作为f-k滤波器的门槛,利用f-k滤波方法压制倏逝波干扰,提高成像质量.
2 任意广角波动方程深度延拓成像的数值实现 2.1 AWWE叠前偏移成像采用AWWE进行叠前深度延拓成像时,分别采用下行波方程和上行波方程将震源波场和记录波场沿深度方向延拓,在同一个深度上将两个波场互相关得到该深度上的像.因此,震源波场和记录波场分别满足定解问题(1)和(2),
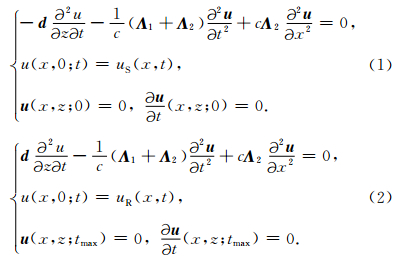
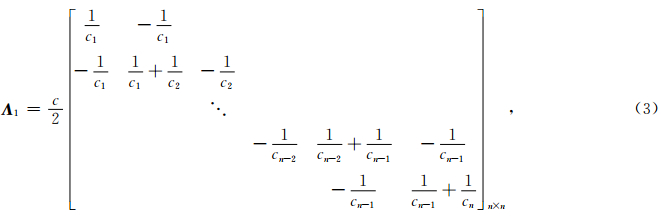

此外,参考速度的个数也直接影响AWWE的精度.增加参考速度的个数,同时适当选取参考速度与传播速度的比值,可以显著地提高AWWE的精度,从而增大成像倾角.为方便叙述,文中简记带n个参考速度的AWWE为AWWEn.
图 1描述了精确的单程波算子,AWWE2、AWWE3以及AWWE5归一化的慢度曲线,图 1a为实部,图 1b为虚部,考虑到近似单程波算子的虚部都为零,图中用AWWEn概括之.从图 1a可以看出,参考速度为(c,4c)的AWWE2已经具有很高的精度,其成像倾角大约为80°.图 1b表明,当水平慢度大于1时,精确的单程波算子的垂直慢度为纯虚数,而近似的单程波算子的垂直慢度却仍为实数,这 种近似误差造成了单程波数值计算中的倏逝波干扰.
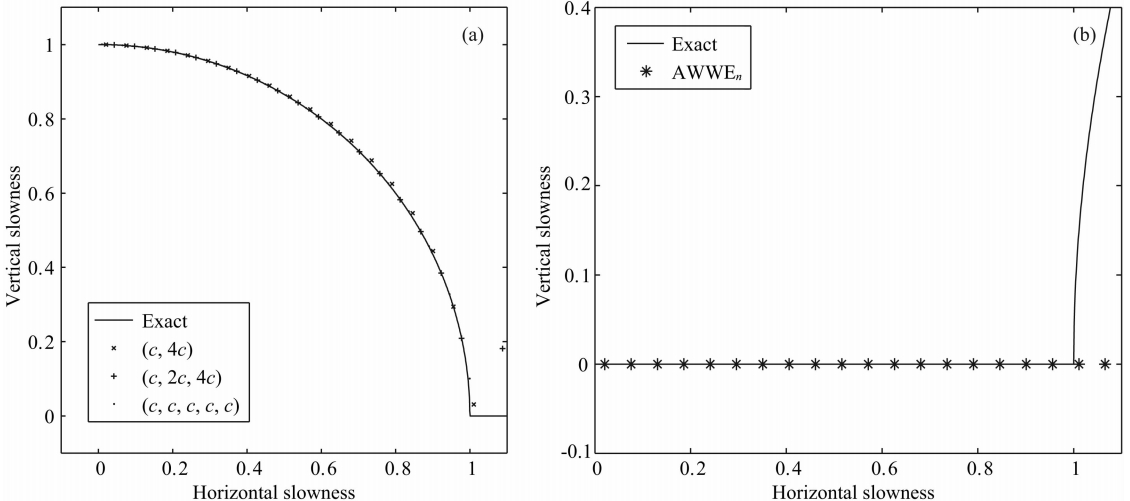 | 图 1 带不同参考速度的AWWE精度分析,(a)为实部,(b)为虚部Fig. 1 Accuracy of AWWE with various numbers of reference velocity including real part(a) and imaginary part(b) |
考虑到方程(1)和(2)的离散方案类似,这里只以上行波方程为例进行说明.定义差分算子如下:

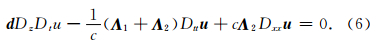

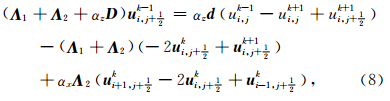
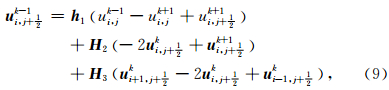
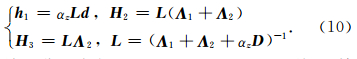
该差分格式由Guddati和Heidari(2005)给出,精度为 O(Δt2+Δz2+Δx2),其稳定性条件为cmaxΔt≤ Δx,cmax为波在介质中传播的最大速度.下行波方程(1)对应的深度延拓时间正向外推差分格式也可以类似得到.利用方程(9)进行计算时,需要计算逆矩阵 L =(Λ 1+ Λ 2+αz D)-1,考虑到αz是随空间变化的,因此计算过程中需要反复求逆,并需要反复计算矩阵 H 2和H 3,这极大地降低了AWWE的计算效率,并且随着参考速度个数的增加,其计算量显著地增加.
本文从方程(8)出发,修改计算格式,将求逆的次数减少为一次,从而能显著地提高计算效率.注意到方程(3)和(4),在网格剖分确定的情况下,如果参考速度ci=λic,其中λi为恒定的常数,则矩阵 Λ 1和Λ 2为恒定的矩阵.事实上λi为恒定的常数这一假设是合理的,后述数值实验将予以证实.在上述假设的前提下,将方程(8)修改为
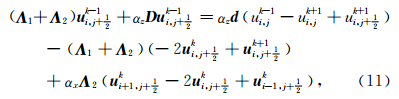
该方程可进一步写为
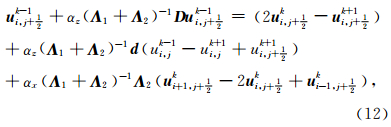
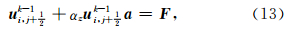
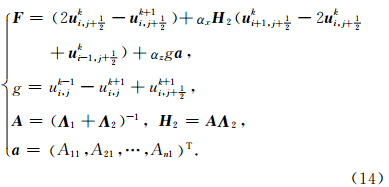
方程(13)和(14)中的矩阵 A 和 H 2不随空间变化,因此只需要计算一次.表 1列出了方程(13)和方程(9)的计算量,单位是15°单程波方程计算量的倍数.从表中可以看出,采用改进后的计算方案AWWE的计算效率显著提高,AWWE2的计算量仅仅为15°单程波方程的1.67倍,AWWE5的计算量甚至比采用原方案的AWWE3的计算量还要小.
|
|
表 1 差分格式改进前后的计算量比较(二维情形)Table 1 Computational efficiency comparison between the improved scheme and the existing scheme in 2D case |
Chen等(2013)推导了AWWE的PML匹配方程并给出了相应的有限差分计算格式,解决了AWWE正演模拟(偏移)中截断边界的问题.本文不重述PML的推导过程,而是直接给出分裂式的PML匹配方程.与内部区域类似,PML区域的差分计算公式也可作相应改进,以提高PML区域的计算效率.下行波方程(1)对应的PML匹配方程为
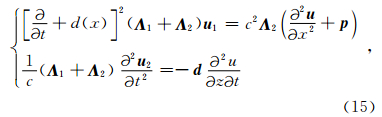
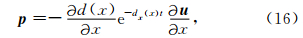
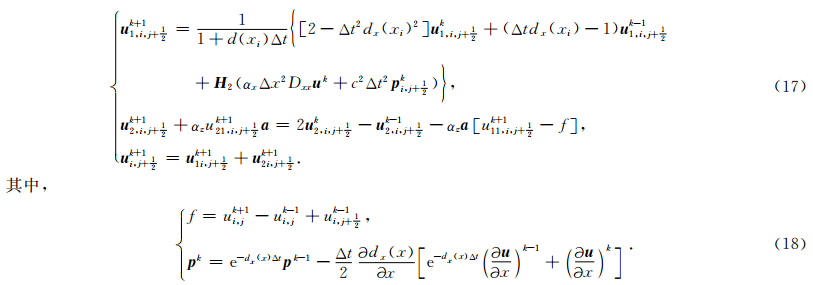
倏逝波是单程波方程数值计算中都存在的问题,在引言中已经说明了其产生的原因,并用图 1b进行了解释.抑制倏逝波的常用方法是倾角滤波,即 f-k滤波,在设计f-k滤波器时需要一个视速度作为门槛.基于观察和实验发现,当AWWE的参考速度有微小扰动时,非倏逝波场几乎不发生变化.将微小扰动参考速度前的波场与微小扰动之后的波场相减,残留波场主要反映的是倏逝波的能量.将残差波场(后称残差记录)变换到f-k域得到其振幅谱,该振幅谱能清晰地反映倏逝波的能量分布,因此能提供一个合理的视速度作为f-k滤波器的门槛.
基于以上考虑,在AWWE叠前偏移的过程中采用如下方法压制倏逝波的干扰:先将波场延拓一次得到记录u1(x,t),然后微小扰动参考速度(选取的扰动量为10-4),重新做一次延拓,得到记录u2(x,t),这两个记录的差记为Δu(x,t),称为残差记录.根据残差记录Δu(x,t)的振幅谱获得一个合理的视速度,然后设计光滑的扇形滤波器对记录u1(x,t)滤波以压制倏逝波成分,再用滤波后的记录进行后续的深度延拓,其流程如图 2所示.
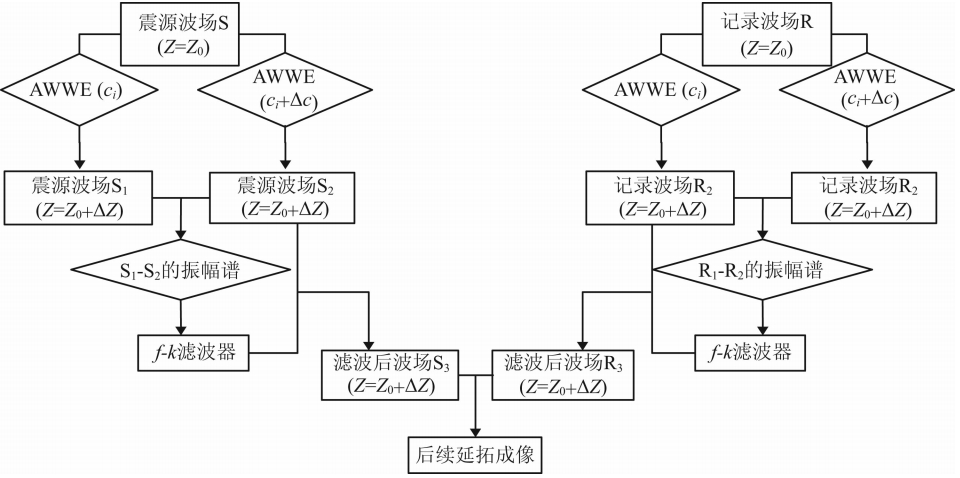 | 图 2 加入f-k滤波处理后的偏移流程Fig. 2 The migration flow with an f-k filtering procedure |
严格意义上,在深度延拓的过程中需要逐层进行滤波,但逐层滤波会额外增加计算量.出于以上考虑,本文只在某些深度上加入上述滤波处理,尽管减少了滤波次数,但抑制倏逝波干扰的效果仍然很明显,后续数值实验将予以证实.
4 数值实验 4.1 AWWE正演模拟图 3为二维SEG/EAGE盐丘速度模型,网格大小(Δx,Δz)=(5 m,4 m),由于高速盐丘体的存 在,横向上速度存在剧烈变化.图 4a和4b为AWWE2 模拟盐丘模型中的下行波场的波场切片,参考速度(c1,c2)=(c,4c),震源靠近左边界,左边界采用PML吸收边界(Chen et al., 2013).图 4a和4b的时刻相同,分别采用改进前的差分计算公式(9)和改进后的计算公式(13)进行计算,两图在相同的色标范围内显示.图 4说明改进之后的计算方案仍能稳定、精确地模拟下行波场,与改进前的计算结果完全一致.此外,在该算例中,采用改进后的计算方案,使用相同层数的PML,PML区域的计算效率也提高了7.6%.
 | 图 3 二维SEG/EAGE盐丘速度模型,网格大小(Δx,Δz)=(5 m,4 m)Fig. 3 2D SEG/EAGE salt velocity model with a grid size of(5 m,4 m) |
 | 图 4 AWWE2模拟二维SEG/EAGE盐丘模型中的下行波场切片(a)采用改进前的计算方案,(b)采用改进后的计算方案.Fig. 4 Snapshots propagated by downward propagating AWWE2 in 2D SEG/EAGE salt model(a) and (b)are respectively calculated by using the original calculation scheme and the improved scheme. |
图 5为AWWE3模拟均匀介质中的下行波场切片,以x=1500 m为界限(图中黑线),左侧区域选取的三个参考速度依次为传播速度的1倍,2倍和4倍,而右侧区域三个参考速度依次为传播速度的0.8倍,1.5倍和2.4倍,因此参考速度与传播速度的比例随空间是变化的.很明显,在分界处产生了虚假反射,该反射并非由波在介质中的传播速度差异造成,而是由于左右区域参考速度与传播速度的比值不一致造成的.同理,当波的传播速度剧烈变化,而参考速度取固定值时,也会产生虚假反射.因此,前文假设参考速度是传播速度的常数倍是合理的.
 | 图 5 不合理的参考速度设置引起的虚假反射Fig. 5 Spurious artifacts caused by unreasonable setting of reference velocities |
为了检验AWWE的成像能力以及f-k滤波方法压制倏逝波的效果,采用二维SEG/EAGE盐丘模型(图 3)进行验证.离散网格大小为(Δx,Δz)=(5 m,4 m),利用该模型合成12炮地震数据,炮间距250 m,每炮501道接收,道间距5 m,记录时间2.5 s,震源采用主频为25 Hz的雷克子波.利用参考速度为(c,4c)的AWWE2的偏移算子进行深度延拓偏移成像,其成像结果为图 6a,该成像结果有很强的倏逝波干扰.为了抑制倏逝波干扰,在深度延拓开始之前分别对地表的震源波场和记录波场进行 一次f-k滤波,用地表所在网格层的最大速度作为滤波器的视速度,其成像结果为图 6b,对比图 6a,倏逝波得以抑制,成像质量明显改善.为了进一步抑制倏逝波的干扰,在深度分别为4 m、8 m和12 m的网格层上对震源和记录波场各进行了一次f-k滤波,滤波器的视速度利用残差记录的振幅谱获得,其 流程如图 2所示,最终的成像结果如图 6c所示.对 比图 6b,在200~400 m的深度范围内倏逝波的干扰进一步被压制,如图 6b中白色箭头所指.在图 6c的基础上,在440 m深度上对震源和记录波场再次 进行f-k滤波,滤波器的视速度利用残差记录的振幅谱获得,其成像结果为图 6d.与图 6c相比,盐丘正上方的小断块内(图 6d中白色箭头所指)的倏逝波干扰更弱.图 6e与图 6d不同,在440 m深度上进行f-k滤波时采用横向上的最大速度作为滤波器的视速度,由于视速度选取不合理,导致440 m以下深度不能准确成像.
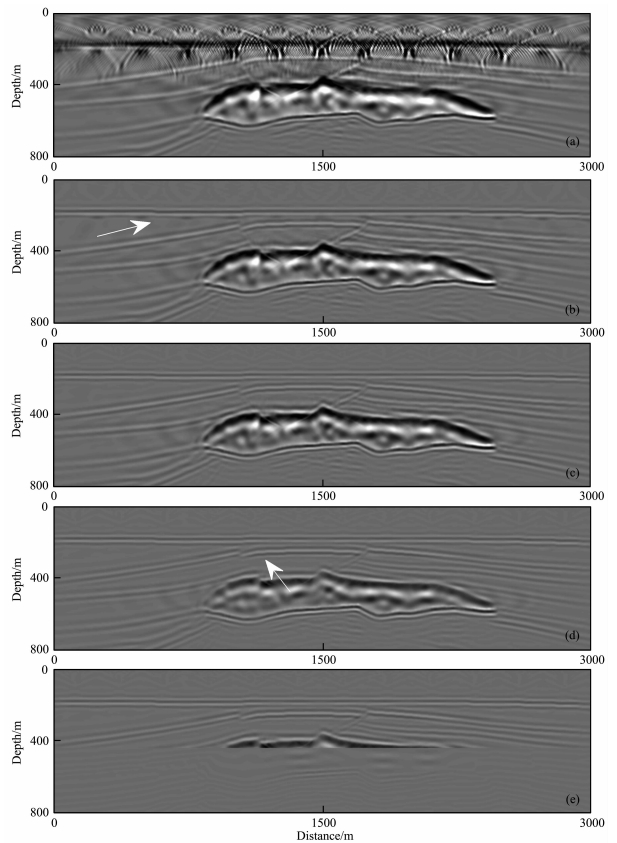 | 图 6 SEG/EAGE盐丘速度模型的偏移结果(a)无滤波;(b)在地表进行f-k滤波;(c)在4 m、8 m和12 m的深度上进行f-k滤波;(d)在4 m、8 m、12 m和440 m的深度上进行f-k滤波;(e)在4 m、8 m、12 m和440 m的深度上进行f-k滤波,第四次滤波的视速度取该深度上速度的最大值.Fig. 6 Migration results of the SEG/EAGE salt model(a)Without f-k filtering;(b)f-k filtering at surface;(c)f-k filtering at depth of 4 m,8 m, and 12 m;(d)f-k filtering at depth of 4 m,8 m,12 m, and 440 m;(e)f-k filtering at depth of 4 m,8 m,12 m, and 440 m,with the lateral maximum velocity being the apparent velocity in the last f-k filtering. |
图 7是利用残差记录的振幅谱获取440 m深度上f-k滤波器视速度门槛值的示意图.图 7a是将地表的雷克子波震源延拓至深度440 m得到的记录,利用参考速度为(c,4c)的下行AWWE2延拓算子;图 7b是将地表的雷克子波震源延拓至深度440 m得到的记录,利用参考速度为(1.0001c,4.0001c)的下行AWWE2延拓算子;图 7c是图 7a与图 7b的差,即残差记录;图 7d是残差记录的振幅谱,其中虚线为拾取的视速度1300 m·s-1,实线为所在深度横向上的最大速度4185 m·s-1,用最大速度作为滤波器的门槛会滤掉有效的高倾角成分,从而损害滤波层以下地层的成像,如图 6e所示.
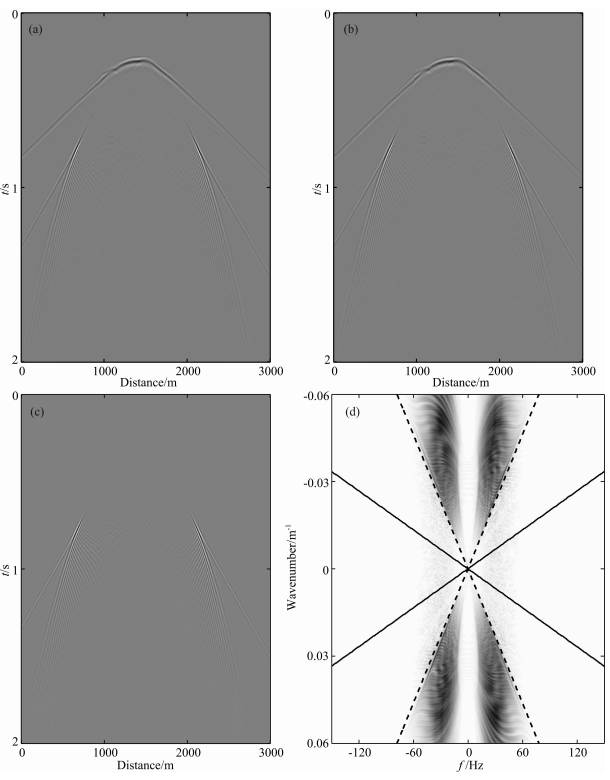 | 图 7 利用残差记录的振幅谱获取440 m深度上f-k滤波器的视速度(a)参考速度为(c,4c)的AWWE2算子延拓后的记录;(b)参考速度为(1.0001c,4.0001c)的AWWE2算子延拓后的记录;(c)残差记录;(d)残差记录的振幅谱,虚线代表视速度为1300 m·s-1,实线代表视速度为4185 m·s-1.Fig. 7 Obtaining apparent velocity threshold at depth of 440 m using the amplitude spectrum of residual wavefield(a)The wavefield downward-propagated by AWWE2 with reference velocities (c,4c);(b)The wavefield downward-propagated by AWWE2 with reference velocities (1.0001c,4.0001c);(c)Residual source wavefield;(d)f-k amplitude spectrum of(c),the dashed line represents an apparent velocity 1300 m·s-1, and the solid line 4185 m·s-1. |
为了进一步验证AWWE对陡倾角构造的成像能力以及f-k滤波方法的有效性,用Marmousi模 型(图 8)进行偏移试验.速度模型的网格大小为 (Δx,Δz)=(10 m,5 m),使用参考速度为(c,4c)的AWWE2算子进行偏移成像,数值计算采用文中改进之后的差分计算方案.51炮合成地震数据的偏 移结果(没有滤波处理)为图 9a,仅在前四个网格深度上加入f-k滤波处理之后的成像结果为图 9b,两图在相同的色标范围内显示,两图的成像结果都证 实了AWWE偏移算子对高陡构造的成像能力.在 深度延拓过程中只进行了数次f-k滤波,其增加的计算量基本可以忽略,但其压制倏逝波干扰进而提高成像质量的效果十分明显.
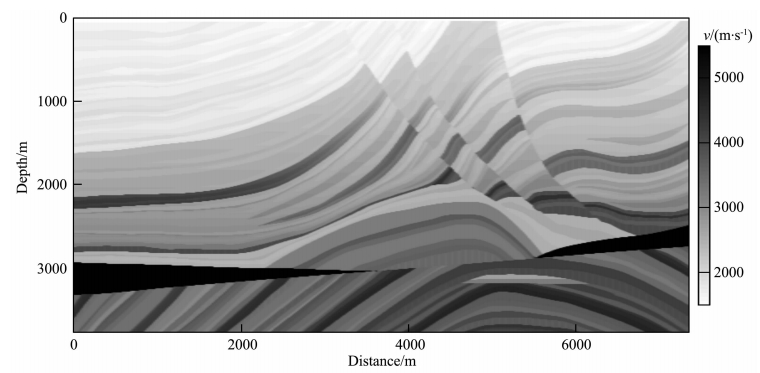 | 图 8 Marmousi速度模型Fig. 8 Marmousi velocity model |
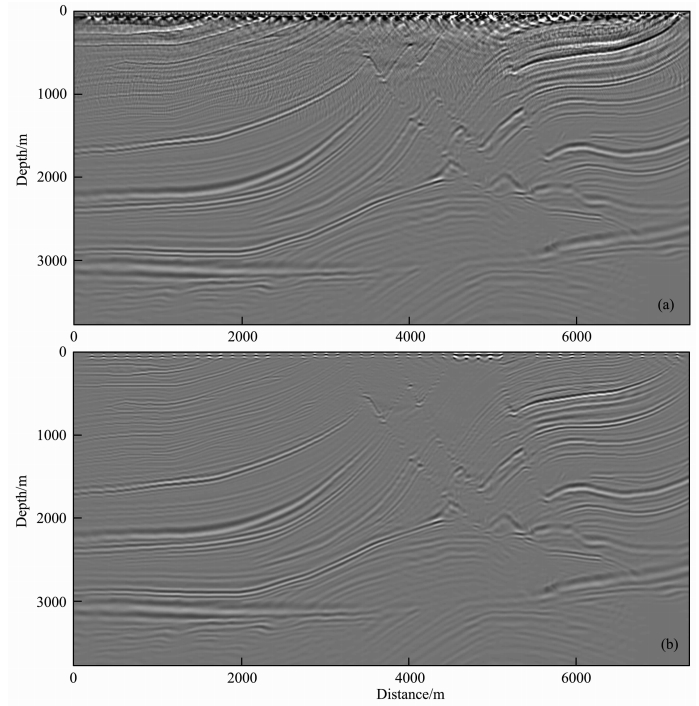 | 图 9 Marmousi模型偏移结果,(a)无滤波处理,(b)进行4次f-k滤波处理Fig. 9 The migration results of Marmousi model,(a)without and (b)with four times f-k filtering |
AWWE是一种高精度的单程波方程,其成像倾角接近90°,可以对高陡构造准确成像,但是其计算量较大,特别是增加参考速度的个数时,计算量会显著增加.本文通过分析和数值实验证实,参考速度必须为背景速度的常数倍以避免虚假反射,基于此分析,本文改进了现有的有限差分计算方案,能避免重复的矩阵求逆并减少矩阵相乘运算的次数,从而显著地提高了AWWE的计算效率.在分析倏逝波产生原因的基础上,采用了f-k滤波方法来抑制倏逝波对成像结果影响,在设计扇形滤波器时,根据残差记录的振幅谱来获取视速度的门槛值.数值实验说明,即使速度横向变化,残差记录的振幅谱也能很好地描述倏逝波的能量分布,从而提供合理的视速度门槛信息.合成数据的偏移试算证实,进行少数几次f-k滤波处理就能很好地抑制倏逝波干扰,提高成像质量.
| [1] | Amazonas D, Costa J C, Schleicher J, et al. 2009. Wide-angle FD and FFD migration using complex padé approximations. Geophysics, 72(6): S215-S220. |
| [2] | Bamberger A, Engquist B, Halpern L, et al. 1988. High-order paraxial wave-equation approximations in heterogeneous media. SIAM J. Appl. Math. , 48(1): 129-154. |
| [3] | Baysal E, Kosloff D D, Sherwood J W C. 1983. Reverse time migration. Geophysics, 48(11): 1514-1524. |
| [4] | Biondi B. 2002. Stable wide-angle Fourier finite-difference downward extrapolation of 3-D wavefields. Geophysics, 67(3): 872-882. |
| [5] | Chen H M, Zhou H, Lin H, et al. 2013. Application of perfectly matched layer for scalar arbitrarily wide-angle wave equations. Geophysics, 78(1): T29-T39. |
| [6] | Claerbout J F. 1976. Fundamentals of Geophysical Data Processing. Oxford: Scientific Publications. |
| [7] | Clapp R G. 2009. Reverse time migration with random boundaries. 79th Ann. Inernat Mtg., Soc. Expi. Geophys. Expanded Abstracts, 2809-2813. |
| [8] | Collins M D, Westwood E K. 1991. A higher-order energy-conserving parabolic equation for range-dependent ocean depth, sound speed, and density. J. Acoust. Soc. Am. , 89(3): 1068-1175. |
| [9] | Fletcher R P, Fowler P J, Kitchenside P, et al. 2006. Suppressing unwanted internal reflections in prestack reverse-time migration. Geophysics, 71(6): E79-E82. |
| [10] | Gazdag J, Sguazzero P. 1984. Migration of seismic data by phase-shift plus interpolation. Geophysics, 49(2): 124-131. |
| [11] | Gazdag J. 1978. Wave equation migration with the phase-shift method. Geophysics, 43(7): 1342-1351. |
| [12] | Guddati M N, Heidari A H. 2005. Migration with arbitrarily wide-angle wave equations. Geophysics, 70(3): S61-S70. |
| [13] | Guddati M N. 2006. Arbitrarily wide-angle wave equations for complex media. Comput. Methods Appl. Mech. Eng. , 195(1-3): 65-93. |
| [14] | Han B A. 1998. Comparison of four depth migration methods. 66th Ann. Internat Mtg., Soc. Expi. Geophys. Expanded Abstracts, 1104-1107. |
| [15] | He B S, Zhang H X, Han L H. 2008a. Prestack reverse-time depth migration of two acoustic wave equation and comparison between both. Oil Geophys. Prosp. (in Chinese), 43(6): 661-684. |
| [16] | He B S, Zhang H X, Zhang J. 2008b. Prestack reverse-time depth migration of arbitrarily wide-angle wave equations. Acta Seismologica Sinica (in Chinese), 30(5): 491-499. |
| [17] | Jin S W, Xu S R, Wu R S. 2002. Wave equation based prestack depth migration using generalized screen propagator. Chinese J. Geophys. (in Chinese), 45(5): 684-690. |
| [18] | Kosloff D D, Baysal E. 1983. Migration with the full acoustic wave equation. Geophysics, 48(6): 677-687. |
| [19] | Liu X W, Liu H. 2002. Status and progress on wave equation migration methods. Progress in Geophysics (in Chinese), 17(4): 582-591. |
| [20] | Ma Z T. 1983. A splitting-up method for solution of higher-order migration equation by finite-difference scheme. Chinese J. Geophys. (Acta Geophysica Sinica) (in Chinese), 26(4): 377-389. |
| [21] | Milinazzo F A, Zala C A, Brooke G H. 1997. Rational square-root approximations for parabolic equation algorithms. J. Acoust. Soc. Am. , 101(2): 760-766. |
| [22] | Ristow D, Rühl T. 1994. Fourier finite-difference migration. Geophysics, 59(12): 1882-1893. |
| [23] | Sandberg K, Beylkin G. 2009. Full-wave equation depth extrapolation for migration. Geophysics, 74(6): WCA121-WCA128. |
| [24] | Stoffa P L, Fokkema J T, de Luna Freire R M, et al. 1990. Split-step Fourier migration. Geophysics, 55(4): 410-421. |
| [25] | Sun Q F, Du Q Z. 2011. The frequency-space domain prestack depth migration with arbitrarily wide-angle wave equation. Oil Geophys. Prosp. (in Chinese), 46(6): 890-896. |
| [26] | Zhou H, Lin H, Sheng S B, et al. 2012. High angle prestack depth migration with absorption compensation. Applied Geophysics, 9(3): 293-300. |
| [27] | 何兵寿, 张会星, 韩令贺等. 2008a. 两种声波方程的叠前逆时深度偏移及比较. 石油地球物理勘探, 43(6): 661-684. |
| [28] | 何兵寿, 张会星, 张晶. 2008b. 任意广角波动方程叠前逆时深度偏移. 地震学报, 30(5): 491-499. |
| [29] | 金胜汶, 许士勇, 吴如山. 2002. 基于波动方程的广义屏叠前深度偏移. 地球物理学报, 45(5): 684-690. |
| [30] | 刘喜武, 刘洪. 2002. 波动方程地震偏移成像方法的现状与进展. 地球物理学进展, 17(4): 582-591. |
| [31] | 马在田. 1983. 高阶方程偏移的分裂算法. 地球物理学报, 26(4): 377-389. |
| [32] | 孙歧峰, 杜启振. 2011. 任意广角波动方程频率-空间域叠前深度偏移成像. 石油地球物理勘探, 46(6): 890-896. |
 2014, Vol. 57
2014, Vol. 57


