地球物理学报  2014, Vol. 57 Issue (4): 1041-1048   PDF    
引用本文
江颖, 徐建桥, 孙和平. 2014. 深内部地球结构对内核平动振荡本征周期的影响. 地球物理学报, 57(4): 1041-1048, doi: 10.6038/cjg20140403   
JIANG Ying, XU Jian-Qiao, SUN He-Ping. 2014. The influence of deep interior structure on the eigenperiod of inner core’s translational oscillations. Chinese Journal Geophysics, 57(4): 1041-1048, doi: 10.6038/cjg20140403   
深内部地球结构对内核平动振荡本征周期的影响
江颖1,2, 徐建桥1, 孙和平1    
1. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室, 武汉 430077;
2. 中国科学院大学, 北京 100049
投稿时间:2013-4-25    最后修改时间: 2013-11-11 .
基金项目：国家重点基础研究发展计划（973计划）（2014CB845902）、国家自然科学基金（41321063和41274085）资助.
第一作者简介：江颖，女，1986年生，现主要从事地球内核平动振荡、超导重力数据分析及其应用研究.E-mail：jiangyingchen@126.com
摘要：地球固态内核的平动振荡是地球的基本简正模之一，又称Slichter模，其本征周期大约为几个小时，与地球内部结构密切相关.为了研究影响内核平动振荡的本征周期与内部结构的依赖关系，本文利用球对称、非自转、弹性和各向同性地球模型（SNREI），通过自由振荡运动方程的数值积分，以地球模型PREM为基础，理论上系统研究了地球内部介质（包括密度、地震波速等）分布异常对Slichter模本征周期的影响.数值结果表明，Slichter模周期随着内外核边界（ICB）密度差的增加以类似于双曲线的特征显著减小，当ICB密度差从597 kg·m-3减小到200 kg·m-3时，周期增大66.44%，当ICB密度差从597 kg·m-3增大到1000 kg·m-3时，周期减小21.48%；Slichter模周期随着核幔边界（CMB）密度差的增大而缓慢增大；相对于PREM，地球模型1066A在ICB和CMB的密度差分别相差45.321%和1.132%，内部地震波速度和密度梯度也存在差异，但是，当密度差减小到1066A模型提供的数值时，得到的Slichter模周期与基于1066A获得的结果（4.599 h）非常接近，差异分别只有3.762%和0.037%；表明Slichter模本征周期与地球内部介质的精细结构关系不大，而对ICB的密度差非常敏感.内、外核P波波速分布异常对Slichter模周期的影响基本相当，当内核和外核P波波速均增加5%时，Slichter周期分别减小1.02%和1.69%，P波波速分别减小5%时，Slichter模周期分别增加1.27%和1.847%，内核S波波速分布异常比P波波速分布异常对Slichter模周期的影响小1个量级；与地核相比，地幔中的地震波速异常对Slichter模本征周期的影响小1~2个量级；表明地核中地震波速异常对Slichter模周期的影响很小，目前有关Slichter模周期理论计算的差异主要来自于所采用的地球模型中内核边界的密度差的差异，本文结果可以为Slichter模的研究、探测及其对地球深内部结构的约束提供理论依据.
关键词： Slichter模本征周期     内外核密度差     核幔边界密度差     地震波波速分布异常    
The influence of deep interior structure on the eigenperiod of inner core’s translational oscillations
JIANG Ying1,2, XU Jian-Qiao1, SUN He-Ping1    
1. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, CAS, Wuhan 430077, China;
2. University of Chinese Academy of Sciences, Beijing 100049, China
Abstract: The translational oscillation of the solid inner core, which is also called Slichter mode, is one of the fundamental normal modes of the Earth. It has an eigenperiod of several hours which is closely related to the Earth's interior structure. Based on the equations for free oscillations of a spherical, non-rotating, elastic and isotropic (SNREI) Earth, and the PREM Earth model, we systematically investigate the influences on Slichter mode's eigenperiod caused by the Earth's interior medium (including density and seismic velocity) in theory. The numerical results indicate that the eigenperiod of Slichter mode reduces significantly, approximately following a hyperbola, with the increase of the density difference across the inner-outer core boundary (ICB). When the density difference reduces from 597 to 200 kg·m-3, the eigenperiod increases 66.44%. When the density difference increases to 1000 kg·m-3, the eigenperiod reduces 21.48%. The eigenperiod of Slichter mode increases slowly with the density difference of the core-mantle boundary (CMB) increasing. Relative to PREM, the density differences of the 1066A model at ICB and CMB are 45.321% and 1.132% respectively. The interior seismic velocity and density gradient are also different between the PREM model and 1066A model. When the density difference reduces to the value provided by 1066A model, the results are very close to the value from the 1066A (4.599 h), and the differences are 3.762% and 0.037% respectively. The results indicate that the eigenperiod of Slichter mode is extremely sensitive to the density contrast across ICB. The influences caused by abnormal distribution of P-wave velocity in inner core and outer core are nearly the same. When P-wave velocity in inner core and outer core increases 5%, the eigenperiod reduces 1.02% and 1.69% respectively, and when it reduces 5%, the eigenperiod increases 1.27% and 1.847%. The influence caused by abnormal distribution of S-wave velocity is 1 order of magnitude smaller than that caused by P-wave velocity. The influence caused by abnormal distribution of seismic velocity in mantle is 1~2 order of magnitude smaller than that caused in core. The results indicate that the influence caused by abnormal distribution of seismic velocity in core is very small, at present, the differences of calculated Slichter mode's eigenperiod come mainly from the different density contrast across the ICB of the adopted Earth model. In this paper, the results can provide a theoretical basis for the researching and detecting of Slichter mode, and constraint for the interior structure of the Earth.
Key words: Slichter mode's eigenperiod     Density contrast across ICB     Density contrast across CMB     The abnormal distribution of seismic velocity    

1 引言

地球简正模观测和研究是了解地球全球动力学过程和内部结构的基础.一方面，地球的一切受迫运动实际上是各种简正模“共振”运动以特定方式的叠加；另一方面，地球简正模运动综合反映了地球内部介质分布及内部圈层耦合的特征，其观测与研究是认识地球内部结构、物理参数分布和主要圈层耦合机制的重要依据(Wahr，1981).地球固态内核的平动振荡是地球的基本简正模之一，对于非自转、球对称地球模型，简并的Slichter模是周期最长的一阶球型振荡模，由Slichter(1961)首先指出其出现的可能性，又称Slichter模.与传统的地球自由振荡简正模不同，Slichter模不以弹性应力为恢复力，而是以重力(液核流体的浮力)作为主要恢复力，其本征周期大约为几个小时(Xu J Q et al，2005).Slichter模可能是由深部大地震激发的，大地震发生伴随着的地幔一阶球型扰动将导致核幔边界的相应形变，由可压缩的流体外核传递到内外核边界，进而激发Slichter模；也可能是由于液核物质在内外核边界上的非对称结晶导致内核质心的微小变化，地球重力场将驱动内核在其平衡位置附近平动振荡.Slichter模的观测与研究是认识地球受迫运动和内部动力学过程的基础，是了解地球大尺度内部结构、特别是内外核相互作用及其机理的重要依据.

Slichter模的本征周期(频率)可能与地球深内部构造和圈层结构密切相关，许多科学家基于不同 的地球模型研究了Slichter 模的本征周期(Slichter，1961； Xu J Q et al，2005；Busse，1974；Smith，1976；Rogister，2003；Dahlen，1968；Dahlen and Sailor， 1979；Rieutord，2002；Smylie and Rochester， 1981).Busse(1974)假设固态球形内核位于以刚性同心球面为边界的自转、均匀、不可压缩、非黏性流体中心，研究了内核平动振荡，并发现本征周期与内外核密度差(ΔρICB)之间存在非常强的依赖关系.Smith(1976)利用弹性引力运动方程广义球谐函数展开法，基于DG597模型计算了地球平动振荡的本征周期并且理论上研究了自转微椭地球固态内核平动振荡问题.Smith(1976)的数值结果表明液态外核的分层和固体内核的弹性特征对内核平动的本征周期的影响比较显著.Rogister(2003)将本征位移的无穷耦合链分别截取3项和5项，基于PREM模型和1066A模型解算Slichter模的本征周期，并得出了两种截断方式在4位有效数字上保持相同的精度.Rogister(2003)提出如果固体内核处于外核中的刚性平动振荡，那么主要的恢复力是内核的浮力，并且指出内外核密度差对本征周期的影响非常大.Dahlen采用“二阶扰动”理论研究了自转、椭球地球的简正模，详细讨论了由于自转和椭率的谱峰分裂特征并计算得出简并的Slichter模的本征周期(Dahlen，1968；Dahlen and Sailor， 1979).Rieutord(2002)假设核幔边界和固体内核均为刚性的，研究了Slichter模，并探讨了ICB 附近流体的黏性对内核平动振荡(包括谱峰分裂和品质因子)的影响.Smylie和Rochester(1981)采用有限元方法，在“亚地震波”近似的假设下，引入位移势函数，建立液核运动变分原理，分别基于CORE11和1066A地球模型计算了核模.其他一些科学家得到的Slichter模的本征周期的结果都相近(Slichter，1961；Xu J Q et al，2005；Busse，1974；Smith，1976；Rogister，2003；Dahlen，1968；Dahlen and Sailor， 1979)，Rieutord(2002)可能是忽略了内核的形变，导致结果和其他科学家的结果差异较大.目前存在的主要问题是由于对深内部地球结构的了解远远不够，相比于地震简正模，Slichter模的本征周期的计算结果相差较大，这种差异主要来自于地球内部结构的哪些因素有待进一步澄清.

本文基于球对称、非自转、弹性和各向同性地球模型(SNREI)，讨论地球内部结构的差异对Slichter模的本征周期的影响.分别计算内外核密度差、核幔边界密度差、地核和地幔内P波、S波波速对其本征周期的影响，探讨内部结构的不同差异对Slichter模的影响有多大，进而更好地了解地球深内部结构，更为基于超导重力仪的实际观测资料检测Slichter模提供理论依据(Xu et al., 2010；Smylie，1992；Smylie et al., 1992; Smylie，1999；Rochester and Peng， 1993；Peng，1997；Courtier et al., 2000；Rosat et al., 2003；Sun H P，2004；Rosat et al., 2006；Guo et al., 2006；Ding and Shen， 2013；Shen and Ding， 2013；Jiang et al., 2013；Hinderer et al., 1995).

2 地球内部物理参数的变化对Slichter模本征周期的影响

地球内核平动振荡的运动满足相互耦合的Navier弹性平衡方程、Poisson方程和弹性本构方程，采用Alterman 等人(1959)的基本变量代换，即可简化成6阶线性常微分方程组

式中， y =(y1，y2，y3，y4，y5，y6)T为本征函数解向量，其中y1、y3分别表示径向、横向位移，y2、y4分别表示径向、横向应力，y5、y6分别表示引力位扰动和引力扰动.基于PREM模型(含海洋)，采用龙格库塔数值积分法，获得Slichter模的本征周期为5.420047 h，而基于PREM模型(固体地球)得到的计算结果为5.42005 h，两者相差很小，与其他方法得出的结果相差不大.

2.1 地球内部密度分布差异对Slichter模本征周期的影响

为研究地球内部密度分布差异对Slichter模本征周期的影响，我们首先讨论内外核密度差对其本征周期的影响.在PREM模型中，内核中密度(ρIC)是半径的二次方程，外核中密度(ρOC)和下地幔中密度(ρM)是半径的三次方程：

其中x为距地心距离，R(6371 km)为地球半径，r为归一化半径.

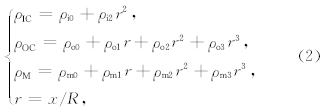
在内外核边界的密度突跳为：

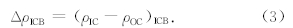
为了计算内外核密度差对Slichter模本征周期的影响，基于PREM模型，保持地核和地幔的总质量不变，并且使核幔边界的密度差保持不变，只改变地球内外核边界的密度差.在(2)式中改变常数项ρi0和ρo0，而ρi2、ρo1、ρo2、ρo3保持常数不变(地核内部密度的梯度分布不变)，计算出内外核的密度差及相应的Slichter模本征周期.计算结果如图 1实线和表 1所示，从计算结果可以看出：Slichter模本征周期对内外核边界的密度跳跃非常敏感，随着密度差的增加，以类似于双曲线的特征减小.当内外核密度差减小到200 kg·m-3时，周期增大66.44%，当内外核密度差增大到1000 kg·m-3时，周期减小21.48%.在1066A模型中，内外核边界密度差为868 kg·m-3，而PREM模型中内外核边界密度差为597.3 kg·m-3，相对于PREM模型来说，两者相差45.321%，基于两个模型计算出的Slichter模本征周期相差15.148%.尽管PREM和1066A两个地球模型在地球内部波速(Lamé参数)和密度梯度结构存在比较大的差异，但有趣的是，当内外核边界密度差减小到1066A模型提供的数值时，得到的 Slichter模周期与基于1066A获得的结果(4.599 h)非常接近，差异仅有3.762%.这就意味着Slichter模本征周期与地球内部介质的精细结构关系不大，但对于内核边界的密度差非常敏感，其观测与研究可作为约束该参数的重要依据.
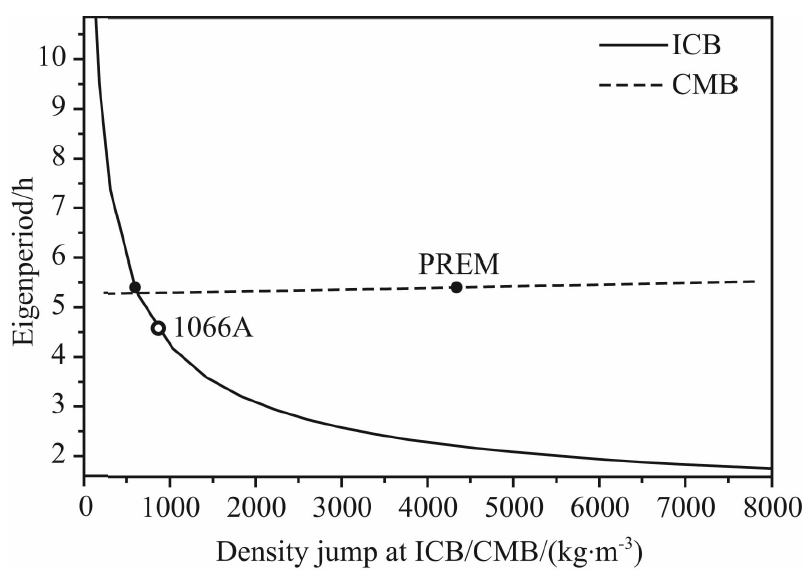图 1 内外核密度差和核幔边界密度差对Slichter模本征周期的影响Fig. 1 Relationship between the eigenperiod of the S lichter mode and the density contrast across the ICB/CMB

在核幔边界的密度差异为：

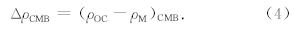
为了计算核幔边界对其本征周期的影响，我们保证地核和地幔的总质量不变，同时使内外核密度差保持不变，只改变核幔边界的密度差，在(2)式中改变常数项ρo0和ρm0，而ρo1、ρo2、ρo3、ρm1、ρm2、ρm3保持常数不变(即整个地球内部的密度梯度分布保持不变)，计算出核幔边界的密度差及相应的Slichter模本征周期.计算结果如图 1虚线和表 1所示，从计算结果可以看出：Slichter模本征周期随着核幔边界密度差的增大而缓慢增大，核幔边界密度差比内 外核边界密度差对Slichter模本征周期的影响小得 多.在1066A模型中核幔边界的密度差为4386 kg·m-3，而PREM模型中核幔边界密度差为4336.9 kg·m-3，相对于PREM模型来说，两者相差1.132%.当核幔边界密度差减小到1066A模型提供的数值时，得到的Slichter模周期与基于1066A获得的结果(4.599 h)非常接近，差异仅有0.037%.主要原因是内核平动振荡的运动是地球内核在液态外核中运动，主要恢复力为地球引力，在静力平衡状态下地球的引力等于液核的浮力，所以对内外核边界的密度更敏感.

表 1 地球内部密度分布差异与Slichter模本征周期的变化 Table 1 Differences of interior density and the changes of the Slichter mode′s eigenperiod
2.2 地核中P波波速对Slichter模本征周期的影响

为了研究地震波速对Slichter模本征周期的影响，我们首先讨论在地核中的P波波速变化对Slichter模本征周期的影响.在PREM模型中，内核中P波波速(VPI)是半径的二次方程，外核中P波波速(VPO)是半径的三次方程：

其中，Q为变化因子.

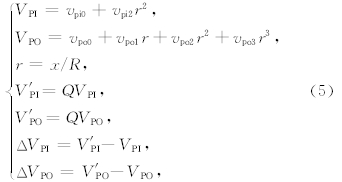
首先讨论在内核中P波波速对Slichter模本征周期的影响，由式(5)改变变化因子Q，使vpi2保持不变，依次调整vpi0的大小来计算不同变化因子Q而引起的速度变化，并计算相应的周期变化，结果如图 2(PIC对应的线型)所示；在外核中，改变变化因子Q，使vpo1、vpo2和vpo3保持不变依次调整vpo0的大小来计算不同变化因子Q而引起的速度变化，并计算相应的周期变化，结果如图 2(POC对应的线型)所示；用相同的方法，得出在整个地核中P波波速改变相应的Slichter模本征周期的变化，如图 2实线所示.在地震学的研究中，一般认为地球内部波速异常的变化范围是±5%，为了方便讨论我们将这个范围扩大一倍，因此令变化因子Q在0.9~1.1范围内变化.由结果可知，随着P波波速的变化因子增大计算得到的Slichter模本征周期缓慢减小.由表 2清晰可知，当内、外核P波波速变化因子相同时，内核P波波速变化引起Slichter模本征周期的变化百分比要略小于外核P波波速变化造成的影响.当波速同样都增加5%时，内核中P波波速的增加使计算得到的周期减小1.019%，外核中P波波速的增加使计算得到的周期减小1.687%，地核中P波波速的增加使计算得到的周期减小2.650%；当 波速同样都增加10%时，内核中P波波速的增加使 计算得到的周期减小1.852%，外核中P波波速的增加使计算得到的周期减小3.227%，地核中P波波速的增加使计算得到的周期减小4.885%；反之，当波速同样都减小5%时，内核中P波波速的减小使计算得到的周期增加1.271%，外核中P波波速的减小使计算得到的周期增大1.847%，地核中P波波速的减小使计算得到的周期增大3.194%；当波速同样都减小10%时，内核中P波波速的减小使计算得到的周期增加2.892%，外核中P波波速的减小使计算得到的周期增加3.865%，地核中P波波速的减小使计算得到的周期增大7.124%.对Slichter模来说，地球内核的运动近似一个刚性的运动.当它在液态外核中运动时，由于流体压力的变化，使其形状有微小的变形，同时，由于内核和外核都是可压缩的，内核在其平衡位置附近的运动导致ICB附近介质的微小的体膨胀，从而使得它们的密度也发生微小的扰动，因此对Slichter模本征周期有影响.

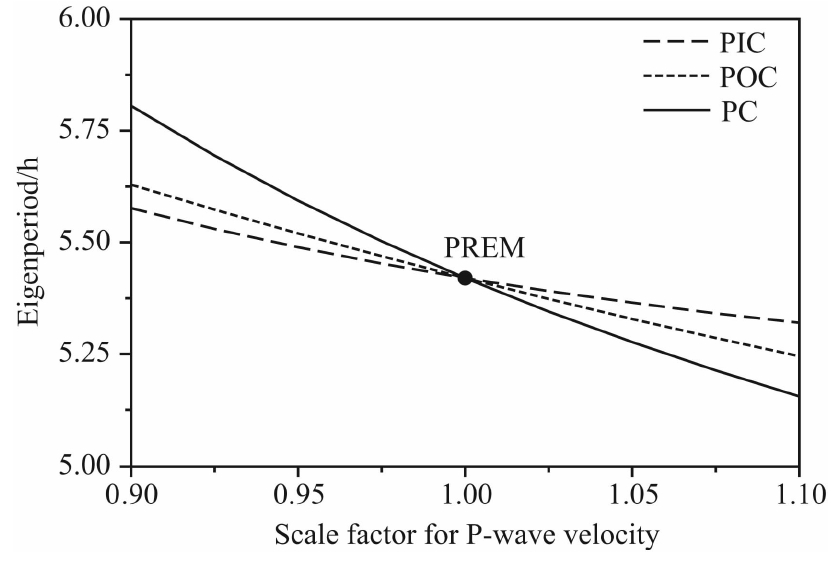图 2 地核内P波波速变化因子与Slichter模本征周期的变化Fig. 2 Relationship between the scale factor for P-wave velocity in core and eigenperiod of the Slichter mode

表 2 P/S波波速变化因子与Slichter模本征周期的变化 Table 2 The scale factor for P/S-wave velocity and changes of the Slichter mode′s eigenperiod
2.3 地核中S波波速对Slichter模本征周期的影响

在PREM模型中，内核中S波波速(VSI)是半径的二次方程，外核中S波波速为0：

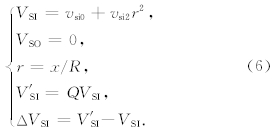
讨论在内核中S波波速对Slichter模本征周期的影响，改变变化因子Q，使vsi2保持不变，依次调整vsi0的大小来计算不同变化因子Q而引起的速度变化，并计算相应的周期变化，结果如图 3虚线所示.同样考虑到实际情况，变化因子Q的变化范围为0.9~1.1，当地核中S波波速变化因子增大时，Slichter模本征周期增大，但是幅度非常小.当波速增加5%时，S波波速的增加使计算得到的周期只增加0.160%；当波速增加10%时，S波波速的增加使计算得到的周期只增加0.335%；反之，当波速减小5%时，S波波速的减小使计算得到的周期只减小0.147%；当波速减小10%时，S波波速的减小使计算得到的周期只减小0.282%.由表 2可以清晰看出，当地核中P波和S波波速变化因子相同时，P波波速变化引起Slichter模本征周期的变化比S波造成的影响要大一个数量级.

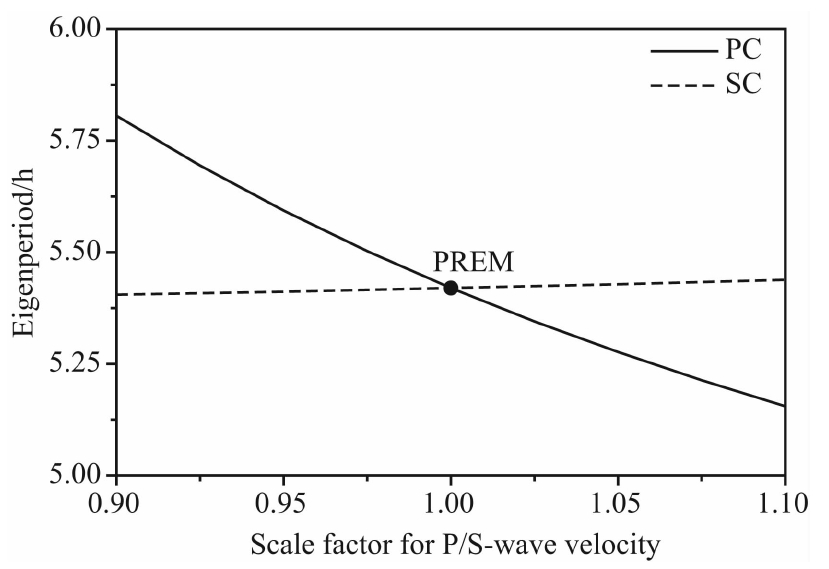图 3 地核内P波和S波波速变化因子与Slichter模本征周期的变化Fig. 3 Relationship between the scale factor for P/S- wave velocity in core and eigenperiod of the Slichter mode
2.4 地幔中P/S波波速对Slichter模本征周期的影响

利用PREM模型，采用相同的方法，只改变地幔中地震波的波速，来讨论地幔中地震波的变化对Slichter模本征周期的影响.由图 4得出，随着P波波速变化因子的增大，Slichter模本征周期减小；而随着S波波速变化因子的增大，Slichter模基本上没有什么变化，更接近于一条直线.由表 2知，地幔 中地震波波速的变化对Slichter模本征周期的影 响非常小，不足0.003%，P波波速变化引起的Slichter模本征周期的变化比S波波速变化的影响略大一点.当波速同样都增加5%时，地幔中P波波速的增加使计算得到的周期减小0.880×10-3%，而S波波速的增加使计算得到的周期减少0.142×10-3%；当波速同样都增加10%时，地幔中P波波速的增加使计算得到的周期减小1.433×10-3%，而S波波速的增加使计算得到的周期增加0.043×10-3%；反之，当波速同样都减少5%时，地幔中P波波速的减少使计算得到的周期增加1.150×10-3%，而S波波速的减少使计算得到的周期增加0.227×10-3%；当波速同样都减少10%时，地幔中P波波速的减少使计算得到的周期增加2.626×10-3%，而S波波速的减少使计算得到的周期增加0.596×10-3%.地球内核平动主要表现为地核中的径向形变，地幔中形变非常小，这也是地幔中地震波速的改变对其本征周期影响较小的主要原因.地球内核平动振荡的运动局限在内核附近，相对来说地幔结构对它的影响很微弱，几乎可以忽略不计.

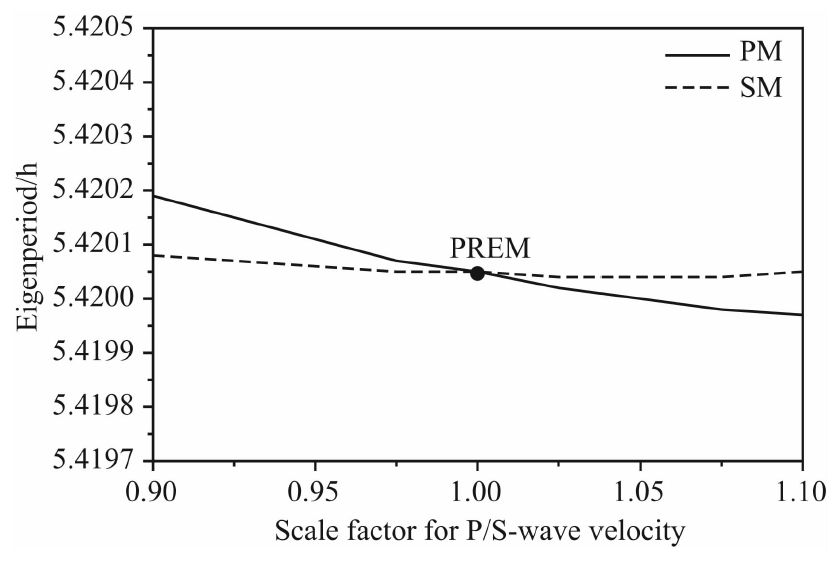图 4 地幔中P波和S波波速变化与Slichter模本征周期的变化Fig. 4 Relationship between the scale factor for P/S-wave velocity in mantle and eigenperiod of the Slichter mode
3 结语及讨论

Slichter模是地球的基本简正模之一，其观测与研究是我们了解地球深内部构造，特别是内外核边界附近密度结构的重要依据.通过上述讨论可以得出以下结论： (1)在地核中，随着P波波速的变化因子增大计算得到的Slichter模本征周期缓慢减小；当波速同样都增加5%时，内核中P波波速的增加使计算得到的周期减小1.019%，而外核中P波波速的增加使计算得到的周期减小1.687%；当波速同样都减小5%时，内核中P波波速的减小使计算得到的周期增加1.271%，而外核中P波波速的减小使计算得到的周期增大1.847%；内、外核P波波速分布异常对Slichter模周期的影响基本相当.

(2)由于液核中S波波速为零，内核主要是平动运动，因此剪切力的影响非常小.在地核中，当S波波速变化因子增大时，Slichter模本征周期增大，但是幅度非常小.当波速增加5%时，S波波速的增加使计算得到的周期只增加0.160%；当波速减小5%时，S波波速的减小使计算得到的周期只减小0.147%.当地核中P波和S波波速变化因子相同时，P波波速变化引起Slichter模本征周期的变化比S波造成的影响要大一个数量级.总体来说，由于内核平动振荡的运动特殊性，地震波的变化对Slichter模的影响非常微弱，之所以有影响是因为内核发生微小形变，在现有的观测条件下是可以不考虑的.

(3)在地幔中，随着P波波速变化因子的增大，Slichter模本征周期减小；而随着S波波速变化因子的增大，Slichter模本征周期先减小后增大.地幔中地震波波速的变化对Slichter模本征周期的影响非常小，P波波速变化引起的Slichter模本征周期的变化比S波波速变化的影响略大一点.地球内核平动主要表现为地核中的径向形变，地幔中形变非常小，这也是地幔中地震波速的改变对其本征周期影响较小的主要原因.相对于局限在内核附近的内核平动振荡，地幔的结构对它的影响微弱，不足0.003%，因此几乎可以忽略不计.

(4)数值结果表明计算得到的Slichter模本征 周期随着内外核边界密度差的增加以类似于双曲线 的特征减小，当内外核密度差减小到200 kg·m-3时，周 期增大66.44%，当内外核密度差增大到1000 kg·m-3 时，周期减小21.48%；Slichter模本征周期随着核幔边界密度差的增大而缓慢增大；1066A模型相对于PREM模型在ICB和CMB的密度差分别相差45.321%和1.132%，但是密度差减小到1066A模型提供的数值时，得到的Slichter模周期与基于1066A获得的结果(4.599 h)非常接近，差异分别只有3.762%和0.037%；也就是说Slichter模本征周期与地球内部介质的精细结构关系不大，但对于内核边界的密度差非常敏感.主要原因是内核平动振荡是地球内核在液态外核中运动，Slichter模以地球引力为恢复力，以流体浮力作为驱动，因此对内外核边界的密度跳跃非常敏感.

由于人们对于地球深内部的了解还远远不够，想要采用现有地球模型准确推算Slichter模周期不是很现实.对Slichter模的观测，有助于约束地球3D结构，特别是内外核密度跳跃.尽管已有不少学者致力于探测Slichter 模(包括三重分裂)(Xu et al., 2010；Smylie，1992；Smylie et al., 1992;Smylie，1999；Rochester and Peng， 1993；Peng，1997；Courtier et al., 2000；Rosat et al., 2003；Sun H et al，2004；Rosat et al., 2006；Guo et al., 2006；Ding and Shen， 2013；Shen and Ding， 2013；Jiang et al., 2013；Hinderer et al., 1995)，但尚未出现普遍公认的观测结果.本工作有助于更加深入地了解地球内部结构，从影响Slichter模本征周期的因素入手，得到更精准的地球模型，为基于超导重力仪的实际观测资料检测Slichter模提供理论依据.

致谢 感谢比利时Liege大学的Carlo Denis教授和法国科研中心(CNRS)斯特拉斯堡地球物理研究所的Yves Rogister教授提供有关地球简正模的理论计算软件.

参考文献
[1] Alterman Z, Jarosch H, Pekeris C L. 1959. Oscillation of the earth. Proc. Roy. Soc. A, 252(1268): 80-95, doi: 10.1098/rspa.1959.0138.
[2] Busse F H. 1974. On the free oscillation of the Earth's inner core. J. Geophys. Res., 79(5): 753-757, doi: 10.1029/JB079i005p00753.
[3] Courtier N, Ducarme B, Goodkind J, et al. 2000. Global superconducting gravimeter observations and the search for the translational modes of the inner core. Phys. Earth Planet. Inter., 117(1-4): 3-20, doi: 10.1016/S0031-9201(99)00083-7.
[4] Crossley D J, Rochester M G, Peng Z R. 1992. Slichter modes and love numbers. Geophys. Res. Lett., 19(16): 1679-1682, doi: 10.1029/92GL01574.
[5] Dahlen F A. 1968. The normal modes of a rotating, elliptical Earth. Geophys. J. Int., 16(4): 329-367, doi: 10.1111/j.1365-246X.1968.tb00229.x.
[6] Dahlen F A, Sailor R V. 1979. Rotational and elliptical splitting of the free oscillation of the Earth. Geophys. J. Int., 58(3): 609-623, doi: 10.1111/j.1365-246X.1979.tb04797.x.
[7] Ding H, Shen W B. 2013. Search for the Slichter modes based on a new method: Optimal sequence estimation. J. Geophys. Res.: Solid Earth, 118(9): 5018-5029, doi: 10.1002/jgrb.50344.
[8] Guo J Y, Dierks O, Neumeyer J, et al. 2006. Weighting algorithms to stack superconducting gravimeter data for the potential detection of the Slichter modes. J. Geodyn., 41(1-3): 326-333, doi: 10.1016/j.jog.2005.08.014.
[9] Hinderer J, Crossley D J, Jensen O A. 1995. A search for the Slichter triplet in superconducting gravimeter data. Phys. Earth Planet Inter., 90(3-4): 183-195, doi: 10.1016/0031-9201(95)05083-N.
[10] Jiang Y, Xu J Q, Sun H P. 2013. Detection of inner core translational oscillations using superconducting gravimeters.1 Journal of Earth Science, 24(5): 750-758, doi: 10.007/s12583-013-0370-x.
[11] Peng Z R. 1997. Effects of a mushy transition zone at the inner core boundary on the Slichter modes. Geophys. J. Int., 131(3): 607-617, doi: 10.1111/j.1365-246X.1997.tb06602.x.
[12] Rieutord M. 2002. Slichter modes of the Earth revisited. Phys. Earth Planet. Inter., 131(3-4): 269-278,doi:10.1016/S0031-9201(02)00039-0.
[13] Rochester M, Peng Z. 1993. The Slichter modes of the rotating Earth: A test of the subseismic approximation. Geophys. J. Int., 113(3): 575-585, doi:10.1111/j.1365-246X.1993.tb04653.x.
[14] Rogister V. 2003. Splitting of seismic-free oscillations and of the Slichter triplet using the normal mode theory of a rotating, ellipsoidal Earth. Phys. Earth Planet. Inter., 140(1-3): 169-182, doi: 10.1016/j.pepi.2003.08.002.
[15] Rosat S, Hinderer J, Crossley D, et al. 2003. The search for the Slichter mode: comparison of noise levels of superconducting gravimeters and investigation of a stacking method. Phys. Earth Planet. Inter., 140(1): 183-202, doi: 10.1016/J.PEPI.2003.07.010.
[16] Rosat S, Rogister V, Crossley D, et al. 2006. A search for the Slichter triplet with superconducting gravimeters: Impact of the density jump at the inner core boundary. J. Geodyn., 41(1): 296-306, doi: 10.1016/j.jog.2005.08.033.
[17] Slichter L B. 1961. The fundamental free mode of the Earth's inner core. Proceedings of the National Academy of Sciences of the United States of America, 47(2): 186-190.
[18] Smith M L. 1976. Translational inner core oscillations of a rotating, slightly elliptical Earth. J. Geophys. Res., 81(17): 3055-3064, doi: 10.1029/JB081i017p03055.
[19] Smylie D E. 1992. The inner core translational triplet and the density near the Earth's center. Science, 255(5052): 1678-1682, doi: 10.1126/science.255.5052.1678.
[20] Smylie D E. 1999. Viscosity near Earth's solid inner core. Science, 284(5413): 461-463, doi: 10.1126/science.284.5413.461.
[21] Smylie D E, Hinderer J, Richter B, et al. 1993. The product spectra of gravity and barometric pressure in Europe. Phys. Earth Planet. Inter., 80(3): 135-157, doi: 10.1016/0031-9201(93)90044-A.
[22] Smylie D E, Jiang X. 1993. Core oscillations and their detection in superconducting gravimeter records. J. Geomagnet. Geoelectr., 45(11-12): 1347-1369.
[23] Smylie D E, Jiang X, Brennan B J, et al. 1992. Numerical calculation of modes of oscillation of the Earth's core. Geophys. J. Int., 108(2): 465-490, doi:10.1111/j.1365-246X.1992.tb04629.x.
[24] Smylie D E, Rochester M G. 1981. Compressibility, core dynamics and the subseismic wave equation. Phys. Earth Planet. Inter., 24(4): 308-319, doi: 10.1016/0031-9201(81)90118-7.
[25] Shen W B, Ding H. 2013. Detection of the inner core translational triplet using superconducting gravimetric observations. Journal of Earth Science, 24(5): 725-735, doi: 10.1007/s12583-013-0369-3.
[26] Sun H P, Xu J Q, Ducarme B. 2004. Detection of the translational oscillation of the earth's solid inner core based on the international SG observations. Chinese Sci. Bull. (in Chinese), 49(11): 1165-1176, doi:10.1360/03wd0242.
[27] Wahr J M. 1981. A normal mode expansion for the forced response of a rotating earth. Geophys. J. R. Astr. Soc., 64(3): 651-675, doi: 10.1111/j.1365-246X.1981.tb02689.x.
[28] Xu J Q, Sun H P, Fu R S. 2005. Detection and study of the translational oscillations of the Earth's solid inner core. Advances in Earth Science (in Chinese), 20(7): 740-745.
[29] Xu J Q, Sun H P, Zhou J C. 2010. Experimental detection of the inner core translational triplet. Chinese Sci. Bull., 55(3): 276-283, doi: 10.1007/s11434-009-0479-6.
[30] 孙和平, 徐建桥, Ducarme B. 2004. 基于国际超导重力仪观测资料检测地球固态内核的平动振荡. 科学通报, 49(8): 803-813 .
[31] 徐建桥, 孙和平, 傅容珊. 2005. 地球固体内核平动振荡的研究和检测. 地球科学进展, 20(7): 740-745.