地球物理学报  2014, Vol. 57 Issue (4): 1032-1040 PDF    
引用本文
冉将军, 许厚泽, 钟敏等. 2014. 利用GRACE重力卫星观测数据反演全球时变地球重力场模型. 地球物理学报, 57(4): 1032-1040, doi: 10.6038/cjg20140402   
RAN Jiang-Jun, XU Hou-Ze, ZHONG Min et al. 2014. Global temporal gravity filed recovery using GRACE data. Chinese Journal Geophysics, 57(4): 1032-1040, doi: 10.6038/cjg20140402   
利用GRACE重力卫星观测数据反演全球时变地球重力场模型
冉将军1,2, 许厚泽1, 钟敏1, 冯伟1,2, 沈云中3,4, 张兴福5, 易维勇6    
1. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室, 武汉 430077;
2. 中国科学院大学, 北京 100049;
3. 同济大学测绘与地理信息学院, 上海 200092;
4. 同济大学空间信息科学及可持续发展应用中心, 上海 200092;
5. 广东工业大学土木与交通工程学院, 广州 510006;
6. 慕尼黑工业大学, 德国慕尼黑 80333
投稿时间:2013-6-6    最后修改时间: 2014-1-28 .
基金项目：国家重大科学研究计划（2013CB733305，2012CB957703），国家自然科学基金（41174066，41021003），中国科学院国家外专局“创新团队国际合作伙伴计划”（KZZD-EW-TZ-05）和国家留学基金（2011491203）资助.
第一作者简介：冉将军，男，1986年生，中国科学院测量与地球物理研究所博士研究生，主要从事地球重力场模型的确定和卫星定轨方面的研究.E-mail：j.ran@tudelft.nl
通讯作者：钟敏，男，1964年生，博士生导师，研究员，主要从事动力大地测量和时变重力场研究.E-mail：zmzm@whigg.ac.cn
摘要：本文基于短弧长法开发了一套由低轨卫星数据解算重力场的系统ANGELS（ANalyst of Gravity Estimation with Low-orbit Satellites），成功用GRACE Level1B数据解算出全球时变重力场模型（第一版IGG-CAS系列模型），并与国际三大知名重力卫星相关研究机构：美国德克萨斯大学空间中心CSR （Center for Space Research）、德国GFZ地学研究中心（GeoForschungsZentrum）和美国宇航局JPL喷气推进实验室（Jet Propulsion Laboratory）发布的全球时变重力场模型（RL05模型）进行了详细的比较分析.通过每阶大地水准面差距的对比结果表明，IGG-CAS模型的精度接近RL05模型的精度.对以上四家机构在2004—2010年的时变重力场模型经过相同的去条带和高斯滤波处理，可以发现四家GRACE反演陆地水时变信号的空间分布十分接近，在长江流域反演的陆地水时变信号，两两之间的相关系数均大于0.8.通过反演撒哈拉沙漠干旱地区的时变信号来评估反演的精度水平，IGG-CAS、CSR-RL05、GFZ-RL05和JPL-RL05反演结果的均方差分别为1.5 cm、1.1 cm、1.1 cm和1.2 cm等效水柱高.综合表明IGG-CAS时变重力场反演模型的精度接近于目前国外主要机构最新公布的时变重力场模型.
关键词： GRACE     时变重力场     IGG-CAS     等效水柱高     短弧长法    
Global temporal gravity filed recovery using GRACE data
RAN Jiang-Jun1,2, XU Hou-Ze1, ZHONG Min1, FENG Wei1,2, SHEN Yun-Zhong3,4, ZHANG Xing-Fu5, YI Wei-Yong6    
1. State Key Laboratory of Geodesy and Earth's Geodynamics, Chinese Academy of Sciences, Wuhan 430077, China;
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. College of Surveying and Geo-informatics, Tongji University, Shanghai 200092, China;
4. Center for Spatial Information Science and Sustainable Development, Tongji University, Shanghai 200092, China;
5. Faculty of Civil and Transportation Engineering, Guangzhou 510006, China;
6. Institute of Astronomical and Physical Geodesy, Technical University Munich, Munich 80333, Germany
Abstract: The first version of IGG-CAS series temporal gravity field model is recovered in this paper using GRACE data with a software named ANGELS (ANalyst of Gravity Estimation with Low-orbit Satellites) which is based on short-arc approach, and compared with the RL05 version of temporal gravity models from three famous research institutes well known in satellite gravity research, including the CSR (Center for Space Research), GFZ (GeoForschungs Zentrum), and JPL (Jet Propulsion Laboratory). The accuracy of IGG-CAS model is close to RL05, according to the geoid height comparison per degree. After applying the same de-stripe and Gauss filter to the four series temporal gravity models (IGG-CAS, GFZ, CSR and JPL) from Jan 2004 to Dec 2010, the time signal of continental water recovered from those four models are very similar. Especially, the correlation coefficients of the signal of Yangtze River valley among the four models are higher than 0.8. The square roots of the signals in Sahara desert region from the IGG-CAS, CSR-RL05, GFZ-RL05, and JPL-RL05 are 1.5 cm, 1.1 cm, 1.1 cm, and 1.2 cm in terms of equivalent water height, respectively. To sum up, it shows that the IGG-CAS model reaches almost the same accuracy level when compared with the kind of products which are released by other famous institutes in the world (CSR, GFZ and JPL).
Key words: GRACE     Temporal gravity field     IGG-CAS     Equivalent water height     Integrated equation approach    

1 引言

GRACE(Gravity Recovery And Climate Experiment)自2002年发射后，持续十多年来给地球科学相关领域提供了地球表层质量时空分布的信 息(Wouters et al., 2008; Chen et al., 2004; Tapley et al., 2003). 这些信息对冰川学、水文学、大地测量学以及地球物理等学科的发展起到了很大的推动作用.而GRACE卫星直接观测数据并不是直接反映地球表层质量分部信息，而是所搭载的各种仪器在地球重力场影响下的观测数据，比如星载加速计数据、卫星姿态数据、微波测距系统数据和GPS接收机数据等.如何从这些原始数据中提取出需要的地球质量分布信号一直是科学界的研究难题与热点之一.

到目前为止，国际上仅有少数几家机构可以完成这项复杂工作，主要是美国德克萨斯大学奥斯汀 分校空间研究中心CSR(Center for Space Research)、 德国地学研究中心GFZ(GeoForschungsZentrum)、美国宇航局喷气推进实验室JPL(Jet Propulsion Laboratory)、法国国家空间局、荷兰代尔夫特理工大学和德国波恩大学等.国内的相关同行也为GRACE模式下利用实测数据进行重力场模型的反演做出了大量的工作和贡献，如章传银等(2003)、周旭华(2005)、罗佳(2003)、王正涛(2005)、张兴福(2007)、邹贤才(2007)、郑伟(2007)、郑伟等(2009)、徐天河(2004)、肖云(2006)、肖云等(2006)和游为等(2011)分别利用动力学两步法和一步法、基线法、能量法和短弧长法等进行了静态地球重力场的反演工作，取得了很大的研究进步.此外，Zhao等(2011)介绍了经验参数对动力学法反演时变地球重力场的影响.本文通过处理JPL发布的GRACE Level 1B数据，基于短弧长法开发了一套由低轨卫星数据解算 重力场的系统ANGELS(ANalyst of Gravity Estimation with Low-orbit Satellites)，反演出的时变重力场模型精度接近国际同行最新发布的时变重力场模型精度.

短弧长法最早由Schneider(1968)在1968年提出，并将此方法用于定轨，且把短弧长法引进到重力场确定领域；在CHAMP和GRACE等重力卫星成功发射后，Mayer-Gürr(2006)把此法成功地用于处理这两类重力卫星的实测数据.游为等(2011)分析了联合轨道与星间距离的积分方程反演地球重力场的方法，但未对星间距离变率做出讨论，也没有对短弧长法本身的误差特性进行分析.本文深入分析了短弧长法的误差特性，及其相较于动力学法的优势所在，并利用短弧长法，根据实测GRACE卫星轨道与星间距离变率数据，有效提取出了地球质量分布的时变重力场信号，接近国际水平.

2 基于短弧长法的重力反演模型及其误差分析2.1 反演模型

人造卫星绕地球质心飞行，遵循牛顿运动定律.将卫星飞行轨迹划分成多个弧段，各弧段边界点位置向量 r A、 r B和与弧段中其他位置向量 r(τ)的关系，以及地球重力位系数的联系之间，可以建立如下函数模型(Mayer，2007):

式中，r ·(τ)表示τ时刻的速度； f(τ′)表示卫星在τ′ 时刻所受到的加速度合力，包括中心引力、地球非球形引力、固体潮、海潮、大气阻力、太阳光压、地球反照辐射压等.

 式(3)可重新整理为

 表示卫星在时刻所受到的加速度合力，包括中心引力、地球非球形引力、固体潮、海潮、大气阻力、太阳光压、地球反照辐射压等.而地球非球形引力所导致的加速度与地球重力场球谐系数间存在直观的线性关系:

式里，β 表示展开到某一阶次的地球重力场球谐系数. G 表示卫星所受加速度与地球重力位系数的关系.

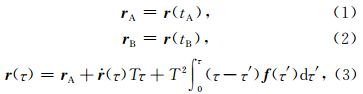
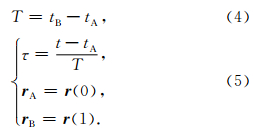
综合上述函数关系，可得如下位置与重力位系数之间的函数模型:

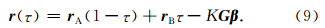
对于GRACE卫星的低低卫卫跟踪模式，把两颗卫星的基线在视线方向做投影，可得到星间距离与星间距离变率的函数关系:

式中，1和2分别表示两颗GRACE卫星. ρ和ρ · 分别表示星间距离和星间距离变率.

动力学法与短弧长法在弧段选择上存在一定差别.目前国际上用动力学法反演地球重力场的主要机构通常把弧长选择为24 h.而短弧长法的弧长选择则不应大于卫星的飞行周期的二分之一，常以30 min弧长为佳.由轨道积分的性质可知，积分弧段越长，积分所得的参考轨道与卫星实测轨道的差值就越大.对于此类型误差的改正，国际上有不少相应的处理方法，如荷兰代尔夫特理工大学采用轨道拟合的方式降低误差(Liu，2008).虽然短弧长法的弧段仅选择30 min，但仍然存在积分误差.本文采用梯度改正方法来降低该类误差的影响，其基本思想是把卫星在位置 r(τ)处的力模型在运动学轨道处一阶Tayor展开，略去二阶以上的高阶项，再对此展开项进行多次积分，得到相应的轨道改正项.再把此轨道改正项加到由弧段边界值算出的参考轨道里，得到更精确的参考轨道.

式中， Δ f(τ，τ′)表示力模型的梯度项，r 为真实轨道，由于真实轨道无法获得，因此用运动学轨道 r k 代替，r ＾ 为由弧段边界值计算的参考轨道，Δ r(τ′)即为梯度改正项.联合式(6)，对上式进行整理并写成矩阵形式，可得

式中，T 为梯度改正项的矩阵表达形式，I 表示单位矩阵，K 矩阵同式(7)，B和b 的形式如下.

 则通过梯度改正后的轨道得

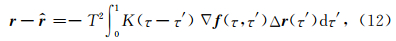
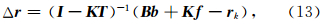
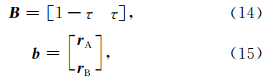
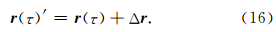
通过联合(10)、(11)和(16)可建立融合轨道与星间距离或距离变率反演地球重力场的函数模型(冉将军等，2012).

2.2 误差分析

利用实测重力卫星数据反演地球重力场模型时，参考轨道的正确程度直接影响到重力场模型的反演精度.而参考轨道深受轨道误差和设计矩阵误差等误差源的影响.因此，下面通过设计3个算例，对短弧长法的这两种误差源进行分析.

为了进行误差分析，根据式(9)设计如下3个算例.算例一，首先计算出一个弧段的开普勒轨道 r true作为真实轨道；然后用边界位置 r A，r B以及加速度 f = Gβ(由于真实轨道为开普勒轨道，所以此处加速度仅考虑中心引力)积分出参考轨道 r(τ)； 最后可以得到开普勒轨道 r true与参考轨道 r(τ)的差值，结果如图 1所示，其中error-free_x、error-free_y和error-free_z分别表示该差值的X，Y和Z分量.从图 1可知，该项差值只有10-9量级.

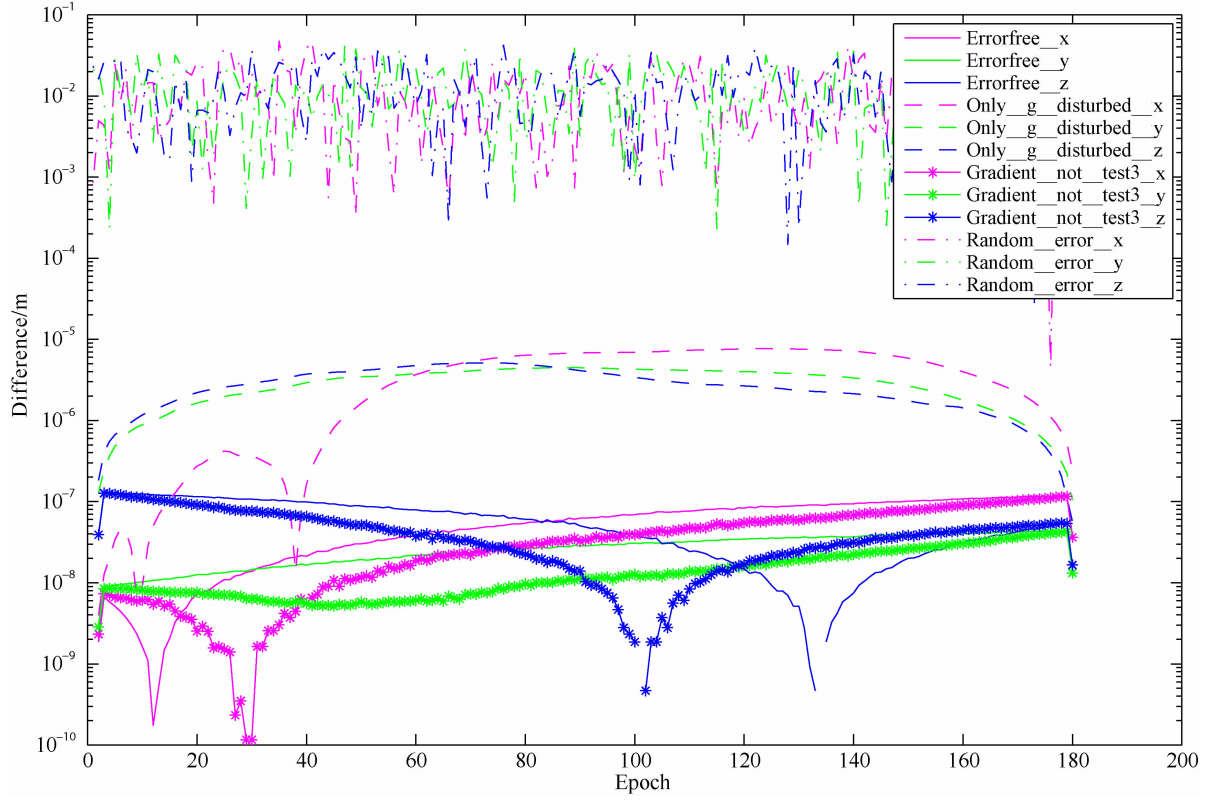图 1 短弧长法各种误差源分析(纵坐标取以10为底对数)Fig. 1 Error source analysis of short arc approach(lg10 scaled)

为了了解设计矩阵 G 的误差对参考轨道的影 响，设计了算例二.用加入了均值为0，方差为1.73×10-2 m 误差(如r and om_error_x，r and om_error_y和r and om_error_z所示)的开普勒轨道计算设计矩阵 G，再利用 G 根据式(9)算出一组新的参考轨道. 此参考轨道与无误差的开普勒轨道差值的X，Y和Z分量如图 1里only_G_disturbed_x，only_G_disturbed_y和only_G_disturbed_z.此项差值为10-6量级.

在实测数据处理中，卫星的位置通常采用GPS定轨，而目前GPS的定轨精度通常在2~3 cm左右，远低于GRACE星间距离变率数据在微米量级的设计精度.本文所述梯度改正的目的在于对轨道进行改正，以减少轨道误差对重力场反演的影响.算例三利用式(13)算出的梯度改正对算例二加入了误差的轨道进行改正，从而得到新的参考轨道.该参考轨道与无误差开普勒轨道的差值如图 1里gradient_not_test3_x，gradient_not_test3_y和gradient_not_test3_z所示.其量级在10-9到10-7量级.相比于没经过梯度改正的算例二在10-6量级的残差，经过梯度改正后，取得了至少一个量级的改善. 3 利用GRACE实测数据反演时变地球重力场模型

本文以ITG-GRACE2010为静态参考重力场模型，采用JPL提供的高精度的轨道数据、加速度计数据、星间距离变率数据、卫星姿态数据以及GFZ发布的大气与海洋混叠模型进行月重力场信号的提取.由于卫星在轨飞行时不仅监测到了地球表层的质量变化，同时也会因为固体潮，海潮，极潮和相对论效应等产生摄动.因此需要采用较为准确的模型进行扣除，以得到“干净”的时变重力场信号.

本文采用的背景模型详见表 1.

表 1 重力场模型确定时的背景模型 Table 1 Background models for gravity field determination

利用本文所述函数模型，结合GRACE观测数 据，解算了第一版的IGG-CAS系列时变重力场模 型.为了比较第一版IGG-CAS时变重力场模型的精度，随机选择了2009年9月份发布GRACE时变重力场模型的官方机构CSR，JPL和GFZ的RL05版本与IGG-CAS做比较，结果如图 2所示.从图中画出的每阶大地水准面差距可知，从2到59阶，IGG-CAS与其他模型的每阶大地水准面差距相当.到60阶时，各模型的每阶大地水准面差距从大到小的排列顺序为： GFZ-RL05，JPL-RL05，IGG-CAS和CSR-RL05. 4 IGG-CAS时变重力场模型验证与地球物理解释

为了进一步验证本文的IGG-CAS时变重力场模型，我们选择2004年至2010年共84个月时变重力场模型为例，将其与CSR、GFZ和JPL公布的最新RL05版本的GRACE数据产品进行了比较分析.首先用卫星激光测距(SLR)结果替换了二阶项(Cheng and Tapley， 2004)，并加入了Swenson等(2008)计算的地心改正项；采用Swenson和Wahr(2006)提出的滑动窗口方法分别去除同一次的奇数阶和偶数阶位系数的相关性，减少南北方向“条带”误差的影响；并使用了500 km高斯平滑来降低高阶位系数的噪声(Jekeli，1981)；最终转化为全球分布的等效水柱高变化(Wahr，1998).鉴于篇幅所限，本文仅随机画出四家时变重力场模型在2006年1月和2007年12月的时变信息，如图 3和图 4所示.由图可知，IGG-CAS反演得到的2006年1月和2007年12月的全球时变重力场信号(等效水柱高)与CSR、GFZ和JPL公布的时变重力场结果在空间分布上符合得很好.例如，在亚马逊流域和刚果河流域等季节性陆地水变化较大的地区，四家GRACE 反演结果的空间分布十分接近.我们进一步利用2004—2010年的四家GRACE反演结果计算得到了时变重力场变化的周年振幅和长期趋势.如图 5所示，不同机构反演的全球质量变化周年振幅的空间分布较为一致，振幅较大的地区主要在南美的亚马逊河流域、非洲的尼日尔河流域和东南亚的季风区.如图 6所示，不同机构得到的全球质量长期变化趋势的空间分布也十分一致，并成功观测到印度北部、阿拉斯加、格林兰和西南极等地区的质量亏损信号，以及北美等地的冰川均衡调整导致的质量增加信号等.

图 2 GFZ-RL05，JPL-RL05，CSR-RL05和IGG-CAS每阶大地水准面信号比较Fig. 2 Goid height of GFZ-RL05，JPL-RL05，CSR-RL05 and IGG-CAS

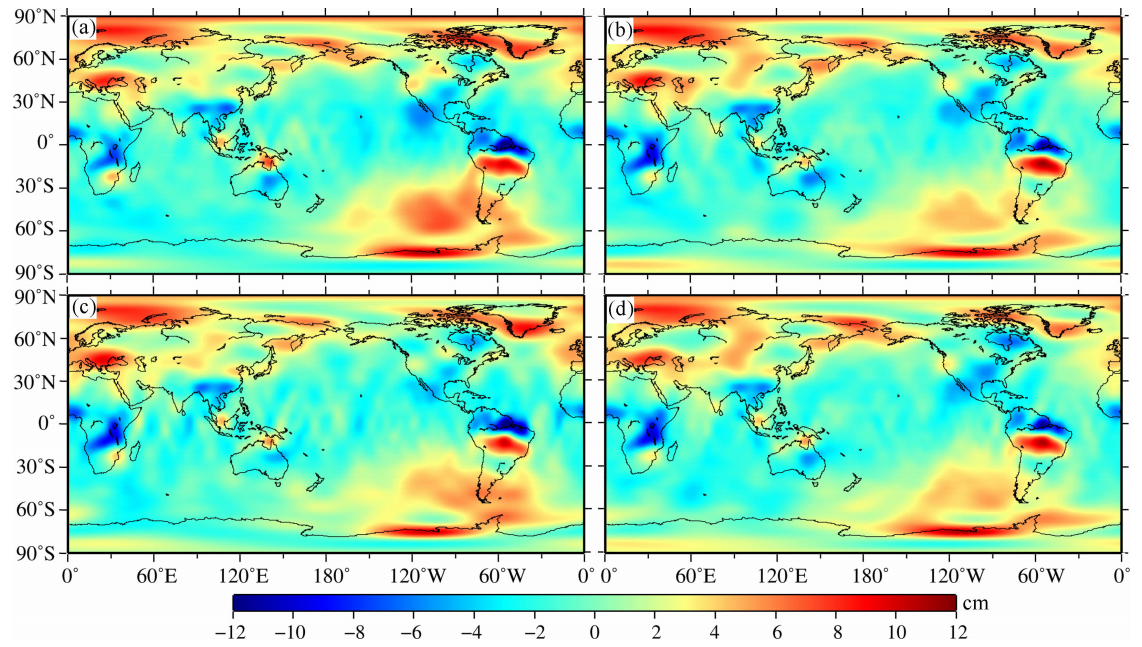图 3 2006年1月GRACE反演的时变重力场计算得到的全球质量分布异常(等效水柱高，单位：cm). (a)IGG-CAS，(b)CSR，(c)GFZ和(d)JPL Fig. 3 Mass anomaly from GRACE in Jan 2006(equivalent water height in cent-meter): (a)IGG-CAS，(b)CSR，(c)GFZ and (d)JPL

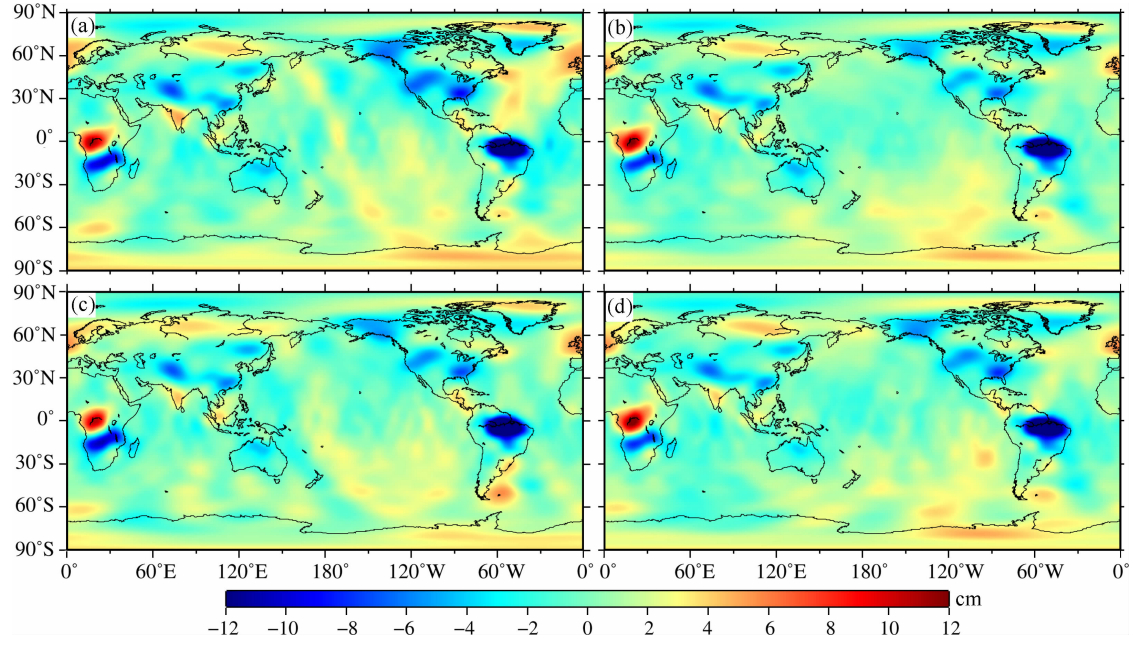图 4 2007年12月GRACE反演的时变重力场计算得到的全球质量分布异常(等效水柱高，单位：cm). (a)IGG-CAS，(b)CSR，(c)GFZ和(d)JPL Fig. 4 Mass anomaly from GRACE in Dec 2007(equivalent water height in cent-meter) (a)IGG-CAS，(b)CSR，(c)GFZ and (d)JPL

此外，我们利用四家GRACE时变模型对亚马 逊流域、长江流域以及非洲撒哈拉沙漠地区的陆地水变化信号进行了估计.采用Oki和Sud(1998)提供的流域数据得到亚马逊流域和长江流域的范围； 撒哈拉地区选择了经纬度范围为(10°E—20°E，20°N—30°N)的沙漠地区.如图 7a所示，在亚马逊流域，四家结果都表现出一致的周年变化和年际变化.2004至2010年，IGG-CAS得到的亚马逊流域陆地水周年振幅为14±1 cm等效水柱高，略小于其他三家的结果(CSR为16±1 cm等效水柱高、GFZ为15±1 cm等效水柱高和JPL为16±1 cm等效水柱高).在长江流域，四家结果的周年信号也基本一致.2004—2010年，CSR、GFZ和JPL三家结果符合得较好，相关性大于0.97；IGG-CAS与CSR、GFZ和JPL结果的相关性分别为0.87、0.84和0.86.沙漠地区的时变重力场信号相对较小，因此不同机构反演的沙漠地区的时变结果可以用来评估其反演的精度水平.图 6c给出四家机构反演的撒哈拉沙漠地区的时变信号.2004—2010年，IGG-CAS、CSR、GFZ和JPL反演结果的均方差分别为1.5 cm、1.1 cm、1.1 cm和1.2 cm等效水柱高.IGG-CAS时变重力场模型结果的精度与其他三家的结果在同一水平.

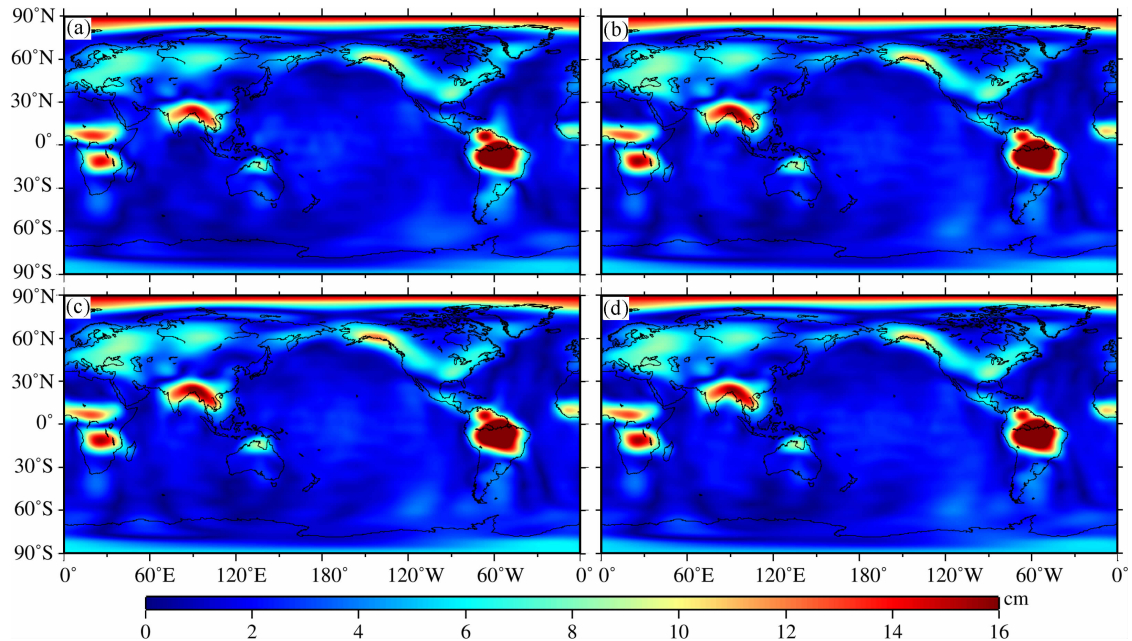图 5 基于(a)IGG-CAS、(b)CSR、(c)GFZ和(d)JPL反演的时变重力场计算得到的2004—2010年的全球质量变化周年振幅(等效水柱高，单位：cm) Fig. 5 Annual amplitude of mass anomaly from 2004 to 2010 calculated by GRACE monthly models from (a)IGG-CAS，(b)CSR，(c)GFZ and (d)JPL(equivalent water height in cent-meter)

图 6 基于(a)IGG-CAS、(b)CSR、(c)GFZ和(d)JPL反演的时变重力场计算得到的2004—2010年的全球质量变化趋势(等效水柱高，单位：cm/yr) Fig. 6 Mass anomaly trend from 2004 to 2010 calculated by GRACE monthly models from(a)IGG-CAS，(b)CSR，(c)GFZ and (d)JPL(equivalent water height in cent-meter)
5 结论

本文分析了短弧长法的重力反演理论及其误差源，并利用此方法解算了第一版的IGG-CAS系列时变重力场模型，且与GFZ，CSR和JPL发布GRACE时变重力场模型做了详细的比较，得到如下结论.

(1)通过误差分析表明，利用梯度改正能提高参考轨道的精度.

(2)从每阶大地水准面差距的角度比较，IGG-CAS模型精度接近GFZ，JPL和CSR发布的RL05模型.

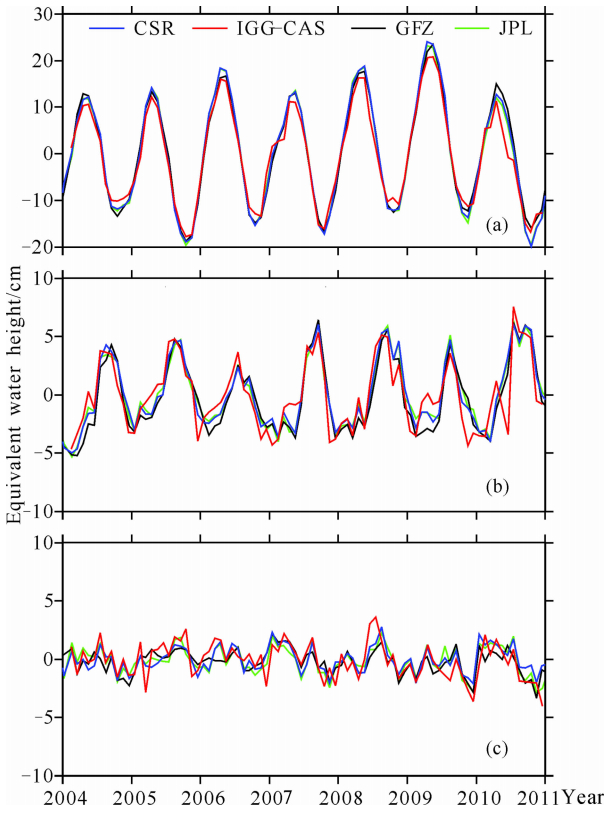图 7 在(a)亚马逊流域，(b)长江流域和(c)撒哈拉沙漠 地区，基于CSR、IGG-CAS、GFZ和JPL反演的时变重 力场计算得到的陆地水变化(等效水柱高，单位：cm) Fig. 7 Water storage changes of(a)Amazon river，(b)Changjiang river and (c)Sahara desert calculated by GRACE monthly solutions from IGG-CAS，CSR，GFZ and JPL(equivalent water height in cent-meter)

(3)通过把四家模型做相同的去条带与高斯滤波处理，发现IGG-CAS时变重力场结果与CSR、GFZ和JPL等公布的结果在时空分布上具有很好的一致性.例如，在长江流域时变信号的时间序列相关系数均大于0.8.

(4)通过进一步比较四家模型的时变信号在2004至2010年间的周年振幅可知：IGG-CAS，CSR-RL05，GFZ-RL05和JPL-RL05，亚马逊流域陆地水周年振幅分别为14±1 cm，16±1 cm、15±1 cm和16±1 cm等效水柱高.

(5)通过反演撒哈拉沙漠干旱地区的时变信号来评估重力场模型的精度水平，可以发现，IGG-CAS、CSR、GFZ和JPL在撒哈拉沙漠反演结果的均方差分别为1.5 cm、1.1 cm、1.1 cm和1.2 cm等效水柱高.

综合表明IGG-CAS时变重力场反演模型的精度接近目前国外主要机构最新公布的时变重力场模型的精度.

致谢 感谢NASA JPL以及德国GFZ提供的GRACE Level 1B 数据以及荷兰Fugro公司柳响林博士给予的帮助.

参考文献
[1] Chen J L, Wilson C R, Tapley B D. 2006. Satellite gravity measurements confirm accelerated melting of Greenland ice sheet. Science, 313(5795): 1958—1960, doi: 10.1126/science.1129007.
[2] Cheng M K, Tapley B D. 2004. Variations in the Earth's oblateness during the past 28 years. J. Geophys. Res., 109(B9): B09402, doi: 10.1029/2004JB003028.
[3] Jekeli C. 1981. Alternative methods to smooth the Earth's gravity field. Rep. 327, Dep. of Geod, Department of Geodetic Science and Surveying, The Ohio State University, Columbus.
[4] Liu X L. 2008. Global Gravity Field Recovery from Satellite-to-Satellite Tracking Data with the Acceleration Approach . Delft: Delft University of Technology.
[5] Luo J.2003.Theory and Methodology of Earth Gravity Field Determination Using Satellite-to-Satellite Tracking(in Chinese). Wuhan: Wuhan University.
[6] Mayer-Gürr T. 2006. Gravitationsfeldbestimmung aus der Analyse kurzer Bahnbgen am Beispiel der Satellitenmissionen CHAMP und GRACE . Bonn: Institute für Theoretische Geodsie der Universitt Bonn.
[7] Oki T, Sud Y C. 1998. Design of Total Runoff Integrating Pathways (TRIP)—A global river channel network. Earth Interact., 2(1): 1-37.
[8] Ran J J, Xu H Z, Shen Y Z, et al. 2012. Expected accuracy of the global gravity field for next GRACE satellite gravity mission. Chinese J. Geophys. (in Chinese), 55(9): 2898-2908.
[9] Schneider M. 1968. A general method of orbit determination, Report 1279. Royal Aircraft Establishment, Hants, UK. 1-4.
[10] Swenson S, Chambers D, Wahr J. 2008. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res., 113(B8): B08410, doi: 10.1029/2007JB005338.
[11] Swenson S, Wahr J. 2006. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett., 33(8): L08402, doi: 10.1029/2005GL025285.
[12] Tapley B D, Chambers D P, Bettadpur S, et al. 2003. Large scale ocean circulation from the GRACE GGM01 Geoid. Geophys. Res. Lett., 30(22), doi: 10.1029/2003GL018622.
[13] Wahr J, Molenaar M, Bryan F. 1998. Time variability of the Earth's gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res., 103(B12): 30205-30229.
[14] Wang Z T. 2005. Theory and Methodology of Earth Gravity Field Recovery by Satellite-to-Satellite Tracking Data (in Chinese). Wuhan: Wuhan University.
[15] Wouters B, Chambers D, Schrama E J O. 2008. GRACE observes small-scale mass loss in Greenland. Geophys. Res. Lett., 35(20): L20501, doi: 10.1029/2008GL034816.
[16] Xiao Y. 2006. Research on the earth gravity field recovery from satellite-to-satellite tracking data. Acta Geodaetica et Cartographica Sinica (in Chinese), 35(4): 408.
[17] Xiao Y, Xia Z R, Wang X T, et al. 2006. Error analyses for recovery of the earth's gravity field by HL-SST technique. Acta Geodaetica et Cartographica Sinica (in Chinese), 35(2): 106-111.
[18] Xu T H. 2004. Gravity field recovery from orbit and accelerometer data(in Chinese).Zhengzhou: PLA Information Engineering University.
[19] You W, Fan D M, Huang Q.2011. Analysis of short-arc integral approach to recover the Earth's gravitational field. Chinese J. Geophys. (in Chinese), 54(11): 2745-2752.
[20] Zhang C Y, Hu J G, Dang Y M, et al. 2003. Gravity field recovery method with several kinds of satellite tracking data. Geomatics and Information Science of Wuhan University (in Chinese), 28(S1): 137-141.
[21] Zheng W. 2007. Theory and methodology of Earth's gravitational field recovery based on satellite gravity measurement (in Chinese).Wuhan:Huazhong University of Science and Technology.
[22] Zheng W, Xu H Z, Zhong M, et al. 2009. Optimal design of orbital altitude in satellite-to-satellite tracking model. Journal of Geodesy and Geodynamics (in Chinese), 29(2): 100-105, 110.
[23] Zhou X H. 2005. Study on satellite gravity and it's application (in Chinese). Wuhan: Institute of Geodesy and Geophysics, Chinese Academy of Sciences.
[24] Zhang X F. 2007. The Earth's field model recovery on the basis of satellite-to-satellite tracking missions(in Chinese). Shanghai: Tongji University.
[25] Zhao Q L, Guo J, Hu Z G, et al. 2011. GRACE gravity field modeling with an investigation on correlation between nuisance parameters and gravity field coefficients. Adv. Space Res., 47(10): 1833-1850, doi: 10.1016/j.asr.2010.11.041.
[26] Zou X C. 2007. Theory of satellite orbit and Earth gravity field determination(in Chinese). Wuhan: Wuhan University.
[27] 罗佳. 2003. 利用卫星跟踪卫星确定地球重力场的理论和方法[博士论文]. 武汉: 武汉大学.
[28] 冉将军, 许厚泽, 沈云中等. 2012. 新一代ＧＲＡＣＥ重力卫星反演地球重力场的预期精度. 地球物理学报, 55(9): 2898-2908.
[29] 王正涛. 2005. 卫星跟踪卫星测量确定地球重力场的理论与方法[博士论文]. 武汉: 武汉大学.
[30] 肖云. 2006. 基于卫星跟踪卫星数据恢复地球重力场的研究. 测绘学报, 35(4): 408.
[31] 肖云, 夏哲仁, 王兴涛. 2006. 高低卫卫跟踪模式恢复地球重力场的误差分析. 测绘学报, 35(2): 106-111.
[32] 徐天河. 2004. 利用CHAMP卫星轨道和加速度计数据推求地球重力场模型[博士论文]. 郑州: 中国人民解放军信息工程大学.
[33] 游为, 范东明, 黄强. 2011. 卫星重力反演的短弧长积分法研究. 地球物理学报, 54(11): 2745-2752.
[34] 章传银, 胡建国, 党亚民等. 2003. 多种跟踪组合卫星重力场恢复方法初探. 武汉大学学报(信息科学版), 28(特刊): 137-141.
[35] 郑伟. 2007. 基于卫星重力测量恢复地球重力场的理论和方法[博士论文]. 武汉: 华中科技大学.
[36] 郑伟, 许厚泽, 钟敏等. 2009. 卫-卫跟踪测量模式中轨道高度的优化选取. 大地测量与地球动力学, 29(2): 100-105, 110.
[37] 周旭华. 2005. 卫星重力及其应用研究[博士论文]. 武汉: 中国科学院测量与地球物理研究所.
[38] 张兴福. 2007. 应用低轨卫星跟踪数据反演地球重力场模型[博士论文]. 上海: 同济大学.
[39] 邹贤才. 2007. 卫星轨道理论与地球重力场模型的确定[博士论文]. 武汉: 武汉大学.