2014, Vol. 57
2. 吉林大学电子科学与工程学院, 长春 130012;
3. 大庆钻探工程公司测井公司, 大庆 163412
2. College of Electronic Science and Engineering, Jilin University, Changchun 130012, China;
3. Wireline Logging Company, Daqing Drilling Engineering Company, Daqing 163412, China
自然伽马测井是进行地层划分、岩性识别以及泥质含量计算等一种重要方法.为降低统计涨落对测量结果的影响，常规自然伽马仪器主要采用直径和长度分别为0.05 m和0.3 m的NaI晶体作为探测器，其纵向分辨率大约为0.6 m，通过高分辨率处 理能够得到的最大纵向分辨率大约为0.3 m(Tikhonov et al, 1979; 汪宏年等，1996；汪宏年等，1997).随着油气资源需求增加以及油气勘探开发的不断深入，迫切需要研制开发新一代的高分辨率测井仪器，解决薄交互储层、裂缝以及页岩气等非常规储层测井评价和解释中遇到的新问题.最近，我们研制出一种新型高分辨率伽马测井仪器，该新型仪器的最大特点在于：不仅缩短探测器中NaI晶体的长度，而且在NaI晶体外表面上加装一定大小的屏蔽铅板进一步降低围岩影响，此外，为研究井眼泥浆影响，采用居中和贴井壁两种测量.通过数值模拟方法系统考察不同条件下仪器的响应特征以及纵向分辨率变化规律，设计出纵向分辨率0.2 m的高分辨率自然伽马测井仪器.为克服NaI晶体长度减小对计数率和测量精度的不利影响(陶宏根等，2012)，在整个自然伽马测井仪器的井下部分安装了四个尺寸和结构完全相同的NaI晶体，能够同时测量出四条相同分辨率的自然伽马测井曲线，以便利用测井资料的合成技术降低统计涨落效应影响、保证在高分辨率基础上仍然具有较高的测量质量.
由于在NaI晶体外表面的一部分加装了屏蔽铅板，探测器只能接收到地层中的部分自然伽马射线.当仪器贴井壁时，放射性源的空间分布相对于仪器的对称性也遭到破坏，仪器响应的计算变成三维问题.此外，伽马仪器的测井响应不仅与地层中铀钍钾的含量、伽马射线能谱、岩石散射和吸收有关外，还与伽马射线的散射路径有关.从理论上说，根据地层中的铀钍钾含量、岩石散射和吸收特点以及井眼和仪器结构，通过求解Boltzmann传输方程可以获 得自然伽马测井响应(Tittman et al., 1979; Tzortzis et al., 2003; Manduci et al., 2010; Vlastou et al., 2006).然而由于地球化学特征的复杂性，完全准确模拟自然伽马响应仍然是极端复杂的工作，即使借助于复杂的Monte Carlo技术和矩量法等现代数值模拟方法也难以准确模拟出复杂地层条件下真实自然伽马测井响应(吴文圣等，2007；周继宏等，2012；黄隆基，1985；黄隆基，2000；黄隆基等，1997；Kerr et al.,1988; Bertozzi et al., 1981; Conaway et al., 1978; 龚大兴等，2011). 因此，常规自然伽马测井响应数值往往采用无限多个水平薄板产生的单色自然伽马通量的叠加，伽马测井仪器的脉冲响应是点状函数(z－zd)=0.5αexp(－α z－zd )关于仪器长度、采样间距等的积分(α为常数，表示地层的吸收系数)，井中的自然伽马测井记录可以表示为仪器脉冲响应与地层伽马强度的褶积形式(Huang et al., 1997; Sheng et al., 1987; Scott et al., 1961; Cavalier et al., 2007; Gadeken et al., 1990; Wahl et al., 1983; 王斌等，2006).为了便于进行复杂地层条件下自然伽马测井响应的数值模拟，基于单能窄束原理可以用关于光子体密度n(r)的扩散方程逼近Boltzmann传输方程(Tittman et al., 1979)，利用该扩散方程的近似解，考察井眼环境和自然伽马测井仪器的探测深度(王斌等，2006)以及含有井眼情况下水平层状地层自然伽马测井响应(刘国庆等，2002；谢仲生等，2000).
本文将进一步推广单能窄束原理中的算法，建立当NaI晶体的部分外表面上加装了屏蔽铅板以及仪器在居中和贴井壁等测量方式下，自然伽马测井响应函数的三维数值模拟方法.考察NaI晶体尺寸、屏蔽铅板和测速变化以及居中和贴井壁等情况下对仪器响应特征和纵向分辨率的影响，为实现0.2 m高分辨率伽马测井仪器设计提供合适的仪器参数，并通过数值模拟结果与模型井和井场测量结果对相关算法和仪器特征进行检验.
图1是含有井眼的水平层状介质与新型高分辨率自然伽马测井仪器结构示意图，其中地层界面深度、地层密度和伽马源强度分别为Zi、di和Qi(i=1,2,3,…,N),μi是伽马射线吸收系数.井眼半径为b、泥浆密度和吸收系数分别为dmd和μmd.为便于比较不同测量方式对仪器纵向分辨率的影响，本文将分别讨论居中和贴井壁两种测量方式下的数值模拟方法.对于居中型仪器，仅在NaI晶体的上下底面加装屏蔽铅板，减低围岩影响，而在贴井壁仪器中，不仅NaI晶体的上下底面上且在其靠近井轴的半个侧面上也加装屏蔽铅板，即只有靠近井壁的半个晶体侧面能够接收到伽马射线，其它部分全部被屏蔽.为描述的方便起见，假定NaI晶体的长度和半径分别为lT和bT，上下底面上屏蔽铅板的半径为bL，且将晶体表面没有被屏蔽的部分用ST表示.
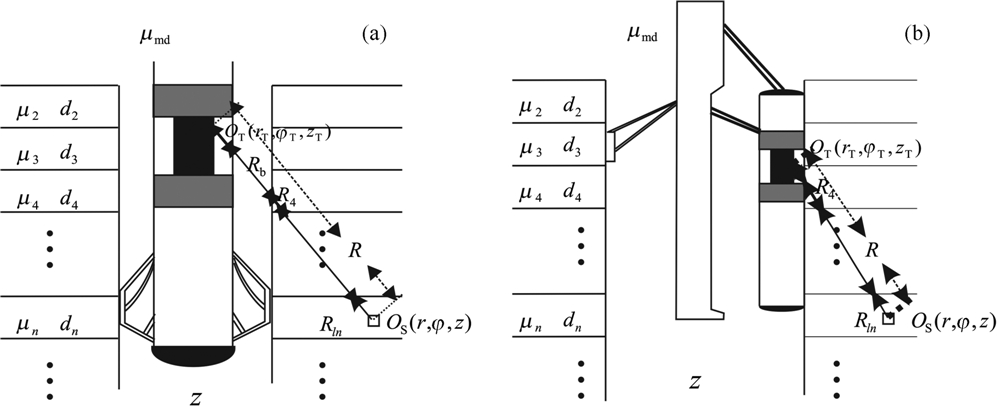 | 图1 层状地层模型与仪器结构示意图 (a) 居中屏蔽探测器； (b) 贴井壁屏蔽探测器. Fig.1 Schematic of formation and GR tools (a) At borehole axis; (b) Cling to borehole. |
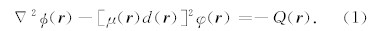
r =(x,y,z)=(ρ,θ,z)是空间坐标， Qφ(r )是地层 中自然伽马源强度，对于图1所示的层状模型，伽马源强度Qφ(r )、吸收系数μφ(r )和密度dφ(r )均是分片常数分布的.且函数Qφ(r )具有轴对称性，因此可以表示为
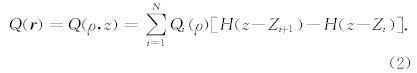
其中,Qi(ρ)=QiH(ρ－b)是地层i中的伽马源强度，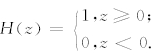
为阶跃函数.
利用伽马光子体密度φ(r )在地层边界上的连续条件(Vlastou et al., 2006)，以及铅板对伽马射线的屏蔽作用(即铅板表面上伽马通量的法向分量为零)，通过求解方程(1)可以获得NaI 晶体表面附近的φ(r )值的大小与分布，探测器晶体表面接受到的光子通量I是通量密度jφ(r )=－ Δ φ(r )在晶体表面上的面积分
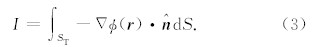
是晶体表面单位外法向向量.显然,伽马仪器的测井响应与伽马光子通量I成正比.
由于井中探测器与铅板的几何结构较为复杂，严格求解方程(1)会涉及到井下探测器晶体与铅板表面上边界条件的设定问题，导致一个极为复杂的边值问题.因此准确求解方程(1)是非常困难的.本 文采用一种近似求解方法，通过引入水平层状介质中的Green函数
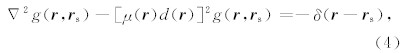
δ( r － r s)是Dirac函数,g( r , r s)是位于 r s的点状源在层状介质中产生的伽马光子空间分布.如果忽略伽马射线在地层界面上的反射与折射效应，方程(4)的近似解为
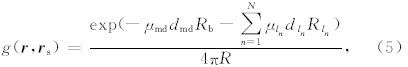
其对应通量向量密度Green函数为
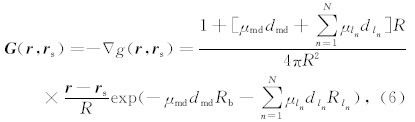
其中，R=‖ r － r s‖是 r 和 r s间的距离，Rb和Rln是连接 r 和 r s的直线中分别位于井眼和地层中的线 段ln,n=1,2,…,N的长度(见图1)，μmddmd和μlndln 分别是井眼和地层中的各个线段ln,n=1,2,…,N上的吸收系数与密度乘积.
近似解(5)是基于层状介质中单能窄束射线理论得到的，由于忽略了伽马光子的散射效应，所以从发射的伽马光子均沿直线传播.
利用叠加原理，方程(1)的解可以表示为
空间任意点上的光子通量密度为
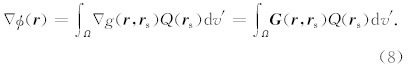
由于晶体表面附近铅板的屏蔽作用(见图2)，探测器只能够接收到周围地层的一部分伽马射线.为计算在测量深度zR上屏蔽探测器上的总光子通量，需要确定没有被屏蔽的晶体表面ST(zR)以及该表面每一点 r T上能够探测到的有效地层区域Ωeff( r T)(即发射的伽马射线能够照射到 r T点的地层区域).为方便起见，假定测量深度zR与NaI晶体中心位置相同.
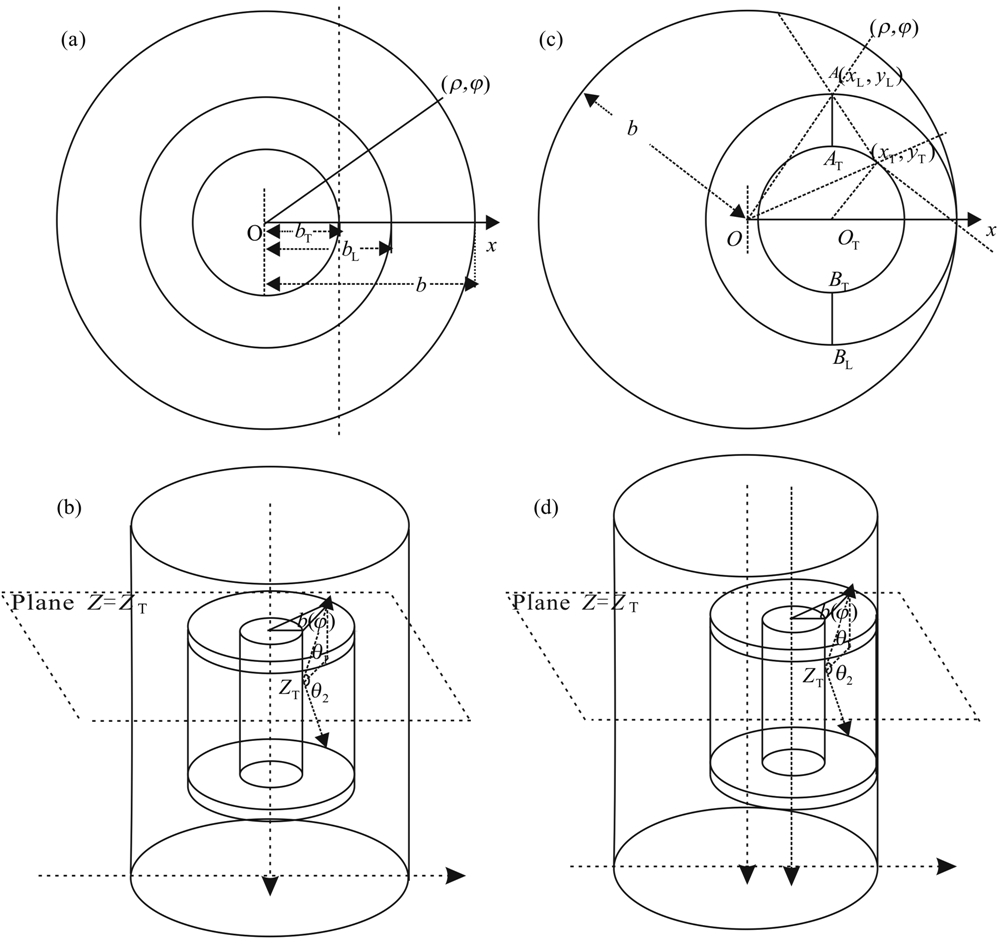 | 图2 居中上下屏蔽探测器和贴井壁开窗屏蔽探测器的有效积分区域和屏蔽角(a)和(c)井眼俯视图； (b)和(d)井眼立体图. Fig.2 The effective integration region or shielding angle of the detector at borehole axis or cling to borehole wall (a) & (c) The top view of borehole； (b) & (d) The perspective view of borehole. |
由于居中屏蔽探测器中没有被屏蔽的晶体表面是整个NaI晶体的整个柱面(见图2b)，柱面上的点构成的区域可表示为
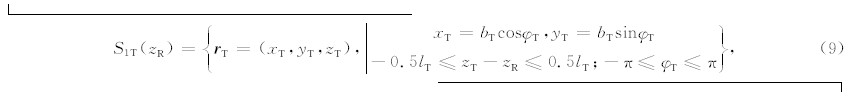
对于柱面上 r T∈S1T(zR)，其对应的有效地层探测区域Ω1,eff( r T)是地层中能够直接照射到该点上的所有伽马射线发射源组成的区域.由于假定伽马射线直线传播，该有效探测区间也是从 r T点能够看到的地层区域.为确定Ω1,eff( r T)大小，首先过 r T点作一个与晶体表面的切平面，切平面的右侧地层(见图2a)对应区域为
Ω1,0( r T)=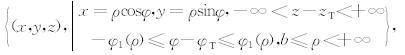
其中，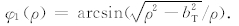
不难看出只有从区域Ω1,0( r T)中发射的射线才可能照射到 r T点上.此外，由于上下铅板的屏蔽作用，从Ω1,0( r T)中发射伽马射线，也有一部分被屏蔽掉.为此，从 r T出发作连接上下圆形铅板外沿的曲面，两个曲面围成的右侧区域与Ω1,0( r T)相交的部分构成 r T的有效探测区域Ω1,eff( r T)，从该区域中发射的伽马射线将能够照射到晶体表面.因为屏蔽铅板外沿是一个以井轴上(0,0,zR－0.5lT)为圆心、半径为bL的圆环，该圆环上的任意点 r L=(xL,yL)到 r T=(xT,yT) 的距离可表示为：
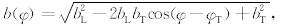且屏蔽角θ1和θ2满足条件tanθ1=(zT+0.5lT－zR)/b(φ)和tanθ2=(0.5lT+zR－zT)/b(φ)(见图2b), 从图2b可以看出Ω1,eff( r T)可表示为
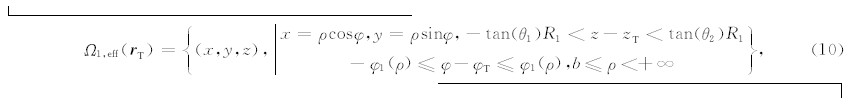
其中，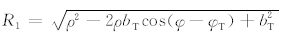
是空间发射源 r 与晶体表面 r T间的水平距离.
贴井壁仪器中的NaI晶体在上下底面和靠近井轴的半个侧面上均加装了屏蔽铅板(见图2d)，测 量时整个探测器被推靠到井壁.由于NaI晶体更靠近地层，其分辨率应该比居中型探测器高且受井 眼泥浆的影响会更小.我们仍然以井轴作为z轴， 探测器和井壁的切线与井轴平行, 井轴到该切线 的水平连线作为x轴方向，这时探测器轴线和上下底面铅板中心在水平面上的位置OT为(b－bL,0)， 晶体表面屏蔽与非屏蔽部分的分界线分别用AT 和BT表示(见图2c)，其在水平面上的位置分别 为(b－bL,b)和(b－bL,－b)，利用图中的几何关系，未屏蔽晶体柱面S2T(zR)构成的区域可用方程表示为
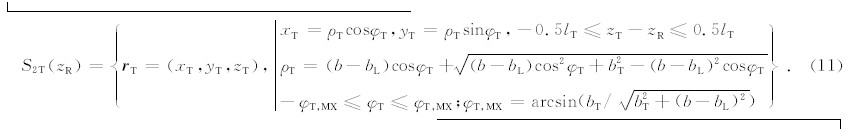
由于仪器偏心,未屏蔽晶体柱面上的 r T ∈ S2T(zR)对应的有效地层探测区域Ω2,eff( r T)的表达式将变得较为复杂.为讨论方便，首先考虑仅有侧向屏蔽作用情况下， r T ∈ S2T(zR)点的有效探测区域Ω2,0( r T). 未屏蔽的晶体表面是以OT为圆心半径为bT 的半个圆柱面，其方程为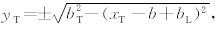
柱面上的切线斜率为dyT/dxT=kT=－(xT－b+bL)/yT，因此过(xT,yT)点的切线方程可表示为y=yT+kT(x－xT).侧面边界AL和BL在水平面上的位置分别为(b－bL,bL)和(b－bL,－bL)(图2d)，(xT,yT)和(b－bL,bL)连线的斜率为kc=(bL－yT)/(b－bL－xT)，该连线方程的表达式为y=yT+kc(x－xT)， 显然切线y=yT+kT(x－xT)和连线y=yT+kc(x－xT)围成的扇形区域为 r T点所能有效探测区域Ω2,0( r T)，经过推导该区域可以表示为 Ω2,0( r T)=
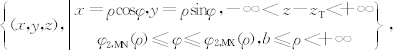
其中φ2,MX和φ2,MN分别是方程sinφ2,MX－kTcosφ2,MX=(yT－kTxT)/ρ和sinφ2,MN－kccosφ2,MN=(yT－kcxT)/ρ的解.
为进一步确定上下铅板的屏蔽作用，利用铅板边界点(xL,yL)对应的方程(xL－b+bL)2+y2L=b2L，并令xL=ρLcosφ和yL=ρLsinφ，则可得到边界点(xL,yL)在极坐标系下的方程ρL=(b－bL)+
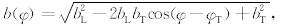，(xT,yT)和(xL,yL) 间距离屏蔽角θ1和θ2满足的条件为tanθ1=(zT+0.5lT
－zR)/b(φ)和tanθ2=(0.5lT+zR－zT)/b(φ).因此，
有效探测区域Ω2,eff( r T)可以表示为
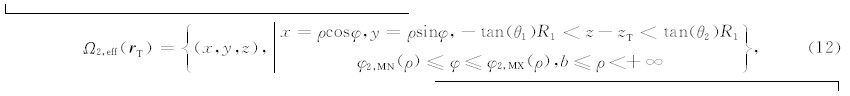
即有效探测区域内的任意点 r 与晶体表面 r T的连线与水平面的夹角θ必须位于屏蔽角θ1和θ2之间，
这里的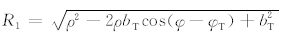是空间发射源 r 与晶体表面
r T点间的水平距离.
对于方形NaI晶体，假设各边的长度分别为aTx、aTy和aTz， 在居中和贴井壁两种不同情况下，晶体表面每一点上的有效探测区域可用类似方法建立，为简短 起见，这里仅给出未被屏蔽的晶体表面对应区域的方程.
对于居中屏蔽探测器中，NaI晶体的上下两个矩形表面被屏蔽，未被屏蔽的部分是晶体的四个矩形侧面，这四个距形侧面构成的区域可表示为
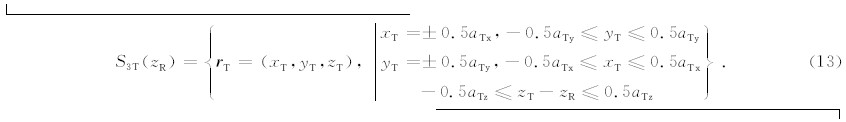
对于贴井壁屏蔽探测器中，在晶体表面只留有一个侧面开口，因此没有被屏蔽的晶体表面是整个NaI晶体靠近开口方向的一个侧面，该侧面上所有点构成的区域可表示为
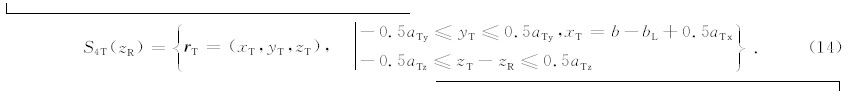
根据仪器居中和贴井壁两种情况下，能够接收伽马射线的晶体外表面大小以及晶体外表面每一点 r T对应有效探测区域，通过积分可以确定出每个深度点上探测器能够测量到的伽马射线的通量.
对于居中屏蔽型探测器，晶体表面任意点 r T处的伽马射线强度表示为有效探测区域Ω1,eff( r T)上所有发射源伽马强度的叠加，因此可以表示为如下三重积分
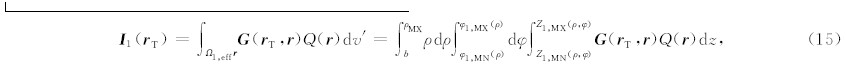
在测量位置zR处，居中屏蔽探测器上的总伽马通量
nT是晶体表面的单位外法向向量.
同样地，对于贴井壁屏蔽探测器晶体表面任意点 r T处的伽马射线强度可表示为如下有效探测区域Ω2,eff( r T)上的三重积分
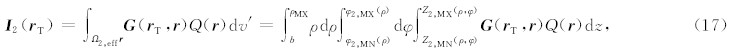
且该探测器上的总伽马通量为
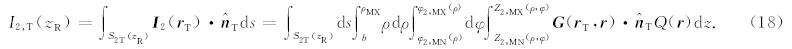
方程(16)和(18)的计算涉及到一个三重体积分和一个二重面积分，因此只能借助于数值积分方法.为提高计算效率并保证计算精度，将整个放射性地层在柱坐标下剖分(见图3)，且在纵向方向采用等间距离散剖分方式，在径向采用指数等间距离散，此外，对探测器晶体表面按均匀网格进行离散.对于晶体表面的每个离散节点，确定其有效探测区域以及有效探测区域对应的剖分网格，利用简单的积分和逼近三重体积分，然后对晶体表面的每个离散节点上计算结果求和，得到屏蔽探测器的伽马响应.
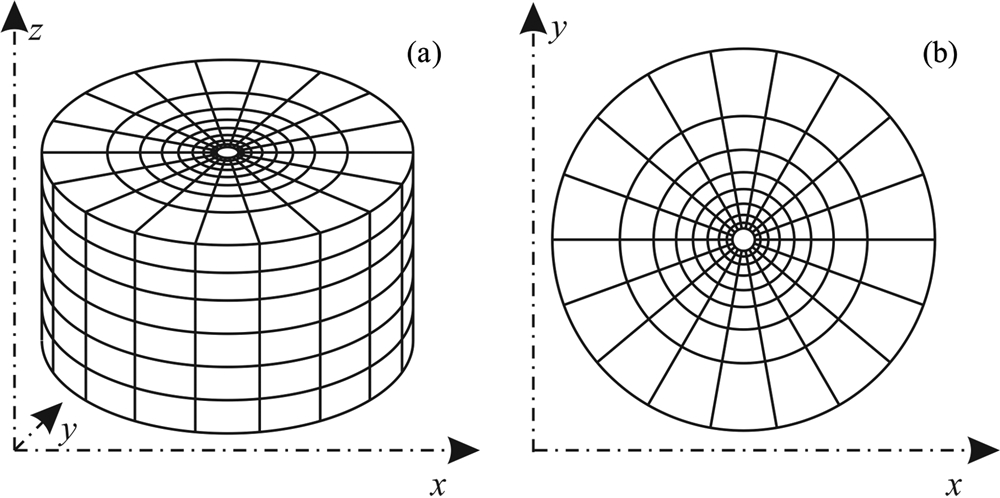 | 图3 三维离散模型 Fig.3 Discretization of 3D model |
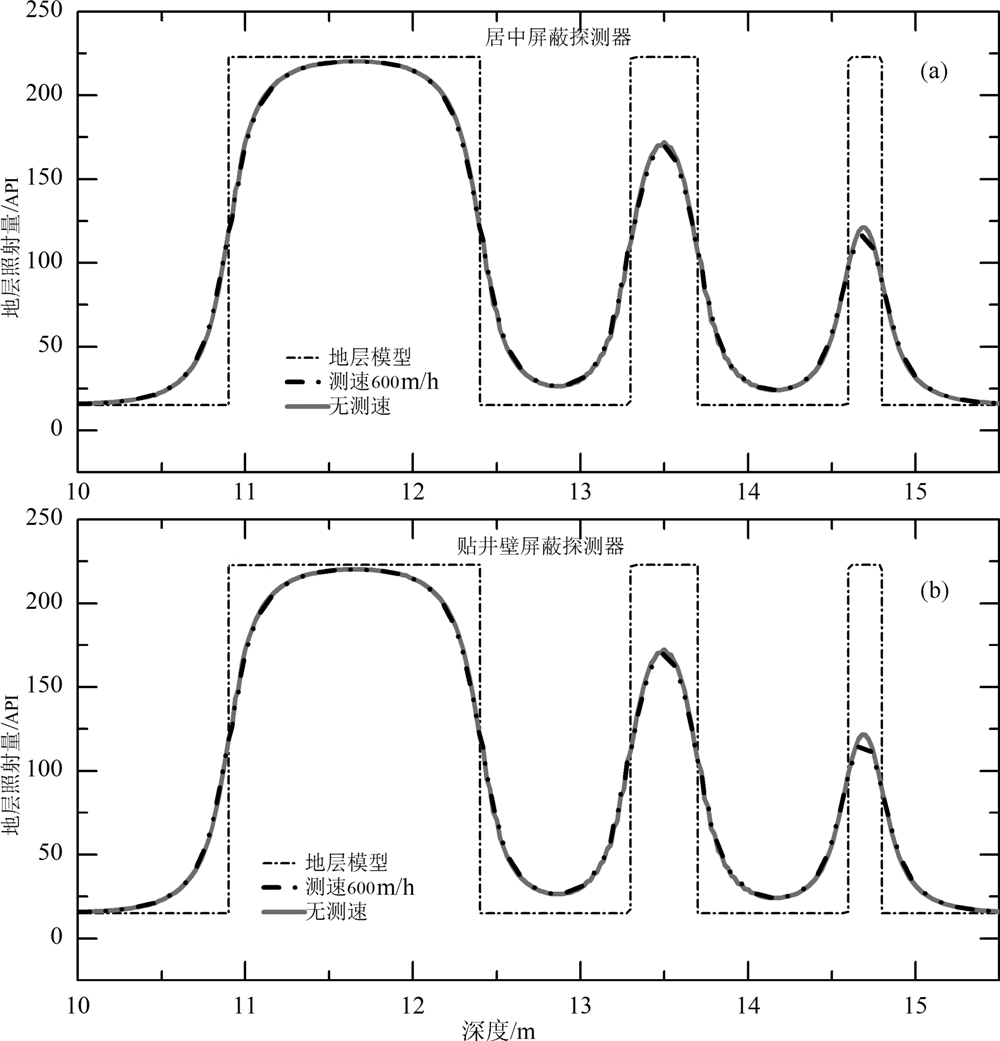
公式(16)和(18)给出的是仪器静止状态下的测井响应，然而在实际测量状态下，整个仪器在井中按一定的速度均匀移动并按照固定时间间隔进行连续采样，同时将相邻的几个采样记录进行平均以便提高测量精度，所以在仪器真实响应的数值模拟中需要考虑测速的影响.设测井速度为v、深度采样间距为Δ、时间采样间隔为τ，且假定用连续n个采样结果的平均值作为仪器的输出，这时深度点zR处的真 实测井记录是在zR附近n个连续采样结果的平均：
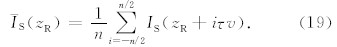
首先利用模型井上的实际测量结果与数值模拟结果的对比，检验前面模拟算法的有效性并确定相关参数.然后通过理论模型模拟结果对居中屏蔽和贴井壁屏蔽探测器的响应进行对比，考察晶体长度、形状变化对纵向分辨率的影响，最后给出新型高分辨率伽马测井仪器的井场实际测量结果与常规伽马测井、微电极等测井记录的对比.
为设计高分辨率自然伽马测井仪器并对仪器响应特征和相关数值模拟结果进行有效检验,大庆测井研究所专门建立了模型井,模型井由厚度分别为1.5 m、0.4 m和0.2 m，伽马强度均为223 API的三个高放层组成,且每个高放层被厚度为0.9 m、伽马强度为15 API的低放层隔开，构成一个7层水平 层状模型，模型井长度是5.2 m、井眼直径为0.203 m. 在数值模拟过程中假定地层吸收系数μ=0.07.图4是居中屏蔽探测器在该模型井中的实际测量结果与数值模拟结果的对比，其中，晶体半径和长度分别为 0.05 m和0.1 m，测速为60 m/h、采样间距0.02 m. 结果显示两者吻合得非常好，在高放层合成数据与实测结果间的相对误差为3.5 %.
 | 图4 居中屏蔽情况下的理论合成曲线与模型井实测曲线对比 Fig.4 Comparison of the synthetic response of the shielding GR tool with the measured results in the model well |
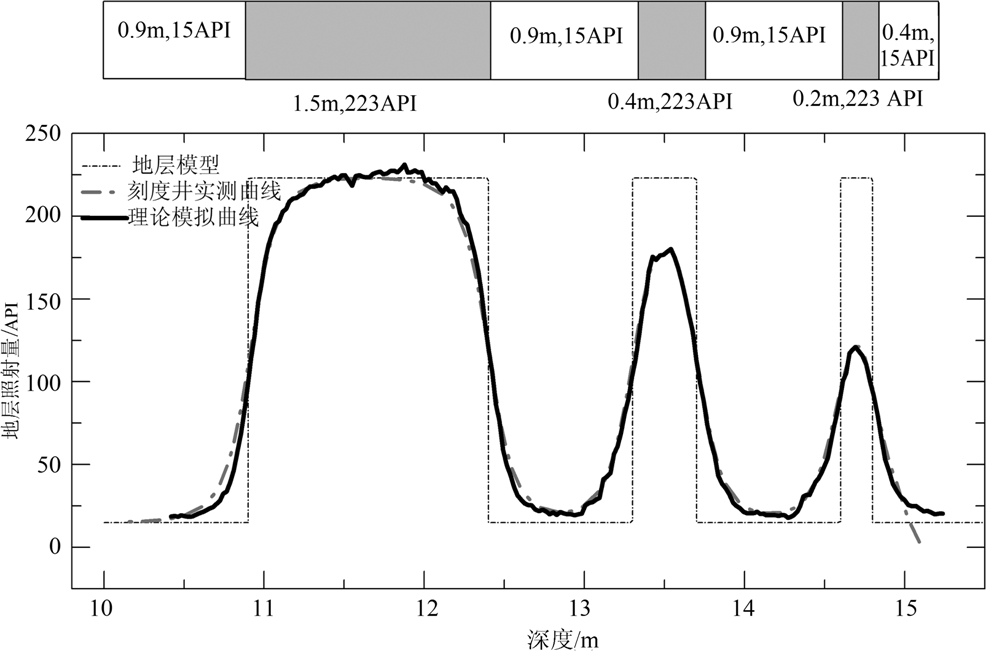
贴井壁屏蔽探测器中推靠臂的长度较长，在模型井中难以进行连续测量，因此没有获得模型井中贴井壁屏蔽探测器的实测数据，为了对两种不同测量方式的测量结果进行对比，我们对比了不同测速情况下居中屏蔽探测器和贴井壁屏蔽探测器在模拟井中的数值模拟结果(见图5)，结果显示，两种探测器对应的数值模拟结果相差很小，贴井壁屏蔽探测器在提高纵向分辨率方面并没有非常大的改进，但测速变化对薄层上的伽马响应影响较大，测速增加会导致薄层上的响应明显降低.所以在薄储层上必须严格控制测井速度,否则,分辨率再高的仪器也难 以获得理想的测量效果.
 | 图5 测速对屏蔽探测器响应的影响 Fig.5 The influence of logging velocity on the response of the GR tools |
为进一步考察新型仪器的探测深度，我们计算了居中无屏蔽、居中屏蔽以及贴井壁屏蔽三种探测器的径向微分几何因子和径向积分几何因子(图6).在计算几何因子过程中三种探测器中的晶体尺寸完全相同.三种探测器的径向探测特性几乎完全 一致，伽马响应的70%信号来自于距离探测器0.3 m以内的地层贡献.
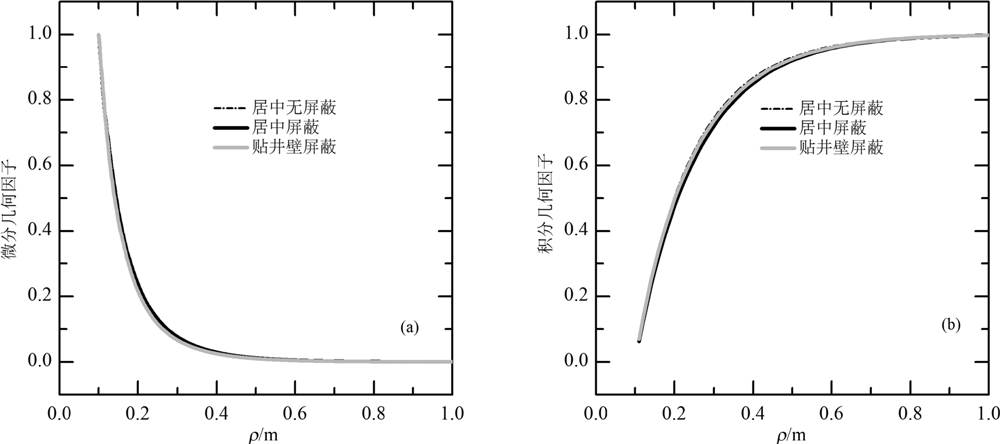 | 图6 不同类型探测器径向几何因子的对比 Fig.6 Comparison of radial geometric factors of different types of GR detectors |
从理论上说，探测器晶体长度越短其分辨率会越高，但晶体上接收到的计数率也相应降低，从而影响测量精度，因此，需要优化高分辨率自然伽马测井仪器中的相关参数.为选择合适的仪器参数，针对居中和贴井壁屏蔽两种不同测量方式，通过数值模拟方法系统考察晶体长度和半径大小、屏蔽铅板尺寸变化等对仪器纵向分辨率的影响，并根据探测器上伽马通量大小以及变化规律，设计出较为理想的仪器参数，保证在0.2 m高放射性薄层中，探测器的伽马通量不小于其放射性强度的十分之一.如果伽马通量太小，则计数率很低，导致统计涨落误差增大.为此，在假定晶体半径、屏蔽铅板大小不变的情况下，利用上述模型井参数分别计算出晶体长度0.3、0.1和0.05 m的探测器上的伽马射线通量(见图7)，结果显示晶体长度越小计数率越低.为进一步了解不同长度晶体上的伽马通量与地层放射性强度和地层层厚的关系，计算出每个地层的放射性强度与该层中间的伽马射线通量比值，图7c和7d分别是居中和贴井壁屏蔽的测量方式对应的不同晶体长度探测器的计算结果，从图可以看出，在0.4 m高放射性地层上，0.05 m晶体的放射性强度与伽马 射线通量的比值仍然大于10，说明0.05 m晶体作为探测器，其分辨率虽然较高但其计数率很低，必然影响测量质量.而0.1 m晶体的放射性强度与伽马射线通量的比值在0.2 m的高放射性地层上仍然小于10，且在0.2和0.4 m的高放性层上的比值相差不到一倍，说明0.1 m晶体的分辨率仍然较高，因此，我们选择0.1 m晶体作为高分辨率伽马仪器的探测器.当然与0.3 m晶体探测器相比其计数率仍然较低，为保证自然伽马仪器既具有较高的分辨率，同时又能够有较高的计数率，新型高分辨率自然伽马仪器采用四个长度为0.1 m晶体构建一个复合探测器，四个探测器同时测量并分别获得分辨率较高但计数率相对较低的四条伽马测井曲线，利用数据合成技术降低统计涨落误差影响进而获得高分辨率自然伽马测井曲线.
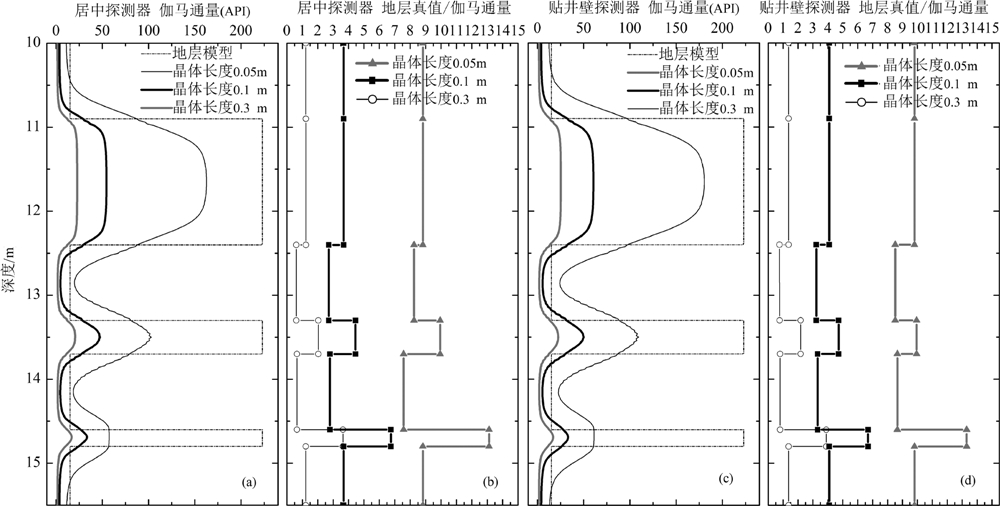 | 图7 不同晶体长度的自然伽马探测器响应特征的对比 Fig.7 The comparison of the responses of GR tools with different lengths of crystal |
自然伽马探测器可以选用圆柱形或方形晶体.为比较不同形状晶体的仪器响应，假定圆柱形和方形晶体的高度均为0.1 m，仪器居中且屏蔽铅板大小相同，圆柱晶体的直径为0.05 m而方形晶体截面的边长也为0.05 m，方形晶体比圆柱晶体的体积稍大一点.图8是两种不同形状晶体在同一模型上的数值模拟结果，结果显示两者的响应几乎相同.但圆柱形晶体比方形晶体体积小，更便于安装，因此，我们选用圆柱形晶体作为自然伽马仪器的探测器.
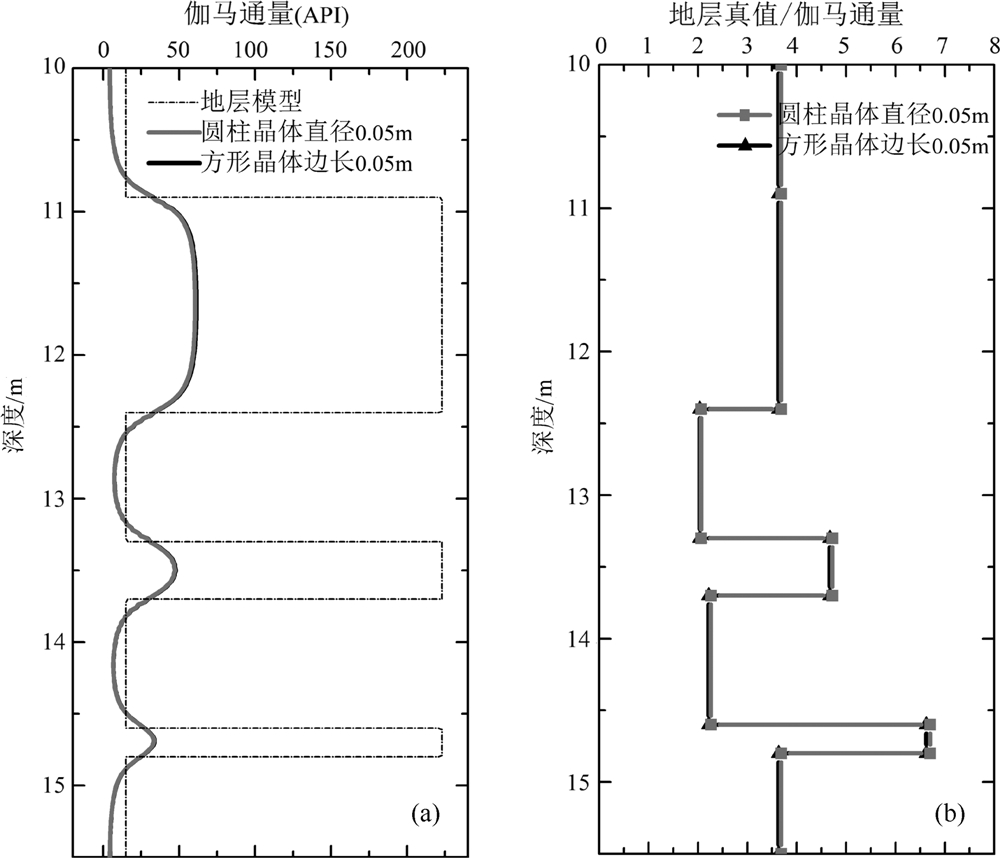 | 图8 不同晶体形状的自然伽马探测器响应特征的对比(晶体高度0.1 m) Fig.8 The comparison of the responses of GR tools with different geometrical shape of NaI crystal |
利用长度为0.1 m的NaI晶体研制出居中和贴井壁屏蔽的两台工业用实验样机，每台仪器的井下部分均由4个尺寸和结构完全相同并彼此分离的NaI探测器，同时测量出4条相同分辨率的自然伽 马测井曲线GR1、GR2、GR3和GR4.图9是大庆某 井上新的自然伽马仪器测量结果与其它测井记录的对比.其中左边的第一道为实测的两条高分辨率伽马曲线GR1和GR4，由于存在统计涨落误差，两条曲线间存在较大差异，因此，需要通过曲线合成技术从四条高分辨率伽马曲线计算其高分辨率合成曲线GRAV，图中的第3道是合成曲线GRAV和常规自然伽马曲线GR的对比，结果显示GRAV曲线的分辨率比常规自然伽马曲线GR的分辨率高得多.为了进一步检验GRAV曲线是否是地下地层的真实反映，在第二和第四道上分别给出了分辨率较高的微球型聚焦曲线MSFL和微电极(RMN和RMG)的测井曲线，从图可以清楚看出，GRAV曲线的分辨率与微球型聚焦曲线和微电极分辨率几乎相同， 且在A、B、C、D 四个取芯薄层上(厚度0.2 m左右)， 高分辨率自然伽马测井曲线GRAV均有明显显示.
本文基于单能窄束伽马射线算法与稳态扩散方程，研究建立了居中和贴井壁两种测量方式下屏蔽探测器响应的三维数值模拟技术，数值模拟结果与模型井上实验结果间的相对误差为3.5 %，证明了该算法的有效性.
在水平层状地层垂直井眼情况下的数值模拟证明，居中屏蔽探测器与贴井壁屏蔽探测器在纵向分辨率和探测深度方面基本相同，影响仪器纵向分辨率的最主要参数为晶体长度，虽然长度为0.05 m的NaI晶体探测器分辨率更高，但由于其接收到的伽马通量太低，导致起伏涨落误差变大，对测量精度会有不利影响.因此，选择长度为0.1 m的NaI晶体同时采用四个探测器的组合方式进行测量，并结合数据合成技术能够获得分辨率高且稳定的自然伽马测井曲线.
| [1] | Cavalier L, Raimondo M. 2007. Wavelet deconvolution with noisy eigenvalues. IEEE Transactions on Signal Processing, 55(6): 2414-2424. |
| [2] | Conaway J G, Killeen P G. 1978. Quantitative uranium determinations from gamma-ray logs by application of digital time series analysis. Geophysics, 43(6): 1536-1550. |
| [3] | Gadeken L L, Merchant G A, Jacobson L A, et al. 1990.The utility of combining Smoothing and deconvolution in Processing algorithm for Well Log Data. IEEE Nuclear Science, 810-816. |
| [4] | Gong D X, Yi H S, Wu C H, et al. 2011. High-frequency carbonate depositional cycles and its response to the gamma ray well logging data and sea-level change in Permian Nanpanjiang Basin. Progress in Geophysics, 26(1): 287-293. |
| [5] | Huang L J. 1985. Principles of Radioactive Well Logging (inChinese). Beijing: Publication Press of China University of Petroleum. |
| [6] | Huang L J. 2000. Principles of Nuclear Well Logging (in Chinese). Dongyin: Publication Press of China University of Petroleum. |
| [7] | Huang L J, Hu Q D. 1997. The then-bed response of natural Gamma-ray spectral log. Chinese J. Geophys. (in Chinese), 40(2): 272-279. |
| [8] | Kerr S A, Worthington P F. 1988.Nuclear logging techniques for hydrocarbon, mineral, and geological applications. IEEE Transactions on Nuclear Science, 35(1): 794-799. |
| [9] | Liu G Q, Liu J, Zhang M L, et al. 2002. A processing method of GR logs with high resolutions. WLT (in Chinese), 26(3): 194-197. |
| [10] | Manduci L, Tenailleau L, Trole J L. 2010. Self-attenuation correction factors for bioindicators measured by r-spectrometry for energies E<100 keV. Nuclear Instruments and Methods in Physics Research, A613: 90-94. |
| [11] | Scott J H, Dodd P H, Droullard R F, et al. 1987. Quantitative interpretation of Gamma-ray logs. Geophysics, 1961, 26(2): 182-191. |
| [12] | Sheng P, White B, Nair B, et al. Bayesian deconvolution of gamma-ray logs. Geophysics, 52(11): 1535-1546. |
| [13] | Tao H G, Shang Q L, Liu C W, et al. 2012. Optimizing design of new high resolution Gamma-ray logging device and data processing technique. Journal of Jilin University (Earth Science Edition) (in Chinese), 42(4): 906-913. |
| [14] | Tikhonov A H. 1979. Solution of Ill-Posed Problems (in Chinese). Wang B C, translation. Beijing: Geological Publish House, 34-112. |
| [15] | Tittman J, Wahl J S. 1965. The physical foundations of formation density logging (gamma-gamma). Geophysics, 30(2): 284-294. |
| [16] | Tzortzis M, Tsertos H, Christofides S, et al. 2003. Gamma-ray measurements of naturally occurring radioactive samples from cyprus characteristic geological rocks. Radiation Measurements, 37(3): 221-229. |
| [17] | Vlastou R, Ntziou I T, Kokkoris M, et al. 2006. Monte Carlo simulation of r-ray spectra from natural radionuclides recorded by a NaI detector in the marine environment. Applied Radiation and Isotopes, 64(1): 116-123. |
| [18] | Wahl J S. 1983. Gamma-ray logging. Geophysics, 48(11): 1536-1550. |
| [19] | Wang B, Fan X M. 2006. Application of numerical simulation in the rocks influence the Gamma-ray logging. Journal of Jilin University (Earth Science Edition) (in Chinese), 36(Sup): 166-168. |
| [20] | Wang H N, Li Z B, Chang M C. 1996. The integrated processing system to enhance vertical resolution of geophysical well logs and its application. WLT (in Chinese), 20(6): 441-448. |
| [21] | Wang H N, Li Z B, Chang M C, et al. 1997. Regularized algorithm for enhancement of vertical resolution of natural Gamma-ray log. Chinese J. Geophys. (in Chinese), 40(6): 847-856. |
| [22] | Wu W S, Xiao L Z. 2007. Monte Carlo simulation in developing nuclear logging instruments. Nuclear Electronics & Detection Technology (in Chinese), 27(5): 974-977. |
| [23] | Xie Z S, Zhang S H. 2000. Physical Theory of Nuclear Reactor and Numerical Method (in Chinese). Xian: Publication Press of Xian Jiaotong University. |
| [24] | Zhou J H, Yuan R. 2012. Automatic test method for abnormal data of formation resistivity logging through casing. Progress in Geophysics, 27(3): 1189-1194. |
| [25] | 龚大兴, 伊海生, 吴驰华等. 2011. 南盘江盆地二叠系高频沉积旋回的测井响应及海平面变化趋势. 地球物理学进展, 26(1): 287-293. |
| [26] | 黄隆基. 1985. 放射性测井原理. 北京: 石油工业出版社. |
| [27] | 黄隆基. 2000. 核测井原理. 东营: 石油大学出版社. |
| [28] | 黄隆基, 胡庆东. 1997. 自然伽马能谱测井薄层响应. 地球物理学报, 40(2): 272-279. |
| [29] | 刘国庆, 刘江, 张美玲等. 2002. 自然伽马测井曲线高分辨率处理方法. 测井技术, 26(3): 194-197. |
| [30] | 陶宏根, 商庆龙, 刘长伟等. 2012. 新型高分辨率自然伽马测井仪器的优化设计与资料处理技术. 吉林大学学报, 42(4): 906-913. |
| [31] | Tikhonov A H著, 王秉忱译. 1979. 不适定问题的解法. 北京: 地质出版社, 34-112. |
| [32] | 王斌, 范晓敏. 2006. 围岩对自然伽马测井影响的数值模拟. 吉林大学学报(地球科学版), 36(Sup): 166-168. |
| [33] | 汪宏年, 李舟波, 常明澈. 1996. 地球物理测井综合高分辨率处理系统及其应用. 测井技术, 20(6): 441-448. |
| [34] | 汪宏年, 李舟波, 常明澈等. 1997. 提高自然伽马测井曲线分辨率的正则化方法. 地球物理学报, 40(6): 847-856. |
| [35] | 吴文圣, 肖立志. 2007. 核辐射测井中的Monte Carlo数值模拟. 核电子学与探测技术, 27(5): 974-977. |
| [36] | 谢仲生, 张少泓. 2000. 核反应堆物理理论与计算方法. 西安: 西安交通大学出版社. |
| [37] | 周继宏, 袁瑞.2012.过套管电阻率测井异常测量值的自动检验方法. 地球物理学进展, 27(3): 1189-1194. |