2. 中国科学院地质与地球物理研究所, 北京 100029
2. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
电阻率测深法是资源环境和水文工程勘查的常用方法,用于探测地下地层结构.电阻率测深的正演模拟和反演解释技术一直是国内外研究者关注的对象.近年来,地下电性成像技术得到获得快速发展,科研工作者研制出了多种二维反演软件,中国地质大学(罗延钟,2006)、廊坊物化探研究所(王华军等,2000)、Loke工作组(Loke等,1995)等开发的反演软件获得广泛应用.这些软件可以完成对异常体的定性和定位,能反映出地层构造的特征.但绝大多数二维反演的结果,无法自动完成对地层结构的解释.反演图像是电阻率连续变化的等值线图,是地下介质的电性成像,没有明确的地层结构信息,需要数据处理人员根据经验结合地质信息解释地层结构和各地质单元的电性.例如探测断裂构造时,反演结果主要包括断裂的位置、宽度、倾向和埋深,断裂两侧的地层参数等.实际上这些最终信息都是由数据处理人员推测得到的.
为了降低对数据处理人员经验的依赖,通过反演直接获取地层结构关键参数,有必要尝试与传统方法差异较大的非线性反演.
电阻率测深数据二维反演问题中,初始模型的设置是主要困难之一.设计简单的模型,在拟合过程中容易向最先出现的区域最优解靠近;设置复杂的模型常带有主观性,而且无法程序化.国内外的研究者们进行了大量的尝试,提出了设置层状模型或块状模型的思路.(阮百尧等,1999;苏朱刘等,2005;徐凯军等,2006;Auken et al.,2004;黄俊革等,2005;底青云等,2003)
本文作者提出了一种基于统计学和遗传算法的电阻率测深二维反演算法(程勃和底青云,2012a,b),先用统计学判断地层结构并建立初始模型,再用遗传算法修改模型参数.该方法的特点在于建立初始模型时充分利用了实测电阻率测深数据所包含的地层结构信息,反演结果中有明确的地层结构以及每个地质单元的电阻率.
研究证明:对于相对简单的理论模型和野外实测数据,该方法获得了较理想的反演解释结果.但要使该方法适用于复杂地层结构,建模部分还需要进一步完善:
(1)设计逐级统计判断模型结构的机制,并将水平梯度、电测深曲线类型等信息,也纳入到统计内容中.在初次判断地层结构类型之后,设计第二级的分段统计判断方法,使统计学特征值和异常体空间位置联系起来;
(2)增加了水平梯度信息统计的权重分配、对地层分区后局部范围内的统计学特征值、测深曲线类型再次统计,给出局部地层的详细层参数;
(3)增加加入先验信息模块,利用岩石的电性信息、钻孔资料等地质信息参与建立初始模型,使初始模型更加接近实际地层结构.
应用逐次统计判断法建立的初始模型,较充分地利用了原始数据中所包含的地电结构信息,与实际地层结构联系紧密,减少了修改层参数方面的计算量.本文以含断裂的层状模型为例,研究统计学建模反演的效果.
复杂地层结构条件下,统计学方法建模主要步骤分为:初次统计判断地层结构;二次统计确定空间位置和地层分区范围;加入先验性信息;建立初始模型.统计学建模主要流程如图1所示.
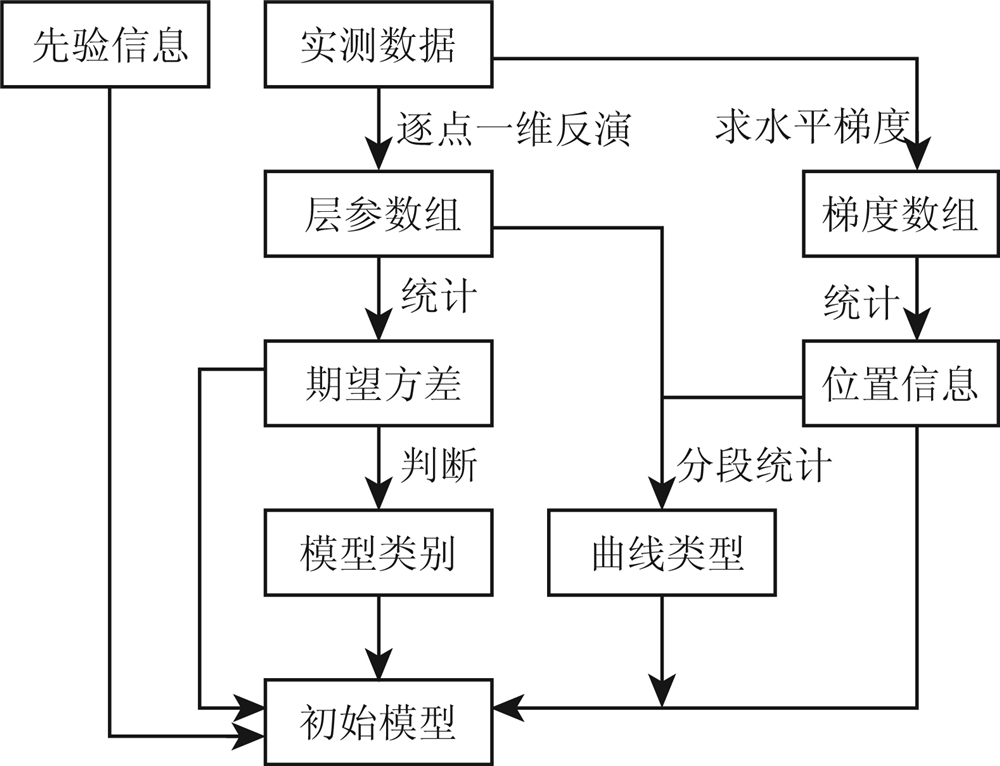 | 图1 统计学建模流程图 Fig.1 The process of statistic modeling |
在初次统计建模之后,如果地层结构被判断为含横向变化(如存在断裂)时,需要确认异常体的位置、宽度及异常体(断裂)两侧的地层结构和层参数.为此,统计电阻率测深数据各极距视电阻率的水平方向梯度.水平梯度的极值位置信息可以辅助完成初始模型结构类别判断,并获得断裂或岩性接触面的初始位置.数值模拟结果和实测资料证明,浅部的局部异常体,同样会造成水平梯度出现极值,可能造成对主要异常体位置判断失误.因此在水平梯度统计过程中对深部信息赋予较大的统计权重.
以低阻断裂为例,断裂左边界确定函数为
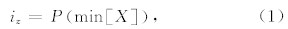
断裂右边界确定函数为
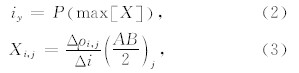
其中, Δρi,j Δi 为视电阻率在水平方向上的变化率, AB 2 j为权重因子,i为测点号,j为极距号.P(x)的作用是求x在测线上的位置.
通过对含有直立异常体模型的尝试性反演发现,初次统计的层参数数学期望不适合作为初始模型层参数初值,特别是直立异常体两侧结构差异较大的情况.
为了建立较接近真实的初始模型,在统计部分增加了对直立异常体两侧测点的一维反演层参数统计,分别统计两侧的测深曲线类型、同类型曲线的数量及所占总曲线数量 的份额.由此,以占较大份额的曲线类型作为断裂某一侧的初始地层电性结构.分别求出两侧层参数的数学期望,作为初始层参数.
测区的先验性信息,包括地质构造、地层岩性及地球物理信息,是地球物理勘探资料解释中必须参考的信息.了解地质资料并参考专业地质人员的意见,是获得先验性信息的主要途径.例如,测区的基本地层结构;各层的岩性(电性)特征;断裂的走向、倾向、破碎程度和含水性;测区内的钻孔资料等,都是重要的先验性信息.结合先验信息判断地层结构,能降低局部和浅部异常体对整体地层结构判断的干扰.
按照2.1—2.3节的步骤设计了反演初始模型后,利用所获得的先验性信息修正模型.本文在之前的研究基础上,增加了加入先验信息模块.例如根据地质资料限制地层结构的变化范围;在断裂倾角已知的条件下在初始模型中设置断裂的倾角;根据断裂的破碎或含水情况,参考地下水的电阻率设置断裂的初始电阻率;根据钻孔资料设置具体测点的地层深度;根据某种特定基岩的电阻率设置基岩电阻率等.
这些信息的加入,使初始模型更接近实际的地电结构.在反演过程中,有先验信息的参数不参与遗传变异,子模型数量减少,对提高反演速度也有一定的作用.
为证明复杂地层结构条件下统计学建模方法的可行性,以理论模型为例进行试算.
图2是一个层状大地中存在倾斜断裂的模型示意图.覆盖层厚4.5~7.5 m,电阻率300 Ωm,在断裂左侧凹陷,在断裂右侧凸起;覆盖层下的断裂,电阻率10 Ωm,位于测线的130 m到150 m之间,向 小号点方向倾斜,倾角45°;第二层厚度为左侧2.5 m, 右侧4 m,起伏与覆盖层相似,电阻率100 Ωm;第三层电阻率1000 Ωm.设计测线长度300 m,电阻率测深点共计31个,点距10 m.
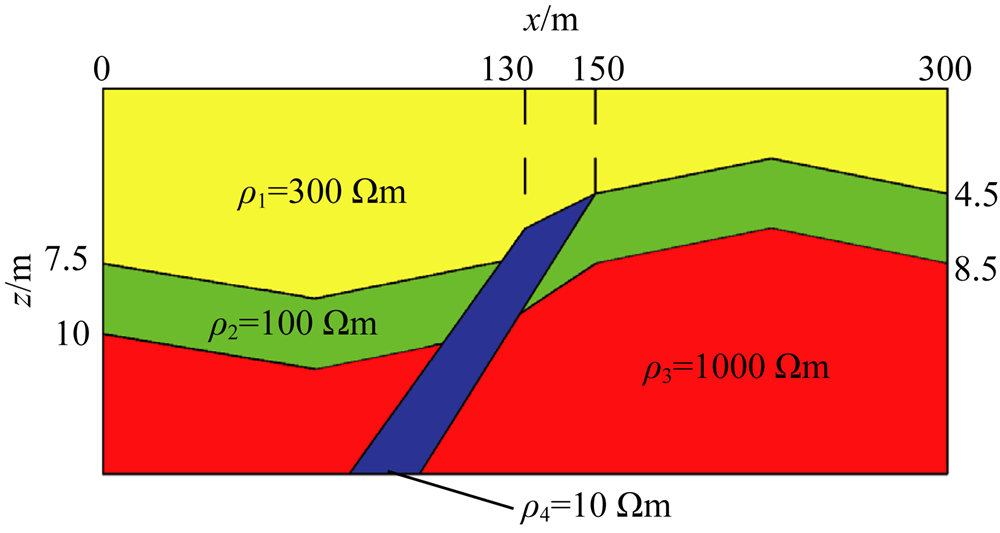 | 图2 有断裂存在的模型示意图 Fig.2 The sketch map of a model with fault |
图3是图2模型的对称四极测深装置有限元数值模拟结果,图中等值线标注的数值为视电阻率.本文中视电阻率断面图的标注和单位均与此图相同.可以看出在测线150 m附近有显著的低阻异常,异常左侧等值线稀疏,右侧等值线密集.仅根据图3不能直观分辨出地层结构.
对各测深点数据进行的单点一维反演,层数设定为3.表1是31个测点的一维反演统计结果,可以发现第一层层参数的方差比较小,后两层电阻率方差比较大,根据判断规则,判断地层中存在断裂结构类型.
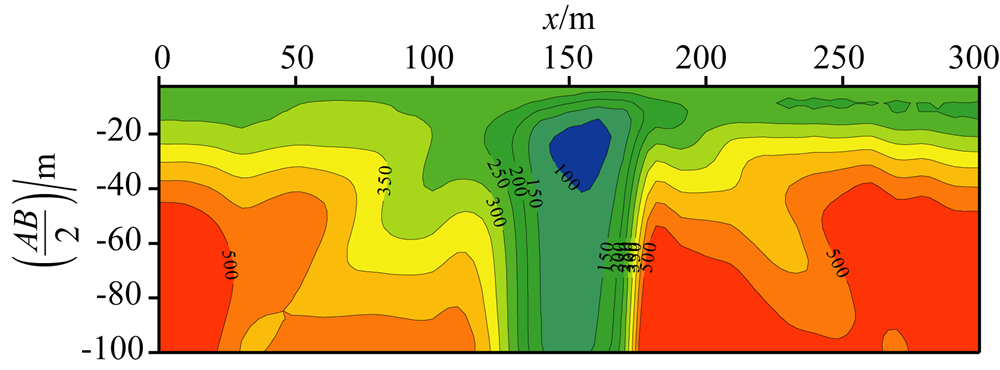 | 图3 断裂模型模拟结果(单位:Ωm) Fig.3 The stimulation result of a model with fault |
|
|
表1 一维反演参数统计结果 Table 1 The layer parameters′ statistic result |
计算并统计各极距视电阻率的水平方向梯度,部分极距的计算结果如图4所示.在图中水平位置120~130 m处出现水平梯度极小值,在170 m处出现了水平梯度的极大值,梯度极小值位置随极距增大向小号点方向移动,而各极距的极大值位置不变.参考理论模型正演研究结果,可以判断低阻断裂存在.根据以上的分析判断,并利用公式(1)、(2)统计判断低阻断裂的左边界和右边界.初步确定断裂范围为测线的130 m到170 m部分.
为了判断断裂两侧的地层结构,统计断裂两侧 测点的测深曲线类型.并分别统计两侧的第二层厚度和第二、第三层电阻率作为初始模型的初值.表2为断裂两侧测深曲线类型及参数统计结果.两侧的地层结构均以H型为主.由于断裂的存在,靠近断裂的测深点测深曲线形态发生变化,部分测点的一维反演层参数出现了畸变,影响到统计出来的数学期望值大小关系.例如表3中断裂右侧层电阻率期望 2大于 3,而曲线类别统计结果显示断裂右侧测深曲线主要为H型.在层参数统计结果与曲线类型统计结果矛盾的情况下,地层结构判断以曲线类别统计结果为准.
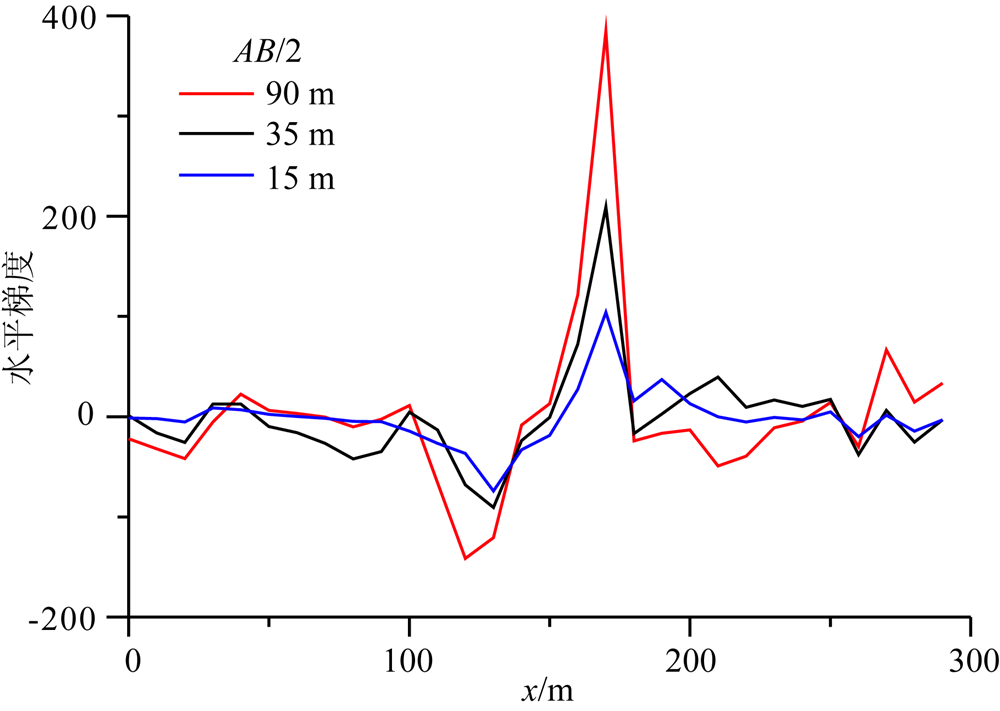 | 图4 部分极距的视电阻率水平梯度 Fig.4 The gradient of apparent resistivity |
由表2可知,断裂左、右侧测深曲线均以H型 为主.因此,断裂两侧的地层结构被判定为H型,再 分别统计两侧的H型测点的层参数,如表3所示.采用重新统计得到的厚度和电阻率期望值构建初始模型.
|
|
表2 断裂两侧测深曲线类型及一维反演层参数数学期望 Table 2 The curve type and layer parameters′ expect for each side |
图5为综合以上统计判断结果建立的初始模型.断裂部分电阻率初值根据水平梯度及两侧电阻率初值推算.
以初始模型为基础,生成基因(参数)变异的子模型,每个子模型有且只有一个基因发生变异.电阻率基因每次变异当前值的10%,位置参数每次变异一个网格,断裂的倾向有45°、65°、90°、105°、135°等5个档位,每次变异为相邻的一个.用有限单元法对所有子模型进行正演,统计每个子模型与图3数据的拟合误差,选择拟合误差最小的子模型存活并开始下一轮繁殖.
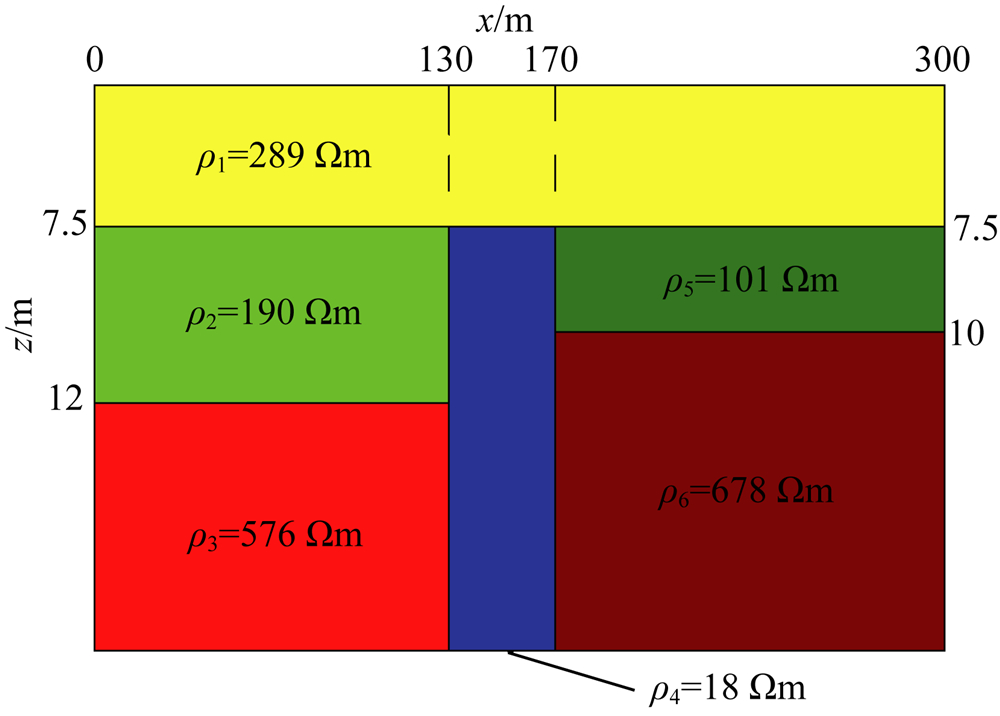 | 图5 初始模型示意图 Fig.5 The sketch map of initial model |
在反演过程中,还需要计算整体误差和局部误差,以选择优先调整的参数.当拟合误差无法降低时各部分电阻率停止变化,对各点层厚度进行调整.为 了防止相邻点厚度剧烈变化,相邻点厚度变化幅度被控制在一个网格以内.
|
|
表3 断裂两侧H型测点层参数数学期望 Table 3 The layer parameters of H type curve expect for each side |
反演结果如图6a所示,拟合误差低于5%.在反演结果中,地层结构、断裂的倾向都与目标模型(图2)相符合,各部分的电阻率也基本相符.图6b为RES2DINV软件反演的结果,其中断裂存在,断裂位置信息较容易判断,断裂的倾向不明确,两侧的地层结构没有具体的层参数.
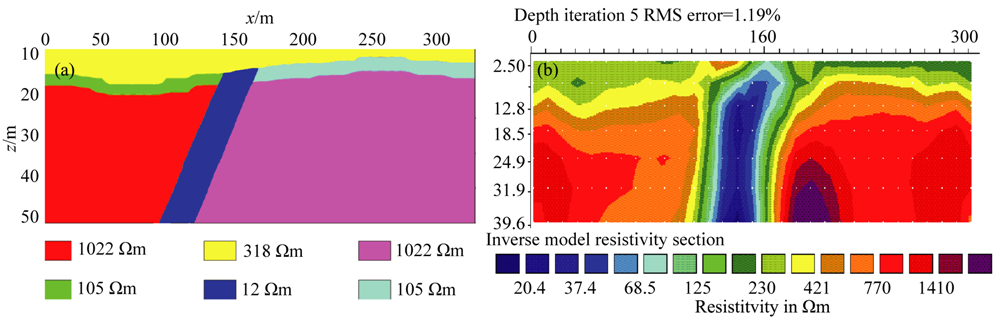 | 图6 反演结果 (a) 统计学建模反演; (b)线性反演(使用RES2DINV软件) Fig.6 The inversion result |
百色—合浦断裂是广西境内主要断裂之一,有记载以来,共发生过大于4.7级地震7次,在城市规划及地震安全性评价工作中,确定隐伏的百色—合浦断裂的位置、产状和地层结构是地质勘察工作的重要任务.为研究该断裂在合浦某规划区覆盖层下的位置,采用高密度电阻率法进行探测.
工作区地形平坦,覆盖层为第四系河漫滩及I级阶地;根据地质资料,断裂可能在测区内穿过.区域性地质研究结果表明:断裂走向北西约310°~320°,倾向南西,倾角约65°.断裂一侧的基岩为志留系中统文头山群的粉砂岩夹页岩、细砂岩;另一侧的基岩为志留系下统连滩群的片岩、细砂岩、粉砂岩与页岩互层.参考地质情况,在测区内垂直断裂走向布置高密度电法测线,总长度为1500 m.测量采用A-MN和MN-B两种三极装置,这些数据可以换算为对称四极测深的数据.
图7a是实测资料(测线305~605 m范围)中,存在明显低阻异常的视电阻率断面图.可以看出在测线380 m和470 m附近,存在两处较明显的低阻异常,但无法确定哪一个是断裂引起的异常.图7b为RES2DINV软件反演的结果,图中的电性分布显示出测区在探测深度范围内的地层结构,主要是三层K型.但该反演结果没有明确地指示出断裂存在的位置及地层的层参数.
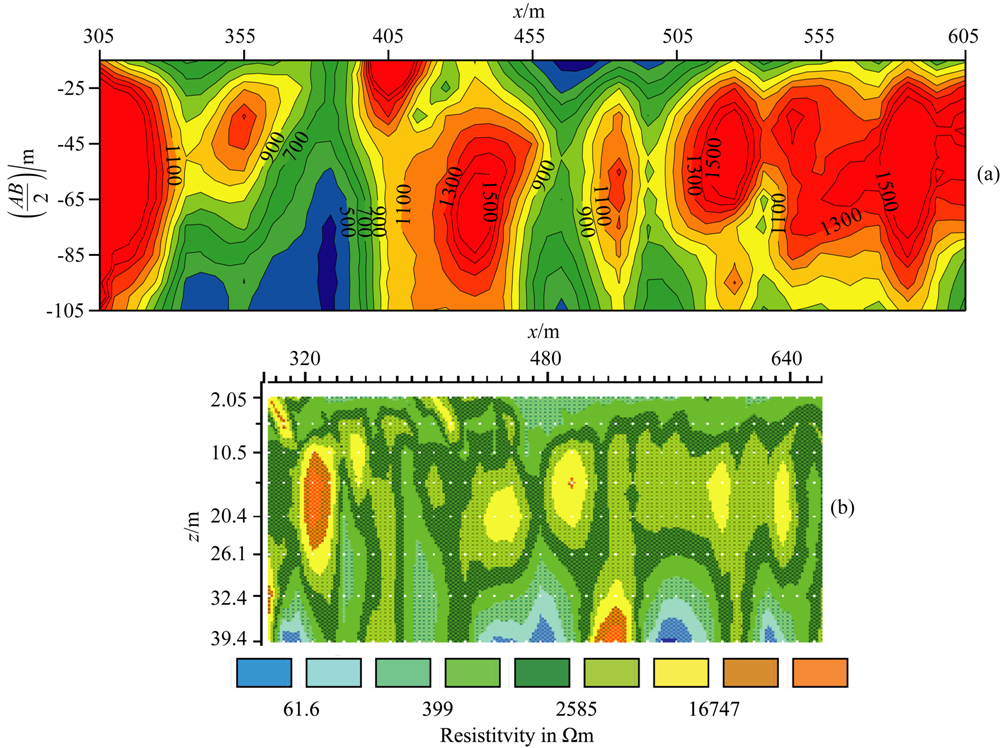 | 图7 实测数据及线性反演结果 (a) 实测数据断面等值线图; (b) RES2DINV软件反演结果 Fig.7 The field data profile and linear inversion result |
根据对实测数据的分析,设在探测深度范围内大地为3层结构.表4是31个测点一维反演获得的层参数的期望和方差,根据判断规则,统计结果符合有横向电性变化的多种模型,结合地质资料进一步判断,确定为有覆盖层的含断裂的层状结构.
|
|
表4 一维反演层参数的统计结果 Table 4 The layer parameters′ statistic result |
为了获得断裂的位置,计算并统计了各极距视电阻率的水平方向梯度,并统计获得极值,增加深部信息的权重,利用(1)和(2)式确定断裂的左右边界.
经计算在测线450 m处出现了水平梯度的极小值,且为负值,在水平位置460 m处出现水平梯度极大值,且为正值,该结果与算例中图4极为相似,符合断裂存在的视电阻率分布特征.因此采用450 m和460 m为断裂的初始边界,根据先验信息,初始模型中的断裂倾角为65°.根据地质资料,断裂含水,由此设置断裂电阻率初值为100 Ωm.
为了确定断裂两侧的地层结构,统计断裂两侧测点的测深曲线类型,并统计两侧测点的第二层厚度和第二、第三层电阻率的数学期望,统计结果如表5所示.断裂两侧的曲线类型大部分为K型,由此确定断裂两侧地层结构均为K型.
|
|
表5 断裂两侧测深曲线类型及一维反演层参数数学期望 Table 5 The curve type and layer parameters′ expect for each side |
根据统计判断的地层结构类型、水平梯度及二 次的统计结果及先验信息设置的初始模型如图8所示.
对图8中初始模型的8个层参数、2个断裂位置,生成基因(参数)变异的子模型,遗传算法反演流程与第3节中理论算例相同.在反演过程中,有先验信息支持的断裂倾角不参与变异.
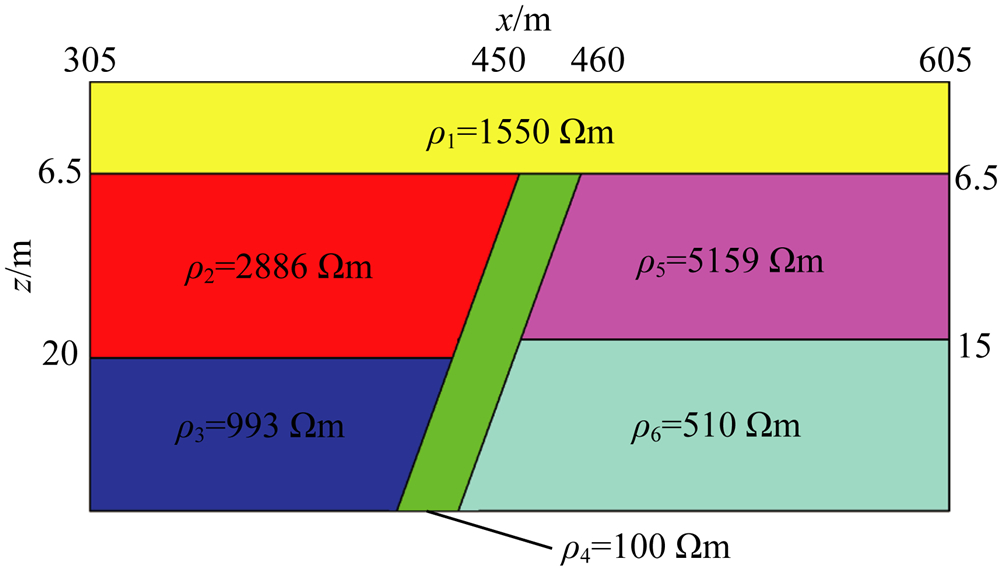 | 图8 初始模型示意图 Fig.8 The sketch map of the initial model |
反演结果如图9所示.反演结果表明:断裂顶端位于测线的455~470 m范围内,埋深为7.5 m.断裂两侧地层结构接近,都是中间层为高阻,底层为低阻.断裂两侧,中间层电阻率差异不大,而底层差异较大.断裂的电阻率与覆盖层接近.反演结果反映出断裂两侧覆盖层下地层结构的电性差异.
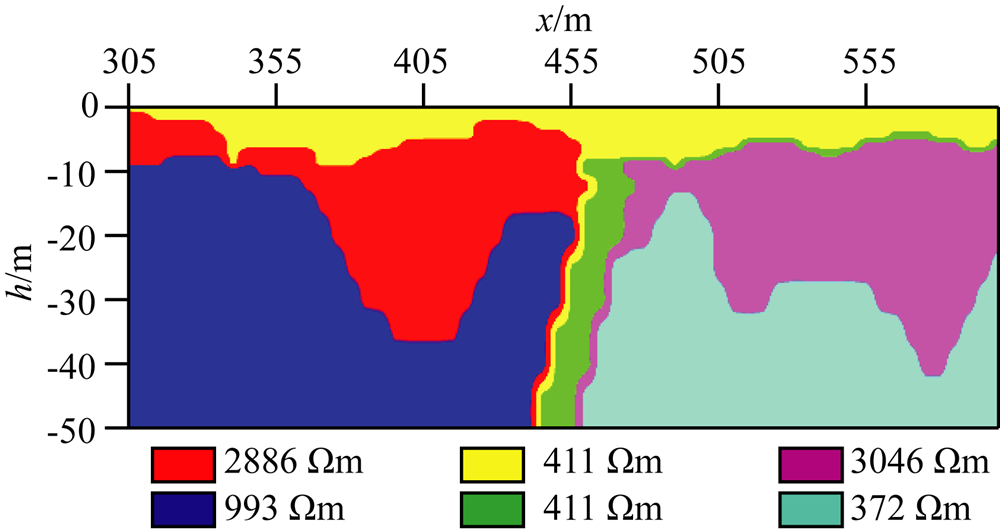 | 图9 实测数据反演结果 Fig.9 The inversion result of field data |
图10是以图9反演结果为模型的有限元正演数据断面,与实测数据(图7a)的拟合误差为22%.虽然拟合误差较高,但在反演结果给出了工作任务 所需要的关键信息.经钻探验证,断裂位置是准确的.
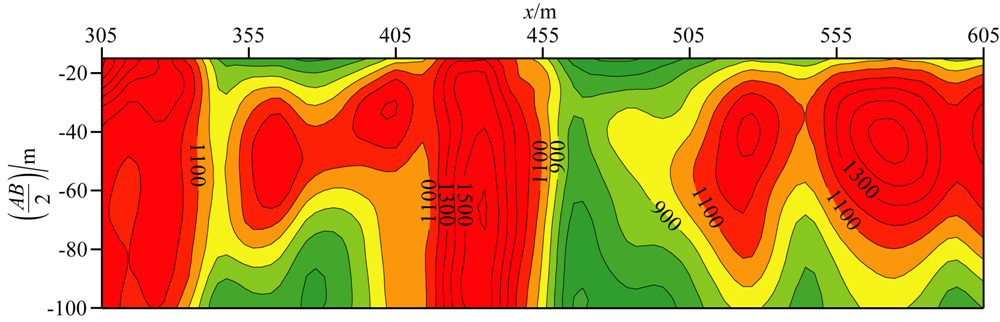 | 图10 反演结果正演视电阻率断面 Fig.10 The stimulation result of the final model |
通过理论算例和实测数据处理结果可以看出,统计学有效完成了对地质结构的判断;水平梯度的计算和统计完成了对断裂的定性和定位;测深曲线类型统计为建立更接近实际的初始模型提供了依据;先验信息参与到初始模型的建立和反演过程中.应用统计学、水平梯度计算和先验信息融合的方法尽可能利用了视电阻率实测数据和地质信息,建立了最大限度接近真实的初始模型,提高了反演的速度和质量.
初始模型建立后,使用遗传算法配合有限元正演模拟调整模型参数,完成了非线性反演.在反演结果中,断裂有明确的位置、埋深、倾向及电性,断裂两侧有明确的地层结构、层电阻率和层厚度.这样的反 演结果,更有利于人们认识和利用电阻率测深的成果.
由于影响岩土层电性变化因素很多,自然界中地下电性结构的非常复杂.本研究探索复杂地层结构条件下,利用统计学方法建模的可行性,对于更加复杂的地层结构以及含有各种干扰因素的野外实测数据,统计学建模法还需要进一步完善.
致谢 衷心感谢赵国泽、王妙月、石昆法、杨生、汤吉老师对本文提出的建议!| [1] | Auken E, Christiansen A V. 2004. Layered and laterally constrained 2D inversion of resistivity data. Geophysics, 69(3): 752-761. |
| [2] | Cheng B. 2012. 2D inversion of resistivity sounding base on GA and statistic [Ph. D's thesis]. Beijing: Institute of Geology and Geophysics, Chinese Academy of Science. |
| [3] | Cheng B, Di Q Y. 2012a. 2D inversion of resistivity sounding base on GA and statistic. Progress in Geophysics (in Chinese), 27(2): 788-795. |
| [4] | Cheng B, Di Q Y. 2012b. 2D inversion of resistivity sounding base on partial derivative and statistic. Oil Geophysical Prospecting (in Chinese), 47(6): 1006-1013. |
| [5] | Di Q Y, Ni D L, Wang R, et al. 2003. High-density resistivity image. Progress in Geophysics (in Chinese), 18(2): 323-326. |
| [6] | Huang J G, Bao G S, Ruan B Y. 2005. A study on anomalous bodies of DC resistivity sounding in tunnel. Chinese J. Geophys. (in Chinese), 48(1): 222-228. |
| [7] | Loke M H, Barker R D. 1995. Least-squares deconvolution of apparent resistivity pseudosections. Geophysics, 60(6): 1682-1690. |
| [8] | Luo Y Z. 2006. 2.5-D inversion software for high density resistivity. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 28(3): 188-193. |
| [9] | Ruan B Y, Murikami Y, Xu S Z. 1999. 2D inversion programs of induced polarization data. Computing Techniques for Geophysical[KG2*2]and Geochemical Exploration (in Chinese), 21(2): 116-125. |
| [10] | Su Z L, Hu W B, Yan L J. 2005. The forward modified inversion of resistivity and induced polarization sounding. Geophysical Prospecting for Petroleum (in Chinese), 44(2): 194-198. |
| [11] | Wang H J, Luo Y Z. 2000. Windows version software system designing of 2D man-machine interactive inversion for conventional DC electric method. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 22(4): 356-360. |
| [12] | 程勃, 底青云. 2012a. 基于偏导数和统计学方法的电阻率测深二维反演. 石油地球物理勘探, 47(6): 1006-1013. |
| [13] | 程勃, 底青云. 2012b. 基于遗传算法和统计学的电阻率测深二维反演研究. 地球物理学进展, 27(2): 788-795. |
| [14] | 底青云, 倪大来, 王若等. 2003. 高密度电阻率成像. 地球物理学进展, 18(2): 323-326. |
| [15] | 黄俊革, 鲍光淑, 阮百尧. 2005. 坑道直流电阻率测深异常研究. 地球物理学报, 48(1): 222-228. |
| [16] | 罗延钟. 2006. 高密度电阻率法的2.5维反演软件. 物探化探计算技术, 28(3): 188-193. |
| [17] | 阮百尧, 村上裕, 徐世浙. 1999. 电阻率/激发极化率数据的二维反演程序. 物探化探计算技术, 21(2): 116-125. |
| [18] | 苏朱刘, 胡文宝, 严良俊. 2005. 电阻率和极化率测深法的正演修正法反演. 石油物探, 44(2): 194-198. |
| [19] | 王华军, 罗延钟. 2000. 常规直流电法二维人机联作反演软件系统WINDOWS版的设计与实现. 物探化探计算技术, 22(4): 356-360. |
 2014, Vol. 57
2014, Vol. 57

