2. 中国科学院大学, 北京 100049
2. Graduate University, Chinese Academy of Sciences, Beijing 100049, China
探地雷达是一种利用高频脉冲电磁波来探测介质内部物质分布规律的地球物理方法(陈义群和肖柏勋, 2005;李嘉等,2007;李华等,2010;Slob et al.,2010). 因为探地雷达的探测原理和方法与地震勘探相似,所以我们可以利用地震数据处理方法来处理探地雷达数据.但是,与地震勘探不同的是,雷达子波在地下介质的传播过程中,它的衰减和频散比地震子波要严重,特别是它的高频成分(底青云等,2000).衰减和频散会使雷达子波的能量减弱,主频降低,时域波形变宽,进而会减小探地雷达的勘探深度和勘探分辨率(Turner,1994;Oden et al.,2007;Economou and Vafidis,2010).同时,雷达子波的这种强衰减和频散特性会限制一些地震数据处理方法在探地雷达数据处理中的应用,如偏移、反褶积等(Irving and Knight,2003).因此,在探地雷达数据处理中,消除探地雷达数据的子波衰减和频散具有重要意义.
地震勘探中,消除地震子波的衰减和频散的常用方法是反Q滤波(赵建勋,1986;余振等,2009;姚振兴等,2003;Wang,2006).该方法需要正确求取地下介质的Q参数大小.实际地震数据处理中,求取Q参数时,一般假定Q与地震子波的频率无关,地震子波的衰减与频率成线性关系(Tonn,1989,1991).但是,在探地雷达数据处理中,这一条件不能得到很好地满足.其次,雷达子波在地下介质的传播过程中,其衰减和频散比较严重,时域波形变化快, 这也增加了求取Q参数的难度(Turner and Siggins,1994). 实际探地雷达数据处理中,正确求取地下介质的Q参数很困难,导致反Q滤波方法不能很好地消除雷达子波的衰减和频散.
雷达子波在地下介质的传播过程中,可以将地下介质视为一个等效滤波器,且该等效滤波器为最小相 位滤波器(Futterman,1962;Aki and Richards,1980). 雷达子波的衰减和频散可以视为等效滤波器的滤波作用结果.本文在假设地下介质反射系数是随机的前提下,利用等效滤波器具有最小相位这个特性,通过求取等效滤波器的振幅谱来求取等效滤波器的反滤波器.最后利用该反滤波器对探地雷达数据进行反滤波,消除地下介质对雷达子波的滤波影响,从而实现消除探地雷达数据的子波衰减和频散. 理论模型计算和实测探地雷达数据处理都能验证该方法能很好地消除探地雷达数据的子波衰减和频散.
探地雷达数据中,单道雷达记录x(t)可以表示为:
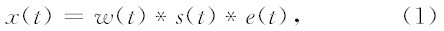
(1)式中,w(t)为雷达子波,s(t)为探地雷达记录系统响应时间函数,e(t)为地下介质响应时间函数.
e(t)可进一步表示为:
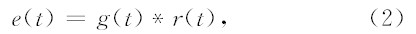
(2)式中,r(t)为地下介质的反射系数时间序列,g(t)为引起雷达子波衰减和频散的地下介质等效滤波器时间函数.
由(1)和(2)式,x(t)可表示为:
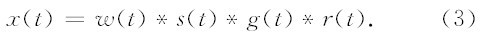
实测探地雷达数据中,w(t)*s(t)可近似用空气直达波d(t)来代替.x(t)可近似表示为:
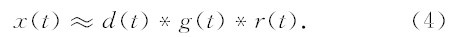
在频率域中,可以将(4)式改写为:
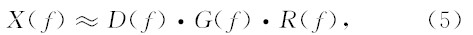
(5)式中,X(f),D(f),G(f),R(f)对应的分别为x(t),d(t),g(t),r(t)的傅里叶变换.
对(5)式两边分别取模,可以得到:
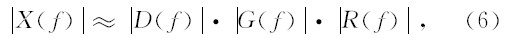
(6)式中,∣ X(f) ∣,∣ D(f) ∣,∣ G(f) ∣,∣ R(f) ∣ 对应的分别为x(t),d(t),g(t),r(t)振幅谱.
假定地下介质的反射系数时间序列是随机的白噪序列,可以得到:

联立(6),(7)式,得到等效滤波器的振幅谱∣ G(f) ∣ 为:
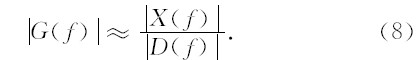
因为地下介质等效滤波器为最小相位滤波器,即g(t)为最小相位信号.对g(t)进行离散采样,得到采样 信号g(n),n=0,1,2,3,…,∞.g(n)的Z变换为:
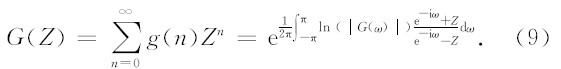
最小相位信号的频谱取对数后,对应的仍然是一个物理可实现信号(Kolmogorov,1939;程乾生,1993).令
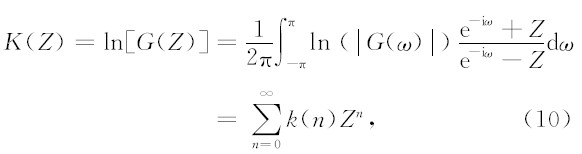
因为
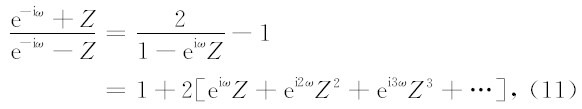
所以
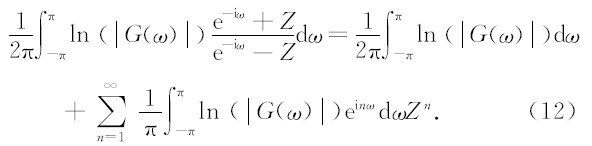
对比(10)和(12)式,求得k(n)为:
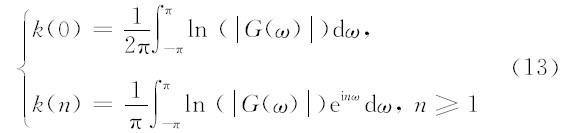
(10)式两边对Z取微商,得到:
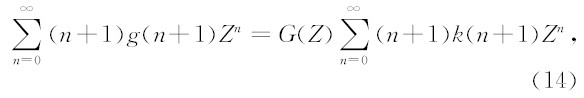
由Z变换和褶积的关系,可以得到:

在(10)式中取Z=0,得到:g(0)=ek(0).最后,g(n)可以通过(16)式计算出.
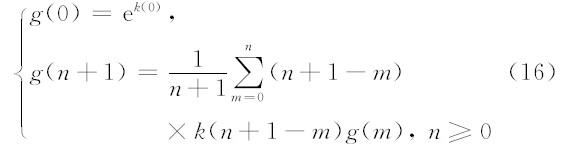
实际计算时,k(n)可以通过FFT计算得到.为了保证求解过程的稳定,通常用∣ G(ω) ∣ +ε(ε>0)来代替∣ G(ω) ∣.
令地下介质等效滤波器的反滤波器时间函数为h(t),h(t)满足以下条件:
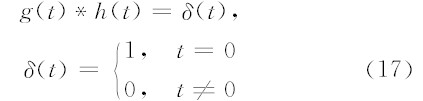
h(t)可以利用最小平方反滤波方法计算得到(何樵登和熊维纲,1990).具体的计算公式为:
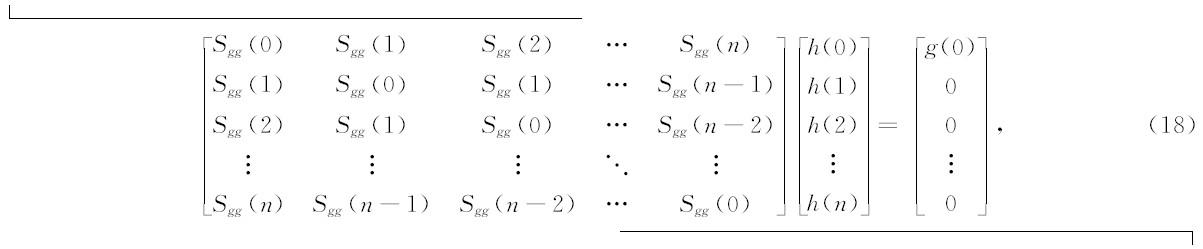
(18)式中,Sgg为g(n)的自相关函数.实际计算(18)式时,可以利用莱文森递推公式来求解.为了保证求解过程的稳定,通常用(1+λ)Sgg(0)(λ>0)来代替Sgg(0).
计算出h(t)后,利用h(t)对x(t)进行反滤波,消除g(t)对x(t)的影响,从而实现消除探地雷达数据的子波衰减和频散.滤波结果y(t)为:
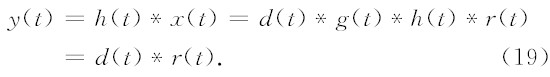
为了模拟雷达子波在地下介质中的传播特性,本文采用如下性质的有耗介质来模拟地下介质.
有耗介质的复介电常数ε*r(ω)与频率的关系可以利用Debye公式来描述(方广有等,1998;刘四新和曾昭发,2007):
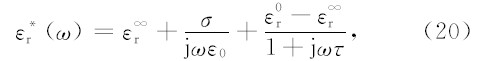
(20)式中,ε0为真空的相对介电常数.ε0r和ε∞r分别表示的是有耗介质的低频和高频相对介电常数.τ为驰豫时间.σ为有耗介质的电导率.
因为探地雷达一般在非磁性介质中开展工作,所以本文假设有耗介质的磁导率μ与真空的磁导率μ0相等.同时,本文假设有耗介质的电导率与频率无关(Irving and Knight,2003).
本文利用FDTD算法分别模拟了雷达子波在有耗介质和无损介质中的传播特性,有耗介质的介质参数分别为:ε0r=9,ε∞r=7.5,σ=0.001 S/m,μ=μ0,τ=2 ns.无损介质的介质参数分别为:ε=9,σ=0,μ=μ0.模拟时选用的是中心频率为100 MHz 高斯脉冲雷达子波,发射器与接收器的距离分别设置为:2 m,4 m,6 m,8 m,10 m,12 m.图1和图2分别为雷达子波的时域波形和振幅谱.
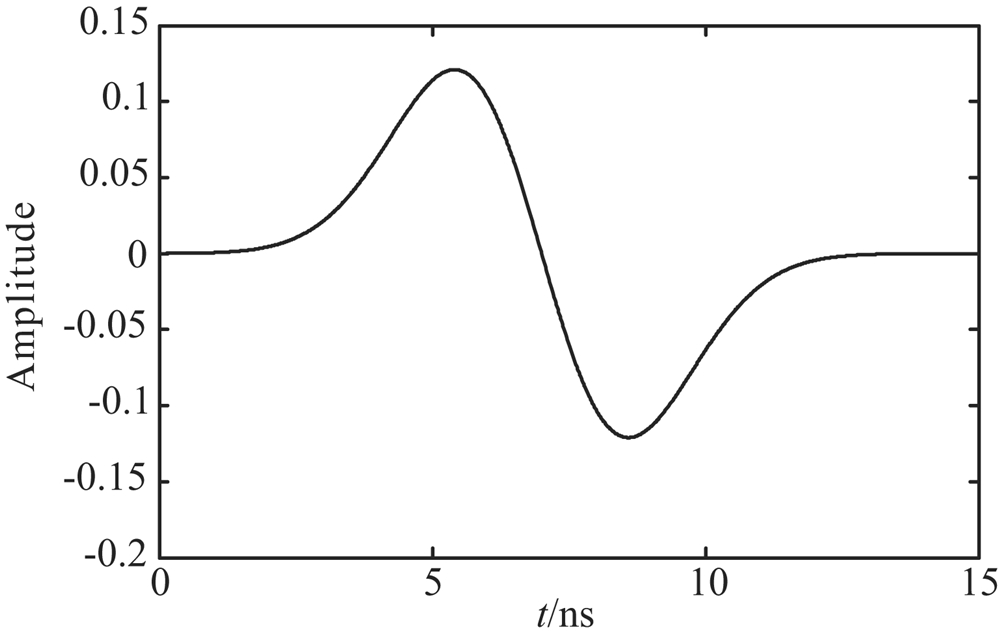 | 图1 雷达子波时域波形图 Fig.1 Time domain waveform of radar wavelet |
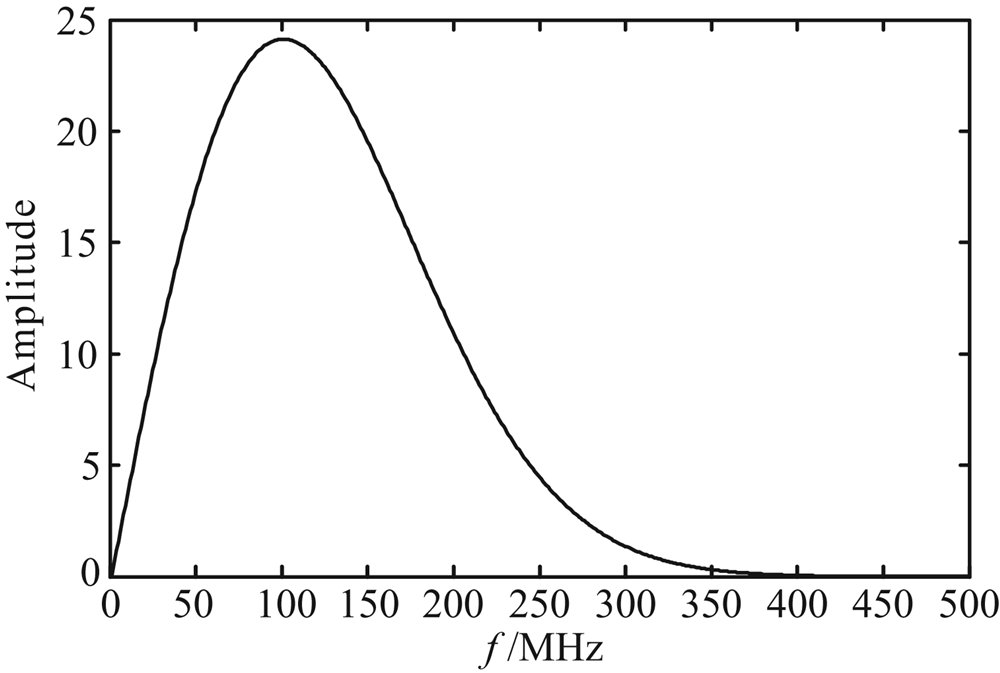 | 图2 雷达子波振幅谱 Fig.2 Amplitude spectrum of radar wavelet |
图3和图4分别为雷达子波在有耗介质和无损介质中传播一维FDTD模拟结果.为了便于图形显示,本文对各个接收器记录到的雷达子波按道数显示在同一图中.
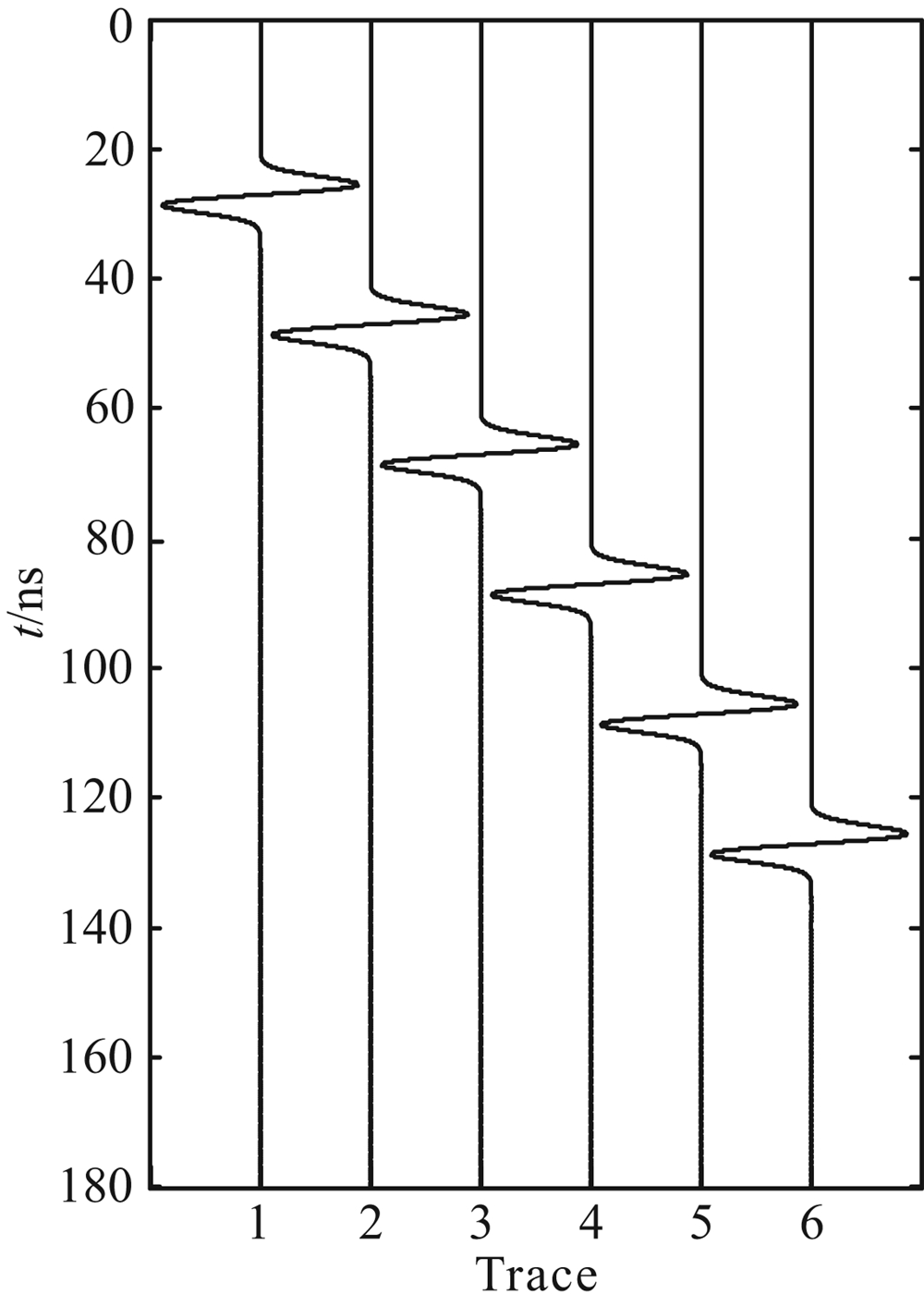 | 图3 雷达子波在无损介质中传播FDTD模拟结果 Fig.3 FDTD simulation result of radar wavelet propagating in lossless media |
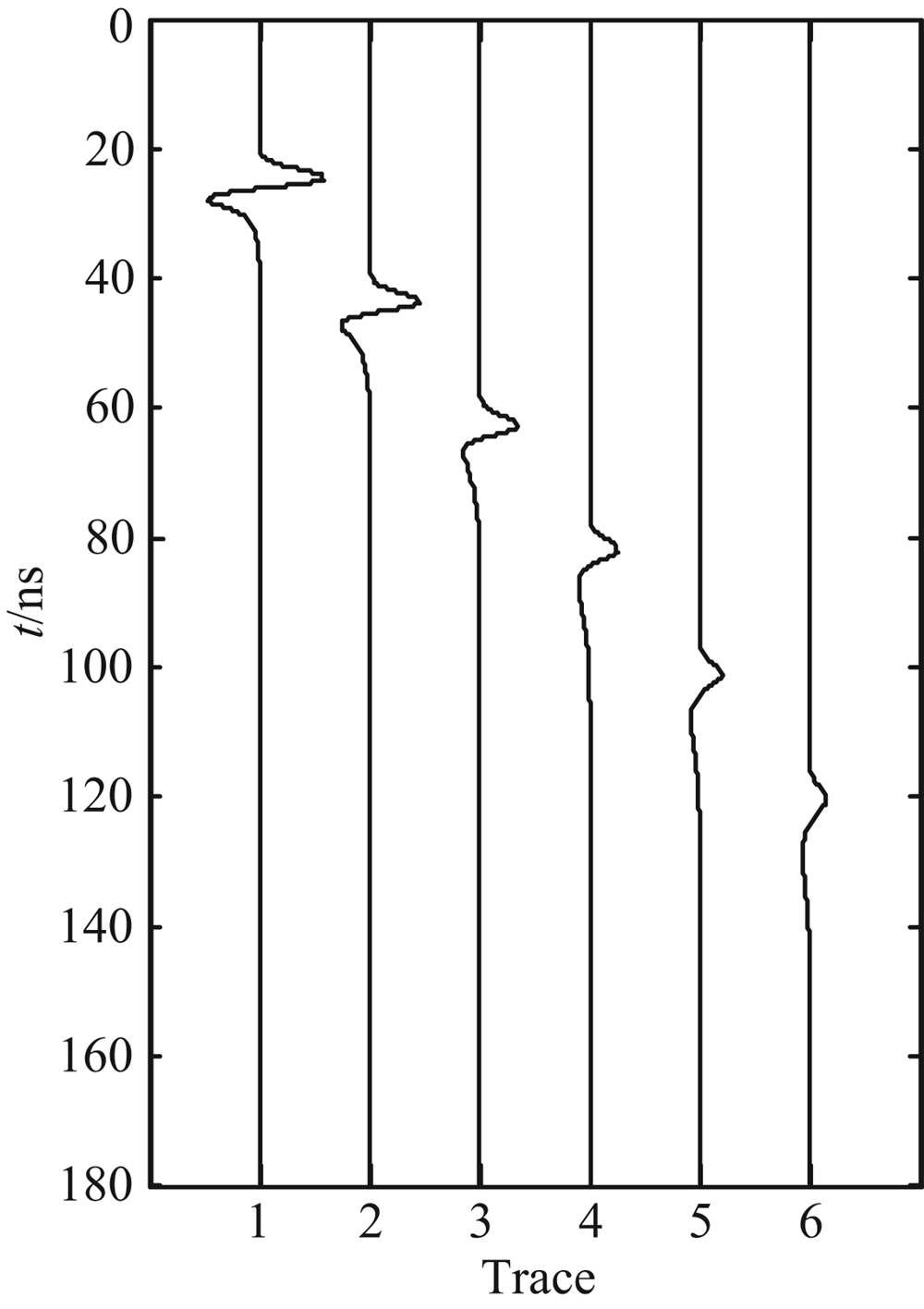 | 图4 雷达子波在有耗介质中传播FDTD模拟结果 Fig.4 FDTD simulation result of radar wavelet propagating in lossy media |
图5为有耗介质中各个接收器记录的雷达子波振幅谱.从图4和图5中可以看出,雷达子波在有耗介质中传播时,随着传播深度的增加,雷达子波的振幅逐渐降低,能量逐渐减弱,雷达子波能量的衰减会降低探地雷达的勘探深度.同时,雷达子波的主频也会随着传播深度的增加而逐渐降低,雷达子波的时域波形逐渐变宽,探地雷达的勘探分辨率逐渐减小.
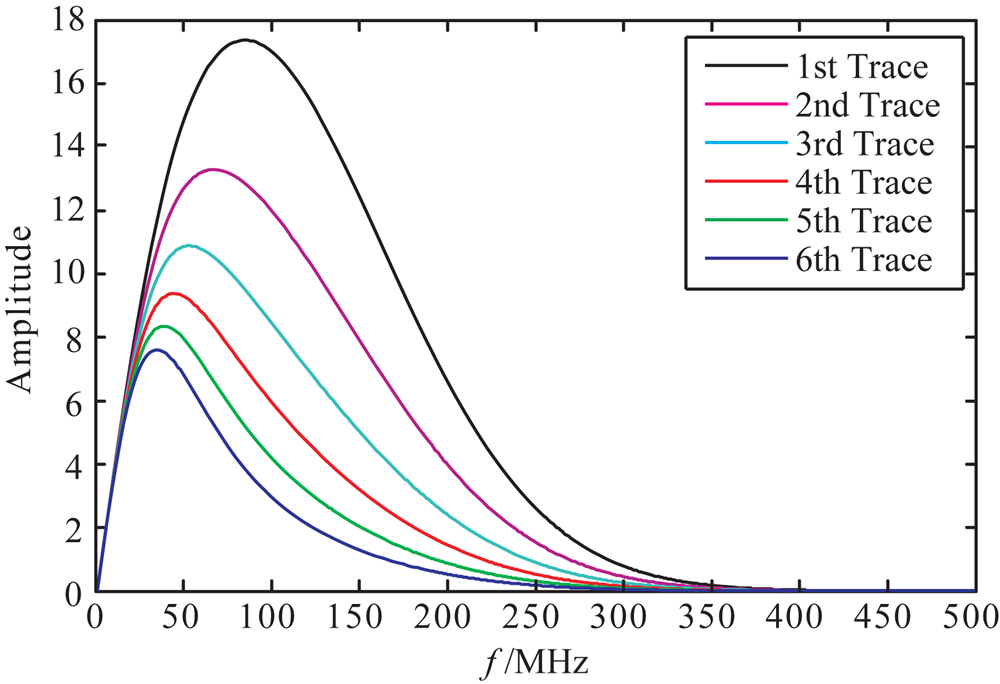 | 图5 有耗介质中各个接收器记录的雷达子波振幅谱 Fig.5 Amplitude spectrum of radar wavelets recorded by each receiver in lossy media |
对有耗介质中各个接收器记录到的雷达子波分别进行反滤波处理,图6为反滤波处理结果.对比分析图3、图4和图6,在有耗介质中传播的雷达子波经过反滤波处理后,雷达子波的振幅能够得到很好地恢复.对比分析反滤波前后的雷达子波振幅谱(图7),可以看出,雷达子波的主频得到提升,时域波形变窄,探地雷达的勘探分辨率得到提高.
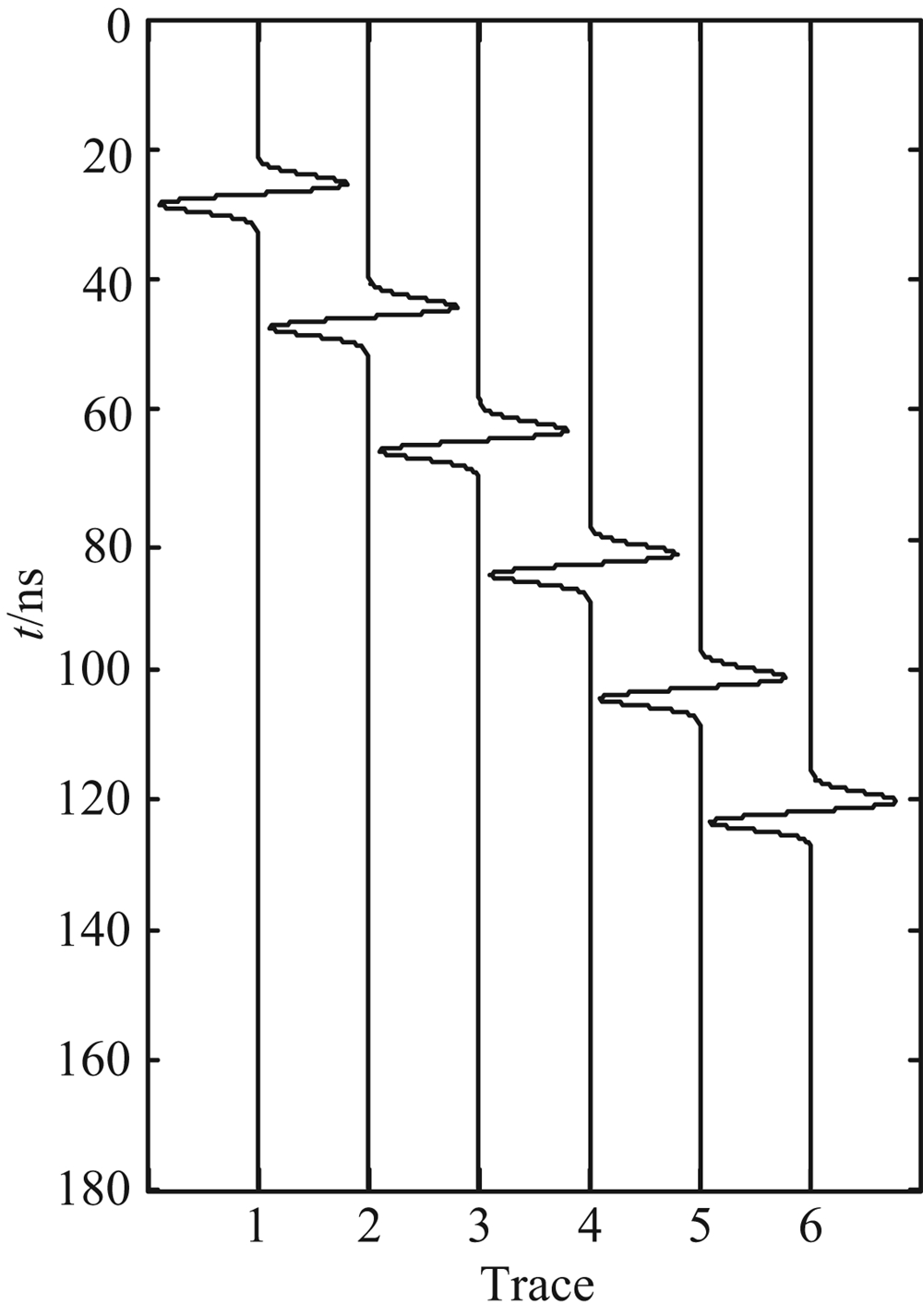 | 图6 图4所示的FDTD模拟结果的反滤波结果 Fig.6 Inverse filtering result of FDTD simulation result as Fig.1 shows |
 | 图7 有耗介质中第6道雷达子波振幅谱(实线所示)和反滤波后振幅谱(虚线所示) Fig.7 Amplitude spectrum, pre-inverse filtered (as solid line shows) and post-inverse filtered (as dotted line shows), of the sixth trace radar wavelet in lossy media |
实际探地雷达勘探中,探地雷达的发射天线和接收天线一般置于介质表面.探地雷达记录到的一 般是地下介质的回波信号.为了更好地了解有耗地下介质对实际探地雷达探测结果的影响,本文用FDTD分别模拟了有耗和无损两种地下介质的回波信号.FDTD模拟时选用的雷达子波如图1所示.图8为模拟时选用的地下介质模型.
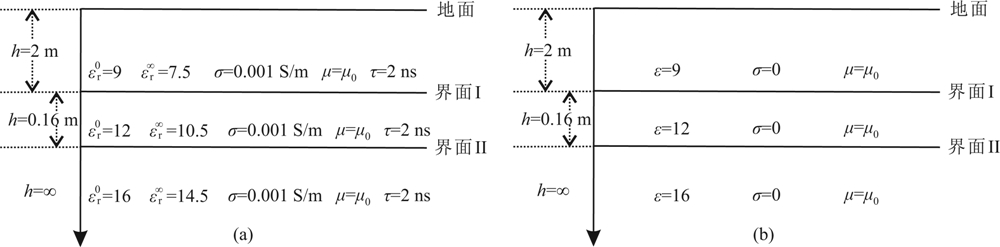 | 图8 地下介质模型 (a) 有耗地下介质模型; (b)无损地下介质模型. Fig.8 Ground media model (a) Lossy ground media model; (b) Lossless ground media model. |
图9和图10分别为FDTD模拟的有耗和无损两种地下介质单道回波信号.
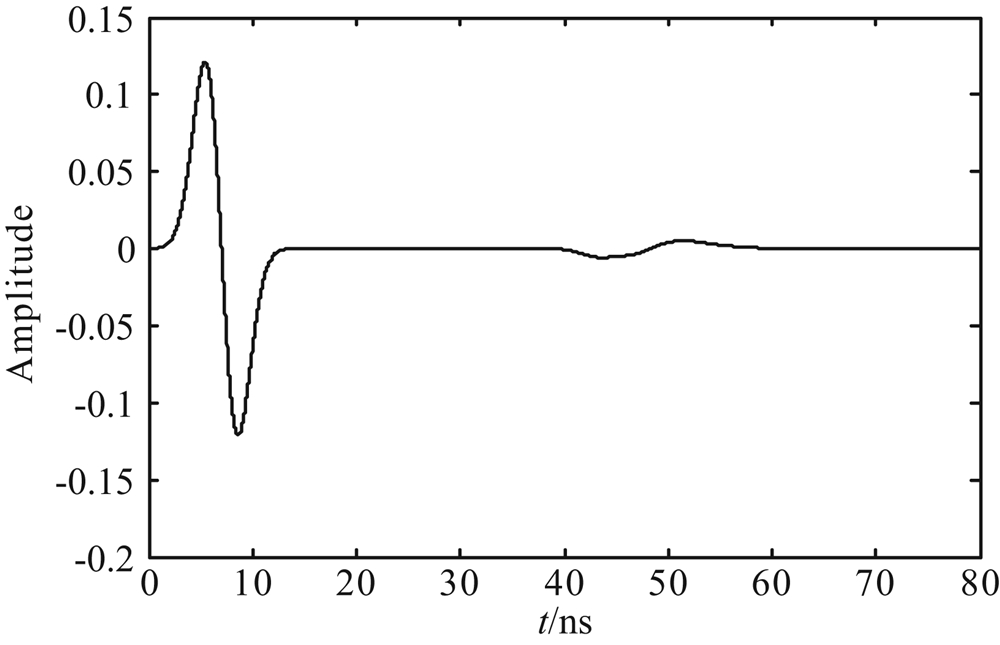 | 图9 有耗地下介质单道回波信号 Fig.9 Lossy ground media single trace echo signal |
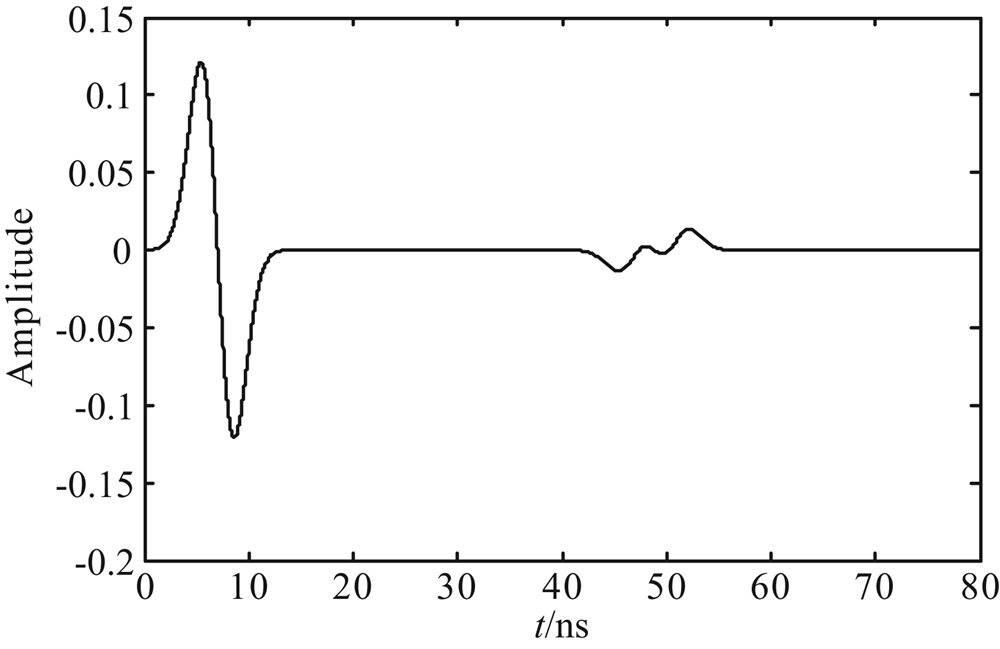 | 图10 无损地下介质单道回波信号 Fig.10 Lossless ground media single trace echo signal |
在图10中,我们可以从无损地下介质单道回波信号中识别出界面I和界面II.但是在图9中,由于雷达子波的衰减和频散,我们很难在有耗地下介质单道回波信号中识别出界面I和界面II.对有耗地下介质单道回波信号进行反滤波处理,图11为处理结果.
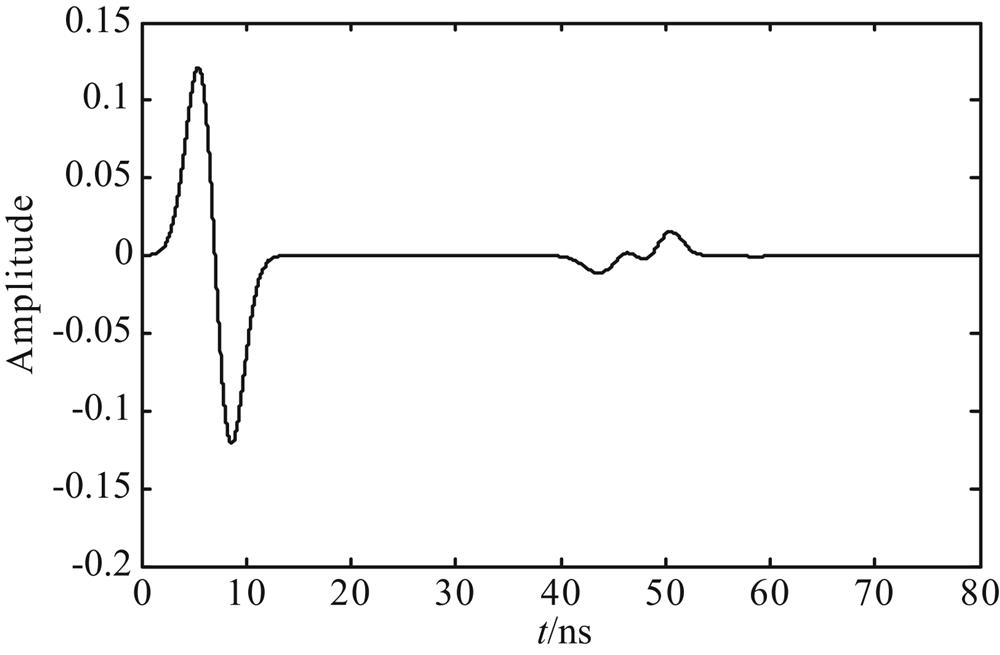 | 图11 有耗地下介质单道回波信号反滤波处理结果 Fig.11 Inverse filtering result of lossy ground media single trace echo signal |
经过反滤波处理后,界面I和界面II的反射信 号振幅得到增强,同时由于反滤波提高了反射信号主频,界面I和界面II在图11中可以清楚地被识别出.对比分析图9、图10和图11,可以得出,有耗地下介质单道回波信号经过反滤波处理后,可以很好地消除有耗地下介质对雷达子波的影响,从而消除了雷达子波的衰减和频散,进而提高了探地雷达在有耗地下介质中的勘探深度和勘探分辨率.
图12为某一湖区实测探地雷达数据.测量时,天线中心频率选用150 MHz,时间窗口为500 ns,采样点数为512,总的记录道数为141道.
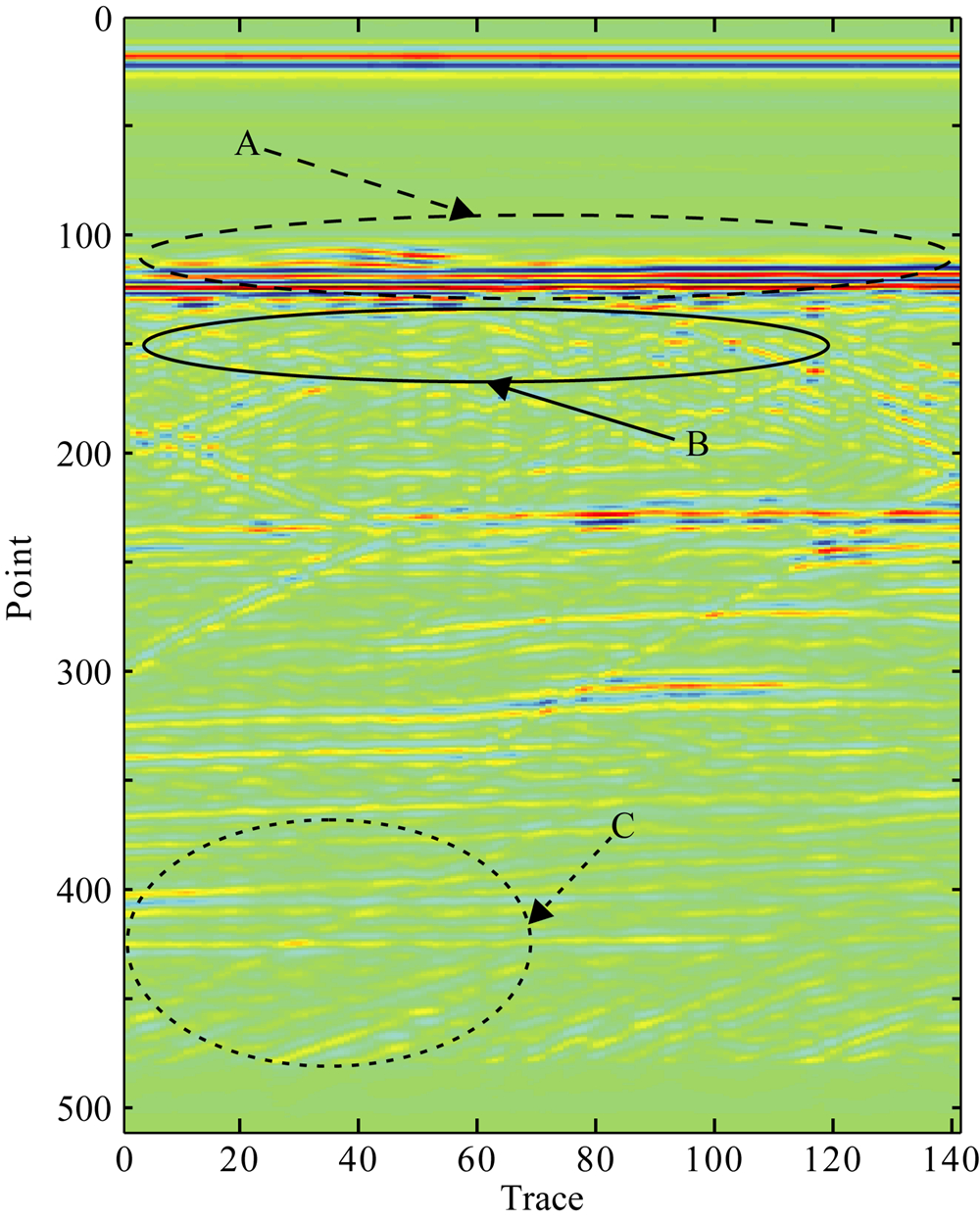 | 图12 实测探地雷达数据 Fig.12 Ground Penetrating Radar data |
对湖区实测探地雷达数据进行反滤波处理,处 理结果为图13.对比分析图12和图13中A区域,湖区实测探地雷达数据经过反滤波处理后,湖底淤泥沉积序列反射回波信号变得更加清晰,我们可以更清楚地划分湖底淤泥沉积层.
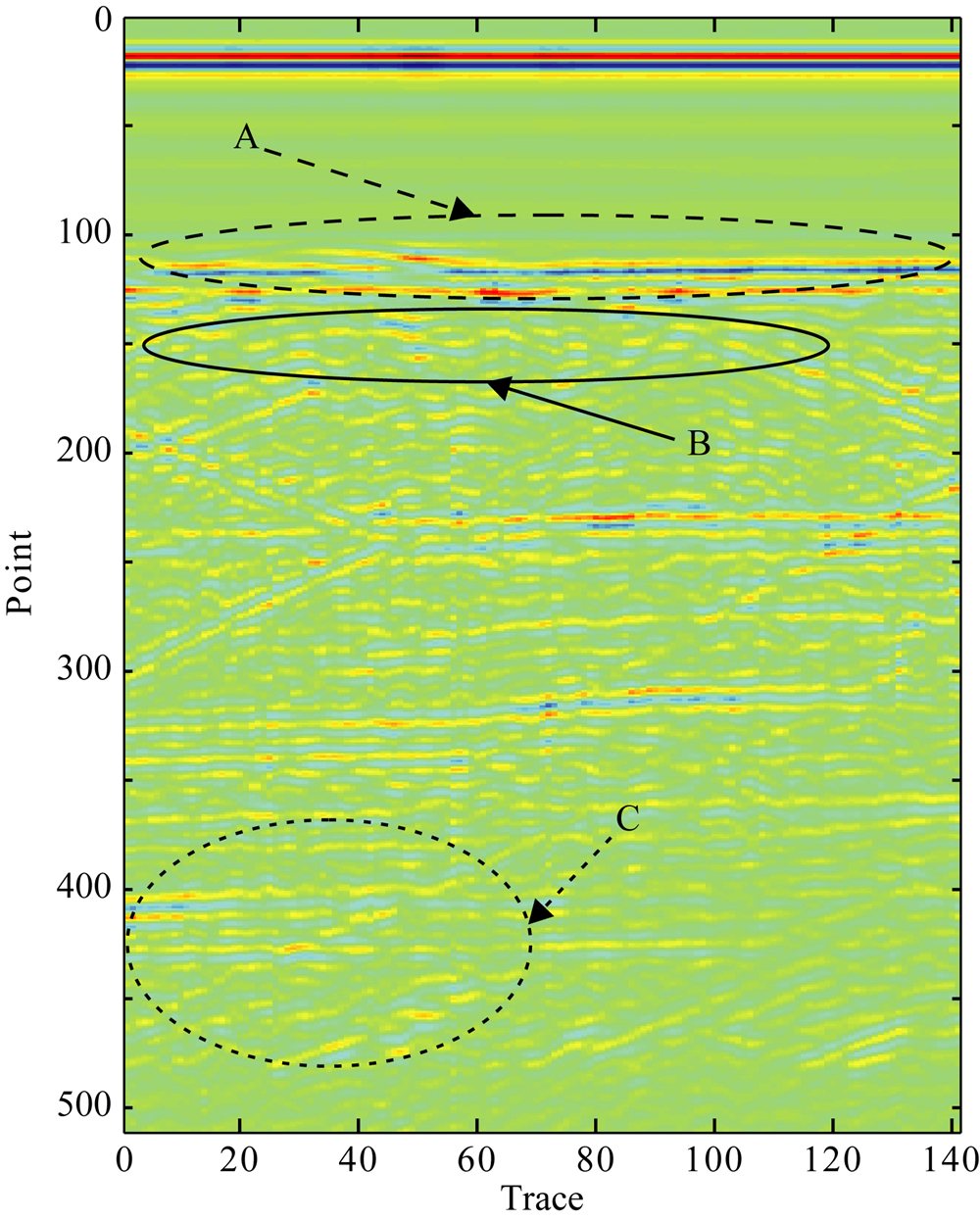 | 图13 实测探地雷达数据反滤波处理结果 Fig.13 Inverse filtering result of Ground Penetrating Radar data |
在图12中B区域,由于湖水和湖底淤泥沉积序列引起雷达子波发生衰减和频散,湖底淤泥沉积序列底部反射层的反射回波信号模糊甚至缺失,我们很难了解湖底淤泥沉积序列底部反射层的性质.但是在图13中B区域,由于反滤波消除了湖水和湖底淤泥沉积序列引起的雷达子波的衰减和频散,湖底淤泥沉积序列底部反射层的反射回波信号变得清晰.通过反滤波处理,我们可以很好地解释和划分湖底淤泥沉积序列底部反射层.对比分析图12和图13中C区域,可以发现,由于反滤波消除了雷达子波的衰减和频散,深部反射层的回波信号得以增强,探地雷达的勘探深度得到提升.
雷达子波的衰减和频散会给探地雷达勘探带来严重影响,降低探地雷达的勘探深度和勘探分辨率.鉴于利用传统反Q滤波方法消除雷达子波的衰减和频散存在很大困难,本文提出了一种消除探地雷达数据的子波衰减和频散的反滤波方法.新方法以 地下介质反射系数是随机数为前提,充分利用了地下介质等效滤波器为最小相位滤波器这个特性.本文通过理论模型计算和实测探地雷达数据处理,证明了新方法能很好地消除探地雷达数据的子波衰减和频散.利用该方法,能很好地提高探地雷达的勘探深度和勘探分辨率.
| [1] | Aki K, Richards P G. 1980. Quantitative Seismology, Vol.1: Theory and Methods. W. H. Freeman and Company, 173-175. |
| [2] | Cheng Q S. 1993. The Theory of Digital Signal Processing (in Chinese). Beijing: Petroleum Industry Press. |
| [3] | Chen Y Q, Xiao B X. 2005. On the status quo and development of ground penetrating radar. Chinese Journal of Engineering Geophysics (in Chinese), 2(2): 149-155, doi: 10.3969/j.issn.1672-7940.2005.02.015. |
| [4] | Di Q Y, Xu K, Wang M Y. 2000. The attenuated radar wave migration with finite element method. Chinese Journal of Geophysics (in Chinese), 43(2): 257-263, doi: 10.3321/j.issn:0001-5733.2000.02.014. |
| [5] | Economou N, Vafidis A. 2010. Spectral balancing GPR data using time-variant bandwidth in the t-f domain. Geophysics, 75(3): J19-J27, doi: 10.1190/1.3374464. |
| [6] | Futterman W I. 1962. Dispersive body waves. Journal of Geophysical Research, 67(13): 5279-5291, doi: 10.1029/JZ067i013p05279. |
| [7] | Fang G Y, Zhang Z Z, Wang W B. 1998. Numerical simulation of Ground Penetrating Radar. Journal of Microwaves (in Chinese), 14(4): 288-295. |
| [8] | He Q D, Xiong W G. 1990. Course in Applied Geophysics—Seismic Exploration (in Chinese). Beijing: Geological Publishing House. |
| [9] | Irving J D, Knight R J. 2003. Removal of wavelet dispersion from ground-penetrating radar data. Geophysics, 68(3): 960-970, doi: 10.1190/1.1581068. |
| [10] | Kolmogorov A N. 1939. Sur I'interpolation et I'extrpolation des suites stationnaires. Comptes Rendus de I'Acadamie des Sciences, 208: 2043-2045. |
| [11] | Li H, Lu G Y, He X Q, et al. 2010. The progress of the GPR and discussion on its future development. Progress in Geophysics (in Chinese), 25(4): 1492-1502, doi: 10.3969/j.issn.1004-2903.2010.04.043. |
| [12] | Li J, Guo C C, Wang F M, et al. 2007. The summary of the surface ground penetrating radar applied in subsurface investigation. Progress in Geophysics (in Chinese), 22(2): 629-637, doi: 10.3969/j.issn.1004-2903.2007.02.043. |
| [13] | Liu S X, Zeng Z F. 2007. Numerical simulation for ground penetrating radar wave propagation in the dispersive medium. Chinese Journal of Geophysics (in Chinese), 50(1): 320-326, doi: 10.3321/j.issn:0001-5733.2007.01.040. |
| [14] | Oden C P, Powers M H, Wright D L, et al. 2007. Improving GPR image resolution in lossy ground using dispersive migration. IEEE Transactions on Geoscience and Remote Sensing, 45(8): 2492-2500, doi: 10.1109/TGRS.2006.888933. |
| [15] | Slob E, Sato M, Olhoeft G. 2010. Surface and borehole ground-penetrating-radar developments. Geophysics, 75(5): A103-A120, doi: 10.1190/1.3480619. |
| [16] | Tonn R. 1989. Comparison of seven methods for the computation of Q. Physics of the Earth and Planetary Interiors, 55(3-4): 259-268, doi: 10.1016/0031-9201(89)90074-5. |
| [17] | Tonn R. 1991. The determination of the seismic quality factor Q from VSP data: a comparison of different computational methods. Geophysical Prospecting, 39(1): 1-27, doi: 10.1111/j.1365-2478.1991.tb00298.x. |
| [18] | Turner G. 1994. Subsurface radar propagation deconvolution. Geophysics, 59(2): 215-223, doi: 10.1190/1.1443583. |
| [19] | Turner G, Siggins A F. 1994. Constant Q attenuation of subsurface radar pulses. Geophysics, 59(8): 1192-1200, doi: 10.1190/1.1443677. |
| [20] | Wang Y H. 2006. Inverse Q-filter for seismic resolution enhancement. Geophysics, 71(3): V51-V60, doi: 10.1190/1.2192912. |
| [21] | Yao Z X, Gao X, Li W X. 2003. The forward Q method for compensating attenuation and frequency dispersion used in the seismic profile of depth domain. Chinese Journal of Geophysics (in Chinese), 46(2): 229-233, doi: 10.3321/j.issn:0001-5733.2003.02.016. |
| [22] | Yu Z, Wang Y C, He J, et al. 2009. A review of inverse Q filtering methods. Progress in Exploration Geophysics (in Chinese), 32(5): 309-314, 325. |
| [23] | Zhao J X. 1986. The application of inverse Q filtering. Oil Geophysical Prospecting (in Chinese), 21(4): 410-421. |
| [24] | 程乾生. 1993. 信号数字处理的数学原理. 北京: 石油工业出版社. |
| [25] | 陈义群, 肖柏勋. 2005. 论探地雷达现状与发展. 工程地球物理学报, 2(2): 149-155, doi: 10.3969/j.issn.1672-7940.2005.02.015. |
| [26] | 底青云, 许琨, 王妙月. 2000. 衰减雷达波有限元偏移. 地球物理学报, 43(2): 257-263, doi: 10.3321/j.issn:0001-5733.2000.02.014. |
| [27] | 方广有, 张忠治, 汪文秉. 1998. 脉冲探地雷达的模拟计算. 微波学报, 14(4): 288-295. |
| [28] | 何樵登, 熊维纲. 1990. 应用地球物理教程——地震勘探. 北京: 地质出版社. |
| [29] | 李华, 鲁光银, 何现启等. 2010. 探地雷达的发展历程及其前景探讨.地球物理学进展, 25(4): 1492-1502, doi: 10.3969/j.issn.1004-2903.2010.04.043. |
| [30] | 李嘉, 郭成超, 王复明等. 2007.探地雷达应用概述.地球物理学进展, 22(2): 629-637, doi: 10.3969/j.issn.1004-2903.2007.02.043. |
| [31] | 刘四新, 曾昭发. 2007. 频散介质中地质雷达波传播的数值模拟.地球物理学报, 50(1): 320-326, doi: 10.3321/j.issn:0001-5733.2007.01.040. |
| [32] | 姚振兴, 高星, 李维新. 2003. 用于深度域地震剖面衰减与频散的反Q滤波方法.地球物理学报, 46(2): 229-233, doi: 10.3321/j.issn:0001-5733.2003.02.016. |
| [33] | 余振, 王彦春, 何静等. 2009. 反Q滤波方法研究综述.勘探地球物理进展, 32(5): 309-314, 325. |
| [34] | 赵建勋. 1986. 反Q滤波的应用. 石油地球物理勘探, 21(4): 410-421. |
 2014, Vol. 57
2014, Vol. 57


