电离层是地球大气层被太阳射线电离的部分,因它能够影响无线电波的传播而受到人们的重视.人们对电离层的了解主要来自探测技术,其中斜向探测能够对远离发射点的电离层进行监测.正因为如此,在海洋和荒凉贫瘠的地方,其上空的电离层也可以得到很好的实时监测.斜向探测能够获得描述收发站之间电波传播群时延对频率关系的电离图,通过分析这种探测电离图,可以获取电离层垂直剖面信息和收发站之间的电离层水平结构信息.
斜测电离图的反演一直是人们关注的对象,国内外许多学者对斜测电离图的反演做过研究.最初是以Gething为代表的学者用Martyn等效虚高定理和修正的正割定理将斜测电离图换算为垂直电离图,再用垂直入射反演理论得到斜入射反射中点的电离层剖面(Smith,1970;Rao,1973; Gething and Maliphant,1967),由于Martyn等效虚高原理只有在假设地球面和电离层是平面的前题下才成立,所以这种反演方法只适用于短距离传播的情况.为了克服这个难题,Rao (1975)提出了直接反演斜测电离图的方法,该方法用单层QP模型来表征斜测链路中继点的电离层电子浓度剖面,结合球面电离层下的正割定理和等效路径定理以及QP模型下的射线路径参数表达式之后,应用Rao(1974)的迭代反演方法推导出斜测描迹对应的大圆距离以及中继点的电离层QP模型参数.但是,由于Rao用的是斜测描迹中的X波,导致反演得到的临界频率要偏大,再加上该反演方法对初始电离层模型参数的选取要求比较苛刻,对测量误差也非常敏感,算法本身并不稳定.柳文等(2003)在Rao反演算法的基础上引入了解线性不稳定问题的正则化方法,较好地改善了反演算法的不稳定性.Reilly(1985)基于改进的球面电离层下的等效路径定理,应用分片法对斜测电离图进行了反演,并用合成的斜测数据进行验证.后来,Reilly和Kolesar(1989)对1985年Reilly提出的反演方法进行了改进(简称R-K方法),用比等效路径定理更精确的解析方法求解群路径和大圆距离,用合成的斜测电离图对反演方法进行了验证.Phaninong等(1995)在R-K方法的基础上考虑了地磁场效应,对比分析加入地磁场效应和忽略地磁场效应的反演结果,得出前者的反演结果更加接近真 实情况.Heaton等(2001)用R-K方法对Cove Radio 到Malvern这条链路的斜测数据进行了反演,并将斜测反演结果与部署在Chilton(离链路中继点20 km)的垂测仪的数据进行了比较.通过实测数据的验证发现了R-K方法的不足:很难得到F层峰高附近的电子浓度分布.
随着计算科学的发展,近10年左右,许多新的非线性反演方法得到了发展.谢树果(2001)首次把遗传算法应用于斜向返回电离层参数的反演研究当中,这种方法具有其他传统反演方法没有的优势,无需将反演问题线性化,可以容易地利用已知或先验信息对解做出约束,减少反演问题解的非唯一性.随后徐彤(2006)、宋鹏和徐彤(2008)用遗传算法对单层合成的斜测电离图进行反演,比较观测数据在加噪声和不加噪声两种情况下的反演结果,得出遗传反演算法具有一定的抗噪能力.Benito等(2008)分别用遗传算法和模拟退火算法对实测的仰角扫描斜返电离图进行反演,比较这两种算法的反演结果得出:遗传算法反演得到最佳解所需的时间比模拟退火所需的时间快9倍左右,而且遗传算法反演的结果更接近真实值,所以Benito认为未来遗传算法将会被广泛使用.但是,遗传算法本身有两个严重的缺陷:首先是“过早收敛”,所谓“过早收敛”是指在搜索的初期,由于优良个体急剧增加使种群失去多样性,从而造成程序陷入局部最优,达不到寻找全局最优解的目的;其次是局部搜索能力差,研究发现遗传算法可以很快地到达最优解的90%,但寻找到真正的最优解却要花较长时间.宋君等(2011)利用模拟退火算法对实测扫频斜返电离图进行反演,在Benito的基础上,对反演方法进行修改,使其能够反演扫频电离图前沿.但是,模拟退火算法全局搜索能力很差,需要进行大量的迭代运算才可能得到好的反演结果.此外,Benito等(2008)在文章中证明了,相比遗传算法来说,模拟退火算法的反演效果并不理想.
为了克服遗传算法和模拟退火算法的不足,在计算科学领域,有学者将遗传算法和模拟退火算法结合起来组成一种新的优化方法——混合遗传算法.因为遗传算法和模拟退火算法之间存在着直接互补性,体现在:遗传算法把握总体的能力较强,但局部搜索能力较差;模拟退火算法具有较强的局部搜索能力,但全局搜索能力差.所以,可以将遗传算法和模拟退火算法相互结合起来,取长补短.此外,很多学者从各种不同的角度出发,证明了混合遗传算法比遗传算法和模拟退火算法优越.桂卫华等(2001)通过比较三种算法的求解结果,得出混合遗传算法可以提高求得全局最优解的计算精度.吴浩扬等(2000)通过比较混合遗传算法和遗传算法,寻找到最优解所需的平均运行次数,得出混合遗传算法不仅能增强全局收敛性,还能加快遗传进化速度.周丽和黄素珍(2005)、Wang等(2009)通过比较混合遗传算法与遗传算法运行中的最佳适应度值和平均适应度值的变化,得出混合遗传算法是一个高精度高效率的算法,能显著提高遗传算法的优化性能.但是,这些文章都没有具体地从稳定性的角度来分析混合遗传算法.
本文将混合遗传算法应用于斜测电离图的反演中.采用忽略地磁场效应和电子碰撞的准抛物(QP)模型作为反演的电离层模型( Dyson and Bennett,1988),用遗传算法、模拟退火算法和混合遗传算法分别对合成的斜测图和实测电离图进行反演,并对三种算法的反演结果进行比较和验证.文中不仅比较了三种算法的反演结果和寻找到最优解所需的迭代次数,还从另外一种角度出发,通过改变种群大小和总迭代次数来比较这两个参数值的变化给三种算法的反演结果带来的影响,从而反映三种算法的稳定性,关于这种比较目前很少有学者关注过.文中实验及其比较结果表明:混合遗传算法在反演的 准确度和稳定性上要优于遗传算法和模拟退火算法.
当不考虑电离层的水平不均匀性时,常用QP模型来描述电子浓度分布.我们假设电离层电子密度为准抛物模式,表示如下:
在单层QP模型下,探测频率为 f 、发射仰角为 β 的信号的群路径 p′ 和电波接收点与发射点之间的地面距离 D 可以精确地计算出来,Croft and Hoogasian(1968)在文献中给出了群路径 p′ 和地面距离 D 的解析解,它们的表达式如下: 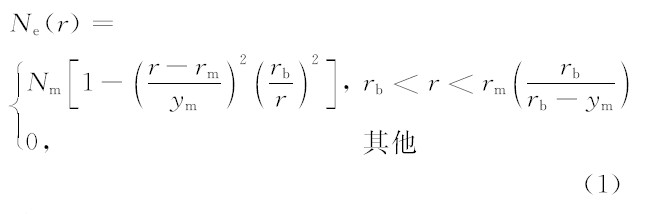
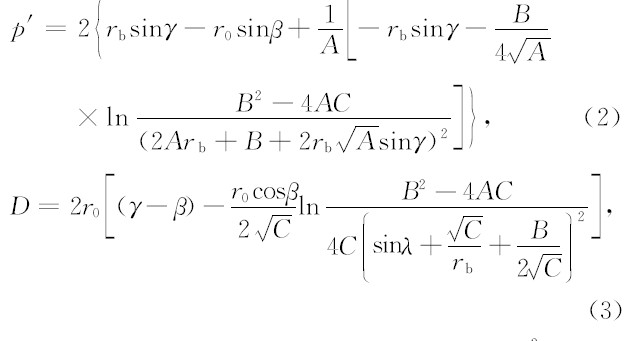
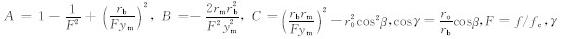 为射线在电离层底的入射角,r0=6370 km为地球半径.对于斜向探测,接收站与发射站之间的地面距离是确定的;对于确定的地面距离,可以由(3)式计算出电波的发射仰角β.由于(3)式是一个超越方程,可以用迭代法计算β,令β=0,以一定的步长增加 β 的值,增加到π/2为止,计算与每个 β 值对应的地面距离.将所有的地面距离值与已知的地面距离相比较,保留差值满足一定精度的地面距离对应的 β 值.用这 种方法可以精确地得到电波高低射线对应的仰角 β.
为射线在电离层底的入射角,r0=6370 km为地球半径.对于斜向探测,接收站与发射站之间的地面距离是确定的;对于确定的地面距离,可以由(3)式计算出电波的发射仰角β.由于(3)式是一个超越方程,可以用迭代法计算β,令β=0,以一定的步长增加 β 的值,增加到π/2为止,计算与每个 β 值对应的地面距离.将所有的地面距离值与已知的地面距离相比较,保留差值满足一定精度的地面距离对应的 β 值.用这 种方法可以精确地得到电波高低射线对应的仰角 β.
遗传算法在运行早期个体差异较大,当采用经典的轮盘赌方式进行选择时,早期容易使个别好的个体后代充斥整个种群,造成早熟;在遗传算法后期,所有个体的适应度趋向一致,使得优秀个体产生的后代优势不明显,从而整个种群进化停滞不前.混合遗传算法优势就是当遗传算法出现上述现象时,将模拟退火算法引入遗传算法中,在优选交叉和变异个体的过程中进行一定的“扰动”,剥夺局部最优值对整个种群的控制权,使得搜索沿着全局最优的方向进行.
(1)编码方案
采用多参数级连浮点数编码,即对QP层三个参数 fc,rm,rb 中的每个参数分别进行浮点数编码,然后按照一定的顺序连接在一起.每个编码就是一个个体,其中每个参量为基因.
(2)构建目标函数
构建反演问题的目标函数是为了确定适应度函数.本文取对应频率上理论计算得到的群路径与实际观测值的方差之和作为目标函数 Φ(fc,rm,rb), 目标函数表示如下:
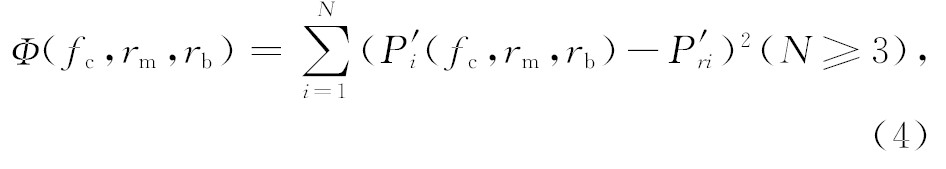
(3) 模型扰动规则
利用Ingber(1989)提出的依赖于温度的似Cauchy 型概率分布来产生新模型,对初始模型进行修改,即在参数空间 (fc,rm,rb) 内产生一组新电离层模型参数 (fc1,rm1,rb1). 产生的新模型如下所示:
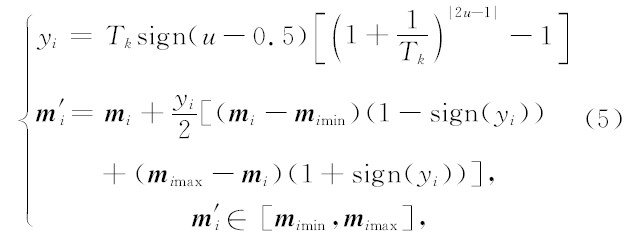
(4) 状态接受概率准则
本文采用Metropolis准则对新模型进行选择接受(Kirkpatrick et al.,1983).新状态被接受的概率取决于新旧模型目标函数的差值以及全局控制参数——温度 T. 反演过程中,模型参数为 m i 时对应的目标函数为 σp, 模型参数为 m ′ i 时对应的目标函数为σ′ p,则Metropolis准描述如下:(a)令 Δσp=σ′ p-σp, 如果 Δσp≤0, 则接受新状态σ′ p;(b)如果 Δσp>0, 则计算概率 ρ(Δσp)=exp - Δσp kBT . 将 ρ(Δσp) 与一个位于区间[0,1]上的一个随机数进行比较,若随机数小于 ρ(Δσp), 则接受新状态σ′ p,反之则舍弃新状态,保留旧状态σp.
(5)设定降温方式
根据不同的反演对象,可以选择不同的降温方式. 在本文的斜测电离图反演中,采用下式进行降温:

(6)程序运行终止条件
当退火温度 Tk 下降到小于事先设定的终止温度 Te 时,程序终止运行,输出此时寻找到的最优解,作为斜测电离图的反演结果.
3.2 斜测电离图反演步骤首先设定电离层参数搜索空间 (fc,rm,rb), 然后选取合适的群体大小GroupSize、交叉概率 Pc、变异概率Pm、 初始温度 T0、 终止温度 Te、 温度衰减因子α,接着在斜测电离图描迹上选取若干个探测数据作为输入数据,反演开始.一般来说,选取的数据点越多反演结果越接近真实值,但数据点过多会降低反演算法的计算效率.综合考虑反演结果和计算效率,本文选取5个数据点 (f1,P′ r1),(f2,P′ r2),(f3,P′ r3),(f4,P′ r4),(f5,P′ r5) 作为观测数据输入,具体反演步骤如下:
(1)在给定的电离层参数搜索空间中,随机产生 N 个电离层参数模型,组成初始群体Group1,并令遗传代数k=0.
(2)对于每个电离层参数模型,根据第2节中介绍的仰角计算方法,确定仰角β,得到该模型下采样频率为 f1,f2,f3,f4,f5 对应的理论群路径 P′ 1,P′ 2,P′ 3,P′ 4,P′ 5, 然后根据(4)式计算它的目标函数值.
(3)把目标函数值转换成适应度值,根据适应度值,对初始群体进行选择、交叉和变异操作,得到新的群体Group2.
(4)对Group2中的每个电离层参数模型加以扰动,产生新的电离层参数模型Group3,然后采用Metropolis准则进行判断,是接受新模型,还是保留旧模型.
(5)将Group2和Group3合并成一个群体Group4, 重复步骤(2),然后把目标函数值转换成适应度值,按照适应度值对Group4中的所有个体排序,取前 N 个个体作为下一代群体Group5,遗传代数k加1.
(6)降温.采用3.1.5节中介绍的降温方式,得到第k代温度 Tk.
(7)当温度满足 Tk
其基本框图见图 1.
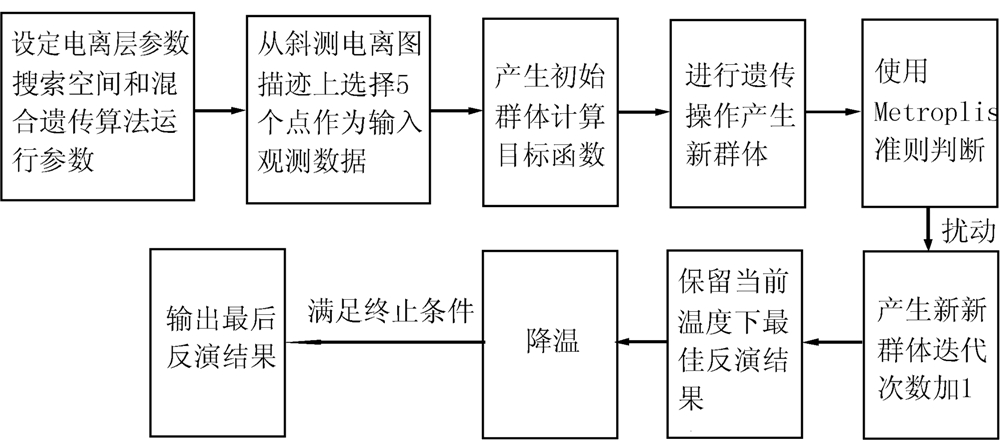
图 1 斜测电离图反演框图
Fig.1 The inversion flowchart of oblique ionogram
为了验证该算法在斜测电离图反演中的有效性,本文分别采用模拟退火算法(SA)、遗传算法(GA)和混合遗传算法(HGA)对同一张合成的斜测电离图进行反演,并对三种算法的反演结果进行了对比研究.
4.1 合成电离图设准抛物模型参数为:fc=10.5 MHz,rb=6550 km,ym=6700 km,假设收发站之间的地面距离为1630.0 km.对不同频率解超越方程(3),得到电波射线入射角β,代入(2)式,合成的斜测电离图见图 2所示.
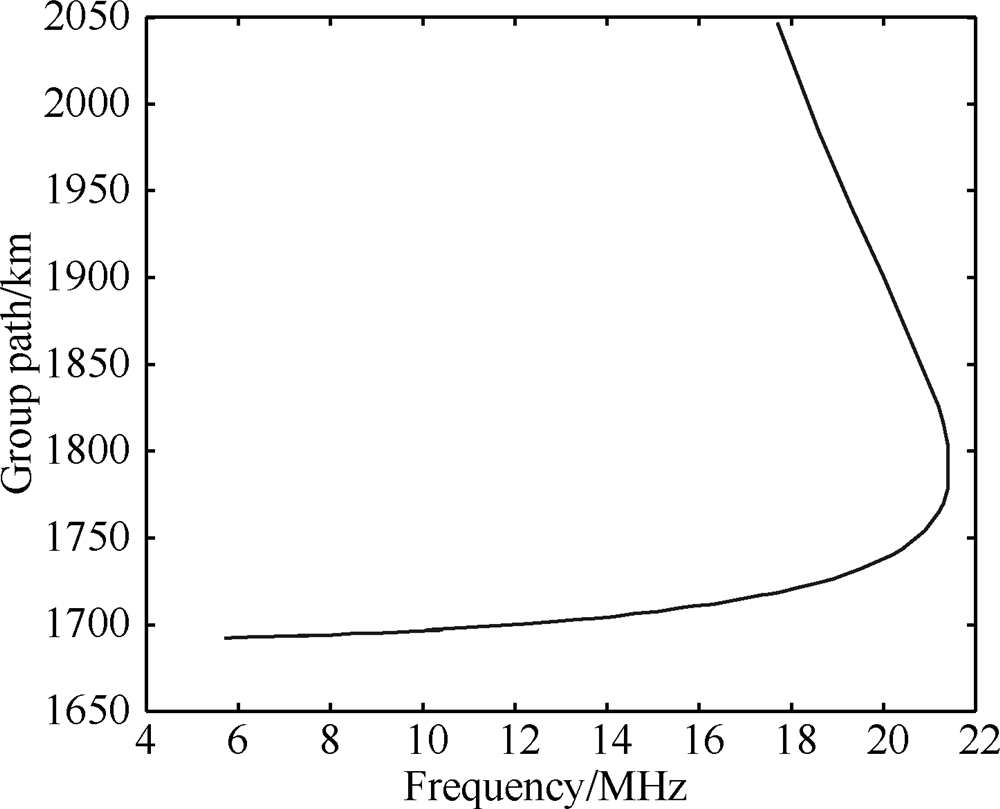 |
图 2 合成的斜测电离图 Fig.2 The synthetic oblique ionogram |
在合成的斜测电离图描迹上选取5个数据点作为输入数据,其中两个点来自高角波,三个点来自低角波.参照给定的QP模型参数,本文给出的参数搜索空间为:fc=8~12 MHz;rb=6530~6570 km;rm=6680~6720 km.
4.2 反演结果与分析为了更好地体现混合遗传算法反演的效果,统一设置三种不同算法的运行参数,使它们具有相同的群体大小,相同的进化代数,相同的参数搜索空间.特别是,混合遗传算法具有和遗传算法相同的遗传算子、交叉概率、变异概率,具有和模拟退火算法相同的初始温度、终止温度和温度衰减因子.需要强调一下,对于模拟退火算法来说,群体大小相当于每个温度下的重复迭代次数.三种算法运行参数的初始设定值如下:群体大小N为100,迭代次数k为55,初始温度为2000 ℃,终止温度为0.01 ℃,温度衰减因子为0.8,Pc为0.5,Pm为0.1.
4.2.1 反演结果在统一初始参数的情况下,利用三种不同算法分别对合成的斜测电离图进行反演.以每种算法重复反演10次为例,得到的三个反演参数的平均值与真实值的偏差d、标准误差 δ 及得到最佳反演结果所需的平均迭代次数k见表1,其中 dfc和δfc,drb 和 δrb,drm和δrm 分别为 fc,rb,rm 的偏差和标准偏差,K为最佳平均迭代次数.
| 表1 遗传算法、模拟退火算法和混合遗传算法的反演结果 Table 1 The inversion results of the GA, SA and HGA |
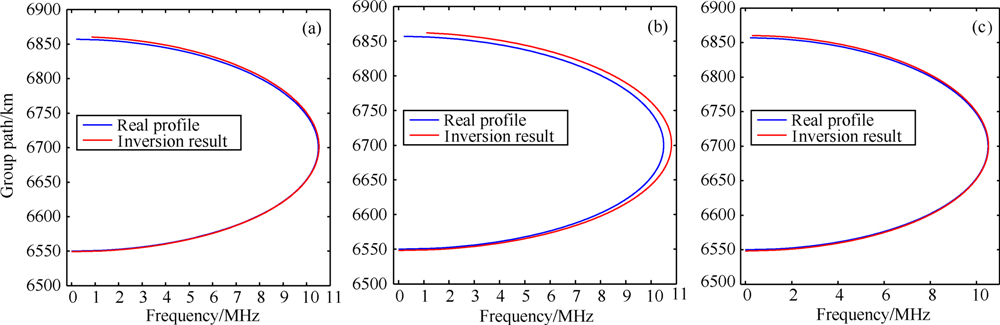 |
图 3 反演所得电子浓度剖面与真实剖面(a) 遗传算法;(b)模拟退火算法;(c)混合遗传算法. Fig.3 The resulting electron density profiles and the real profile (a)GA;(b)SA;(c) HGA. |
从表1可知,用遗传算法和混合遗传算法反演得到的模型参数的偏差和标准误差很小,特别是fc的偏差和标准误差基本接近于0,相比之下,用模拟退火算法反演得到的模型参数的偏差和标准误差很大.三种算法反演采用的总迭代次数都是55次,但它们得到最优解需要的平均迭代次数相差悬殊,其中遗传算法和模拟退火算法需要的迭代次数分别是 46.8次和53.5次,而混合遗传算法只需要23.0次. 图 3给出了用三种算法反演所得电子浓度剖面与真实剖面的比较结果,从中可以看出(b)图中的两条描迹明显吻合得不好,(a)图和(c)图吻合得很好.以上结果说明,模拟退火算法的反演结果不准确,遗传算法在反演过程中进化速度缓慢,相比之下,混合遗传算法不仅反演结果准确,还明显地加快了进化速度,提高了求得全局最优解的计算效率.
4.2.2 算法参数的改变及其影响(1) 群体大小的改变
群体大小的取值可以直接影响群体的多样性,而维护群体的多样性可以预防“过早收敛”现象的发生.群体大小N取值较小时,可以提高算法运算的速度,但与此同时降低了群体的多样性,可能会引起“过早收敛”现象发生;N取值较大时,又会使得算法的运行效率降低.表1给出了群体大小为100时三种算法的反演结果,其中遗传算法和混合遗传算法的反演结果都很理想.将群体大小分别设置为50和150,三种算法的反演结果见表2,其中 dfc、drb、drm、δfc、δrb、δrm、K 含义同表1.
| 表2 群体大小N=50、150,迭代次数k=55时,遗传算法、模拟退火算法和混合遗传算法的反演结果 Table 2 The inversion results of GA, SA and HGA at the population size 50,150 and the iteration times 55 |
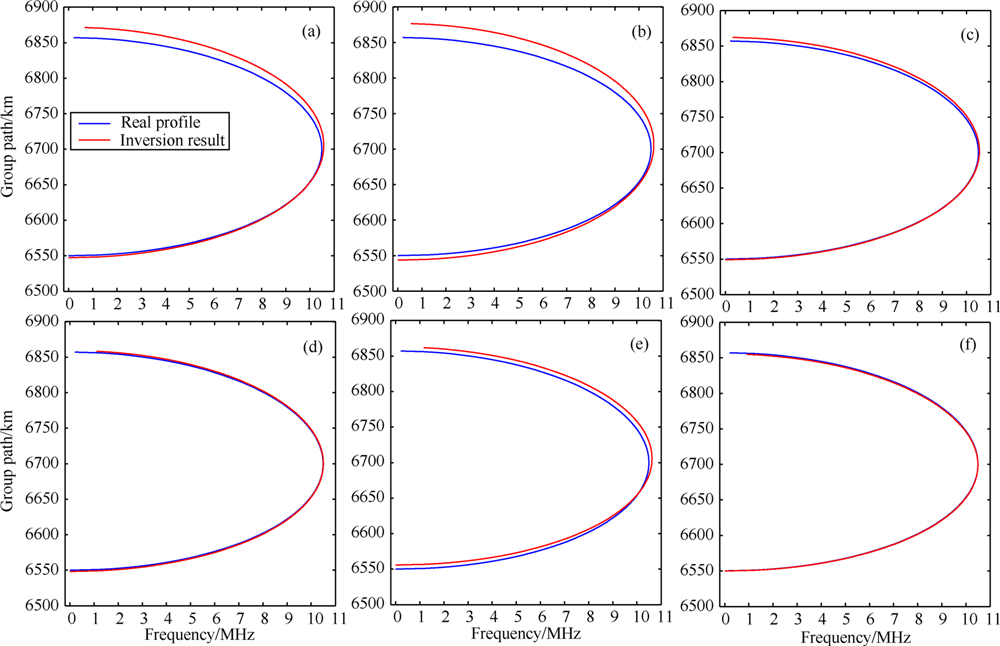 |
图 4 群体大小N=50、150时,遗传算法、模拟退火算法和混合遗传算法反演所得电子浓度剖面与真实剖面 (a)遗传算法,N=50;(b)模拟退火算法,N=50;(c)混合遗传算法,N=50;(d)遗传算法,N=150;(e)模拟退火算法,N=150;(f)混合遗传算法,N=150. Fig.4 The resulting electron density profiles of GA, SA and HGA, and the real profiles at the population size 50,150 (a)GA, N=50;(b) SA, N=50; (c) HGA, N=50; (d) GA, N=150; (e) SA, N=150; (f) HGA, N=150. |
(2)迭代次数的改变
每种算法得到最佳反演结果都需要一定的迭代次数.迭代次数取值过小,反演的结果可能是局部最优解;迭代次数取值过大,则会导致反演算法的运算效率降低.所以,迭代次数的取值对于提高计算精度和效率至关重要.表1给出了迭代次数k为55次时,三种算法的反演结果.将k分别设置为30和70(对于模拟退火算法和混合遗传算法来说,通过改变 初始温度的值来改变迭代次数),三种算法的反演结果见表3,其中 dfc、drb、drm、δfc、δrb、δrm、K含义同表1.
将k=30和k=70时三种算法反演得到的模型参数分别代入QP模型,得到利用反演参数合成的电子浓度剖面图,将该剖图与图 1做比较,比较结果见图 5.
| 表3 迭代次数k=30、70,群体大小N=100时,遗传算法、模拟退火算法和混合遗传算法的反演结果 Table 3 The inversion results of GA, SA and HGA at the iteration times 30,70 and the population size 100 |
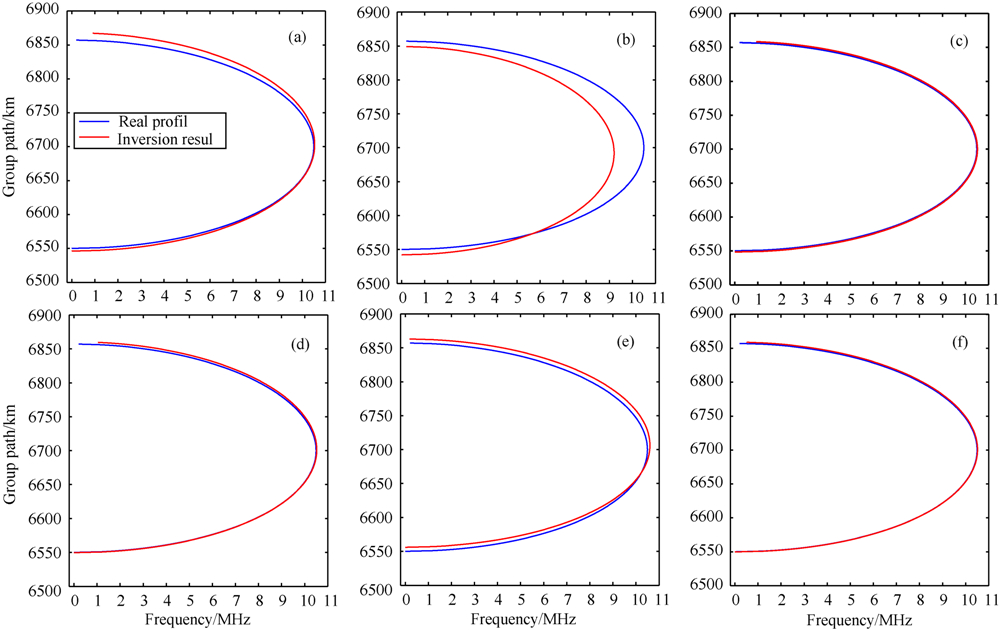 |
图 5 迭代次数k=30、70时,遗传算法、模拟退火算法和混合遗传算法反演所得电子浓度剖面与真实剖面 (a)遗传算法,k=30;(b)模拟退火算法, k=30;(c)混合遗传算法, k=30;(d)遗传算法, k=70;(e)模拟退火算法, k=70;(f)混合遗传算法, k=70. Fig.5 The resulting electron density profiles of GA, SA and HGA, and the real profiles at the iteration times 30,70 (a)GA, k=30;(b) SA, k=30; (c) HGA, k=30; (d) GA, k=70; (e) SA, k=70; (f) HGA, k=70. |
(3) 结果分析
由表1、表2可知,群体大小N由100变为50后, 遗传算法的反演结果以fc为参考,从0.03变为 0.08,反演参数的偏差和标准偏差相比改变前扩大了3倍左右,模拟退火算法的反演结果仍然不理想,混合遗传算法反演结果与改变前基本一致.群体大小由100变为150后,遗传算法的反演结果与改变前没有大的变化,模拟退火算法的反演结果依旧不理想,混合遗传算法的反演结果以fc为参考,从0.02变为0.00,反演参数的偏差和标准偏差大体上比改变前小,虽然群体大小改变前的反演结果很好,但是改变后的结果更优.将图 3和图 4结合起来比较,可以清楚地看到群体大小由50变为150的这个过程中,遗传算法反演得到的电子浓度剖面与真实剖面越来越接近,最后与真实剖面完全重合,模拟退火算法反演得到的电子浓度剖面有接近真实剖面的趋势,但它们始终没有重合,相比之下,混合遗传算法反演得到的电子浓度剖面一直都与真实剖面吻合得很好.
由表1和表3可知,迭代次数由55次变为30次后,遗传算法的反演参数偏差和标准偏差均变 大,特别是rb的偏差和标准误差分别从0.37、2.3695 增加到3.67、6.5932,模拟退火的反演结果也均变大,比改变前的结果更糟糕,混合遗传算法的反演结果基本没变.迭代次数由55次增大为70后,遗传算法的反演结果与改变前没有大的变化,模拟退火算法反演参数的偏差比改变前增加了3倍左右,标准偏差比改变前缩小4倍左右,混合遗传算法的反演参数的偏差和标准偏差大体上比改变前小,反演结果更理想.将图 3和图 5结合起来比较,可以清楚地看到迭代次数的改变给三种算法反演所得电子浓度剖面带来的影响,该影响跟群体大小变化产生的影响是一样的,在这里不重复描述.
以上结果说明,群体和迭代次数小的变动不能改善模拟退火算法的反演结果,遗传算法在群体和迭代次数较小的情况下容易陷入局部最优,取得好的反演结果需要较大的群体和迭代次数,而群体和迭代次数越大需要的反演时间就越多,这就需要经过多次实验来选取合适的群体大小和迭代次数.相比遗传算法来说,混合遗传算法的反演结果不易受到群体和迭代次数大小改变的影响,在群体和迭代次数比较小的情况下也能取得好的反演结果,降低了对参数选取的依赖性和人为因素的干扰,充分体现了混合遗传算法在实际应用中的价值.
5 实测电离图的反演为了进一步验证混合遗传算法在斜测电离图反演上的优越性,本文分别利用遗传算法、模拟退火算法和混合遗传算法对武汉大学电离层实验室获得的2010年8月25至26日实测数据进行反演.实验中用到了三部WISS(武汉大学电离层探测系统):WISS-1、 WISS-2和WISS-3,分别部署在武汉大学电离层实验室(30.5°N,114°E)、广东省深圳市罗湖区(22.5°N,114.1°E)和江西省宜春市(27.7°N,114.3°E).WISS-1和WISS-2分别用来发射和接收斜向探测信号,用于电离层的斜向探测.WISS-3在斜测链路中继点附近,用来进行电离层垂直探测以获得此处上空的电离层临界频率,用于验证斜向探测电离图反演结果.本次实验共获得26张斜测电离图,其中日落期间的斜测电离图来自26日.26日上 午10点到晚上8点,Dst指数在0~-20之间变 化,表明了背景电离层较为平静,没有明显的地磁扰动.
图 6所示是3部WISS在2010年8月26日下午3点获取的一对探测数据.从图 6b中我们可以清 晰看到F2层的垂测回波描迹,并且可以测得 f0F2=9.45 MHz.从图 6a中可以清晰看到F2层的斜测回波描迹,其中高角O波和高角X波发展完好.反演开始之前,需要在斜测回波描迹上选取5个点作为输入数据,低角波上选取3个点,高角O波上选取2 个点,然后根据第3节中讲述的反演步骤对实测电离图进行反演.遗传算法的反演结果是:fc=8.997 MHz; rb=6565.0321 km;rm=6641.7978 km; Δfc=0.4531 MHz.模拟退火算法的反演结果是: fc= 10.347 MHz;rb=6596.1859 km;rm=6692.3718 km; Δfc=0.8974 MHz.混合遗传算法的反演结果是:fc=9.2465 MHz;rb=6580.8237 km;rm=6660.5666 km;Δfc=0.2045 MHz.图 7给出了采用三种算法的反演结果合成的斜测电离图与真实值合成的斜测电离图比较结果.图 8给出了三种算法反演所得电子浓度剖面,从中可以直接读出三种算法反演得到的fc.
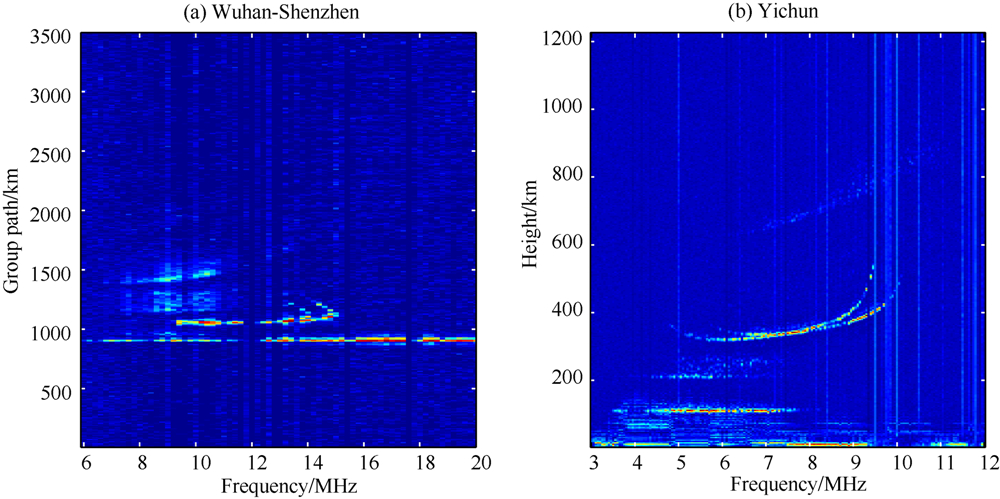 |
图 6 2010年8月26日15点斜向探测电离图(a)和垂测图(b) Fig.6 The oblique ionogram (a) and vertical ionogram (b) at 3:00pm, Aug.26, 2010 |
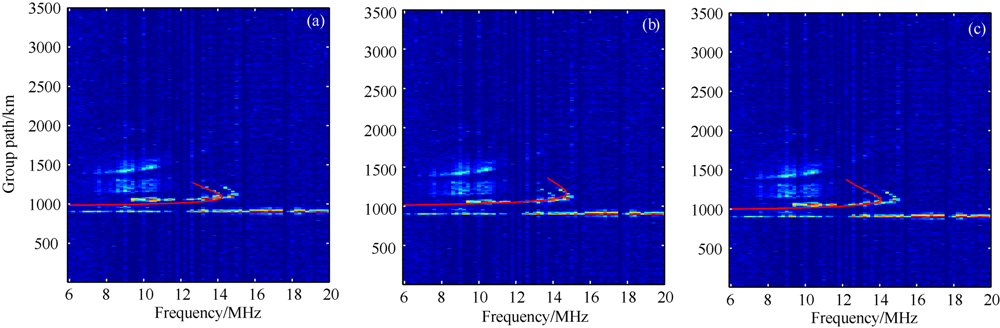 |
图 7 反演得到的模型参数值合成的斜测电离图与实测电离图比较结果(a)遗传算法;(b)模拟退火算法;(c)混合遗传算法. Fig.7 The compared results between measured ionograms and synthetic oblique ionograms (a)GA;(b)SA;(c)HGA. |
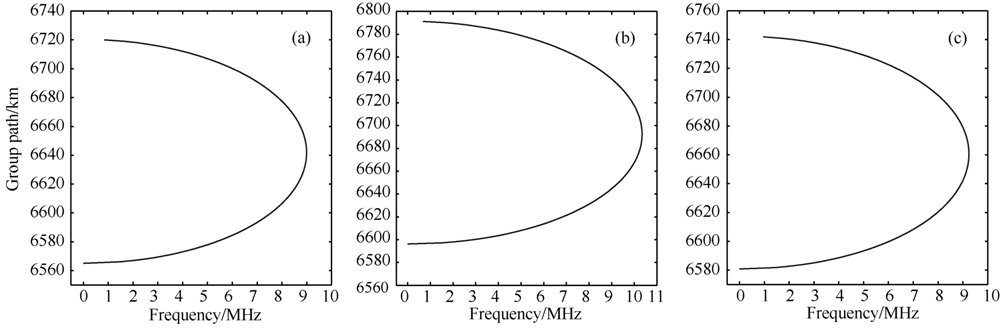 |
图 8 反演所得电子浓度剖面(a)遗传算法;(b)模拟退火算法;(c)混合遗传算法. Fig.8 The resulting electron density profiles(a)GA;(b)SA;(c) HGA. |
遗传算法、模拟退火算法和混合遗传算法反演得到的fc与垂测结果的误差分别为:0.4531 MHz、0.8974 MHz和0.2045 MHz,由此可知,混合遗传算法的反演结果最接近垂测结果.图 7给出了三种算法反演得到的模型参数值合成的斜测电离图与实测电离图的比较,可以看出(c)图吻合得最好,高角波部分完全重合,低角波部分基本重合,相比之下,(a)图低角波部分没有重合,(b)图高角波部分没有重合.以上结果表明,混合遗传算法的反演效果优于遗传算法和模拟退火算法,在实测电离图反演中具有明显优势.
本次实验共对26张斜测电离图进行了反演.将三种算法反演得到的fc与其对应的垂测结果进行差值比较(以垂测结果为基准),得到三种算法的fc的误差统计结果,如图 9所示.
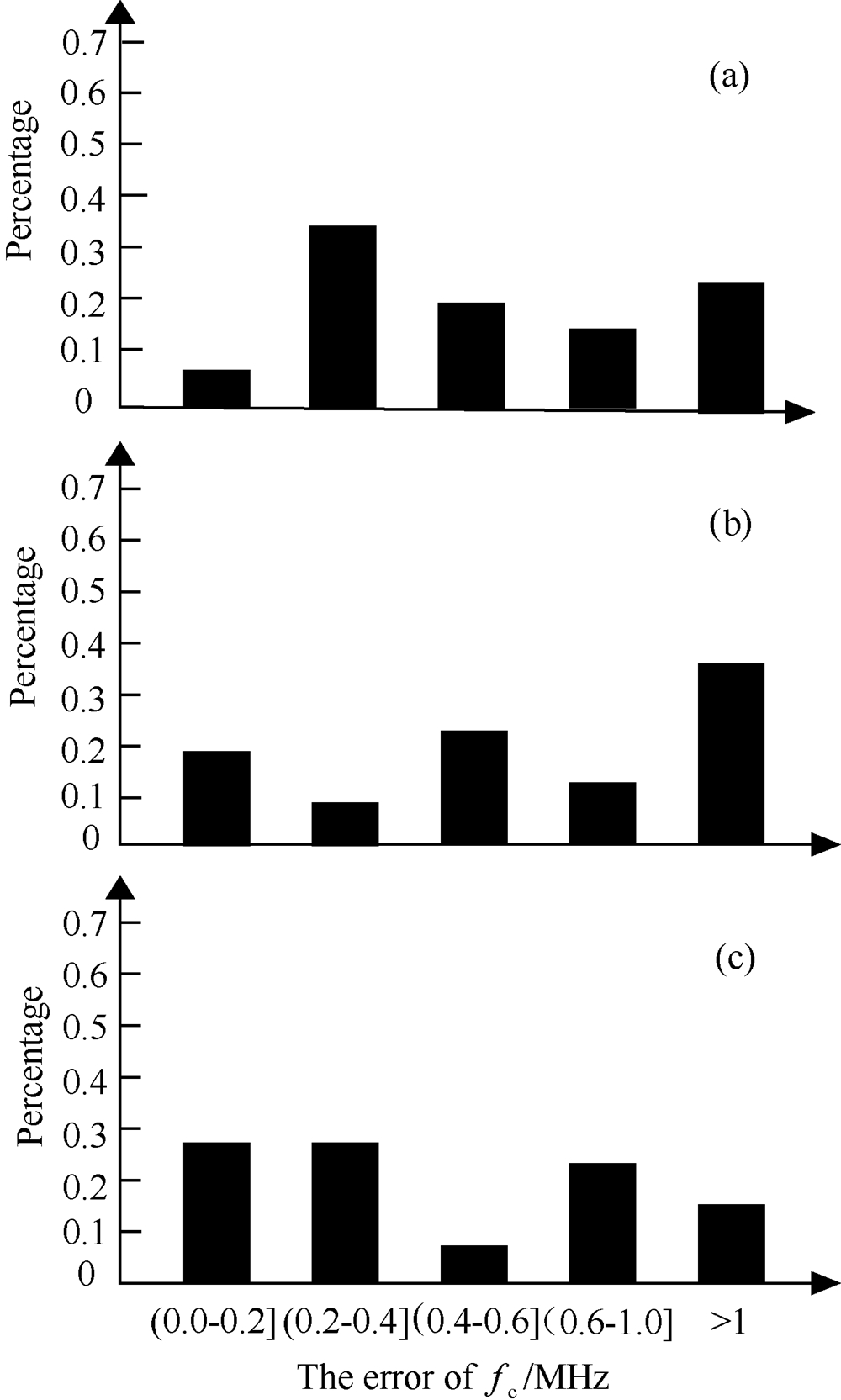 |
图 9 三种算法的反演结果统计(a)遗传算法;(b)模拟退火算法;(c)混合遗传算法. Fig.9 Statistical results(a) GA;(b) SA;(c) HGA. |
文中使用的斜向探测装置工作于扫频模式,扫频步进为0.2 MHz.本文指定fc的误差允许范围是:0.0~1.0 MHz,与国际无线电科学联盟UESI提出的±5Δ标准(Δ是斜测电离图的分辨率)一致.如果fc的误差超过1.0 MHz,说明反演结果不正确;fc的误差在0.0~0.4 MHz之间,则说明反演 结果相当精确.从图 8可知,混合遗传算法有84.62% 的反演结果控制在误差范围之内,高于模拟退火算 法(65.38%)和遗传算法(76.93%),并且混合遗传算法有超过一半的反演结果相当精确,远远 高于模拟退火算法(26.92%),遗传算法则有42.31% 的反演结果相当精确.可见,三种算法的反演结果依次是混合遗传算法优于遗传算法,遗传算法优于模拟退火算法,其中混合遗传算法的反演结果是最为精确的,这充分说明了混合遗传算法在斜测电离图反演上的优越性.
6 结论在统一设置算法参数的情况下,本文采用遗传算法、模拟退火算法和混合遗传算法对同一张合成的斜测电离图进行反演,通过比较三种算法的反演结果和得到最佳反演结果所需的迭代次数,得出混合遗传算法是一种进化速度快、反演精度高的优化算法.随后,通过比较分析群体大小和总迭代次数的改变对三种算法反演结果的影响,得出混合遗传算法在反演的过程中具有一定的稳定性.特别是在减小群体大小和总迭代次数时,混合遗传算法能够有效地减小参数的选取对反演结果的影响,降低了反演算法对参数选取的依赖性和人为因素的影响.文中还比较分析了上述三种算法在实测电离图中的反演情况,得出混合遗传算法的反演结果与垂测结果最接近,合成的斜测电离图与实测电离图最吻合.
进一步,文中对26张实测电离图进行了反演,统计分析了三种算法的反演结果,结果显示三种算法大部分反演结果都控制在误差范围之内,但仍然都有部分反演结果超过了1MHz.分析产生这一现象的原因,发现反演误差较大的斜测电离图,其探测时段大体处于17 ∶ 00~19 ∶ 30LT之间,这一时期正好为日落时期.从日落期间的宜春频高图上可以观测到类似‘satellite traces’描迹(Li et al.,2012),再加上在此期间电离层变化剧烈(一个半小时内临频变化达到2.8 MHz), 表明反演的部分误差来自于电离层的结构扰动.由于本文采用的QP模型中没有加入扰动项,所以无论是哪一种反演方法,在此期间的反演结果都会存在很大的误差.然而,正确地分析日出日落的数据可以获得更多的电离层变化信息,所以这将是后续工作需要考虑的地方.值得一提的是,混合遗传算法只有15.38%的反演结果超过了1 MHz,低于模拟退火算法(34.62%)和遗传算法(23.07%),这说明了反演误差的来源不仅仅与斜测电离图的探测时段有关,还与算法本身的寻优能力和稳定性有关.因此,混合遗传算法的寻优能力和稳定性要优于遗传算法和模拟退火算法,在实测电离图反演中具有明显优势,是一种值得推广应用的反演方法.
另外,文中采用单层QP模型来表示斜测电离图中F2层的电子浓度分布,事实上斜测电离图还存在F1层和E层(Es层).清晰地获得含有F1层的斜测电离图,采用多层QP模型作为电离层模型,并在模型中加入扰动项,将有助于反演结果精度的进一步提高,使混合遗传算法在实际应用中具有更强的适用性和应用价值,这也是以后需要进一步努力的地方.
| [1] | Benito E, Saillant S, Molini J P, et al. 2008. Inversion of backscatter ionograms optimization by using simulated annealing and genetic algorithms. Geoscience and Remote Sensing Symposium, IEEE International, 1127-1130, doi:10.1109/IGARSS.2008. 779553. |
| [2] | Croft T A, Hoogasian H. 1968. Exact ray calculations in a quasi-parabolic ionosphere with no magnetic field. Radio Science, 3(1): 69-74. |
| [3] | Dyson P L, Bennett J A. 1988. A model of the vertical distribution of the electron concentration in the ionosphere and its application to oblique propagation studies. Journal of Atmospheric and Terrestrial Physics, 50(3): 251-262. |
| [4] | Gething P J D, Maliphant R G. 1967. Unz's application of Schlomilch's integral equation to oblique incidence observations. Journal of Atmospheric and Terrestrial Physics, 29(5): 599-600. |
| [5] | Gui W H, Huang T S, Yang C H. 2001. An improved Genetic Algorithm and its application in raw material purchase of nonferrous enterprise. Mining and Metallurgical Engineering (in Chinese), 21(3): 59-62. |
| [6] | Heaton J A T, Cannon P S, Rogers N C, et al. 2001. Validation of electron density profiles derived from oblique ionograms over the United Kingdom. Radio Science, 36(5): 1149-1156, doi:10.1029/1999RS002423. |
| [7] | Ingber L. 1989. Very fast simulated re-annealing. Mathematical and Computer Modelling, 12(8): 967-973. |
| [8] | Kirkpatrick S, Gelatt C D, Vecchi M P. 1983. Optimization by simulated annealing. Science, 220(4598): 671-680. |
| [9] | Li G Z, Ning B Q, Abdu M A, et al. 2012. Precursor signatures and evolution of post-sunset equatorial spread-F observed over Sanya. J. Geophys. Res., 117(A8): A08321, doi:10.1029/2012JA017820. |
| [10] | Liu W, Jiao P N, Wang J J. 2003. A inverse algorithm of oblique ionogram and its stability. Chinese Journal of Radio Science (in Chinese), 18(6): 597-601, doi:10.3969/j. issn. 1005-0388. 2003. 06. 001. |
| [11] | Phaninong B, Chen J, Dyson P L, et al. 1995. Inversion of oblique ionograms including the Earth's magnetic field. Journal of Atmospheric and Terrestrial Physics, 57(14): 1715-1721. |
| [12] | Rao N N. 1973. A note on the analysis of oblique ionograms. Journal of Atmospheric and Terrestrial Physics, 35(8): 1561-1563. |
| [13] | Rao N N. 1974. Inversion of sweep-frequency sky-wave backscatter leading edge for quasiparabolic ionospheric layer parameters. Radio Science, 9(10): 845-847, doi:10.1029/RS009i010p00845. |
| [14] | Rao N N. 1975. Analysis of discrete oblique ionogram traces in sweep-frequency sky-wave high resolution backscatter. Radio Science, 10(2): 149-153, doi:10.1029/RS010i002p00149. |
| [15] | Reilly M H, Kolesar J D. 1989. A method for real height analysis of oblique ionograms. Radio Science, 24(4): 575-583, doi:10.1029/RS024i004p00575. |
| [16] | Reilly M H. 1985. Ionospheric true height profiles from oblique ionograms. Radio Science, 20(3): 280-286, doi:10.1029/RS020i003p00280. |
| [17] | Smith M S. 1970. The calculation of ionospheric profiles from data given on oblique incidence ionograms. Journal of Atmospheric and Terrestrial Physics, 32(6): 1047-1056. |
| [18] | Song J, Zhao Z Y, Zhou C, et al. 2011. Inversion of HF sweep-frequency backscatter ionograms. Chinese J. Geophys. (in Chinese), 54(8): 1953-1959, doi:10.3969/j. issn. 0001-5733. 2011. 08. 002. |
| [19] | Song P, Xu T. 2008. Inversion of oblique sounding for ionospheric parameters based on genetic algorithm. Modern Electronics Technique (in Chinese), 31(19): 16-18. |
| [20] | Wang Z F, Cui D H. 2009. A hybrid algorithm based on genetic algorithm and simulated annealing for solving portfolio problem. International Conference on Business Intelligence and Financial Engineering, 106-109, doi:10.1109/BIFE. 2009. 34. |
| [21] | Wu H Y, Chang B G, Zhu C C, et al. 2000. A multigroup parallel genetic algorithm based on simulated annealing method. Journal of Software (in Chinese), 11(3): 416-420. |
| [22] | Xie S G. 2001. A study on the ionospheric parameter inversion of backscatter ionograms[Ph. D. thesis](in Chinese). Wuhan: School of Electronic Information of Wuhan University. |
| [23] | Xu T. 2006. Study on genetic inverse method for ionospheric parameters from VI and oblique ionograms[Master's thesis](in Chinese). Xi'an: School of Scinece of Xi'an Electronic and Science University. |
| [24] | Zhou L, Huang S Z. 2005. Study of hybrid genetic algorithm based on simulated annealing. Application Research of Computers (in Chinese), 22(9): 72-73. |
| [25] | 桂卫华, 黄泰松, 阳春华. 2001. 一种改进遗传算法及其在企业原料采购优化中的应用. 矿冶工程, 21(3): 59-62. |
| [26] | 柳文, 焦培南, 王俊江. 2003. 斜测电离图反演及其不稳定性研究. 电波科学学报, 18(6): 597-601, doi:10.3969/j.issn.1005-0388. 2003. 06. 001. |
| [27] | 宋君, 赵正予, 周晨等. 2011. 高频返回散射扫频电离图的反演. 地球物理学报, 54(8): 1953-1959, doi:10.3969/j.issn. 0001-5733. 2011. 08. 002. |
| [28] | 宋鹏, 徐彤. 2008. 基于遗传算法斜向探测电离层参数反演研究. 现代电子技术, 31(19): 16-18. |
| [29] | 吴浩扬, 常炳国, 朱长纯等. 2000. 基于模拟退火机制的多种群并行遗传算法. 软件学报, 11(3): 416-420. |
| [30] | 谢树果. 2001. 斜向返回探测电离层参数反演方法研究[博士论文]. 武汉: 武汉大学电子信息学院. |
| [31] | 徐彤. 2006. 垂直和斜向探测电离层参数反演遗传算法研究[硕士论文]. 西安: 西安电子科技大学理学院. |
| [32] | 周丽, 黄素珍. 2005. 基于模拟退火的混合遗传算法研究. 计算机应用研究, 22(9): 72-73. |
 2014, Vol. 57
2014, Vol. 57


