地球物理学报  2014, Vol. 57 Issue (2): 671-678   PDF    
引用本文
薛国强, 王贺元, 闫述, 周楠楠. 瞬变电磁场时域格林函数解. 地球物理学报,2014,57(2): 671-678, doi: 10.6038/cjg20140230   
XUE Guo-Qiang, WANG He-Yuan, YAN Shu, ZHOU Nan-Nan. Time-domain Green function solution for transient electromagnetic field. Chinese Journal Geophysics,2014,57(2): 671-678, doi: 10.6038/cjg20140230   
瞬变电磁场时域格林函数解
薛国强1, 王贺元2, 闫述3, 周楠楠1    
1. 中国科学院矿产资源研究重点实验室, 中国科学院地质与地球物理研究所, 北京 100029;
2. 辽宁工业大学理学院, 锦州 121001;
3. 江苏大学计算机科学与通信工程学院, 镇江 212013
投稿时间:2013-5-6    最后修改时间: 2013-8-1 .
基金项目：国家973重点基础研究发展计划（2012CB416605）、国家自然科学基金（41174090）和国家重大科研装备研制项目（ZDYZ2012-1-05-04）资助.
第一作者简介：薛国强，男，1966年生，研究员，主要从事瞬变电磁法的研究与应用.E-mail：ppxueguoqiang@163.com
摘要：近源时间域电磁场具有信号强、探测深度大、精度高等优点，但传统勘探电磁场理论中偶极子近似在近源会引起较大误差，导致这一优势的发挥受到了制约.开展直接时间域电磁场解析式研究，是解决这一问题的途径之一.本文提出在点电荷微元假设下，引入时域格林函数，求取瞬变电磁场时间域解析解.采用积分运算法，把电磁场阻尼波动方程的求解问题转化为求其格林函数积分形式解的问题；建立辅助路径解决奇点问题，利用复分析中的约当引理、留数定理和广义函数等理论和方法，推导计算出时间域格林函数的时空四重广义积分.得到达朗贝尔方程的直接时域格林函数精确解析式，与传统方法“比拟”出的公式具有相同的形式，验证了本文推导的时域格林函数解析公式的正确性；推导出扩散方程的直接时间域解析解.通过与时变点电荷源时间域的电磁响应近似表达式进行对比，得出本文所推导的公式计算精度较高的结论；建立了全空间回线源瞬变电磁场问题的直接时间域求解公式.为解决全场区瞬变电磁场精细探测直接时域解析问题提供了基础理论.
关键词： 瞬变电磁场     点电荷     时域格林函数     达朗贝尔方程     扩散方程    
Time-domain Green function solution for transient electromagnetic field
XUE Guo-Qiang1, WANG He-Yuan2, YAN Shu3, ZHOU Nan-Nan1    
1. Key Laboratory of Mineral Resources, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
2. College of sciences, Liaoning University of Technology, Jinzhou 121001, China;
3. School of Computer Science and Telecommunication Engineering, Jiangsu University, Zhenjiang 212013, China
Abstract: Time-domain near-source electromagnetic method has the merit of strong signal, deep detecting depth and high accuracy. However, the method meet problem, because dipole approximation in the near-source will cause greater error based on traditional electromagnetic theory. Studying direct time domain electromagnetic field analytical formula derivation is one way of solving the problem. Based on point charge hypothesis, TEM field analytical solution has been derived by introducing time-domain Green function in this paper. Integral formula has been used to transform electromagnetic field damping wave equation into Green function integral form. Auxiliary path has been constructed for solving singularity problem. 4-tuple generalized integral formula of time-domain electromagnetic field response has been arrived by using Jordan's lemma, the residue theorem and generalized function method. Direct-time-domain exact solution of D'Alembert equations firstly has been derived, whose form is agree with the traditioanl "matching" result, which show that the method of time-domain electromagnetic field based on Green function is right. Then, the direct-time-domain formula of diffusion function also has been given. After the copmaresion the numerical result between point charge Green function exact sulotion and approximate solution,it can be concluded that the derivation formula in this paper has higher precision. Furtherly, the full-space TEM direct-time-domain solution due to loop-source has been derived using integral method. The achievement lay a theoretical fundation for solving the problem of TEM All-Zone detection with directy time domain analytical solution.
Key words: Transient electromagnetic field     Point charge     Time-domain Green functions     D’Alembert equation     Diffusion equation    

1 引言

在近源情况下，CSAMT法无法将辐射场从占主要优势的自有场中分离出来,故仅有某些场分量可进行几何测深(曼和凯勒, 1987; 陈明生和闫述, 2005),对于瞬变电磁法，当采用低频占优的阶跃波激发时,电流关断后得到辐射场，即远区场, 获得近源深部探测能力(牛之琏,2007; 薛国强等, 2013)和较高的信噪比.为地下深部矿产资源精细探测提供了一种施工便利、探测深度大、场信息量丰富的新的手段.近年来,近源探测得到了极大的 关注(薛国强等, 2013; Nestor and Alumbaugh, 2011; Evan et al., 2012).

在传统的勘探电磁场理论研究中,大多在偶极子假设前提下,根据频率域解析解,得到时间域解(Knight and Raiche, 1982；Raiche, 1987). 在电磁场近源区,偶极子近似解与精确解之间存在较大误差(薛国强等, 2011),偶极子假设理论无法适应近源情况下精确勘探的需要.研究点电荷微元假设下的瞬变电磁场直接时间域解具有重要意义.

纳比吉安(1992)给出了单位点源的频率域格林函数,通过反付氏变换,得到全空间直流点源静电场时域格林函数和时间域电磁场波动方程解析解，并将无穷小偶极源作为点源代入格林函数表达式,得到瞬态偶极元电磁场响应.由于推导时需将点源放在坐标原点,只给出了单位点源的响应,未考虑源尺寸大小以及不同位置源激发时响应,无法处理大尺度的长接地导线源和大回线源.电动力学中采用“比拟”法求取波动方程时域解,首先给出时间域点电荷源波动方程的通解,与静态场的点电荷的电位解析式相比较,得到通解中的待定系数，由此得到波动场的推迟标量位函数(冯恩信, 2005).

瞬变电磁场直接时间域响应研究手段有解析和 数值模拟方法(闫述等, 2002; Wang and Hohmann, 1993)，对于解析法，从时变点电荷出发的直接时间域格林函数求解扩散方程的研究,目前还未有更多的相关报道.为避免频时变换实现过程中的计算误差,与以往“比拟”法或者先在频率域推导格林函数思路的不同,本文利用时间域格林函数直接推导电磁场波动方程解析解，同时，首次推导出扩散方程的直接时间域解析式,并给出了全空间回线源瞬变电磁直接时间域响应式.研究成果为瞬变电磁法的进一步发展和实际勘探提供新的理论基础.

2 电磁场格林函数基本解

在均匀、线性、各向同性的媒质中有源的麦克斯韦方程组为(方文藻等, 1993)

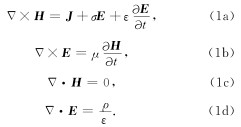
式中,J 为电流源密度矢量, ρ为自由电荷密度. E 是电场强度 (V/m), H是磁场强度 (Wb/m2). v2=1/εμ， (ν为光速)μ,ε分别为磁导率和介电常数.

由麦克斯韦方程组(1),可得到电磁场矢量阻尼波动方程(方文藻等, 1993)

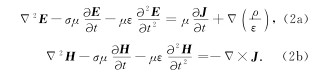
当场变化很快或介质电阻率趋于无穷时,(2)式变为达朗贝尔波动方程(方文藻等, 1993)

当场变化比较慢并在良导介质中传播时,(2a)式和(2b)式分别为扩散方程(方文藻等, 1993)

当点电荷位于坐标原点时,(2)式对应的频率域格林函数为(纳比吉安, 1992)

式中，r=(x2+y2+z2)1/2表示到坐标原点的距离.

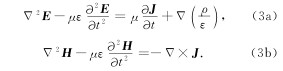
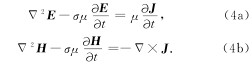
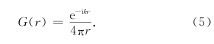
对(5)式进行付氏反变换,得到时间域格函数(纳比吉安, 1992)

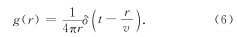
通过“比拟”方法，可得到更普遍的、点电荷不位于坐标系原点的解析解. (4)式对应的标量位函数的通解为(冯恩信, 2005)

式中, c1是待定系数.R= | r － r ′ |. r ′为源点到原点的距离.

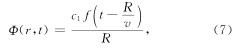
由于静态点电荷势函数为(冯恩信, 2005)

令(7)式中的t= 0, 将(7)和(8)“比拟”后，确定出式(7)中的系数c1，由此得波动场的推迟标量位函数(冯恩信, 2005)

3 波动方程直接时域解

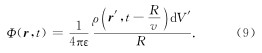
电磁场达朗贝尔波动方程为(冯恩信, 2005)

为了直接推导出方程(10)时域格林函数的解析形式,将方程(10)右端项用δ 函数表示成积分形式. 通过积分算符对δ函数的作用,并令源点x′=(x′,y′,z′), 场点x=(x,y,z),经推导得出方程(10)对应的格林函数形式

其中K为三维空间积分变量,K0为时间积分变量. 故方程(10)的格林函数解为

(12)式中的格林函数的物理意义为：在t′时刻位于x′的单位强度源在t时刻在点x处所产生的场. 对所有源引起的场及所有时刻响应进行积分,便得到给定时空坐标的场量u(x,t).

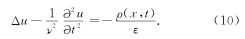
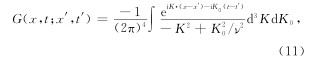
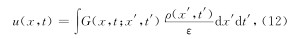
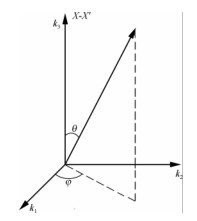
下面通过具体计算格林函数(11)式中右端的时空四重积分给出格林函数的解析式，选用如图1所示的球坐标, 图中x－x′为极轴.

图 1 球坐标系统示意图 Fig. 1 Sphere coordinates system

首先对(12)式中的角度部分积分，由于 K·(x－x′)= K x－x′ cosθ=r x－x′ cosθ(这里r= K 指极径)，利用

可得

再对(12)式中径向部分进行积分,将r积分变为沿整个实轴的积分

将(13)中分母分解因式得

当积分(14)式分母等于零时，在实轴上存在两个一阶奇点.为解决这一问题,引入辅助路径CR和Cε,积分回路的选择如图 2所示,利用约当引理和留数定理求得

再利用δ 函数的积分表示得

因此方程(10)的解为

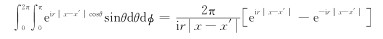
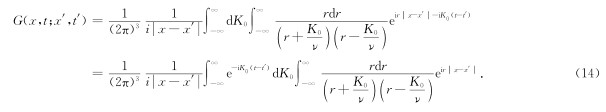
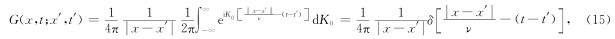
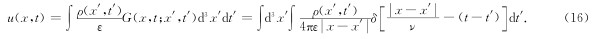
利用δ函数的性质，可以求出对t′的积分

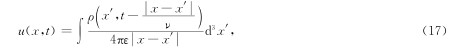
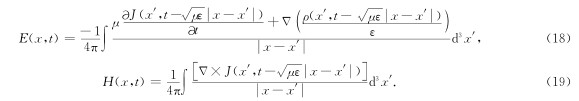
(17)式是达朗贝尔方程直接时间域推迟势的公式.与经典电磁场理论(冯恩信, 2005)中由“比拟”方法得到的公式(9)一致.说明本文方法是正确的.进一步地,由(17)和(3)式, 得到电场和磁场分量时间域的响应解析公式


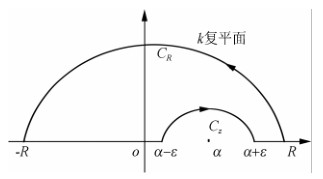
图 2 积分路径示意图 Fig. 2 Integral path diagram
4 扩散方程直接时域解

方程(4)对应的标量形式扩散方程(冯恩信, 2005)

经推导得到扩散方程 (20) 的形式Green函数为

与前面达朗贝尔方程格林函数解的讨论类似,经积分运算得到

所以扩散方程 (20)的解

由(22)式得扩散方程(4)的电场和磁场响应解析公式

其中

5 计算结果对比与分析

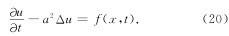
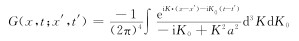
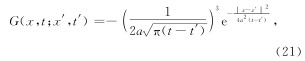
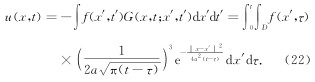
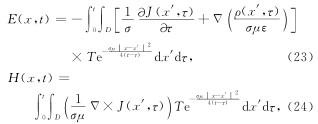
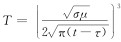
本文分别给出了全空间时变点电荷源的直接时间域波场方程和扩散方程的电磁响应表达式.已经证实由“比拟“法得到的波动场直接时域格林函数(冯恩信, 2005)公式(9)与经过严格数学推导所得出的精确解析解公式(17)具有相对的形式. 对于所推导出来的直接时间域扩散方程，将通过与纳比吉安(1992)近似计算结果进行对比，以说明文中结果的正确性.

经反拉氏变换和类比法，纳比吉安(1992)给出似稳态情形下扩散场直接时域格林函数的近似公式式中，g(r,t)表示扩散场时域格林函数响应.

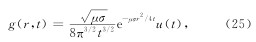
分别对格林函数精确表达式(21)式和似稳态情形下近似表达式(25)式进行计算，并画出响应值随时间变化曲线.

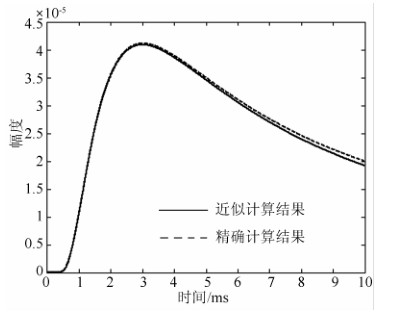
图 3给出了导电率为0.01 S/m的全空间中，距源100 m处G(x,t;0,0)随时间的变化曲线.图中实线表示根据公式(25)的近似计算结果.虚线表示根据公式(21.)的精确计算结果. 对比两种公式的计算结果曲线,可以明显看出两种曲线基本吻合.

图 3 Green函数关于时间的变化曲线 Fig. 3Variation curves of Green function versus time

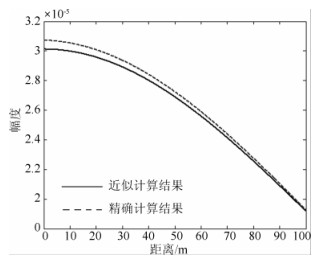
图4给出了导电率为0.01 S/m的全空间中，时间t=10 ms格林函数精确表达式(21)式和似稳态情形下近似表达式(25)随距离变化曲线.图中实线表示根据公式(21)的计算结果.虚线表示根据公式(25)的计算结果.容易看出距离较小时存在误差，距离较大时两曲线基本吻合.从而验证了远场区情况下,在点电荷假设下直接时域格林函数精确解析解与格林函数近似解是一致的，而在近源情况下存在明显误差.说明本文推导出来的格林函数精确解具有较高的精度.

图 4 Green函数关于距离的变化曲线 Fig. 4 Curves of Green function versus distance
6 回线源直接时域解

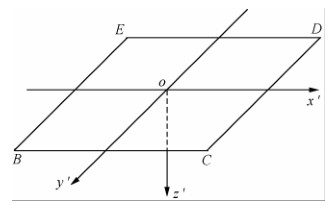
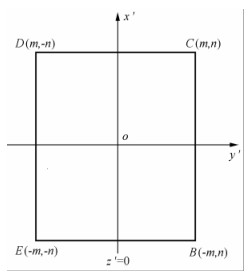
当发射源形式给定后,通过时域电磁场强度公式(23)和(24)可以得到任意场点处由点电荷发射源产生的总电磁场强度.针对大定源回线装置,建立如图5的三维坐标系.采用与矩形回线偶极子源积分 相同的研究思路(Poddar, 1983; Xue et al., 2012), 将整个回线源分成四段直线段EB,BC,CD,DE构成，当z=0时，可简化成平面坐标系(图6).

图 5 瞬变电磁回线源三维示意图 Fig. 5 TEM square loop source 3D system

图 6 瞬变电磁回线源二维示意图 Fig. 6 TEM square loop source 2D system

在整个回线源上产生电磁场是沿四条直线段上的点电荷产生的电磁场的迭加，源点x′=(x′,y′,z′)位于四条直线段上，场点x=(x,y,z)为任意点. 由此可得EB段参数方程为

弧长微元

由第一型曲线积分的计算公式经(23)和(24)式沿EB计算积分,得大回线源EB段扩散电磁场方程时域解为

其中

BC段参数方程为

同理，可得BC段扩散电磁场方程时域解为

其中，

CD段参数方程为

CD段扩散电磁场方程时域解为

其中

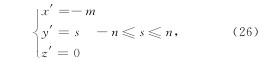
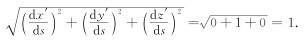
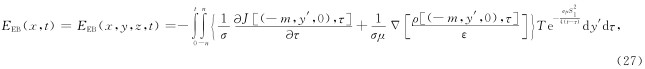
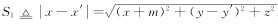
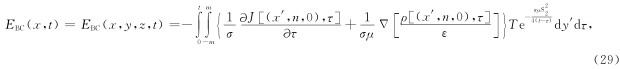
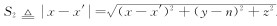
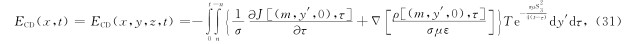
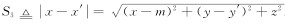
DE段参数方程为

DE段扩散电磁场方程时域解为

其中

同样地,各段的磁场分别为

扩散场总电场强度为

扩散场总磁场强度为

由此，可通过积分计算出任意场点处发射源产生的扩散场总电磁场强度.

7 结论

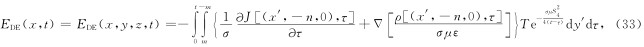
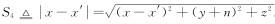
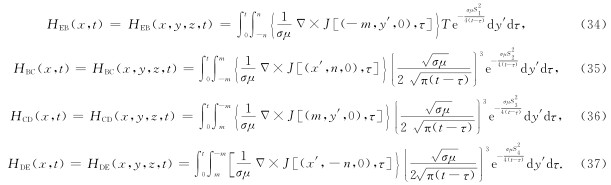
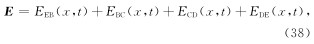
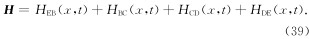
为了对瞬变电磁精细解释提供理论基础,本文经过严格数学推导得到麦克斯韦方程的时间域解析式,并给出了全空间回线源瞬变扩散电磁场直接时间域响应式.与纳比吉安文献中研究相比,本文直接采用时间域格林函数进行推导,避免了偶极子假设下由频域转到时域引起的误差；与电动力学中采用“比拟”法求取波动方程时域解相比,本文的直接推导算法更显得数学上的严密性. 这种方法克服了偶极子假设下只适用远场区的不足,也回避了引入位函数等繁琐的理论推导.研究成果完善了时间域电磁场理论,为瞬变电磁法的进一步发展和实际勘探提供新的理论基础.

附录 1 约当引理(Jordan′s lemma) 设f(z)=eiazg(z)是定义在上半圆周CR={z ∶ z=Reiωθ,θ∈〖0,π〗}上的复值连续函数，a＞0，则有

2 留数定理 设f(z)在围线或复围线C所围的区域D内，除z1,z2,…,zn外，解析，在闭域 =D+C除z1,z2,…,zn外连续，则

其中Res(f,zk)表示奇异点zk处的留数.

3 δ 函数定义及性质

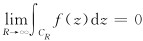
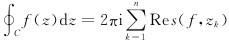
三维空间中动点r=(x,y,z)和定点r′=(x′,y′,z′)，δ 函数定义为

并且

其中dr=dxdydz，或者等价地定义为

δ 函数的积分表示为

其中四维矢量 x =( x ,t)， x =(x1,x2,x3)，x′=(x′,t′)，x′=(x′1,x′2,x′3)，K=(K1,K2,K3)，Kαxα=K1x1+K2x2+K3x3－K0t=K·x－K0t.

参考文献
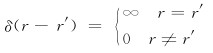
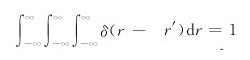
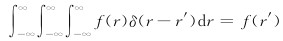
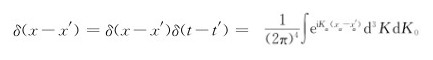
[1] Chen M S, Yan S. 2005. Analytical study on field zones, record rules, shadow and source overprint effects in CSAMT exploration. Chinese Journal of Geophysics (in Chinese), 48(4): 951-958.
[2] Evan S U, David A, Jerry M H, Chen J P. 2012. Numerical modeling analysis of short-offset electric-field measurements with a vertical electric dipole source in complex offshore environments. Geophysics, 77(5): E329-E34.
[3] Fang W Z, et al. 1993. Theory of TEM Sounding (in Chinese). Xi'an: Press of North-west Industry University, 1-5, 93-94.
[4] Feng E X. 2005. Electromagnetic Fields and Electromagnetic Waves (Second Edition). Xi'an: Xi'an Jiaotong University Press (in Chinese), 84, 144, 53-54, 124, 134, 143.
[5] Kaufman A A, Keller G V. 1987. Frequency and transient soundings. (in Chinese), Translated by Wang J M. Beijing: Geological Publishing House, 164-167.
[6] Knight J H, Raiche A P. 1982. Transient electromagnetic calculations using the Gaver-Stehfest inverse laplace transform method. Geophysics, 47(1): 47-50.
[7] Nabighian M N. Ed. 1992. Electromagnetic Methods in Applied Geophysics, Volume 1, Theory Society of Exploration Geophysicists. (in Chinese) Translated by Zhao J X, Wang Y J. Beijing: Geological Publishing House, 155-159.
[8] Nestor H C, Alumbaugh D. 2011. Near-source response of a resistive layer to a vertical or horizontal electric dipole excitation. Geophysics, 76(6): F353-F371.
[9] Niu Z L. 2007. Theory of Time Domain Electromagnetic Method (in Chinese). Changsha: Press of Central South University, 198-217.
[10] Poddar M. 1983. A rectangular loop source of current on multilayered earth. Geophysics, 48(1): 107-109.
[11] Raiche A P. 1987. Transient electromagnetic field computations for polygonal loops on layered earth. Geophysics, 52(6): 785-793.
[12] Wang T, Hohmann G W. 1993. A finite-difference, time-domain solution for three-dimensional electromagnetic modeling. Geophysics, 58(6): 797-809.
[13] Xue G Q, Bai C Y, and Yan S. 2012. Deep sounding TEM investigation method based on a modified fixed central-loop system. Journal of Applied Geophysics (in Chinese), 76: 23-32.
[14] Xue G Q, Chen W Y, Zhou N N, et al. 2013. Short-offset TEM technique with a grounded wire source for deep sounding. Chinese Journal of Geophysics (in Chinese), 56(1): 255-261, doi:10.6038/cjg20130126.
[15] Xue G Q, Yan S, Zhou N N. 2011. Theoretical study on the error caused by dipole hypothesis of Large-loop TEM response. Chinese Journal of Geophysics (in Chinese), 54(9): 2389-2396,doi:10.3969/j.issn.0001-5733.2011.09.022.
[16] Yan S, Chen M S, Fu J M. 2002. Direct Time-Domain numerical analysis of transient electromagnetic fields. Chinese Journal of Geophysics (in Chinese), 45(2): 275-284.
[17] 陈明生, 闫述. 2005. CSAMT 勘探中场区、记录规则、阴影及场源复印效应的解析研究. 地球物理学报, 48(4): 951-958.
[18] 方文藻等. 1993. 瞬变电磁法测深原理. 西安: 西北工业大学出版社, 1-5, 93-94.
[19] 冯恩信. 2005. 电磁场与电磁波(第2版). 西安: 西安交通大学出版社, 144, 53-54, 124, 134, 143.
[20] 考夫曼, 凯勒. 1987. 频率域和时间域电磁测深, 王建谋译. 北京: 地质出版社, 164-167.
[21] 米萨克 N 纳比吉安主编. 1992. 勘查地球物理电磁法 第一卷 理论. 赵经祥, 王艳君译. 北京: 地质出版社, 155-159.
[22] 牛之琏. 2007. 时间域电磁法原理. 长沙: 中南大学出版社, 198-217.
[23] 薛国强, 陈卫营, 周楠楠等. 2013. 电性源瞬变电磁全场域探测方法. 地球物理学报, 56(1): 255-261,doi:10.6038/cjg20130126.
[24] 薛国强, 闫述, 周楠楠. 2011. 由偶极子假设引起的大回线源瞬变电磁响应偏差分析. 地球物理学报54(9): 2389-2396,doi:10.3969/j.issn.0001-5733.2011.09.022.
[25] 闫述, 陈明生, 傅君眉. 2002. 瞬变电磁场的直接时域数值分析. 地球物理学报, 45(2): 275-284.