2. 中国科学院大学, 北京 100049;
3. 中国气象局国家空间天气监测与预警中心, 北京 100081
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. National Center for Space Weather, China Meteorological Administration, Beijing 100081, China
电离层LBH日辉辐射是由光电子与氮气分子碰撞激发而产生的,是电离层在远紫外辐射波段中最强的分子辐射信号.从空间对此信号进行观测,不仅可以监测高层大气中氮气(或氧气)分子的密度(Meier, 1991),还可以获得电离层中光电子通量的信息(Oran and Strickland, 1978),从而为高层大气状态的监测提供了一种强有力的方法.因此,LBH辐射被广泛用作星载遥感仪器的观测目标,比如DMSP卫星上的SSUSI(Paxton et al., 1992),TIMED卫星上的GUVI(Paxton et al., 1999),以及IMAGE卫星上的WIC(Mende et al., 2000)等.中国风云三号(FY-3)卫星上即将搭载广角极光成像仪(视场角为130°),首次对极光LBH辐射和电离层LBH日辉辐射进行探测,从而对极光活动及电离层的空间天气状况进行监测预报.
准确理解LBH辐射产生的物理过程,从而建立合理的计算模型,这是获得可靠的地球物理参数信息的重要保证.Mcewen等人(1966)率先讨论了LBH波带的辐射强度分布,但只给出了初步的理论计算公式.Conway(1992)研究了氮气分子的自吸收效应对LBH波带辐射传输过程的影响,指出氧气分子的吸收作用远大于氮气分子的自吸收作用.Dashkevich等人(1993),Eastes(2000)讨论了氮气分子激发态之间的耦合效应对LBH波带辐射的影响.Strickland等(1995, Evans等(1995在前人工作的基础上,给出了比较通用的LBH日辉辐射的计算模型.
当前,紫外波段的辐射传输模型及相应计算代码的研制仍然是国际上研究的热点(Huffman,1992).然而,能够用于远紫外波段辐射的计算代码 很少,比较通用的只有AURIC(Atmospheric Ultraviolet Radiance Integrated Code),即大气紫外辐射积分代码,它是由美国计算物理公司CPI(Computational Physics, Inc.)与空军Phillips实验室联合开发的(Link et al.,1992;Strickland et al.,1992).AURIC在计算LBH日辉柱辐射率时将沿观测视线LOS方向的太阳天顶角作为常数,Strickland等人(1999)指出AURIC模式不适用于太阳天顶角大于90°的观测情况.AURIC仅仅适用于SSUSI等瞬时扫描型小视场的LBH日辉辐射计算.以DMSP/SSUSI和TIMED/GUVI的11.8°瞬时扫描视场为例,设观测点高度为830 km,观测视场投影至155 km海拔处的高层大气时,观测视场内太阳天顶角的最大差值约是1.2°(计算过程见附录A).然而,当瞬时扫描视场比较大时,对于FY-3上的广角极光成像仪,视场角是130°,在同样的观测位置,观测视场内太阳天顶角的最大差值约达50°(见附录A),就需要考虑太阳天顶角变化带来的影响,而不能再将其作为常数来处理.
为了满足大视场LBH日辉辐射特性研究的需要,本文给出了一种改进的LBH日辉柱辐射率计算方法RAURIC(Revised algorithm of AURIC).该方法考虑了观测视线方向上太阳天顶角的变化,克服了AURIC对LBH日辉柱辐射率计算的局限性.本文第2节首先对LBH辐射的谱带结构作了简要分析,然后详细描述了LBH日辉柱辐射率的计算方法.第3节计算了140~180 nm波段的LBH日辉柱辐射率,同时将RAURIC计算结果与AURIC进行了比较,然后对比较结果作了详细讨论.最后,第4节对本文工作进行了简要总结.
LBH带(Lyman-Birge-Hopfield Bands)辐射,如(1)式所示,是氮气分子由激发态(α1Πg)至基态(X1Σ+g)的跃迁而产生的,此为电偶极禁止跃迁.由选择定则可知,在这两个态之间可以发生的是电四极矩跃迁和磁偶极矩跃迁(Conway, 1992).每个LBH带由(O,P,Q,R,S)五个分支组成,其中(P,Q,R)三个分支是由磁偶极矩跃迁与电四极矩跃迁混合组成的,对应于ΔJ=-1,0,1;其余两个分支(O,S)则为纯电四极矩跃迁,对应于ΔJ=-2,2.
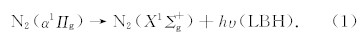
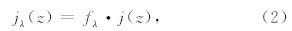
处于α1Πg态的氮气分子的产生速率j(z),可采用电子碰撞直接激发理论来计算,其值等于g因子与氮气分子密度的乘积,即
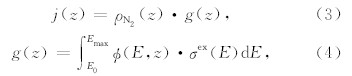
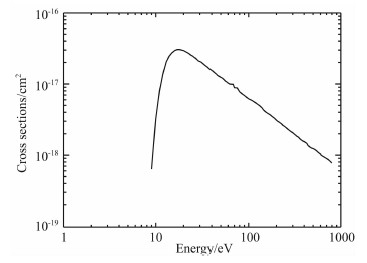 | 图1 α1Πg态的激发截面 Fig.1 Excitation cross sections of the α1Πg state |
从空间对LBH日辉辐射进行观测,观测量为LBH日辉柱辐射率.某一观测视线LOS方向的柱辐射率Iλ,可由(5)式表达(单位为Rayleigh):
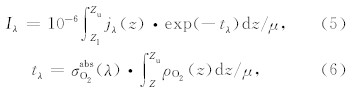
 | 图2 观测几何 Fig.2 Observation geometry |
LBH体辐射率的计算在2.1节中已经讨论过,下一步需要计算的是LBH带光子由发射点传输至观测点处而不被散射的几率.LBH带光子的辐射传输过程,主要考虑氧气分子的吸收,而忽略氮气分子自身的吸收,即氮气分子对于LBH带光子是“光学薄”的(Conway, 1992).因此LBH带光子的散射几率,可通过计算氧气分子的吸收光学厚度来解决.本文使用的氧气分子吸收截面的数据(Strickland et al.,1999)如图3所示.
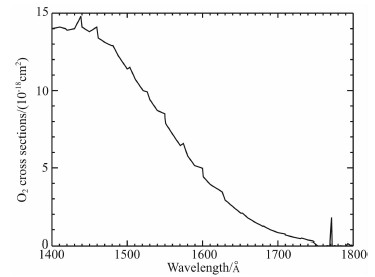 | 图3 氧气分子的吸收截面 Fig.3 Absorption cross sections of molecular oxygen |
电离层LBH日辉柱辐射率的具体计算步骤,如图4所示.
第一步,确定输入参数.输入参数包括:日期(Year、Day)、 时间(UT)、地磁活动参数(Ap)、太阳 10.7 cm射电通量值(F10.7)及其81天平均值(〈F10.7〉).
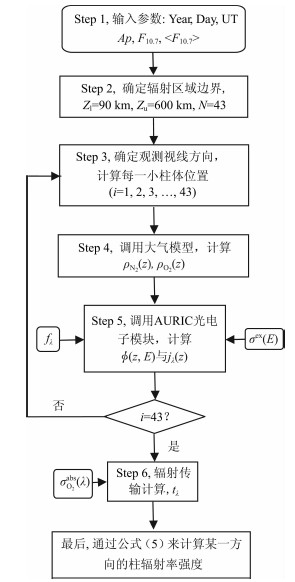 | 图4 柱辐射率计算流程图 Fig.4 Flowchart of calculation of column emission rates |
Year、Day、UT、Ap、F10.7和〈F10.7〉用于计算高层大气密度分布.为了研究不同太阳活动下LBH辐射的特征,我们分别选取了太阳活动极大年和太阳活动极小年两种情况,如表1所示.
第二步,确定LBH辐射产生区域的边界.电离层LBH日辉辐射产生于向阳侧的高层大气区域.因为海拔高度在90 km以下的低层大气对远紫外波段的LBH辐射具有强烈的吸收作用,同时考虑到500~600 km的海拔高度时氮气分子已经非常稀薄,从而可以忽略对LBH日辉辐射的贡献,故选取Zl=90 km,Zu=600 km作为辐射产生区域的下、上边界.在该区域内,采用球面几何描述的大气模型,即使用球面对该区域进行划分.各个球面之间间隔的确定,根据高层大气密度结构的变化情况,采用“由密到疏”的原则给定(Bush and Chakrabarti, 1995).本文采用AURIC的划分方法将90~600 km 范围内的高层大气区域分为43层.
第三步,确定观测视线LOS的方向.首先需要给定观测点的位置坐标(H,,λ),即观测点的海拔高度,纬度及经度坐标.然后需要给定观测角的大小,但这时还不能确定观测视线LOS的方向.因为采用的是球几何大气模型,还需要给定具体的观测方位,才能确定某一观测视线LOS的方向.因此,我们定义一个观测方位角β:以观测点的东向观测方位为起始线,逆时针方向转向观测视线LOS的方向,转过的角度即观测方位角β.
接下来,需要计算每个小柱体上下表面处的经度与纬度坐标.本文将辐射区域分为43层,那么沿观测视线LOS方向就划分为43个小柱体.因为辐射区域的分层已经完成,所以每个小柱体上下表面处的海拔高度就确定了.
对于每个小柱体上下表面处的经度与纬度坐标的确定,本文采用的是垂直方位投影技术.此处,以小柱体上表面处为例说明经度与纬度的确定过程.由观测点向小柱体上表面对应的海拔高度处作一垂直投影平面,根据观测角的大小,以及观测视线LOS的方向,可以确定小柱体上表面处在投影平面中所对应的水平坐标与垂直坐标(x,y).这时根据垂直投影坐标的转换公式(详见附录B),可以将上表面处的水平坐标与垂直坐标(x,y)转换为纬度与经度坐标(Glat,Glon).对于小柱体下表面处的经度与纬度坐标的确定,同样遵循这个过程.
当小柱体上下表面处的位置坐标确定之后,还需要确定的是每个小柱体沿观测视线LOS方向的观测角的大小.本文采用的是球几何大气模型,根据观测角的定义,沿观测视线LOS方向的各个小柱体处当地的天底方向是变化的,所以对应的观测角是不同的.对于小柱体上下表面处的观测角的计算,由观测点的坐标与小柱体上下表面处的坐标,可以确定观测视线LOS方向的矢量坐标,然后由小柱体上下表面处的垂直方向的矢量坐标,计算出小柱体上下表面处的观测角μ的大小.
第四步,调用大气模型MSISE-00计算每个小柱体的密度参数.当小柱体上下表面处的经度、纬度坐标确定之后,(Glat,Glon)连同表1中给定参数以及该大气区域的上下边界及分层数作为输入参数,调用大气模型MSISE-00计算出小柱体上下表面处的氮气分子密度ρ<sub>N2(z)与氧气分子密度ρO2(z).
第五步,计算每个小柱体的体辐射率.对于每个小柱体体辐射率的计算,我们调用AURIC体辐射率计算模块来完成.与AURIC原算法不同的是,此处每个小柱体体辐射率的计算中均考虑了太阳天顶角的变化.AURIC在计算沿观测视线LOS方向的柱辐射率时将太阳天顶角作为常数,这种处理方式只有当观测视线LOS方向为天底方向时是完全合理的.因此,对于每个小柱体体辐射率的计算,均调用AURIC体辐射率计算模块来计算天底方向的对应值,这样不同天底方向上的小柱体所对应的太阳天顶角也是不同的.每个小柱体的体辐射率计算完成之后,输入对应的fλ数据,根据(2)式,计算出对应的LBH带的体辐射率jλ.
对于每个小柱体参数的确定均采用梯形积分法,即,每个小柱体的氮气分子密度ρ<sub>N2,氧气分子密度ρ<sub>O2,观测角μ以及体辐射率jλ均为每个小柱体上下表面处对应的平均值.
第六步,辐射传输计算.对于LBH带的辐射传输过程,只考虑氧气分子的吸收.已知氧气分子密度及吸收截面数据,根据(6)式,可计算出每个小柱体传输至观测点处的光学厚度tλ.
最后,将确定的各个参数代入(5)式进行计算,就可以得到某一观测视线LOS方向的LBH日辉柱辐射率.
综上所述,我们将这种基于AURIC代码改进的LBH日辉柱辐射率计算方法称为RAURIC模式.RAURIC模式对于AURIC辐射算法的局限性主要有两点改进:一是增加了观测方位角,从而在观测角相同时可对不同的观测方位进行计算,解决了AURIC计算结果对称的局限性;二是考虑了沿观测视线LOS方向上太阳天顶角的变化,这对于LBH带的辐射计算非常重要,因为LBH辐射强度与太阳天顶角密切相关(Huffman,1992),从而使得RAURIC模式适用于大视场观测的情况.
为验证LBH辐射算法,本文应用RAURIC模式计算了电离层140~180 nm波段的LBH日辉辐射,计算结果包括:天底方向的柱辐射率;其他观测方向的体辐射率与柱辐射率.同时,对RAURIC与AURIC的计算结果进行了比较、分析与讨论.
天底方向柱辐射率的计算结果如图5所示,左右两栏分别对应表1中所给定的两组参数所描述的大气模型,观测点的海拔高度为830 km,经度坐标自上而下依次为0°,20°,50°,纬度坐标的范围均为-80°~80°(采用地理坐标系).
|
|
表1 大气模型参数 Table 1 Parameters of atmosphere model |
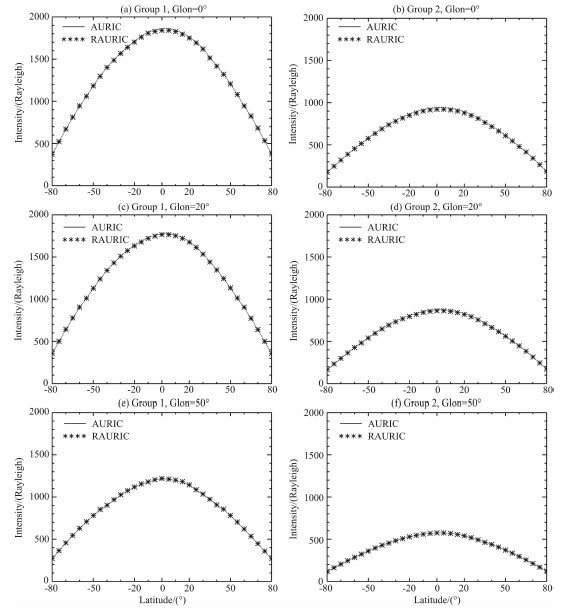 | 图5 RAURIC与AURIC在天底方向的比较 Fig.5 Comparison of RAURIC and AURIC in nadir |
由图5可以看出,不论是在太阳活动与地磁活动较强的情况下(左边一栏),还是在太阳活动与地磁活动较弱的情况下(右边一栏),RAURIC与AURIC的LBH柱辐射率计算结果在天底方向上都具有很好的一致性.
其他观测方向的柱辐射率计算结果如图6所示,左右两栏分别对应Group 1与Group 2两组参 数所描述的大气模型.观测点的海拔高度为830 km, 纬度与经度坐标自上而下分别为(20°,20°),(35°,35°),(50°,50°),观测角的变动范围均是0°~60°.本文采用的是球面几何大气模型,当观测角相同时(天底方向除外),还存在观测方位的不同.因此,我们选取了东西南北四个方位的柱辐射率进行计算,对应的观测方位角β分别为0°,180°,270°,90°.
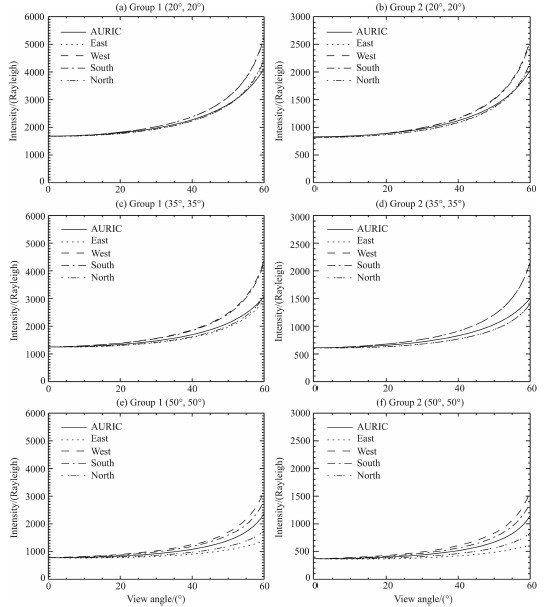 | 图6 RAURIC与AURIC在其他观测方向的比较 Fig.6 Comparison of RAURIC and AURIC in other lines of sight |
从图6中可以看出,在所有观测位置,当观测角比较小时(大约20°),太阳天顶角的变化比较小,RAURIC与AURIC的计算结果非常接近.但是,随着观测角的增大(大约40°),太阳天顶角的变化也增大,RAURIC与AURIC的计算结果的区别越来越明显.如图6a,6b中,东、北方位的太阳天顶角变化比西、南方位变化较大,所以与AURIC计算结果的区别就比较明显;图6c,6d中,RAURIC与AURIC计算结果的区别比图6a,6b更明显.随着观测角的进一步增大,如图6e,6f所示,四个方位的太阳天顶角变化都非常显著,RAURIC与AURIC的柱辐射率计算结果的差别就越来越大.图5与图6的结果反映出RAURIC模式与AURIC柱辐射率计算方法的区别,具体讨论如下.
电离层LBH日辉辐射是由光电子与氮气分子碰撞激发而产生的,LBH辐射与太阳天顶角密切相关(Huffman,1992).因此,在计算某一观测视线LOS方向的LBH日辉柱辐射率时需要考虑太阳天 顶角的变化.为了说明太阳天顶角的变化对LBH日辉辐射的影响,我们选取观测点位于海拔高度830 km,纬度与经度坐标为(50°,50°)且观测角为60°时,分别对东西南北四个方位的LBH体辐射率进行了计算,如图7所示.
由图7可知,对LBH日辉体辐射率贡献最大的海拔高度范围大约是120~220 km.同时,在此海拔高度范围内,AURIC与东西南北四个方位的LBH日辉体辐射率有明显的区别,这是因为(在此高度范围内)四个方位的太阳天顶角是不同的,详见以下讨论.
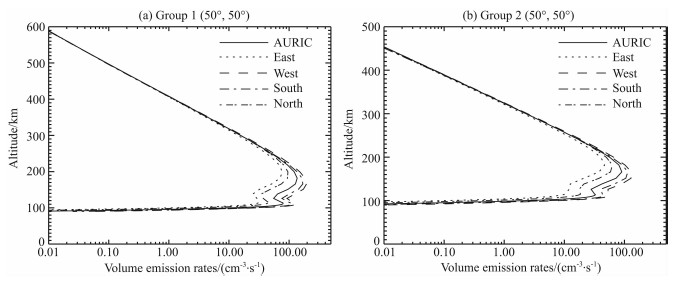 | 图7 与AURIC体辐射率的比较 Fig.7 Comparison with volume emission rates of AURIC |
为了进一步说明太阳天顶角对LBH日辉辐射的影响,我们选取固定海拔高度处来讨论g因子与太阳天顶角SZA的关系.如图8所示,海拔高度分别为150 km与180 km处的g因子,太阳天顶角的变化范围为0°~90°,g因子通过(4)式进行计算,图8a,8b分别对应Group 1与Group 2两组参数所描述的大气模型.
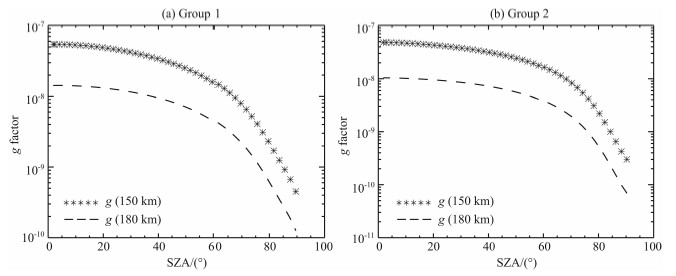 | 图8 g因子与太阳天顶角SZA的关系 Fig.8 Relationship between g factor and SZA |
由图8可知,在不同的海拔高度处,g因子随太阳天顶角的变化趋势是一致的.同时,在太阳天顶角小于40°时,g因子变化比较平缓;然而,当太阳天顶角大于40°时,g因子的变化就比较显著了.接下来,我们说明图6e,6f中太阳天顶角随观测角的变化情况,结果如图9所示,其中纵坐标为观测视线LOS方向上下边界处对应的太阳天顶角.
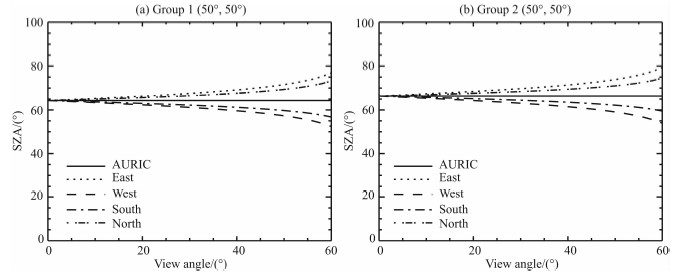 | 图9 观测角与太阳天顶角的关系 Fig.9 Relationship between view angle and SZA |
由图9可以看出,AURIC将太阳天顶角作为常数处理,因而随观测角的变化为直线;RAURIC模式考虑了太阳天顶角的变化,当观测角比较小时,太阳天顶角的变化亦不明显,但是当观测角比较大时,太阳天顶角在各个方位的变化就比较显著了.当观测角为60°且观测方位为东时,RAURIC与AURIC太阳天顶角的差值大约是13°,而g因子相差近一个数量级.因此,当观测视场比较小时,将太阳天顶角作为常数处理是近似成立的;而当观测视场比较大时,不能将太阳天顶角作为常数处理,就需要考虑太阳天顶角的变化.
由以上讨论可知,当观测方向为天底方向时,RAURIC与AURIC在天底方向上都将太阳天顶角作为常数来处理,因此,二者对LBH柱辐射率计算结果是一致的(图5);在其他观测方向上,RAURIC模式考虑了观测视线LOS方向上太阳天顶角的变化,当观测视场比较大时,RAURIC与AURIC计算结果的差别比较大(图6),需要使用RAURIC模式进行计算.
本文针对大视场观测模式,基于现有通用的大气紫外辐射积分代码AURIC模式,提出了一种改进的电离层LBH日辉柱辐射率计算方法,即RAURIC模式.RAURIC模式对大视场且太阳天顶角不大于90°时的体辐射率计算方法进行了改进,考虑了沿观测视线方向上的太阳天顶角变化对体辐射率的影响,并没有修改AURIC模式中的光电子通量计算模块.RAURIC模式在计算体辐射率时仍需要调用AURIC模式中原有的光电子通量计算模块,而这一模块仅仅适用于太阳天顶角不大于90°的情况,因此RAURIC模式目前还只适用于太阳天顶角不大于90°的电离层圆盘观测时的LBH日辉辐射计算,而不适合太阳天顶角大于90°的临边探测情况.
RAURIC模式为电离层LBH日辉图像模拟技术与数据反演技术的研制奠定了基础,从而为研究广角极光成像仪的电离层LBH日辉图像对于空间天气事件(马淑英等,2002;徐文耀,2009)的响应情况以及极光图像中的杂光去除技术(Strickland et al., 1994; Gladstone, 1994)奠定了基础.
附录A如附图1所示,地球半径R=6371.0 km,观测点A的海拔高度H=830 km.
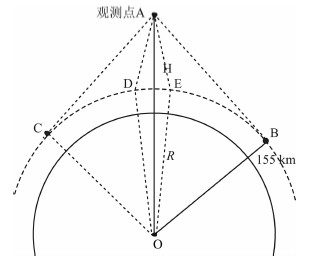 | 附图1 几何示意图 Appendix Fig.1 Geometrical sketch map |
(1)小视场对应太阳天顶角的变化
当观测点A的视场张角∠DAE为11.8° (DMSP/SSUSI和TIMED/GUVI两台仪器的瞬时扫描视场)时,∠OAE=5.9°.观测视线AD、AE与海拔高度为155 km处的球面大气相交时(典型的LBH带投影高度),OD、OE对应交点处的天底方向,因此D、E两点之间的太阳天顶角之差等于OD、OE之间的夹角.
在三角形ΔOAE中,根据正弦定理得

(2)大视场对应太阳天顶角的变化
当观测点A的视场张角∠CAB为130°(FY-3气象卫星广角极光成像仪的瞬时扫描视场)时,观测视线AB、AC约与海拔高度为155 km处的球面大气相切;因为CO、BO为C、B两点处的天底方向,所以C、B两点之间的太阳天顶角之差等于CO、BO之间的夹角∠COB.计算过程如下:
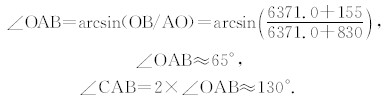
垂直方位投影建立了地理经纬度坐标(Glat, Glon)与投影平面的水平方向及垂直方向坐标(x,y) 之间的转换关系,以下是由投影坐标(x,y)至经纬度坐标(Glat,Glon)的转换方程(Snyder,1987),

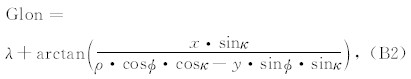
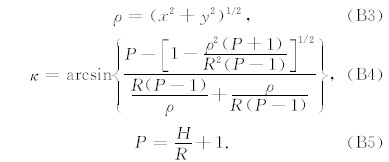
| [1] | Ajello J M, Shemansky D E. 1985. A reexamination of important N2 cross sections by electron impact with application to the dayglow: the Lyman-Birge-Hopfield band system and NI (119.99 nm). J. Geophys. Res., 99(A10): 9845-9861, doi: 10.1029/JA090iA10p09845. |
| [2] | Bush B C, Chakrabarti S. 1995. A radiative transfer model using spherical geometry and partial frequency redistribution. J. Geophys. Res., 100(A10): 19627-19642, doi: 10.1029/95JA01209. |
| [3] | Conway R R. 1992. Self-Absorption of the N2 Lyman-Birge-Hopfield bands in the far ultraviolet dayglow. J. Geophys. Res., 87(A2): 859-866, doi: 10.1029/JA087iA02p00859. |
| [4] | Dashkevich Z V, Sergienko T I, Ivanov V E. 1993. The Lyman-Birge-Hopfield bands in aurora. Planet. Space Sci., 41(1):81-87, doi: 10.1016/0032-0633(93)90019-X. |
| [5] | Evans J S, Strickland D J, Paxton L J. 1995. Satellite remote sensing of thermospheric O/N2 and solar EUV, 2. Data analysis. J. Geophys. Res., 100(A7): 12227-12233, doi: 10.1029/95JA00573. |
| [6] | Eastes R W. 2000. Emissions from the N2 Lyman-Birge-Hopfield bands in the Earth's atmosphere. Phys. Chem. Earth, 25(5-6): 523-527, doi: 10.1016/S1464-1917(00)00069-6. |
| [7] | Gladstone G R. 1994. Simulations of DE 1 UV airglow images. J. Geophys. Res., 99(A6): 11441-11448, doi: 10.1029/93JA03525. |
| [8] | Huffman R E. 1992. Atmospheric Ultraviolet Remote Sensing. London: Academic Press. |
| [9] | Link R, Strickland D J, Daniell R E. 1992. AURIC airglow modules: phase 1 development and application. SPIE, Ultraviolet Technology IV, 1764: 132-1441, doi: 10.1117/12.140843. |
| [10] |
Mcewen D J, Nicholls R W. 1966. Intensity distribution of the Lyman-Birge-Hopfield band system of N2. Nature, 209(5026): 902, doi: 10.1038/209902a0. Meier R R. 1991. Ultraviolet spectroscopy and remote sensing of the upper atmosphere. Space Sci. Rev., 58(1): 1-185, doi: 10.1007/BF01206000. |
| [11] | Mende S B, Heetderks H, Frey H U, et al. 2000. Far ultraviolet imaging from the IMAGE spacecraft. 2. wideband FUV imaging. Space Sci. Rev., 91(1): 271-285, doi: 10.1023/A:1005227915363. |
| [12] | Ma S Y, Liu H X, Schlegel K. 2002. A comparative study of magnetic storm effects on the ionosphere in the polar cap and auroral Oval-F-Region negative storm. Chinese J. Geophys. (in Chinese), 45(2): 160-169. |
| [13] | Oran E S, Strickland D J. 1978. Photoelectron Flux in the Earth's Ionospheric. Planet. Space Sci., 26(1): 81-87, doi: 10.1016/0032-0633(78)90056-9. |
| [14] | Paxton L J, Meng C I, Fountain G H, et al. 1992. Special Sensor Ultraviolet Spectrographic Imager (SSUSI): An instrument description. SPIE, 1745: 2-15, doi: 10.1117/12.60595. |
| [15] | Paxton L J, Christensen A B, Humm D C, et al. 1999. Global ultraviolet imager (GUVI): measuring composition and energy inputs for the NASA Thermosphere Ionosphere Energetics and Dynamics (TIMED) mission. SPIE, 3756: 265-276, doi: 10.1117/12.366380. |
| [16] | Snyder J P. 1987. Map Projections—a Working Manual. Reston: U.S. Geological Survey. |
| [17] | Strickland D J, Evans J S, Bishop J, et al. 1992. Atmospheric ultraviolet radiance integrated code (AURIC): Current capabilities for rapidly modeling dayglow from the far UV to the near IR. SPIE, 2831: 184-199, doi: 10.1117/12.257195. |
| [18] | Strickland D J, Cox R J, Barnes R P, et al. 1994. Model for generating global images of emission from the thermosphere. Appl. Opt., 33(16): 3578-3594, doi: 10.1364/AO.33.003578. |
| [19] | Strickland D J, Evans J S, Paxton L J. 1995. Satellite remote sensing of thermospheric O/N2 and solar EUV, 1. Theory. J. Geophys. Res., 100(A7): 12217-12226, doi: 10.1029/95JA00574. |
| [20] | Strickland D J, Bishop J, Evans J S, et al. 1999. Atmospheric ultraviolet radiance integrated code (AURIC): Theory, software architecture, inputs, and selected results. J. Quant. Spectrosc. Radiat. Transfer, 62(6): 689-742, doi: 10.1016/S0022-4073(98)00098-3. |
| [21] | Xu W Y. 2009. Variations of the auroral electrojet belt during substorms. Chinese J. Geophys. (in Chinese), 52(3): 607-615." |
| [22] | 马淑英, 刘会欣, Schlegel K. 2002. 磁暴期间极光椭圆与极盖区电离层效应比较研究——F区负暴. 地球物理学报, 45(2): 160-169. |
| [22] | 徐文耀. 2009. 亚暴期间极光电集流带的变化. 地球物理学报, 52(3): 607-615. |
 2014, Vol. 57
2014, Vol. 57


