伽利略卫星是由伽利略于1610年1月7日首次发现的木星的四个大型卫星,分别为木卫一至木卫四,该发现是天文学史上的一个里程碑.自探测到木卫一的十米波以来(Bigg,1964),大部分研究者的目光都集中在木卫一上,对木卫一的轨道环境、粒子成分都有深入研究.木卫一等离子体环的发现说明了木卫一是木星磁层中一个重要的等离子体源(Kupo et al., 1976),之后的研究中发现,木卫二是 仅次于木卫一的等离子体源(Eviatar and Paranicas, 2005). 然而,木卫二一直未引起过多关注,直到伽利略号飞船探测到木卫二表面比较年轻,并且可能存在全球性的冰下液态海洋时(Khurana et al., 1998),木卫二成为了研究的焦点.
木卫二是伽利略卫星中最小的一颗,其半径Reu=1.56×106 m,轨道半径约为9.38Rj(木星半径Rj=71492 km),位于木星磁层中木卫一等离子体环的外边缘.理论上由于木星磁轴与自转轴大约有10°的夹角,在木星快速自转的过程中,木卫二附近的等离子体环境应随自转而呈周期性变化.1996年12月,伽利略飞船飞临木卫二,获取了等离子体成分、密度与磁场强度等数据.磁场数据表明木卫二附近磁场大约为325 nT至460 nT,并且也观测到了11.23 h的周期变化(Schilling et al., 2008).特别的是,与木卫一相似,在木卫二附近探测到磁场减弱了大约50 nT,相比木卫一小了一个数量级(Kivelson et al., 1996a),由于压力主要由磁压贡献,所以减弱的磁场形成了压力槽.粒子数据表明在木卫二附近 平均离子数为130 cm-3,温度大约为100 eV(Kivelson et al., 1997).
木卫二轨道公转速度为14 km·s-1,磁层共转速度约为117 km·s-1.轨道速度远小于磁层共转速度,二者相对于木星都是逆时针运动,因此存在103 km·s-1的速度差.换个角度,这相当于木卫二在静止磁层中快速穿越磁通量管,在此过程中,由于木卫二的阻挡,等离子体流会在下游形成一个尾迹,与在水中的阻碍物后形成的水纹相似.同时,由于木卫二表面是固态海洋,本身只有微弱的磁场,因此等离子体流与卫星附近中性粒子相互碰撞会引起中性粒子电离,在感应电场的作用下加速形成电流,最终注入到木星电离层(Kivelson et al., 1999).与木卫一的理论相似,木卫二与磁层的相互作用也可以分为两个不同的理论:一是电磁回路理论(Piddington and Drake, 1968),赤道面等离子体与电离层存在电磁回路驱使赤道面等离子体随木星共转,电流在磁 通量管中发展,观测到的周期性现象侧面说明了这 一点;二是阿尔芬侧翼理论(Neubauer,1980; Southwood et al., 1980),木卫二在与背景等离子体相对运动时,木卫二附近产生的电流等由阿尔芬波携带向木星传播,电流在阿尔芬侧翼发展.
无论哪种理论都有电流向木星电离层注入,该过程引发了木卫二的极光足迹.与木卫一明亮而细长的足迹不同,由于木卫二附近等离子体密度远远小于木卫一,且磁场强度也远比木卫一附近小,所以木卫二的极光足迹在哈勃拍摄的紫外图像上只有一个斑点再加上微弱的尾迹(大约1~2经度)(Clarke et al., 2002).极光形态也意味着木卫二与磁层的作用过程比较短,在木卫二下游形成的尾迹也很弱.
木卫二轨道处离子回旋半径大约是10 km,比木卫二的半径小两个数量级,同时粒子与木卫二的作用时间(数十秒)也远大于粒子回旋周期(2 s),满足MHD(磁流体力学,magnetohydrodynamics)模拟的要求,虽然重离子的粒子效应对粒子速度分布和磁通量有一定影响(Lipatov et al., 2013),但本文关注的尺度较大,并不需要非常精确的粒子分布,总体而言对于木卫二尾迹的影响并不明显.目前已经有很多不同的MHD模拟了木卫二与磁层的相互作用(Kabin et al., 1999; Liu et al., 2000),甚至模拟了周期性时变过程(Schilling et al., 2007).上述模拟范围通常集中在木卫二附近区域(几个Reu),并未考虑木星电离层的影响.因此本文欲通过MHD模拟重现木卫二至木星电离层总的演化过程.考虑到受影响的磁通量管相对木星而言只是很小的一部分,并且磁通量管需要由赤道连接到极区,因此比较适合用长度很长、宽度很小的模拟方法.参考Chen(2007)等人对木卫一尾迹的研究,在此选择推广的“细丝运动理论”为核心进行演化过程的模拟.下面将分别介绍使用的磁场模型、细丝理论以及模拟的结果,并进行讨论和总结.2 理论模型 2.1 磁场模型
本文选用基于Caudal(1986)自洽模型扩展的稳态模型.该模型要求磁轴和自转轴重合,虽然如1节所述,木卫二的粒子环境受磁轴倾角调制,但从大尺度平均效果来讨论木卫二与磁层作用时可以怱略倾角的影响,因此可认为重合条件是符合的.在此基础上可自然地认为背景等离子体分布是各向同性的.综上,选用此稳态模型是比较合理的.
稳态模型从稳态MHD方程出发
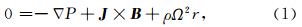
细丝理论曾成功应用于模拟粒子输运过程,包括土星、木星以及地球的粒子输运过程(Chen,2003;王翼和陈出新,2008;Chen and Wolf, 1999).细丝是自身厚度与宽度相比可以忽略,宽度与所处的环境尺度相比也可以忽略的细长磁通量管.从拉格朗日观点看,可以把细丝分成若干粒子微团,当把焦点集中在各个粒子微团,跟踪微团的运动就可以得到细丝的演化过程.以前的应用用于模拟径向运动,而本文是用于沿木卫二轨道平面的运动,因此需要对该理论进行合适的修改以适应不同的情况.
木卫二的尾迹可以看作同一时间不同磁通量管的位形分布,也可以看作是一根扰动磁通量管随时间的演化分布,二者是统一的.本文假设木卫二的尾迹中的物理量沿尾迹距离固定而随时间不变,同时尾迹中的磁通量管仅在沿轨道的壳层曲面内运动,则背景磁场可简化为沿木卫二轨道壳层的二维磁场分布.同时假设磁通量管在背景磁场中运动不会引起背景磁场的大幅扰动(除了轻微的加热过程).本文选取即将受到扰动的磁通量管作为细丝,模拟细丝随时间的变化过程.文中采用如下坐标系,e x指向细丝的运动方向,e y=(- B /B)× e x指向木星,e z= e x× e y,原点位于木卫二所在位置.由此定义,细丝位于xz曲面内,该曲面也就是木卫二处的磁壳面.
本文理论推导从运动方程出发,在所关注的环境内不需要考虑相对论效应,且不考虑科里奥利力(Yang et al., 1994),那么宏观磁流体力学运动方程可以写为
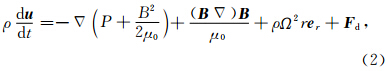
对于选取的细丝,其位置可以认为是质量与时间的函数x = x(m,t),m是细丝从赤道平面到所考虑位置的质量总和.细丝的速度可以表示为
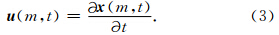
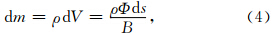
由于细丝沿着磁力线,考虑到式(4),我们可以将磁场B =Bd x /ds重写为
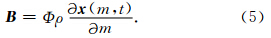

为了积分式(2),需要考虑细丝与背景的相互作用.我们用下标med表示背景的物理量,对于背景 磁场,式(6)依然是成立的,仅需要注意各物理量应使用下标med.由于假设背景处于平衡态,式(2)中左边 第一项可以忽略,同时拖曳力对背景的影响比较微弱,右边最后一项也可以忽略,则背景运动方程可以写为
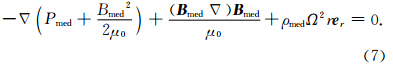
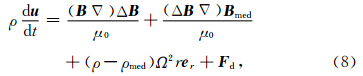
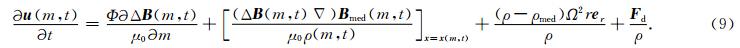
式(9)中的拖曳力表现为两方面,一是细丝前后的压力差.细丝的加速过程是随着尾迹距离的增大而单调递减,在此过程中,前面细丝的压力总大于后面的压力,由于压力主要部分为磁压,一个显然的结果就是下游会出现压力槽,这与伽利略飞船的探测结果一致(Kivelson et al., 1997).压力槽对细丝的相互作用可等效为一个拖曳力F d1,在后面的结果中发现其影响较小,基本可以忽略.二是细丝侧面的摩擦力.摩擦力大小与细丝的速度成正比,令η为黏滞系数,dS为细丝的横截面积,R表示细丝y方向的半宽度,则黏滞力可以表示为
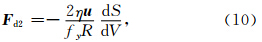

在细丝运动过程中,当细丝容积变化或由于摩擦力而加热的时候就会引起能量的转移.由热力学第一定律,对单位质量的细丝其能量方程可以写为
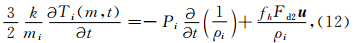
由于对称性,只需要考虑木星电离层处的边界.在边界处细丝携带的电流为
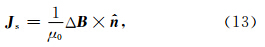
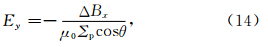

第2节已经建立了数值模拟的理论过程.再次强调在拉格朗日观点下,我们可以认为细丝是一连串的粒子微元构成.因此在模拟过程中,可以将细丝用一系列点来代替,这些微元点的运动代表了细丝的演化过程.需要注意在模拟过程中假设细丝运动关于赤道面是对称的.
由于阿尔芬波速度在木星电离层处很高,因此按一般模拟习惯将电离层顶设置在3Rj处(Fedder et al., 1991).这将导致细丝携带的电流被截断一部分,然而考虑到电流在电离层顶与帕特森电流形成回路,同时细丝中是理想导电的,那么只要将3Rj的电导率设置成与电离层顶处电导率相同,则从能量角度来看该截断并不会影响细丝的运动过程.同时提高电离层位置也会减小阿尔芬波在细丝中的传播时间,考虑到电离层附近的高阿尔芬速度和相比整条细丝的长度,其截断时间约为3 s,可以不考虑其对细丝运动的影响.
在模拟中我们将细丝分割成300个质量微元,未扰动细丝在赤道面上的大小设为1Reu,等离子体温度和磁场强度与未扰动的背景相同,在本文所用的木星磁场模型中,等离子体密度沿z方向减小(见图 1).扰动后的细丝初始速度分布如图 2所示,赤道面上的细丝速度设定为与伽利略飞船观测值一 致.具体模拟中各可调参数互相影响,决定着最终模拟结果. 基于前人的研究成果,取Σp=1 S,fh=0,经过测试取fy=0.5得到一个比较合理的结果(见图 3),fy的影响后面将进行讨论,其中fh=0暗示绝热过程.
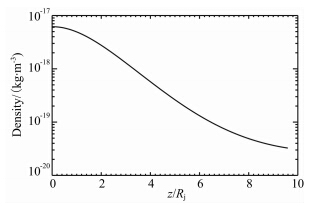 | 图 1 沿细丝的等离子体密度分布Fig. 1 Plasma density distribution along an unperturbed filament |
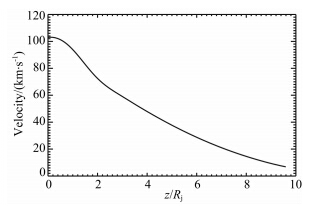 | 图 2 相对于背景磁力线沿细丝的初始速度分布Fig. 2 Initial azimuthal velocity distribution along the perturbed filament |
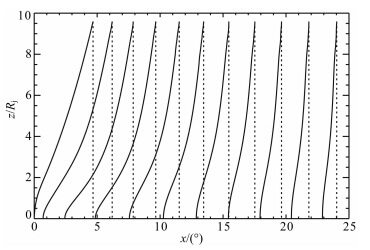 | 图 3 木卫二尾迹中扰动细丝的位形 虚线为电离层顶位置与细丝一致的背景磁力线.Fig. 3 Shape of the perturbed filament in Europa′s wake Dashed lines indicate the background magnetic field lines. |
图 3中左边第一根实线是扰动细丝刚脱离与木卫二作用的初始位形,随后的曲线是细丝随时间演化的过程,相邻曲线间的间隔为270 s.初始位形与背景磁力线的夹角大约为4°,是一根背景磁细丝在另外的模拟过程中经过大约720 s时间被木卫二拖曳形成的,磁细丝根部即将离开零点位置,表示此时的细丝刚好脱离木卫二而自由运动,对应于尾迹模拟的0时.
细丝运动模拟过程中,扰动的细丝自模拟开始 就逐渐加速,图 3中细丝形状的变化过程可以看出 大约运动2160 s以后,细丝形状逐渐与背景磁力线 平行.这种现象很多学者在之前的工作中就已经预 言到,并且其他的MHD模拟也重现了这一现象(Schilling et al., 2008).扰动的细丝在木卫二的拖曳作用下形成拉伸的弓形,能量存储在拉伸的磁通量管中,当细丝脱离木卫二时在磁张力的作用下加速.另一方面,底部细丝的位形呈现不明显的波动状,这是由于底部的速度变化以阿尔芬波速度向电离层顶传递.由于木卫二轨道处阿尔芬波速较小,同时粒子密度也较小,导致细丝加速过程比较快(见图 4),因此细丝的波动过程并不明显.我们也模拟了木卫二的压力槽对细丝加速的影响,但因为木卫 二的磁场降低大约只有50 nT,约为背景磁场的1/8,对细丝加速影响很小,模拟最终结果未在本文列出.
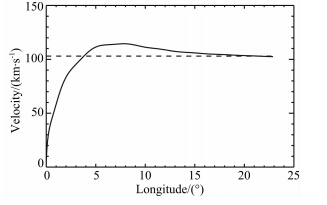 | 图 4 赤道面细丝相对于木卫二的速度变化 虚线表示背景磁力线相对木卫二的速度.Fig. 4 Equatorial velocity distribution of Europa′s plasma wake in Europa′s reference frame Dotted line indicated the background velocity in Europa′s reference frame |
图 4显示了赤道面细丝的加速过程,模拟过程中我们重点模拟细丝在背景磁场中的运动,背景磁场相对木卫二有稳定的速度如图虚线所示.模拟开始细丝在磁张力作用下很快就加速到背景磁力线的速度,由于黏滞力较小,细丝加速并未停止,细丝速度超过背景磁力线的速度,之后才逐渐减速,最终与背景磁力线重合.重合后就表示细丝在赤道面上与背景磁力线没有相对运动,细丝所代表的磁通量最终也融入了背景磁通量管.
细丝的运动携带着电流向电离层顶注入,其电流大小如图 5所示.可以清楚地看到电流仅间隔7 个经度(大约1000 s左右)就很快衰减到0.Kivelson等(1996b)在分析伽利略飞船对木卫一的观测时估计木卫一携带的电流表达式为
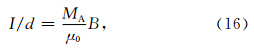
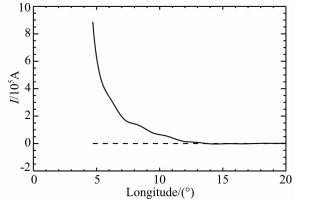 | 图 5 电离层顶注入电流分布Fig. 5 Field-aligned current distribution in Europa′s reference frame |
本文首先介绍了木卫二附近的探测结果.木卫二表面存在固态海洋,内部可能存在液态海洋因此呈现出导电性,但本身磁场很弱.木卫二在公转过程中与磁层中等离子体相互作用引起木星表面附近的中性粒子电离,在感应电场作用下加速而进入到木星磁层中.探测结果显示木卫二附近平均离子质量为18.5 amu(单位原子质量),我们在模拟中是用两种成分来代替: 21 amu的冷等离子体和16 amu的热 等离子体.木卫二在木星磁层中以相对103 km·s-1 的速度穿行,在这过程中阻碍磁力线穿越,就像平静水流中的一块阻碍物在下游形成水纹一样,木卫二上游磁场比平均磁场增强30 nT左右,而在下游形成一个磁场减弱区域.上游磁通量管被木卫二拖曳而拉伸,当跨过木卫二后在磁张力和压力作用下加速,最终又回归到稳定态.虽然整个过程是同一时间一系列磁通量管的运动,但转换一个角度,则可以看成一根磁通量管随时间的变化过程.因此很自然的,我们可以通过模拟一根磁通量管的演化过程而得到整个尾迹的形态,这也表明了本文使用细丝模拟的合理性.
细丝理论在建立过程中作了很多假设,比如稳态的对称的背景磁场,细丝南北两个半球对称,等离子体压力各向同性等.这些假设都有其合理性,在不需要模拟微观运动的情况下都是基本成立的.细丝理论已经成功应用于粒子的径向输运模拟等过程,可以看作是一个比较成熟的MHD模拟方法.本文在模拟木卫一尾迹的基础上修改以应用于木卫二尾迹的模拟.在模拟过程中有几个可调参量,影响着最终的模拟结果.其中最重要的是表征黏滞力的系数fy和帕特森电导Σp,虽然本文只详细描述了一种特定参数的运动过程,但在我们的工作中还得到了不同的参数结果.fy与尾迹的尺度关系密切,大的fy会使细丝快速静止,但过大的fy又会使扰动的细丝不能回复初始的平直位形.而Σp影响电离层顶细丝的移动速度,这也可以从式(15)中看出,过小的电导率会使细丝迅速达到受力平衡,表现在扰动的细丝不仅在赤道面加速,也会在电离层顶反向加速.
本文中为了方便模拟简单地认为细丝在y方向上没有相对运动,在有关径向输运的模拟中可知细丝可以在y方向上背离木星而运动.此处我们重点在于木卫二的尾迹运动,y方向上的运动相对于轨道方向的运动而言是比较小的,即使考虑也只会使尾迹与轨道形成一个微小角度,而且从模拟结果来看,尾迹范围比较小,因此不考虑y方向的运动是可以理解的.
细丝的运动过程在模拟结果中是比较清楚的,与Chen分析木卫一的尾迹相似,未扰动的细丝与木卫二的相互作用大约720 s,似乎更倾向于场向电流的模型.但在电流的分布中又存在波动的影响,这可能是阿尔芬波的调制作用引起的.另一方面,电流分布相比与木卫一的模拟结果有很大区别.木卫一的模拟结果显示,电流与速度显现明显的周期结构,其衰减时间也远远大于木卫二的衰减时间.模拟中木 卫一附近的粒子质量密度大约为7.7×10-17kg·m-3,磁场强度约为1940 nT,而木卫二附近的粒子质量密度大约为2.3×10-18kg·m-3,磁场强度约为460 nT,与木卫一相比小了一个量级.计算出的阿尔芬速度 木卫一处为197 km·s-1,木卫二处为273 km·s-1. 扰动过程中卫星的动能转化为磁通量管向木星电离层注入的能量,具体存在为两个过程.一是等离子体的动能,在木星坐标系中看,扰动的磁通量管释放时等离子体具有很大的初始速度,在重新回复静止的过程中等离子体存在动能差.二是磁能,扰动过程中卫星的动能一部分转化为磁能存储在拉伸的磁力线中.磁通量管脱离卫星影响时这两种能量释放以电流的方式注入到木星电离层顶引发极光.虽然连接木卫二的磁通量管长度更长,但木卫一距离木星5.9Rj,比木卫二近了3.5Rj,自转角速度是木卫二的2倍,当地磁场强度是木卫二处的4倍,等离子体密度也更高,因此在扰动过程中转移到等离子体的动能更大,磁通量管在与木卫一的相互作用中也积累了更多的磁能.具体计算也证实了这一结论,木卫一扰动磁通量管中等离子体的动能大约为2.0×1014J,木卫二扰动磁通量管中等离子体的动能大约为2.3×1013J,二者中的磁能大约为1012量级,相比动能是小量. 木卫一与木卫二足迹在木星电离层上位置相差不大,但木卫二足迹处磁场的z分量是木卫一的两倍多,x分量几乎相同,由式(15)可以看出木星电离层顶木卫二的磁通量管运动更快.考虑到电离层的电导率都取为1 S,木卫一能量高,则电流强度更高,持续时间更长(见文献(Chen,2007)中的图 10).与之形成对比的是木卫二因为积累的能量较小,电流强度较弱,持续时间很短,表现在图 5中电流很快就衰减到0.而且能量传递需要时间,赤道面的能流沿磁通量管向木星电离层传递,到达木星电离层时形成的极光足迹与卫星位置有一个滞后,这也已经被观测所证实.
细丝的初始位形设置为拉伸的弓形,这个位形可能是需要改进的.在木卫二与背景磁通量管的作用过程中,于木卫二附近会形成大约与背景夹角20°的柱状扰动区域.磁通量管在此区域内被木卫二拖曳,如果此区域能延伸到电离层顶并且磁通量管的跨越速度足够小,以使磁通量管在未离开扰动区域时阿尔芬波已经传播到电离层,那么此位形是比较合理的.然而目前为止并没有过多的探测结果支持这一假设.对于一根磁通量管,可能的情况是赤道面附近磁通量管被拖曳,其影响范围大约到达几个Rj处就已经开始脱离木卫二.从另一角度来说,也就是初始位形可能是下部被拉伸而上部保持平直的位形.这可能会对模拟结果有一定影响,将在以后的工作中验证.5 总结
本文通过细丝理论模拟,发现木卫二的尾迹理论不应该简单地归结为电磁回路理论或者阿尔芬翼理论,二者存在共同作用和相互影响.电流的波动现象与阿尔芬翼理论相近,但在本文模拟中磁力线与木卫二的接触时间较大,形成的角度也比阿尔芬理论预计的更大,这说明其中受到电磁回路的影响.模拟结果显示一根经过720 s的时间扰动的磁通量管被木卫二拖曳成角度大约为4°的拉伸磁通量管并脱离木卫二而加速,之后经过大约2160 s的运动而重归于稳定.扰动磁通量管的速度先快速增加并超过了相对速度而后逐渐减小到与背景速度一致.磁通量管中释放的能量大约为2.3×1013J,所形成的电流在五个经度跨度内快速由9×105A衰减为0.取其1/e初始电流处为可观测的尾迹,则理论上木卫二尾迹只有一到两个经度范围,这与观测到的木卫二极光足迹基本一致,该范围与木卫一尾迹相比明显更小.通过以上模拟结果表明,细丝理论在模拟木卫二的尾迹中是比较成功的.
| [1] | Bigg E K. 1964. Influence of the satellite Io on Jupiter's decametric emission. Nature, 203(4949): 1008-1010. |
| [2] | Caudal G. 1986. A self-consistent model of Jupiter's magnetodisc including the effects of centrifugal force and pressure. J. Geophys. Res., 91(A4): 4201-4221. |
| [3] | Chen C X, Wolf R A. 1999. Theory of thin-filament motion in Earth's magnetotail and its application to bursty bulk flows. J. Geophys. Res., 104(A7): 14613-14626. |
| [4] | Chen C X. 2003. Numerical simulation of the Io-torus-driven radial plasma transport. J. Geophys. Res., 108(A10):1376, doi: 10.1029/2002JA009460. |
| [5] | Chen C X. 2007. Simulations of field-aligned currents: Application of theory of thin filament motion to Io's plasma wake. J. Geophys. Res., 112(A3), A03204, doi: 10.1029/2006JA011599. |
| [6] | Chen C X. 2013. Theoretical constraints on the cross-tail width of bursty bulk flows. Ann. Geophys., 31(12): 2179-2192. |
| [7] | Clarke J T, Ajello J, Ballester G, et al. 2002. Ultraviolet emissions from the magnetic footprints of Io, Ganymede and Europa on Jupiter. Nature, 415(6875): 997-1000. |
| [8] | Eviatar A, Paranicas C. 2005. The plasma plumes of Europa and Callisto. Icarus, 178(2): 360-366. |
| [9] | Fedder J A, Mobarry C M, Lyon J G. 1991. Reconnection voltage as a function of imf clock angle. Geophys. Res. Lett., 18(6): 1047-1050. |
| [10] | Hill T W. 1979. Inertial limit on corotation. J. Geophys. Res. -Space, 84(A11): 6554-6558. |
| [11] | Kabin K, Combi M R, Gombosi T I, et al. 1999. On Europa's magnetospheric interaction: A MHD simulation of the E4 flyby. J. Geophys. Res.-Space, 104(A9): 19983-19992. |
| [12] | Khurana K K, Kivelson M G, Stevenson D J, et al. 1998. Induced magnetic fields as evidence for subsurface oceans in Europa and Callisto. Nature, 395(6704): 777-780. |
| [13] | Kivelson M G, Khurana K K, Walker R J, et al. 1996a. A magnetic signature at Io: Initial report from the Galileo magnetometer. Science, 273(5273): 337-340. |
| [14] | Kivelson M G, Khurana K K, Walker R J, et al. 1996b. Io's interaction with the plasma torus: Galileo magnetometer report. Science, 274(5286): 396-398. |
| [15] | Kivelson M G, Khurana K K, Joy S, et al. 1997. Europa's magnetic signature: Report from Galileo's pass on 19 December 1996. Science, 276(5316): 1239-1241. |
| [16] | Kivelson M G, Khurana K K, Stevenson D J, et al. 1999. Europa and Callisto: Induced or intrinsic fields in a periodically varying plasma environment. J. Geophys. Res.-Space, 104(A3): 4609-4625. |
| [17] | Kupo I, Mekler Y, Eviatar A. 1976. Detection of ionized sulfur in the Jovian magnetosphere.Astrophys J. , 205: L51-L54. |
| [18] | Lipatov A S, Cooperb J F, Paterson W R, et al. 2013. Jovian plasma torus interaction with Europa. Plasma wake structure and effect of inductive magnetic field: 3D hybrid kinetic simulation. Planetary and Space Science, 77: 12-14. |
| [19] | Liu Y F, Nagy A F, Kabin K, et al. 2000. Two-species, 3D, MHD simulation of Europa's interaction with Jupiter's magnetosphere. Geophys. Res. Lett., 27(12): 1791-1794. |
| [20] | Lu B, Chen C X. 2010. The causation of bright spots polarward of Jupiter's aurora oval. Chinese J. Geophys.(in Chinese), 53(11): 2544-2550, doi: 10.3969/j.issn.0001-5733.2010.11.002. |
| [21] | Neubauer F M. 1980. Nonlinear standing Alfvén wave current system at Io: Theory. J. Geophys. Res., 85(A3): 1171-1178. |
| [22] | Piddington J H, Drake J F. 1968. Electrodynamic effects of Jupiter's satellite Io. Nature, 217(5132): 935-937. |
| [23] | Schilling N, Neubauer F M, Saur J. 2007. Time-varying interaction of Europa with the jovian magnetosphere: Constraints on the conductivity of Europa's subsurface ocean. Icarus, 192(1): 41-55. |
| [24] | Schilling N, Neubauer F M, Saur J. 2008. Influence of the internally induced magnetic field on the plasma interaction of Europa. J. Geophys. Res.-Space, 113(A3), A03203, doi: 10.1029/2007JA012842. |
| [25] | Southwood D J, Kivelson M G, Walker R J, et al. 1980. Io and its plasma environment. J. Geophys. Res.-Space, 85(A11): 5959-5968. |
| [26] | Wang Y, Chen C X. 2008. Numerical simulation of radial plasma transport in the Saturn's magnetosphere. Chinese J. Geophys. (in Chinese), 51(3): 635-642. |
| [27] | Yang Y S, Wolf R A, Spiro R W, et al. 1994. Numerical simulation of torus-driven plasma transport in the Jovian magnetosphere. J. Geophys. Res.-Space, 99(A5): 8755-8770. |
| [28] | 卢斌, 陈出新. 2010. 木星极光区亮斑形成机制. 地球物理学报, 53(11): 2544-2550, doi: 10.3969/j.issn.0001-5733.2010.11.002. |
| [29] | 王翼, 陈出新. 2008. 土星磁层等离子体径向输运的数值模拟. 地球物理学报, 51(3): 635-642. |
 2014, Vol. 57
2014, Vol. 57


