2. 武汉轻工大学电气与电子工程学院, 武汉 430023
2. School of Electrical and Electronic Engineering, Wuhan Polytechnic University, Wuhan 430023, China
1 引言
热层中性风是电离层-热层系统非常重要的一个参数,它影响着热层、电离层乃至等离子体层的形态结构,在热层和电离层动力学过程、电离层-热层的耦合过程中具有决定性的作用(Makela et al., 2011; Wu et al., 2012; 解海永等,2014; 余涛等,2014).全面了解热层中性风时空分布特征,在地球环境科学、大气动力学以及空间天气等研究工作中有着极其重要的作用(Yuan et al., 2010; Liu et al., 2014).与广泛开展的带电粒子测量相比,中性风观测还十分有限(Huang et al., 2012),现有的观测结果大多是关于水平风场的,有关垂直风观测的报道比较少见.研究表明垂直中性风对大气成分、大气动力学、电动力学的影响要远甚于水平风(Anderson et al., 2011),观测数据的匮乏导致人们对垂直风的了解远不如对水平风透彻,比如,垂直风突然变大的现象在极地高纬度地区时有发生,但有关其驱动机制仍不清楚(Price et al., 1995; Innis et al., 1996; Kurihara et al., 2009; Mingalev et al., 2012).
法布里-珀罗干涉仪(FPI)是测量热层风场的主要地基设备之一(Cooper et al., 2009; Englert et al., 2012; 王英鉴等,2014),由它对不同峰值高度的气辉辐射进行干涉成像,通过记录的多普勒频移信息计算得到中性风.其中,比较典型的两个波段是630.0 nm和557.7 nm,对应的峰值高度是250 km和97 km(Hern and ez, 1966).FPI测量的中性风一般是视线方向的水平风场(Shiokawa et al., 2003),要观测垂直风有难度.一个原因是利用地基设备测垂直风时,观测天顶角受到一定的限制,使得测量的空间点有限,另一个原因是垂直风速比水平风速小得多(通常量级为10 m·s-1)(Cooper et al., 2009; Larsen and Meriwether, 2012),要想对其进行直接测量,对仪器和天气条件的要求十分苛刻.比如,测量垂直风时,需要将FPI视场正对上方天顶,同时还要满足两个条件,一是天空无云或少云,二是天顶上方无其他光辐射(Smith et al., 1995a,1995b).此外,计算垂直风时,需要确定多普勒频移为零的参考基准,一般是假设水平风场是均匀的,一定时段内垂直风的均值为零来确定这一基准(Aruliah and Rees, 1995; Smith et al., 1995a,1995b; Cooper et al., 2009).然而,垂直风在多数情况下存在短期波动,平均垂直风更是表现出随地磁、季节和太阳活动周期的系统性变化(Aruliah and Rees, 1995).研究表明,当水平风场为均匀时,低纬度地区垂直风为5~10 m·s-1,而当水平风场为非均匀时,低纬度地区垂直风为20~50 m·s-1,高纬度地区垂直风可高达100 m·s-1以上(Laakso et al., 1995).显然,简单地利用观测期间垂直风的均值为零的假设来确定零参考基准存在一定的问题.国际上,有关垂直风计算方法的研究开展了一些,其中Burnside等(1981)基于大量的假设建立了垂直风与水平辐散的一种简单关系,而这些假设或许并不成立,其建立的垂直风与水平辐射的关系可信度值得怀疑(Cooper et al., 2009).考虑到高热层(330~340 km)离子密度的损耗,Laakso等(1995)用电场和等离子密度数据反演出的赤道附近垂直风达15~30 m·s-1,其反演结果明显超出了预期值.Anderson等(2011)基于南极莫森站全天空FPI与戴维斯站扫描式FPI由同一地点的视线风速来反演垂直风速,但得到的垂直风偏小.
基于Sipler等(1995)提出的由两台扫描式FPI计算单点矢量风的方法,考虑垂直风测量对空间分辨率的需求,本文提出了一种从单台全天空FPI干涉仪的观测数据反演垂直风的方法.本文建立的垂直风反演算法,不需要不合理的假设垂直风为零,单台全天空FPI即可观测垂直风,也不用限制FPI的观测方位,这将提升FPI观测数据的产出和利用率,不仅可为全面描述垂直风提供数据支持,也可为热层大气建模、中性成分等相关研究提供坚实的基础.
2 垂直中性风的理论模型及数据输出 2.1 理论模型图 1给出了基于全天空FPI干涉图计算矢量风场的示意图.在图 1a中,O为观测点,R1和R2为两个相邻的视线观测方向,其夹角为Δθ.V1和V2是沿此两个方向的视线风速(远离观测点方向为正,指向观测点方向为负),面OR1R2上的二维风速用V2D表示,且定义V2D与R1和R2之间的夹角分别为θ2D和θ2D-Δθ.不难得到V2D在R1和R2方向上的投影分量为:
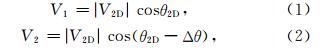
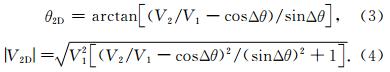
从式(3)和式(4)可以知道,在获得两个视线风速及其夹角后,可计算出此二视线所在平面内的二维风速以及该风速所对应的夹角.对于三维风场,可通过在三维空间内任意一个面上的风速投影及这个面法线上的风速分量计算得到.如图 1b所示,OA和OB是同一干涉环上两个相邻的视线方向,对应视线风速为V1和V2,求出面OAB上的矢量风V2D,在高一级次的干涉环上取点C,令点C满足AC⊥AB,设面OAB的法线为AD1.根据多普勒频移理论,只有在观测视线方向上产生的风速变化才会引起多普勒频移,由于AD1同时垂直于视线OA和OB,故沿法线AD1的风速分量VAD1与面OAB上的矢量风V2D相关性为零,则风速分量V2D和VAD1的合成矢量即为该点的矢量风.求得沿OA和OB方向的视线风速后即可按式(3)和式(4)计算出V2D,但无法直接求得AD1方向上的风速分量.但是,我们可以通过获得OC上的视线风速VOC,根据式(3)和式(4)求得面OAC内的二维风速VOAC及其对应的角度,再将VOAC在AD1方向上进行投影,得到VAD1.由于面OAC垂直于面OAB,且视面OAC垂直于地平面,因此可直接通过投影计算得到VAD1在水平方向AD3和垂直方向AD2上的分量.将这两个分量分别与VOAB在水平方向和垂直方向上的分量进行矢量相加,即可最终得到三维风场的水平分量和垂直分量.
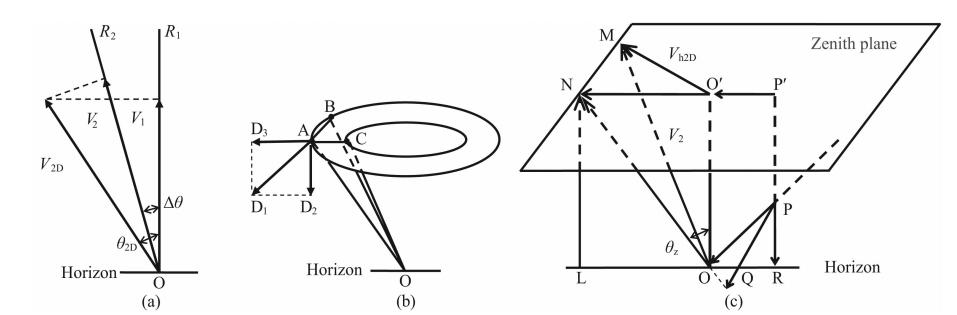 | 图 1 基于全天空FPI干涉图计算矢量风场 Fig. 1 Illustration of vertical neutral wind deduced from all-sky FPI |
求解三维矢量风如图 1c所示,ON方向为图 1a中R1指向方向,对应的天顶角为θZ,OM为图 1a中V2D的方向,则OM和ON的夹角为θ2D,Vh2D为V2D在天顶所在水平面的对应风速,其矢量大小分别用 O'M和 OM表示,PO为面OMN的法线,沿此法线的风速分量用PO表示,可算得:
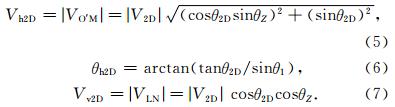
设沿OC方向的视线风速为V3,R1和R3的夹角为Δθ′,则三维风场在面PON上的矢量风投影V′ 2D、该投影风速与PO的夹角θ′ 2D、该投影风速在水平和垂直方向的分量V′ h2D、V′ v2D分别为:
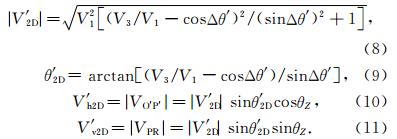
P′O′ 为PO在天顶面的投影,LN和PR分别为ON和PO在竖直方向的投影.由图 1a分析可知,两个风速分量OM和PO的矢量和即为空间三维风速,将此两个风速分别向水平面和竖直方向投影,可得水平风和垂直风.
2.2 数据输出根据2.1节介绍的垂直风计算模型,本文利用北极黄河站的FPI实际观测数据计算了该地区垂直风.中国北极黄河站,位于78°55′N、11°56′E,从每年的11月份直到次年的2月份,北极黄河站处于极夜期间,特别适合进行光学观测.武汉大学安装在北极黄河站的全天空FPI(图 2)采用了大视场鱼眼镜头,具有与挪威UNIS大学的FPI相似的观测极盖和极光区边界的能力(Zhang et al., 2013).
 | 图 2 中国北极黄河站全天空FPI框图(a)和观测室(b) Fig. 2 Schematic diagram(a) and observation room(b) of all-sky FPI at Chinese Yellow River station |
北极黄河站的全天空FPI干涉图包含8级以上干涉环,为了等距离计算天空中各点三维风速,选取第1、3、5、7级干涉环进行计算处理.经标定后可计 算出四个干涉环对应的天顶角依次为0.3462、0.6558、0.8746和1.0549 rad,即对应的天顶半径为 84.8314、152.4484、191.8218和217.4627 km(气辉高度为250 km时).将第1、3、5、7级干涉环分为10、20、30、40个等分,按本文提出的垂直风计算方法,计算得到该干涉图对应的垂直风场(图 3).
 | 图 3 干涉环级次的选取处理(a)与垂直风示例(b) Fig. 3 Illustration of interferometer image processing(a) and vertical neutral wind results(b) |
FPI干涉图风场反演中,误差来源主要是系统误差和数据处理误差.对于FPI设备的系统误差和干涉图数字图像处理的误差在文献(Hu et al., 2014)中已有阐述.本文所提出的算法中,理论上我们可以在同一级干涉环上任意选取两点进行处理,但算法编程实现时对径向视线风速点的选取会受相邻两级干涉环的距离限制而与理想的“极小间距”存在差异.假设两个取样点的视线风速差值大小为ΔV,则式(2)应修正为:
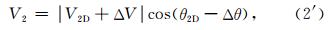
式(3)、(4)修正为
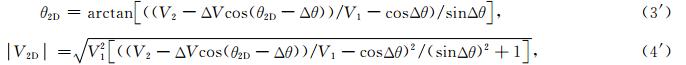
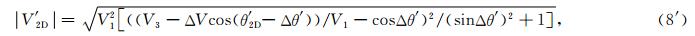
表 1说明了同一级干涉环上不同两点的视线风速的差值对垂直风误差的影响.由此可见,当视线风 在50~200 m·s-1变化时,若所选两点风速值变化范围在5~10 m·s-1时,其垂直风误差为9~20 m·s-1. 或可在设计FPI硬件系统时满足相邻级次干涉环“极小间距”的要求,比如,成像系统更小的焦距会在成像面上得到更多的干涉环.事实上,如果暂不考虑这一点,仅从FPI设备误差和数字图像处理误差的角度来看,由本文算法计算得到的垂直风能满足风场分析要求,3.2节的实验结果就是佐证.
|
|
表 1 取样两点视线风速差值对垂直风误差的影响 Table 1 Two points′ velocity of sight influence vertical wind error |
北极黄河站全天空FPI在2012年1月13日到2012年2月26日观测的是630.0 nm波段的气辉,2012年11月到2013年2月观测的是557.7 nm波段的气辉.考虑气辉干涉图质量,本文分别选取了2013年1月1—31日的低热层(97 km高度)观测数据和2012年1月16—19日的高热层(250 km高度)观测数据用2.1节提出的方法来计算低热层和高热层的垂直风,并且对受暴风雪天气或月盈时月光影响较大的FPI原始干涉图进行了剔除.
3.2 黄河站垂直风数据结果分析与讨论在热层中性风的研究中,许多观测表明垂直风存在突然变大的现象,但目前尚无足够的观测数据 来解释其驱动机制(Larsen and Meriwether, 2012),同时,观测数据的匮乏也制约着观测数据的可靠性验证,迄今尚缺乏有效的直接验证垂直风观 测的手段(Laakso et al., 1995; Cooper et al., 2009). 科学家普遍认同,若垂直风一天中表现为时间的函数,或者表现为给定事件(如极光)的函数,则可认为计 算结果是可信的(Smith et al., 1995a,1995b),或者不同地点、不同手段测得的热层垂直风显示出高度的一致性,也可认为计算结果是可信的(Larsen and Meriwether, 2012).
基于2.1节的反演方法计算了黄河站上空的热层垂直中性风,分别给出了低热层和高热层垂直风的时间变化系列,其数据的时间分辨率10 min,得到的结果如图 4至图 9所示(图中仅给出了正北方位的垂直风).图 4和图 5分别给出了低热层和高热层垂直风风向、风速以及地磁ap指数的时间变化情况.图 6和图 7给出的是对多天的垂直风的观测平均值,图 8和图 9考虑了垂直风的突变特性,给出的是垂直风的小时平均值.
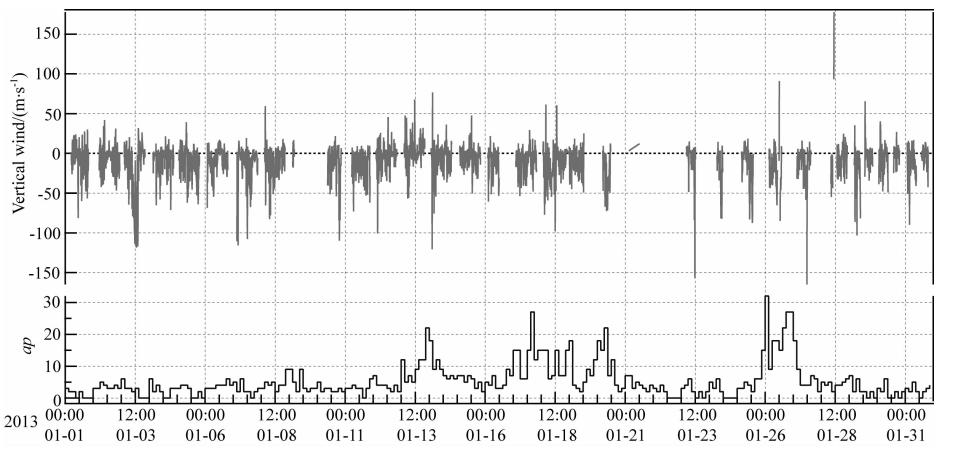 | 图 4 低热层中性垂直风观测值 Fig. 4 Vertical neutral winds observed in lower thermosphere |
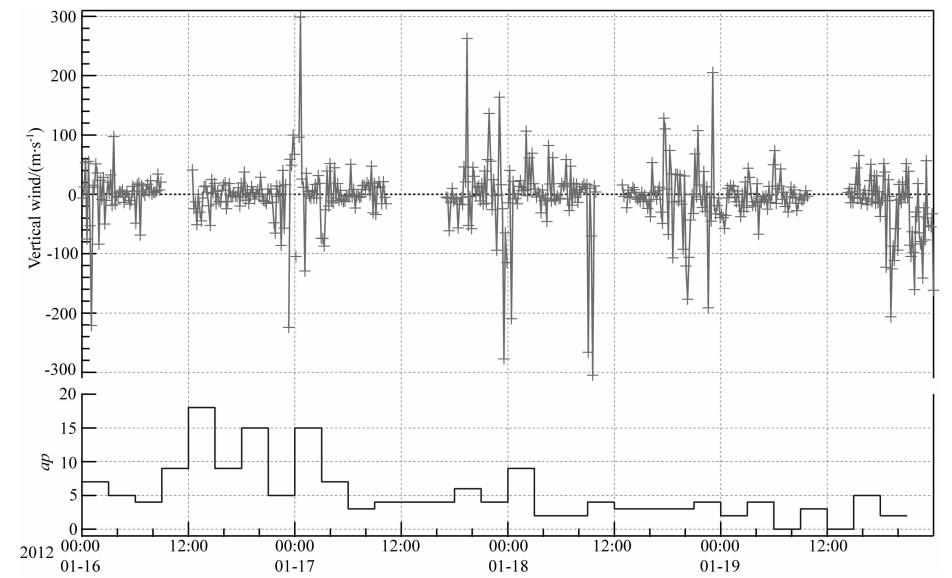 | 图 5 高热层中性垂直风观测值 Fig. 5 Vertical neutral winds observed in upper thermosphere |
 | 图 6 低热层中性垂直风的平均值(2013年1月) Fig. 6 Average vertical neutral winds in lower thermosphere(January 2013) |
 | 图 7 高热层中性垂直风的平均值(2012年1月16—19日) Fig. 7 Average vertical neutral winds in upper thermosphere(January 16—19,2012) |
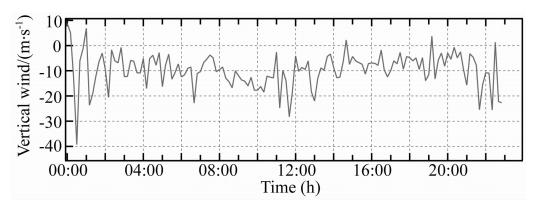
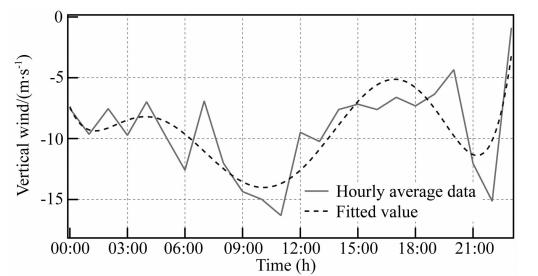 | 图 8 低热层中性垂直风的小时平均值(2013年1月) Fig. 8 Hourly average vertical neutral winds in lower thermosphere(January 2013) |
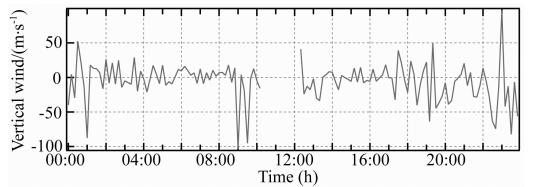
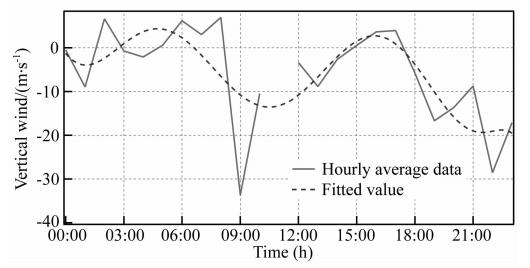 | 图 9 高热层中性垂直风的小时平均值(2012年1月16—19日) Fig. 9 Hourly average vertical neutral winds in upper thermosphere(January 16—19,2012) |
从图 4中看到,2013年1月13日18 ∶ 00左右,低热层风场达到100 m·s-1,对应的ap指数为22.但在1月17日18 ∶ 00左右,ap指数达到27的极大值,但对应的低热层风场仅为50 m·s-1.观察分析图 5,也有类似的现象,即ap指数达到极大值时,并非一定会伴有垂直中性风的扰动.这说明地磁活动虽然对热层风场有影响,但垂直风的扰动并非只受地磁活动的影响.从图 4和图 5中还可看到垂直风有许多的短期波动,在强地磁活动开始后,低热层会出现高达100 m·s-1以上的强风速,高热层更甚,会出现300 m·s-1以上的强风速.在低热层这一扰动过程会持续一小时甚至更长的时间,比如2013年1月3日12 ∶ 00到14 ∶ 00,而高热层垂直风的扰动更多的是表现为脉冲行为.
从图 6和图 7中的垂直风观测平均值看到,低热层垂直风一般小于高热层垂直风,但差值并不大,且低热层垂直风扰动幅值也同样小于高热层的扰动.从图 8和图 9中的垂直风小时平均值看到,北极 黄河站区域低热层和高热层的垂直中性风表现出明显的半日潮特性,其幅值分别为40 m·s-1和15 m·s-1,垂直风同样或类似的时间演变特性也被其他学者观测到(Smith et al., 1995a,1995b; Cooper et al., 2009; Larsen and Meriwether, 2012).
综上所述,基于本文的算法计算得到的垂直风,表现出与地磁和时间的联合变化特性,而且与其他学者发现的规律相一致.
4 结论本文基于全天空FPI干涉图建立了一个中性风矢量风场模型,给出了计算中性垂直风的算法.基于本文提出的算法计算了北极黄河站的垂直风,结果表明,高热层与低热层的垂直风平均幅值分别为40 m·s-1和15 m·s-1,且垂直风日变化表现出有规律的时间演变特性,且与地磁ap指数的变化有一定的相关性,在地磁活动强烈时,低热层垂直风会出现高达100 m·s-1的扰动,高热层甚至会达到300 m·s-1的扰动,这些特征与其他学者的观测结果相一致.
本文提出的热层中性垂直风的反演计算方法,不需要假设垂直风在一段时间内的均值为零(已被许多观测所证实并不总是成立),也不需要两台FPI同步观测,更有意义的是,本方法不要求FPI设备观测垂直风时必须是观测天顶上方,这使提供大量的、覆盖更多空域的垂直风观测数据成为了可能.
前人的工作中,计算垂直风时一般只给出了1σ不确定度,缺乏相应的误差分析.事实上,在低纬地区,水平风场为均匀时,垂直风可低至5~10 m·s-1,如此低的量级要求更高的计算精度,在下一步的工作中,将进一步提高我们的算法计算精度.
致谢 感谢国家海洋局极地办和中国极地研究中心对北极黄河站开展热层中性风FPI观测的支持.
| [1] | Anderson C, Davies T, Conde M, et al. 2011. Spatial sampling of the thermospheric vertical wind field at auroral latitudes. J. Geophys. Res., 116(A6): A06320. |
| [2] | Aruliah A L, Rees D. 1995. The trouble with thermospheric vertical winds: geomagnetic, seasonal and solar cycle dependence at high latitudes. J. Atmos. Terr. Phys., 57(6): 597-609. |
| [3] | Burnside R G, Herrero F A, Meriwether J W, et al. 1981. Optical observations of thermospheric dynamics at Arecibo. J. Geophys. Res., 86(A7): 5532-5540. |
| [4] | Cooper S L, Conde M, Dyson P. 2009. Numerical simulations of thermospheric dynamics: divergence as a proxy for vertical winds. Ann. Geophys., 27: 2491-2502. |
| [5] | Englert C R, Harlander J M, Brown C M, et al. 2012. Coincident thermospheric wind measurements using ground-based Doppler Asymmetric Spatial Heterodyne (DASH) and Fabry-Perot Interferometer (FPI) instruments. J. Atmos. Sol-Terr. Phys., 86: 92-98. |
| [6] | Hernandez G. 1966. Analytical description of a Fabry-Perot photoelectric spectrometer. Appl. Opt., 5(11): 1745-1748. |
| [7] | Hu G Y, Ai Y, Zhang Y G, et al. 2014. First scanning Fabry-Perot interferometer developed in China. Chin. Sci. Bull., 59(5-6): 563-570, doi: 10.1007/s11434-013-0093-5. |
| [8] | Huang Y Y, Makela J J, Swenson G R. 2012. Simulations of imaging Fabry-Perot interferometers for measuring upper-atmospheric temperatures and winds. Appl. Opt., 51(17): 3787-3800. |
| [9] | Innis J L, Greet P A, Dyson P L. 1996. Fabry-Perot spectrometer observations of the auroral oval/polar cap boundary above Mawson, Antarctica. J. Atmos. Terr. Phys., 58(16): 1973-1988. |
| [10] | Kurihara J, Oyama S, Nozawa S, et al. 2009. Temperature enhancements and vertical winds in the lower thermosphere associated with auroral heating during the DELTA campaign. J. Geophys. Res., 114(A12): A12306. |
| [11] | Laakso H, Aggson T L, Herrero F A, et al. 1995. Vertical neutral wind in the equatorial F-region deduced from electric field and ion density measurements. J. Atmos. Terr. Phys., 57(6): 645-651. |
| [12] | Larsen M F, Meriwether J W. 2012. Vertical winds in the thermosphere. J. Geophys. Res., 117(A9): A09319. |
| [13] | Liu X, Xu J Y, Zhang S R, et al. 2014. Thermospheric planetary wave-type oscillations observed by FPIs over Xinglong and Millstone Hill. J. Geophys. Res., 119(8): 6891-6901, doi: 10.1002/2014JA020043. |
| [14] | Makela J J, Meriwether J W, Huang Y Y, et al. 2011. Simulation and analysis of a multi-order imaging Fabry-Perot interferometer for the study of thermospheric winds and temperatures. Appl. Opt., 50(22): 4403-4416. |
| [15] | Mingalev I V, Mingalev V S, Mingaleva G I. 2012. Numerical simulation of the global neutral wind system of the Earth' middle atmosphere for different seasons. Atmosphere, 3(1): 213-228. |
| [16] | Price G D, Smith R W, Hernandez G. 1995. Simultaneous measurements of large vertical winds in the upper and lower thermosphere. J. Atmos. Terr. Phys., 57(6): 631-643. |
| [17] | Shiokawa K, Kadota T, Otsuka Y, et al. 2003. A two-channel Fabry-Perot interferometer with thermoelectric-cooled CCD detectors for neutral wind measurement in the upper atmosphere. Earth. Planets. Space, 55(5): 271-275. |
| [18] | Sipler D P, Biondi M A, Zipf M E. 1995. Vertical winds in the midlatitude thermosphere from Fabry-Perot interferometer measurements. J. Atmos. Terr. Phys., 57(6): 621-629. |
| [19] | Smith R W, Hernandez G. 1995a. Upper thermospheric temperatures at South Pole. Adv. Space. Res., 16(5): 31-39. |
| [20] | Smith R W, Hernandez G. 1995b. Vertical winds in the thermosphere within the polar cap. J. Atmos. Terr. Phys., 57(6): 611-620. |
| [21] | Wang Y J, Wang Y M, Wang H M. 2014. Simulation of ground-based Fabry-Perot interferometer for the measurement of upper atmospheric winds. Chinese J. Geophys. (in Chinese), 57(6): 1732-1739, doi: 10.6038/cjg20140605. |
| [22] | Wu Q, Wang W, Roble R G, et al. 2012. First daytime thermospheric wind observation from a balloon-borne Fabry-Perot interferometer over Kiruna (68N). Geophys. Res. Lett., 39(14): L14104, doi: 10.1029/2012gl052533. |
| [23] | Xie H Y, Yu T, Wang T B, et al. 2014. Modeling study on the coupling effect of the horizontal electric field and winds in the ionosphere. Chin. J. Space. Sci. (in Chinese), 34(4): 406-414, doi: 10.11728/cjss2014.04.406. |
| [24] | Yu T, Mao T, Wang Y G, et al. 2014. Two-dimension theoretical modeling of ionospheric dynamo and its preliminary application. Chinese J. Geophys. (in Chinese), 57(5): 1357-1365, doi: 10.6038/cjg20140501. |
| [25] | Yuan W, Xu J Y, Ma R P, et al. 2010. First observation of mesospheric and thermospheric winds by a Fabry-Perot interferometer in China. Chin. Sci. Bull., 55(35): 4046-4051. |
| [26] | Zhang H, Ai Y, Zhang Y G, et al. 2013. First observation of thermospheric neutral wind at Chinese Yellow River Station in Ny-Ålesund, Svalbard. Chin. Sci. Bull., 58(11): 1310-1315. |
| [27] | 王英鉴, 王咏梅, 王后茂. 2014. 高层大气测风用地基F-P干涉仪的数值模拟. 地球物理学报, 57(6): 1732-1739, doi: 10.6038/cjg20140605. |
| [28] | 解海永, 余涛, 王铁邦等. 2014. 电离层水平电场与风场的耦合模拟研究. 空间科学学报, 34(4): 406-414, doi: 10.11728/cjss2014.04.406. |
| [29] | 余涛, 毛田, 王云冈等. 2014. 二维电离层发电机理论模式及其初步应用. 地球物理学报, 57(5): 1357-1365, doi: 10.6038/cjg20140501. |
 2014, Vol. 57
2014, Vol. 57

