1 引言
地球空间内磁层、电离层和热层的相互耦合过程与动力学过程通常表现出十分复杂的时空变化特征.跨越亚洲和美洲的120°E/60°子午圈因其间的地磁与地理坐标的偏离(与地磁场构型有关)非常显著且方向相反而备受地球物理研究领域关注,它是当前世界上主要中高层大气、电离层、磁层和行星际空间环境观测设备集中的位置(图 1),其中120°E的子午圈正是国家“子午工程计划”中布设地基观测设备链的位置(陈泽宇和吕达仁,2007).由美国麻省理工学院海斯塔克天文台和中国科学院国家空间科 学中心发起的MERINO(MEridian ciRcle INternational Observation)观测,是沿120°E/60°W子午圈的全球联网观测项目,旨在提高人们在空间天气和气候监测的能力和促进相关研究成果.
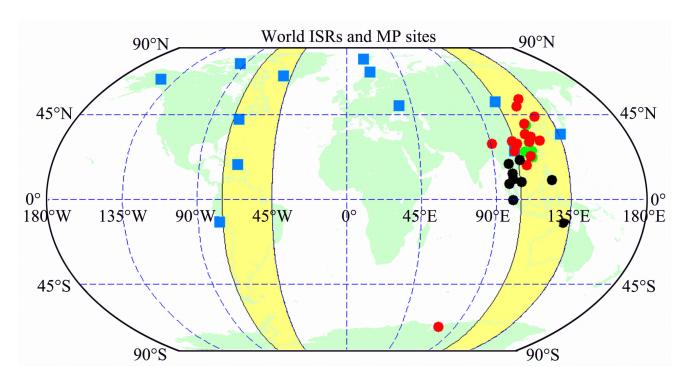 | 图 1 MERINO国际联测站点分布 红色:中国“子午工程”台站,蓝色:非相干散射雷达,黑色:亚洲其他观测台站. Fig. 1 MERINO network Red markers:Chinese Meridian Chain sites,blue squares: ISRs in the Northern Hemisphere,dark dots: Observational networks in Southeast Asia. |
在MERINO联测中,热层中性风是一个十分重要的观测参数,它显著地影响着热层、电离层乃至等离子体层的形态结构,在热层和电离层动力学过程、电离层-热层的耦合过程中具有决定性的作用(Makela et al., 2011; Wu et al., 2012),在大气上下相邻圈层的能量交换中也具有重要地位(Larsen and Meriwether, 2012).与广泛开展的带电粒子测量相比,针对中性风的观测还十分有限(Huang et al., 2012),针对热层中性风的探测手段也十分有 限(王英鉴等,2014).FPI(Fabry-Perot interferometer)干涉仪以其成本低、能耗小、测量手段直接等特点,成为热层中性风测量比较理想的探测设备,该仪器可对80~300 km高度范围内的热层中性风进行探测,这是其他地基手 段无法实现的.FPI探测目前已成为全球对80~300 km高度的大气风场和温度进行测量的主要方法之一(Cooper et al., 2009).国际上对基于FPI的热层风场观测研究起步较早(Armstrong,1969;Meriwether et al., 1973;Hern and ez, 1980),我国近年来也相继开展了地基FPI风场观测(胡国元,2010; Yuan et al., 2010; Zhang et al., 2013; Hu et al., 2014).王英鉴等(2014)基于计算机模拟气辉干涉图在FPI测风误差的评价方面做了一些有益的工作.但是,相关文献中对FPI测风精度的分析和描述不尽相同,或者是语焉不详,对FPI仪器研制的参考作用有限.
本文介绍了武汉大学SFPI干涉测风仪,分析了SFPI在MERINO第一轮观测中的结果,并与同台站的空间中心流星雷达测风数据进行了对比,详细的误差分析为FPI测风系统的精度评价和仪器研制提供了有益参考.
2 武汉大学SFPI和数据处理方法介绍 2.1 武汉大学SFPI武汉大学较早涉足了FPI研究(Ai et al., 1998),于2009年自主研制成功国内首台机动式双通道扫描FPI干涉测风仪.目前SFPI布置在中国科学院廊坊临近空间环境野外科学综合观测研究站(39.38°N,116.65°E),正常执行常规观测.图 2给出了武汉大学SFPI干涉测风仪的系统框图,表 1是SPFI的设备参数.SFPI观测热层风场时,扫描系统可设定为按5个方向进行观测,分别是天顶角为0°的天顶方向和天顶角为45°的东、西、南、北方向.两个平面镜M1、M2分别绕水平轴和竖直轴旋转配合,在程序控制下把上述5个方向的气辉辐射信号导入能对无穷远成像的聚焦透镜,光线经反射镜M3入射到标准具前的准直透镜,出射光以一定倾角入射到标准具,从标准具透射出的光线经成像透镜,再经半透半反的分光镜后,经过各自干涉滤光片后在CCD中进行光电转换,干涉图像被保存在PC机上,图中MG是波长为632.8 nm的校准激光器.
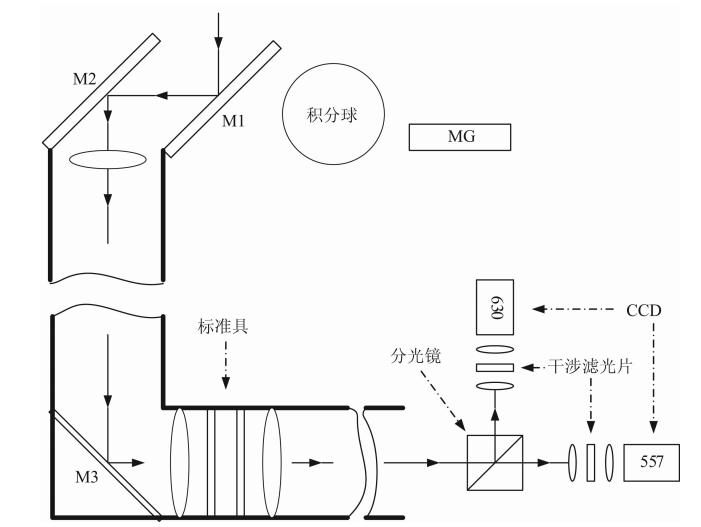 | 图 2 武汉大学SFPI原理框图 Fig. 2 Schematic diagram of SFPI |
|
|
表 1 SFPI设备主要参数 Table 1 SFPI key parameters |
MERINO安排有两轮联测,第一轮是世界标准时2014年3月24日零时始到4月6日24时止.武汉大学SFPI自2009年部署在廊坊野外观测站以来,一直正常执行着日常观测,我们择取了规定时间 段内的数据提交到联测数据库.图 3是3月23日CCD记录的气辉干涉图(图像经过了灰度范围调整以便于 显示和打印).图 3中的点状亮斑是天空星云,557.7 nm 波段的气辉观测时CCD进行的是2×2的像素合并(binning),630.0 nm波段气辉辐射较弱,进行了4×4的像素合并以增强干涉图的信噪比.
 | 图 3 SFPI记录的气辉干涉图(左:557.7 nm,2×2 binning;右:630.0 nm,4×4 binning) Fig. 3 Interferogram of SFPI(left:557.7 nm,2×2 binning;right:630.0 nm,4×4 binning) |
对于地基扫描式FPI,从干涉图反演大气风场有3类方法:
(1)基于傅里叶级数和实验标定获得FPI系统传递函数,建立FPI光强传递模型,用最小二乘法拟合气辉光强廓线求得视线风速和标准偏差. 如MiniME(Makela et al., 2011),Arecibo FPI(Burnside and Tepley, 1989),Millstone Hill FPI(Sipler et al., 1991).其难点是标准光源的制备以及传递函数的正确表达十分困难.
(2)从Fabry-Perot干涉仪原理出发,分析风速引起的多普勒频移对入射光波长的改变,表现在CCD生成的干涉图上则是干涉环半径的变化,即风速是零风速时干涉环半径、风速引起多普勒频移后 的干涉环半径以及系统成像焦距的函数.如Ramfjord FPI(Nakajima et al., 1995).这种方法测量视线风速的前提是获取一个参考零风速干涉图,通常的做法是用特定波长的激光光源来生成参考干涉图,或者用一段时间内的天顶观测值平均来获取参考半径,但被认为会引入10~20 m·s-1的系统误差(Aruliah and Rees, 1995).
(3)由同一天顶角下相对方向测量获得.如采用北向测量和南向测量给出南北向风速,采用东向测量和西向测量给出东西向风速,即风速是相对两 个方向观测的干涉环半径与系统成像焦距的函数,如Tromso FPI(Shiokawa et al., 2012).这种方法避开了参考零风速,对标准具腔长漂移也有一定的抵消.SFPI 采用了这种方法来计算水平风场(胡国元,2010).
3 个例观测结果与误差分析分析MERINO联测期间中性风与磁场、电场的相互耦合和动力学过程显然有积极意义,这一工作将在第二轮联测结束后进行.本文只开展第一轮12天的观测期间个例观测结果的分析与讨论.在廊坊观测站,布置有Meteor radar(流星雷达),它通过观测流星余迹的反射回波来反演100 km以下大气风场和温度(易稳等,2014),中科院空间中心提供了98 km高度上的水平风供我们进行对比分析.
3.1 个例观测结果这里选择MERINO第一轮联测第一天的观测 数据进行分析.武汉大学SFPI同时记录在557.7 nm(峰值高度被认为是97 km)和630.0 nm(峰值高度被认为是250 km)两个波段的气辉辐射.Meteor radar可提供90~100 km高度范围内每2 km高度上的水平风,图 4和图 5里参与比较的是98 km高度的经向风和纬向风.
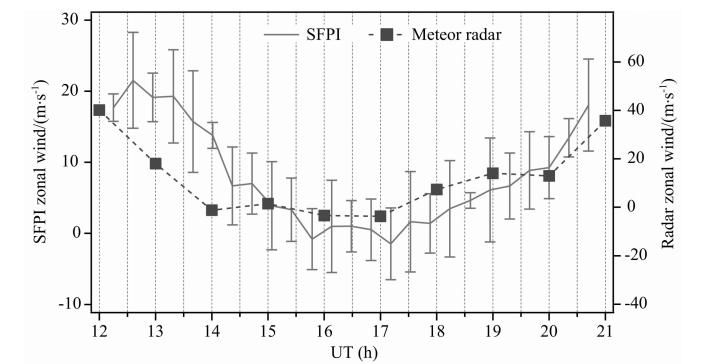 | 图 4 2014年3月24日SFPI与Meteor radar观测的低热层纬向风速对比 Fig. 4 Zonal winds in lower thermosphere from SFPI vs. Meteor radar at March 24,2014 |
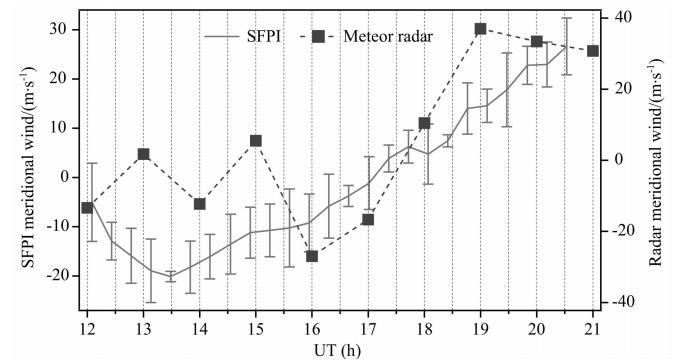 | 图 5 2014年3月24日SFPI与Meteor radar观测的低热层经向风速对比 Fig. 5 Meridional winds in lower thermosphere from SFPI vs. Meteor radar at March 24,2014 |
从图 4和图 5可以看出,武汉大学SFPI与中科院空间中心Meteor radar观测的水平经向风和纬向风的趋势变化高度吻合,而在数值上流星雷达观测的值较大,这与两种设备观测的高度有差异有关,而且也符合热层高度越高风速越大的经验认识.
在24日的观测中,SFPI风速测量的误差分别 小于8 m·s-1(557.7 nm)和7.8 m·s-1(630.0 nm),低热层水平经向风幅值大于纬向风,而高热层水平经向风幅值则小于纬向风.有意思的是,两个高度上的纬向风风向基本未变,而经向风则存在反向变化.
3.2 误差分析对于给定的FPI设备,其测风理论精度与设备参数有关,是可以计算的.但在实际反演风场时,方法不同以及图像处理的精度不同,实际测风误差要大于理论误差,通常是由风速计算的标准偏差给出(表 2).但对FPI测风理论精度的分析,对于评估实际测风系统和指导FPI仪器设计仍然十分重要.
|
|
表 2 国际FPI系统反演风速和误差评定的方法 Table 2 Wind derive method and error definition of several FPIs |
(1)标准具通光孔径D和成像物镜焦距f
以SFPI为例,其设备参数如表 1所列,入射光波长λ为630.0 nm时,第m级干涉环的出射角θ符合mλ=2dcosθ,CCD成像面上第m级干涉环的半径为r=ftanθ≈fθ.表 3列出了干涉环级次对应的出射角及半径.可见,共有三级干涉环能完全成像在CCD接收面,但内环的半径值相对而言太小,在气辉干涉图中几乎成一亮斑,因此,不予考虑最高级次干涉环,将m数为47618的干涉环看作内环.实际上设备的f设计值就是遵循该原则由干涉条纹数(最大出射角)和CCD像面尺寸共同确定的.
|
|
表 3 干涉环级次对应的出射角及半径 Table 3 Emergence angle and radius according to the annular ring index |
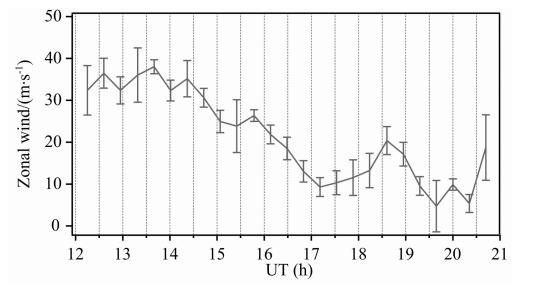 | 图 6 2014年3月24日SFPI观测的高热层纬向风 Fig. 6 Zonal winds in upper thermosphere from SFPI at March 24,2014 |
 | 图 7 2014年3月24日SFPI观测的高热层经向风 Fig. 7 Meridional winds in upper thermosphere from SFPI at March 24,2014 |
从等倾干涉原理出发,不难推导出视线风速的精度为(Hu et al., 2014):
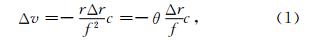
式中,c是真空中的光速.由(1)式可知,波长变化量、风速测量精度与条纹半径变化量呈近似线性关系,在f以及入射光λ已确定的条件下,斜率与干涉条纹级数(半径)有关,表 4给出了内环和次级环的条纹半径变化量与波长变化及风速之间的数值关系,显然,靠近干涉中心的条纹(内环)的测量精度明显高于外环.实际处理干涉图时像素的定位精度达到0.1像素,则视线风速的测量精度最高可达到3.76 m·s-1.
|
|
表 4 测风精度与干涉环半径变化的关系 Table 4 Ring radius change influence wind error |
由(1)式还可知道,测风精度随成像物镜焦距的增加而线性提高,但会牺牲通光量和条纹数目,这对 弱气辉条件下的观测不利,也不利于通过FPI数值模型来拟合气辉廓线求解风速.因此,在FPI仪器设计之初,就需要考虑标准具通光孔径D和成像物镜焦距f的合理组合.
(2)标准具腔长d和腔长温度漂移特性
同前理,基于F-P等倾干涉公式对d、θ求全微分,由于θ极小,可近似得到


(3)影响FPI测风精度的其他因素
FPI测风精度除与上述硬件设备参数和运行环境有关外,还与观测模式、CCD的暗电流和图像处理的精度有关.比如,可以通过CCD在关闭镜头后记录一张暗电流图像作为背景噪声图像,观测时减去背景图像得到干涉图可以显著提高信噪比,有利于提高测风精度.在气辉辐射较弱时,设置CCD工作在Binning图像读出模式下,可极大提高灵敏度、输出速度,但图像的解析度将降低,会降低FPI测风精度.光学元件的加工和安装误差也会带来测风的系统误差,虽然在FPI的测风模型中可以加以考虑,但定量衡量它们仍存在困难.反演风速时对气辉辐射廓线峰值坐标以及干涉环圆心的处理精度也会对最终的风速标准偏差带来影响.
4 结论
本文介绍了武汉大学SFPI干涉测风仪在MERINO联合观测中的工作,并与同基站的流星雷达测风数据进行了验证,详细分析了FPI测风系统的误差计算与评估.本文经过分析指出,在FPI仪器设计之初,就需要考虑标准具通光孔径D和成像物镜焦距f的合理组合,在目前CCD和标准具规格的限制下,增加f会提高测风精度,但会牺牲通光量,可通过设置CCD为Binning读出模式来提高灵敏度.在FPI观测风场时,要对设备的工作环境温度进行控制,特别是控制标准具的温度漂移.FPI测风设备的精度可以理论推导,但实际测风误差还与反演算法、元器件的加工和安装精度有关,国际通用的误差评价方法是用统计偏差来表示.
致谢 感谢中国科学院空间科学与应用研究中心对SFPI在廊坊站日常观测的支持以及对MERINO观测期间流星雷达数据的提供.
| [1] | Ai Y, Ishii M, M K, et al. 1998. Airglow observation by Fabry-Perot interferometer. J. Wuhan Univ. (Nat. Sci. Ed)., 3(2): 175-180. |
| [2] | Armstrong E B. 1969. Doppler shifts in the wavelength of the OI [lambda] 6300 line in the night airglow. Planet. Space Sci., 17(5): 957-974. |
| [3] | Aruliah A L, Rees D. 1995. The trouble with thermospheric vertical winds: geomagnetic, seasonal and solar cycle dependence at high latitudes. J. Atmos. Terr. Phys., 57(6): 597-609. |
| [4] | Burnside R G, Tepley C A. 1989. Optical observations of thermospheric neutral winds at Arecibo between 1980 and 1987. J. Geophys. Res., 94(A3): 2711-2716. |
| [5] | Chen Z Y, Lü D R. 2007. Seasonal variations of the MLT tides in 120°E meridian. Chinese J. Geophys. (in Chinese), 50(3): 691-700, doi: 10.3321/j.issn:0001-5733.2007.03.006. |
| [6] | Cooper S L, Conde M, Dyson P. 2009. Numerical simulations of thermospheric dynamics: divergence as a proxy for vertical winds. Ann. Geophys., 27: 2491-2502. |
| [7] | Hernandez G. 1980. Measurement of thermospheric temperatures and winds by remote Fabry-Perot spectrometry. Opt. Eng., 19(4): 518-532. |
| [8] | Hu G Y. 2010. Development of mobile Doppler imaging Fabry-Perot interferometer for atmospheric wind measurement (in Chinese)[Ph. D. thesis]. Wuhan: Wuhan University. |
| [9] | Hu G Y, Ai Y, Zhang Y G, et al. 2014. First scanning Fabry-Perot interferometer developed in China. Chin. Sci. Bull., 59(5-6): 563-570, doi: 10.1007/s11434-013-0093-5. |
| [10] | Huang Y, Makela J J, Swenson G R. 2012. Simulations of imaging Fabry-Perot interferometers for measuring upper-atmospheric temperatures and winds. Appl. Optics., 51(17): 3787-3800. |
| [11] | Larsen M F, Meriwether J W. 2012. Vertical winds in the thermosphere. J. Geophys. Res., 117(A9): A09319, doi: 10.1029/2012JA017843. |
| [12] | Makela J J, Meriwether J W, Huang Y, et al. 2011. Simulation and analysis of a multi-order imaging Fabry-Perot interferometer for the study of thermospheric winds and temperatures. Appl. Optics., 50(22): 4403-4416. |
| [13] | Meriwether J W, Heppner J P, Stolarik J D, et al. 1973. Neutral winds above 200 km at high latitudes. J. Geophys. Res., 78(28): 6643-6661. |
| [14] | Nakajima H, Okano S, Fukunishi H, et al. 1995. Observations of thermospheric wind velocities and temperatures by the use of a Fabry-Perot Doppler imaging system at Syowa Station, Antarctica. Appl. Optics., 34(36): 8382-8395. |
| [15] | Shiokawa K, Otsuka Y, Oyama S, et al. 2012. Development of low-cost sky-scanning Fabry-Perot interferometers for airglow and auroral studies. Earth, Planets and Space, 64(11): 1033-1046. |
| [16] | Sipler D P, Hagan M E, Zipf M E, et al. 1991. Combined optical and radar wind measurements in the F region over Millstone Hill. J. Geophys. Res., 96(A12): 21255-21262. |
| [17] | Wang Y J, Wang Y M, Wang H M. 2014. Simulation of ground-based Fabry-Perot interferometer for the measurement of upper atmospheric winds. Chinese J. Geophys. (in Chinese), 57(6): 1732-1739, doi: 10.6038/cjg20140605. |
| [18] | Wu Q, Wang W, Roble R G, et al. 2012. First daytime thermospheric wind observation from a balloon-borne Fabry-Perot interferometer over Kiruna (68N). Geophys. Res. Lett., 39(14), L14104, doi: 10.1029/2012gl052533. |
| [19] | Yi W, Chen J S, Ma C B, et al. 2014. Observation of upper atmospheric temperature by Kunming all-sky meteor radar. Chinese J. Geophys. (in Chinese), 57(8): 2423-2432, doi: 10.6038/cjg20140804. |
| [20] | Yuan W, Xu J Y, Ma R P, et al. 2010. First observation of mesospheric and thermospheric winds by a Fabry-Perot interferometer in China. Chin. Sci. Bull., 55(35): 4046-4051. |
| [21] | Zhang H, Ai Y, Zhang Y, et al. 2013. First observation of thermospheric neutral wind at Chinese Yellow River Station in Ny-Ålesund, Svalbard. Chin. Sci. Bull., 58(11): 1310-1315. |
| [22] | 陈泽宇, 吕达仁. 2007. 东经120°E中间层和低热层大气潮汐及其季节变化特征. 地球物理学报, 50(3): 691-700, doi: 10.3321/j.issn:0001-5733.2007.03.006. |
| [23] | 胡国元. 2010. 机动式法布里-珀罗多普勒成像干涉测风仪的分析与研制[博士论文]. 武汉: 武汉大学. |
| [24] | 王英鉴, 王咏梅, 王后茂. 2014. 高层大气测风用地基F-P干涉仪的数值模拟. 地球物理学报, 57(6): 1732-1739, doi: 10.6038/cjg20140605. |
| [25] | 易稳, 陈金松, 马春波等. 2014. 昆明全天空流星雷达观测中高层大气温度. 地球物理学报, 57(8): 2423-2432, doi: 10.6038/cjg20140804. |
 2014, Vol. 57
2014, Vol. 57

