2. 中国地震局地震预测研究所, 北京 100036
2. Institute of Earthquake Science, China Earthquake Administration, Beijing 100036, China
1 引言
近些年来,地震电离层异常效应研究已成为地震科学领域和电离层科学领域的研究热点之一(Pulinets and Boyarchuk, 2004; Hayakawa and Hobara, 2010; 申旭辉等,2007).随着电离层探测站点的增多,全球定位系统(GPS)反演技术的发展,以及相关监测卫星的使用,科学家们观测到了更多强震前后的电离层数据.对这些数据进行分析研究,人们发现多种震前电离层参数发生了扰动,如电子浓度(刘静等,2011; Pulinets and Legen′ka,2003),F2层临频foF2(Zhao et al., 2008; Liu et al., 2000),F2层虚高hmf2(Liu et al., 2006; Hsiao et al., 2009),电子浓度总含量TEC(Yu et al., 2009;Zhu et al., 2010)离子浓度温度(Akhoondzadeh et al., 2010; Li and Parrot, 2013),以及电离层电磁辐射背景中 超低频VLF(Zhang et al., 2012; Ho et al., 2013),极低频ELF(Serebryakova et al., 1992),直流DC-甚低频ULF(Zhang et al., 2011,2014)波段等.
任何异常现象的出现都与一定的物理或化学机制相联系,地震电离层异常效应也不例外.到目前为止,对其机理的解释目前主要集中在两方面.一方面为声重力波扰动产生异常,由地震引起的声重力波从下到上传到电离层,在电离层中形成行进式扰动(TID),所以电离层参数的扰动形态具有波状特征(Shalimov and Gokhberg, 1998; Molchanov et al., 2004). 另一方面为异常电场效应,由地表岩石破裂引起的一系列复杂的物理化学反应,在电离层处形成异常的直流电场,继而扰动其他电离层参数.因为电离层场向电导率近似无限,异常电场及其引起电离层参数扰动将在局地和磁共轭地区同时发生(Pulinets et al., 2000; Sorokin et al., 2011,2005,2007; Freund,2011).Horie等(2007)在对苏门达腊地震数据分析中发现电离层扰动具有波状特征,而且Rozhnoi等(2007)也给出了震前声重波的观测证据.另一方面,张学民等(2011,2014),Gousheva等(2008)用卫星数据发现了震前电离层出现准静电场的扰动,且多篇论文报道不同地震的电离层异常均出现了磁共轭效应(Ruzhin et al., 1998; Liu et al., 2011).这些观测结果表明地震电离层效应十分复杂,电场和声重波都对电离层产生了干扰现象.在电离层异常机制研究中可以假设这两种机制相互独立,分别进行针对性的研究.在本文中,不考虑声重力波扰动机制的影响,重点关注地震引起电离层异常电场机制.
对地震孕育过程中大气中发生异常电场现象的研究已有近百年的历史(丁鉴海等,2006).学者们普遍认为这是伴随摩擦过程中岩石破碎发生的效应,其机制可分为压电效应理论(Freund,2011),热电效应理论(申俊峰等,2010)和化学气体释放(Pulinets et al., 2000; Sorokin et al., 2001).本文将采用Sorokin等(2001,2006,2007)给出的一个地震电离层的电动力学机制,该机制认为震前地壳岩石破碎,将排放氡等放射性物质,而这些放射性气体显著增大低层大气的电离辐射现象,一方面改变了大气层底部的电导率分布,另一方面也电离出更多的离子.这些离子将附在气体分子或液体分子上形成带电气溶胶,带电气溶胶在垂直对流及重力作用下上升输运,在大气层低层形成附加电流(external current).而附加电流将显著增大大气层-电离层电路里的传导性电流,并最终对电离层直流电场产生扰动.在考虑附加电流对称分布和电离层层电导率均匀分布且各向同性(只考虑Peterson电导率)的情况下,Sorokin等(2005)给出了电离层异常电场的理论解.求解发现,附加电流引起的电离层异常电场能达到~10 mV/m.
但在真实情况中,电离层层电导率各向异性且不均匀,在E层导电层中,Hall电导率值反而比Peterson电导率更高,因此不能简单地忽略Hall电导率的作用.考虑到地震电离层效应的尺度范围,电离层被看作为球面薄层更符合实际,而非先前模型(Sorokin et al., 2005,2006)中所假设的平面薄层.为了考虑更普遍的情况,本文将基于大气层-电动力学的理论,计入各向异性的层电导率的影响,将模型方程推广到球坐标系中,建立新的电离层异常电场模型.在新的模型中,通过引入一个电离层层电导率经验公式,对附加电流引起的电离层电场异常进行分析与研究.
2 物理模型氡气等惰性气体从土壤中渗透进入大气,是底部大气辐射的主要来源.有文献指出,震前5—7天 内,都观测到近地空气里氡气含量显著上升(Heinicke et al., 1995; Virk and Singth, 1994).这些氡气等放射性气体在低层大气中放射电离,增大该区域的离子含量,同时受对流、扩散等作用向上扩散.基于这些事实,Sorokin和Chmyrev(2010)提出大气层-电离层耦合电动力学模型,认为从土壤排放出来的附电气体及放射性物质垂直对流会形成附加电流,该附加电流显著增强了大气层-电离层电路里传导电流,并最终对电离层电场进行扰动.
2.1 底部充电区域电场方程考虑到近地大气有附加电流铅直流动,持续时 间大于大气电场弛豫时间(τ0=ε0/σ0)情况下,方程 满足欧姆定律和电荷守恒条件:

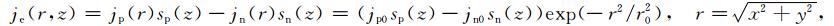
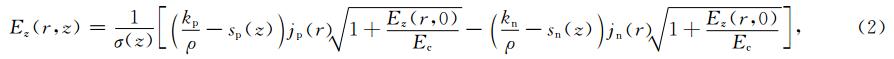
将电离层视为薄层,考虑到共轭性,即可由(1)—(2)式推出电离层水平电场方程(Sorokin et al., 2005,2006):
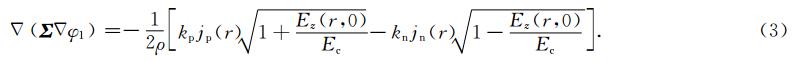
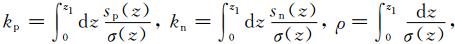 φ1为电离层电势,z1为电离层薄层海拔高度,这里设z1=110 km,Σ 为电离层层电导率张量.Ec为大气中电场阀值,由静电力、重力、黏滞力的平衡计算得到.根据Sorokin等(2001)的计算,Ec=450 V/m.
φ1为电离层电势,z1为电离层薄层海拔高度,这里设z1=110 km,Σ 为电离层层电导率张量.Ec为大气中电场阀值,由静电力、重力、黏滞力的平衡计算得到.根据Sorokin等(2001)的计算,Ec=450 V/m.如果设层电导率均匀分布且各向同性,张量 Σ 可以用一个Σp常量来表示,(3)式化简为
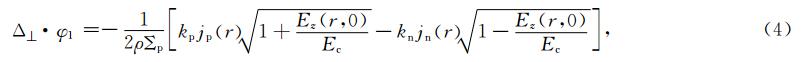
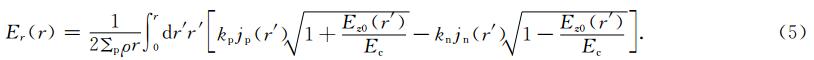
在真实的电离层,Σ 张量是各向异性且随着时空变化,因此难以采用理论方法求解(3)式.再考虑到基于球坐标的经验公式或观测数据同化模式能较为真实地提供 Σ 的值,下面我们将把(3)式扩展到球面坐标式中,并采用松弛迭代数值方法来求解新坐标系下的方程.
将电离层看成一球面薄层,设局地笛卡尔坐标中x轴磁南向,y轴磁东向.震心坐标(0,0)位于球面坐标(θ0,λ0),θ表示的是地磁余纬,λ表示地磁经度.则球面坐标和局地笛卡尔坐标系的变换公式为

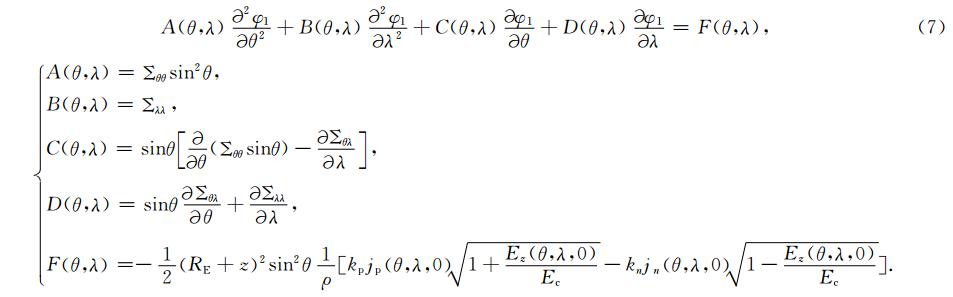
在地磁坐标下,电离层层电导率张量可写为
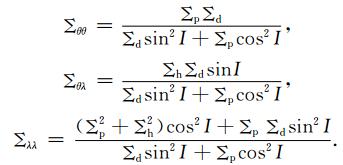
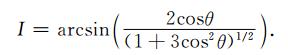
方程(7)是一般线性椭圆型偏微分方程,因为已经考虑到电离层电势的等共轭性,所以求解该方程可以在一个半球上求解.设在南北方向余纬θ的边界条件为
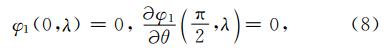
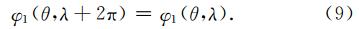
计算中网格均匀划分,间隔是0.1°.采用松弛迭代法即可由方程(3),(7),(8),(9)解出电离层电势φ1,继而求得电离层薄层的水平电场Ex,Ey:
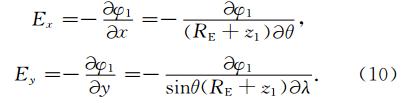
电离层电导率主要取决于带电粒子浓度、电子、离子的磁回旋频率及其与中性粒子的碰撞频率相对大小,具有明显的时间和空间上的不均匀性(Yu et al., 2003).本文采用Nopper和Carovillano(1979)所使用的电离层层电导率经验公式,该公式给出不同纬度及经度(地方时)下层电导率的分布,可以用来初步比较不同时空下该附加电流激发电离层电场的特征.
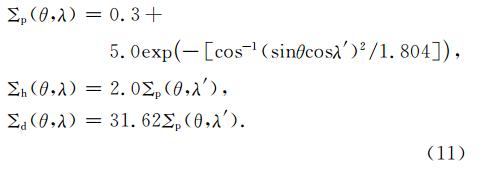
在这个模式中,为了方便比较,我们采用Sorokin等(2005)的附加电流参数设置,设大气底层中附加电流的高度分布及大气电导率分布如下:
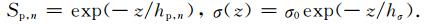
在地表处,附加电流有以下计算公式:
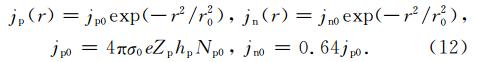
为了研究分析震前附加电流理论所造成的电离层异常电场的时空特征,本文针对以下情况进行数值模拟.(1)电离层电导率各向同性时附加电流所激发电离层异常电场特征.(2)不同纬度之间电离层异常电场差异.(3)白天和夜晚之间电离层异常电场的差异.
4.1 均匀层电导率时异常电场计算结果首先为了了解附加电流在模型里的作用以及验证数值方法是否正确,我们先考虑一种最简单的情况:假设电离层电导率是各向同性的,层电导率设为Σθθ=Σλλ=1 Ωm,Σθλ=2 Ωm.代入方程(3)得到
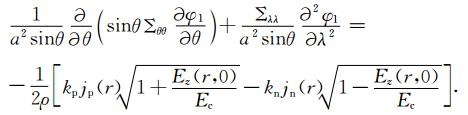
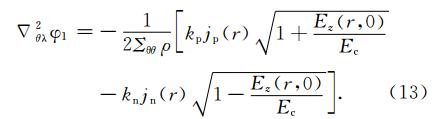
由(13)式对比(4)式可看出,各向同性电导率的例子就是Sorokin等(2005)模型里所计算的例子,只是他将电离层考虑成平面薄层而本文考虑为球面薄层.并且为了求解的普遍性,我们采用数值解法替换理论解.因此,这个例子可以用来检验新的出发方程和数值解法.
图 1给出均匀电导率情况下的计算结果,南北方向上北向为正,东西方向上东向为正.经检验,在设置迭代次数10000次后,松弛迭代因子w=1和理论解的最大误差约为0.2%.该附加电流激发起的异常电场 E 方向由震心向外,场值以震心为圆心呈圆形分布.在震心附近,异常电场值较小,并随着水平距离r的增大迅速增大,附加电流区域边缘处达到最大值然后缓慢下降,其最大值强度接近10 mV·m-1.图 2a给出了随水平距离变化的异常电场,图 2b是引起电离层异常电场的附加电流分 布,对比a、b可以看出,附加电流所激发的电离层异常电场分布距离远远大于自己在地表处的水平分布距离.这表明,观测到的地震电离层电场异常范围将远大于地震孕育区的区域.这种现象和前人的观测一致(Liu et al., 2011).
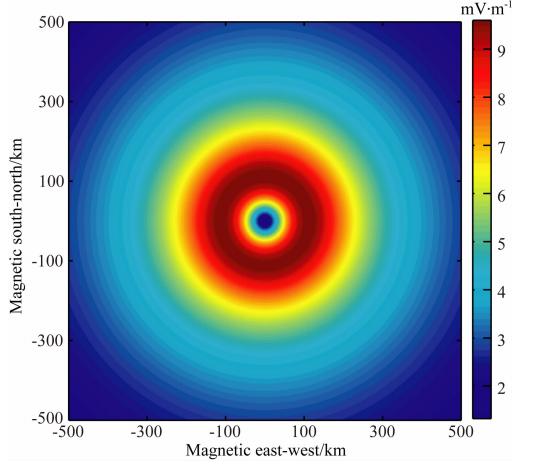 | 图 1 各向同性层电导率情况下异常电场的分布 Fig. 1 Spatial distribution of anomalous electric field with homogeneous conductivity |
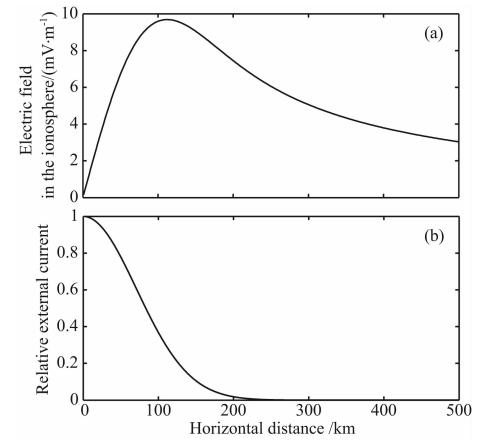 | 图 2 随着水平距离变化的异常电场强度(a)和额外电流的分布(b) Fig. 2 Dependence of the anomalous electric field in the ionosphere on horizontal distance(a) and external current(b) |
在真实的电离层中,层电导率具有明显的不均匀特征.这就会使得生成的电场形态、方向各不相同.我们将采用(9)式的层电导率经验模型,来研究纬度不同时,电场形态的变化,以及这种变化对电离层造成的干扰.
图 3给出的是地磁经度315°(LT 21 ∶ 00)时,不同地磁纬度计算的电场结果.第一行表示磁纬40°,第二行磁纬30°,第三行磁纬20°,第四行磁纬10°.而第一列表示的是总电场强度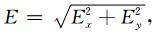 第二列表示磁南北向电场强度 | Ex |,第三列表示磁东西向电场强度 | Ey | .纬度40°时,因为层电导率的各向异性,异常电场E的形态与图 1相比变成了椭圆型,且随着纬度的降低,电场E的形态也逐渐变成了东西侧偶极子式.这是因为南北向电场值 | Ex | 随着纬度下降的速度比 | Ey | 快得多(图 3),因此异常电场E的分布形态越来越接近 | Ey | 的形态.而Ex电场值迅速下降是因为高电导率的磁力线在靠近磁赤道时会逐渐变为南北水平线,使得在南北向的电导率变大,进而减小该方向电场Ex.从图 3还可看出当电导率张量存在梯度时,Ex和Ey强度分布也不是对称分布.几乎所有纬度上都是南向(赤道向)电场强于北向电场,而在近赤道区域10°、20°,东边异常电场明显强于西边异常电场.这也许和方程(7)里的C,D系数正负相关,但因偏微分方程的复杂性,还需要进一步研究.
第二列表示磁南北向电场强度 | Ex |,第三列表示磁东西向电场强度 | Ey | .纬度40°时,因为层电导率的各向异性,异常电场E的形态与图 1相比变成了椭圆型,且随着纬度的降低,电场E的形态也逐渐变成了东西侧偶极子式.这是因为南北向电场值 | Ex | 随着纬度下降的速度比 | Ey | 快得多(图 3),因此异常电场E的分布形态越来越接近 | Ey | 的形态.而Ex电场值迅速下降是因为高电导率的磁力线在靠近磁赤道时会逐渐变为南北水平线,使得在南北向的电导率变大,进而减小该方向电场Ex.从图 3还可看出当电导率张量存在梯度时,Ex和Ey强度分布也不是对称分布.几乎所有纬度上都是南向(赤道向)电场强于北向电场,而在近赤道区域10°、20°,东边异常电场明显强于西边异常电场.这也许和方程(7)里的C,D系数正负相关,但因偏微分方程的复杂性,还需要进一步研究.
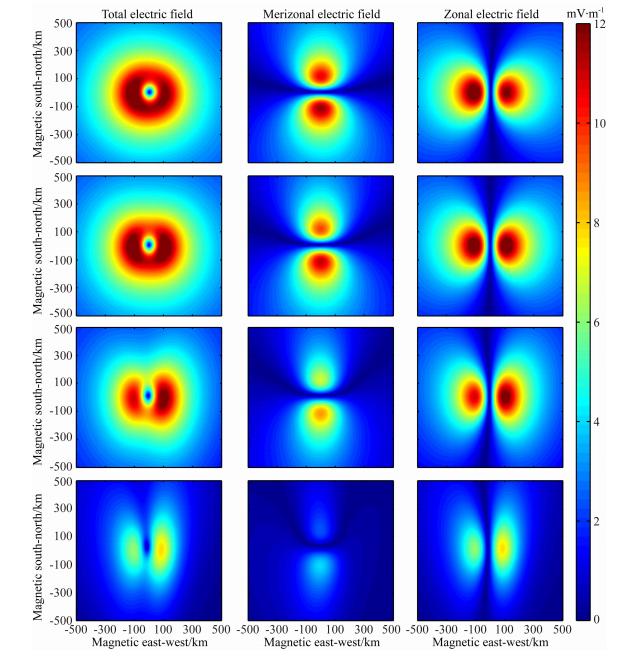 | 图 3 不同纬度、震区上空电离层异常电场水平分布 图中第一行表示磁纬40°,第二行表示磁纬30°,第三行表示磁纬20°,第四行表示磁纬10°. Fig. 3 Electric field structure in the ionosphere over seismically active fault zone calculated for different magnetic latitudes First row:40°,second row: 30°,third row: 20°,fourth row: 10°. |
在靠近赤道的区域,附加电流引起的异常电场 主要是东西向电场,显示左右两侧偶极子形态变化.该异常电场能通过磁力线近乎无损地到达F层,并驱使F层等离子体(主要是O+离子)做 E × B 漂移运动.而在低纬度地区,E × B 漂移现象和喷泉现象紧密相关.东向电场将使等离子体(主要是O+离子和电子)向上漂移N2和O2高度较低的高层大气中,增强赤道喷泉效应.而西向电场将等离子体向下漂移,减弱赤道喷泉效应.它们都将会扭曲同个子午面上的赤道异常形态,扰动该区域的电离层参数.因此在低纬度引起的电离层异常现象会向南北(经度方向)两端延伸.
4.3 白天晚上引起水平异常电场的差异图 4给出了在纬度50°上,地震异常电场随着当地时的变化.从图中可以看出,假设地震在地表上生成同样的附加电流分布情况时,激发的电离层异常电场有明显的日夜变化.夜间值比日间值大10倍左右.这是因为电离层层电导率Σp、Σh高于晚上电离层层电导率,且其形态也大不一样,因此生成的电场值大小及形态皆有很大的差别.
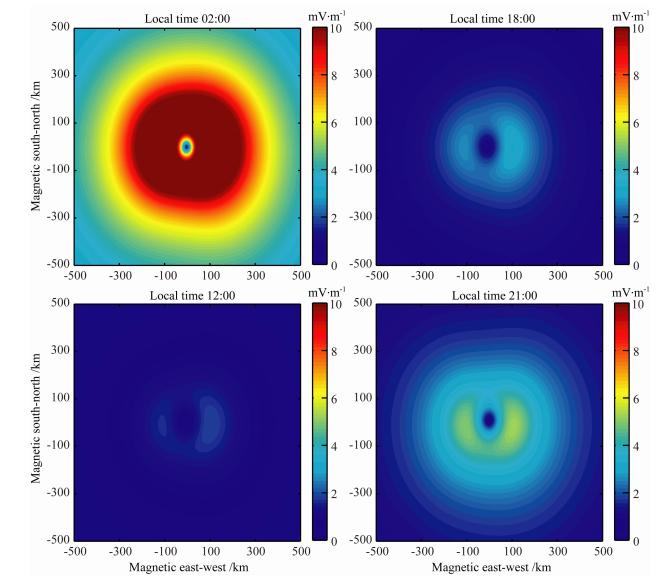 | 图 4 随时间变化的电离层异常电场 Fig. 4 Anomalous electric field in ionosphere variation with time |
以上表明只考虑同样分布的附加电流情况时,引起的电离层异常电场或由异常电场激发起的其他参数干扰晚上现象将比白天更显著.有些观测似乎 可以印证这一点.Zolotov等(2012)对日本(2011.3)、 土耳其(2011.10)、智利及阿根廷(2011.1)地震前TEC扰动进行分析时,发现扰动都在入夜时开始出现,日出后消失,Ouzounov等(2013)对2008—2009年度在希腊发生的四次M>6.0地震观测研究表明,TEC异常发生时间处在LT16—LT04时段,以上的观测结果都可以被电离层层电导率的日夜变化所解释.且Kuo等(2011)对震前p-holes(positive hole)机制研究发现,在相同的岩石电流源的情况下,晚上电离层干扰比白天高10倍左右.但是也有相反的例子,徐彤等(2012)和Liu等(2006)统计研究表明,震前前兆foF2异常集中在下午时段.这可能是在真实情况下,地震电离层异常不仅和电场有关,还和声重 波、当地天气、岩石种类等有关,这需要进一步的研究.
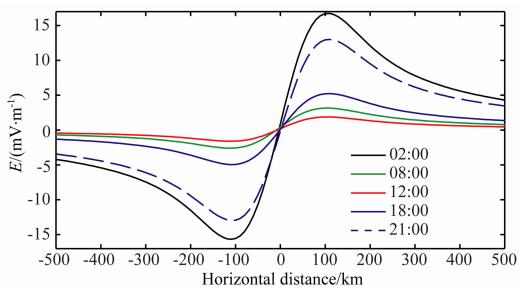 | 图 5 震心磁东西方向上纬向电场随时间变化 Fig. 5 Zonal electric field in the epicenter magnetic east-west direction variation with time |
基于低层大气层-电离层电动力学耦合理论,本文将附加电流理论推导出来的电离层电势方程扩展到球面坐标系中,建立新的电离层异常电场模型. 在建立新的模型中,考虑到电离层层电导率张量为各向异性,难以理论求解,因此采用松弛迭代法求解该模型.经检验,模型是可靠而准确的.对地震电离层异常电场的模拟研究中发现:
(1)附加电流引起电离层异常电场范围远大于附加电流在地表上的分布.
(2)在低纬度地区,异常电离层电场主要是磁东西向(磁纬向),分布在震心的东西侧,显偶极子形状.这样的异常电场将加强或减弱喷泉效应,继而影响该子午面上的赤道异常现象,因此该电场造成的电离层扰动将沿着子午线向南北延扩,加深或减弱赤道异常现象.
(3)在扰动源相同的情况下,异常电场夜晚值比白天值高出10倍,昼夜差异十分明显.
| [1] | Akhoondzadeh M, Parrot M, Saradjian M R. 2010. Electron and ion density variations before strong earthquakes (M>6.0) using DEMETER and GPS data. Nat. Hazards Earth Syst. Sci., 10(1): 7-18. |
| [2] | Ding J H, Shen X H, Fan W Y, et al. 2006. Seismo electromagnetism precursor research progress. Chin. J. Radio Sci. (in Chinese), 21(5): 791-801. |
| [3] | Freund F. 2011. Pre-earthquake signals: Underlying physical processes. J. Asian Earth Sci., 41(4): 383-400. |
| [4] | Gousheva M, Danov D, Hristov P, et al. 2008. Quasi-static electric fields phenomena in the ionosphere associated with pre-and post earthquake effects. Nat. Hazards Earth Syst. Sci., 8(1): 101-107. |
| [5] | Hayakawa M, Hobara Y. 2010. Current status of seismo-electromagnetics for short-term earthquake prediction. Geomat. Nat. Hazards Risk, 1(2): 115-155. |
| [6] | Heinicke J, Koch U, Martinelli G. 1995. CO2 and radon measurements in the Vogtland Area (Germany)—A contribution to earthquake prediction research. Geophys. Res. Lett., 22(7): 771-774. |
| [7] | Ho Y Y, Liu J Y, Parrot M, et al. 2013. Temporal and spatial analyses on seismo-electric anomalies associated with the 27 February 2010 M=8.8 Chile earthquake observed by DEMETER satellite. Nat. Hazards Earth Syst. Sci., 13(12): 3281-3289. |
| [8] | Horie T, Yamauchi T, Yoshida M, et al. 2007. The wave-like structures of ionospheric perturbation associated with Sumatra earthquake of 26 December 2004, as revealed from VLF observation in Japan of NWC signals. J. Atmos. Sol. Terr. Phys., 69(9): 1021-1028. |
| [9] | Hsiao C C, Liu J Y, Oyama K I, et al. 2009. Ionospheric electron density anomaly prior to the December 26, 2006 M7.0 Pingtung earthquake doublet observed by FORMOSAT-3/COSMIC. Phys. Chem. Earth, 34(6): 474-478. |
| [10] | Kuo C L, Huba J D, Joyce G, et al. 2011. Ionosphere plasma bubbles and density variations induced by pre-earthquake rock currents and associated surface charges. J. Geophys. Res., 116: A10307, doi: 10.1029/2011JA016628. |
| [11] | Liu J, Wan W X, Huang J P, et al. 2011. Electron density perturbation before Chile M8.8 earthquake. Chinese J. Geophys. (in Chinese), 54(11): 2717-2725. |
| [12] | Li M, Parrot M. 2013. Statistical analysis of an ionospheric parameter as a base for earthquake prediction. J. Geophys. Res., 118(6): 3731-3739. |
| [13] | Liu J Y, Chen Y I, Pulinets S A, et al. 2000. Seismo-ionospheric signatures prior to M≥6.0 Taiwan earthquakes. Geophys. Res. Lett., 27(19): 3113-3116. |
| [14] | Liu J Y, Chen Y I, Chuo Y J, et al. 2006. A statistical investigation of preearthquake ionospheric anomaly. J. Geophys. Res., 111: A05304, doi: 10.1029/2005JA011333. |
| [15] | Liu J Y, Le H, Chen Y I, et al. 2011. Observations and simulations of seismoionospheric GPS total electron content anomalies before the 12 January 2010 M7 Haiti earthquake. J. Geophys. Res., 116: A04302, doi: 10.1029/2010JA015704. |
| [16] | Nopper R W, Carovillano R L. 1979. On the orientation of the polar cap electric field. J. Geophys. Res., 84(A11): 6489-6492. |
| [17] | Molchanov O, Fedorov E, Schekotov A, et al. 2004. Lithosphere-atmosphere-ionosphere coupling as governing mechanism for preseismic short-term events in atmosphere and ionosphere. Nat. Hazards Earth Syst. Sci., 4(5-6): 757-767. |
| [18] | Ouzounov D P, Pulinets S A, Davidenko D A, et al. 2013. Space-borne observations of atmospheric pre-earthquake signals in seismically active areas. Case study for Greece 2008-2009. Thales, in honor of Prof. Emeritus Michael E Contadakis, 1: 259-265. |
| [19] | Pulinets S A, Boyarchuk K A, Hegai V V, et al. 2000. Quasielectrostatic model of atmosphere-thermosphere-ionosphere coupling. Adv. Space Res., 26(8): 1209-1218. |
| [20] | Pulinets S A, Boyarchuk K A. 2004. Ionospheric Precursors of Earthquakes. Berlin: Springer. |
| [21] | Pulinets S A, Legen'ka A D. 2003. Spatial-temporal characteristics of large scale disturbances of electron density observed in the ionospheric f-region before strong earthquakes. Cosmic Res., 41(3): 221-230. |
| [22] | Rozhnoi A, Solovieva M, Molchanov O, et al. 2007. Observation evidences of atmospheric Gravity Waves induced by seismic activity from analysis of subionospheric LF signal spectra. Nat. Hazards Earth Syst. Sci., 7(5): 625-628. |
| [23] | Ruzhin Y Y, Larkina V I, Depueva A K. 1998. Earthquake precursors in magnetically conjugated ionosphere regions. Adv. Space Res., 21(3): 525-528. |
| [24] | Serebryakova O N, Bilichenko S V, Chmyrev V M, et al. 1992. Electromagnetic ELF radiation from earthquake regions as observed by low-altitude satellites. Geophys. Res. Lett., 19(2): 91-94. |
| [25] | Shalimov S, Gokhberg M. 1998. Lithosphere-ionosphere coupling mechanism and its application to the earthquake in Iran on June 20, 1990. A review of ionospheric measurements and basic assumptions. Earth Planet. Inter., 105(3): 211-218. |
| [26] | Shen J F, Shen X H, Liu Q. 2010. The thermoelectric effect of magnetite: a new model for abnormal Geo-Electricity from the formation and occurrence of earthquake. Chin. J. Mineral Petrol. (in Chinese), 30(4): 21-27. |
| [27] | Shen X H, Wu Y, Chan X J. 2007. Remote sensing application in earthquake science and general proposal for earthquake satellite project in China. Recent Developments in World Seismology (in Chinese), (8): 38-45. |
| [28] | Sorokin V M, Chmyrev V M, Yaschenko A K. 2001. Electrodynamic model of the lower atmosphere and the ionosphere coupling. J. Atmos. Sol. Terr. Phys., 63(16): 1681-1691. |
| [29] | Sorokin V M, Chmyrev V M, Yaschenko A K. 2005. Theoretical model of DC electric field formation in the ionosphere stimulated by seismic activity. J. Atmos. Sol. Terr. Phys., 67(14): 1259-1268. |
| [30] | Sorokin V M, Yaschenko A K, Hayakawa M. 2006. Formation mechanism of the lower-ionospheric disturbances by the atmosphere electric current over a seismic region. J. Atmos. Sol. Terr. Phys., 68(11): 1260-1268. |
| [31] | Sorokin V M, Yaschenko A K, Hayakawa M. 2007. A perturbation of DC electric field caused by light ion adhesion to aerosols during the growth in seismic-related atmospheric radioactivity. Nat. Hazards Earth Syst. Sci., 7(1): 155-163. |
| [32] | Sorokin V M, Chmyrev V M. 2010. Atmosphere-ionosphere electrodynamic coupling. // The Atmosphere and Ionosphere. Netherlands: Springer, 97-146. |
| [33] | Virk H S, Singh B. 1994. Radon recording of Uttarkashi earthquake. Geophys. Res. Lett., 21(8): 737-740. |
| [34] | Xu T,Hu Y L, Wu J, et al. 2012. Statistical analysis of seismo-ionospheric perturbation before 14 Ms≥7.0 strong earthquakes in Chinese subcontinent. Chinese. J. Radio Sci. (in Chinese), 27(3): 507-512. |
| [35] | Yu T, Wan W, Liu L. 2003. A theoretical model for ionospheric electric fields at mid-and low-latitudes. Sci. China Ser. G, 46(1): 23-32. |
| [36] | Yu T, Mao T, Wang Y G, et al. 2009. Study of the ionospheric anomaly before the Wenchuan earthquake. Chin. Sci. Bull., 54(4): 1080-1086. |
| [37] | Zhang J G, Yao L, Liu X C, et al. 2012. Research on frequency spectrum characteristics of VLF electromagnetic field in earthquake ionosphere. Journal of Geodesy and Geodynamics (in Chinese), 32(3): 110-115. |
| [38] | Zhang X, Shen X, Zhao S, et al. 2014. The characteristics of quasistatic electric field perturbations observed by DEMETER satellite before large earthquakes. J. Asian Earth Sci., 79(Part A): 42-52. |
| [39] | Zhang X, Zeren Z, Parrot M, et al. 2011. ULF/ELF ionospheric electric field and plasma perturbations related to Chile earthquakes. Adv. Space Res., 47(6): 991-1000. |
| [40] | Zhao B Q, Wang M, Yu T, et al. 2008. Is an unusual large enhancement of ionospheric electron density linked with the 2008 great Wenchuan earthquake?J. Geophys. Res., 113: A11304, doi: 10.1029/2008JA013613. |
| [41] | Zhu F Y, Wu Y, Zhou Y Y, et al. 2010. Statistical analysis of pre- earthquake ionospheric TEC disturbance. J. Geod. Geodyn. (in Chinese), 30(5): 19-23. |
| [42] | Zolotov O V, Namgaladze A A, Prokhorov B E. 2012. Total electron content disturbances prior to Great Tohoku March 11, 2011 and October 23, 2011 Turkey Van earthquakes and their physical interpretation. Proceedings of the MSTU, 15(3): 583-594. |
| [43] | 丁鉴海, 申旭辉, 潘威炎等. 2006. 地震电磁前兆研究进展. 电波科学学报, 21(5): 791-801. |
| [44] | 刘静,万卫星,黄建平等. 2011. 智利8.8级地震的震前电子浓度扰动. 地球物理学报, 54(11): 2717-2725. |
| [45] | 申俊峰, 申旭辉, 刘倩. 2010. 磁铁矿热电效应: 地震地电异常的新模式. 矿物岩石, 30(4): 21-27. |
| [46] | 申旭辉,吴云,单新建. 2007. 地震遥感应用趋势与中国地震卫星发展框架. 国际地震动态, (8): 38-45. |
| [47] | 徐彤, 胡艳莉, 吴健等. 2012. 中国大陆14次强震前电离层异常统计分析. 电波科学学报, 27(3): 507-512. |
| [48] | 余涛, 毛田, 王云冈等. 2009. 汶川特大地震前电离层主要参量变化. 科学通报, 54(4): 493-499. |
| [49] | 张建国, 姚丽, 刘晓灿等. 2012. 地震电离层VLF电磁场频谱特征研究. 大地测量与地球动力学, 32(3): 110-115. |
| [50] | 祝芙英, 吴云, 周义炎等. 2010. 震前电离层TEC异常扰动统计分析. 大地测量与地球动力学, 30(5): 19-23. |
 2014, Vol. 57
2014, Vol. 57


