经过多年发展,全球定位系统(Global Positioning System,GPS)高精度双频接收机已经成为电离层测量的常规手段(Lanyi and Roth,1988; Coco et al.,1991; Sardón and Zarraoa,1997; Ma and Maruyama,2003; Otsuka et al.,2001; Liu and Gao,2004; 张东和和萧佐,2000; Xiao et al.,2012; Zhang et al.,2012; Liu et al.,2012).由GPS观测数据提取的电离层电子总含量(Total Electron Content,TEC)也成为描述电离层形态的重要参量(Wan et al.,2012).由于在利用GPS数据获得电离层垂直TEC过程中有一些假设条件,而这些假设条件在一定程度上会影响到获得的TEC的精度,因此关于基于GPS数据提取的电离层TEC的精度问题的研究从未停止.一些学者针对电离层对这些假设条件的满足程度对提取的电离层TEC精度的影响开展研究;另一些学者将GPS方法提取的TEC与其他探测手段或模型预测的结果进行比较,以检验该方法 的有效性(Ho et al.,1997; Vladimer et al.,1997).
传统的利用GPS观测量解算高精度的电离层TEC主要经过三个步骤:(1)使用地面接收机对L1和L2两个频段(1575.42 MHz和1227.60 MHz)信号的伪距观测量和载波相位观测量,计算出沿信号传播路径积分的斜向电子总含量(简称斜TEC);(2)在电离层单层薄壳模型假定下,利用映射函数将斜TEC转化为垂直方向上的电子总含量(简称TEC)并(3)同时估算卫星和接收机的硬件延迟偏差(Differential Code Biases,DCB).
在上述各步骤中,都有一些针对电离层的假设条件,这些假设条件不可避免地会引入误差,从而影响到解算的电离层TEC的精度和可靠性.由于GPS载波信号为L波段,在光学近似条件下,步骤一可以获得高精度的斜向电离层TEC,但在电离层中存在强闪烁的情况下,这种假设条件会造成一定的TEC误差.此外,研究表明,差分硬件延迟的估算过程需要电离层满足时空缓变的假设条件,这种缓变假设条件的满足程度决定于电离层状态.早期的研究者认为卫星DCB较为稳定,在较长时间内不会显著改变(Lanyi and Roth,1988; Coco et al.,1991).然而近年来的研究表明,目前方法估算的卫星和接收机的DCB会随观测环境和电离层状态的变化而改变(Coster et al.,2013; Zhang et al.,2009,2010,2014; Hernández-Pajares et al.,2009),是基于GPS数据提取电离层TEC的主要误差源.另一部分误差来源于斜TEC向垂直TEC的转化.目前广泛使用的转化方法是建立在电离层薄壳模型(也称单层模型)的基础上.这一模型假定电离层的厚度可以忽略,所有电子都集中在一个确定高度的薄壳内.如果在信号穿过电离层的范围内,电子密度的水平梯度可以忽略,那么就可以推导出垂直TEC与斜TEC的关系,从而得到穿刺点(GPS信号的传播路径与薄壳的交点被称为穿刺点,Ionospheric Pierce Point,IPP)位置处的垂直TEC.
在薄壳模型中,薄壳的高度是影响误差大小的重要参数.Birch等(2002)认为,尽管前人把这一高 度选为350 km至400 km,但更高的高度(介于600 km和1200 km之间)是更适宜的.Lanyi和Roth(1988)认为在太阳活动低年的夜间,电离层的平均高度甚至高达2000 km以上.Rama Rao等(2006)研究了印度地区的电离层形态特点,分析了薄壳高度在250 km和750 km之间变化时造成的解算的电离层TEC误差,鉴于薄壳高度的不确定性会在小仰角卫星的数据中产生较大误差,建议在测量中卫星的仰角应大于50°.Niranjan等(2007)结合了多种手段的观测,指出薄壳模型中的水平均匀假设是适用的;在印度地区,薄壳的高度随时间和季节在750 km和1500 km之间变化.
薄壳高度的选取会对GPS测量TEC的结果产生重要影响,在实际电离层TEC解算过程中,这一问题还关系到卫星最小仰角的选择.但由于不可能获得一个真实的从电离层D层到GPS卫星高度的电子密度的剖面,关于薄壳高度的选择一直是基于GPS数据解算电离层TEC方法中关注的一个问 题.本文利用Global Core Plasma Model(简称GCPM)这一等离子体模型来对电离层和等离子体层的电子密度分布进行仿真,借此分析最佳薄壳高度的选择.第2节将简要介绍所使用的模型和计算方法;第3节将给出仿真计算结果和分析;第4节为总结.
2 模型和方法 2.1 Global Core Plasma ModelGPS卫星的轨道高度大致为20200 km,载波信号传播的范围涵盖了电离层和等离子体层,因而在分析电离层薄壳高度的问题时需要使用涵盖电离层和等离子体层的模型.现在已有多种成熟的半经验和经验的等离子体模型可供使用.在众多模型中GCPM被选中进行这一研究.GCPM由Gallagher等(2000)开发.它建立在多颗卫星的观测基础之上,由关于电离层、等离子体层、等离子体层顶、槽区和极盖区的多个经验模型综合而成.这一模型主要以Kp指数为输入参量,能够提供电离层和等离子体层范围内的特定时间和地点的电子、氢离子、氦离子和氧离子密度.经过多年发展,该模型能够反映地磁活动、地方时、季节、太阳活动和太阳活动周变化等带来的影响.目前最新的版本为2.4版,该模型在电离层高度上使用国际参考电离层模型(International Reference Ionosphere,IRI)2007版的输出结果.相比于其他等离子体模型,该模型具有以下优势:(1)作为一个经验模型,GCPM能够提供比理论模型更贴近实际的计算结果,同时其计算速度也更快;(2)GCPM的输出量及其导数是连续的;(3)该模型的源代码完全开放,易于获取,可以根据研究需要进行修改.在本工作中,通过修改GCPM的源代码,我们将较新的IRI 2012模型移植进入GCPM之中,以代替较老的IRI 2007模型.当选取的时间在2007年之后时,老版本的模型只能根据预测的太阳活动情况进行计算,而新版本的模型更新了空间环境参量数据库,能够提供更可靠的计算结果.图 1给出了太阳活动高年(2002年)和低年(2008年)由GCPM模型得到的电子密度剖面.
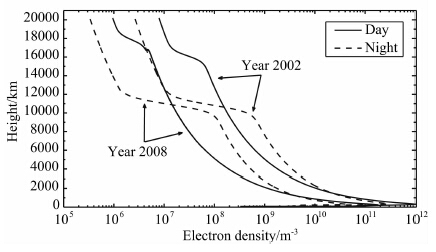 | 图 1 GCPM模型计算得到的2002年和2008年世界时
春分日零时,20°N不同地方时处的电子密度剖面图 实线表示白天(MLT=14 ∶ 00),虚线表示凌晨(MLT=05 ∶ 00). Fig. 1 Electron density profiles at 20°N,calculated from GCPM. The time is at 00:00 UT,vernal equinox,in 2002 and 2008 The solid lines show the day-time profiles(MLT=14 ∶ 00) while the dash lines show the night-time(MLT=05 ∶ 00). |
由图 1可见,从地面到GPS轨道高度(20200 km),电子主要集中在300 km附近的电离层F区内,这是薄壳模型得以应用的基础.同时也可以看到,随着昼夜交替和太阳活动的变化,不同高度的电子在TEC中所占比重也会显著变化.可以预见,有效的薄壳高度也会在一定区间内变化.这一变化的区间和规律在现实应用中具有重要意义.
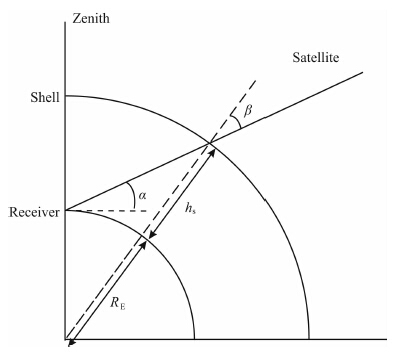
2.2 检验薄壳高度的计算方法图 2为利用薄壳模型计算垂直TEC的几何图,RE为地球半径,hs为薄壳高度,α为卫星仰角,β为IPP处卫星的天顶角.当卫星相对地面接收机的仰角为α时,角度β满足:
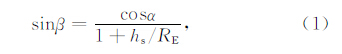
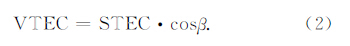
 | 图 2 利用薄壳模型计算垂直TEC的几何图
Fig. 2 Geometry for the conversion from slant TEC to vertical TEC
|
薄壳模型中的薄壳高度应取为多少,很大程度上依赖于经验.然而,两个理论计算的高度可以提供参考.其一是质心高度,即根据从地面到GPS卫星轨道高度的电子密度剖面,计算出的电子密度分布的质心高度;其二是积分中值高度,该高度之上(到GPS卫星)的电子总含量与该高度之下(到地面)的电子总含量相等.
利用GCPM模型可以对这两个高度进行计算.图 3给出了这两种高度的全球分布示例.其中(a)(c)分别为2002年和2008年春分日世界时零时,积分中值高度的全球分布图;(b)(d)分别为2002年和2008年春分日世界时零时,质心高度的全球分布图.由图 3可见,两者随经纬度的分布基本是一致的,质心高度通常大于积分中值高度.与太阳活动高年(2002年)相比,在太阳活动低年(2008年),无论是质心高度还是中值高度都比太阳活动高年时更高.这表明,在太阳活动低年,等离子体层中的电子(即较高高度的电子)在TEC中所占比重更大.
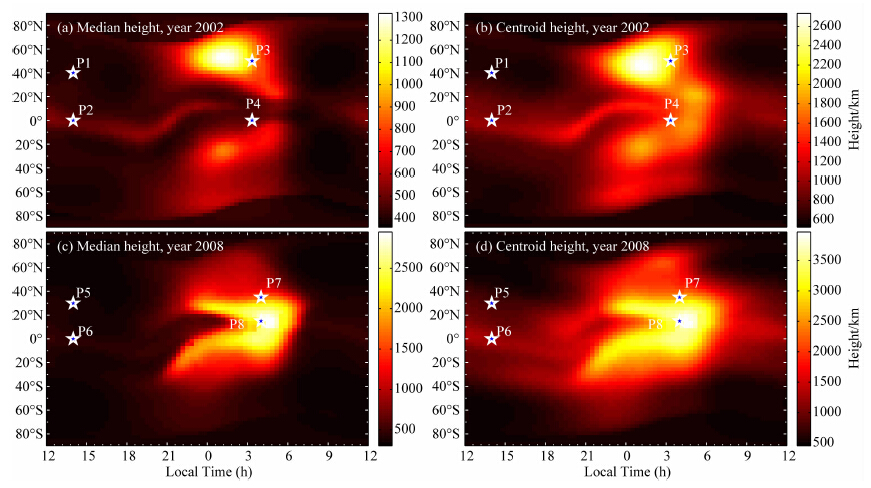 | 图 3 GCPM模型计算得到的积分中值高度和质心高度全球分布图.所选的时刻均为春分日世界时零点
(a)2002年积分中值高度全球分布图;(b)2002年质心高度全球分布图; (c)2008年积分中值高度全球分布图;(d)2008年质心高度全球分布图.Fig. 3 Global distribution of centroid height and median height calculated from GCPM at 00:00 UT,vernal equinox (a)The median height distribution in 2002;(b)The centroid height distribution in 2002; (c)The median height distribution in 2008;(d)The centroid height distribution in 2008.
|
图 4和图 5分别为2002年和2008年全球TEC分布图.值得注意的是,日落后的一段时间(大约18LT至03LT),低纬地区TEC分布图与质心高度(或中值高度)的分布图具有“互补”性.即TEC较高的地方,质心高度(或中值高度)较低.在白天,电离层F层(高度约为300 km)的电子含量在总电子含量中占主要部分;日落后,电离层中的复合过程会快速地消耗掉电子,从而使TEC降低.然而,在更高的高度上,电子的复合速率较慢,从而使更高高度的电子在总电子含量中所占比重上升,因而质心高度和积分中值高度都显著上升.这样就出现了TEC降低的同时质心高度(和中值高度)升高的现象.
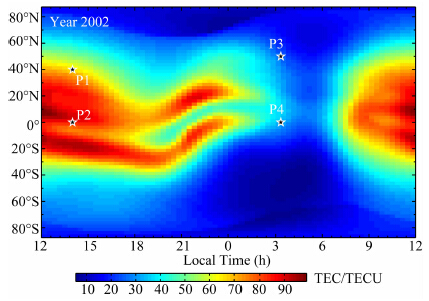 | 图 4 GCPM模型计算得到的TEC全球分布图.
时间为2002年春分日,00 ∶ 00 UT
Fig. 4 Global TEC map calculated from GCPM at 00 ∶ 00 UT,vernal equinox in 2002
|
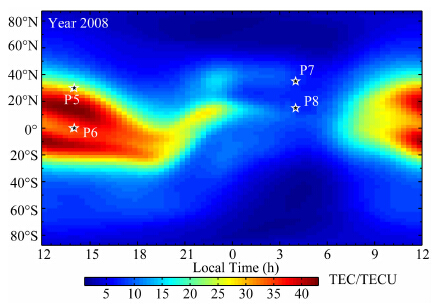 | 图 5 GCPM模型计算得到的TEC全球分布图.
时间为2008年春分日,00 ∶ 00 UT
Fig. 5 Global TEC map calculated from GCPM
at 00 ∶ 00 UT,vernal equinox in 2008
|
质心和中值高度可以作为薄壳高度的参考.可以预计,在晚间质心高度变化显著的区域,有效的薄壳高度也应当有显著变化.另外,由于薄壳模型依赖于水平均匀假设,在TEC梯度较大的区域内,薄壳高度的选取就成为一个值得关注的问题.
综合考虑TEC和质心高度的全球分布情况,在2002年和2008年的春分日,各选取4个代表点,即图 3—5中的P1—P8.这8个点的地理纬度和经度见表 1.其中P1、P2、P5和P6位于日侧,代表了TEC水平梯度较大的地区;而P3、P4、P7和P8位于夜侧,代表了质心高度的水平梯度较大的地区.在3.2—3.4节中,将对这8个代表点的薄壳有效高度进行分析.
| | 表 1 图 3—5中所选取各点的地理位置 Table 1 Geographic latitudes and longitudes of the eight selected points in Fig. 3—5 |
在薄壳高度的选择问题上,目前现实的做法是选取一个固定的高度.例如,喷气推进实验室(Jet Propulsion Laboratory,JPL)所选取的薄壳高度是450 km,而麻省理工学院(MIT)提供的全球TEC图所用的薄壳高度为400 km.可以预见,当卫星位于不同方位角时,由于电离层通常在不同方位角上有不同的形态,这一固定的薄壳高度会在不同的方位角上带来不同的误差.
假设接收机位于P1点处.卫星的方位角在0°至360°间变化(间隔15°);仰角在20°至85°间变化(间隔5°).对于每一对确定的方位角和仰角,可以 计算出薄壳模型转化得到的垂直TEC与“真实值” 的相对误差.这一误差随方位角和仰角的分布见图 6,其中薄壳高度为固定值450 km.
图 6的一个显著特征是,当卫星位于北侧时,TEC会被低估;位于南侧时,TEC被高估.这种南北的不对称性应该是由两个方向上电子密度剖面的不同造成的.如图 7所示,P1位于40°N.在其南侧,较低高度(约400 km)的电子占有较大比重;而在北侧,更高高度的电子比重更大.可以推测,有效的薄壳高度在南侧较低,而在北侧较高.当卫星位于北侧时,人为选定的薄壳高度可能会低于有效的薄壳高度.由公式(1)可知,薄壳高度hs偏小会导致角β偏大.再由公式(2)可见偏大的角β会导致转化得到垂直TEC偏小,从而使TEC被低估.南侧的情况正好相反.
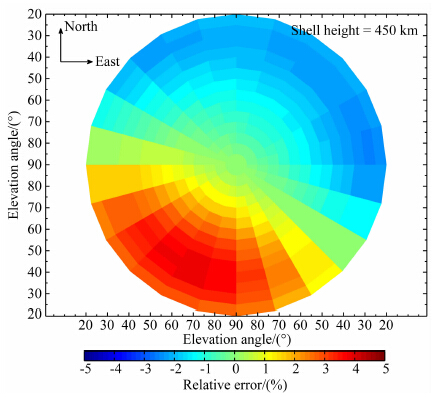 | 图 6 当薄壳高度取450 km时,P1点处TEC 相对误差随卫星方位角和仰角的变化Fig. 6 Relationship of relative error and satellite′s elevation, azimuth angles. The shell height is 450 km |
这种方位角不对称性的根源还是电子密度的水平梯度.在水平梯度较大的区域,很可能会存在类似的现象.北半球位于赤道异常峰以北的台站,其周围的电子密度分布往往类似于图 7.这些台站有可能也存在这种对南北两侧TEC估计“不对称”的现象.这种不对称性会使基于GPS数据得到的TEC比真实值具有更大的水平梯度.
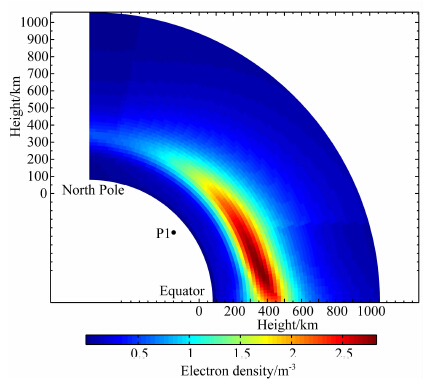 | 图 7 北半球150°W扇面的电子密度剖面.时间为2002年春分日00 ∶ 00 UT (14 ∶ 00 LT) Fig. 7 Electron density profile in the plane of the meridian 150°W,north hemisphere. The time is 00 ∶ 00 UT(14 ∶ 00 LT),vernal equinox in 2002 |
图 8给出了表 1中P1—P4四个点的最佳薄壳高度和相对误差随仰角的变化,这四个点对应着白天和夜晚情况.针对每一个点,对于每一个卫星仰角都能计算出一个最佳的薄壳高度.这一最佳高度是如此地选取,使得在不同方位角上的转换的垂直 TEC与模型计算的“真实TEC”相对误差的平均值 最小.由这四个计算实例可以看到,最佳的薄壳高度随仰角的变化不具有普适的规律性.在P1和P3的例子中,薄壳高度随仰角降低而降低.但在P2中,情况却完全相反.P4的结果更为复杂,随着仰角的 降低,薄壳高度先增加而后减小.但是,所有的计算实例都给出了相同的趋势:随着卫星仰角降低,通过薄壳模型转换得到的垂直TEC与“真实值”的相对误差是逐渐增大的.
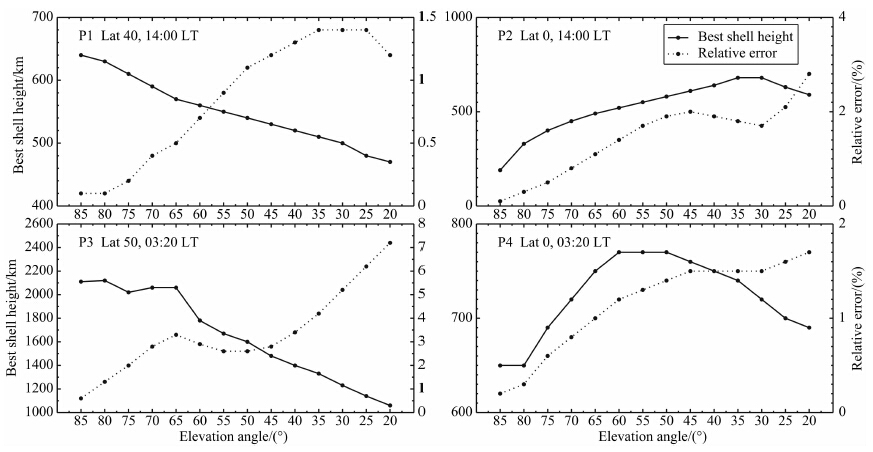 | 图 8 最佳薄壳高度(实线)和相对误差(点线)随卫星仰角的变化
Fig. 8 The relationship between the best shell height(solid),relative error(dotted) and elevation angle |
通过白天(P1和P2)与晚上(P3和P4)数据的对比,可以看到:在白天,薄壳高度较为稳定(一般为数百公里),转化带来的相对误差也比较小(不超过3%);但在夜晚,薄壳高度会呈现出较大的变化(最高可以超过2000 km),而且相对误差也会增大(最大超过7%).这一昼夜变化与图 3中的质心高度(及中值高度)的变化规律是相符合的.在白天,质心高度(及中值高度)较为稳定,相应的薄壳高度也变化不大;而在夜晚,质心高度(及中值高度)变化剧烈,最佳薄壳高度也呈现出同样的规律.
3.4 最佳薄壳高度的个例分析在本小节中,“最佳薄壳高度”具有如下含义:对于固定的地面接收机,最佳的薄壳高度使得不同方位角、仰角卫星的相对误差的平均值最小.
按照这一定义,可以分别计算P1至P8八个点上的最佳薄壳高度.例如,P1的薄壳高度,使得不同方位角和仰角的相对误差之平均最小.图 9给出了各点平均相对误差随薄壳高度的变化.图中同时给出了薄壳高度取穿刺点处的质心高度或中值高度时,不同方位角和仰角的相对误差的平均值.其中水平实线代表薄壳高度取质心高度时的TEC相对误差,水平虚线代表薄壳高度取积分中值高度时的TEC相对误差.当虚线在实线之下时,表示该固定高度的平均相对误差小于质心或中值高度的误差.
由图 9可以看到,中值高度和质心高度孰好孰坏并不确定.而且,两者都不是薄壳高度的最佳选择.在白天(即P1、P2、P5和P6)尽管TEC的水平梯度很大,但是最佳薄壳高度的变化范围较小.这一变化范围为500 km至750 km.由P1和P2对比可知,在太阳活动高年(2002年),中纬度地区的最佳薄壳高度应比低纬度地区偏低约100 km.同样,由 P5和P6对比可知,在太阳活动低年(2008年),中 纬度地区的最佳薄壳高度比低纬度地区偏低约200 km. 无论中纬还是低纬度地区,太阳活动低年的最佳薄壳高度都比高年时偏高.在夜间(P3、P4、P7和P8),最佳薄壳高度呈现出更强的变化性.四个点的最佳高度从700 km(P4)、1200 km(P7)、1500 km(P3)到超过2000 km(P8).
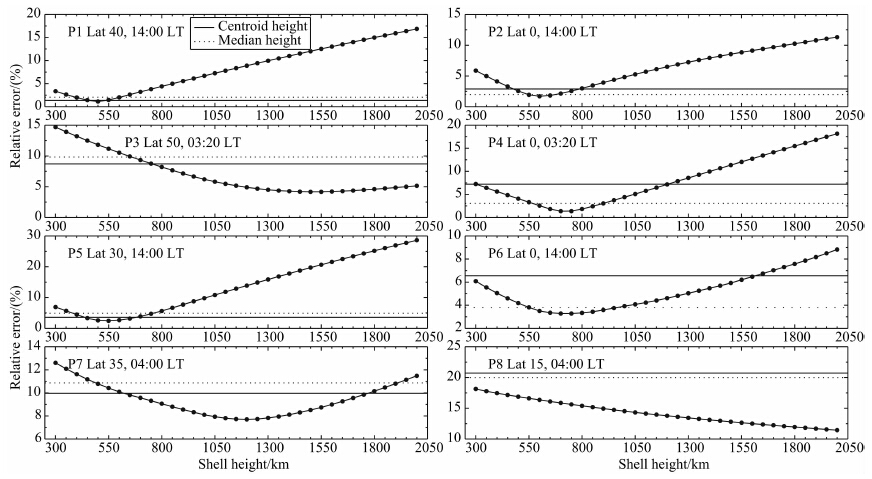 | 图 9 TEC平均相对误差随薄壳高度的变化
水平实线给出了取质心高度时TEC的相对误差;水平虚线给出了取积分中值高度时TEC的相对误差. Fig. 9 Mean relative errors of TEC with different shell heights The horizontal solid line shows the relative error of TEC by centroid height. The horizontal dotted line shows the relative error of TEC by median height. |
在前面的工作中,对具有代表性的点进行了个例分析.从中可以看到,薄壳高度具有较大的变化 性.然而在实际应用中,通常选取某一固定的高度. 这一固定的高度应当如何选取,是本小节所探讨的问题.
为了使结果具有普遍性,这里假设接收机位于更大的范围内:从180°W到180°E(间隔30°),0°到60°N(间隔5°).相对于这些位置的接收机,卫星的方位角为0°、90°、180°和270°,仰角变化范围为30°到60°(间隔10°).已有研究表明(Birch et al.,2002; Rama Rao et al.,2006),在大仰角的情形下,转换误差对薄壳高度的选取不敏感.因此,这里没有考虑仰角大于60°的情形.
给定接收机的位置、卫星方位角和仰角,就可以计算出一个转换带来的相对误差.所有相对误差的平均值可以作为衡量薄壳高度优劣的指标.图 10给出了不同的薄壳高度带来的相对误差.在2002年这一太阳活动高年,最佳的薄壳高度为560 km,此时平均的相对误差为5.11%.而在2008年这一太阳活动低年,最佳高度为695 km,平均相对误差为8.70%.
这种太阳活动周的变化是可以理解的.在太阳活动低年,由于太阳辐射强度变弱,电离层中的电子含量较太阳活动高年偏低,因而更高高度的等离子体层中的电子在TEC中所占比重上升.这就使得有效的薄壳高度上升.
在当前条件下,在基于GPS解算电离层TEC方法中还不能引入一个变化的电离层薄壳高度,而任何一个固定高度的薄壳模型都不可避免地引入转换误差.图 11和图 12给出了薄壳高度取图 10中的 最佳高度时(即2002年取560km,2008年取695 km),2002年和2008年的绝对误差随纬度和地方时的分 布.可见在2008年这一太阳活动低年,薄壳模型带来的绝对误差不超过2 TECU(1 TECU=1016 m-2). 但是在2002年这一太阳活动高年,绝对误差可以超过8 TECU.误差较大的地区主要集中于午夜附近的中、高纬度地区.
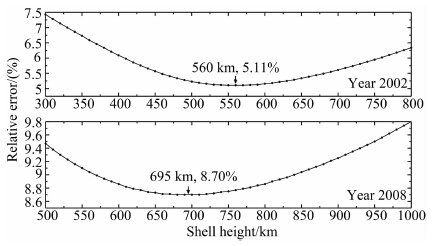 | 图 10 转换的电离层TEC平均相对误差随薄壳高度的变化
Fig. 10 Relationship between mean relative error of converted ionospheric TEC and the corresponding shell height |
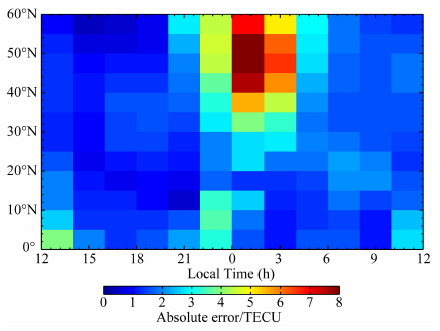 | 图 11 薄壳高度为560 km时转换的电离层TEC与电离层TEC“真实值”的绝对误差随接收机纬度和地方时的分布(2002年)
Fig. 11 Distribution of absolute error of converted ionospheric TEC with latitude and local time in 2002. The shell height is 560 km |
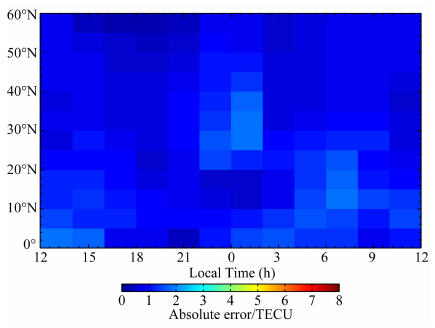 | 图 12 薄壳高度为695 km时转换的电离层TEC与电离层TEC“真实值”的绝对误差随接收机纬度和地方时的分布(2008年)Fig. 12 Distribution of absolute error of converted ionospheric TEC with latitude and local time in 2008. The shell height is 695 km |
在基于GPS数据提取电离层总电子含量(TEC)的过程中,电离层薄壳高度的选择对解算电离层垂直TEC的精度有很大的影响.在保留这一模型的前提下,通过选择合理的薄壳高度对提高解算电离层TEC的精度是有意义的.本文利用等离子体GCPM模型,对太阳活动高年(2002)和太阳活动低年(2008)情况下电离层有效薄壳高度的选择进行了仿真计算.结果表明,最佳的薄壳高度在2002年为560 km,而在2008年为695 km.通过对全球八个具有代表性地点的仿真计算,揭示了有效薄壳高度更复杂的变化特点.在白天,最佳薄壳的高度变化不大(500 km至750 km);但在夜晚,最佳薄壳高度会在数百公里至超过2000 km的大范围内变化.此外,本文还对不同卫星仰角情况下斜向TEC转换为垂直TEC的误差进行了分析,随着卫星仰角的增加,薄壳模型带来的转换误差基本上是单调减少的.最后,对全球不同地点的电离层TEC的仿真研究表明,在电子密度水平梯度较大的地区,应用电离层薄壳模型时会导致电子密度较高处的TEC被高估,而 电子密度较低处的TEC被低估,在分析基于GPS数据提取的 电离层TEC空间变化时要认识到这一点.
致谢 GCPM模型的源代码由D.L. Gallagher博士提供.他对模型的使用和修改方法也提供了宝贵意见.
| [1] | Birch M J, Hargreaves J K, Bailey G J. 2002. On the use of an effective ionospheric height in electron content measurement by GPS reception. Radio Science, 37(1): 15-1-15-19, doi: 10.1029/2000RS002601. |
| [2] | Coco D S, Coker C, Dahlke S R, et al. 1991. Variability of GPS satellite differential group delay biases. IEEE Transactions on Aerospace and Electronic Systems, 27(6): 931-938, doi: 10.1109/7.104264. |
| [3] | Coster A, Williams J, Weatherwax A, et al. 2013. Accuracy of GPS total electron content: GPS receiver bias temperature dependence. Radio Science, 48(2): 190-196. |
| [4] | Gallagher D L, Craven P D, Comfort R H. 2000. Global core plasma model. J. Geophys. Res., 105(A8): 18819-18833, doi: 10.1029/1999JA000241. |
| [5] | Hernández-Pajares M J, Juan M, Sanz J, et al. 2009. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geod., 83(3-4): 263-275, doi 10.1007/s00190-008-0266-1. |
| [6] | Ho C M, Wilson B D, Mannucci A J, et al. 1997. A comparative study of ionospheric total electron content measurements using global ionospheric maps of GPS, TOPEX radar, and the Bent model. Radio Science, 32(4): 1499-1512, doi:10.1029/97RS00580. |
| [7] | Lanyi G E, Roth T. 1988. A comparison of mapped and measured total ionospheric electron content using global positioning system and beacon satellite observations. Radio Science, 23(4): 483-492, doi: 10.1029/RS023i004p00483. |
| [8] | Liu J, Liu L B, Zhao B Q, et al. 2012. Empirical modeling of ionospheric F2 layer critical frequency over Wakkanai under geomagnetic quiet and disturbed conditions. Sci. China Tech. Sci., 55(5): 1169-1177, doi: 10.1007/s11431-012-4801-1. |
| [9] | Liu Z Z, Gao Y. 2004. Ionospheric TEC predictions over a local area GPS reference network. GPS Solutions, 8(1): 23-29, doi: 10.1007/s10291-004-0082-x. |
| [10] | Ma G, Maruyama T. 2003. Derivation of TEC and estimation of instrumental biases from GEONET in Japan. Ann. Geophys., 21(10): 2083-2093, doi: 10.5194/angeo-21-2083-2003. |
| [11] | Niranjan K, Srivani B, Gopikrishna S, et al. 2007. Spatial distribution of ionization in the equatorial and low-latitude ionosphere of the Indian sector and its effect on the pierce point altitude for GPS applications during low solar activity periods. J. Geophys. Res., 112(A5), A05304, doi: 10.1029/2006JA0119895194/angeo-21-2083-2003. |
| [12] | Otsuka Y, Ogawa T, Saito A, et al. 2001. A new technique for mapping of total electron content using GPS network in Japan. Earth, Planets and Space, 54(1): 63-70. |
| [13] | Rama Rao P V S, Niranjan K, Prasad D S V V D, et al. 2006. On the validity of the ionospheric pierce point (IPP) altitude of 350 km in the Indian equatorial and low-latitude sector. Ann. Geophys., 24: 2159-2168, doi: 10.5194/angeo-24-2159-2006. |
| [14] | Sardón E, Zarraoa N. 1997.Estimation of total electron content using GPS data: How stable are the differential satellite and receiver instrumental biases? Radio Science, 32(5): 1899-1910. |
| [15] | Vladimer J A, Lee M C, Doherty P H, et al. 1997. Comparisons of TOPEX and Global Positioning System total electron content measurements at equatorial anomaly latitudes. Radio Science, 32(6): 2209-2220, doi: 10.1029/97RS02277. |
| [16] | Wan W X, Ding F, Ren Z P, et al. 2012. Modeling the global ionospheric total electron content with empirical orthogonal function analysis. Sci. China Tech. Sci., 55(5): 1161-1168, doi: 10.1007/s11431-012-4823-8. |
| [17] | Xiao R, Xu J S, Ma S Y, et al. 2012. Abnormal distribution of ionospheric electron density during November 2004 super-storm by 3D CT reconstructions from IGS and LEO/GPS observations. Sci. China Tech. Sci., 55(5): 1230-1239, doi: 10.1007/s11431-012-4791-z. |
| [18] | Zhang D H, Xiao Z. 2000. A method of calculating TEC with GPS data and its application to the ionospheric disturbances. Chinese J. Geophys. (in Chinese), 43(4): 451-458. |
| [19] | Zhang D H, Zhang W, Li Q, et al. 2010. Accuracy analysis of the GPS instrumental bias estimated from observations in middle and low latitudes. Ann. Geophys., 28: 1571-1580, doi: 10.5194/angeo-28-1571-2010. |
| [20] | Zhang D H, Mo X H, Ercha A, et al. 2012. Case study of ionospheric fluctuation over mid-latitude region during one large magnetic storm. Sci. China Tech. Sci., 55(5): 1198-1206, doi: 10.1007/s11431-012-4785-x. |
| [21] | Zhang D H, Shi H, Jin Y Q, et al. 2014. The variation of the estimated GPS instrumental bias and its possible connection with ionospheric variability. Sci. China Tech. Sci., 57: 67-79, doi: 10.1007/s11431-013-5419-7. |
| [22] | Zhang W, Zhang D H, Xiao Z. 2009. The influence of geomagnetic storms on the estimation of GPS instrumental biases. Ann. Geophys., 27: 1613-1623, doi: 10.5194/angeo-27-1613-2009. |
| [23] | 张东和, 萧佐. 2000. 利用GPS计算TEC的方法及其对电离层扰动的观测.地球物理学报 |
 2014, Vol. 57
2014, Vol. 57


