1 引言
极区中层夏季回波(PMSE)是发生在极区中层80~90 km高度范围内异常强的雷达反射回波.1979年,Ecklund和Balsley首次用MST雷达观察到了这种现象,它出现在每年夏季的5月中旬到8月中旬.雷达和火箭的联合探测实验表明,极区中层是由电子﹑离子﹑带电尘埃粒子以及浓度相对很高的分子组成的弱电离尘埃等离子体系(Rapp and Lübken,2004;La Hoz, et al., 2005;Havnes et al., 2001;Chilson and Kirkwood, 2001;Ress et al., 2000;Hosokawa et al., 2004;Havnes et al., 2001;蒋成进和李芳,2006).Roger等考虑了尘埃粒子的作用,理论推导出了一个新的反射率表达式,并由此推断在极区中层高度上PMSE和尘埃粒子浓度之间存在着紧密的关系(Varney et al., 2011),实际观测也证实了这一结论(Hervig et al., 2011;Morris et al., 2012).实验发现,在80~90 km的高度范围内,这种弱电离的尘埃等离子体有明显的分层结构,进一步的研究表明,PMSE现象的产生与这些特殊的分层结构有非常密切的联系(Rapp 2004;La Hoz, et al., 2005;Havnes et al., 2001;Chilson and Kirkwood, 2001;Ress et al., 2000;Hosokawa et al., 2004;Havnes et al., 2001;蒋成进和李芳,2006;李海龙等,2010;李辉等,2009).弱电离尘埃等离子体分层结构形成的原因主要有两种观点:大气湍流理论认为,大气扰动引发了带电尘埃粒子浓度的起伏,带电尘埃粒子的起伏带动了电子和离子,进而导致了这种不规则的分层结构.然而实验的观测统计表明,在85 km以下的PMSE现象与大气湍流之间的相关性不强(Hill et al., 1999);另一种观点认为,不规则分层结构是尘埃等离子体不稳定性演变的一种结果性(Pfaff et al., 2001;Shimogawa and Hlllzworth, 2009;Ogawa et al., 2011).在引入外电场的情形下,Angelo讨论了极区中层的离子声波和尘埃声波的特性,得出了不稳定是分层结构形成的原因的结论(N. D,2005).极区中层外电场的存在问题,目前还没有通过实验给予证实.本文研究不考虑外电场时,极区中层尘埃声波的不稳定性问题.
研究尘埃等离子体不稳定性的途径之一是分析尘埃等离子体纵波色散关系.以往的尘埃等离子体纵波色散关系主要是针对实验室尘埃等离子体的,这些理论一般不适用于极区中层大气这样的弱电离尘埃等离子体(Ma and Yu, 1994;Tsytovich and Angelis, 1999;Ivlev et al., 1999;Zhang and Xue, 2008).与实验室尘埃等离子体不同,极区中层的带电粒子与中性分子的碰撞频率远大于带电粒子之间的碰撞频率,与相应的带电粒子的等离子频率在量级上接近(石雁祥等,2008).因而,在建立尘埃等离子体不稳定性的纵波色散关系时,必须将带电粒子与中性分子的碰撞作为一个主要的因素加以考虑,同时要考虑电子和离子对带电尘埃粒子的充电作用.本文在统计力学框架下(Ichimaru,1973),考虑了碰撞和充电两种因素,建立了极区中层弱电离尘埃等离子体的纵波色散关系,分析了极区中层尘埃声波的不稳定性.
2 基本理论考虑一种未磁化﹑非简并﹑弱电离的尘埃等离子体.它由电子﹑一次电离的离子﹑带负电的尘埃粒子和分子组成.忽略尘埃粒子之间的库仑耦合作用(极区中层尘埃耦合系数远小于1),在弱电离尘埃等离子体中,带电粒子α的分布函数的微扰δfα由Alexandrov等(1984)给出:
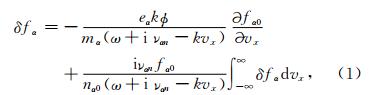
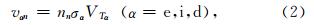
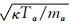 是带电粒子的热速度;nn是分子的浓度;σα是分子的碰撞截面.计算中常取σα=5×10-21m2.
是带电粒子的热速度;nn是分子的浓度;σα是分子的碰撞截面.计算中常取σα=5×10-21m2.
设由纵波而引起的带电粒子的密度扰动为 α,则
α,则
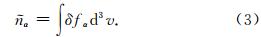
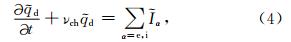
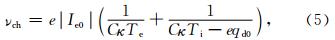
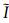 α是与扰动相关联的电子和离子对尘埃粒子的充电电流(Shukla and Mamun, 2002):
α是与扰动相关联的电子和离子对尘埃粒子的充电电流(Shukla and Mamun, 2002):
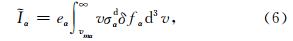
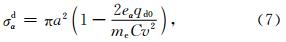
 α以及尘埃粒子的电量扰动
α以及尘埃粒子的电量扰动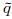 d与自洽场φ满足Poisson′s方程:
d与自洽场φ满足Poisson′s方程:
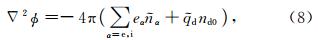
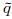 d以exp(-iωt +ikx)规律变化.利用(3)—(8)式以及qd
d以exp(-iωt +ikx)规律变化.利用(3)—(8)式以及qd d≈qd0
d≈qd0 d的关系(q=q0+
d的关系(q=q0+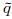 )可得到
)可得到

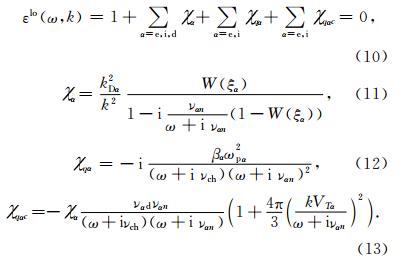

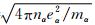 是带电粒子α的等离子频率,kDα=ωpα/VTα是α粒子的德拜波数;其他各量为
是带电粒子α的等离子频率,kDα=ωpα/VTα是α粒子的德拜波数;其他各量为
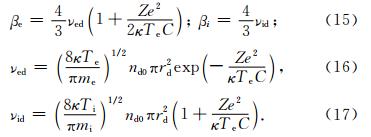
为简化(10)式,需要对有关参量做出量级上的估计.由Rapp and Lübken(2004)给出了极区中层大气不同高度的带电粒子的浓度,如表 1所示,其中的尘埃粒子给出的是电荷数浓度(即尘埃粒子的浓度乘以它的电荷数);此外,尘埃粒子的半径大小分布在10~50 nm之间,计算时统一取30 nm.由Havnes等(2001)给出极区80~90 km的大气分子的浓度在5×1014~6×1013cm-3之间并随高度升高而减小,计算时统一取2×1014cm-3;大气温度取130 K;分子质量取空气分子量,那么离子质量mi=5×10-23g; 电子质量me=9.1×10-29g;尘 埃粒子质量md= 3.05×10-16g,带电荷数Z约为1.
|
|
表 1 极区中层大气尘埃等离子体的测量参数 Table 1 The parameters of dust plasmas in the polar mesosphere |
根据以上的测量参数,计算出极区中层相关各参量如表 2所示.
|
|
表 2 极区中层大气相关参量的定量估计 Table 2 Estimating for related parameters of polar mesosphere in quantity |
表 2中,ωpe,ωpi,ωpd分别代表电子、离子、尘埃粒子的等离子体频率;νch代表电荷弛豫速率;νen,νin,νdn分别代表电子、离子、尘埃粒子与中性分子的碰撞频率.
根据表 2中的参数,考虑满足kVTd<<|ω+iνdn|<
式中 而
运用费拉里法可求(19)式一元四次方程的解析解(徐诚浩,2012),这里省略求解过程.表 3给出k= 0.01 kDd时不同高度尘埃声波的复角频率的四种模式.
从表 3可以看出,复角频率的形式为ω=ωr+iωi(ωr是实部,ωi是虚部),对以exp(-iωt +ikx)规 律变化的尘埃声波,将ω=ωr+i ωi代入exp(-iωt +ikx)可知,复角频率的虚部大于零表示它所对应的模式是增长的(不稳定的);复角频率虚部小于零的模式对应于尘埃声波的衰减模式.表 3中,不同高度尘埃声波的四个模式中,复角频率的虚部大于零的模式有两个.需要说明的是,为突出不稳定波模的主要模式,这里把极区中层尘埃声波的色散关系简化成了一元四次方程,由此给出的解表明,极区中层以exp(-iωt +ikx)规律变化的尘埃声波有不稳定的模式.为给出尘埃声波的振荡频谱以及振幅随时间变化规律的直观描述,以 85.5 km高度为例,将振幅归一化,令Y(t)=exp(0.1ωit)sin(ωrt),可得尘埃声波随时间(单位:s)变化的规律如图 1所示,为 表现尘埃声波随时间逐步增长的规律,这里将ω的虚部降低了一个量级.k在0.001~0.01 kDd范围内变化时,给出四种模式的尘埃声波角频率(实部,单位:Hz)随k的变化规律如图 2所示.
本文同时考虑碰撞和充电两种因素,建立了极区中层弱电离尘埃等离子体的色散关系.研究发现,极区中层大气高度为80~90 km处的尘埃声波有不稳定的波模.这一不稳定性与Langmuir波﹑尘埃离子声波相互耦合,演变和发展可能是极区夏季中层特殊分层结构的一种形成机制;实验测量表明:85.5 km和87.5 km两高度的尘埃粒子浓度很大,关于不稳定尘埃声波复角频率的虚部与尘埃粒子浓度的关系需要作进一步的研究.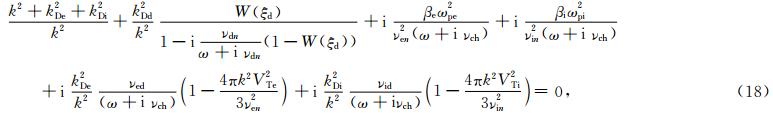
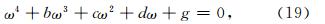
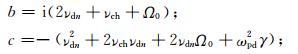
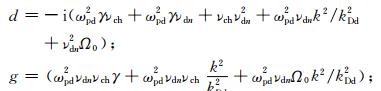
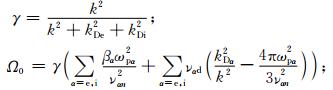
![]()
表 3 k=0.01 kDd时的复角频率
Table 3 Complex angle frequency when k=0.01 kDd
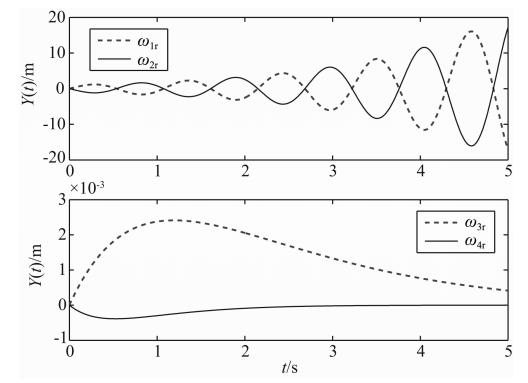
图 1 振幅Y(t)随时间的变化曲线
Fig. 1 Amplitude-time curve
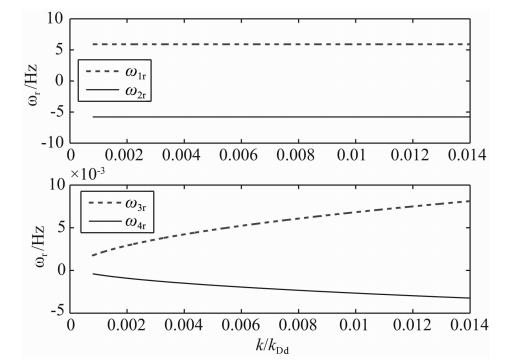
图 2 角频率(实部)随k的变化曲线
Fig. 2 Angle frequency-k curve
| [1] | Alexandrov A F, Bogdankevich L S, Rukhadze A A. 1984. Principles of Plasma Electrodynamics. New York: Springer-Verlag. |
| [2] | Chilson P B, Kirkwood S, Häggström I. 2001. Frequency domain interferometry mode observations of PMSE using the EISCAT VHF radar. Ann. Geophys., 18: 1599-1612. |
| [3] | D'Angelo N. 2005. IA/DA waves and polar mesospheric summer echoes. Phys. Lett. A., 336(2-3): 204-209. |
| [4] | Havnes O, Brattli A, Aslaksen T, et al. 2001. First common volume observations of layered Plasma Structures and polar mesospheric summer echoes by rocket and radar. J. Geophys. Res., 28(8): 1419-1422. |
| [5] | Havnes O, Aslaksen T, Brattli A. 2001. Charged dust in the earth's middle atmosphere. Physica Scripta, T89: 133-137. |
| [6] | Hervig M E, Rapp M, Latteck R, et al. 2011. Observations of mesospheric ice particles from the ALWIN radar and SOFIE. J. Atmos. Sol.-Terr. Phys., 73(14-15): 2176-2183. |
| [7] | Hill R J, Gibson-Wilde D E, Weme J A, et al. 1999. Turbulence-induced fluctuations in ionization and application to PMSE. Earth Planets Space, 51(7-8): 499-513. |
| [8] | Hosokawa K, Ogawa T, Yukimatu A S, et al. 2004. Statistics of Antarctic mesospheric echoes observed with the SuperDARN Syowa Radar. Geophys. Res. Lett., 31: L02106. |
| [9] | Ichimaru S. 1973. Basic Principles of Plasma Physics: A Statistical Approach. London: Benjamin. |
| [10] | Ivlev A V, Samsonov D, Goree J, et al. 1999. Acoustic modes in a collisional dusty plasma. Phys. Plasmas., 6(3): 741-750. |
| [11] | Jiang C J, Li F. 2006. A study on properties of gravity waves in space dust plasma. Chinese J. Geophys. (in Chinese), 49(5): 1250-1256. |
| [12] | La Hoz C, Havnes O, Næsheim L I, et al. 2006.Observations and theories of Polar mesospheric summer echoes at a Bragg wavelength of 16 cm. J. Geophys. Res.,111(D0):4203-4259. |
| [13] | Li H, Wu J, Wu J, et al. 2009. Study on the sharp boundary of layered dust structure in the summer polar Mesopause. Chin. J. Polar Res. (in Chinese), 21(4): 272-278. |
| [14] | Li H R, Wang M Y, Wu J, et al. 2010. Preliminary experiment analysis about PMSE artificial electron heating and overshoot. Chinese J. Geophys. (in Chinese), 53(12): 2836-2842. |
| [15] | Ma J X, Yu M Y. 1994. Langmuir wave instability in a dusty plasma. Phys. Rev. E., 50(4): 2431-2433. |
| [16] | Morris R J, Höffner J, Lübken F J, et al. 2012. Experimental evidence of a stratospheric circulation influence on mesospheric temperatures and ice-particles during the 2010-2011 austral summer at 691S. J. Atmos. Sol.-Terr. Phys., 89: 54-61. |
| [17] | Ogawa T, Kawamura S, Murayama Y. 2011. Mesosphere summer echoes observed with VHF and MF radars at Wakkanai, Japan (45.41N). J. Atmos. Sol.-Terr. Phys., 73(14-15): 2132-2141. |
| [18] | Pfaff R, Holzworth R, Goldberg R, et al. 2001. Rocket probe observations of electric field irregularities in the polar summer mesosphere. Geophys. Res. Lett., 28(8): 1431-1434. |
| [19] | Rapp M, Lübken F J. 2004. Polar mesosphere summer echoes (PMSE): review of observations and current understanding. Atmos. Chem. Phys., 4: 2601-2633. |
| [20] | Ress D, von Zahn U, von Cossart G, et al. 2000. Daytime Lidar measurements of the stratosphere and mesosphere at the Alomar observatory. Adv. Space Res., 26(6): 893-902. |
| [21] | Shi Y X, Wang J, Wu J, et al. 2008. Characteristic parameters estimation of two weakly ionized dusty plasma. Chin. J. Radio Sci. (in Chinese), 23(1): 95-99. |
| [22] | Shimogawa M, Hlllzworth R H. 2009. Electric field measurements in a NLC/PMSE region during the MASS/ECOMA campaign. Ann. Geophys., 27: 1423-1430. |
| [23] | Shukla P K, Mamun A A. 2002. Introduction to Dust Plasma Physics. London: IOP Publishing Ltd. |
| [24] | Tsytovich V N, de Angelis U. 1999. Kinetic theory of dusty plasma. I. General approach. Phys. Plasmas, 6(4): 1093-1106. |
| [25] | Varney R H, Kelley M C, Nicolls M J, et al. 2011. The electron density dependence of polar mesospheric summer echoes. J. Atmos. Sol. -Terr. Phys., 73(14-15): 2153-2165. |
| [26] | Xu C H. 2012. Classical Mathematical Problems and Galois Theory (in Chinese). Harbin: Harbin Industrial University Press. |
| [27] | Zhang L P, Xue J K. 2008. The instability of dust acoustic waves in inhomogeneous dusty plasmas with non-adiabatic dust charge fluctuation. Chin. Phys. B, 17(7): 2594-2599. |
| [28] | 蒋成进, 李芳. 2006. 空间尘埃等离子体中的重力波特性. 地球物理学报, 49(5): 1250-1256. |
| [29] | 李辉, 吴健, 吴军等. 2009. 极区夏季中层顶尘埃分层的锐边界结构研究. 极地研究, 21(4): 272-278. |
| [30] | 李海龙, 王茂琰, 吴健等. 2010. PMSE人工电子加热和过冲实验的初步研究. 地球物理学报, 53(12): 2836-2842. |
| [31] | 石雁祥, 王菊, 吴健等. 2008. 对两种弱电离尘埃等离子体特征参量的定量估计. 电波科学学报, 23(1): 95-99. |
| [32] | 徐诚浩. 2012. 古典数学难题与伽罗瓦理论. 哈尔滨: 哈尔滨工业大学出版社. |
 2014, Vol. 57
2014, Vol. 57


