1 引言
曲率属性作为一个描述地层弯曲程度的几何属性,是三维地震资料构造解释的重要工具(印兴耀和周静毅,2005).它可以用来识别地层弯曲、地层不连续性以及预测裂缝的发育(张凤旭等,2007),对背斜、向斜的走向及规模刻画清晰,尤其在裂缝预测方面,曲率属性已成为从地震属性角度来预测裂缝的主要方法.
Price和Cosgrove(1990)给出应力与曲率和杨氏模量的定量计算关系,奠定了通过曲率来预测应力的理论基础.Lisle(1994)通过实际露头资料统计,指出高斯曲率和裂缝在成因上的相关性,从而在实际资料上对曲率和裂缝的关系做了一定的验证.Roberts(2001)提出了层面曲率的计算方法,同时系统地阐述了多种曲率属性如高斯曲率、最大正曲率、最小负曲率的定义以及各自的特点.但层面曲率由于是基于人工解释层位所计算的,受到人工解释因素的影响,会带来一些不存在的构造假象.为此,Al-Dossary(2006)提出了三维曲率属性的计算方法,将Roberts(2001)基于层位计算倾角的方法改为基于原始地震数据,并通过相似性扫描的方法来计算曲面的一阶导数,将曲率属性的算法推广到了全三维,并称之为体曲率.Chopra和Marfurt(2011)提出了欧拉曲率属性,计算不同方位的最大正曲率和最小负曲率,能够凸显方位差异信息.Chpora和Marfurt(2012,2013)提出了振幅曲率,将原来计算构造曲率时输入的inline和crossline方向的倾角转换为inline和crossline方向相干加权能量的梯度,计算出横向振幅的曲率属性,用振幅曲率对地质上的差异压实从地震属性领域进行了解释,实现了更加精细的三维地震属性解释.Chen 等(2012)在小波域对曲率属性进行了多尺度分解,并将多尺度信息进行融合.Gao 等(2013)推导了曲率梯度属性,并结合曲率属性对断层进行了精细的识别和描述.体曲率属性的提出使得曲率在应用方面又得到了很大的拓宽.Chopra和Marfurt(2007)将曲率属性成功地应用到哥伦比亚某区块进行了三维地震解释,尤其是裂缝预测工作.Guo等(2010)将曲率属性应用于Woodford美国典型页岩气区块进行了裂缝密度和裂缝发育方位的预测,效果显著.Hunt(2010,2011)根据曲率和地应力的关系,将曲率与杨氏模量、曲率与拉梅参数结合对地应力和裂缝密度进行预测,并根据测井资料和交会分析综合提出了一种通过方位AVO和曲率属性对裂缝密度进行定量估计的方法.
倾角扫描技术是曲率属性提取中的一项关键技术,它决定了曲率提取效果的精度.关于倾角扫描,已经发展了很多方法.在这些方法中,主要有三个分支,一是基于相似性(Marfurt,1998)的扫描方法,二是基于复地震道分析(Barnes, 1996,2000)的扫描方法,三是基于梯度结构张量(Bakker,1999)的方法.后两者由于其扫描精度限制并没有得到广泛的应用.基于相似性的扫描方式以其较高的计算精度被多数人使用并发展.其中,最早的是由Picou和Utzmann(1962)提出了二维非归一化的互相关扫描,该计算方法是沿着二维地震测线进行倾角扫描,将三维曲面抽象到二维进行倾角估算,所得到的倾角数据呈条带状,且不够精确.Finn(1986)提出了三维倾角和方位角的定义,并在二维对其进行了实践.Marfurt(1998,2000)提出了三维基于相似性的倾角扫描方 法,与相干属性中的C2算法一致,将Finn和Backus(1986)的算法提到了一个真正的三维意义上.由于该算法是采用中心扫描窗,导致计算时对分析点两侧的构造存在一个平滑作用,为了改进这一点,Marfurt(2006)提出了多窗扫描的方式,作为一种稳健的倾角和方位角估计方法,该方法能够对断层两侧倾角的变化扫描相对精确,但是在一些小断层发育的地方,它往往会忽略掉这些构造,并且多窗扫描计算点数是有限的,对于信噪比低的区域或者同相轴比较杂乱的地方,扫描效果不是十分理想.而信噪比对于中心窗的影响是比较小的,因此,本文提出了一种离心窗的倾角扫描方法,将原来的窗口空间布局改为在空间上为窗口中心偏离分析点的四个旋转窗口,时间上为包含分析点的五个纵向滑动窗口,通过变换不同的窗口进行高精度倾角估计,从而能够保证扫描到小的构造变化,同时增加了计算点数,对噪声抵抗力增强,并将原来多窗所进行的45次扫描改为20次扫描,提高了计算效率.通过该方法得到的倾角数据体进行曲率属性提取,在识别断层和其他线性构造方面均取得较好的效果.
2 离心窗倾角扫描原理倾角扫描是曲率计算的一个关键步骤,目前已发展了多种倾角扫描的方法.Marfurt(2006)指出,中心窗扫描会对地质构造带来一定的平滑,或者需要对数据进行预滤波,为了避免这个问题,他提出了多窗扫描的稳健估计方式,但是由于他所改进的多窗空间布局的限制,导致一些小的断层或局部构造容易被忽略,对于这一点可以通过图 1来分析.
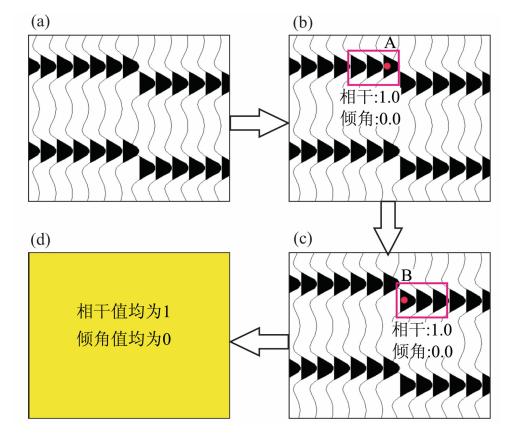 | 图 1 多窗扫描对小断层的忽略示意图(按箭头指示顺序) Fig. 1 The schematic of the ignoration of small fault scanned by multi window style(in the direction of the arrow) |
对图 1中这样一个小断层,如果计算分析点A的倾角,需要在分析点A处进行多窗旋转扫描,最终在图 1b中红色框内取得最大相干值,此时相干值为1.0,倾角值为0;然后计算下一点B的倾角,在分析点B处进行多窗旋转扫描,最终在图 1c中红色框内取得最大相干值,此时相干值为1.0,倾角值为0.而其他点处由于轴的连续性很好,均为水平层,所以相干值均为1.0,倾角值为0.整个剖面扫描结束之后,所有分析点的相干值均为1.0,倾角值均为0,显示剖面轴的连续性很好.而其实剖面自身是存在断层的,多窗扫描由于有些窗只取了分析点一侧的信息,导致将此断层忽略,事实上这样的断层是广泛存在的,因为空间一个采样间隔往往达到几百米.因此,并不能忽略这种小的构造.此外,多窗由于其计算点数的限制,所提取的属性受地震资料噪声的影响比较严重.
为了改进这些问题,综合多窗和中心窗的优势,本文提出一种离心窗扫描的方法.窗口的空间和时间布局见图 2.
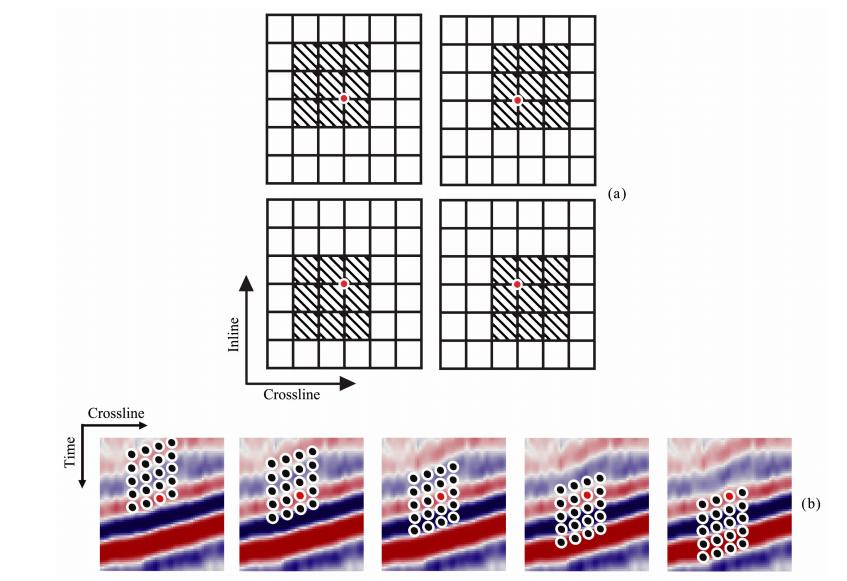 | 图 2 离心窗(a)空间分布和(b)时间分布 Fig. 2 The spatial distribution(a) and time distribution(b)of eccentric window |
采用围绕分析点的四个偏离中心的离心窗进行扫描.避免了单独考虑分析点一侧信息所带来的对小断层的忽略,在示意图中的体现是所选取的窗并不是只有点一侧的信息,因此不会忽略掉图 1中类似的小断层等构造.并且,分析窗空间点数的增加,对噪声的抵抗能力增强.
选定了扫描窗口之后,通过相似性扫描的方法计算倾角,通过复数道的方式构建相似系数计算公式,得到
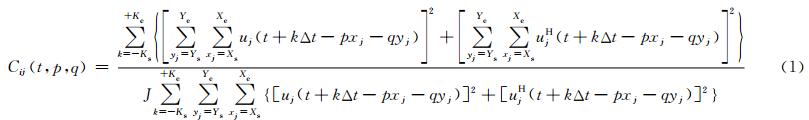
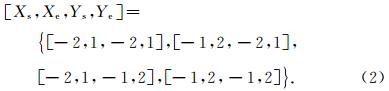
在选定横向窗口之后,需要对每一个横向窗口在纵向上进行扫描.从剖面上看,是变换不同的视倾角p和q,根据各参与计算的道与分析点的inline和crossline方向的距离以及p、q的关系,确定各道所对应的中心位置,然后取出时窗大小的数据,用公式(1)计算相似性的值.相似性值越高说明所取波形的相似程度越高,Cij最大为1.0.扫描到最大的相似性值时对应的p和q即为该分析点处同相轴的视倾角向量.由于本文采用四个离心窗进行旋转扫描,并在纵向进行移位扫描,分析点最终的相干值是取所有扫描窗口的最大值.
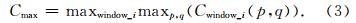
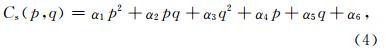
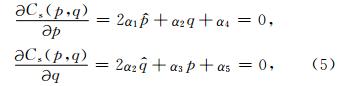
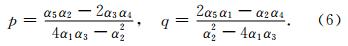
三维地震资料可以看作振幅关于空间位置和时间采样点的函数u(t,x,y),那么u的梯度可以表示成下面的形式
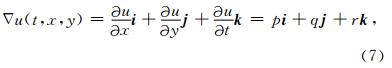
在曲率属性计算中,需要寻找反射点所在曲面的曲率,本文通过Roberts(2001)提出的二元二次拟合方程对曲面进行拟合(公式(8)).其中z(x,y)表示曲面的高度值,a~e表示象征曲面形态的系数,f表示纵向位移量,我们已知x、y和z的数值对应关系,需要拟合它们的函数关系,通过公式(8)进行拟合.
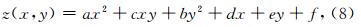
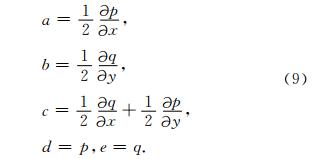
由于f是一个纵向位移量,因此不会影响到曲率值的大小,所以无需计算.由公式(9)可以看出,需要计算的是地震反射振幅的一阶导数和二阶导数,反射振幅的一阶导数即视倾角向量,反射振幅的二阶导数即视倾角向量的一阶导数.
根据2节中由离心窗倾角扫描方法求取的倾角数据,下面需要对该倾角数据求取一阶导数.在求取时,可以通过差分或者傅氏变换求取,本文通过傅氏变换求取.根据傅氏变换的微分性质,对空间域求取某变量的一阶导数,相当于在波数域乘ik因子(公式(10),其中F表示傅里叶变换),因此利用这个性质将倾角数据变换到波数域,然后乘ik因子之后进行反变换求取空间域的导数.同时,通过分数阶导数的方法进行多尺度曲率属性分解.

其中,α为尺度控制因子,一般为0~1之间,值越大表示尺度越小,如α为0.25时为大尺度信息,反映地层弯曲,背斜向斜的走向、规模等,α为1时为小尺度信息,反映断层、构造上的微妙变化.
这样,通过倾角扫描和波数域导数求解,就可以得到u关于x和y方向的一阶、二阶导数信息,即a~e参数已获得,然后根据Robert(2001)给出的各曲率属性的计算公式进行曲率属性的提取.在计算中,因为傅里叶变换对突变点是非常敏感的,而扫描的倾角数据往往存在一些差异较大的点,因此应用中值滤波的方法对倾角数据进行预处理,去掉了突变点所带来的吉普斯效应影响.
本文主要提取的是最大正曲率和最小负曲率属性,二者的计算公式如下:
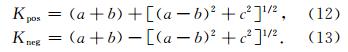
为了验证方法的有效性,设计一个断层模型.分别用多窗和离心窗对模型进行倾角扫描,得到相似 性值的剖面如图 3.本文是用相似性扫描的效果来衡量倾角扫描的精度,这是因为相似性值是在变换扫描倾角的同时所得到的,相似性值的精度越高,说明所扫描到的倾角的值就越准确,是最接近同相轴倾角的值,因此,下面通过对比相似性扫描的效果来反映倾角扫描精度.
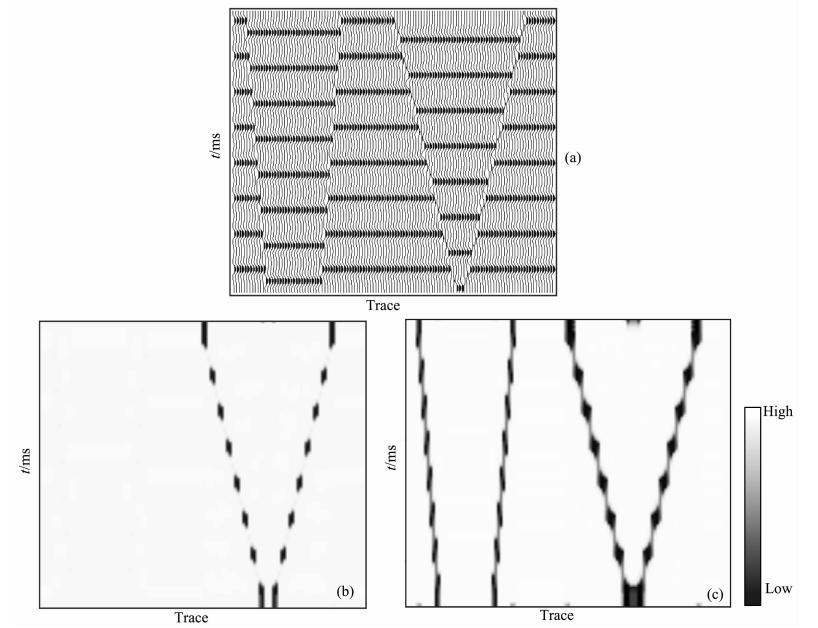 | 图 3 断层模型相似性扫描 (a)模型地震记录;(b)多窗扫描的相似性;(c)离心窗扫描的相似性. Fig. 3 The semblance scanning of a fault model (a)Seismic profile of fault model;(b)Semblance scanned by multi window;(c)Semblance scanned by eccentric window. |
该模型中,左边两条断层横向断距为1个道间距,右边两条断层横向断距为3个道间距.离心窗和多窗在扫描时所跨越的数据范围一致,均为25道.可以看出,多窗精度较高,对于规模较大的断层可以扫到,但是细小的断层则被忽略.而离心窗扫描能够保证扫描的精确度,对模型中左侧的两个断层扫描的非常清晰.我们通过比较二者相干值的大小也可以看出,多窗扫描中,右侧两个断层的相干值在0.85左右,而离心窗右侧断层的相干值在0.65左右,在相干属性中,我们希望不连续的地方相干值越低越好.由此充分说明,离心窗能更好地突出相似性差的部位.
该模型验证了离心窗的应用效果,说明该方法 是可取的,下面针对实际资料进行测试.
5 实际资料测试 5.1 倾角扫描下面取某区块的资料进行实际验证.图 4a展示了该区一条测线,发育一个小的背斜,背斜右侧有一些细小断层,对该数据体分别用多窗和离心窗进行相似性扫描.得到结果如图 4.
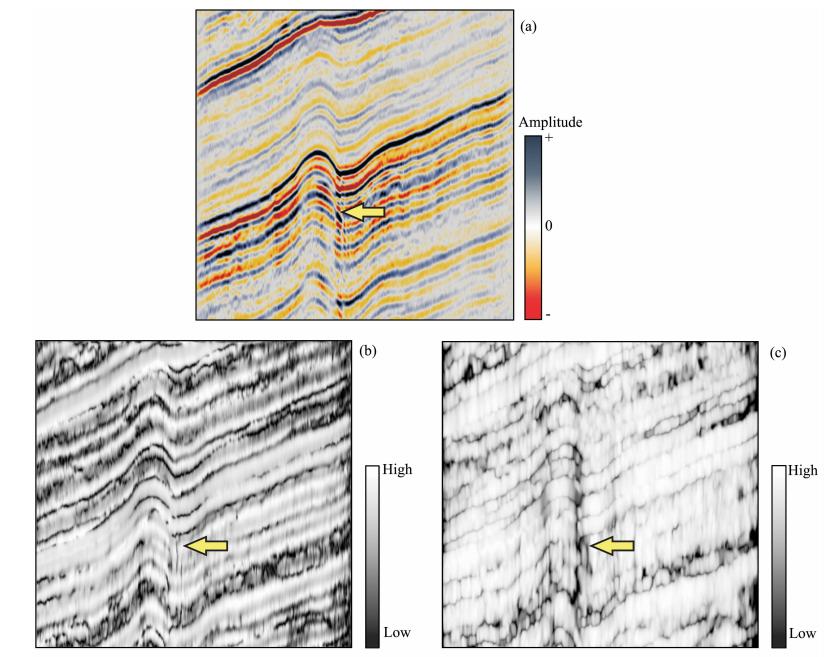 | 图 4 不同扫描方式得到的相似性剖面 (a)原始地震剖面;(b)多窗扫描;(c)离心窗扫描. Fig. 4 The semblance section scanned through different windows (a)Original seismic section;(b)The semblance profile scanned by multi window; (c)The semblance profile scanned by eccentric window. |
图 4a是地震剖面,图 4b,4c分别是多窗和离心窗的扫描结果.箭头所指处仔细看是有一个小的断层发育的,多窗扫描基本是看不出这个细小的构造,并且在同相轴杂乱的地方受噪声影响比较严重.离心窗扫描的相似性中该处的细小断层明显,相似性剖面整体较白,受噪声的影响较小.充分说明,离心窗在扫描精度和信噪比上是优于多窗的.从扫描窗口大小看,离心窗是比多窗要大.在一般的叠后的地震剖面中,有效信号是远大于噪声所占的比例的.因此,窗口较小时,所圈定的有效信号并不多,噪声所占比例会较大,窗口越大,所圈定的有效信号会越多,因为有效信号是具有相似性的,而噪声是不具有相似性的,因此,窗口越大,有效信号的相似性会越强,因而最终相似性会越高,从而图片越白,对应于图 4c的情况.图 4b则由于有效信号较少,因此相似性小,图片较黑.Marfurt(2006)应用主成分滤波对多窗扫描进行了改造,使得其取得较好的效果.在不经过任何处理的情况下,多窗扫描是存在一定问题的.尤其对于中国东部的资料,多发育横向断距不是很大的断层,因此高精度的描述小断层位置和空间延展是非常必要的.
图 5为通过多窗和离心窗所扫描的倾角切片.离心窗在对背斜形态、转折端的刻画上清晰明了,多窗扫描的结果噪点太多,受噪声干扰太大,并且一些小的线性构造几近忽略或被噪声掩盖.充分说明离心窗扫描方式相对稳定,保证了扫描精度和信噪比.因此,选用离心窗进行倾角扫描是非常有必要的.
 | 图 5 inline和crossline方向的视倾角 (a)原始地震剖面;(b)time=0.07 ms的振幅切片;(c)多窗扫描的inline方向的视倾角p;(d)多窗扫描的crossline 方向的视倾角q;(e)离心窗扫描的inline方向的视倾角p;(f)离心窗扫描的crossline方向的视倾角q. Fig. 5 The apparent dip of inline and crossline direction (a)Original seismic profile;(b)Amplitude slice at time 0.07 ms;(c)Apparent dip p of inline direction scanned by multi window;(d)Apparent dip q of crossline direction scanned by multi window;(e)Apparent dip p of inline direction scanned by eccentric window;(f)Apparent dip q of crossline direction scanned by eccentric window. |
在由倾角数据计算曲率属性时,需要对倾角数据作预处理,去掉一些差异较大的噪点的影响,否则会因为傅氏变换带来一些细小的震荡.本文应用中值滤波对倾角数据进行改造.将地震倾角切片作为数字图像进行中值滤波处理.中值滤波的原理是(Liu,2006;Bednar,1983; 王伟等,2012):在处理第i个像素点时,首先选取滤波窗口内的灰度中值mi,以mi为中心选取一个灰度区间[mi-d,mi+d],将滤波窗口内的所有落在选定灰度区间内的点作平均,并将结果作为最终的滤波输出,数学表示为
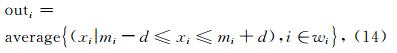
图 6展示了某切片沿inline方向的视倾角p向量中值滤波的结果.中值滤波在尽可能保留原有构造的前提下去掉了一些差异较大的点,使得数据更接近真实情况.
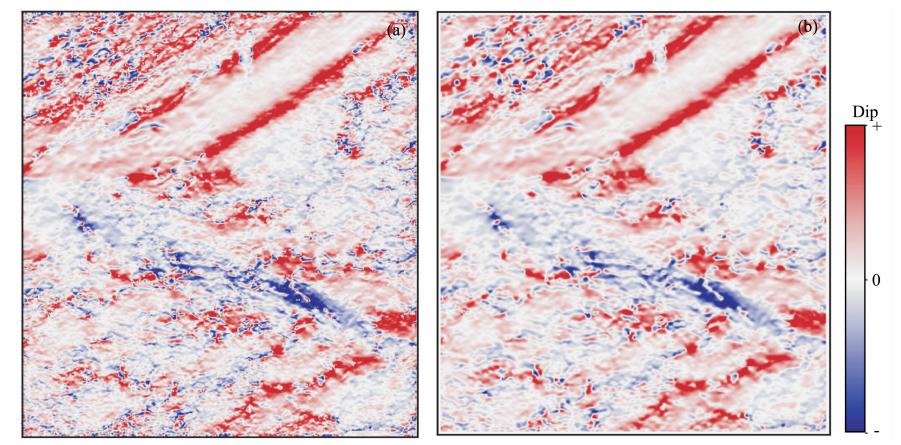 | 图 6 中值滤波前(a)、后(b)的倾角数据对比 Fig. 6 Comparation of dip verctor before(a) and after(b)median filtering |
图 7是经过中值滤波和未经过中值滤波的倾角所计算出的曲率属性的对比.一个最为突出的特点是,中值滤波去除了大量的条带现象,并且较好地保留了原始的构造信息.
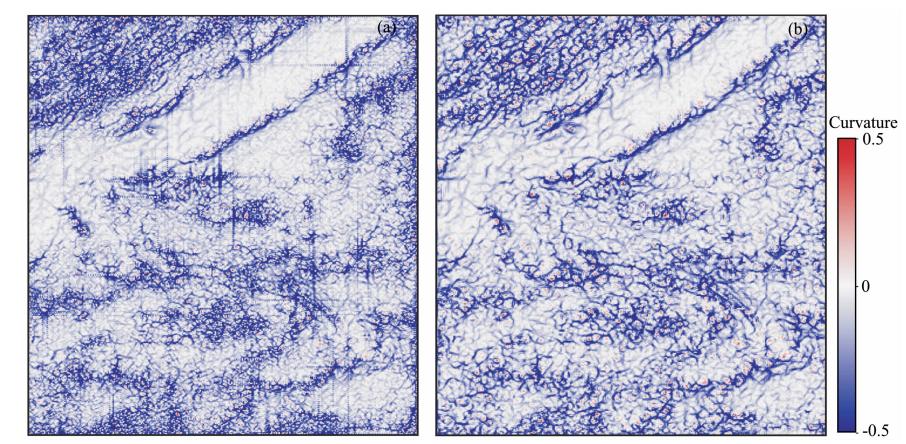 | 图 7 中值滤波前(a)、后(b)计算的曲率属性 Fig. 7 Curvature attribute calculated from dip verctor before(a) and after(b)median filtering |
曲率属性越来越多的受到地震解释工作者的关注,它不仅在构造解释,也在裂缝预测方面有很好的辅助作用.本文利用离心窗扫描得到的倾角数据体进行曲率属性提取,并将之与多窗扫描的倾角所计算出的曲率属性进行对比,在由倾角求取曲率时需要对倾角数据做中值滤波.
对该区一时间切片提取曲率属性,在波数域尺度选择时,选取尺度因子α=1,即小尺度的信息,小尺度更多的是反映构造细节上的变化,凸显塌陷、隆起、断层等小的细节构造,分别提取了最大正曲率和最小负曲率属性.得到结果见图 8.
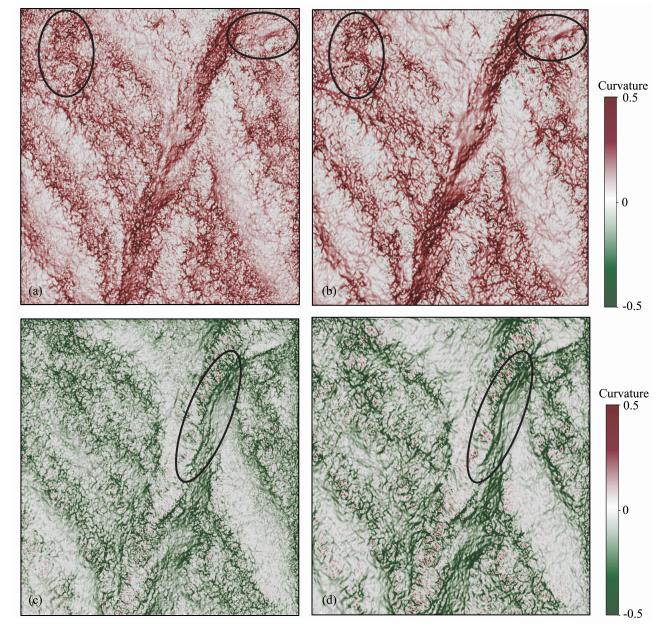 | 图 8 基于不同扫描方式计算的曲率属性切片 (a)由多窗扫描倾角计算的最大正曲率属性;(b)由离心窗扫描倾角计算的最大正曲率属性; (c)由多窗扫描倾角计算的最小负曲率属性;(d)由离心窗扫描倾角计算的最小负曲率属性. Fig. 8 Curvature attribute based on different scanning style (a)Kpos attribute calculated from multi window dip scanning style;(b)Kpos attribute calculated from eccentric window dip scanning style;(c)Kneg attribute calculated from multi window dip scanning style;(d)Kneg attribute calculated from eccentric window dip scanning style. |
分析图 8可以看出,由多窗倾角扫描所计算的最大正曲率和最小负曲率属性存在的问题是构造现象杂乱,典型线性构造模糊.由离心窗倾角扫描所计算的两种曲率属性信噪比要高于多窗所计算的,并且从图 8中黑色椭圆内以及图 9(对图 8c,8d两图黑色圈内的局部放大)白色箭头所指处可以看到离心窗扫描所提取的属性优化了多窗中比较模糊的地方,使得一些线性构造,如沟壑、断层等可以突显出来,便于三维地震资料解释.对于一些塌陷位置,也 能得到较好的体现.综合说明离心窗扫描所得到的 倾角数据体是相对比较精确的,由该倾角数据体所计算的曲率属性精度也是非常高的.
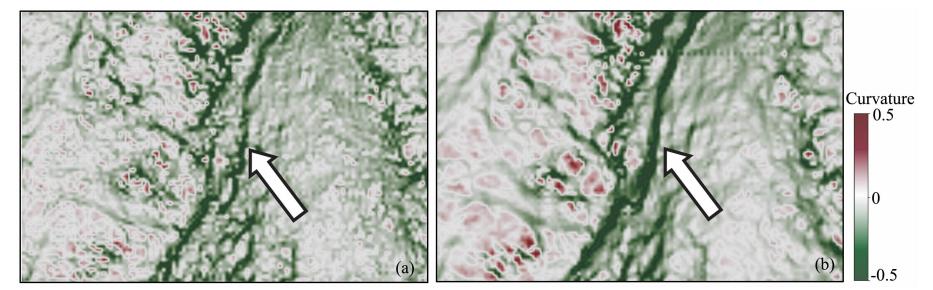 | 图 9(a)图 8c和(b)图 8d黑色圈内局部放大 Fig. 9 Partial enlarged view of the black circle in(a)Fig. 8c and in(b)Fig. 8d |
本文针对曲率属性计算方法中的关键步骤倾角扫描问题做了改进,提出了基于离心窗的倾角扫描方法,避免了多窗扫描对细节构造的忽略,降低了地震资料的噪声对曲率属性提取的影响,并有效地提高了计算效率,通过实际资料测试证明是一个可行的方法.在实际应用中,也可以根据资料自身的特点进行选择.如果所研究的地区地质构造较为简单,小断层发育较少,可以仍然选用中心窗扫描的方式,中心窗扫描在计算效率上是明显高于多窗和离心窗扫描的,只是精度较低.而如果所研究的地区地质构造复杂,小断层发育广泛,那么需要采用本文所提出的的离心窗扫描方式,可以较好地体现构造的细节、不连续性信息.曲率属性作为一种预测裂缝的地震属性,主要在页岩地层中适用,根据曲率的分布状况对应地层弯曲程度,从而预测地应力的分布以及裂缝的发育,对裂缝型油气藏识别具有可靠的指导作用.
| [1] | Al-Dossary S, Marfurt K J. 2006. 3D volumetric multispectral estimates of reflector curvature and rotation. Geophysics, 71(5): 41-51. |
| [2] | Bakker P, van Vliet L J, Verbeek P W. 1999. Edge preserving orientation adaptive filtering.// IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Fort Collins, CO: IEEE, 535-540. |
| [3] | Barnes A E. 1996. Theory of 2-D complex seismic trace analysis. Geophysics, 61(1): 264-272. |
| [4] | Barnes A E. 2000. Attributes for automating seismic facies analysis. 2000 SEG Annual Meeting, 553-556. |
| [5] | Bednar J B. 1983. Applications of median filtering to deconvolution, pulse estimation, and statistical editing of seismic data. Geophysics, 48(12): 1598-1610. |
| [6] | Chen X H, Yang W, He Z H, et al. 2012. The algorithm of 3D multi-scale volumetric curvature and its application. Applied Geophysics, 9(1): 65-72. |
| [7] | Chopra S, Marfurt K J. 2007. Volumetric curvature attributes add value to 3D seismic data interpretation. The Leading Edge, 26(7): 856-867. |
| [8] | Chopra S, Marfurt K J. 2011. Observing fracture lineaments with Euler curvature. SEG Technical Program Expanded Abstracts 2011. Society of Exploration Geophysicists, 990-994. |
| [9] | Chopra S, Marfurt K J. 2012. Seismic attribute expression of differential compaction. The Leading Edge, 31(12): 1418-1422. |
| [10] | Chopra S, Marfurt K J. 2013. Structural curvature versus amplitude curvature. The Leading Edge, 32: 178-184. |
| [11] | Finn C J, Backus M M. 1986. Estimation of three-dimensional dip and curvature from reflection seismic data. 1986 SEG Annual Meeting, 335-358. |
| [12] | Gao D L. 2013. Integrating 3D seismic curvature and curvature gradient attributes for fracture characterization: Methodologies and interpretational implications. Geophysics, 78(2): O21-O31. |
| [13] | Guo Y X, Zhang K, Marfurt K J. 2010. Seismic attribute illumination of Woodford Shale faults and fractures, Arkoma Basin, Oklahoma. Annual International Meeting-Society of Exploration Geophysicists, 2: 1372-1376. |
| [14] | Hunt L, Reynolds S, Brown T, et al. 2010. Quantitative estimate of fracture density variations in the Nordegg with azimuthal AVO and curvature: A case study. The Leading Edge, 29(9): 1122-1137. |
| [15] | Hunt L, Reynolds S, Hadley S, et al. 2011. Causal fracture prediction: Curvature, stress, and geomechanics. The Leading Edge, 30(11): 1274-1286. |
| [16] | Lisle R J. 1994. Detection of zones of abnormal strains in structures using Gaussian curvature analysis. AAPG Bulletin, 78(12): 1811-1819. |
| [17] | Liu C, Liu Y, Yang B J, et al. 2006. A 2D multistage median filter to reduce random seismic noise. Geophysics, 71(5): 105-110. |
| [18] | Marfurt K J, Kirlin R L, Farmer S L, et al. 1998. 3-D seismic attributes using a semblance-based coherency algorithm. Geophysics, 63(4): 1150-1165. |
| [19] | Marfurt K J. 2006. Robust estimates of 3D reflector dip and azimuth. Geophysics, 71(4): P29-P40. |
| [20] | Marfurt K J, Kirlin R L. 2000. 3-D broad-band estimates of reflector dip and amplitude. Geophysics, 65(1): 304-320. |
| [21] | Picou C, Utzmann R. 1962. La "coupe sismique vectorielle". Geophysical Prospecting, 10(4): 497-516. |
| [22] | Price N J, Cosgrove J W. 1990. Analysis of Geological Structures. Cambridge: Cambridge University Press, 304-330. |
| [23] | Roberts A. 2001. Curvature attributes and their application to 3D interpreted horizons. First Break, 19(2): 85-100. |
| [24] | Wang W, Gao J H, Chen W C, et al. 2012. Random seismic noise suppression via structure-adaptive median filter. Chinese Journal of Geophysics (in Chinese), 55(5): 1732-1741. |
| [25] | Yin X Y, Zhou J Y. 2005. Summary of optimum methods of seismic attributes. Oil Geophysical Prospecting (in Chinese), 40(4): 482-489. |
| [26] | Zhang F X, Zhang F Q, Liu C, et al. 2007. A technique for elaborate explanation of faulted structures: three-directional small subdomain filtering. Chinese Journal of Geophysics (in Chinese), 50(5): 1543-1550. |
| [27] | 王伟, 高静怀, 陈文超等. 2012. 基于结构自适应中值滤波器的随机噪声衰减方法. 地球物理学报, 55(5): 1732-1741 . |
| [28] | 印兴耀, 周静毅. 2005. 地震属性优化方法综述. 石油地球物理勘探, 40(4): 482-489 . |
| [29] | 张凤旭, 张凤琴, 刘财等. 2007. 断裂构造精细解释技术——三方向小子域滤波. 地球物理学报, 50(5): 1543-1550. |
 2014, Vol. 57
2014, Vol. 57

