2. 中国石油川庆钻探工程有限公司地球物理勘探公司, 成都 610213
2. CNPC CDEC Sichuan Geophysical Company, Chengdu 610213, China
1 引言
传统的各向异性层析成像是在弱各向异性假设下,主要利用走时信息进行单参数线性反演.近十年来,各向异性层析成像发展到利用多种地震信息、在不同域、采用非线性方法进行反演,但多参数联合反演一直是各向异性层析中的主要难题.Chapman与Pratt(1992)基于线性扰动理论,导出了二维非均匀弱各向异性介质中的射线走时方程,该方程仅依赖于有限的几个参数.Chapman与Pratt同时指出,基于地表观测数据很难将这几个参数同时反演出来.Pratt与Chapman(1992)利用井中观测数据,在对 模型中的梯度和二阶梯度做平滑后,用SVD(Singular Value Decomposition,奇异值分解)方法实现了各向异性介质中Qp波的线性层析.Watanabe等(1996)采用四周全方位观测方式,实现了VTI介质中三参数的同步反演.Gholami等(2010)指出,即使利用四周全方位观测的地震数据,二维波动方程层析也很难将vS0,vP0,ε,δ同时反演出来,其中ε刻画的是水平和垂直方向vP的变化率,δ刻画的是vP垂直入射时相速度的二阶导数.Sieminski等(2007)在研究了各向异性介质中体波的走时层析核函数的敏感性后指出,各向异性介质的走时层析更依赖于射线路径、入射角和传播方向,而非直接依赖于观测系统.可见,各向异性层析的难点不在于反演算法本身,而在于多参数的相互影响.了解不同参数对观测信息的贡献大小,并采取一定 的参数化手段与策略是成功实现多参数反演的关键.
前人在各向异性介质地震层析成像中做了一定的参数化方面的研究.Fowler(2003)研究了一种参数化方法,使得P波相速度基本独立于横波相速度,但是缺乏精确的P波群速度表达式.为了排除反演过程中更难掌握和含有更多噪声的横波影响,Grechka与Mateeva(2007)采用慢度和偏振方向参数化方法,从VSP(Vertical Seismic Profiling,垂直 地震剖面)数据中估计局部各向异性参数.Richardson等(2008)基于vP0,ε,δ参数化方式,在反演过程中固定各向异性参数,只更新速度参数.Zhou等(2011)基于慢度,ε,δ参数化方式,发现速度的反演分辨率 高于各向异性参数的反演分辨率,而且多参数同步 层析的反演结果优于单参数层析的反演结果.Sieminski等(2007)采用Born散射和面波模式耦合方法研究了各向异性介质中的面波走时层析成像,并指出在反演过程中要尽量采用与速度有关的参数化方法.Plessix与Cao(2011)通过对VTI介质纵波层析的Hessian矩阵作特征值分析后也指出,采用vnmo与vh是较为合适的参数化方法.但以上研究并没有从理论上分析不同的参数化方式对层析反演的影响,也没有对“合理”的参数化方式进行理论解释.
在各向异性层析反演策略方面,前人也做了大量的研究.Watanabe等(1996)在全波形反演研究中先做各向同性单参数反演,再在此基础上完成各向异性多参数反演.Richardson等(2008)也提出类似的反演策略,即在各向同性条件下反演v0,再在地下结构变化较小的地方用一维联合反演得到ε与δ,然后再固定各向异性参数,在后续的反演过程中只更新速度.Gholami等(2010)在频率域各向异性 全波形反演研究中提出逐层反演v0.Koren等(2008)为了在成像道集上利用剩余速度分析更新各向异性介质中的背景速度,用长偏移距反演ε,用短偏移距反演δ.Bakulin等(2010)则通过加入平滑后的井数据约束反演深度域的各向异性参数.可见,尽管做了大量的研究但仍未获得一种合适的、统一的反演策略.Crampin(2003)指出,反演各向异性参数需要利用多分量数据,同时他利用三分量地震数据中的横波分裂作为分析地震各向异性的关键指标.Bale 等(2009)则采用坐标旋转,联合PP反射和PS反射获得介质各向异性的强度和方向,从而改善成像质量.
综合以上研究现状,本文采用与vS0无关的纵波群速度近似表达式,利用局部最优化理论,实现了VTI介质中多参数联合走时层析反演.为了克服多参数层析反演中不同参数对地震波走时的不同影响,在理论上分析并比较了两种参数化方法的核函数特点.同时,为了实现多参数反演,本文给出了一种普适性的层析反演策略.
2 方法原理在各向同性介质中,基于L2范数的P波走时层析目标函数Φ(s)表达为
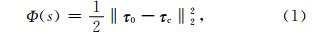
以上反演问题即找到使目标函数取极小值的慢度s.公式(2)、(3)分别为该目标函数所对应的最速下降方向 p和步长t(Liu et al., 2014).
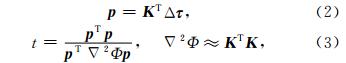
模型的迭代更新公式为
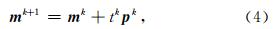
为了利用上述非线性反演方法计算VTI介质中的各向异性参数,本文首先使用传统的Thomsen参数化(s0,ε,δ)方式,利用球谐级数展开表达群慢度(Sayers,1995)
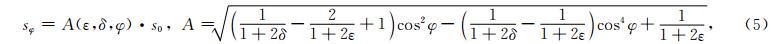
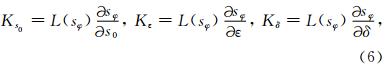
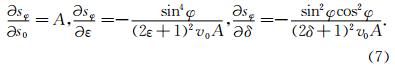
本文对另外一种参数化方式,即垂直慢度s0、水平慢度sh与NMO慢度sn进行了分析.s0、sh、sn与ε、δ的关系如式(8)所示,
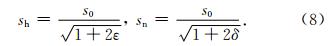
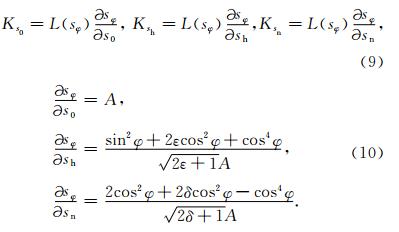
理论分析与数值计算结果(图 1b)表明,这三个新的核函数的数量级比较接近.这说明,这三个参数对地震波走时的影响比较接近,因此有可能把它们同时反演出来,即第二种参数化方法要优于第一种参数化方法.
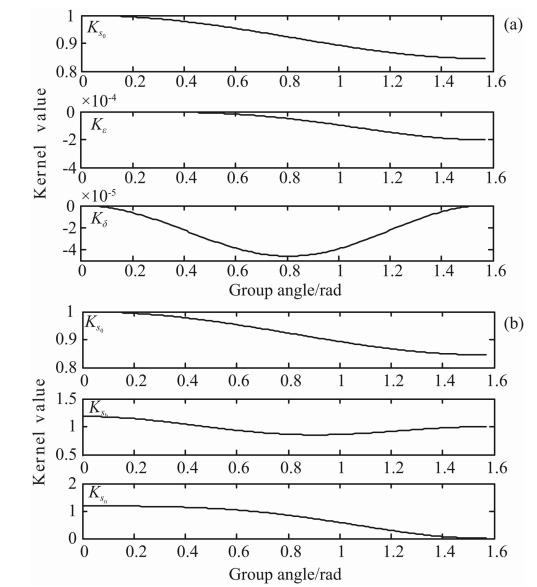 | 图 1 均匀VTI介质中(v0,ε,δ)参数化核函数(a)和(v0,vh,vn)参数化核函数(b)与入射角的关系 Fig. 1 Fréchet kernels of parameterizations(a)(v0,ε,δ) and (b)(v0,vh,vn)as a function of incident angle in homogeneous VTI medium |
为了测试上述非线性反演方法及第二种参数化方式的有效性,我们首先固定δ为精确值,进行v0和ε双参数反演.该部分的所有实验都基于相同的理论模型(图 2)与相同的观测方式.观测系统为每边放炮,其余三边接收,无反射数据.每一边100炮,共400炮,300个接收点均匀分布在其余的三边,炮点间隔与检波点间隔都是20 m.模型离散化为200×200 个网格,离散间隔为10 m×10 m.为了保证快速收敛,本文采用共轭梯度(CG)算法(徐果明,2003).真实模型与初始模型如图 2所示.两种参数化方式的反演结果如图 3所示.从反演结果可以看出,第二种参数化得到的反演结果比第一种参数化 反演结果形态更准确,精度更高.但需要注意的是,两种参数化反演得到的ε与真实模型差距都比较大.
 | 图 2 真实速度模型(a),初始速度模型(b),真实ε模型(c),初始ε模型(d) Fig. 2 Real v0(a),initial v0(b),real ε(c), and initial ε(d) |
 | 图 3 第一种参数化方式反演得到的v0(a),第二种参数化方式反演得到的v0(b),第一种参数化方式反演得到的ε(c),第二种参数化方式反演得到的ε(d) Fig. 3 Obtained v0 by the first parameterization(a),obtained v0 by the second parameterization(b),obtained ε by the first parameterization(c), and obtained ε by the second parameterization(d) |
一个合适的参数化方法只是从数学上提高了弱参数ε与δ对走时的影响.在物理上,ε与δ对走时的弱影响是无法改变的.因此多参数联合反演仍需结合一定的反演策略以提高弱参数的反演精度.本次VTI多参数走时层析实验中,我们借鉴杨积忠等(2014)在变密度声波方程双参数FWI(Full Waveform Inversion,全波形反演)中提出的两步法策略,即第一步同时反演v0和ε,然后将第一步反演得到的v0作为第二步反演的初始速度模型,舍弃第一步反演得到的ε,而是将第一步的初始ε再次作为第二步反演的初始ε.最后,将第二步反演的v0和ε作为最终的结果.采用这种策略的原因在于:在第一步反演没有一个好的初始速度模型的情况下很难得到一个较好的ε反演结果,甚至得到一个更糟的ε结果;但经过第一步的反演,可以得到一个较好的速度模型,这样将该速度模型作为第二步的初始模型,则可以联合反演得到一个较好的ε结果;同时,v0在第二步的反演中自身也会有所改善.
图 4是两种参数化的第二步反演结果,可以看出,v0在第一步的基础上又得到了改善,同时ε的准确性相对于第一步反演结果有了大幅的提高.为了定量比较两种参数化方式的优劣及两步法策略的有效性,水平方向800 m与1000 m处的速度剖面被提取出来,如图 5所示.可以看到,无论是在异常体处还是在背景上,第二种参数化方法的反演结果明显比第一种参数化的反演结果精度更高.同时第二步v0反演分辨率得到了提高,与第一步相比,第二步的ε反演结果有明显的提高.
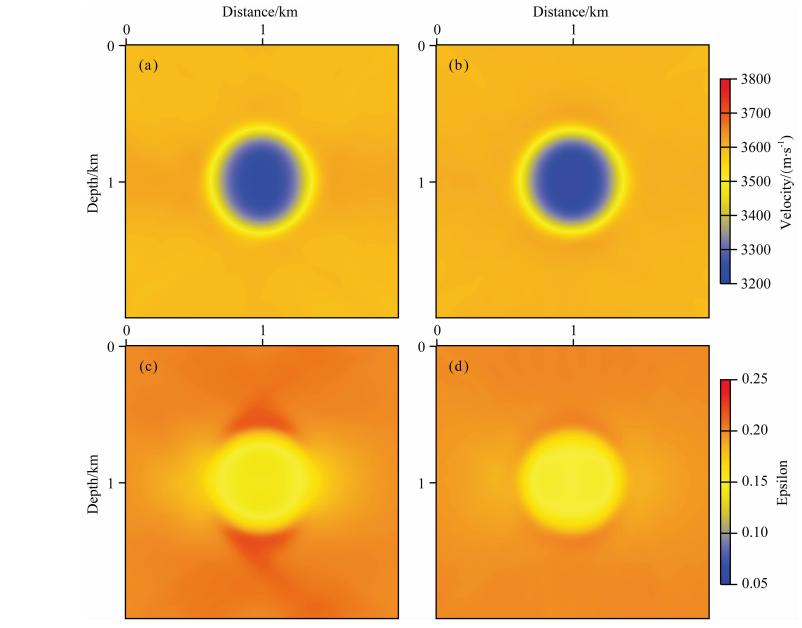 | 图 4 第一种参数化第二步v0反演结果(a),第二种参数化第二步v0反演结果(b),第一种参数化第二步ε反演结果(c),第二种参数化第二步ε反演结果(d) Fig. 4 Obtained v0 by the first parameterization(a),obtained v0 by the second parameterization(b),obtained ε by the first parameterization(c), and obtained ε by the second parameterization(d)after the second round |
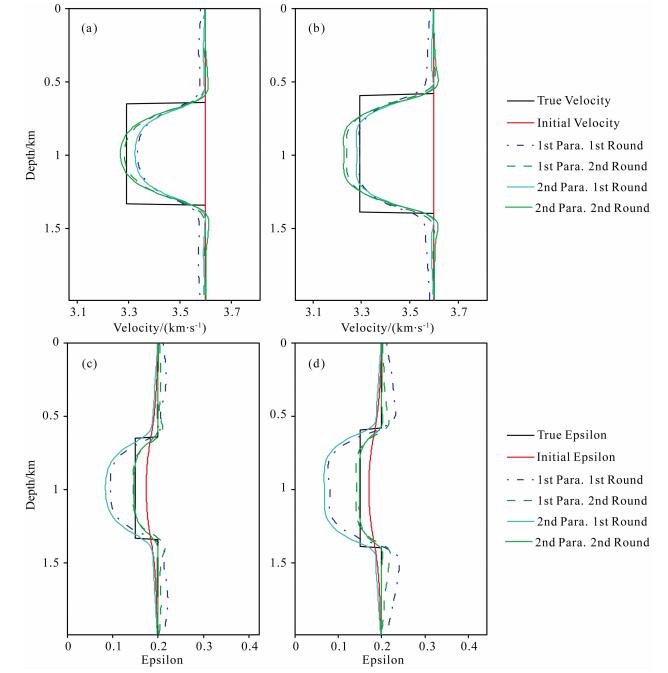 | 图 5 水平位置800 m处(a,c)和1000 m处(b,d)的速度反演剖面(a,b)与ε反演剖面(c,d). 虚线代表第一种参数化方法,实线代表第二种参数化方法,蓝线代表第一步反演,绿线代表第二步反演 Fig. 5 Vertical sections of obtained v0(a,b) and ε(c,d)at x=800 m(a,c) and x=1000 m(b,d)by the first parameterization(dash lines) and second parameterization(solid lines)after the first round(blue lines) and second round(green lines) |
为了进一步测试两步法的适用性,设计了一个二维复杂起伏地表理论模型,真实与初始速度模型和ε模型如图 6所示.复杂模型试验中反演的模型参数为v0和ε,在整个反演的过程中δ参数不更新 且始终保持真实值.层析反演采用第二种参数化方法.
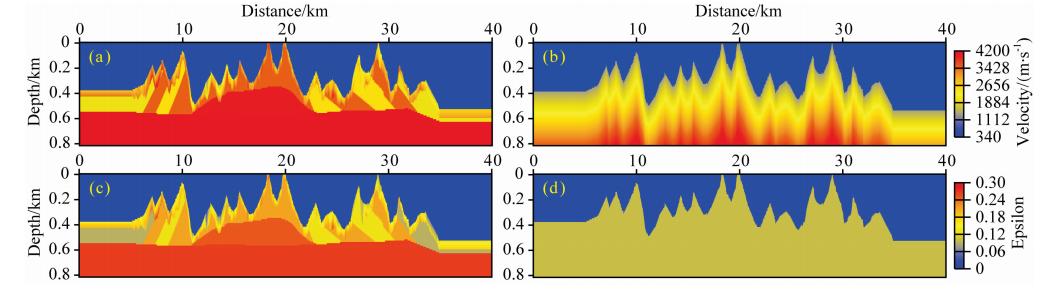 | 图 6 二维复杂起伏地表真实速度模型(a),初始速度模型(b),真实ε模型(c),初始ε模型(d) Fig. 6 2D complex near-surface topographic model. Real velocity(a),initial velocity(b),real ε(c),initial ε(d) |
模型离散为4001×61个网格,离散间隔为10 m× 10 m,速度从1800 m·s-1变化到4000 m·s-1. 为了提高覆盖率,采用非规则观测系统.第一个炮点位 于水平方向0 m处,炮点间隔50 m,检波点间隔10 m,共模拟800炮.单边放炮,两边接收.最大偏移距5000 m,最小偏移距0 m.初始速度模型为从地表1500 m·s-1开始的梯度模型,ε初始模型为0.1的均匀模型.采用上述两步法得到的反演结果如图 7、图 8所示.
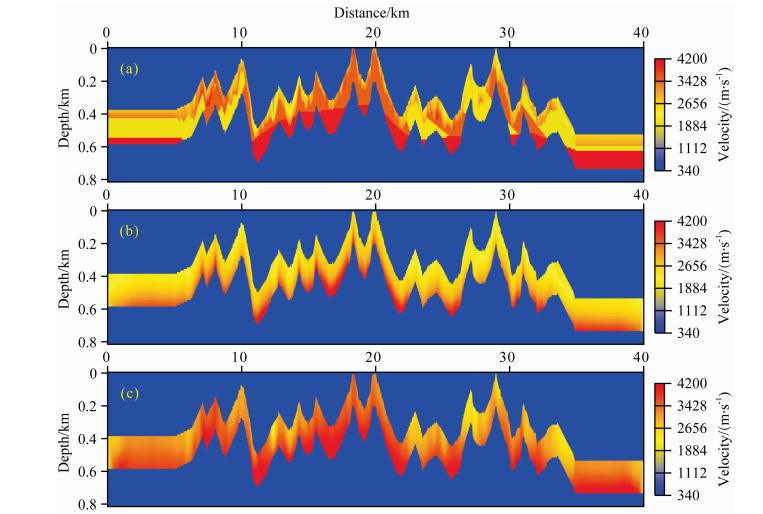 | 图 7 地表以下200 m深度范围内的速度结构 (a)二维复杂起伏地表模型,(b)第一轮反演结果,(c)第二轮反演结果 Fig. 7 Velocity structure within 200 m in depth from surface (a)Real velocity of the above 2D complex near-surface velocity model with topography,(b)Tomographic velocity after the first round,(c)Tomographic velocity after the second round |
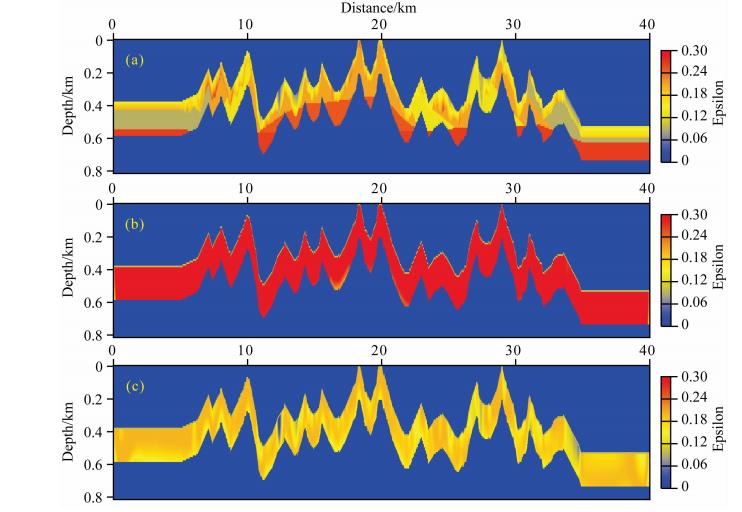 | 图 8 地表以下200 m深度范围内的ε模型 (a)二维复杂起伏地表模型,(b)第一轮反演结果,(c)第二轮反演结果. Fig. 8 Epsilon structure within 200 m in depth from surface (a)Real epsilon of the above 2D complex near-surface epsilon model with topography;(b)Tomographic epsilon after the first round;(c)Tomographic epsilon after the second round. |
为了定量分析对比两步法的反演效果,本文提取了地表以下不同深度处的速度和ε剖面.受篇幅限制,此处仅展示了地表以下40 m处的反演剖面,如图 9所示.速度剖面图 9a表明,在初始速度(红线)离真实速度(黑线)较远的情况下,第一轮速度反演结果(蓝线)在向着正确的方向收敛.应用反演策略后,第二轮的速度反演结果(绿线)更加接近真实速度,且反演精度与分辨率都得到了提高.ε剖面图 9b表明,在均匀的初始ε模型(红线)下,由于第一轮初始速度与真实速度相差较大,导致第一轮的ε反演结果(蓝线)偏离真实模型(黑线)很远,甚至更新方向完全是错误的.应用反演策略后,由于速度初始模型(第一轮速度反演结果)精度较高,第二轮的ε反演向正确的方向收敛,最终反演结果(绿线)与真实ε模型(黑线)吻合得相当好.
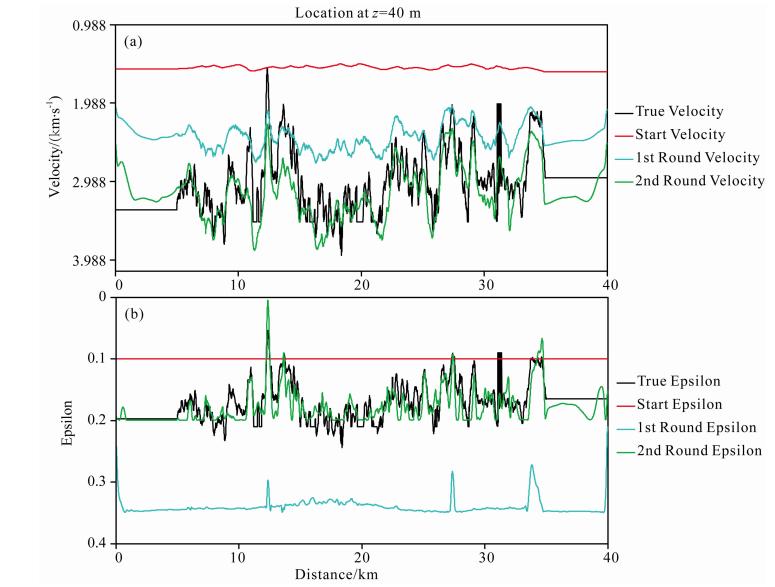 | 图 9 二维复杂起伏地表理论模型与地表下40 m深度处的速度反演剖面(a)与ε反演剖面(b) Fig. 9 Velocity(a) and Epsilon(b)sections of the real model(black),the initial model(red), and the obtained results after the first round(blue) and the second round(green)in 40 m depth beneath the surface |
为了进行三参数反演,可以将两步法策略扩展为三步法.第一步,初始模型为v0,ε0,δ0,进行三参数同步反演得到v1,ε1,δ1;第二步,将第一步反演得到的速度v1作为初始速度,其余两个参数的初始模型仍为ε0,δ0,然后进行三参数同步反演得到v2,ε2,δ2;第三步,将第二步反演结果中的v2,ε2作为初始模型,δ的初始模型依然为δ0,再进行三参数同步反演得到v3,ε3,δ3,并将其作为最终反演结果.该实验中,速度与ε的初始模型与前文简单模型两步法实验中的初始模型相同.δ的初始模型通过对真实模型平滑得到,平滑强度与构造ε初始模型时的平滑强度相同.采用上述非线性反演方法,应用第二种参数化方式及三步法策略,本文成功反演得到了v、ε和δ,如图 10所示.可以看出,经过三步反演得到了较好的v和ε.δ较初始模型无论形态还是精度上都得到了较大的提升,但与v和ε的反演效果相比,δ的反演效果较差.这可能是由δ参数物理上对走时的强烈不敏感性造成的.需要注意的是,除参数化方式与反演策略外,在寻优算法中利用更加准确的搜索方向(Liu et al., 2014)同样可以提高弱参数的反演精度,该研究成果将在后续文章中发表.
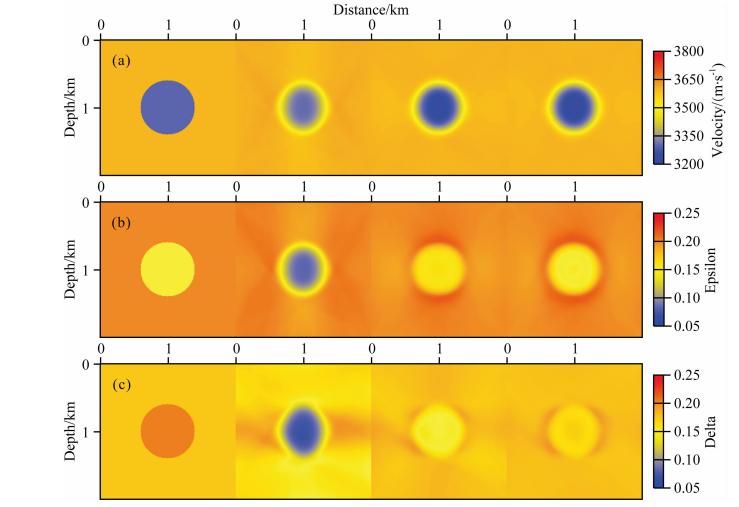 | 图 10 简单理论模型三步法.(a)速度反演结果,(b)ε反演结果,(c)δ反演结果. 从左到右分别为真实模型、第一轮反演结果、第二轮反演结果与第三轮反演结果 Fig. 10 Obtained results of v(a),obtained results of ε(b),obtained results of δ(c)with triple-round strategy by the second parameterization. The columns from left to right are the real models and the results after the first round,the second round and the third round respectively |
本文基于球谐展开表示的群速度公式,利用非线性反演算法联合反演VTI介质中的Thomsen参数.在多参数反演中,参数化非常重要.对核函数的理论分析与数值试验表明,(s0,sh,sn)的参数化方式比(s0,ε,δ)的参数化方式更适合于VTI介质多参数联合走时反演.影响反演效果的另一个因素是反演策略.本文采用两步法策略成功地反演出了v和ε,三步法策略也展示出反演所有参数的潜力.
| [1] | Bakulin A, Woodward M, Nichols D, et al. 2010. Localized anisotropic tomography with well information in VTI media. Geophysics, 75(5): D37-D45. |
| [2] | Bale R, Gratacos B, Mattocks B, et al. 2009. Shear wave splitting applications for fracture analysis and improved imaging: Some onshore examples. First Break, 27(9): 73-83. |
| [3] | Chapman C H, Pratt R G. 1992. Traveltime tomography in anisotropic media—I. Theory. Geophysical Journal International, 109(1): 1-19. |
| [4] | Crampin S. 2003. The new geophysics: Shear-wave splitting provides a window into the crack-critical rock mass. The Leading Edge, 22(6): 536-549. |
| [5] | Fowler P J. 2003. Practical VTI approximations: A systematic anatomy. Journal of Applied Geophysics, 54 (3-4): 347-367. |
| [6] | Gholami Y, Ribodetti A, Brossier R, et al. 2010. Sensitivity analysis of full waveform inversion in VTI media. 72nd EAGE Conference & Exhibition SPE. |
| [7] | Grechka V, Mateeva A. 2007. Inversion of P-wave VSP data for local anisotropy: Theory and case study. Geophysics, 72(4): D69-D79. |
| [8] | Koren Z, Ravve I, Gonzalez G, et al. 2008. Anisotropic local tomography. Geophysics, 73(5): VE75-VE92. |
| [9] | Liu Y Z, Xie C, Yang J Z. 2014. Gaussian beam first-arrival waveform inversion based on Born wavepath. Chinese J. Geophys. (in Chinese), 57(9): 2900-2909. |
| [10] | Plessix R E, Cao Q. 2011. A parametrization study for surface seismic full waveform inversion in an acoustic vertical transversely isotropic medium. Geophysical Journal International, 185(1): 539-556. |
| [11] | Pratt R G, Chapman C H. 1992. Traveltime tomography in anisotropic media—II. Application. Geophysical Journal International, 109(1): 20-37. |
| [12] | Richardson M, Ionescu G, Huang T, et al. 2008. The benefit of TTI tomography for dual azimuth data in gulf of Mexico. SEG Conference & Exhibition. |
| [13] | Sayers C M. 1995. Anisotropic velocity analysis. Geophysical Prospecting, 43(4): 541-568. |
| [14] | Sieminski A, Liu Q Y, Trampert J, et al. 2007. Finite-frequency sensitivity of surface waves to anisotropy based upon adjoint methods. Geophysical Journal International, 168(3): 1153-1174. |
| [15] | Watanabe T, Hirai T, Sassa K. 1996. Seismic traveltime tomography in anisotropic heterogeneous media. Journal of Applied Geophysics, 35(2-3): 133-143. |
| [16] | Xu G M. 2003. The Inversion Theory and Its Application (in Chinese). Beijing: Seismological Press. |
| [17] | Yang J Z, Liu Y Z, Dong L G. 2014. A multi-parameter full waveform inversion strategy for acoustic media with variable density. Chinese J. Geophys. (in Chinese), 57(2): 628-643. |
| [18] | Zhou C G, Jiao J R, Lin S, et al. 2011. Multiparameter joint tomography for TTI model building. Geophysics, 76(5): WB183-WB190. |
| [19] | 刘玉柱, 谢春, 杨积忠. 2014. 基于Born波路径的高斯束初至波波形反演. 地球物理学报, 57(9): 2900-2909. |
| [20] | 徐果明. 2003. 反演理论及其应用. 北京: 地震出版社. |
| [21] | 杨积忠, 刘玉柱, 董良国. 2014. 变密度声波方程多参数全波形反演策略. 地球物理学报, 57(2): 628-643. |
 2014, Vol. 57
2014, Vol. 57

