断层自发破裂传播问题主要是研究在应力场的作用下,断层面上滑动速率和应力状态的时空演化.为了理解这种发生在震源的物理过程以及近场强地面运动,我们通常将发生在成熟断层带的地震简化为在摩擦表面上剪切破裂的传播,并采用合适的数值方法进行模拟.自Madariaga(1976)研究圆形断层动力学破裂以来,大量有关自发破裂传播的研究已证实数值模拟是研究断层动态破裂过程行之有效的方法(Cochard and Madariaga, 1994;Fukuyama and Madariaga, 1998;Aochi et al., 2000; Day et al., 2005;Kaneko et al., 2007).
断层自发破裂过程的数值模拟需要结合摩擦定律.早期的线性滑动弱化摩擦定律(linear slip weakening friction law)(Ida,1972)是由理论推导得出,在该摩擦定律下摩擦系数随着滑动位移的增大而线性地减小;而速率状态摩擦定律(Rate- and state-dependent friction law)(Dieterich,1979;Ruina,1983)是由岩石实验观测得出的,主要描述了摩擦力随着滑动速率、滑动状态等因素变化的规律,从而可以更好地解释地震断层的摩擦性质.现今震源动力学研究多使用速率状态摩擦定律来模拟整个地震周期的断层活动(Marone,1998),包括成核(Roy and Marone, 1996)、地震断层破裂(Bizzarri and Cocco, 2005;Tinti et al., 2005)以及震后滑移(Lapusta and Liu, 2009)等过程.该摩擦定律也与断层泥(Marone et al., 1990)、小地震重复发生(Chen and Lapusta, 2009)等实际观测现象相符合.一方面,自发破裂传播对速率状态摩擦定律中本构参数a与b的变化较为敏感,不同的参数取值往往会导致破裂行为的差异.另一方面,尽管a与b在实验室条件下测定的数量级约为0.01,a-b的值多分布在-0.01~0.03之间,但岩石成分、温压、断层泥厚度等多种因素均会影响摩擦表面的性质(Marone,1998;Marone et al., 1990),使得a和b存在一定变化范围.因此,探究本构参数a、b的取值对自发破裂传播的影响有助于我们在模拟裂纹动态扩展时选择合适的参数,从而更好地了解发震时刻断层面上的物理过程.
在大部分有关速率状态摩擦定律的数值模拟研究中(Roy and Marone, 1996;Bizzarri and Cocco, 2003;Bizzarri and Cocco, 2005;Tinti et al., 2005;Kaneko et al., 2007;Chen and Lapusta, 2009;Lapusta and Liu, 2009),a与b的取值随研究者和研究目的的不同而变化.一般来说,a的取值范围分 布在0.008~0.015,而b的取值范围分布在0.012~0.019(为了控制变量个数,我们暂不讨论另一本构参数L),但是鲜有研究详细地论述本构参数a与b对破裂传播行为的影响.Bizzarri与Cocco(2003)曾讨论了二维小尺度断层切平面方向上(断层长20m),本构参数a与b对动态裂纹传播的影响,发现a的减小和b的增大会导致滑动速率峰值的增大.但基于尺度的考虑,仍需要研究三维真实断层规模(10~100 km)下的情形,以便将结论推广至地震破裂传播.
三维自发破裂传播问题属于混合边界问题,不存在解析解,因此只能依赖数值方法求解.目前自发破裂问题主要采用四种数值解法:有限差分法(Finite-Difference Method,简称FDM)(Bizzarri and Cocco, 2005;Day et al., 2005;Dalguer and Day, 2007),有限元法(Finite-Element Method,简称FEM)(蔡永恩等,1999;Oglesby et al., 2000;陈祖安等,2003;袁杰和朱守彪,2014),谱元法(Spectral Element Method,简称SEM)(Geubelle and Rice, 1995;Kaneko et al., 2007)以及边界积分法(Boundary Integral Method,简称BIM)(Cochard and Madariaga, 1994;Fukuyama and Madariaga, 1998;Fukuyama and Madariaga, 2000;Aochi et al., 2000;Chen and Zhang, 2006;刘启明和陈晓非,2008).作为一种半解析法,BIM在弹性介质自发破裂传播问题上应用广泛.BIM将求解域限制在断层面上,不需考虑边界效应(张海明,2004).此外,积分核处理了网格单元内部Green函数的空间积分,不存在离散化时的平均替代作用,因此该方法也具有计算精度高的优势.与FDM相比,BIM在较大的网格步长下就具有相同的精度.当两种方法的网格都足够精细时,它们的计算精度基本相同(Day et al., 2005).虽然BIM在研究裂纹扩展问题上具有以上优势,但在复杂介质中,Green函数的求解往往比较困难,并且积分核的计算需要对整个断层面进行Green函数的空间积分,因此计算量巨大.但在固定断层几何形状,只修改动力学参数的情况下进行大量计算时,与FDM的重新计算不同,BIM可以重复利用积分核,这样就表现出了计算效率上的优势.
本文采用BIM研究速率状态摩擦定律控制下的断层自发破裂传播问题,讨论了该摩擦定律中本构参数a和b对裂纹扩展的影响,包括滑动速率峰值,剪切应力峰值和破裂传播速度等动力学参数.
2 理论本文将断层模型简化为内插在均匀线弹性全空间中的矩形滑动不连续面.自发破裂传播问题需要在此模型下求解弹性动力学基本方程:
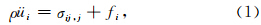
BIM根据位移表示定理(Aki and Richards, 2002),利用滑动面上位错与应力的积分来表示周围弹性介质对破裂扩展的影响,不需处理介质内部的波动传播.这种积分包含断层面上的牵引力与Green函数的时空卷积.如果考虑频率域,该积分只包含牵引力与Green函数的空间卷积.BIM的计算困难在于确定积分中与Green函数相关的积分核,由于复杂介质中理论Green函数难以求出,因此该方法较适于简单弹性介质.但是随着理论推导和运算能力的提高,边界积分方程法也可适用于半空间(Chen and Zhang, 2006;Zhang and Chen, 2006)、孔隙介质(Dunham and Rice, 2008)以及分支断层(Aochi et al., 2000)等多种复杂介质和复杂断层模型.
忽略体力后频率域中的位移表示定理如下:
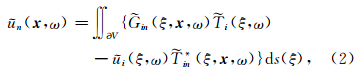
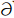 V为研究区域的边界,n为断层滑动方向,ξ为边界上源点坐标,x 为介质内部场点坐标,是表示Green函数的二阶张量,
V为研究区域的边界,n为断层滑动方向,ξ为边界上源点坐标,x 为介质内部场点坐标,是表示Green函数的二阶张量,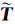 *是Green函数在边界上的牵引力,
*是Green函数在边界上的牵引力,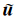 ,
,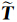 是边界滑动量及其牵引力.代入齐次边界条件,并利用Green函数的空间互易性和连续性以及剪切破裂中水平牵引力在位移间断面的连续性,可以得到
是边界滑动量及其牵引力.代入齐次边界条件,并利用Green函数的空间互易性和连续性以及剪切破裂中水平牵引力在位移间断面的连续性,可以得到
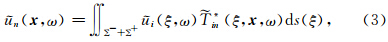
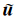 关于 x 求m方向上的偏导,并将与Green函数所对应的断层面牵引力代入右侧,就可以得到BIM的计算公式
关于 x 求m方向上的偏导,并将与Green函数所对应的断层面牵引力代入右侧,就可以得到BIM的计算公式
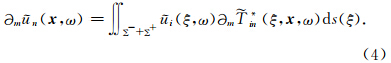
断层上下两盘发生相对滑动时阻碍滑动的摩擦力可用速率状态摩擦定律描述.该定律由滑动速率在10-8~10-3m·s-1下岩石摩擦实验的结果拟合而成(Marone et al., 1990;Marone,1998),现已广泛地应用在震源动力学数值模拟上(Bizzarri and Cocco, 2005;Liu and Rice, 2005;Tinti et al., 2005;Kaneko et al., 2007;Chen and Lapusta, 2009).速率状态摩擦定律认为剪切应力会受到滑动速率与状态变量的影响,包括瞬时速率突变的直接影响和状态变量的长期影响.该类摩擦定律有多种形式,本文研究选取格式较简洁并且最符合实验结果的 Dieterich-Ruina定律(Dieterich,1979;Ruina,1983):
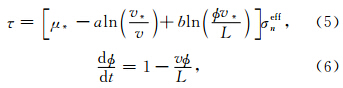
当滑动处于稳定状态时,状态变量记作φss,满足 =0:
=0:
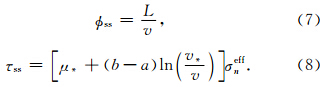
在速率状态摩擦定律中,滑动速率的突变会导致摩擦系数的突变,而且二者正相关,这种阻碍速率突变的直接效应受控于参数a.突变后如果滑动速率保持恒定,摩擦系数也会逐渐趋向平稳,这种长期演化效应又被称为稳定状态速率依赖性,这种依赖性可正可负,受控于a-b的值.a-b控制着摩擦滑动的稳定性.当a-b<0,高速稳定状态的摩擦系数要低于低速时的,即滑动遵循速率弱化摩擦,从而产生黏滑.反之,a-b>0对应的是稳定滑动即蠕滑.发震时,破裂迅速在断层上的传播可看作黏滑,因此通常情况下,主破裂区域a-b<0.
3 数值算法 3.1 边界积分法的算法实现整理式(4)可得滑动面动剪切应力,将全空间Green函数代入后利用箱状离散法(Fukuyama and Madariaga, 1998)进行时空离散得到
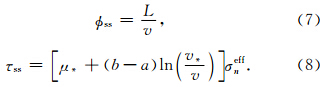
当空间网格步长Δs与时间步长Δt满足wα=vPΔt/Δs<1/2时,同一时刻相邻网格间无相互影响,(9)式右侧求和项中的瞬时项(n=k)只剩同位单元Cijk;ijk1vlmn1,因此绝对剪切应力τ(abs)31可以表示为(张海明,2004)
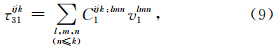
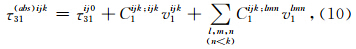
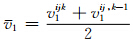 代替可得
代替可得


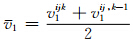 ,以同样的方法计算出k+1时刻的vij,k+11,τ(abs)ij,k+11后,循环计算直至达到最大时刻第kmax步,计算结束.
3.2 高频振荡的抑制
,以同样的方法计算出k+1时刻的vij,k+11,τ(abs)ij,k+11后,循环计算直至达到最大时刻第kmax步,计算结束.
3.2 高频振荡的抑制 作为半解析方法,BIM的理论公式在其假设条件下是严格成立的,但处理自发破裂问题时需要对断层进行网格剖分,并认为同一网格内速度均匀.将连续的积分转为离散的加权求和可能会引入计算误差,随着计算误差的积累,最终出现滑动速率的高频振荡.这种高频振荡会降低计算结果的收敛性.图 1是断层上具有代表性的某网格及其相邻网格的滑动速率,即v1(i,j,k)与v1(i-1,j,k),v1(i+1,j,k)随时间k的变化.
边界积分方程法的发散性主要源自对断层的简 单离散化,但很难定量地解释(Tada and Madariaga, 2001). 图 1右上角的小图是大图中黑色框所示位置的放大,观察可知当某网格的滑动速率波动时,其相邻网格往往会出现相位差为π/2的波动,最终,单个网格的微小波动造成整个断层面计算结果的高频振荡.
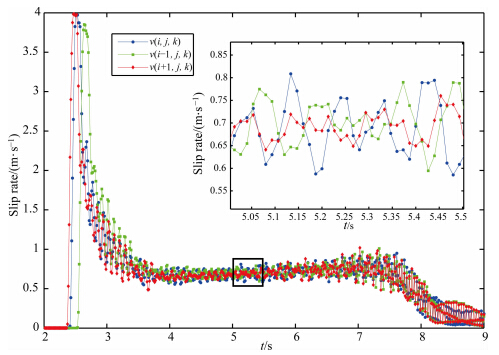 | 图 1 无高斯滤波时相邻三点滑动速率随时间变化Fig. 1 Slip rate evolutions at three neighboring points without Gaussian filtering |
假设这种高频振荡具有高斯噪音的成分,类似FDM利用黏性阻尼项来压制数值计算的发散(Dalguer and Day, 2007),我们利用高斯滤波来抑制这种振荡.振荡多发生在滑动速率到达峰值之后,因此在减速过程中,本文对k时刻的vijk1与其相邻的8个网格加权平均(在断层边界处不对网格进行处理)后得到滤波后的vijkfilter:
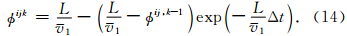
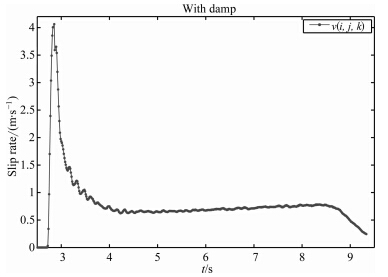 | 图 2 采用高斯滤波后同一点(i,j)的滑动速率变化Fig. 2 The slip rate evolution at the same point(i,j)processed by Gaussian filter |
自发破裂问题缺乏解析解,只能通过对比不同数值方法的模拟结果来验证其精确性(Day et al., 2005).南加州地震中心(Southern California Earthquake Center简称SCEC)发布一系列自发破裂数值模拟代码验证工具.通过对比其他研究者利用FDM、FEM、SEM等方法模拟的结果,可以验证本文程序的可靠性.
本小节采用SCEC验证工具中的TPV101计算模型(http://scecdata.usc.edu/cvws/[2014-02-15]),断层规模为30 km×15 km,主破裂区a=0.008,b=0.012,其他主要动力学参数如表 1所示.
| 表 1 TPV101模型动力学参数及初始状态(http://scecdata.usc.edu/cvws/)Table 1 Dynamic parameters and initial state of model TPV101 |
表 1中ρ为介质密度,vP为P波波速,γ为泊松比,μ*是速率状态摩擦定律中参考摩擦系数,v*是参考滑动速率,L为特征长度,v0是断层初始滑 动速率,σn为断层面上的压应力,τ0为初始剪切应力.
断层面上破裂传播速度对地震信号影响较大,因此破裂前锋的到达时间成为验证数值模拟可靠性的指标之一.遵循前人的惯例,选取滑动速率首次达到1.0 mm·s-1为破裂前锋到达.
图 3源自SCEC验证工具中的TPV101基准测试程序,以0.5 s为间隔绘制破裂前锋到达时间的等值线.本文在其上添加由BIM给出的结果,图 3中蓝线所示.
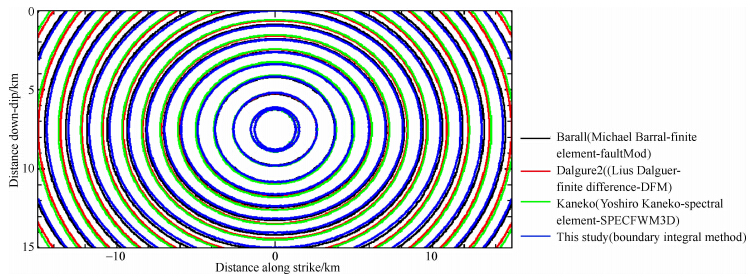 | 图 3 破裂前锋等值线图(FEM,FDM,SEM,BIM),背景图引自http://scecdata.usc.edu/cvws/cgi-bin/cvws.cgiFig. 3 Contours of the arriving time of rupture frontier,given by FEM,FDM,SEM and BIM,the background image is from http://scecdata.usc.edu/cvws/cgi-bin/cvws.cgi |
由图 3可知,不同数值方法模拟出来的破裂传播速率略有不同,但都约等于Rayleigh波波速.本 文BIM程序给出的破裂前锋等值线图与有限元法(图 3中的黑线)给出的结果类似,验证了该程序的可靠性.
4 模型实例与分析本文将模拟不同本构参数a和b下断层的自发破裂传播过程.图 4为断层模型图:矩形平面断层位于线弹性全空间内,断层中央的速率弱化区为主破裂区(a-b<0),在过渡带中,参数a逐渐增大至最外围的速度强化区(a-b>0).通过在半径为3 km的成核区添加随时空连续变化的剪切应力扰动来模拟断层成核过程.由于a=0.011,b=0.014时,破裂仅分布在成核区周围,因此,为便于讨论,选择断层坐标(1.5 km,10 km)为观测点,重点研究该点滑动速率峰值vpeak,剪切应力峰值τpeak,以及破裂传播速度Vrupture对应不同a,b的变化特征.
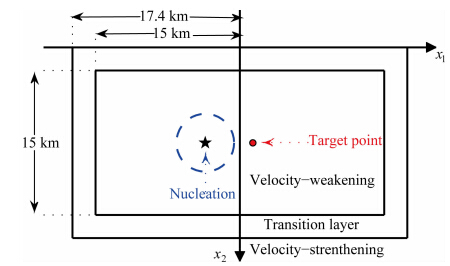 | 图 4 断层模型图Fig. 4 Sketch of a fault model |
本研究假定应力降与断层滑动方向均沿着x1 方向.初始时刻,断层位于稳定状态,以速度v0滑 动,剪切应力τ0在成核区外分布均匀,状态变量τ0随着本构参数a和b的变化而变化.介质参数及初始参量见表 2.考虑到实验室实测结果(Blanpied et al., 1991;Marone,1998),在本研究中,选取a的变 化范围为0.008~0.011,b的变化范围为0.12~0.016.
| 表 2 模型动力学参数及初始状态Table 2 Dynamic parameters and initial state of the model adopted by this study |
在速率状态摩擦定律中,参数a代表状态变量保持恒定时 由滑动速率v突变所导致的摩擦系数的瞬时变化.当地震发生时,滑动速率迅速增至1 m·s-1,甚至更高,因此我们推断a的取值对破裂传播中的速度突变有较大影响.b的取值固定为0.014,a的取值分别为0.008、0.009、0.010、0.011.为了方便讨论,将观测点滑动速率最大值记为vpeak,破裂传播稳定后断层接近匀速滑动时的速率为v2,剪切应力峰值记为τpeak,等效动摩擦力记为τf.
破裂前锋到达观测点后,滑动速率迅速上升至最大值vpeak,后下降至保持匀速滑动,直至由边界反射回来的停止震相使得滑动停止.图 5c表明vpeak和v2均会随着a值的增大而减小.需要注意的是,在本文模型中,当a=0.011,b=0.014时,虽然观测点发生了滑动,但破裂很快就停止在成核区附近,其破裂持续时间较短,滑动速率曲线比较平缓.
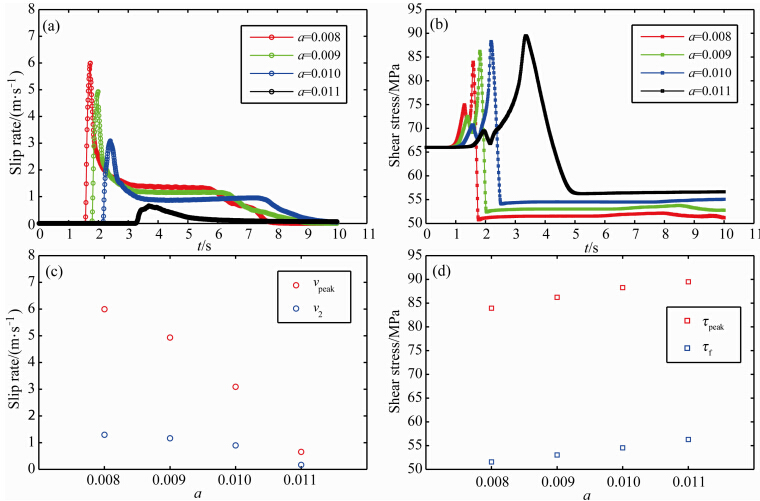 | 图 5 当参数b=0.014时,(a)滑动速率随时间的变化,(b)剪切应力随时间的变化,(c)不同a值下的vpeak与v2,(d)不同a值下的τpeak和τfFig. 5 When b=0.014,(a)the evolution of slip rate,(b)the evolution of shear stress,(c)vpeak and v2 with different value of a,(d)τpeak and τf with different a |
在破裂初期,成核区的应力扰动使剪切应力出现小范围的波动.破裂前锋到达时,由于速度的骤升,τ也开始快速增加直至剪切应力峰值τpeak,随后下降直至等效动摩擦力τf.图 5d说明τpeak和τf均随着a增大而增大.对比图 5a与5b发现τpeak通常出 现在滑动速率v增加较快的时刻,而vpeak往往出现在τ从τpeak减小至τf的过程中.
a的不同也会导致破裂传播速度Vrupture变化.图 6表明Vrupture随着a的增大而减小.通过模拟我们发现Vrupture在断层上的分布不均匀,破裂沿着滑动方向传播较快.除成核区外,本文模拟并未出现超剪切破裂现象(Madariaga and Olsen, 2000;张海明,2004;Kaneko et al., 2007).
 | 图 6 当参数b=0.014时不同a值下的破裂传播速度VruptureFig. 6 When b=0.014,the propagation speed of rupture with different value of a |
通过上述模拟结果,可以证实我们有关a对裂 纹扩展作用的推论.在岩石材料乃至金属材料中,a>0,当滑动速率突然增大时,由a控制的直接作用使摩擦系数也突然增加.因此a越大,τpeak也就越大,从而加强了摩擦力对滑动的阻碍作用,使得vpeak减 小.当破裂前锋到达后,滑动会逐渐趋于稳定状 态.由(8)式可知τf和应力降的大小取决于(b-a)ln(v*/v)σeffn 的值,所以当b-a越大时,τf越小,应力降Δτ也就越大.(b-a)σeffn远大于0有利于应力降的突然释放和强地震的发生,强破裂区往往是速率弱化较剧烈的区域(Boatwright and Cocco, 1996),因此我们认为破裂区(b-a)σeffn的值与滑动速率峰值和应力降呈正相关.相关动力学模拟表明破裂传播速度会随着滑动速率的增大而增大(Bizzarri,2012),所以当b保持恒定时,破裂传播速度会随着a的减小而增大.
4.2 本构参数b的影响速率状态摩擦定律中的状态变量将摩擦系数与滑动历史联系起来,而参数b表征了状态变量驱使滑动向稳定状态演化的作用.为了研究b对断层滑动的影响,我们固定a=0.010,分别研究b=0.016、0.015、0.014、0.013时自发破裂的传播.
滑动速率随时间的演化规律如4.1节所述.图 7表明vpeak和v2随着b的增大而增大.破裂持续 时间由停止震相控制,破裂传播速度越小,停止震相 越晚出现,因此当a=0.010,b=0.013时,断层以v2≈0.6 m·s-1的速度滑动较长时间.剪切应力峰值τpeak虽然有随着b增大而增大的趋势,但并不敏感;τf会随着b的增大而减小,应力降Δτ与之相反.
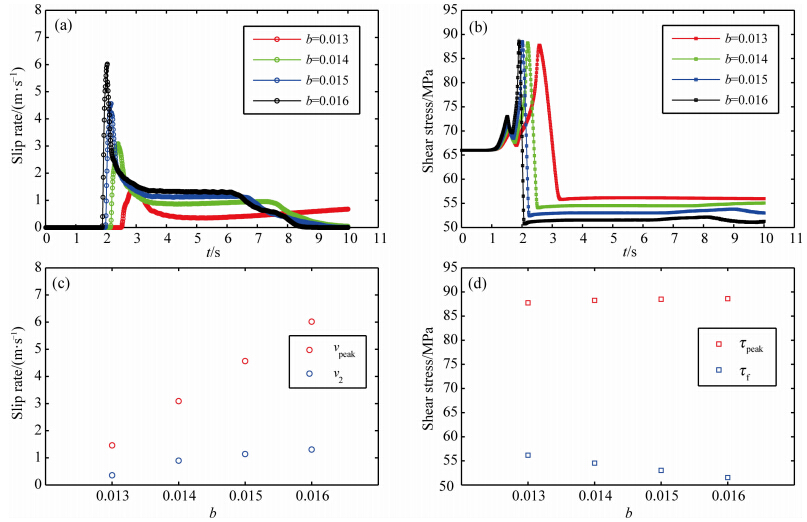 | 图 7 当参数a=0.010时,(a)滑动速率随时间的变化,(b)剪切应力随时间的变化,(c)不同b值下的vpeak与v2,(d)不同b值下的τpeak和τfFig. 7 When a=0.010,(a)the evolution of slip rate,(b)the evolution of shear stress,(c)vpeak and v2 with different value of b,(d)τpeak and τf with different b |
b也会影响破裂传播速度Vrupture,图 8表明Vrupture随着b的减小而减小.破裂从应力扰动的成核区向四周扩展,传播速度从成核区的高速逐渐减低,后随着破裂的扩展而逐渐升高直至破裂前锋达到断层边缘.
 | 图 8 当参数a=0.010时,不同b值下的破裂传播速度VruptureFig. 8 When a=0.010,the propagation speed of rupture with different value of b |
b作用于速率状态摩擦定律中状态变量相关的项bln(v*/L).起初,状态变量由于v的增加而迅速减小,使得bln(v*/L)的值为负,此时剪切应力会在状态变量的降低中逐渐减小.因此,在状态变量快速下降之后,b值越大,剪切应力越小,即对滑动的阻碍作用也越小,滑动速率v,包括vpeak和v2,均会随着的b值的增大而增大.
4.3 a-b的影响(b-a)σeffn是影响滑动稳定性的主要因素,滑动速率峰值vpeak、应力降Δσ以及破裂传播速度均随着(b-a)σeffn的增大而增大.在速度状态摩擦定律中,(b-a)σeffn是否是控制断层破裂行为的唯一因素?为了回答这个问题,我们分别模拟了(b-a)σeffn=0.4 MPa的四种情况:a=0.008,b=0.012;a=0.009,b=0.013;a=0.010,b=0.014以及a=0.011,b=0.015.
图 9表明vpeak和v2会随着a、b具体取值变化而变化.在b-a相同的条件下,a、b的取值越大,vpeak和v2的值越小.因此,滑动速率的演化依赖于速率状态摩擦定律中的参数a和b的单独取值.
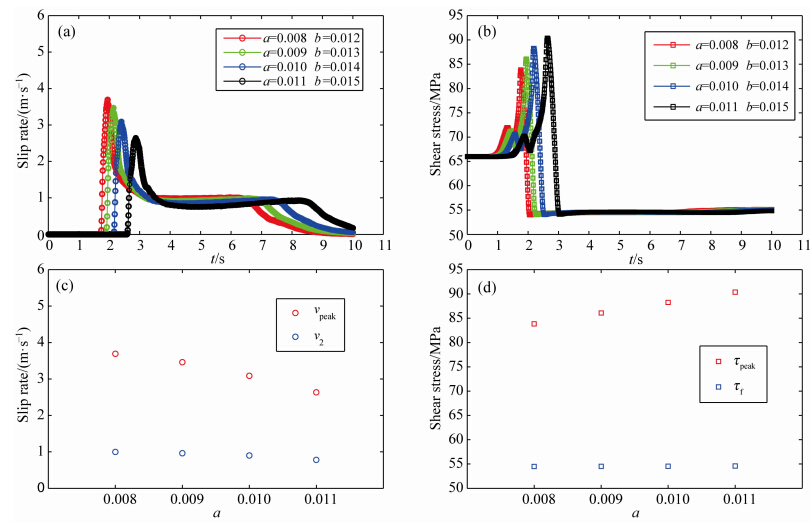 | 图 9 当b-a=0.004时,(a)滑动速率随时间的变化,(b)剪切应力随时间的变化,(c)同一(b-a)值下的vpeak与v2,(d)同一(b-a)值下的τpeak和τfFig. 9 When b-a=0.004,(a)The evolution of slip rate,(b)The evolution of shear stress,(c)vpeak and v2 with same value of (b-a),(d)τpeak and τf with different value of (b-a) |
尽管b-a的值相同,但表征速度变化作用的参数a却不相同,受a控制的τpeak会随着a和b的增大而增大,但受(b-a)σeffn影响的等效动摩擦应力τf和应力降Δσ均不变.
图 10说明尽管b-a相同,也可能出现不同的破裂传播速度Vrupture.a和b的值越小,破裂传播速度越大.这一点也可通过对比图 6中a=0.011,b=0.014的模拟结果与图 8中a=0.010,b=0.013的模拟结果来验证:前者破裂从成核区出发后扩展了一定距离便停止传播,而后者的破裂触发了整个断层面的滑动.
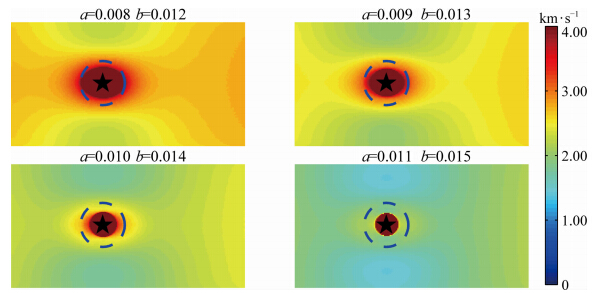 | 图 10 相同(b-a)下的破裂传播速度Fig. 10 The propagation speed of rupture with the same value of(b-a) |
本小节说明(b-a)σeffn并非是影响自发破裂的唯一因素,a和b对破裂扩展区域、滑动速率和剪切应力的演化过程都有影响.综合4.1节和4.2节的结论,我们认为(b-a)σeffn决定等效动摩擦力τf和应力降Δτ的大小,该值越大,断层越容易发生黏滑,从而辐射出巨大的地震波能量,但在同一(b-a)σeffn下,发生滑动的面积有可能不同.即使破裂扩展区域相同,滑动速率峰值vpeak、剪切应力峰值τpeak和破裂传播速度Vrupture也有所不同,通常vpeak和Vrupture同a的大小呈负相关,而τpeak与之呈正相关.
5 结论本文利用BIM实现了对速率状态摩擦定律下断层自发破裂传播问题的模拟,采用高斯滤波压制了由数值计算引起的高频振荡,并通过与SCEC发布的代码验证工具的对比验证了算法的正确性.本文以均匀全空间中平面断层为模型,从滑动速率演化、剪切应力演化以及破裂传播速度等多个方面研究了速率状态摩擦定律中参数a和b对破裂传播的影响.数值模拟结果表明,(b-a)σeffn控制着等效动摩擦应力和发震前后的应力降,参数a对剪切应力峰值影响较大,而参数b表征着状态变量的演化对摩擦力的影响.滑动速率峰值、平均错距及破裂传播 速度通常随着a的减小而增大,随着b的减小而减小.
致谢 感谢Bizzarri Andrea教授的讨论与帮助.感谢两位匿名审稿人提出的建设性修改意见.| [1] | Aki K, Richards P G. 2002. Quantitative Seismology. Sausalito: University Science Books. |
| [2] | Aochi H, Fukuyama E, Matsuura M. 2000. Spontaneous rupture propagation on a non-planar fault in 3-D elastic medium. Pure and Applied Geophysics, 157(11-12): 2003-2027, doi: 10.1007/PL00001072. |
| [3] | Bizzarri A, Cocco M. 2003. Slip-weakening behavior during the propagation of dynamic ruptures obeying rate and state dependent friction laws. Journal of Geophysical Research, 108(B8), doi: 10.1029/2002JB002198. |
| [4] | Bizzarri A, Cocco M. 2005. 3D dynamic simulations of spontaneous rupture propagation governed by different constitutive laws with rake rotation allowed. Annals of Geophysics, 48(2): 279-299, doi: 10.4401/ag-3201. |
| [5] | Bizzarri A. 2012. Rupture speed and slip velocity: what can we learn from simulated earthquakes? Earth and Planetary Science Letters, 317-318: 196-203, doi: 10.1016/j.epsl.2011.11.023. |
| [6] | Blanpied M L, Lockner D A, Byerlee J D. 1991. Fault stability inferred from granite sliding experiments at hydrothermal conditions. Geophysical Research Letters, 18(4): 609-612, doi: 10.1029/91GL00469. |
| [7] | Boatwright J, Cocco M. 1996. Frictional constraints on crustal faulting. Journal of Geophysical Research, 101(B6): 13895-13909, doi: 10.1029/96JB00405. |
| [8] | Cai Y E, He T, Wang R. 1999. Modelling the source dynamic process of the 1976 Tangshan earthquake. Acta Seismologica Sinica (in Chinese), 21(5): 469-477. |
| [9] | Chen T, Lapusta N. 2009. Scaling of small repeating earthquake explained by interaction of seismic and aseismic slip in a rate and state fault model. Journal of Geophysical Research, 114(B1): B01311, doi: 10.1029/2008JB005749. |
| [10] | Chen X F, Zhang H M. 2006. Modelling rupture dynamics of a planar fault in 3-D half space by boundary integral equation method: an overview. Pure and Applied Geophysics, 163(2-3): 267-299, doi: 10.1007/s00024-005-0020-z. |
| [11] | Chen Z A, Bai W M, Lin B H, et al. 2003. Numerical simulation for rupture processes of a series of strong earthquakes (Ms>7) in North China since 1966. Chinese Journal of Geophysics (in Chinese), 46(3): 373-381. |
| [12] | Cochard A, Madariaga R. 1994. Dynamic faulting under rate-dependent friction. Pure and Applied Geophysics, 142(3-4): 420-445, doi: 10.1007/BF00876049. |
| [13] | Dalguer L A, Day S M. 2007. Staggered grid split node method for spontaneous rupture simulation. Journal of Geophysical Research, 112(B2): B02302, doi: 10.1029/2006JB004467. |
| [14] | Day S M, Dalguer L A, Lapusta N, et al. 2005. Comparison of finite difference and boundary integral solutions to three-dimensional spontaneous rupture. Journal of Geophysical Research, 110(B12): B12307, doi: 10.1029/2005JB003813. |
| [15] | Dieterich J H. 1979. Modeling of rock friction 1. Experimental result and constitutive equations. Journal of Geophysical Research, 84(B5): 2161-2168, doi: 10.1029/JB084iB05p02161. |
| [16] | Dieterich J H, Kilgore B D. 1994. Direct observation of frictional contacts new insights for state-dependent properties. Pure and Applied Geophysics, 143(1-3): 283-302, doi: 10.1007/BF00874332. |
| [17] | Dunham E M, Rice J R. 2008. Earthquake slip between dissimilar poroelastic material. Journal of Geophysical Research, 113: B09304, doi: 10.1029/2007JB005405. |
| [18] | Fukuyama E, Madariaga R. 1998. Rupture dynamics of a planar fault in a 3D elastic medium: rate- and slip- weakening friction. Bulletin of the Seismological Society of America, 88(1): 1-17. |
| [19] | Fukuyama E, Madariaga R. 2000. Dynamic propagation and interaction of a rupture front on a planar fault. Pure and Applied Geophysics, 157(11-12): 1959-1979, doi: 10.1007/PL00001070. |
| [20] | Geubelle P H, Rice J R. 1995. A spectral method for three-dimensional elastodynamic fracture problems. Journal of the Mechanics and Physics of Solids, 43(11): 1791-1824, doi: 10.1016/0022-5096(95)00043-I. |
| [21] | Ida Y. 1972. Cohesive force across the tip of a longitudinal-shear crack and Griffith's specific surface energy. Journal of Geophysical Research, 77(20): 3796-3805, doi: 10.1029/JB077i020p03796. |
| [22] | Kaneko Y, Lapusta N, Ampuero J P. 2007. Spectral-element modeling of spontaneous earthquake rupture on rate and state faults: effect of velocity-strengthening friction at shallow depths. Journal of Geophysical Research, 113: B09317, doi: 10.1029/2007JB005553. |
| [23] | Lapusta N, Liu Y. 2009. Three-dimensional boundary integral modeling of spontaneous earthquake sequence and aseismic slip. Journal of Geophysical Research, 114: B09303, doi: 10.1029/2008JB005934. |
| [24] | Liu Q M, Chen X F. 2008. Study on the meshing scheme in the computation of spontaneous faultrupture process. Acta Seismologica Sinica (in Chinese), 30(5): 449-455. |
| [25] | Liu Y J, Rice J R. 2005. Aseismic slip transient emerge spontaneously in three dimensional rate and state modeling of subduction earthquake sequences. Journal of Geophysical Research, 110(B8): B08307, doi: 10.1029/2004JB003424. |
| [26] | Madariaga R. 1976. Dynamics of an expanding circular fault. Bulletin of the Seismological Society of America, 66(3): 639-666. |
| [27] | Madariaga R, Olsen K B. 2000. Criticality of rupture dynamics in 3-D. Pure and Applied Geophysics, 157(11): 1981-2001, doi: 10.1007/PL00001071. |
| [28] | Marone C, Raleigh C B, Scholz C H. 1990. Frictional behavior and constitutive modeling of simulated fault gouge. Journal of Geophysical Research, 95(B5): 7007-7025, doi: 10.1029/JB095iB05p07007. |
| [29] | Marone C. 1998. Laboratory-derived friction laws and their application to seismic faulting. Annual Review of Earth and Planetary Sciences, 26(1): 643-696, doi: 10. 1146/annurev. earth. 26. 1.643. |
| [30] | Oglesby D D, Archuleta R J, Nielsen S B. 2000. The three-dimensional dynamics of dipping faults. Bulletin of the Seismological Society of America, 90(3): 616-628, doi: 10.1785/0119990113. |
| [31] | Roy M, Marone C. 1996. Earthquake nucleation on model faults with rate- and state- dependent friction: effect of inertia. Journal of Geophysical Research, 101(B6): 13919-13932, doi: 10.1029/96JB00529. |
| [32] | Ruina A. 1983. Slip instability and state variable friction laws. Journal of Geophysical Research, 88(B12): 10359-10370, doi: 10.1029/JB088iB12p10359. |
| [33] | Tada T, Madariaga R. 2001. Dynamic modelling of the flat 2D crack by a semi-analytic BIEM scheme. International Journal for Numerical Methods in Engineering, 50: 227-251. |
| [34] | Tinti E, Bizzari A, Cocco M. 2005. Modeling the dynamic rupture propagation on heterogeneous faults with rate and state dependent friction. Annals of Geophysics, 48(2): 327-345, doi: 10.4401/ag-3205. |
| [35] | Yuan J, Zhu S B. 2014. FEM simulation of the dynamic processes of fault spontaneous rupture. Chinese Journal of Geophysics (in Chinese), 57(1): 138-156, doi: 10.6038/cjg20140113. |
| [36] | Zhang H M. 2004. Theoretical study on the spontaneous propagation of 3D seismic rupture on a planar fault in half space . Beijing: Peking University. |
| [37] | Zhang H M, Chen X F. 2006. Dynamic rupture on a planar fault in three-dimensional half space-I. Theory. Geophysical Journal International, 164(3): 633-652, doi: 10.1111/j.1365-246X.2006.02887.x. |
| [38] | 蔡永恩, 何涛, 王仁. 1999. 1976年唐山地震震源动力过程的数值模拟. 地震学报, 21(5): 469-477. |
| [39] | 陈祖安, 白武明, 林邦慧等. 2003. 1966年以来华北地区一系列七级大震破裂过程的数值模拟. 地球物理学报, 46(3): 373-381. |
| [40] | 刘启明, 陈晓非. 2008. 计算断层自发破裂过程的离散网格划分研究. 地震学报, 30(5): 449-455. |
| [41] | 袁杰, 朱守彪. 2014. 断层自发破裂动力过程的有限单元法模拟. 地球物理学报, 57(1): 138-156, doi: 10.6038/cjg20140113. |
| [42] | 张海明. 2004. 半无限空间中平面断层的三维自发破裂传播的理论研究. [博士论文]. 北京: 北京大学地球与空间科学学院. |
 2014, Vol. 57
2014, Vol. 57


