地球物理学报  2014, Vol. 57 Issue (10): 3117-3128   PDF    
引用本文
王正涛, 超能芳. 2014. 利用SWARM卫星高低跟踪探测格陵兰岛时变重力信号. 地球物理学报, 57(10): 3117-3128, doi: 10.6038/cjg20141003   
WANG Zheng-Tao, CHAO Neng-Fang. 2014. Time-variable gravity signal in Greenland revealed by SWARM high-low Satellite-to-Satellite Tracking. Chinese J. Geophysics, 57(10): 3117-3128, doi: 10.6038/cjg20141003   
利用SWARM卫星高低跟踪探测格陵兰岛时变重力信号
王正涛1,2, 超能芳1    
1. 武汉大学测绘学院, 武汉 430079;
2. 武汉大学地球空间环境与大地测量教育部重点实验室, 武汉 430079
投稿时间:2013-12-24    最后修改时间: 2014-9-9 .
基金项目：国家重点基础研究发展计划(973计划)项目(2013CB733301),国家自然科学基金项目(41274032,41474018)资助.
作者简介：王正涛, 1976年生, 博士生导师、副教授, 主要从事物理大地测量学、卫星大地测量学、地磁学等方面的研究. E-mail:ztwang@whu.edu.cn
摘要：GRACE重力卫星任务即将结束,后续GRACE Follow-On卫星计划于2017年发射,在此期间,迫切需要一个新的卫星计划继续对全球时变重力场进行连续监测,以保证时变重力场信息时间序列的连贯性.SWARM计划包括三颗轨道高为300~500 km的近极轨卫星星座,类似于三颗CHAMP卫星,具有接替时变重力场探测的潜力.本文首先分析SWARM(模拟)、CHAMP、GRACE反演至60阶时变重力场球谐系数的误差特性及不同高斯平滑半径对高频误差的抑制效果,然后分别利用SWARM、CHAMP、GRACE的时变重力场模型恢复全球质量变化,结果表明,SWARM模拟观测数据的高频误差低于CHAMP观测数据,探测时变重力场的整体精度优于CHAMP,略低于GRACE探测精度;其次,对比2003年1月—2009年12月期间CHAMP(hl-SST)和GRACE(ll-SST)时变重力场模型反演格陵兰岛冰盖质量变化趋势,结果显示,CHAMP数据得到格陵兰岛冰盖质量变化趋势为-50.2±2.0 Gt/a,GRACE所得结果为-41.2±1.6 Gt/a,两者相差21.8%;最后,对比2000年1月—2004年12月间SWARM模拟数据和"真实"模型数据反演的格陵兰岛冰盖质量变化趋势,结果表明,两者相差19.2%.本文研究表明,利用SWARM hl-SST数据探测时变重力场可以达到20%相对精度水平,有潜力用于填补GRACE和GRACE Follow-On期间探测地球时变重力场的空白.
关键词： 时变重力     格陵兰岛     GRACE     SWARM     高低卫星跟踪    
Time-variable gravity signal in Greenland revealed by SWARM high-low Satellite-to-Satellite Tracking
WANG Zheng-Tao1,2, CHAO Neng-Fang1    
1. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China
Abstract: Amid a termination of the Gravity Recovery and Climate Experiment (GRACE) mission and before the launch of GRACE Follow-On (in 2017), There is an urgent need to have a new satellite for continuous monitoring the global time variable gravity field. SWARM mission, which has three satellites, will orbit Earth at an altitude of 300~500 km on near-polar and near-circular trajectories. This mission shares similarity to that of CHAllenging Minisatellite Payload (CHAMP) mission, and hence, capable of continuous monitoring of the global time variable gravity field. In this paper, we first analyze the error characteristics of the spherical harmonic coefficients up to degree 60 of the variable gravity field and investigate the effect of different Gaussian smoothing radii on the higher degree frequency error for SWARM simulation, CHAMP and GRACE data, followed by inversion of the global mass change from the time variable gravity field model of SWARM, CHAMP, and GRACE data. It shows that the error in the higher degree of SWARM is lower than that CHAMP with the inversion result better than that of CHAMP, while worse than that of GRACE; Second, we get the ice mass loss during January 2003 and December 2009 over the entire of Greenland from CHAMP is -50.2±2.0 Gt/a, whereas -41.2±1.6 Gt/a from GRACE. Their trends differ by 21.8% whereas the trend between SWARM simulation and ‘True’ model over the entire of Greenland differ by 19.2% only. Based on the above result, we conclude that SWARM hl-SST can be detected to the time-variable gravity signal in the 20% relative accuracy level and retrieve time-variable gravity information in the absence of the GRACE twin satellites, and before the launch of GRACE Follow-On.
Key words: Time-variable gravity     Greenland     GRACE     SWARM     hl-SST    
1 引言

GRACE(Gravity Recovery and Climate Experiment)低-低卫星跟踪卫星(ll-SST)任务成功实施，首次实现了高精度高时间分辨率时变重力场探测(Tapley et al.，2004).GRACE任务到目前为止已经连续运行了十二年，获得了丰富的观测资料，极大地提高了人们对气候系统中各个方面(大气、海洋、陆地水和冰雪圈等)质量分布变化的认识，推进了以下领域的研究：全球水循环和陆地水文(胡小工等，2006；杨元德等，2009)、两极冰盖和山岳冰川质量平衡、海水质量及全球海平面变化等，是当今研究全球气候变化取得的重大进展.

GRACE卫星运行已超预期寿命，根据目前载荷运行状态，估计尚可延续至2014或2015年，GRACE后续卫星(GRACE Follow-On)计划于2017年发射(Watkins et al.，2013)，将存在三年左右时变重力场探测空挡.

2013年11月22日，欧洲空间局(ESA)成功发 射了一个地球观测卫星星座SWARM(ESA，2004)，由三颗类似CHAMP(CHAllenging Minisatellite Payload mission)卫星组成，虽然SWARM不是专 用的重力卫星，没有ll-SST星间测距功能，但 SWARM载有精度更高的GNSS(Global Navigation Satellite System)接收机、加速度计等重力探测关键有效载荷，可用于探测地球时变重力场，这将弥补GRACE中断的空白(Weigelt et al.，2012).图 1为21世纪以来的相关低轨卫星运行时间跨度分布.

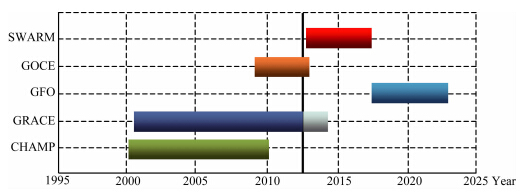图 1 低轨卫星运行时间跨度不同颜色对应纵轴所示的卫星，其中灰色为GRACE预计剩余运行时间.Fig. 1 The time span of related Low Earth OrbitersDifferent colors correspond to different satellite mission，while the gray is the estimated remaining operation-time span of GRACE.

CHAMP卫星是基于高-低卫星跟踪卫星(hl-SST)观测数据，确定中长波地球重力场及其时变场(Reigber et al.，2001).Prange(2010)利用层叠解方法(stacking solutions)，基于CHAMP数据构建的时变重力场序列，可探测地球时变重力信号的趋势项、年际和半年际变化.最近Lin等(2012)研究了 利用COSMIC的hl-SST确定地球时变重力场.尽管通过其他低轨地球探测卫星的星载GNSS接收机确定地球时变重力场，相对于GRACE的精度和分辨率都偏低，但可在一定精度水平上填充地球时变重力场探测的空白.

对CHAMP卫星探测时变重力场能力的研究表明，SWARM卫星的hl-SST观测数据同样具有探测时变重力场的潜能.Wang等(2012)基于SWARM卫星星座模拟研究了其确定地球时变重力场的能力，结果表明，SWARM卫星任务不仅可以确定每月的地球重力场模型，相比于CHAMP卫星，还可以提供星间的相对观测信息，从而大幅度提高重力场模型中长波信号的精度.Reubelt等(2012)基于SWARM标称轨道设计，静态重力场模型、大气、海洋、水文、冰和固体地球物理时变历史资料，模拟研究了格陵兰岛和亚马逊地区冰和水储量的变化，结果验证了SWARM卫星星座有恢复长波 时变重力场的很大潜力.在未来十年，可构建SWARM 卫星时变重力场模型序列，进一步联合GRACE Follow-On数据，有望将反演时变重力场的分辨率和精度提高到一个新水平.

本文首先利用SWARM模拟数据和基于各种地球物理过程数据模拟的时变重力场模型、CHAMP和GARCE观测数据，探讨时变重力场模型的误差特性以及不同高斯平滑半径对高频误差的抑制效果，利用hl-SST和ll-SST方法恢复2004年10月全球质量变化；其次对比分析2003年1月— 2009年12月CHAMP(hl-SST)与GRACE(ll-SST)质量变化，2000年1月—2004年12月SWARM(hl-SST)模拟质量变化与“真实”模型质量变化，探讨基于SWARM卫星hl-SST方法恢复整个格陵兰岛及其小区域冰盖质量变化的可靠性和精度水平，进一步研究SWARM卫星星座探测时变重力场的潜能. 2 时变重力场计算地表质量变化方法

地球外部任意一点(r，θ，λ)的地球引力位(Kusche et al.，2009; Heiskanen and Moritz，1967)，都可以用球谐展开表达：

其中：

r为地球外部点与地心的距离，θ为地心余纬，λ为地心经度，GM为引力常数与地球总质量的乘积，R为地球平均半径，l，m分别为展开的阶和次，L为展开的最高阶数，Clm，Slm为完全规格化的球谐系数，Plm是完全规格化的Legendre缔合函数.

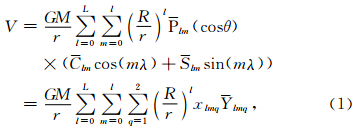
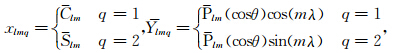
令ρ(r)为地球密度径向分布，则

dV为整个地球体积V的体元，Ω=(θ，λ)，dΩ=sinθdθdλ.

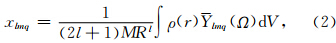
假定ρ(r)随时间变化，表示为ρ(r，t)，需要建立ρ(r，t)与xlmq的关系.有两种方法解决这个问题：拉格朗日方法和欧拉方法.就应用而言，后者是更好的方法.采用欧拉方法，方程(2)可写为：

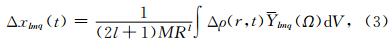
其中Δxlmq(t)为位系数随时间变化，Δρ(r，t)为密度随时间变化，积分为整个地球质量变化.

在全球尺度上，发生在地球表面的气候过程，如 季节性降水降雪和地表水储量变化，质量的径向移 动较之于横向移动，对地球引力场的影响都可以忽略不计.因此，可取近似 r=R，用Δσ(Ω，t)取代Δρ(r，t)，则方程(3)简化为

积分域为整个地球表面.

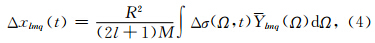
基于Munk和MacDonald(1960)，Δσ由两部分组成，固体地球严格意义上的表面密度变化Δσ0，以及弹性地球加载或卸载产生的密度变化.后一部分可通过Love数kl与Δσ0相联系，假定地球为球形，那么方程(4)变为：

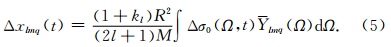
基于Wahr等(1998)，Δσ(θ，λ，t)=Δσ(Ω，t)可展开成

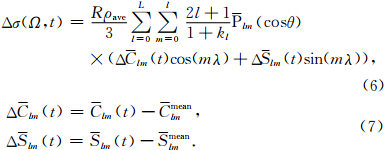
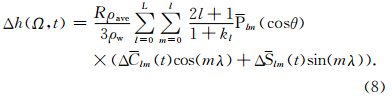
其中 <Clmmean和Slmmean为时间序列球谐系数的平均值，ρave为地球平均密度，等于5517 kg·m-3.当以等效水高表示地球表面质量变化时，方程(6)可写为

考虑到时变重力场模型球谐系数高阶项存在较大误差，而且随着阶数的增加，误差越大，所以本文统一采用简便易行的高斯滤波(图 2).

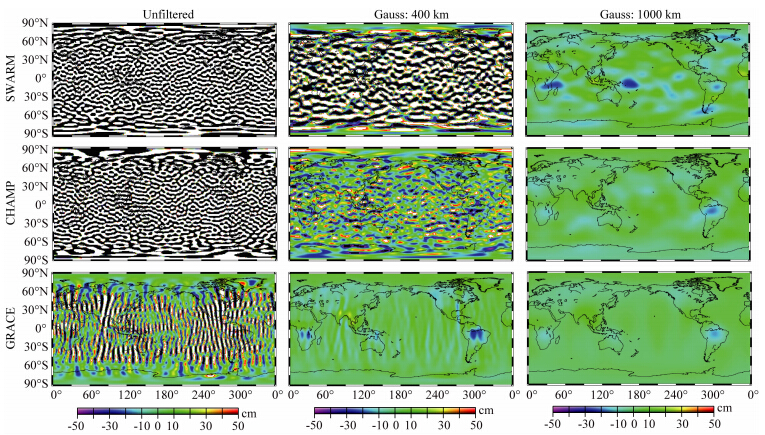图 2 2004年10月以等效水高表示的全球质量变化，包括SWARM模拟结果，CHAMP和GRACE观测结果，以及各自不同半径高斯平滑的效果Fig. 2 The global mass change expressed as the equivalent water height in Oct. 2004 including SWARM simulation result，both CHAMP and GRACE observation results as well as respective Gaussian smoothing effect with different radius

对公式(8)进行空间平滑得到：

Wlm为平滑系数，其对应的平滑函数可由(10)式计算：

其中 Glmc(θ′，λ′)=WlmPlm(cosθ′)cos(mλ′)，Glmc(θ′，λ′)=WlmPlm(cosθ′)sin(mλ′).

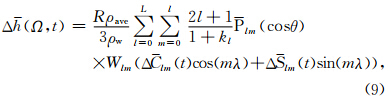
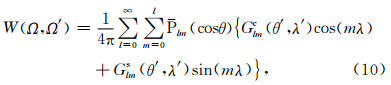
高斯滤波是由Wahr等(1998)基于Jekeli(1981)提出的空间平滑方法.由于这种方法简单且容易实现，所以在GRACE产品早期应用时，这是一种普遍使用的空间平滑方法.高斯滤波平滑函数的表达式为：

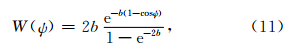
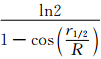其中cosψ=sinθsinθ′cos(λ－λ′)+cosθcosθ′，b=，r1/2=Rψ为“半宽”常数，即平滑半径.平滑系数可由下面的迭代公式计算：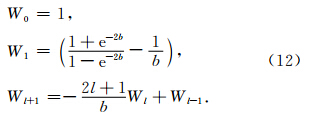

3 数据处理 3.1 月重力场模型

本文采用的数据包括：(1)卢森堡大学(University of Luxembourg)提供的CHAMP 2003—2009年的月重力场模型序列(Weigelt et al.，2013)；(2)德克萨斯大学空间研究中心(CSR，Center for Space Research at the University of Texas)提供的GRACE(RL05)2003—2009年月重力场模型序列(Bettadpur，2012)；(3)斯图加特大学大地测量研究所(Institute of Geodesy，University of Stuttgart)提供：(a)基于SWARM卫星星座标称轨道参数(包括轨道噪声)，根据加入的非保守力、静态重力场模型EIGEN-GRACE02s、大气、海洋、水文、冰以及固体地球物理(固体潮，极潮，冰川均衡调整等)历史观测资料或模型计算的相应动力现象产生的质量或扰动位时变信号，以及噪声和混频误差，由此模拟SWARM hl-SST观测值，进而反演得到2000年1月—2004年12月“观测”月时变重力场模型序列(最高阶次为60)(Reubelt et al.，2012)，下文统称为SWARM模拟数据；(b)基于(a)计算的各类动力现象的时变信号，以及重力场模型EIGEN-GRACE02s模拟得到2000年1月—2004年12月月重力场模型序列，最高阶次为60(Reubelt et al.，2012)，下文统称为“真实”模型数据. 3.2 相关数据处理

本文研究的时变重力场模型包括CHAMP和GRACE月重力场模型，SWARM模拟数据及“真实”模型数据，最高阶次都为60阶.利用由SLR对CHAMP和GRACE卫星的观测数据确定的二阶 带谐系数代替上述模型C20项(Cheng et al.，2012)，同时顾及地心运动的影响，加入基于SLR观测数据得到的地心坐标计算模型一阶项位系数(Wu et al.，2012)，并采用高斯滤波对上述模型进行处理.目前，现有GIA(Glacial Isostatic Adjustment，冰川均衡调整)模型及其改正均有较大的不确定性，GIA模型的建立是基于带推测性的冰载荷历史和地幔黏度，可靠性较差，且GIA相对于年际质量变化趋势的影响很小(Velicogna，2009)，所以本文研究忽略GIA改正.

估计冰盖质量变化趋势，采用以下多项式函数拟合冰盖质量变化时间序列(Baur，2012)：

其中，y(ti)为对应ti时刻的冰盖质量变化，t0为时间序列的初始时刻，pj(j=0，1)为线性拟合系数，fk(k=1，2)为信号频率，Ak和Bk为信号振幅(未知)，二个信号分别代表周年信号、半周年信号，εi为拟合残差.由公式(13)，基于εi平方最小的等权最小二乘估计，求得2+2k个未知参数.

为了更可靠地验证利用SWARM卫星hl-SST观测数据恢复格陵兰岛冰盖质量变化的能力，精细化冰盖质量变化计算，更好地显示冰盖消融区域特征，本文分别将格陵兰岛作为一个区域和划分为多个小区，同样基于Wahr等(1998)和本文第2节的计算模型，分别解算和比较了两种解算结果.其中，区域的划分，采用了Giovinetto和Zwally(2001)，Zwally等(2005)根据卫星测高得到的格陵兰岛表面高程变化分成的19个小区域. 4 数值分析

已有研究(Jacob et al.，2012)以及图 3表明，格陵兰岛是地球上质量变化趋势最显著的区域，这种趋势主要反映冰盖持续消融.由于格陵兰岛冰盖消融对全球海平面上升起着至关重要的作用.因此，连续监测和量化格陵兰岛冰盖质量变化受到全球各界和政府的普遍关注.

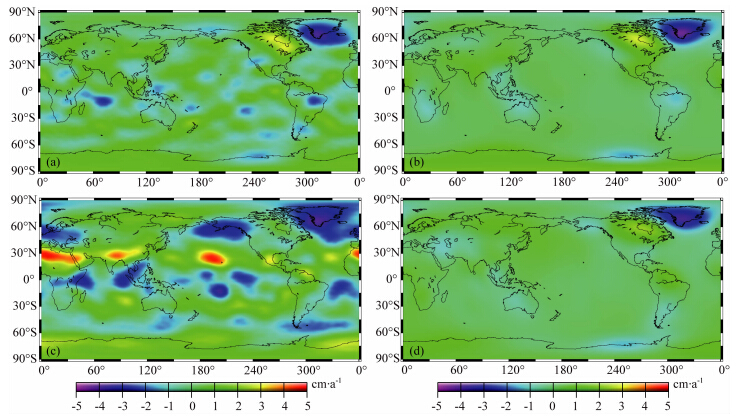图 3 以等效水高表示的全球质量变化趋势(a)SWARM模拟结果(2000年1月—2004年12月)；(b)“真实”模型(2000年1月—2004年12月)；(c)CHAMP观测结果(2003年1月—2009年12月)；(d)GRACE观测结果(2003年1月—2009年12月).Fig. 3 The global mass change trend expressed as equivalent water height(a)SWARM simulation result(Jan. 2000—Dec. 2004);(b)‘True’ model(Jan. 2000—Dec. 2004);(c)CHAMP observation result(Jan. 2003—Dec. 2009);(d)GRACE observation result(Jan. 2003—Dec. 2009).
4.1 全球质量变化

基于式(6)—(12)，利用SWARM模拟数据(2000年1月—2004年12月)，CHAMP hl-SST数据(2003年1月—2009年12月)以及GRACE RL05数据(2003年1月—2009年12月)，其中对RL05数据作了去相关(条带)处理(Swenson and Wahr，2006)，计算了全球质量变化及其趋势.

低轨卫星探测得到的时变重力场具有高频误差大，且随着阶次的增加，误差也增大的特性，采用高 斯平滑可抑制高频误差.图 2表明SWARM、CHAMP、GRACE 时变重力信号误差特性不同，其中GRACE还存在南北条带误差.结果表明，(1)采用400 km的 平滑半径，GRACE数据平滑效果明显优于SWARM和CHAMP；(2)SWARM和CHAMP的高频信号误差远大于GRACE；(3)采用1000 km平滑半径，在陆地水储量变化信号较强的区域，例如亚马逊河流域，三者的符合度较好.

图 3表明，GRACE的全球质量变化(d)非常接近“真实”模型(b)，SWARM和CHAMP的高频噪声大于GRACE，这一特性在信号变化相对较小的海洋地区尤为明显，但在信号变化较大的格陵兰岛、亚马逊河、赞比西河区或东印度区的符合度较好.研究同时发现，由于CHAMP、SWARM高阶噪声过大，导致在北美、欧洲以及亚洲东北区域的结果存 疑.此外，图 3隐含了SWARM模拟和“真实” 模型数据与CHAMP和GRACE观测数据，分别解算全球质量变化趋势可供比较的重叠期，显示了SWARM模拟解整体效果优于CHAMP，但略低于GRACE. 4.2 格陵兰岛冰盖质量变化

为了验证基于SWARM hl-SST数据探测区域性时变重力场和反演质量变化的潜能和精度水平，本节首先分别利用CHAMP hl-SST和GRACE ll-SST数据反演格陵兰岛冰盖质量变化及趋势，旨在确认CHAMP探测时变重力场的能力及其与GRACE时变重力场的差异；进而基于SWARM hl-SST模拟数据和“真实”模型数据分别解算格陵兰岛冰盖质量变化及趋势和两者的差异，同时作为一种内部检核分别作了整体和分区解算. 4.2.1 CHAMP和GRACE对比分析

利用CHAMP和GRACE时变重力场模型确定格陵兰岛整个区域冰盖质量变化，见图 4；将格陵兰岛分为19个区域，确定格陵兰岛每个区域的质量变化，见图 7.

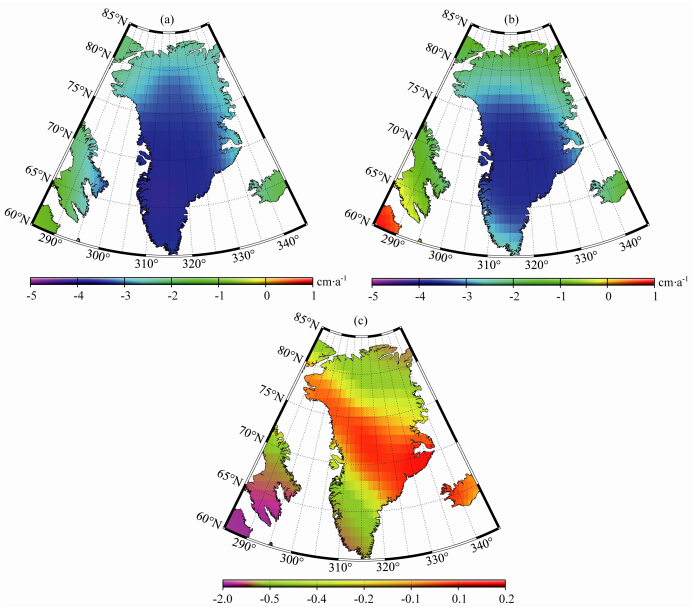图 4 用等效水高表示的格陵兰岛冰盖质量变化趋势:(a)CHAMP数据解，(b)GRACE数据解，(c)CHAMP数据解与GRACE数据解之差Fig. 4 Trend for Greenl and basin-wide ice mass variation in terms of equivalent water height from(a)CHAMP solution，(b)GRACE solution，(c)the differences between CHAMP solution and GRACE one

图 4表明，由于CHAMP的高频误差很大，而GRACE的高频误差相对较小，当利用1000 km高斯平滑时，对于SWARM和CHAMP的hl-SST数据可以很好地抑制高频误差，但对于GRACE的ll-SST数据(最佳高斯平滑半径为400 km)就会将质量变化高频信号平滑掉.

图 5是基于方程(13)计算得到的格陵兰岛质量变化周年振幅、周年相位、半周年振幅及半周年相位变化.其中，周年信号占优，半周年信号很弱，且CHAMP和GRACE的结果非常接近.由此表明，CHAMP的hl-SST可探测到时变重力信号的周年变化和半周年变化，同样可用于建立地球时变重力场模型.图 6显示，CHAMP得到2003—2009年间 格陵兰岛的冰盖质量变化趋势为-50.2±2.0 Gt/a，GRACE为-41.2±1.6 Gt/a，CHAMP和GRACE 相差21.8%(格陵兰岛总的冰盖面积为1.768×106 km2).

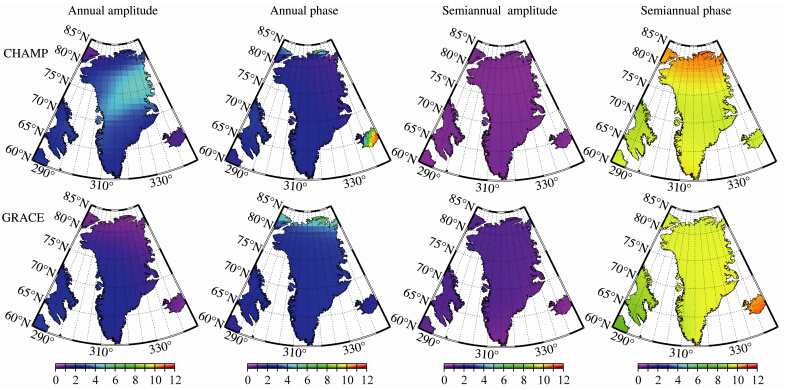图 5 分别由CHAMP和GRACE数据解算的格陵兰岛冰盖质量变化周年振幅、周年相位、半周年振幅及半周年相位Fig. 5 Annual and semi-annual signals(in terms of amplitude and phase)of Greenl and ice mass variation estimated from data of CHAMP and GRACE respectively

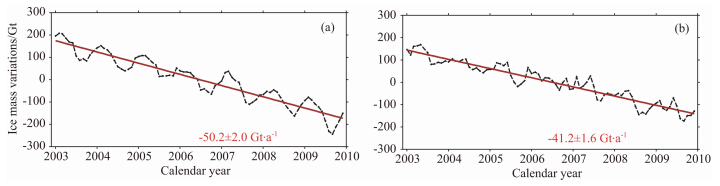图 6 格陵兰岛全区域2003年1月—2009年12月冰盖质量变化及其趋势，(a)CHAMP数据解，(b)GRACE数据解Fig. 6 The Greenl and basin-wide ice sheet mass changes and trends from(a)CHAMP solution and (b)GRACE solution during Jan. 2003—Dec. 2009

图 7显示，格陵兰岛19个子区域冰盖都呈现消融的状态.表 1为CHAMP和GRACE数据解得的格陵兰岛19个子区域冰盖质量年变化趋势，两者差异为-0.9~0.2 cm/a.

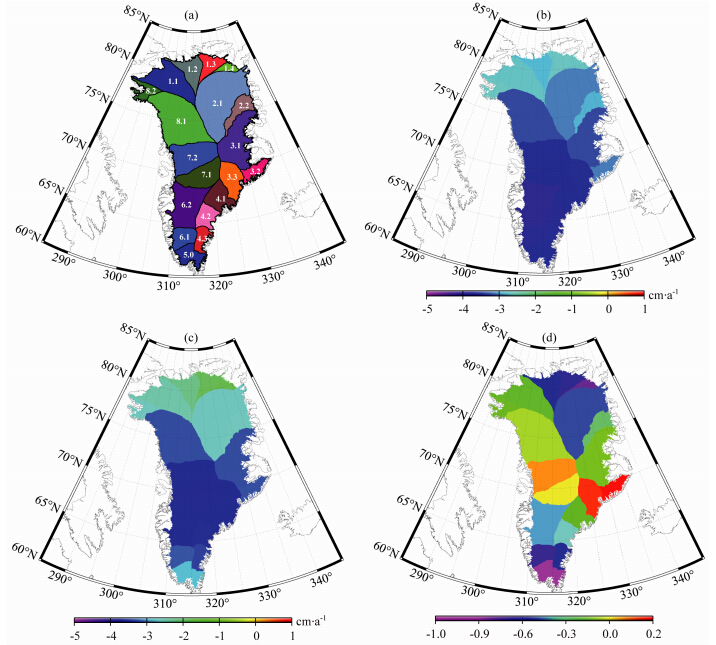图 7 格陵兰岛每个子区域冰盖质量变化趋势，(a)子区域分布，(b)CHAMP数据解，(c)GRACE数据解，(d)CHAMP解与GRACE解之差Fig. 7 Trend for every sub-area ice mass variation in terms of equivalent water height from(a)the distribution of Greenl and sub-areas，(b)CHAMP solution，(c)GRACE solution，and (d)differences between CHAMP solution and GRACE one

表 1 CHAMP和GRACE所得的区域冰盖质量变化趋势(cm/a) Table 1 Change rates(cm/a)from CHAMP and GRACE in drainage systems
4.2.2 SWARM模拟研究

基于SWARM卫星模拟的2000年1月至2004年12月期间月平均重力场模型时间序列，同样分别将格陵兰岛作为一个区域和划分为19个子区域解算冰盖质量变化及其趋势.

图 8和图 9显示，整个格陵兰岛区域冰盖质量 变化及其周年和半周年信号振幅和相位，SWARM模拟值与“真实”模型值都非常接近，模拟的冰盖质量变化趋势要小于“真实”模型值.由于SWARM高频误差很大，当利用1000 km高斯平滑时，虽然可以很好地抑制SWARM高频误差，但也将高频信号平滑掉.图 10表明，SWARM的模拟结果在2000年1月—2004年12月间格陵兰岛的冰盖质量变化为-34.8±6.2 Gt/a，“真实”模型结果为-43.1±3.2 Gt/a，模拟值与“真实”模型值相差19.2%.

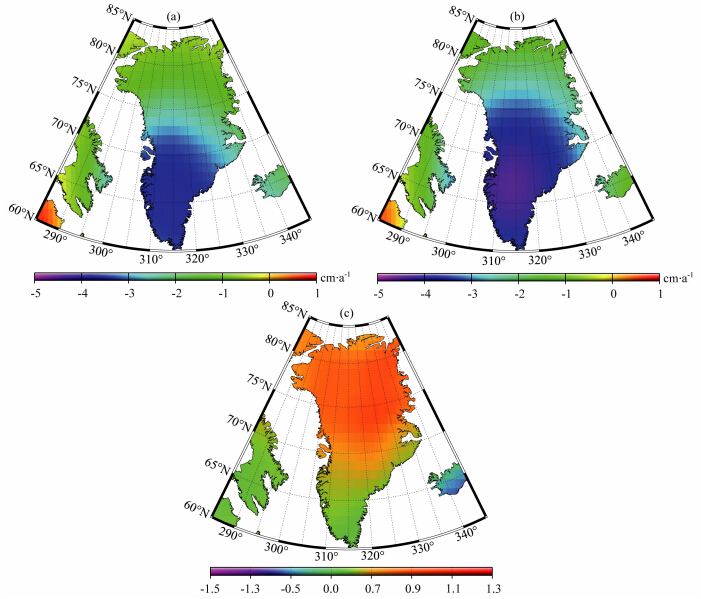图 8 用等效水高表示的格陵兰岛全区域2000年1月—2004年12月冰盖质量变化趋势，(a)SWARM模拟，(b)“真实”模型，(c)SWARM模拟与“真实”模型之差Fig. 8 Trend for Greenl and basin-wide ice mass variation in Jan. 2000—Dec. 2004 expressed as equivalent water height from(a)SWARM simulation，(b)‘True’ model，(c)the differences between SWARM simulation and ‘True’ model

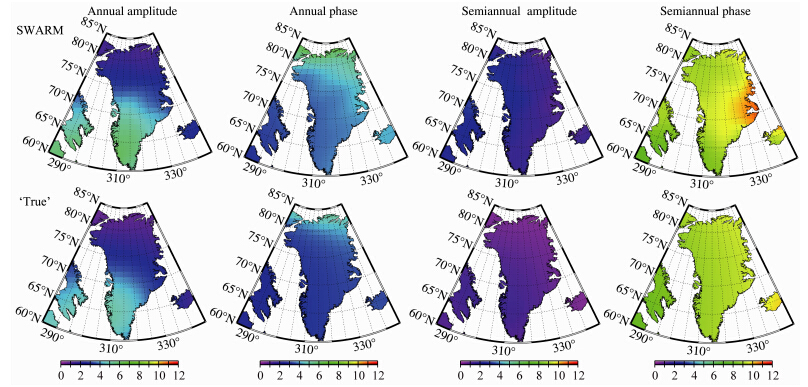图 9 分别由SWARM模拟值及“真实”模型数据解得的格陵兰岛冰盖质量变化周年振幅、周年相位、半周年振幅及半周年相位Fig. 9 Annual and semi-annual signal(in terms of amplitude and phase)of Greenl and ice mass variation estimated from SWARM simulation and ‘True’ model

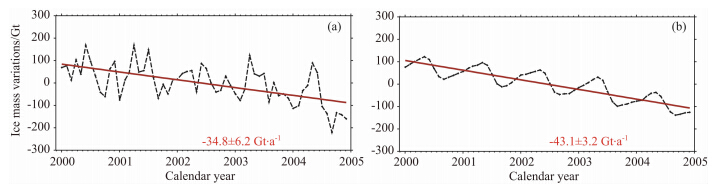图 10 格陵兰岛区域2000年1月—2004年12月的冰盖质量变化及其趋势，(a)SWARM模拟，(b)“真实”模型Fig. 10 The Greenl and basin-wide ice mass variation and trend from(a)SWARM simulation，(b)‘True’ during Jan. 2000—Dec. 2004

图 11中子区域的划分(a)与图 7中的(a)完全相同.图中SWARM模拟解(b)和“真实”模型(c)表明，格陵兰岛19个子区域冰盖都呈现消融的状态.表 2为SWARM模拟解和“真实”模型数据所得的格陵兰岛19个子区域冰盖质量年变化趋势，得出两者之间的差异为0.1~0.9 cm/a.

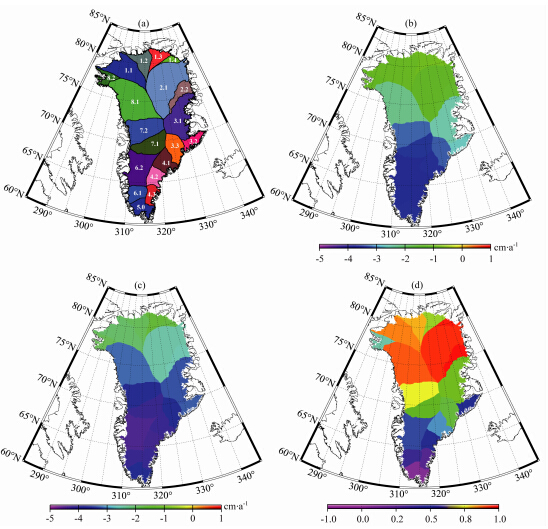图 11 格陵兰岛每个子区域冰盖质量变化趋势：(a)子区域分布，(b)SWARM模拟，(c)“真实”模型，(d)SWARM模拟与“真实”模型之差Fig. 11 Trend for each sub-area ice mass variation in terms of equivalent water height:(a)the distribution of Greenl and sub-areas，(b)SWARM simulation，(c)‘True’ model，(d)the differences between SWARM simulation and ‘True’ model

表 2 SWARM所得的区域冰盖质量变化趋势(cm/a) Table 2 Change rates(cm/a)from SWARM in drainage systems

上述结果显示，21世纪以来，格陵兰岛冰盖质量在持续消融；同时也表明，利用SWARM卫星hl- SST可恢复时变重力场的周年和半周年信号，可用 于对格陵兰岛冰盖质量变化进行连续监测，并可达到一定的精度，由此弥补GRACE任务终止后的空 白，而且SWARM三颗卫星星座的hl-SST数据的时变重力场要优于CHAMP. 5 结语

Baur(2013)的研究表明，CHAMP探测格陵兰岛时变重力场信号，展开至20阶重力场模型时间序列与GRACE观测所得结果最为接近，仅相差 10%，展开至60阶时，与GRACE相差22%；Weigelt等(2013)研究指出，CHAMP卫星只能反映2000 km左右长波重力场的年变化.本文研究表明，展开至60阶，CHAMP和GRACE重力场模型时间序列相差21.8%.因此，可以认为，利用类似于CHAMP卫星hl-SST观测数据，可以在22%的相对误差水平上，等效于GRACE卫星基于ll-SST在约330 km波长(60阶)上对重力场年变化的探测结果，验证了利用类似于CHAMP卫星hl-SST探测时变重力场和地表质量变化的可行性.本文研究结果还表明，基于CHAMP卫星hl-SST探测的时变重力场相比于GRACE其高阶项存在较大噪声污染，需要采用较长的高斯平滑半径.

本文通过探测格陵兰岛冰盖质量变化，进一步验证了SWARM卫星星座探测时变重力场的潜能.SWARM卫星星座相当于3个CHAMP卫星，可以 实现多重hl-SST观测，本文不仅同时利用SWARM 模拟数据、CHAMP和GRACE实测数据计算了2004年10月全球质量变化，并作了分析比较；又分别基于SWARM模拟数据(2000年1月—2004年12月)、CHAMP和GARCE观测数据(2003年1月—2009年12月)估计比较了格陵兰岛冰盖质量变化趋势.研究结果表明：SWARM模拟数据高频噪声低于CHAMP数据，反演的时变重力场模型精度优于CHAMP重力场模型，但略低于GRACE重力场模型，适于探测大尺度长波时变重力场，与“真实”重力场模型或GRACE重力场模型比较，可以达到约20%的相对精度水平.若进一步联合SWARM卫星星座可以成为接续GRACE Follow-On计划探测时变重力场的桥梁，但需要进一步试验研究能否探测 中尺度时变重力场，使其更接近GRACE的探测能力.

致谢 感谢CSR研究中心和卢森堡大学提供的GRACE，CHAMP数据以及Tilo Reubelt提供的SWARM模拟数据.
参考文献
[1] Baur O. 2012. On the computation of mass-change trends from GRACE gravity field time-series. J. Geodyn., 61: 120-128.
[2] Baur O. 2013. Greenland mass variation from time-variable gravity in the absence of GRACE. Geophys. Res. Lett., 40(16): 4289-4293, doi: 10.1002/grl.50881.
[3] Bettadpur S. 2012. Level-2 gravity field product user handbook. GRACE 327-734. The GRACE Project, Cent. for Space Res., Univ.of Texas at Austin, Austin.
[4] Cheng M K, Tapley B D, Ries J C. 2012. Geocenter variations from analysis of SLR data. Reference Frames for Applications in Geosciences, 138: 19-25.
[5] ESA. 2004. Swarm—The Earth's magneticfield and environment explorers. ESA Rep.SP-1279(6), ESA Publication Division, ESTEC, Noordwijk.
[6] Heiskanen W A, Moritz H. 1967. Physical Geodesy. San Francisco: W. H. Freeman and Company.
[7] Hu X G, Chen J L, Zhou Y H, et al. 2006. Monitoring seasonal changes in the Yangtze River water storage by GRACE space observations. Science in China (Series D: Earth Science) (in Chinese), 36(3): 225-232.
[8] Jacob T, Wahr J, Pfeffer W T, et al. 2012. Recent contributions of glaciers and ice caps to sea level rise. Nature, 482(7386): 514-518, doi: 10.1038/nature10847.
[9] Jekeli C. 1981. Alternative methods to smooth the earth's gravity field. Report 327, Department of Geodetic Science and Surveying, Ohio State University, Columbus.
[10] Kusche J, Schmidt R, Petrovic S, et al. 2009. Decorrelated GRACE time-variable gravity solutions by GFZ, and their validation using a hydrological model. Journal of Geodesy, 83(10): 903-913.
[11] Lin T J, Hwang C, Tseng T P, et al. 2012. Low-degree gravity change from GPS data of COSMIC and GRACE satellite missions. J. Geodyn., 53: 34-42, doi: 10.1016/j.jog.2011.08.004.
[12] Munk W H, MacDonald G J F. 1960. The Rotation of the Earth: A Geophysical Discussion. New York: Cambridge University Press.
[13] Prange L. 2010. Global gravity field determination using the GPS measurements made onboard the low Earth orbiting satellite CHAMP . Geodatisch-geophysikalische Arbeiten in der Schweiz, 81.
[14] Reigber C, Lühr H, Schwintzer P. 2001. Announcement of opportunity for CHAMP. Tech. Rep. CH-GFZ-AO-001.
[15] Reubelt T, Baur O, Weigelt M, et al. 2012. On the capability of SWARM for estimating time-variable gravity fields and mass variations. International Symposium on Gravity, Geoid and Height Systems GGHS 2012, Venice, Italy.
[16] Swenson S, Wahr J. 2006. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett., 33(8): L08402, doi: 10.1029/2005GL025285.
[17] Tapley B D, Bettadpur S, Ries J C, et al. 2004. GRACE measurements of mass variability in the Earth system. Science, 305(5683): 503-505, doi: 10.1126/science.1099192.
[18] Velicogna I. 2009. Increasing rates of ice mass loss from the Greenland and Antarctic ice sheets revealed by GRACE. Geophys. Res. Lett., 36(19): L19503, doi: 10.1029/2009GL040222.
[19] Wahr J, Molenaar M, Bryan F. 1998. Time variability of the Earth's gravity field: hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res.103(B12): 30205-30229.
[20] Wang X X, Gerlach C, Rummel R. 2012. Time-variable gravity field from satellite constellations using the energy integral. Geophys. J. Int., 190(3): 1507-1525, doi: 10.1111/j.1365-246X.2012.05578.x.
[21] Weigelt M, Jggi A, Prange L, et al. 2012. Large scale time variability from high-low SST-filling the gap between GRACE and GFO. GRACE Science Team Meeting, Potsdam.
[22] Weigelt M, Van Dam T, Jggi A, et al. 2013. Time-variable gravity signal in Greenland revealed by high-low satellite-to-satellite tracking. J. Geophys. Res. Solid Earth, 118(7): 3848-3859, doi: 10.1002/jgrb.50283.
[23] Watkins M, Flechtner F, Morton P, et al. 2013. Status of the GRACE follow-on mission. Geophys. Res. Abstract, 15, EGU2013-6024.
[24] Wu X P, Ray J, Van Dam T. 2012. Geocenter motion and its geodetic and geophysical implications. J. Geodyn., 58: 44-61, doi: 10.1016/j.jog.2012.01.007.
[25] Yang Y D, E D C, Chao D B, et al. 2009. Seasonal and inter-annual change in land water storage from GRACE. Chinese J. Geophys. (in Chinese), 52(12): 2987-2992.
[26] Zwally H J, Giovinetto M B. 2001. Balance mass flux and ice velocity across the equilibrium line in drainage systems of Greenland. J. Geophys. Res., 106(D24): 33717-33728, doi: 10.1029/2001JD900120.
[27] Zwally H J, Giovinetto M B, Li J, et al. 2005. Mass changes of the Greenland and Antarctic ice sheets and shelves and contributions to sea-level rise: 1992—2002. Journal of Glaciology, 51(175): 509-527.
[28] 胡小工, 陈剑利, 周永宏等. 2006. 利用GRACE空间重力测量监测长江流域水储量的季节性变化. 中国科学D辑, 36(3): 225-232.
[29] 杨元德, 鄂栋臣, 晁定波等. 2009. GRACE估算陆地水储量季节和年际变化. 地球物理学报, 52(12): 2987-2992.