2014, Vol. 57
重力潮汐变化是固体地球在日、月及近地行星等天体引潮力作用下整体形变导致的地球重力场周期性变化，其最大幅度超过2000 nm·s-2，是地球内部结构和介质分布特征的综合反映，是重力时间变化中最主要的部分.重力朝汐变化通常用重力潮汐参数描述，包括无量纲的重力振幅因子δ(即在参考点“真实”地球的重力潮汐变化量与“刚体”地球的重力潮汐变化量之比，为固体潮Love数h和k的线性组合)和相位差Δφ，这些参数可以采用现有的地球模型，通过相互耦合的弹性(或黏弹性)运动方程、扰动引力位Poisson方程和介质本构方程的数值解，理论模拟获得(Wahr，1981; Dehant et al.，1999; Mathews，2001; 徐建桥和孙和平，2003; Métivier and Conrad，2008)；另一方面，它们也可以通过地球表面高精度重力仪的长期连续观测获得(Melchior et al.，1985; 毛慧琴等，1989; 宋兴黎和毛慧琴，1991; Melchior，1994; 许厚泽等，2000; Melchior et al.，1996; 徐建桥等，1999; Xu et al.，2004; 孙和平等，2005).因此，重力固体潮的观测与研究是认识地球内部结构和其他(全球和局部)动力学过程的基础.
事实上，重力固体潮主要包括来自于地球对月球及其它天体的2阶引潮力以及对月球的3阶引潮力的响应，由于三阶重力潮汐变化幅度极小(不足二阶潮汐变化幅度的百分之一)，信噪比很低，并且其信号可以出现在长周期、周日、半日和1/3日等各个潮汐频段.限于仪器的观测精度和观测长度，现有的固体潮实验研究主要集中在2阶潮汐部分，对于3阶潮汐的响应，大部分的研究也仅仅简要罗列出信噪比最高的1/3日频段M3的潮汐参数(Melchior et al，1985; 毛慧琴等，1989; 宋兴黎和毛慧琴，1991; Melchior，1994; 许厚泽等，2000; Melchior et al.，1996; 徐建桥等，1999; Xu et al.，2004; 孙和平等，2005; Xu et al.，2012; Sun et al.，2013).然而，在不同频段，重力固体潮的响应特征可能存在比较大的差异(Dehant et al.，1999).
超导重力仪(SG)具有极高的灵敏度和稳定性、极低的噪音水平和漂移以及极宽的动态频率响应范围，其观测精度可以达到10-2 nm·s-2量级，是目前观测精度和稳定性最高的重力观测仪器，其观测资料，特别是其全球网络观测资料在包括重力固体潮在内的全球地球动力学研究中发挥了非常重要的作用(Hinderer and Crossley，2004; Crossley and Hinderer，2009).随着SG观测资料的长期积累，为精确刻画重力潮汐变化特征提供了可能.
自1979年起，通过广泛的国际合作及多台高精度重力仪在武汉台的长期、连续、对比观测，特别是一台超导重力仪的长期连续观测，建立了高精度的武汉国际重力潮汐基准(宋兴黎和毛慧琴，1991; 许厚泽等，2000)，给出了武汉台O1、K1、M2和S2等主要潮波的重力潮汐参数(包括其振幅因子δ和相位差Δφ).但是，早期在武汉台采用一台LaCoste-Romberg(LCR)G型和三台地球动力学型重力仪进行了半年左右连续对比观测(Melchior et al.，1985; 毛慧琴等，1989; 宋兴黎和毛慧琴，1991; 许厚泽等，2000)，观测精度相对较低；后来，采用了三台高精度LCR ET型重力仪(英国的ET15、德国的ET16和我国的ET21)进行了1年到3年的连续重力观测，其观测精度在10 nm·s-2量级；同时中国唯一的一台GWR TT70型SG也在该台站进行重力固体潮的长期观测，但限于当时比较差的观测环境，其观测精度与LCR ET重力仪相当.因此，在当时观测环境下获得基准值需要进一步精化，以满足目前高精度大地测量观测的要求.1997年底，武汉台SG在生产厂家进行升级改造(升级后编号为C032)，并成功安装在位于武汉市郊的大地测量与地球动力学国家野外观测实验站进行连续观测，至2012年，已经获得了14年多的连续观测资料，为研究区域重力潮汐变化特征奠定了良好的资料基础.同时，需要指出，武汉台是我国正在实施的重大科技支撑项目“中国大陆构造环境监测网络”的基准站，是不同类型重力仪对比观测以及适合中国大陆的固体潮和海潮模型的重要实验和研究基地，武汉国际重力潮汐基准的维持和精化就显得极为迫切和重要.
本文的主要目的是采用武汉台超导重力仪自1997年底至2012年14年多的长期连续观测资料，研究重力潮汐变化特征，精密确定在周日、半日和1/3日频段2阶和3阶重力潮汐参数，修正现有的武汉国际重力潮汐基准，检验现有的潮汐理论和实验模型以及海潮模型在中国大陆区域的有效性，为中国大陆重力网络建设及其相关的科学和应用研究提供更精确的潮汐改正模型和基准. 2 观测资料的处理
武汉台SG C032从1997年11月8日开始正常记录，通过计算机自动采集相关数据(包括重力、气压、温度等)，采样率为1 s，到2012年4月10日，总共获得了14年多的重力连续观测资料，足以刻画该区域重力潮汐变化特征.
与弹簧重力仪类似，SG是相对重力仪，其输出是反映重力实时变化的电压值，尽管仪器生产厂商提供了初步的格值(即输出电压与重力变化之间的转换因子)，但其精度远远无法满足高精度重力观测的需要，必须对它进行精密的格值标定.SG最常见的标定方法是，在大潮期间通过FG5 绝对重力仪与SG同址对比观测(Hinderer et al.，1991; Sun et al.，2001; Riccardi et al.，2012)，根据SG数据的采样率及FG5的特点，控制FG5落体的速率，采用线性回归方法，经过迭代，剔除FG5的异常观测，最后确定SG的格值.SG的标定精度需优于0.3%，这就要求SG和FG5的对比观测需持续3天以上，FG5落体数一般应该超过10000次.在1997-11-08—2012-04-12观测期间，采用FG5绝对重力仪先后4次对SG C032进行格值标定，图 1直观给出了武汉台SG C032在2011年3月3日至7日标定期间与FG5绝对重力仪对比观测，具体标定情况见表 1.结果表明，尽管每次标定的相对精度均优于0.25%，满足高精度重力连续观测的要求，但仪器的格值在长达14年多的时间内发生了显著变化，最大变化幅度接近0.8%，其原因可能是由于SG中各种电子设备和元器件的老化和更新所致，因此，为了获得高精度长期重力观测结果，定期对SG进行标定是非常必要的.
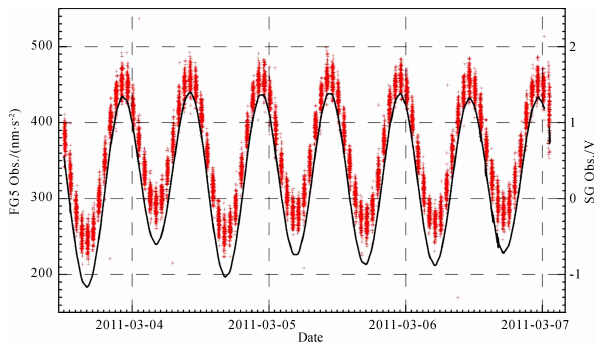 | 图 1 SG C032与FG5对比观测标定周期曲线表示SG C032 观测，离散的+代表FG5观测值.由图可以明显看出，FG5观测的离散度比较大，观测精度明显低于SG. Fig. 1 Calibration of SG C032 by comparison measurements with FG5The periodic curve shows the recordings from SG C032. Discrete symbols + denote the gravity values observed with FG5. From the figure，it is found that the FG5 observations show relatively large dispersion and the precision is obviously lower than those observed with the SG. |
 | 表 1 武汉台SG C032标定情况 Table 1 Information about calibration of SG C032 at Wuhan station |
采用国际地球潮汐中心推荐的重力固体潮观测资料的预处理软件T-Soft(Vauterin，1998)，通过移去—恢复的人—机对话方式，直观剔除并改正观测资料中一些错误数据(如尖峰、突跳、仪器掉格、大地震干扰等)，内插一些由于偶然因素(断电、仪器故障等)引起的较小中断，并采用低通数字滤波器直接将高密度采样资料变换为每小时采样.
利用Eterna3.30标准分析软件(Wenzel，1996)对武汉台SG C032的长期观测序列作调和分析，精密确定重力潮汐参数，数值结果列于表 2和表 3，在调和分析中，采用Hartmann和Wenzel给出的高精度引潮位分波表(Hartmann and Wenzel，1995).重力潮汐观测的最主要的噪音源来自大气的负荷效应，主要来自于台站周边50 km区域的局部大气负荷效应(徐建桥等，1999; Xu et al.，2012; Sun et al.，2013; Merriam，1992; 孙和平，1997; Boy et al.，2002; 罗少聪等2005; Kroner and Jentzsch，1999)，在进行调和分析的同时，对SG C032的观测作了局部大气负荷改正，精密确定了武汉台局部大气重力导纳值为-3.163±0.008 nm·s-2/hPa，这一结果，与以前在武汉台和其他区域台站获得的结果，以及通过全球气压和大气重力格林函数褶积积分的理论模拟计算结果比较接近.分析结果表明，武汉台SG C032重力潮汐观测精度非常高，标准差为1.116 nm·s-2，在周日、半日和1/3日频段的平均 噪音水平分别为0.0201，0.0154和0.0055 nm·s-2. 鉴于武汉台SG C032极高的观测精度、稳定性和频率分辨率，可以精密反映固体地球对2阶和3阶引潮力的响应特征.
| | 表 2 武汉台超导重力仪观测的地球对2阶引潮力的响应(1997-12-24—2012-04-10) Table 2 Response of the Earth to the second-degree tidal forces observed with the SG at Wuhan(1997-12-24—2012-04-10) |
| | 表 3 武汉台超导重力仪观测的地球对3阶引潮力的响应(1997-12-24—2012-04-10) Table 3 Response of the Earth to the third-degree tidal forces observed with the SG at Wuhan(1997-12-24—2012-04-10) |
固体地球对天体引潮力响应的最主要部分就是2阶的潮汐形变.从武汉台SG C032长期观测中分离出了63个2阶潮汐波群信号，其中周日波37个，半日波26个，具体情况见表 2.分析结果表明，2阶 潮波的观测精度很高，其中，4个主要潮波(即O1，K1，M2和S2)重力振幅因子的观测精度均优于0.006%； 其他振幅大于20 nm·s-2的潮波的观测精度也优于0.09%，比武汉基准站其他任何仪器的观测精度都高得多，完全可以作为武汉国际重力潮汐基准维持和精化的依据. 3.1 武汉国际重力潮汐基准的精化
武汉国际重力潮汐基准给出了4个主要潮波重力潮汐参数(许厚泽等，2000)：δ(O1)=1.1780，Δφ(O1)=-0.31°;δ(K1)= 1.1522，Δφ(K1)=-0.46°; δ(M2)= 1.1751，Δφ(M2)=-0.28°; δ(S2)=1.1710，Δφ(S2)=-0.14°. 比较本文结果发现，现有基准的重力振幅因子在半日频段非常准确、可靠，其偏差不足0.07%；在周日频段存在比较明显的偏差，其偏差超过0.13%.理论研究表明，地球对2阶引潮力的响应(表现为Love 数和重力潮汐参数)，在半日频段与频率无关，而在周日频段，由于近周日共振的影响具 有极强的频率依赖性(Wahr，1981; Dehant et al.，1999; Mathews，2001; 徐建桥和孙和平，2003).在前期观测中，除SG TT70持续观测了6年之外，其他仪器连续观测时间一般在半年到1年不等，导致其重力潮汐观测的频率分辨率与SG C032观测无法相比，在进行调和分析时，各潮汐波群包含了大量与主波频率接近的许多潮波.并且，与SG C032相比，前期的观测仪器在精度、灵敏度和稳定性都稍低.但是由于半日潮的重力潮汐参数与频率无关，鉴于M2和S2波群观测极高的信噪比，这两个潮波的现有基准值与SG C032长期观测结果非常接近；而周日波的重力潮汐参数具有极强的频率依赖性，导致O1和K1波的现有基准值存在明显的偏差，需要进一步精化. 3.2 海潮模型的有效性
海潮是海水在天体引潮力作用下周期性涨落.由于全球海洋覆盖了地球表面70%以上的区域，全球海潮负荷将导致地球表面非常显著的形变和重力场变化，并且包含在任何一种固体潮的观测之中，高精度的大地测量(如重力、GPS等)，特别是在沿海地区的测量必须充分考虑海潮负荷效应.海潮负荷效应包括直接效应(海水质量直接吸引力的变化)和间接效应(海水负荷引起地表的形变及地球内部质量分布产生附加引力)两部分.采用经典负荷理论，通过负荷格林函数与海潮潮高全球褶积积分即可获得各海潮潮波的负荷矢量 L(包括振幅L和相位λ)(Farrell，1972; 许厚泽和毛伟健，1988; Agnew，1997). 1980年，Schwiderski采用全球验潮站的观测资料构制了世界上第一个实用的全球海潮模型(Schwiderski，1980)，随着卫星测高技术的发展及其观测资料的积累，国际上许多机构先后发展了一 系列高精度、高空间分辨率的海潮模型(Eanes，1994; Cheng and Andersen，2010; Egbert and Erofeeva，2002; Lyard et al.，2006; Matsumoto et al.，2000; Ray，1999; Savcenko and Bosch 2008; Taguchi et al.，2014). 重力潮汐观测残差主要来自于全球和局部的海洋潮汐的负荷效应，在全球大部分区域，海潮负荷效应达到重力潮汐振幅的1%～2％，特别在一些沿 海地区，其影响更大，可以达到重力潮汐振幅的3%～ 4％.因此，高精度重力潮汐观测可以作为研究不同海潮模型区域有效性的最可靠的手段(Sun et al.，2005).
目前普遍使用的最新全球海潮模型有Fes02，Got04，Ham11A，Nao99，Tpx07，Eot11A，Dtu10，Crs4.0等(Eanes，1994; Cheng and Andersen，2010; Egbert and Erofeeva，2002; Lyard et al.，2006; Matsumoto et al.，2000; Ray，1999;Savcenko and Bosch 2008; Taguchi et al.，2014)，在这些海潮模 型中，均包含Q1，O1，P1，K1，N2，M2，S2和K2等8个振幅最大潮波的等潮图，通过积分格林函数数值方法获得相应的海潮负荷矢量 L .选择Dehant等(1999)基于旋转椭球体、非流体静力平衡地球模型建立的潮汐理论模型作为参考，该模型考虑了地幔介质的非弹性，地幔对流及其导致的边界形变(以观测的地球自由核章动周期和整个地球的动力学扁率控制所选用的参数)等因素的影响.对于某一潮汐波群，SG C032观测矢量与理论模拟矢量之差即为其观测残差矢量 B(其振幅和相位分别记为B和β)，观测残差矢量 B 与海潮负荷矢量 L 之差即为经相应海潮改正后的最终残差矢量 X(其振幅和相位分别记为X和)，X越小表明该海潮模型在该区域越有效.图 2给出了武汉台SG C032观测的上述8个主要潮波的观测残差矢量和各海潮模型的最终残差矢量的振幅 B和X .
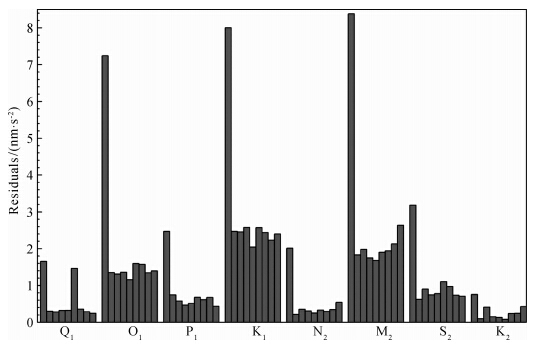 | 图 2 8个主要潮波残差矢量的振幅每组直方图的第一个立柱表示相应潮波观测残差矢量振幅 B，后面8个均为海潮改正后最终残差矢量振幅 X，从左到右依次表示采用的海潮模型分别为Fes02，Got04，Ham11A，Nao99，Tpx07，Eot11A，Dtu10和Crs4.0. Fig. 2 Amplitudes of the residual vectors of eight main tidal wavesThe first upright in each group of histogram denotes amplitude B of the residual vector of the corresponding tidal wave，and the remainders st and for the amplitudes X of the final residual vectors after ocean tide loading correction based on ocean tide models Fes02，Got04，Ham11A，Nao99，Tpx07，Eot11A，Dtu10 and Crs4.0，respectively. |
由图可知，经海潮改正以后，主要潮波的观测残差显著减小，并且不同海潮模型之间也存在差异.对 于Q1波，重力潮汐的理论振幅为52.0049 nm·s-2，除采用Tpx07模型作海潮改正未见明显效果外，采用其他7个海潮模型作海潮改正，其观测残差振幅降低幅度从78%到85%；对于其他几个主要潮波，采用不同海潮模型进行海潮改正后，观测残差振幅下降的幅度基本介于70%与90%之间.换言之，目前的全球海潮模型只能解释武汉台重力潮汐观测残差的70%到90%，剩下的10%~30%可能来自中国沿海局部海潮的负荷效应、台站区域构造导致的对日月引潮力响应的微小差异以及观测仪器微小的标定误差.可以看出，与其它潮波相比，尽管振幅最大的4个主要潮波O1，K1，M2和S2海潮改正后观 测残差显著降低，但最终残差矢量振幅依然很大，为了客观评价某个海潮模型有效性，以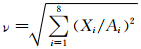
(式中Xi和Ai分别为第i个潮波的最终残差矢量振幅和理论振幅)作为评价海潮模型整体有效性的统计量，ν越小说明相应的海潮模型的区域有效性越强，对于Fes02、Got04、Ham11A、Nao99、Tpx07、Eot11A、Dtu10和Crs4.0等8个海潮模型，ν依次 为0.0125、0.0136、0.0124、0.0113、0.0307、0.0138、0.0128和0.0139，表明除Tpx07海潮模型不太适合中国大陆的海潮负荷改正外，其他7个模型没有实质性的差异，其统计量ν介于0.0113(Nao99)和0.0139(Crs4.0)之间，但相比较而言，在中国大陆采用Nao99作海潮负荷改正的整体精度最高.
Nao99是日本水泽天文台Matsumoto等综合利用5年T/P测高和验潮站数据构制的全球海潮模型，该模型改善了日本岛附近局部浅海区潮汐模型，其空间分辨率为0.5°×0.5°，并且提供了振幅较大的7个周日潮波(即Q1、O1、M1、P1、K1、J1和OO1波)和8个半日潮波(即μ2、N2、ν2、M2、L2、T2、S2和K2波)等潮图(Matsumoto et al.，2000).分别采用这些等潮图，通过积分格林函数即可获得这些潮波的负荷矢量，其他的振幅较小潮波的海潮负 荷矢量通过频率域内插或外推的方法获得(Xu et al.，2004; 周江存等，2009).从SG C032观测的重力潮汐参数剔除各潮波的海潮负荷效应，即可获得固体地球对2阶引潮力的响应，具体数值结果列于表 2. 结果表明，海潮负荷对武汉台重力潮汐观测的影响比较显著，海潮负荷改正后，SG C032观测的重力振幅因子明显降低，其中振幅最大的3个潮波O1，K1和M2振幅因子分别下降了1.8%，1.2%和1.0%，其他潮波振幅因子降低幅度从0.2%到3.8%不等，平均下降幅度达到1.2%，且更接近于重力潮汐理论和实验模型. 3.3 固体潮模型有效性
采用现有的地球模型，通过求解固体地球潮汐运动方程即可获得固体潮理论模型，最新的固体潮理论模型已经顾及到地球的自转、椭率、非弹性、非流体静力平衡和侧向非均匀性等诸多复杂因素的影 响，在固体潮诸多理论模型中，普遍使用的是Dehant等(Dehant et al.，1999)和Mathews(Mathews，2001)给出的模型，分别记为DDW99和M2001，此外，Xu等(Xu et al.，2004)利用全球SG网络观测资料，顾及到潮汐形变特征，建立了一个重力潮汐全球实验模型，记为XSD04.采用武汉台SG C032的长期观测结果是检验这些模型在中国大陆区域的有效性的最佳手段.
由于地球近周日自由摆动的存在，周日潮汐观测出现显著的共振现象、重力潮汐振幅因子具有强烈的频率依赖性，这是固体地球对天体2阶引潮力响应的重要特征之一，图 3直观描述了武汉台SG C032观测结果和最新的潮汐理论和实验模型田谐潮的这一特征.
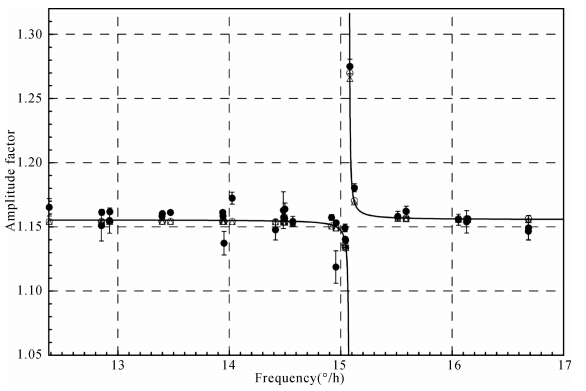 | 图 3 SG C032观测的田谐潮振幅因子与潮汐理论和实验模型的比较带误差棒的·代表SG C032观测结果，实双曲线表示实验模型XSD04结果，○和Δ分别表示理论模型DDW99和M2001结果.Fig. 3 Comparison of the gravimetric factors of the tesseral harmonic tides among the tidal gravity observations from SG C032，theoretical and experimental models for gravity tides · with error bar denotes the SG observations，solid hyperbolic curve for the results of experimental model XSD04，○ and Δ for those of theoretical models DDW99 and M2001，respectively. |
数值结果表明，最新的地球潮汐模型都能非常好地刻画固体地球对引潮力的响应特征.在周日频段，现代潮汐模拟理论通过不同的方式增大流体静力平衡近似下预测的液核动力学椭率约5%，使得这一力学体系中对周日固体潮影响最显著的简正模(近周日自由摆动)的周期与实际观测结果更吻合，而实验模型则是基于全球SG长期观测结果建立的，因此，这些潮汐模型与武汉台SG C032观测结果具有很好的一致性.在周日频段，与SG C032实际观测相比，潮汐理论模型DDW99、M2001和实验模型XSD04的振幅因子平均偏差分别为0.59%，0.62%和0.57%；对于信噪比最高的3个潮波O1、P1和K1(振幅均超过100 nm·s-2)的振幅因子，潮汐理论模型DDW99的偏差分别为0.36%、0.34%和0.47%，M2001的偏差分别为0.38%、0.36%和0.46%，实验模型XSD04的偏差分别为0.29%、 0.26%和0.26%.结果表明，在观测误差和全球海潮模型不确定性的范围内，上述3个潮汐模型都很可靠，可以满足中国大陆高精度重力观测的需要，相比而言，由于实验模型XSD04综合考虑了全球SG 观测结果，与武汉台SG C032 观测结果符合的最好.
固体地球对2阶扇谐引潮力的响应与频率无关，除信号较弱的潮波，SG C032观测的其他潮波重力振幅因子之间相差甚微，其中信噪比最高的3个潮波N2，M2和S2(振幅均超过100 nm·s-2)振幅因子分别为1.16412，1.16410和1.16335，其平均值为1.16386，反映了地球在该频段的平均响应.与之相比，潮汐理论模型DDW99和实验模型XSD04的偏差极小，不足0.15%，而理论模型M2001由于没有顾及地球介质的非弹性，存在显著差异，其偏差达到0.67%.
总之，从武汉基准台SG C032长达14年多的连续观测结果看，最新的潮汐理论和实验模型都能够很好反映固体地球对2阶田谐(周日)引潮力的响应特征，精确预测周日频段的重力潮汐变化；对于2阶扇谐(半日)潮，理论模型M2001存在显著的偏差.因此，对于中国大陆的重力观测，应采用Dehant等(1999)顾及地幔介质非弹性和地球内部非流体静力平衡等特征的潮汐理论模型或Xu等(2004)基于全球SG观测建立的重力潮汐全球实验模型作为参考和改正模型. 4 固体地球对3阶引潮力的响应
武汉台SG C032观测成功分离出15个3阶潮 汐波群，其中3个在周日频段，7个在半日频段，5个在1/3日频段，具体数值结果列于表 3.结果表明，由于周日频段平均噪音水平相对较高，为0.0201 nm·s-2，3MK1波(理论振幅为0.4610 nm·s-2)信噪比比较低，3MQ2波(理论振幅为0.3460 nm·s-2)一方面信噪比比较低，同时其频率非常接近S2波频率，可能受到太阳加热潮的干扰，因此，这两个波群观测结果偏差较大.其他12个波群观测结果都比较可靠，总体来说，1/3日频段的观测精度最高，其中振 幅最大的潮波为M3(理论振幅为9.4322 nm·s-2)，其振幅因子的观测精度优于0.04%；半日频段的观测精度次之，其中振幅最大的两个波群为3Mk2和3MO2(理论振幅均超过6 nm·s-2)，振幅因子的观测精度均优于0.26%；周日频段信号较弱，信号最强的M1波理论振幅仅为1.4423 nm·s-2，观测精度相对较差.
理论研究表明，由于地球的非弹性，3阶重力潮汐振幅因子在不同频段存在微小的差异，在武汉台周日、半日和1/3日频段(分别对应3阶1次、3阶2 次和3阶3次潮汐)重力振幅因子为1.06833，1.07174和1.07345(Dehant et al.，1999).与武汉台观测结果相比，对于3阶1次潮波，信号最强的M1波振幅因子的偏差0.78%，其原因还是在该频段信号相互对比较弱，观测的信噪比较低；对于3阶2次潮波，信号最强的3MK2和3MO2波振幅因子几乎与观测结果相同；对于3阶3次潮波，信号最强的M3波振幅因子的偏差0.68%.总之，考虑到在不同频段3阶潮汐信号的信噪比及相对观测误差，武汉台SG C032观测结果与最新理论预测结果具有很好的一致性，基本反映了非弹性地球对3阶引潮力的响应，由于现有的海潮模型没有系统提供3阶 潮汐等潮图，无法对观测结果作海潮负荷改正，这是 导致理论模型与观测结果存在较大的差异的主要原因. 5 结论及讨论
系统分析处理了武汉台超导重力仪SG C032自1997年11月8日以来14年多的长期连续观测资料，剔除区域大气负荷影响，系统研究了固体地球在该区域对于2阶和3阶引潮力的响应特征，对于重力潮汐基准的维持和精化、以及我国重大科技支撑项目“中国大陆构造环境监测网络”的实施具有重要的参考价值.
通过与FG5绝对重力仪的对比观测，分别在1999、2000、2007和2011年对武汉台SG C032进行过4次格值标定，每次标定的相对精度均优于0.25%，满足高精度重力连续观测的要求，尽管SG是目前观测精度和稳定性最高的重力观测仪器，但由于各种电子设备和元器件的老化和更新等原因，其格值在14年多的时间内发生了显著变化，最大变化幅度接近0.8%，因此，为了获得高精度长期重力观测结果，定期对SG进行标定是非常必要的.
由于目前使用的武汉国际重力潮汐基准建立于2000年，观测仪器在精度、灵敏度和稳定性都稍低，各仪器持续观测时间都相对比较短，各潮汐波群包含了大量与主波频率接近的许多潮波.SG C032长期观测资料调和分析结果表明，重力潮汐观测精度极高，标准偏差达到1.116 nm·s-2，4个主要潮波的观测精度均优于0.005%，完全可以作为武汉国际重力潮汐基准检验和精化的依据.从SG C032 的观测结果看，由于半日潮的重力潮汐参数与频率无关，鉴于M2和S2波群观测极高的信噪比，这两个潮波的基准值与SG C032长期观测结果非常接近；而周日波的重力潮汐参数具有极强的频率依赖性，导致O1和K1波的现有基准值存在明显的偏差，需要进一步精化.
就目前普遍使用的Fes02、Got04、Ham11A、Nao99、Tpx07、Eot11A、Dtu10和Crs4.0等8个海潮模型，采用经典的地表负荷理论和积分格林函数方法计算了全球海潮负荷效应，采用SG C032高精度重力潮汐观测结果研究这些海潮模型在中国大陆的有效性.结果表明，除Tpx07海潮模型不太适合中国大陆的海潮负荷改正外，其他7个模型没有实质性的差异，相比较而言，由于Nao99考虑验潮站数据，改善了日本岛附近局部浅海区潮汐模型，对中国大陆的海潮负荷效应计算的整体精度稍高.此外，由于Nao99提供了振幅较大的15个潮波等潮图(其他海潮模型一般仅提供8个潮波等潮图)，可以更精确模拟海潮负荷效应.因此，建议在中国大陆大地测量采用Nao99作为海潮负荷改正的参考模型.
从武汉台SG C032观测结果看，最新的潮汐理论模型DDW99、M2001和实验模型XSD04都能够很好反映固体地球对2阶田谐(周日)引潮力的响应特征，精确预测周日频段的重力潮汐变化；对于2阶扇谐(半日)潮，理论模型M2001存在显著的偏差(达到0.67%)，DDW99和XSD04的偏差不足0.15%. 因此，对于中国大陆的重力观测，应采用Dehant等(1999)顾及地幔介质非弹性和地球内部非流体静力平衡等特征的潮汐理论模型或Xu等(2004)基于全球SG观测建立的重力潮汐全球实验模型作为固体潮的参考和改正模型.
在武汉台SG C032的14年多连续观测中成功分离出15个3阶潮汐波群，涵盖了周日、半日和1/3日等三个主要潮汐频段.考虑到在不同频段3阶潮汐信号的信噪比及相对观测误差，观测结果与最新理论预测结果具有很好的一致性，基本反映了非弹性地球对3阶引潮力的响应特征.由于现有的海潮模型没有系统提供3阶潮汐等潮图，无法对观测结果作海潮负荷改正，这是导致理论模型与观测结果存在比较大的差异的主要原因.
致谢 武汉台观测和技术保障人员为获得高质量超导重力仪观测资料和其他辅助观测数据付出了辛勤劳动，王晨晨女士对原始观测资料作了精心、细致的预处理，在此表示衷心感谢.| [1] | Agnew D. 1997. NLOADF: A program for computing ocean-tide loading. J. Geophys. Res., 102(B3): 5109-5110. |
| [2] | Boy J P, Gegout P, Hinderer J. 2002. Reduction of surface gravity data from global atmospheric pressure loading. Geophys. J. Int., 149(2): 534-545. |
| [3] | Cheng Y, Andersen O B. 2010. Improvement in global ocean tide model in shallow water regions, Poster, SV.1-68, OST-ST Meeting on Altimetry for Oceans and Hydrology, Lisbon. |
| [4] | Crossley D, Hinderer J. 2009. A review of the GGP network and scientific challenges. J. Geodyn., 48: 299-304. |
| [5] | Dehant V, Defraigne P, Wahr J M. 1999. Tides for a convective Earth. J. Geophys. Res., 104(B1): 1035-1058. |
| [6] | Eanes R J. 1994. Diurnal and semidiurnal tides from TOPEX/POSEIDON altimetry. Eos Trans. AGU, 75(16): 108. |
| [7] | Egbert G D, Erofeeva S Y. 2002. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean. Tech., 19(2): 183-204. |
| [8] | Farrell W E. 1972. Deformation of the Earth by surface loads. Rev. Geophys. Space Phys., 10(3): 761-797. |
| [9] | Hartmann T, Wenzel H G. 1995. The HW95 tidal potential catalogue. Geophys. Res. Lett., 22(24): 3553-3556. |
| [10] | Hinderer J, Florsch N, Mäkinen J, et al. 1991. On the calibration of a superconducting gravimeter using absolute gravity measurements. Geophys. J. Int., 106(2): 491-497, doi:10.1111/j.1365-246X.1991.tb03907.x. |
| [11] | Hinderer J, Crossley D. 2004. Scientific achievements from the first phase (1997—2003) of the Global Geodynamics Project using a worldwide network of superconducting gravimeters. J. Geodyn., 38(3-5): 237-262. |
| [12] | Kroner C, Jentzsch G. 1999. Comparison of different barometric pressure reductions for gravity data and resulting consequences. Phys. Earth Planet. Inter., 115(3-4): 205-2187. |
| [13] | Luo S C, Sun H P, Xu J J. 2005. Theoretical computation of the barometric pressure effects on deformation, gravity and tilt. Chinese J. Geophys. (in Chinese), 48(6): 1288-1294. |
| [14] | Lyard F, Lefevre F, Letellier T, et al. 2006. Modelling the global ocean tides: modern insights from FES2004. Ocean Dynam., 56(5-6): 394-415. |
| [15] | Métivier L, Conrad C P. 2008. Body tides of a convecting, laterally heterogeneous, and aspherical Earth. J. Geophys. Res., 113, B11405,doi: 10.1029/2007JB005448. |
| [16] | Mao H Q, Xu H Z, Song X L, et al. 1989. East-west gravity tidal profile of China. Chinese J. Geophys. (in Chinese), 32(1): 62-69. |
| [17] | Mathews P M. 2001. Love numbers and gravimetric factor for diurnal tides. J. Geod. Soc. Japan, 46(4): 231-236. |
| [18] | Matsumoto K, Takanezawa T, Ooe M. 2000. Ocean tide models developed by assimilating Topex/Poseidon altimeter data into hydrodynamical model: a global model and a regional model around Japan. J. Oceanogr., 56(5): 567-581. |
| [19] | Melchior P, Fang J, Ducarme B, et al. 1985. Studies on the Earth tidal observations in China. Chinese J. Geophys. (in Chinese), 28(2): 142-154. |
| [20] | Melchior P. 1994. A new data bank for tidal gravity measurements (DB 92). Phys. Earth Planet. Inter., 82(2): 125-155. |
| [21] | Melchior P, Deucarme B, Francis O. 1996. The response of the Earth to tidal body forces described by second- and third-degree sphericall harmonics as derived from a 12-year series of measurements with the superconducting gravimeter GWR/T3 in Brussels. Phys. Earth Planet. Inter., 93(3-4): 223-238. |
| [22] | Merriam J B. 1992. Atmospheric pressure and gravity. Geophys. J. Int., 109(3): 488-500. |
| [23] | Ray R D. 1999. A global ocean tide model from TOPEX/POSEIDON altimetry: GOT99. NASA Tech. Mem., 209478, Goddard Space Flight Center, Greenbelt, MD, USA. |
| [24] | Riccardi U, Rosat S, Hinderer J. 2012. On the accu-racy of the calibration of superconducting gravimeters using absolute and spring sensors: A critical comparison. Pure Appl. Geophys., 169(8): 1343-1356, doi:10.1007/s00024-011-0398-8. |
| [25] | Savcenko R, Bosch W. 2008. EOT08a-empirical ocean tide model from multi-mission satellite altimetry, DFGI Report 81, Deutsches Geödtisches Forschungsinstitut (DGFI), Munich. |
| [26] | Schwiderski E W. 1980. Ocean Tides I, Global ocean tidal equations. Marine Geod., 3(1-4): 161-217. |
| [27] | Song X, Mao H. 1991. Study of the tidal gravity standard in Wuchang. Chinese J. Geophys. (in Chinese), 34(3): 381-384. |
| [28] | Sun H P. 1997. Atmospheric gravity Green's functions. Chin. Sci. Bullet. (in Chinese), 42(20): 1712-1719. |
| [29] | Sun H P, Chen X D, Hsu H T, et al. 2001. Accurate determination of calibration factor for tidal gravity observation of a GWR-superconducting gravimeter. Acta Seismol. Sin., 14(6): 692-700, doi:10.1007/BF02718080. |
| [30] | Sun H P, Xu H Z, Zhou J C, et al. 2005. Latest observation results from superconducting gravimeter at station Wuhan and investigation of the ocean tide models. Chinese J. Geophys. (in Chinese), 48(2): 299-307. |
| [31] | Sun H P, Xu J Q, Chen X D, et al. 2013. Results of gravity observations using a superconducting gravimeter at the Tibetan Plateau. Terr. Atmos. Ocean. Sci., 24(4): 541-550. |
| [32] | Taguchi E, Stammer D, Zahel W. 2014. Inferring deep ocean tidal energy dissipation from the global high-resolution data-assimilative HAMTIDE model. J. Geophys. Res.:Oceans,119(7):4573-4592. |
| [33] | Vauterin P. 1998. Tsoft: Graphical & interactive software for the analysis of Earth tide data. // Ducarme B, Paquet P. Proceedings of the 13th International Symposium on the Earth Tides, Brussels. 481-486. |
| [34] | Wahr J M. 1981. Body tides on an elliptical, rotating, elastic and oceanless earth. Geophys. J. R. astr. Soc., 64(3): 677-703. |
| [35] | Wenzel H G. 1996. The nanogal software: data processing package ETERNA 3.3. Bull. Inf. Marées Terrestres., 124: 9425-9439. |
| [36] | Xu H Z, Mao W J. 1988. Correction model of ocean loading tides in Chinese continent. Science in China, Ser. B (in Chinese), 18(9): 984-994. |
| [37] | Xu H Z, Sun H P, Xu J J et al. 2000. International tidal gravity reference values at Wuhan station. Science in China, Ser. D, 43(1): 77-83. |
| [38] | Xu J Q, Hao X H, Sun H P. 1999. Influence of atmospheric pressure on tidal gravity at Wuhan station. Acta Geodaetica et Cartographica Sinica (in Chinese), 28(1): 75-79. |
| [39] | Xu J Q, Sun H P. 2003. Deformation response of a SNREI Earth to surface loads and tidal forces. Chinese J. Geophys.(in Chinese), 46(3): 465-477. |
| [40] | Xu J Q, Sun H P, Ducarme B. 2004. A global experimental model for gravity tides of the Earth. J. Geodyn., 38(3-5): 291-304. |
| [41] | Xu J Q, Chen X D, Zhou J C, et al. 2012. Characteristics of tidal gravity changes in Lhasa, Tibet, China. Chin. Sci. Bull., 57(20): 2586-2594, doi: 10.1007/s11434-012-5130-2. |
| [42] | Zhou J C, Xu J Q, Su H P. 2009. Accurate correction models for tidal gravity in Chinese continent. Chinese J. Geophys. (in Chinese), 52(6): 1474-1482. |
| [43] | 罗少聪, 孙和平, 徐建桥. 2005. 大气变化对位移、重力和倾斜观测影响的理论计算. 地球物理学报, 48(6): 1288-1294. |
| [44] | 毛慧琴, 许厚泽, 宋兴黎等. 1989. 中国东西重力潮汐剖面. 地球物理学报, 32(1): 62-69. |
| [45] | Melchior P, 方俊, Ducarme B等. 1985. 中国固体潮观测研究. 地球物理学报, 28(2): 142-154. |
| [46] | 宋兴黎, 毛慧琴. 1991. 武昌重力潮汐基准研究. 地球物理学报, 34(3): 381-384. |
| [47] | 孙和平. 1997. 大气重力格林函数. 科学通报, 42(15): 1640-1646. |
| [48] | 孙和平, 许厚泽, 周江存等. 2005. 武汉超导重力仪观测最新结果和海潮模型研究. 地球物理学报, 48(2): 299-307. |
| [49] | 许厚泽, 毛伟建. 1988. 中国大陆的海洋负荷潮汐改正模型. 中国科学(B辑), 18(9): 984-994. |
| [50] | 许厚泽, 孙和平, 徐建桥等. 2000. 武汉国际重力潮汐基准研究. 中国科学(D辑), 30(5): 549-553. |
| [51] | 徐建桥, 郝兴华, 孙和平. 1999. 武汉基准台气压对重力潮汐观测的影响. 测绘学报, 28(1): 75-79. |
| [52] | 徐建桥, 孙和平. 2003. SNREI地球对表面负荷和引潮力的形变响应. 地球物理学报, 46(3): 328-343. |
| [53] | 周江存, 徐建桥, 孙和平. 2009. 中国大陆精密重力潮汐改正模型. 地球物理学报, 52(6): 1474-1482. |