2014, Vol. 57
相比于电缆测井技术,随钻测井不仅具有测井成本较低和可以进行地质导向钻井的优点,而且能获得尚未受泥浆浸入影响时的地层信息.如今,随钻电阻率和随钻核磁测井已经发展得比较成熟,但是随钻声波测井却不受石油公司青睐.一个重要原因是在随钻声波测井中会出现在钻铤中传播的波(以下称钻铤波).钻铤波会干扰甚至掩盖从地层中的折射纵波和折射横波,导致无法准确提取地层信息,从而严重影响测井结果.在电缆测井中,为了消除仪器外壳中传播的波对接收信号的影响,通常会在仪器外壳上刻槽,使这部分声波迅速衰减掉.但在随钻声波测井中,钻铤必须保证有足够的强度和刚度来支持钻头进行钻探,且需要给仪器预留足够的安放空间,所以在钻铤上刻槽受到一定约束,不能刻得太深或穿透钻铤,也不能太密.
为了能够消除钻铤波对随钻声波测井结果的影响,Zhu等(2012)提出了随钻动电测井的设想,并在微小模型井中采用超声频率进行了实验测量.在井内激发声波,接收由地层动电效应产生的电磁信号,从中提取地层纵波和横波速度信息,由于动电效应只产生于地层中,井内有可能不出现伴随钻铤声波的电信号,从而可望避开钻铤声信号掩盖地层声信号的问题.基于这种设想,可以不需要在钻铤上刻槽就能实现对地层纵横波速度的测量.但是,至今为止,相关的波场理论分析还很不充分.
随钻动电测井是在电缆动电测井(Zhu et al.,1999; 金鼎等,2010)思想基础上产生的.在井中发射声波,接收来自地层的声信号,同时接收由孔隙地层动电效应产生的声诱导电磁信号,以便获得地层信息的声频(几千赫兹左右频率)动电测井方法,在我国曾称为声电测井(胡恒山和王克协,1999,2000).地层动电效应之所以产生,是因为孔隙地层内的流体通常是电解质溶液,而固体骨架会吸附流体内的带电离子,在流体内形成含净剩电荷的扩散层.当弹性波在孔隙中传播时,会产生孔隙流体相对于固相骨架的流动,这种渗流运动会导致电磁场出现(Pride and Morgan,1991).Pride采用体积平均法,在薄扩散层条件下推导出了描述孔隙岩石弹性-电磁耦合现象的控制方程组(Pride,1994).该方程组中的一个重要参数是动电耦合系数,Li等(1995)通过动电效应测量了砂岩岩样的动态动电耦合系数,王军等开展了类似的实验研究(2010,2012).胡恒山等(1999,2000)最早进行了动电测井波场的理论模拟,他们基于Pride方程组针对充液井孔推导了点声源激发的井孔内外声场和电磁场的解析表达式,并通过计算模拟得到了声场和电磁场的全波波形.随后,胡恒山等(2003)提出了先计算声场,再计算声诱导电磁场的动电测井模拟方法.关于随钻动电测井,目前只能看到Zhan等(2006)进行了理论模拟,他们采用了胡恒山等提出的解耦计算方法,但Zhan忽略了孔隙内流体压强梯度对声波诱导电磁场的影响.为了更准确地模拟随钻动电测井响应,本文考虑弹性波传播过程中,由围压引起的孔隙内流体压强,分析由波动引起的压强梯度对声波诱导电磁场的影响,在计算出随钻动电测井声场和电场的全波之后,考察从声诱导电磁场中提取纵横波速度的可行性.依据计算结果,还将讨论关于软地层井孔中滑行非均匀横波的一个有趣现象.
采用如图1所示的钻铤和井模型,地层是向外无限延伸的,这与Tang等(2002)和崔志文(2004)采用的模型相同,沿径向分布着四层介质,从内而外依次是钻铤内流体、钻铤、钻铤与地层之间流体、井外地层.
 | 图1 随钻声波测井的简化模型 Fig.1 A simplified model of acoustic logging while drilling |
前人在随钻动电测井中,采用了完全弹性固体模型进行模拟(Zhan et al.,2006).为了模拟地层中波的耗散效应,本文采用黏弹性地层模型,并在此基础上考虑孔隙流体流动效应,由平均围压获得孔隙流体压强.采用Biot孔隙地层模型,可以分析声场中慢纵波对声场和动电转换场的影响(Pride,2002; 胡恒山,2003),但是从模拟井孔波衰减的角度看,Biot模型关于纵波和横波衰减的预测都远低于观测值和实验值(Tang et al.,2012;宋永佳和胡恒山,2013),而使用黏弹性模型,通过引入品质因数可以较好地模拟地层实际的耗散效应.因此有必要采用较符合地层衰减特性的黏弹性模型考察波的特性.采用黏弹性地层模型的另一个动机是,可以在退化为弹性地层模型时与前人工作进行比较(Zhan et al.,2006).依据Pride的理论(1994),地层中引起电磁场的声学因素有两个:一是孔隙流体压强梯度,二是固相位移加速度.本文在计算出位移之后,将进一步算出地层围压及其引起的孔隙流体压强分布(陈颙等, 2009),因此从声波诱导产生电磁场的角度看,本文的地层模型反映了动电耦合的主要机制.
如图2所示,声源换能器位于钻铤外表面,换能器高为2z0,厚为h0.在环向上将换能器等分为四片,通过控制每个换能器片上电场的方向,促使每片换能器激发出不同的振动模式.当四片换能器同时径向向外膨胀或是向内收缩时,这种情况下激发的是单极源.若如图2所示,换能器右侧向外膨胀,左侧向内收缩,模拟的是偶极源的情况.
 | 图2 随钻动电测井声源模型(Tang et al.,2002) Fig.2 A schematic model of the multipole source in seismoelectric LWD |
为了能得到数学上的声源表达式,需要对换能器模型进行简化.因为换能器很薄,相对于井孔半径可以忽略不计,所以可以将换能器简化为一个附加在钻铤表面的面声源.考虑换能器激发的声压沿高度按余弦函数分布,则单极换能器源可以表示为(郑晓波,2012)
偶极换能器源可以表示为(郑晓波,2012)
p0是个常数,用于控制声源幅度大小,在本文的计算中令p0=1.0×105 Pa.kz代表的是z轴方向上的波数.S(ω)是余弦包络脉冲声源的频谱函数.
从(2)式可以看出,这种偶极换能器源不是严格的偶极子源,它是由最低阶m=0的偶极、m=1的六极、m=2的十极等更高的多极项构成的,可以看出多极项阶数越高贡献越小,它们的贡献权重分别为1、-1/3、1/5….
在孔隙地层中,动电效应使得声场与电磁场是 相互耦合的.为了简化计算,我们采用胡恒山等(2003) 提出的解耦算法,即先算出声场,再计算声场激发出的电磁场,忽略电磁场激发出的声场.这是因为动电耦合系数是一个非常小的量,在动电测井时,地层中声场诱导产生的电磁场已经比较微弱,由电磁场诱导产生的声场则可以忽略不计.Zhan等使用这种方法计算了随钻动电测井井孔内的声场和电磁场.
首先算出随钻测井的全波声场.在建立模型的解析表达式时,先认为钻铤内外流体为同一种流体,钻铤和地层均是均匀的各向同性固体,通过引入品质因数模拟井内泥浆和井外孔隙介质的耗散效应.
固体中的位移矢量场可用三个势函数φ、 和Γ表示为
流体的位移场可用势函数ψ表示为
使用分离变量法,可以得到四层介质中位移势函数在柱坐标下的多级声场表达式.通过力学边界条件可以确定表达式中的待定系数.声源作为边界条件的一部分引入声场,这与Christophe等(2001)的做法相同.
考虑耗散效应,设泥浆纵波与地层中纵波和横 波的品质因数分别为Qf,Qp,Qs,则波数为复数,即
其中k′ f, k′ p, k′ s分别为泥浆声波波数和黏弹性地层中纵波和横波的波数,kf,kp,ks分别为理想流体声波波数和理想弹性地层中纵波和横波的波数.在计算出井孔内声场之后,可以通过动电效应计算出井内的电磁场.根据Pride理论,在孔隙介质中孔隙流体压强梯度和固相加速度可以引起电流密度变化(Pride,1994):
其中括号内的第二项是作用在孔隙流体中的惯性力.方程中的 E 、 J 分别是电场强度和电流密度, u 是孔隙介质中的固相位移,p是孔隙内流体压强,ρf 是孔隙内流体密度,L是动电耦合系数,ω是角频率.
从(6)式可以看出,地层中有两个因素能诱导产生电场,第一个是孔隙内流体的压强梯度,另一个是孔隙介质固体骨架的固相位移.在使用黏弹性模型进行模拟计算时,孔隙介质的固相位移可以直接使用地层位移代替.对于第一个因素,Zhan在计算中认为使用弹性模型无法获得孔隙流体的压强梯度,因而在计算中将其忽略.其实,在声场计算中可以获得地层的平均围压,孔隙中流体的压强p和孔隙介质围压P存在如下关系(Sava and Revil,2012)：
B是Skempton因子,可以由孔隙地层的基本参数计算获得(详见附录A).
在计算电场时,由于电磁场波长远大于源距和井孔尺寸,则可以将电磁场看作似稳场,即忽略时间的变化,这样由麦克斯韦方程组中电场强度与磁感应强度的关系式可以写为 Δ × E =0.电场是无旋场,引入电势函数有 E =－ ΔφE,则地层内的电势可以写为
φF是地层中的位移势函数.
(8)式在频域和波数域上通解可以写为
A是电势函数中的待定系数,n是声场级数, K是地层的体积弹性模量.
地层内的电势和电流密度可以分别写为
井内电势、电场强度和电流密度可以写为
三个待定系数需要通过三个电场边界条件确定.首先,在井壁处有电势连续φE=φEf和径向电流连续Jr=Jfr.然后,金属钻铤是一个理想导体, 理想导体表面是等电势面, 则电场线垂直于理想导体表面,导体表面的切向电场为零.所以边界条件应该是在钻铤外表面处,切向电场为零Efz=0.而Zhan却使用了Efr=0作为边界条件,这与我们提出的电场边界条件不同.
使用上述三个边界条件,就可以得到电场的三 个待定系数(具体表达式详见附录B), 进而确定电场.
表1给出了模型的几何尺寸和计算声场所需的物理参数.表2则给出了计算电场所需的参数.
|
表1 随钻声场计算参数 Table 1 The parameters in acoustic LWD modeling |
|
|
表2 电场计算所需的井外地层参数 Table 2 Formation parameters in electric field simulation |
动电耦合系数是一个与频率有关的物理量,用来表征弹性声场和电磁场的耦合作用.计算时采用 Pride(1994)给出的动电耦合系数的表达式,其低频极限值可以写为
φ是孔隙度,εF是孔隙内流体的介电常数,ζ是双电层剪切滑移面上的电势,需要通过实验测量, Pride和Morgan给出了拟合关系式(1991):
Cf是孔隙流体的矿化度,α∞是孔隙介质的弯曲度,η是孔隙流体的黏性系数.
是Pride定义的长度,它小于等于Debye长度,且有
kB是Boltzman常数,T是开尔文温度,e是元电子电荷电量,z是电解质溶液的离子价数,N是离子浓度.Λ是一个反映孔道加权体表比的物理量,具有长度的量纲,圆柱型孔道的Λ就等于孔隙半径.
使用实轴积分法(Tsang and Rader,1979),可以得到井内声场和电场的全波波形.图3a和3b分别给出了当地层分别是硬地层和软地层时,中心频率为8 kHz,源距为4 m处钻铤表面接收到的声压图.图中黑色实线是存在耗散时的计算结果,灰色点划线是完全弹性的计算结果.
 | 图3 快速地层(a)和慢速地层(b)中的声场全波图形, 单极源中心频率为8 kHz.P为接收到的径向压强 Fig.3 Synthetic waveforms associated with an 8 kHz monopole source in a fast formation (a) and in a slow formation (b) |
从图3中可以发现,声场中的钻铤波最先出现且幅度很明显.快速地层中,钻铤波掩盖了折射纵波,导致无法提取地层的纵波波速.在流体和井外地层中加入耗散后,地层折射波和导波的幅度均出现明显减弱,但是钻铤波的幅度并没有明显改变,这说明钻铤波在其传播过程中很少受到井内流体和地层耗散效应的影响.同时,当井外地层变化时,可以发现钻铤波没有太大的变化,说明这个波群对地层参数并不敏感.
根据附录A,可得快速地层中Skempton因子 为0.2422,慢速地层为0.2968.图4给出当Skempton 系数为零,即忽略孔隙内流体压强和考虑孔隙内流 体压强结果对比图,源距仍为4 m,中心频率8 kHz, 井外地层为快速地层.
 | 图4 Skempton系数取不同值时钻铤表面径向电场全波波形,单极源中心频率为8 kHz Fig.4 Synthetic waveforms of the electric field associated with an 8 kHz monopole source in the fast formation using different Skempton factor |
图4中的灰色实线是B=0时,即忽略孔隙内流体压强梯度的计算结果,黑色点划线是考虑了压强梯度的结果.图中可以明显看出,如果忽略孔隙流 体压强梯度项,电场斯通利波的幅度将变得十分微弱,这说明孔隙流体压强在声场诱导电磁场过程起到重要作用,在计算模拟时不能将其忽略.
在考虑孔隙流体压强梯度后,将钻铤表面接收 到的声压和径向电场放在一起进行对比,如图5所示.
 | 图5 快速地层中钻铤表面接收到的声压和径向电场的全波波形与时间慢度S图 单极源中心频率为8 kHz. (a)归一化后的声场(灰色实线)与电场(黑色点划线)的阵列图；(b)源距4.0 m处接收到的声压和径向电场的 全波图形；(c)声场的时间慢度图；(d) 电场的时间慢度图.Sf,Ss,Sp分别表示井内流体中声波的慢度，地层横波慢度和地层纵波慢度. Fig.5 Synthetic waveforms and semblance plots of the seismoelectric-LWD with an 8 kHz monopole source in a fast formation (a) Normalized full waveforms of the acoustic pressure (gray solid lines) and the electric fields (black dot lines)； (b) Full waveforms of acoustic field and electric field at 4.0 m； (c) Semblance plot for the acoustic field； (d) Semblance plot for the electric field. |
图5a给出中心频率为8 kHz,快速地层中钻铤表面接收到的声场和电场归一化阵列图.5b是源距4 m处的接收信号,灰色实线代表声场,黑色点划线代表电场.5c和5d分别是声场和电场的时间慢度图.从图5a中可以看出有三个明显的波群,a-a波群是电磁首波波群,相对幅度十分微弱,在时间慢度图上无法显示. b-b波群是单极钻铤波,这个波掩盖了折射纵波,对测井结果造成影响.c-c波群是折射横波,d-d波群是斯通利波.将图5c和图5d对比可以看出，声场和电场的三个波群速度完全相同,说明电场的三个波群是声场三个波群诱导产生的.
Zhan认为钻铤波是在钻铤中传播的,钻铤中没有动电现象,所以钻铤声波不会激发出电场,井内电场不存在钻铤波成分.我们认为这个结论是值得商榷的,声场的钻铤波在沿着钻铤传播时,也可以看作是一个声源,从这个声源激发出的波会辐射到地层中,所以地层中也会有钻铤波的信号.图6给出了中心频率8 kHz时,井壁表面接收到的声压的阵列图和时间慢度图.图6a中可以明显看出存在三个波群,图6b显示了三个波群的速度,a-a波群的速度与 图5中钻铤波的速度相同,说明井壁处也会有钻铤波的存在.地层中的钻铤波同样能激发出电场并返回井中,所以在钻铤表面接收到的电场中仍然会有钻铤波的信号.但是声场中钻铤波主要能量是在钻铤中传播的,辐射进入地层的能量较少,所以电场中钻铤波的相对幅度小于声场中的相对幅度.在图5b中,由计算数据可知电场中钻铤波最大幅值是电场全波最大幅值的10.36%,而声场中为20.95%,声场和电场在相位上还有些差别.
 | 图6 快速地层井壁表面接收到的声压全波波形与时间慢度图单极源中心频率为8 kHz. (a)归一化后的声场；(b)声场的时间慢度图. Fig.6 Synthetic waveforms and semblance plots of the seismoelectric-LWD at the borehole well with an 8 kHz monopole source in a fast formation (a) Normalized full waveforms of the acoustic pressure；(b) Semblance plot for the acoustic field. |
图7给出中心频率为4 kHz时软地层中的全波 声场和电场.图7a中a-a波群仍然是电磁首波,信号十分微弱,没有明显的幅度变化.b-b波群是软地层中的单极钻铤波,在软地层中,电场钻铤波的相对幅度仍然小于声场钻铤波的相对幅度.c-c波群是在钻铤内表面形成的导波(称为内斯通利波),比较图7b和图7c可以发现这个波没有激发出电场.这是因为内斯通利波在钻铤内表面形成并传播,能量基本没有泄露到井外地层中,所以不会在地层中诱导产生电场信号.e-e波群是井壁处的斯通利波.
 | 图7 慢速地层钻铤表面接收到的声压和径向电场 单极源中心频率为4 kHz. (a)接收器距声源中心3 m到4 m处接收到的声场和电场归一化波形阵列图, 灰色实线代表声场, 黑色点划线代表电场；(b)使用STC方法处理得到声场的时间慢度图；(c)使用STC方法处理得到电场的时间慢度图. Fig.7 Synthetic waveforms and semblance plots of the seismoelectric LWD in the slow formation with a 4 kHz monopole source in a slow formation (a) Normalized full waveforms of the acoustic pressure (gray solid lines) and the electric fields (black dot lines)； (b) Semblance plot for the acoustic field；(c) Semblance plot for the electric field. |
图8首先给出中心频率为8 kHz,由偶极换能器源激发,源距3.0 m至4.0 m处,快速地层中声场和电场的计算结果.图8a中a-a波群是电场的首波波群.c-c波群是偶极声场中的弯曲波.d-d波群则是公式(2)中,m=1时的六级声场,其他高阶声场十分微弱,无法显示.
 | 图8 快速地层钻铤表面接收到的声压和径向电场 偶极源中心频率为8 kHz. (a) 接收器距声源中心3 m到4 m处接收到的声场和电场归一化波形阵列图, 灰色实线代表声场,黑色点划线 代表电场；(b) 4.0 m处完全弹性介质和引入衰减后声场的对比图；(c) 声场的时间慢度图；(d) 电场的时间慢度图. Fig.8 Synthetic waveforms and semblance plots of the seismoelectric LWD with an 8 kHz dipole source in a fast formation (a) Normalized full waveforms of the acoustic pressure (gray solid lines) and the electric fields (black dot lines)；(b) Full waveforms of acoustic pressure with the absorption in the fluid and formation considered and pressure when the media are purely elastic at 4.0 m；(c) Semblance plot for the acoustic field；(d) Semblance plot for the electric field. |
需要注意的是,在图8a中的b-b线附近, 电场看上去是一个波群, 而声场中则是由两个波群互相干扰形成的.在声场时间慢度图中可以看出这两个波群的速度比较接近,为了区分这两个波群的性质,图8b比较了完全弹性和引入耗散后4.0 m处声场的全波图形.可以看出前一个波群不受井外地层和井内流体耗散作用的影响,而后一个波群幅度出现了明显减弱,这说明前一个波群是偶极钻铤波,后一个波群是从井壁反射回来的折射横波.若在钻铤中引入耗散,电场中的波形幅度不出现明显变化,说明电场波形中钻铤波信号很小或不出现;若源距增大至5 m,就可见分离的钻铤波与横波,只是钻铤波幅度小而已.可见在图8的特殊情况下钻铤波在地层中引起的电磁场比较微弱,它被伴随地层折射横波的电磁场所掩盖,导致电场中钻铤波难以被识别.
图9给出在中心频率为4kHz,慢速地层中声场与电场的全波图形,图9a中的a-a波群是电磁首波,这幅图中的电磁首波比较明显,这是因为此时的电场幅度较弱, 最大幅度是10－5V/m,比前面的算例小一个数量级.b-b波群是偶极的钻铤波,同样电场钻铤波的相对幅度仍然明显小于声场钻铤波的相对幅度.c-c波群是偶极的弯曲波.
 | 图9 慢速地层钻铤表面接收到的声压和径向电场中心频率 偶极源中心频率为4 kHz. (a) 接收器距声源中心3 m到4 m处接收到的声场和电场归一化波形阵列图, 灰色实线代表声场, 黑色点划线代表电场；(b) 使用STC方法处理得到声场的时间慢度图；(c)使用STC方法处理得到电场的时间慢度图. Fig.9 Synthetic waveforms and semblance plots of the seismoelectric LWD with a 4 kHz dipole source in a slow formation (a) Normalized full waveforms of the acoustic pressure (black solid lines) and the electric fields (red solid lines)； (b) Semblance plot for the acoustic field；(c) Semblance plot for the electric field. |
值得注意的是在图9c 电场时间慢度图中,出现了一个接近地层横波速度的信号,在图9a中由d-d标出.但在声场中并没有出现这个信号.经分析,这个信号是软地层中的临界折射横波(王克协等,1998).软地层声场中存在非均匀的折射横波,这个波的特点是沿着井壁传播,离开井壁后幅度会迅速减小,所以在井内很难接收到这个波的信号.然而在地层中非均匀折射横波仍然可以诱导产生出电场,被激发出的电场并不是非均匀电场,电场信号幅度不受离开井壁距离的影响,所以电场信号可以在井中被接收到.测量软地层中的横波速度一直是实际测井中比较困难的问题,现在大部分声波测井仪器都是通过测量弯曲波的低频极限速度来代替地层横波速度,这种方法存在一定的误差.从上面的结果可以看出,动电测井对软地层横波速度的测量提供了一种新的方法,在工程实际运用上有潜在的价值.
本文对随钻动电测井的声诱导电磁场进行了理论模拟.与前人忽略孔隙压强对渗流和动电效应贡献的做法不同,本文在获得了地层应力后,通过引入Skempton因子计算了孔隙流体压强和声诱导电磁场.模拟结果表明,孔隙流体压强梯度对声波诱导电磁场的影响不可忽略,在斯通利波的动电转换中,孔隙流体压强梯度起主要作用.
地层中也存在以钻铤波速度传播的声信号,它也引起电场,所以钻铤表面的径向电场中会含有钻铤波的成分.但是,电场中钻铤波的相对幅度明显小于声场中钻铤波的相对幅度,在一些情况下甚至不易观察到钻铤波电信号.可见,利用动电效应可以有效地削弱钻铤波的幅度,在一定程度上消除钻铤波对声场的干扰,尽管不能完全消除钻铤波的影响.
比较了慢速地层偶极源激发的声场和声诱导电磁场,发现了一个在声场中难以看见,而在电场中清晰可见的波群.分析表明,它与软地层中非均匀临界折射横波对应.非均匀横波的特点是离开井壁后幅度迅速减弱,导致井内接收不到这个声波信号.然而,非均匀折射横波在井壁上可以诱导电磁场,电磁场的幅度并不随离开井壁的距离而减弱,所以在电场中能看到一个明显的以地层横波速度传播的信号,这样就为软地层横波速度的测量提供了一种新的方法.
Skempton因子B的定义是在不排水(ξ=0)的条件下,孔隙流体压强p的变化与围压P改变的比值,可写成
式中Kc是孔隙介质不排水体积模量,M为Biot定义的模量,它们以及系数α的表达式为
其中φ为地层孔隙度,Kb, Ks和Kf分别为孔隙介质的固相骨架体积模量、固体基质体积模量和孔隙流体体积模量.因此,当给定地层孔隙度和体积模量 Kb、Ks和Kf时,可根据(A1)—(A4)算出Skempton 因子的值.
可以将三个边界条件写成一个线性方程组：
其中
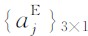为电场势函数的待定系数向量:
为源向量:
其中
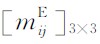中的元素分别为
| [1] | Chen Y, Huang T F, Liu E R. 2009. Rock Phycics (in Chinese). Hefei: Press of University of Science and Technology of China. |
| [2] | Christophe L, Jean M Cr, Olivier L. 2001. Acoustic radiation of cylindrical elastic shells subjected to a point source: Investigation in terms of helical acoustic rays. J. Acoust. Soc. Am. , 110(4): 1783-1791. |
| [3] | Cui Z W. 2004. Theoretical and numerical study of modified Biot′s models, acoustoelectric well logging and acoustic logging while drilling excited by multipole acoustic sources[Ph. D. thesis](in Chinese). Jilin: Jilin University. |
| [4] | Hu H S. 2003. Acoustic head wave on the borehole wall in a porous formation and the causes for its accompanying electromagnetic field. Acta Physica Sinica (in Chinese), 52(8): 1954-1959. |
| [5] | Hu H S, Liu J Q, Wang H B, et al. 2003. Simulation of acousto-electric well logging based on simplified pride equations. Chinese J. Geophys. (in Chinese), 46(2): 259-264. |
| [6] | Hu H S, Wang K X. 1999. Coupled acoustic and electromagnetic waves around a borehole embedded in a porous formation: theory (1). Well Logging Technology (in Chinese), 23(6): 427-432. |
| [7] | Hu H S, Wang K X. Coupled acoustic and electromagnetic waves around a borehole embedded in a porous formation: Part 2. numerical simulation of acoustically induced fields. Well Logging Technology (in Chinese), 2000, 24(1): 3-13. |
| [8] | Jin D, Sun B D, Hu H S, et al. 2010. Electrokinetic logging: State of the art and future challenges. Well Logging Technology (in Chinese), 34(4), 309-313 |
| [9] | Li S X, Pengra D B, Wang P Z. 1995. Onsager′s reciprocal relation and the hydraulic permeability of porous media. Phys. Rev. , E51(6): 5748-5751. |
| [10] | Pride S R, Garambois S. 2002. The role of Biot slow waves in electroseismic wave phenomena. J. Acoust. Soc. Am. , 111(2): 697-706. |
| [11] | Pride S R, Morgan F D. 1991. Electrokinetic dissipation induced by seismic waves. Geophysics, 56(7): 914-925. |
| [12] | Pride S R. 1994. Governing equations for the coupled electromagnetics and acoustics of porous media. Phys. Rev. B. , 50(21): 15678-15696. |
| [13] | Sava P, Revil A. 2012. Virtual electrode current injection using seismic focusing and seismoelectric conversion. Geophysical Journal International, 191(3): 1205-1209. |
| [14] | Song Y J, Hu H S. 2013. Effects of squirt-flow in cracks on drained bulk modulus of porous media. Chinese Journal of Theoretical and Applied Mechanics (in Chinese), 45(3): 1-11 |
| [15] | Tang X M, Chen X L, Xu X K. 2012. A cracked porous medium elastic wave theory and its application to interpreting acoustic data from tight formations. Geophysics, 77(6): D245-D252. |
| [16] | Tang X M. Wang T. Patterson D. 2002. Multipole Acoustic Logging-While-Drilling. SEG Annual Meeting. |
| [17] | Tsang L, Rader D. 1979. Numerical evaluation of the transient acoustic waveform due to a point source in a fluid-filled borehole. Geophysics, 44(10): 1706-1721. |
| [18] | Wang J, Hu H S, Xu X R, et al. 2010. Experimental measurement study on rock permeability based on the electrokinetic effect. Chinese J. Geophys. (in Chinese), 53(8): 1953-1960 |
| [19] | Wang J, Hu H S. 2012. The determination of electrokinetic coupling-coefficient and zeta potential of rock samples by electrokinetic measurements. Advanced Materials Research, 516-517: 1870-1873. |
| [20] | Wang K X, Ma J, Liu J S, et al. 1998. The interpretation about the soft formation glide S wave in acoustic logging. Well Logging Technology (in Chinese), 22(S1): 19-23. |
| [21] | Zhan X, Chi S, Toks?z M N. 2006.Simulation of the converted electric field during multipole logging while drilling (LWD), 76th SEG Annual International Meeting, New Orleans, Louisiana, USA, Expanded Abstracts, 25, 446-450. |
| [22] | Zheng X B. 2012. The full-wave simulation of acoustic logging while drilling[Master thesis](in Chinese). Harbin: Harbin Institute of Technology. |
| [23] | Zhu Z, Haartsen M W, Toksöz M N. 1999. Experimental studies of electrokinetic conversions in fluid-saturated borehole models. Geophysics, 64(5): 1349-1356. |
| [24] | Zhu Z, Wang J, Toks z M N. Multipole seismoelectric logging while drilling (LWD) for acoustic velocity measurements. 74th EAGE Conference & Exhibition incorporating SPE EUROPEC. 2012. |
| [25] | 陈颙 ,黄廷芳,刘恩儒. 2009. 岩石物理学. 合肥: 中国科学技术大学出版社. |
| [26] | 崔志文. 2004. 多孔介质声学模型与多极源声电效应测井和多极随钻声测井的理论与数值研究[博士论文]. 吉林: 吉林大学. |
| [27] | 胡恒山. 2003. 孔隙地层井壁上的声波首波及其诱导电磁场的原因. 物理学报, 52(8): 1954-1959. |
| [28] | 胡恒山, 刘家琦, 王洪滨等. 2003. 基于简化的 Pride理论模拟声电效应测井响应. 地球物理学报, 46(2): 259-264. |
| [29] | 胡恒山, 王克协. 1999. 井孔周围轴对称声电耦合波: (I)理论. 测井技术, 23(6): 427-432. |
| [30] | 胡恒山, 王克协. 2000. 井孔周围轴对称声电耦合波: (II)声电效应测井数值模拟. 测井技术, 24(1): 3-13. |
| [31] | 金鼎, 孙宝佃, 胡恒山等. 2010. 动电效应测井研究现状和展望. 测井技术, 34(4): 309-313. |
| [32] | 宋永佳, 胡恒山. 2013. 裂隙挤喷流对孔隙介质排水体积模量的影响. 力学学报, 45(3): 1-11. |
| [33] | 王军, 胡恒山, 徐小蓉等. 2010. 基于动电效应的岩芯渗透率实验测量. 地球物理学报, 53(8): 1953-1960. |
| [34] | 王克协, 马俊, 刘继生等. 1998. 对声波测井中软地层也存在滑行横波的诠释. 22(增刊): 19-23. |
| [35] | 郑晓波. 2012. 随钻声波测井的全波计算[硕士论文]. 哈尔滨: 哈尔滨工业大学. |