2. 中石油勘探开发研究院西北分院, 兰州 730020;
3. 大庆油田有限责任公司测试技术服务分公司第一大队, 大庆 163000
2. North-west Division, Exploration and Development Research Institute, CNPC, Lanzhou 730020, China;
3. The First Group of Testing Technology Service Division, Daqing Oilfield Co., Ltd, CNPC, Daqing 163000, China
由于近地表低、降速带风化层的横向厚度和速度的变化,以及地震排列上炮点耦合、检波点耦合条件的差异等近地表因素以及地下介质的非均一性和地下构造的复杂性等造成了地震子波相位随时间和空间变化(李振春等,2008).将地震子波校正到零相位,不仅可以改善叠加剖面的质量,而且能够有效提高资料的分辨率.因此,在常规地震数据处理中,有必要进行相位校正方法方面的研究.
关于子波的零相位化,国外研究起步较早,Levy和Oldenburg(1987)、Longbottom等(1988)、White(1988)在Wiggins(1978,1985)提出的盲反褶积的基础上,提出最大方差模准则进行常相位估计.相对盲反褶积方法,该方法自由参数变少,算法更加稳定.从理论上证明了常相位校正只是在不改变地震道包络的前提下改变子波的波形.为了考虑地震子波相位的时变性,Baan等(2008)和陈必远等(1997)采用滑动时窗方法对子波相位进行估计,但是该方法有效的前提是相位变化分段平稳.针对这一问题,Baan等(2009,2010) 、Fomel等(2010)和刘玉金等(2012)进一步将相位估计看作一个最优化反演问题,利用局部地震属性的概念进行非稳态相位估计,从而提高相位估计的精度,改善相位校正的稳定性.针对子波相位受复杂地表因素的影响,国九英等(1995)、高少武等(2001)分别提出了地表一致性相位校正方法.另外,李合群等(2000)同时对相位和时差进行了局部调整从而改善叠加质量.为了消除相位不一致性对叠加产生的影响,宋宗平等(2004)、单联瑜等(2008)在叠前道集中利用常相位校正技术提高叠加剖面的信噪比,改善同相轴的连续性.
综上所述,以往的研究主要集中于常相位校正,当地震子波随时间、空间变化剧烈时,常相位校正方法无法得到正确的零相位子波.滑动时窗进行常相位校正虽然可以在一定程度上解决这一问题,但是由于受分段平稳条件的限制,估计出来的相位角不够准确,进行相位校正时容易出现不稳定的现象.虽然基于局部方差模准则进行相位校正可以较好地考虑子波相位的非稳态性,但是该准则有效的前提是反射系数序列符合随机超高斯分布,具有一定的局限性.基于局部相似度准则采用地震道包络进行相位校正虽然没有这一前提限制,但是计算地震道包络时容易将薄层信息丢失,而且容易出现相位倒转,为了解决这一问题,最好的办法是采用测井合成记录作为模型道在局部相似度准则下进行相位校正,但是测井数据往往有限,针对这一问题,本文结合测井数据和井旁地震记录包络形成模型道,利用局部相似度准则估计出井旁地震数据的局部相位属相,再利用局部倾角信息将井旁地震道的相位信息插值到整个地震剖面,从而得到随时间和空间变化的相位信息,利用该信息即可对整条剖面进行相位校正.相对于线性插值等数学插值方法,平面波预测方法考虑了地震剖面的局部构造信息,因此更为合理.最后通过理论模型和实际资料处理验证本文方法具有更高的精度和更好的稳定性.
对地震数据应用一系列的常相位旋转,根据不同的判别准则,可以估计出数据的相位角.地震道x(t)经过常相位旋转后变为:
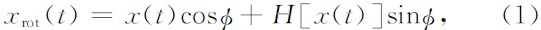
式中,φ为相位旋转角度,可以为常数,也可以随时间变化,H[·] 表示Hilbert变换,采用不同的零相位判别准则,可以得到不同的相位校正方法.
最大方差模准则(White,1988;Wiggins,1978;Wiggins,1985;周兴元,1989)是指地震道经过相位旋转后方差模达到最大时对应的旋转角度为所求的相位角,该准则利用方差模来衡量地震道偏离高斯分布的程度,方差模越大,地震道的非高斯性越强,地震道的相位越接近于零相位.
方差模的定义为:
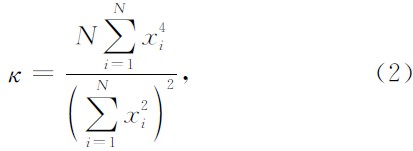
其中xi表示大小为N的时窗内地震振幅值,通过相位角扫描计算该时窗内的方差模,当方差模达到最大时所对应的相位角就是该时窗内子波的相位.
相似系数准则是指地震道经过相位旋转后与标准道的相似度达到最大时对应的旋转角度为所求的相位角.标准道一般利用测井资料合成地震记录得到(Fomel,2007).当没有测井资料可用时,可以选择地震道的包络作为标准道(国九英等,1995).
两个时间序列ai和bi的相似系数定义为:
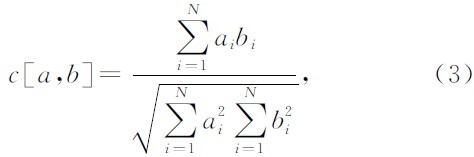
而时间序列ai和常数1的相似系数为:
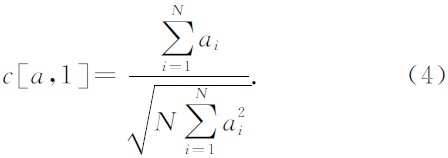
从公式(1)和公式(3)可以看出,方差模可以看作xi2和常数1相似度平方的倒数,也即:
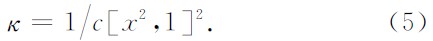
当地震道经过相位旋转成为零相位信号时方差模达到最大,和常数信号的相关性达到最低,因此最大方差模准则可以和相似系数准则统一起来.从公式(2)可以看出,用一个参数来描述两个信号之间的相关性有一定的局限性,采用局部地震属性的思想,可以将公式(3)中的相似系数改为随时间变化的函数,从而描述两个信号相似度的局部变化.
公式(3)可以看作两个最小二乘反演问题解的乘积,
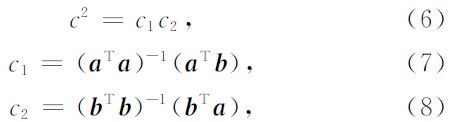
其中a、b分别是信号a(t)、b(t)的向量表示,xTy表示向量x和y点乘.由向量a、b的元素分别构造对角矩阵A、B,对方程局部化后相当于对反演加入正则化条件,标量c1和c2变为向量c1和c2,利用整型正则化,方程(7)、(8)变为:
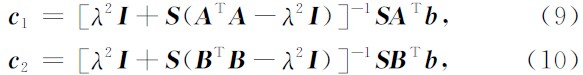
其中S为平滑算子,向量c1和c2各元素对应相乘后得到随时间变化的局部相似度c, 关于整型正则化反演具体细节可以参考文献(Fomel,2007).利用公式(5)和局部相似度的思想,可以计算出地震数据的局部方差模,从而实现非稳态相位估计和校正.
当有测井资料时,首先采用测井资料合成地震记录,由于测井数据记录时间往往短于地震数据记录时间,为此,测井数据记录时间之外的数据用井旁地震道的包络来代替,这样就合成了一道与原地震数据记录时间相同的模型道,根据这个模型道对井旁数据进行局部相似度准则下的非稳态相位估计,得到随时间变化的相位属性.由于实际勘探中,测井数据往往比较少,这就需要考虑如何将井数据处的相位信息插值到其他位置处.为此本文采用平面波预测滤波器算子来解决这一问题.下面详细介绍平面波预测滤波器的基本原理.
平面波预测滤波器来源于描述地震数据的局部 平面波模型,可以用下面的微分方程来描述(Clae rbout,1992):
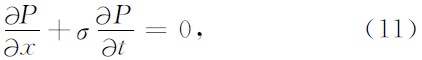
其中P(t,x)为地震波场,σ为随时间和空间变化的局部倾角.当倾角为常数时,(11)式的通解为:
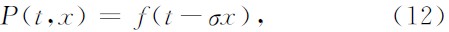
其中f(t)为任意波形,(12)式是从数学上描述了一个平面波.假定倾角σ随时间和空间变化,则可以设 计一个将每个地震道传播到相邻地震道的局部算子.
假定地震剖面s由一系列地震道组成,s=[s1 s2…sN]T.平面波解构滤波器(PWD)算子(Fomel,2002)根据相邻道预测该道数据,并将原始道与预测道相减,数学表达式为:

其中r为剩余量,D为PWD算子,定义为:

其中I为单位算子,P为预测算子,通过沿同相轴倾角方向移动原始道来预测下一道地震数据,Pi,j表示由第i道预测第j道的算子.式(13)可以通过正则化共轭梯度法最小化预测误差r 估计出主要的局部倾角信息.该反演问题的约束条件通常是使得数据空间倾角平滑变化(Fomel,2007).
PWC算子是PWD算子的逆,可以通过递归算法快速实现PWC算子:
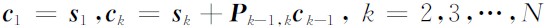
具体推导过程请参考文献(Fomel et al.,2006).
在最大相似度准则下,利用测井数据和井旁地震道包络合成参考道,然后利用参考道对井旁地震道进行相位估计,估计出来的相位信息随时间变化,再根据PWD预测的局部倾角信息,采用平面波预测算子将井旁地震道的相位信息插值到其他位置,即可得到随时间和空间变化的相位属性.如果存在多个测井数据,可以利用相同的方法得到多张相位属性剖面,再对这些相位属性剖面进行平均,则得到最终的局部相位信息,利用该相位信息可对原地震剖面进行相位校正,改善剖面质量,提高资料的分辨率,具体实现流程如图1所示.
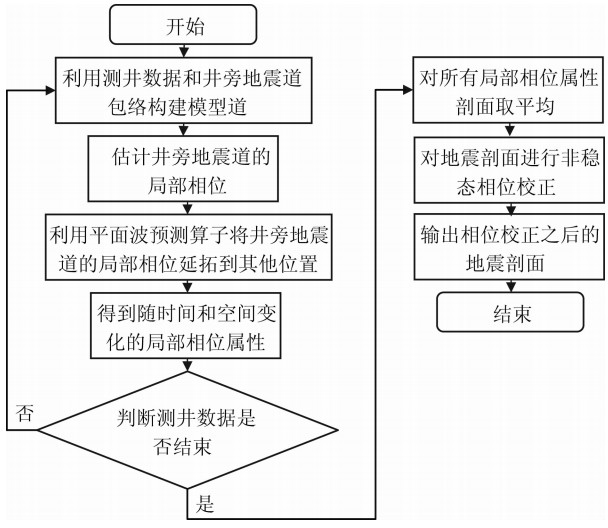 | 图1 井约束非稳态相位校正方法实现流程图 Fig.1 Workflow of well constrained non-stationary phase correction |
相对于局部方差模和包络局部相似度准则,基于井数据的非稳态相位校正方法具有最高的精度,为了证明这一点,我们采用某探区的测井数据进行测试.图2a为波阻抗测井曲线,图2b为反射系数曲线,图2c为与零相位Ricker子波褶积之后的地震记录,图2d为对合成地震记录进行-90°到0°线性变化相位旋转之后的地震记录.下面对图2d所示的地震记录在最大方差模准则、包络最大相似度准则、测井约束最大相似度准则下进行非稳态相位校正,校正结果分别如图3a、图3b、图3c所示,对比可以看出,由于最大方差模有效的前提是反射系数序列符合随机超高斯分布,因此该方法将各个波峰对应的位置作为一个反射层,将其校正为零相位,但是存在薄层时,无法将其校正到正确的相位.包络最大相似度准则受包络计算的影响,同样无法校正薄层地震响应的相位,而井约束相位校正方法的精度最高.图3d为这三种方法估算的相位角对比图,从图中可以看出,测井约束最大相似度准则估计的相位最为 准确,虽然中间位置三种方法估计的相位角比较接近,但两边位置利用最大方差模和包络最大相似度准则无法估计出正确的相位角.
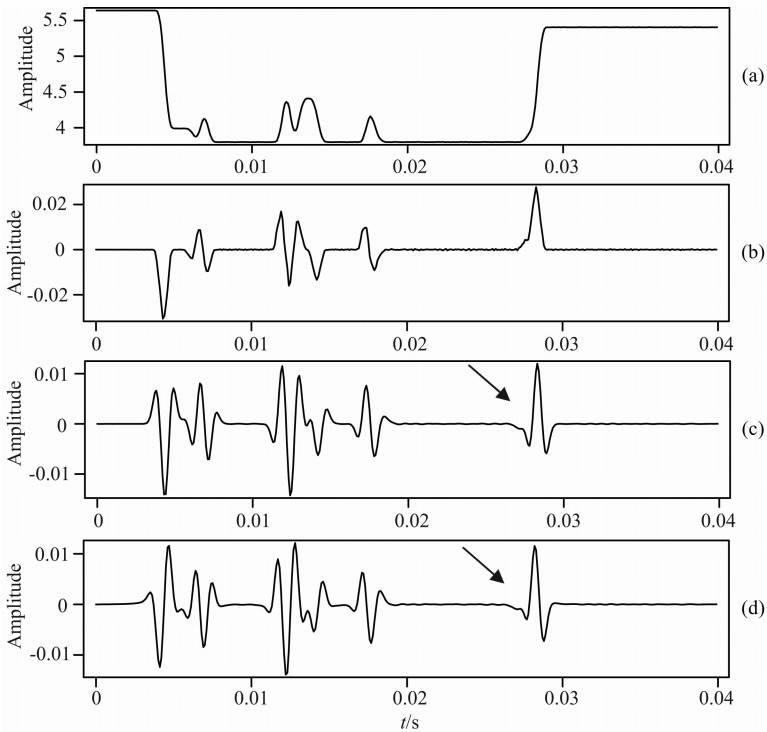 | 图2 一维合成数据 (a)波阻抗测井曲线;(b)反射系数;(c)合成地震记录;(d)经线性相移之后的地震记录. Fig.2 1-D synthetic data (a) Acoustic impedance; (b) Reflectivity; (c) Synthetic trace; (d) Synthetic trace after linear phase shift. |
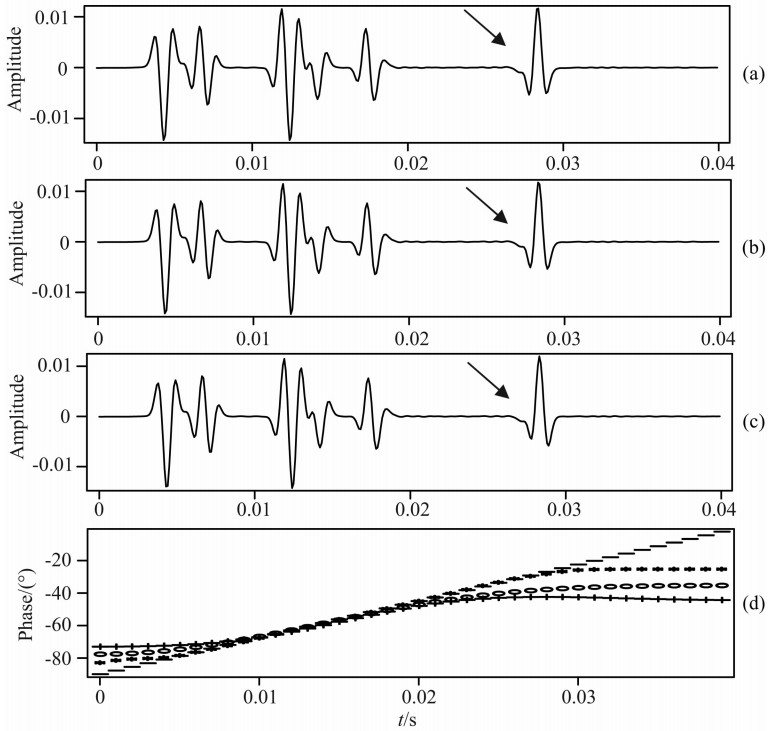 | 图3 一维合成数据相位校正 (a)最大局部方差模准则相位校正结果;(b)包络最大局部相似度准则相位校正结果;(c)测井最大局部相似度准则相位校正结果; (d)三种相位校正方法估算的相位( - :真实相位角;*:测井约束最大相似度法; o :包络最大相似度法; + :最大方差模法). Fig.3 Phase correction on 1-D synthetic data (a) Local kurtosis maximization method; (b) Local similarity maximization method with the envelope; (c) Local similarity maximization method with well logging; (d) Difference between true phase and phase estimated by these three methods ( - : true phase angle; *: local similarity maximization method with well logging; o : local similarity maximization method with the envelope; + : Local kurtosis maximization method). |
为了进一步验证本文方法的有效性,采用凹陷模型进行测试.图4a为模型层速度场,测井数据位于图中五角星所在位置(CDP=320处),其中实线为测井的时间长度.图4b为褶积模型,子波主频为15 Hz,图4c为经过相移之后的地震数据,四个层位的相移量分别为0°、30°、90°和50°.图4d为PWD对图4c估计的局部倾角,从图中可以看出,该倾角场基本反映了凹陷模型的局部构造信息.
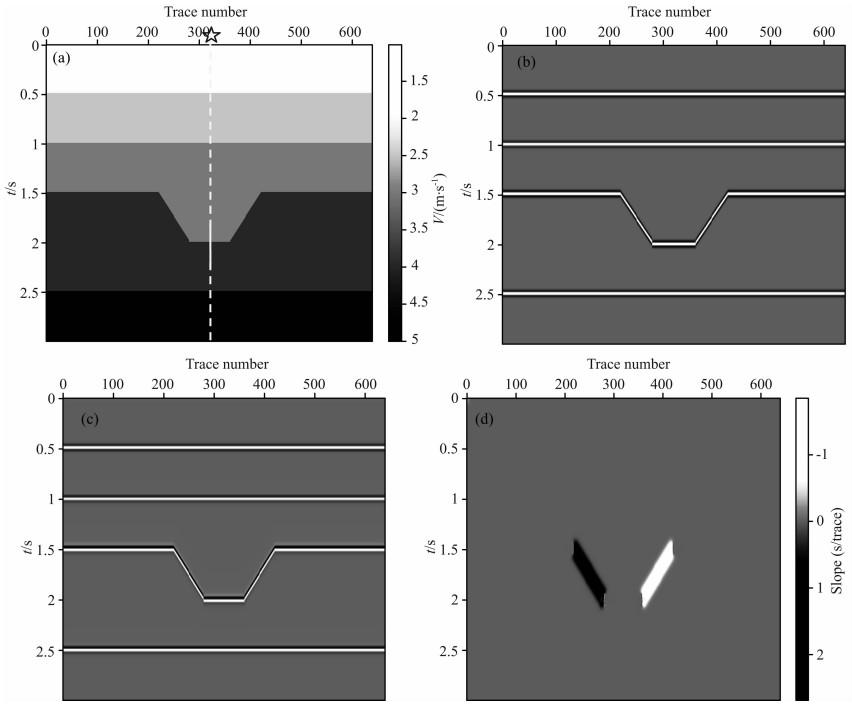 | 图4 二维凹陷模型 (a)层速度场及井位置(垂线所示);(b)褶积模型;(c)对褶积模型进行相移后的结果;(d)对图(c)进行PWD估计的局部倾角场. Fig.4 2-D hollow model (a) Interval velocity field and the well position (as shown in the vertical line); (b) Convolution model; (c) Convolution model after phase shift; (d) Local slope field estimated by PWD. |
下面对该模型数据进行井约束非稳态相位校正,图5a为井数据处的地震道,图5b为测井合成数据和地震道包络合成的参考道,利用该参考道对图5a进行非稳态相位校正,估计的局部相位信息如图5c所示,图5d为相位校正之后的结果,可以看出,四个子波均已校正到零相位.
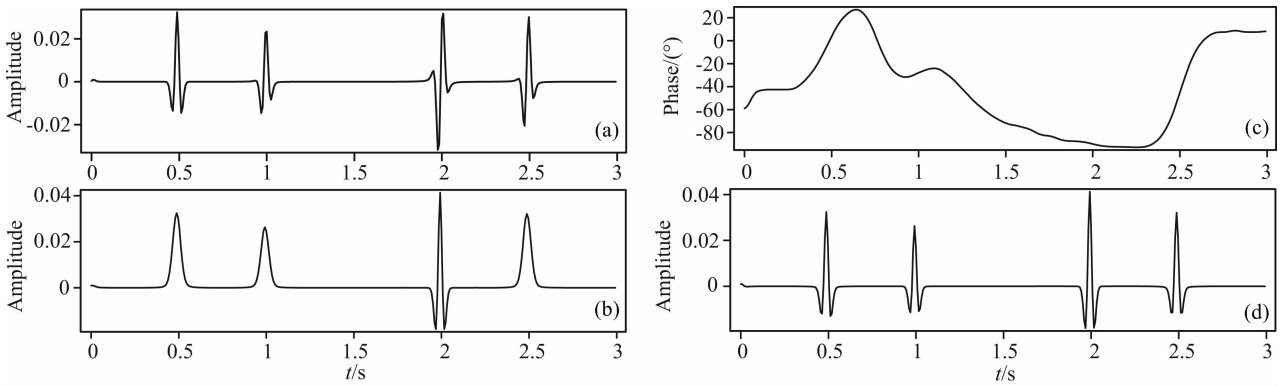 | 图5 单道相位校正 (a)井旁地震道;(b)参考道;(c)基于局部相似度得到的相位角;(d)非稳态相位校正之后的结果. Fig.5 One trace after phase correction (a) The trace near the well; (b) Reference trace; (c) Phase angle estimated by local similarity method; (d) Result after non-stationary phase correction. |
利用测井数据估计出井位置处地震道的局部相位信息以后,常规的做法是将井位置处的相位信息插值到其他地震道,由于该模型只有一口井资料,这种方法只能将井位置处的相位信息复制到其他位置.为了更好地估计其他位置处的相位信息,采用平面波预测滤波器利用地震同相轴的局部倾角信息将该道相位信息延拓到其他地震道.常规方法得到的相位角如图6a所示,本文方法得到的相位角如图6b所示,分别用这两种方法得到的相位信息对输入数据进行相位校正,校正结果分别如图6c和6d所示,其中图6c和图6d右图分别为左图白线(CDP=100)处的地震道数据.从图中可以看出,采用常规方法无法将1.5 s处的同相轴校正到零相位,而利用本文方法则可以很好地将四个反射波同相轴都校正到零相位.
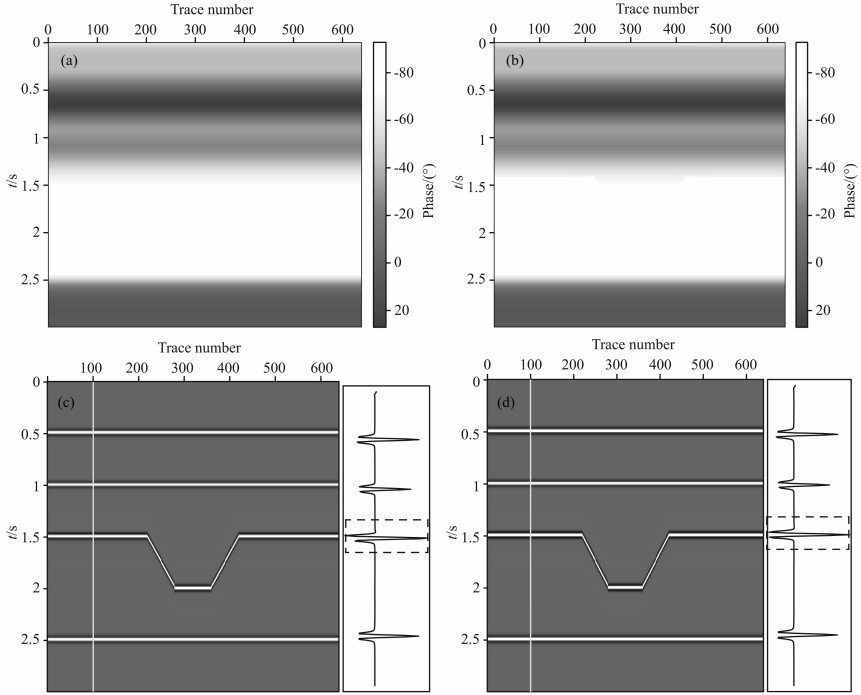 | 图6 二维凹陷模型相位校正 (a)直接插值得到的相位信息;(b)平面波预测方法得到的相位信息;(c)利用图(a)的相位信息相位校正后的结果;(d)利用图(b)的相位信息相位校正后的结果;(e)直接插值法对整个剖面及CDP=100处地震道相位校正的结果;(f)平面波预测法对整个剖面及CDP=100处地震道相位校正的结果. Fig.6 Phase correction on 2-D hollow model (a) Phase estimated by direct interpolation; (b) Phase estimated by plane-wave prediction method; (c) Phase correction using phase in Fig.6a; (d) Phase correction using phase in Fig.6b; (e) The entire profile and the trace at CDP=100 after phase correction by direct interpolation method; (f) The entire profile and the trace at CDP=100 after phase correction by plane-wave prediction method. |
下面对某探区实际资料进行相位校正处理.图7a为原始叠加剖面,图中五角星表示井所在的位置,实线部分为测井的时间范围.图7b为应用PWD估计的局部倾角场.下面采用局部相似度对井旁地震道进行相位估计.图8a为井旁地震数据,图8b为井旁地震数据包络和测井合成数据生成的模型道.估计的相位角如图8c所示,利用该相位角对井旁地震道进行相位校正,校正后的地震道如图8d所示.从图中可以看出,该地震道子波基本校正到零相位,尤其是箭头所示层位(约1.82 s)子波相位校正效果更为明显.
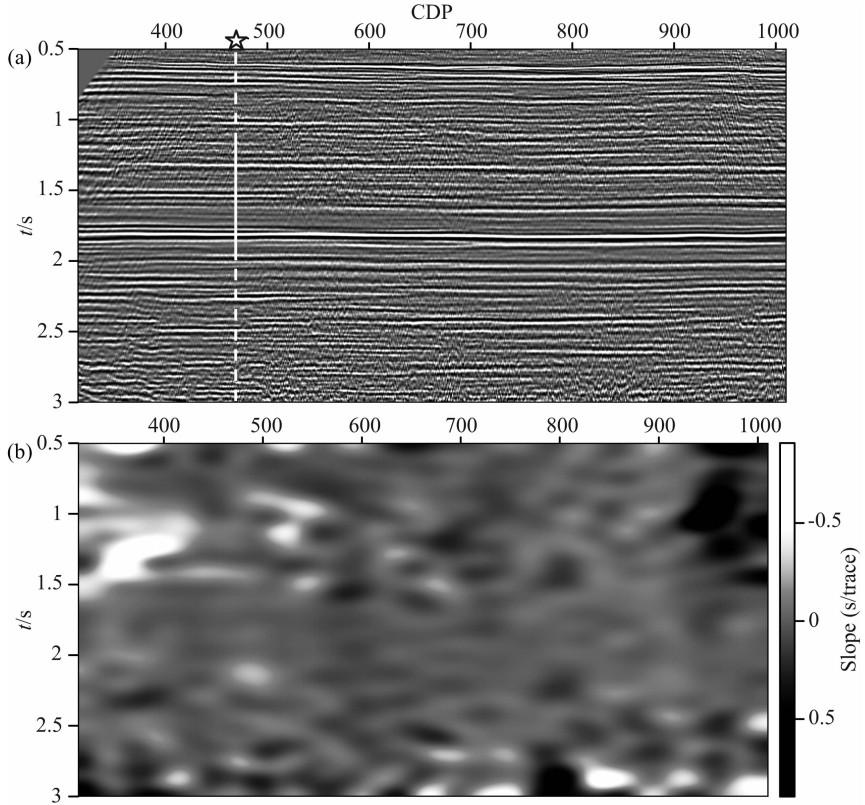 | 图7 二维实际资料 (a)原始叠加剖面;(b)PWD估计的局部倾角场. Fig.7 2-D real data (a) Original stack profile; (b) Local slope field estimated by PWD. |
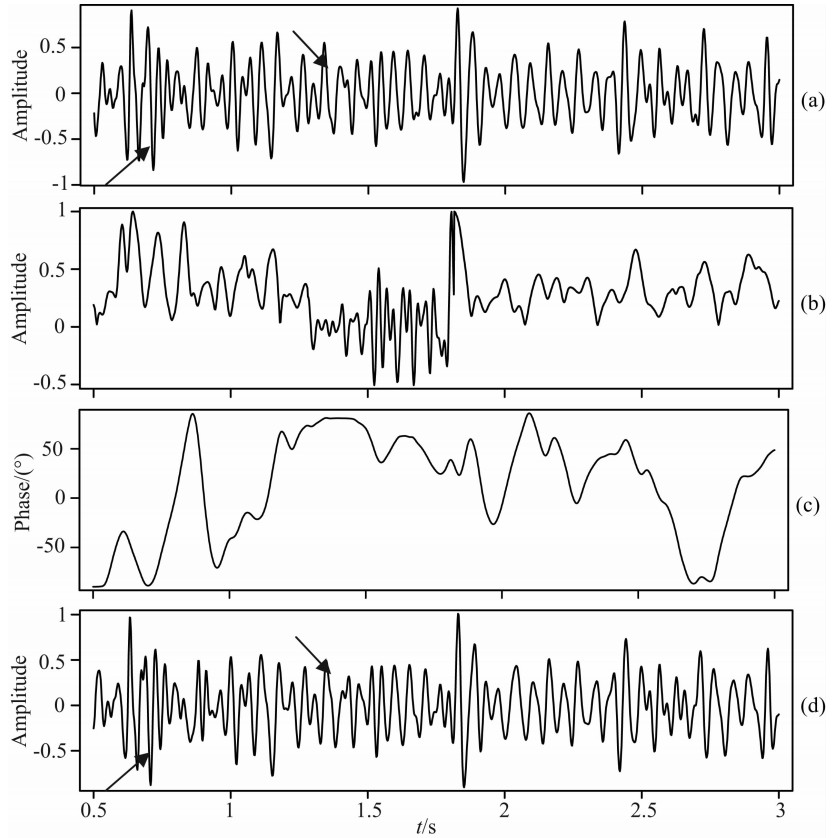 | 图8 井旁道相位校正 (a)井旁地震道;(b)模型道;(c)基于局部相似度得到的相位角; (d)非稳态相位校正之后的结果. Fig.8 Phase correction on the trace near the well (a) Seismic trace near the well; (b) Reference model; (c) Phase angle estimated by local similarity method; (d) Result after non-stationary phase correction. |
利用测井合成数据对井旁数据进行相位估计以 后,采用平面波预测算子将该相位信息插值到其他位置,从而得到整条地震剖面的相位信息,如图9a所示,利用插值后的相位信息对原始叠加剖面进行相位校正,校正结果如图9b所示,图9c、图9d分别为图7a、图9b的局部放大图.从图中可以看出,采用本文所提出的相位校正方法可以有效将地震剖面的子波校正到零相位,从而改善叠加剖面的质量,提高叠加剖面的分辨率.
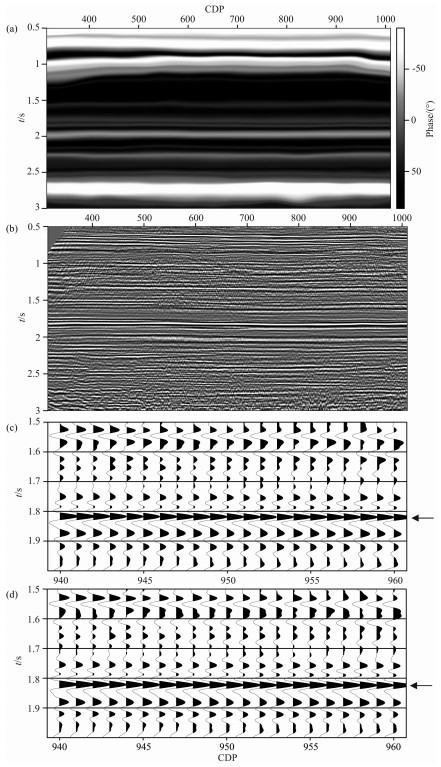 | 图9 二维实际资料相位校正 (a)平面波预测方法得到的局部相位信息;(b)非稳态相位校正之后的结果; (c)对图7a进行局部放大后的结果;(d)对图9b进行局部放大后的结果. Fig.9 Phase correction on 2-D real dataset (a) Local phase estimated by plane-wave prediction method; (b) Results after non-stationary phase correction; (c) Zoom-in of Fig.7a; (d) Zoom-in of Fig.9b |
本文在局部相似度方法的基础上,提出了一种基于井约束的非稳态相位校正方法,通过理论模型和实际资料处理可以得到如下几点结论:
(1)相对于最大方差模和包络最大相似度方法,基于井数据的相位校正方法具有最高的精度;
(2)通过将地震道包络和测井合成记录构建模型道,可以充分利用测井数据的信息对井旁地震道进行相位校正;
(3)采用平面波预测算子可以将井旁地震道的相位信息插值到其他位置,从而得到随时间和空间变化的相位信息,有利于实现整条地震剖面的零相位化,从而改善地震剖面的叠加质量,提高分辨率;
(4)本文数值算例中,主要阐述了单井约束相位校正,实际上,当探区存在多井时,同样可以采用本 文提出的处理流程(图1所示)进行非稳态相位校正;
(5)事实上,利用平面波预测算子也可以将测井数据中包含的其他信息插值到其他位置,充分利用 测井数据精度高的优点,从而达到地震资料和测井 资料相结合进行地下属性反演的目的.
致 谢 作者感谢两位匿名审稿人的宝贵意见.感谢开源工具包Madagascar所有开发人员(http://www.ahay.org/wiki/Main_Page).| [1] | Clae rbout J F. 1992. Earth Soundings Analysis: Processing Versus Inversion. Blackwell Scientific Publications. |
| [2] | Chen B Y, Chen M W, Yi W Q. 1997. Time and space and subsection frequency phase correction. Oil Geophysical Prospecting (in Chinese), 32(1): 103-108. |
| [3] | Fomel S. 2002. Applications of plane-wave destruction filters. Geophysics, 67(6): 1946-1960. |
| [4] | Fomel S. 2007. Shaping regularization in geophysical-estimation problems. Geophysics, 72(2): R29-R36. |
| [5] | Fomel S. 2007. Local seismic attributes. Geophysics, 72(3): A29-A33. |
| [6] | Fomel S. 2010. Local similarity with the envelope as a seismic phase detector. //80th Annual International Meeting: SEG, 1555-1559. |
| [7] | Fomel S, Guitton A. 2006. Regularizing seismic inverse problems by model reparameterization using plane-wave construction. Geophysics, 71(5): A43-A47. |
| [8] | Gao S W, Zhou G Y, Cai J M. 2001. Surface consistant phase correction for reflection wave. Oil Geophysical Prospecting (in Chinese), 36(4): 480-487. |
| [9] | Guo J Y, Zhou X Y. 1995. Surface consistent phase correction in 2D and 3D domains. Oil Geophysical Prospecting (in Chinese), 30(3): 345-350. |
| [10] | Levy S, Oldenburg D W. 1987. Automatic phase correction of common-midpoint stacked data. Geophysics, 52(1): 51-59. |
| [11] | Li F L, Wang C S, Xu B X, et al. 1990. Lp norm deconvolution and its application in seismic exploration. Chinese J. Geophys. (in Chinese), 33(5): 585-592. |
| [12] | Li H Q, Zhou X Y. 2000. Moveout and constant phase correction along with weighed stacking. Oil Geophysical Prospecting (in Chinese), 35(4): 415-418. |
| [13] | Li Z C, Wang X P, Han W G. 2008. Review of phase correction in seismic data processing. Progress in Geophysics (in Chinese), 23(3): 768-774. |
| [14] | Liu Y J, Li Z C, Guo K. 2012.Non-stationary phase correction based on local similarity. Oil Geophysical Prospecting (in Chinese), 47(6): 887-893. |
| [15] | Longbottom J, Walden A T, White R E. 1988. Principles and application of maximum kurtosis phase estimation. Geophysical Prospecting, 36(2): 115-138. |
| [16] | Shan L Y. 2008. Improvement of discriminant criteria for phase correction and its application effect. Geophysical Prospecting for Petroleum (in Chinese), 47(3): 219-224. |
| [17] | Song Z P, Li J J, Zhang L P. 2004. Prestack constant phase correction. Petroleum Geology & Oilfield Development in Daqing (in Chinese), 23(2): 69-70. |
| [18] | Van der Baan M. 2008. Time-varying wavelet estimation and deconvolution by kurtosis maximization. Geophysics, 73(2): V11-V18. |
| [19] | Van der Baan M, Fomel S. 2009. Nonstationary phase estimation using regularized local kurtosis maximization. Geophysics, 74(6): A75-A80. |
| [20] | Van der Baan M, Perz M, Fomel S. 2010. Nonstationary phase estimation for analysis of wavelet character. //72nd Conference and Exhibition, EAGE. |
| [21] | White R E. 1988. Maximum kurtosis phase correction. Geophysical Journal International, 95(2): 371-389. |
| [22] | Wiggins R. 1978. Minimum entropy deconvolution. Geoexploration, 16(1-2): 21-35. |
| [23] | Wiggins R. 1985. Entropy guided deconvolution. Geophysics, 50(12): 2720-2726. |
| [24] | Zhou X Y. 1989. Constant phase correction. Oil Geophysical Prospecting (in Chinese), 24(2): 119-129. |
| [25] | 陈必远, 陈明伟, 易维启. 1997. 时空变分频常相位校正. 石油地球物理勘探, 32(1): 103-108. |
| [26] | 高少武, 周光元, 蔡加铭. 2001. 反射波地表一致性相位校正. 石油地球物理勘探, 36(4): 480-487. |
| [27] | 国九英, 周兴元. 1995. 二维及三维地表一致性相位校正. 石油地球物理勘探, 30(3): 345-350. |
| [28] | 李凤林, 王承曙, 徐伯勋等. 1990. Lp模反褶积及其在地震勘探中的应用. 地球物理学报, 33(5): 585-592. |
| [29] | 李合群, 周兴元. 2000. 时差、常相位校正及加权叠加. 石油地球物理勘探, 35(4): 415-418. |
| [30] | 李振春, 王希萍, 韩文功. 2008. 地震数据处理中的相位校正技术综述. 地球物理学进展, 23(3): 768-774. |
| [31] | 刘玉金, 李振春, 郭恺. 2012. 基于局部相似度的非稳态相位校正方法研究. 石油地球物理勘探, 47(6): 887-893. |
| [32] | 单联瑜. 2008. 相位校正判别准则的改进及应用效果分析. 石油物探, 47(3): 219-224. |
| [33] | 宋宗平, 李建军, 章黎萍. 2004. 叠前常相位校正. 大庆石油地质与开发, 23(2): 69-70. |
| [34] | 周兴元. 1989. 常相位校正. 石油地球物理勘探, 24(2): 119-129. |
 2014, Vol. 57
2014, Vol. 57

