2. 地下信息探测技术与仪器教育部重点实验室(中国地质大学, 北京), 北京 100083;
3. 中国地质大学(北京)数理学院, 北京 100083
2. Key Laboratory of Geo-detection (China University of Geosciences, Beijing), Ministry of Education, Beijing 100083, China;
3. Mathematical College, China University of Geosciences, Beijing 100083, China
由重力异常反演密度界面是位场处理解释中的一大问题.密度分界面与区域构造、储油构造有密切的关系,因此计算密度分界面的起伏或深度的变化在区域构造研究和石油勘探中具有重要的意义.很多学者提出了各种根据已知的重力异常计算密度界面起伏的方法,概括起来主要分为两大类,即空间域反演方法和频率域反演方法.在空间域中比较典型的方法有线性回归法、压缩质面法和等效源法(刘光鼎等,2005; 《重力勘探资料解释手册》编写组,1983).等效源法是先用一系列微元(棱柱体或长方体)构造一个密度界面模型,计算每个棱柱体或长方体产生的异常,然后求和就能得到相应界面产生的重力异常;比较模型产生的重力异常和实测重力异常的差异,反演模型高度的修正量,直到符合要求为止(Neji et al., 1969; Cordell, 1973).但该方法反演的界面具有不连续性并且计算速度慢.1973年,Parker在位场界面正演计算中引入快速傅里叶变换(FFT).Oldenburg (1974)根据Parker公式,提出了一种频率域的密度界面迭代反演方法,由于采用了快速傅里叶变换,计算速度很快.由于这种方法包含一项向下延拓算子,可以利用一个低通滤波器保证迭代的收敛性,这种做法在消除高频震荡的同时必然会对有效信号进行一定的压制,造成反演精度的降低.为了提高反演的精度,一些学者对FFT进行了各种改进.关小平(1991)提出,在空间域中由平板公式给出界面深度的初值,在频率域中用Parker公式正演出拟合实测异常,频率域、空间域交替进行.肖鹏飞(2007)利用迭代法向下延拓替代Parker-Oldenburg反演法中的向下延拓,用上延来替代下延,通过逐次迭代拟合的方法来完成向下延拓运算.王金波(2001)和张会站(2006)等认为在重力位场分解中,可以利用小波多尺度分解替代低通滤波器.张凤旭(2005)提出利用余弦变换代替傅里叶变换研究重力密度界面正、反演问题,能够提高数据处理的速度和精度.这些方法丰富和发展了空间 域和频率域的界面反演理论.但对于Parker-Oldenburg 方法,层间物性只能为常数或横向二维变化,柴玉璞(1990)和冯锐(1986)将Parker-Oldenburg方法推广到物性可随深度变化的三维情况,但界面起伏h(x,y)是以水平面为基准面度量的,如果界面深度 太大在迭代过程中不易收敛.在常密度或密度横向 二维变化情况下,可以通过改变基准面的位置(与以水平面为基准面相比,二者只相差一个常数)来减小h(x,y)的绝对值,使迭代易于收敛.但对于密度随深度变化的三维情况,效果不佳.本文将Parker-Oldenburg方法推广到物性可随深度变化的三维情况,同时可以合理地选取基准面位置,减小界面起伏,保证迭代的收敛性.并且在迭代过程中还可以加入约束条件,例如已知点的深度、密度的上下限等以减少位场反演的多解性.
在直角坐标系中,坐标轴的选取如图1所示,以地面上某一点O作为坐标原点,x-y平面置于水平,z轴垂直向下,即沿重力方向.
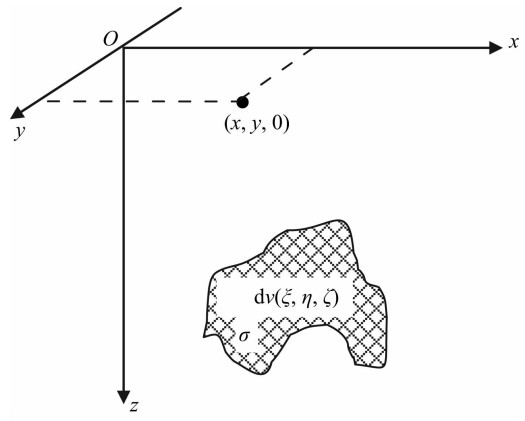 | 图1 场源位置坐标系 Fig.1 Field source location coordinates |
重力异常的扰动源三维坐标为(ξ,η,ζ),观测面为z=0的水平平面,观测点在(x,y,0)处,则重力异常Δg(x,y,0)(以下简记为Δg)可表示为
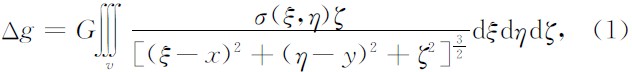
其中G为万有引力常数,σ(ξ,η)为横向二维变化的密度差(即剩余密度),其傅里叶变换为
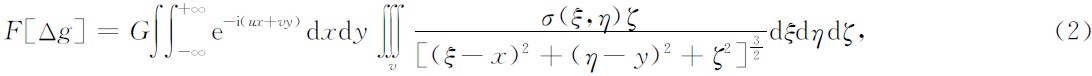
u,v分别表示x,y方向上的波数,改变积分顺序
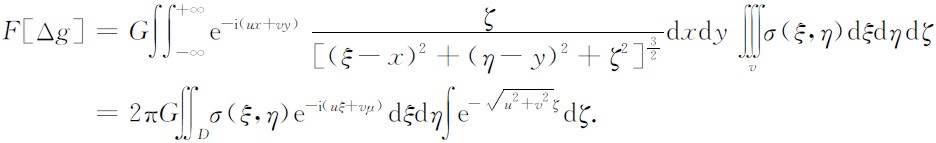
设密度界面h(x,y)的平均深度为z0, 如图2所示,相对于z0的界面起伏深度为Δh(ξ,η)(以下简记为Δh).
 | 图2 三维密度界面示意图 Fig.2 3-D density interface |
则上式中关于ζ的积分上下限分别为z0+Δh和z0,写为
令
 处泰勒展开,并对ζ积分得
处泰勒展开,并对ζ积分得
(4)式就是三维常密度或密度横向二维变化的重力界面异常正演公式.
从(4)式的无限和式中提出n=1的项,并重新排列,得到
(5)式就是与之对应的重力界面反演公式.假定已知地层与下部介质之间的密度差σ(ξ,η),参考面深度z0已知或给定,就可以应用(5)式进行计算.
下面将(4)式推广到σ=σ0(ξ,η)+μ1(ξ,η)ζ+μ2(ξ,η)ζ2的情况,这一密度模式具有相当的普遍性.
根据重力场的叠加性,将由σ0(ξ,η)、μ1(ξ,η)ζ、μ2(ξ,η)ζ2引起的重力场分别表示为Δg0、Δg1、Δg2. 记为
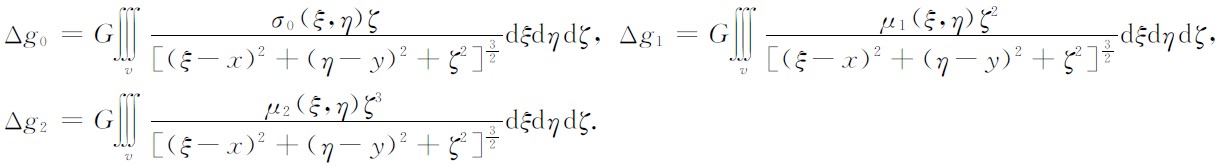
则有

Δg0可由(4)式得到
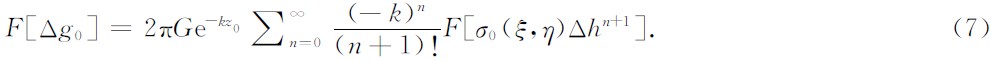
现以Δg1为例进行推导.根据(3)式有
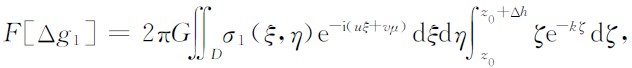
将e-kζ在 ζ=z0处泰勒展开
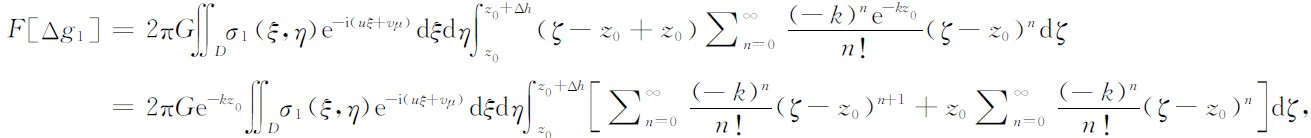
对ζ积分得
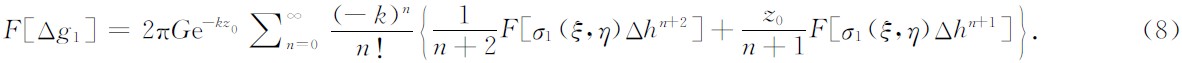
同理可得到
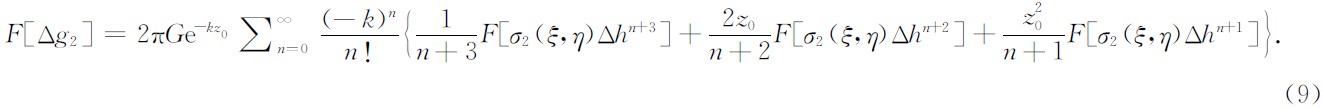
则对应(6)式的总重力异常为
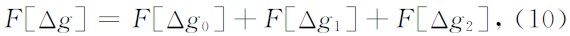
密度在纵向上成n次多项式变化时,原则上亦可推出理论的重力异常正演公式.
将(10)式变形,可得到相应的重力界面反演公式.
设密度分布函数为σ=σ0(ξ,η)eμζ,μ为剩余密度随深度的衰减系数.
采用与上面类似的推导方法,不难得到:
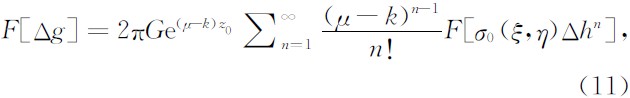
由(11)式同理可得到相应的重力界面反演公式.
有些沉积盆地的剩余密度随深度的增加而减小,而减小的速率也随深度的增加而减小,这种情况可以用指数函数来模拟.当密度随深度的变化关系更加复杂时,则可改用多项式密度模式;或者从深度上划分为几段,每一段对应于一层,再分别用指数函数或多项式函数来近似.
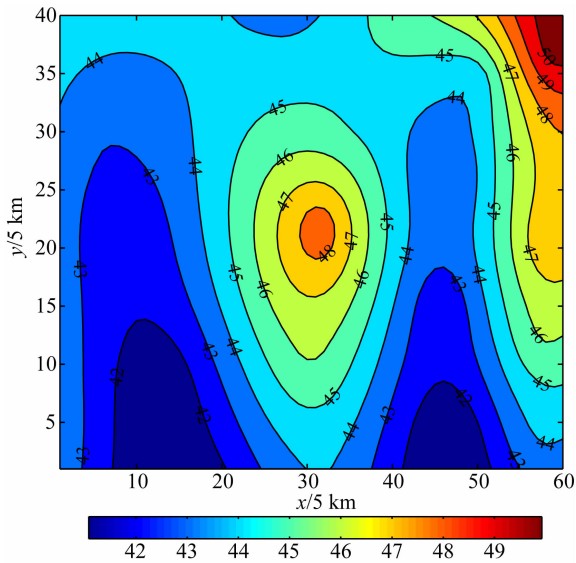
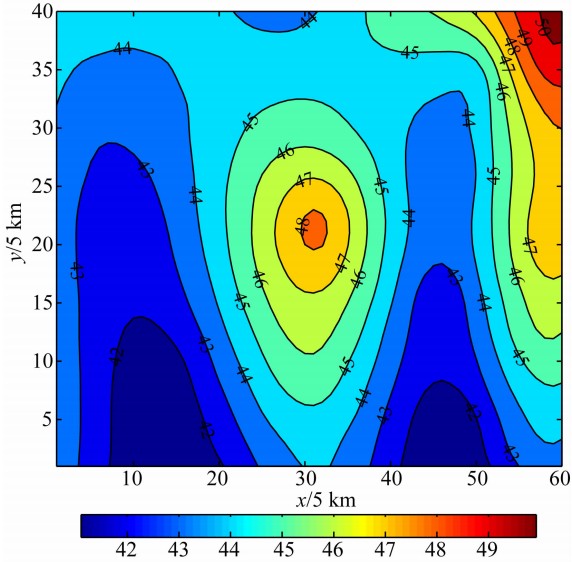
某密度分界面,如图3所示,其密度随深度的变化为指数函数σ=σ0(ξ,η)eμζ,σ0(ξ,η)=-0.8 g/cm3, 衰减系数μ=-0.04/km.此密度界面在地面上引起的理论重力异常(以深度z0=40 km为基准面计算)如图4所示.图5是采用指数密度模式对此重力异常进行反演的结果,由图5可以看出,采用指数模型的反演结果与理论模型基本吻合.为了对比明显,图6与图7是分别对某一条重力剖面采用指数模型和常密度模型进行反演的结果,图6的反演结果与实 际模型吻合得很好.对于常密度模型,分别取σ(ξ,η)=-0.14 g/cm3、 -0.15 g/cm3、-0.16 g/cm3进行反演,结果见图7.当密度差取-0.14 g/cm3时,反演的深度比实际深度普遍要深 0.25 km左右.当密度差取-0.15 g/cm3时,在地形较为平缓处反演结果与实际情况基本吻合,但在地形起伏较大的波峰和波谷处,二者差别较大.当密度差取-0.16 g/cm3 时,反演结果比实际情况普遍要浅,差别最大处达1 km左右.这一理论模型试验说明,如果采用的密度模型与实际密度分布差别较大,那么反演结果就会产生较大的偏差.实际的地层密度在铅锤方向上是变化的,因此,界面的反演应根据不同情况选用合理的变密度模型来进行.
 | 图3 密度界面理论深度分布(单位:km) Fig.3 Theoretical depth of density interface |
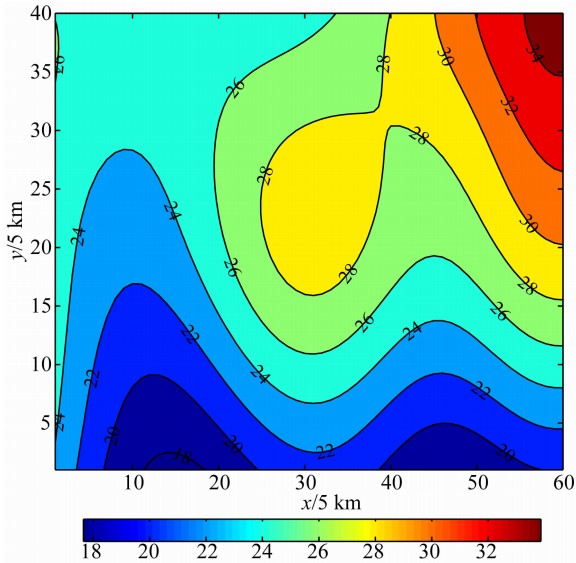 | 图4 理论重力异常分布(单位:mGal) Fig.4 Theoretical gravity anomaly |
 | 图5 反演的密度界面深度分布(单位:km) Fig.5 Inverted density interface |
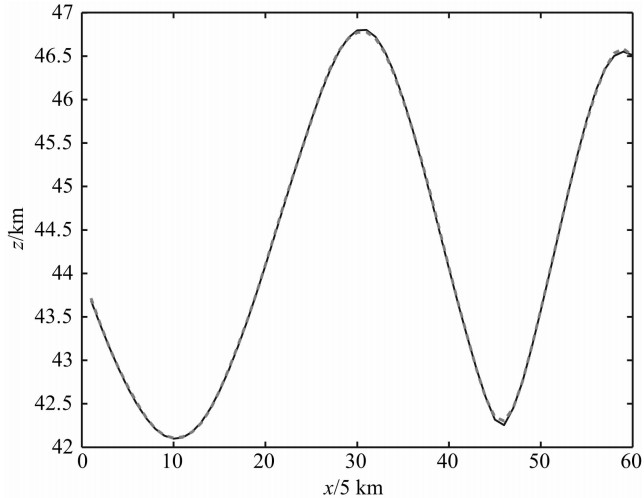 | 图6 采用指数模型反演的密度界面 实线:实际模型, 双划线:反演结果. Fig.6 Inverted density interface with exponential density model Solid line: theoretical depth, dashed line: inversion result. |
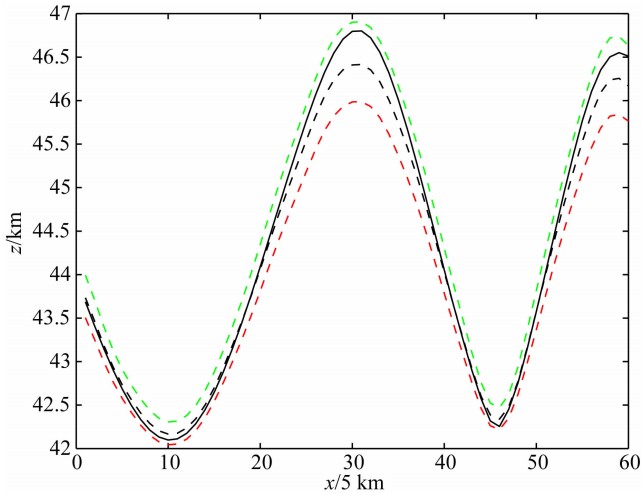 | 图7 采用常密度模型反演的密度界面 黑色实线:实际模型,绿色双划线:σ(ξ,η)=-0.14 g/cm3,黑色双划线:σ(ξ,η)=-0.15 g/cm3,红色双划线:σ(ξ,η)=-0.16 g/cm3. Fig.7 Inverted density interface with constant density model Solid black line: theoretical depth, green dotted line: σ(ξ,η)=-0.14 g/cm3, black dotted line: σ(ξ,η)=-0.15 g/cm3, red dotted line: σ(ξ,η)=-0.16 g/cm3. |
由于华北地区地壳结构在横向上及纵向上均存在不均匀性,本文从变密度模型的角度来研究华北 地区莫霍面的分布情况.利用华北地区的卫星重力异常,经过校正得到华北地区布格重力异常如图8所示.为了提取分离莫霍面所产生的异常,将其分别向上延拓10 km和20 km后所得结果如图9所示.图9中向上延拓10 km后所得异常与我们之前认识的区域布格异常非常接近,且布格重力异常等值线已经清晰可见鄂尔多斯块体、太行隆起、燕山隆起和华北裂谷盆地等明显地区区域.因此上延10 km已经能够将深部异常提取出来,故采用向上延拓10 km后的区域异常作为反演莫霍界面的原始异常数据.对图9a所示的布格重力异常,分别采用常密度模型与指数密度模型进行反演.对于常密度模型,取参考面深度z0=40 km, 壳幔密度差σ(ξ,η)=-0.4 g/cm3.对于指数密度模型σ=σ0(ξ,η)eμζ,同样取参考面深度z0=40 km,σ0(ξ,η)=-0.9 g/cm3, 衰减系数μ=-0.022/km.为了便于观察,分别将常密度模型与指数密度模型反演的结果沿某一剖面取值(应县—淄博剖面),测线的位置见图8和图9的标注,图10是应县—淄博地震测深二维速度结构剖面图.将反演结果与地震测深获得的结果(邓晋福等,2007; 刘昌栓等,1996)进行比较.从图11可以看出,利用指数密度模型反演的结果与地震测深得到的结果整体趋势一致,二者具有很好的一致性,而常密度模型反演的结果与地震资料获得的结果偏差较大.
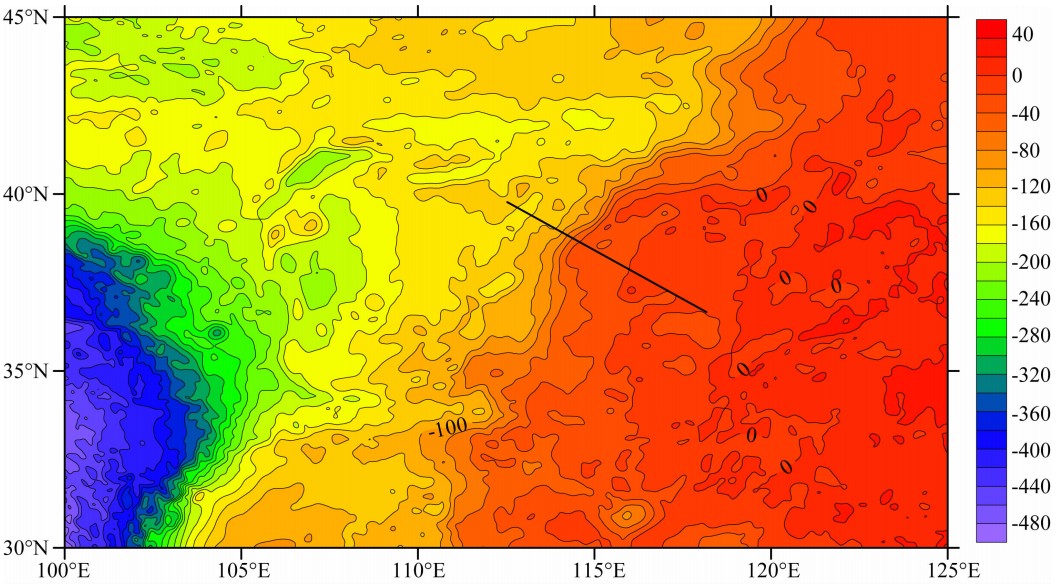 | 图8 华北地区布格重力异常(图中横线为地震测深剖面)(单位:mGal) Fig.8 Bouguer anomaly map of North China (straight line is seismic sounding profile) |
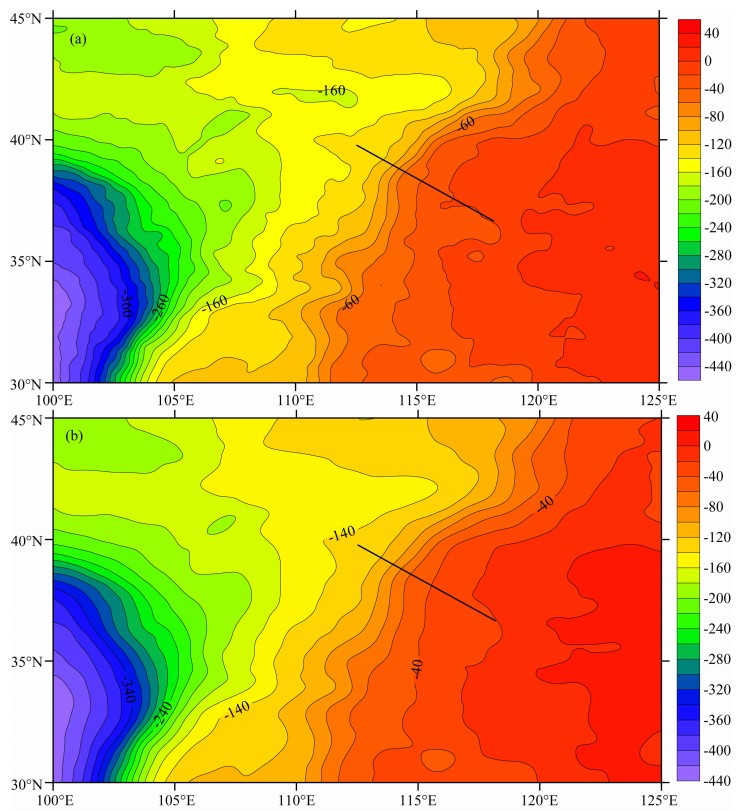 | 图9 (a) 上延10 km 后和(b) 上延20 km 后的华北布格重力异常(图中横线为地震测深剖面)(单位:mGal) Fig.9 Bouguer anomaly map of North China by (a) up continuation to 10 km and (b) up continuation to 20 km (straight line is seismic sounding profile) |
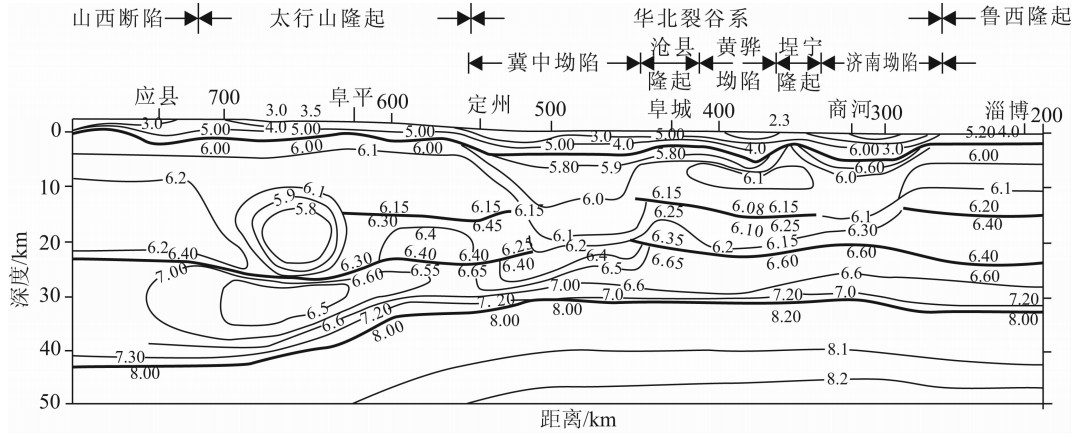 | 图10 应县—淄博地震测深二维速度结构剖面 Fig.10 The explosion seismic sounding profile along Yingxian to Zibo |
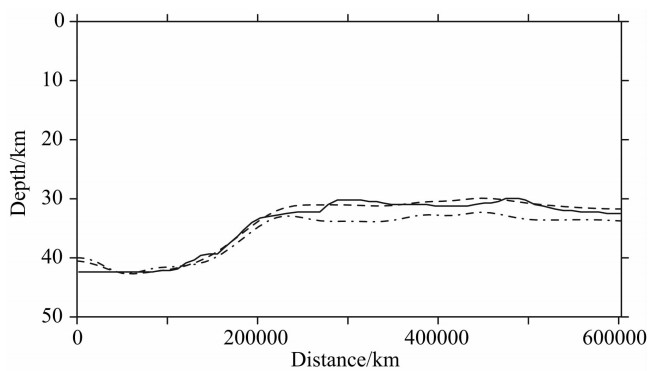 | 图11 重力反演结果与地震测深结果的比较 实线:地震数据,双划线:指数密度模型,点划线:常密度模型. Fig.11 Comparison of Moho depths from gravity and seismic inversion Solid line: seismic result, dashed line: exponential density model, dotted line: constant density model. |
利用常密度模型反演莫霍面的结构只是一种近似假设,即假设界面上下两层的密度差为一常数,是一种简化的模型.本文利用变密度模型来反演莫霍面的结构,考虑了密度随深度的变化情况,所得结果更接近于实际情况.
本文研究的是重力位场的界面正反演问题,将频率域的界面反演方法Parker-Oldenburg公式推广到物性可随深度变化的三维情况.并且在计算中 可以选取地面下某一深度作为基准面,以保证迭代 的收敛性.由模型计算可以看出,该方法计算稳定, 反演精度高,具有良好的效果.利用该方法处理了华 北地区的重力资料,反演结果与地震资料获得的结果吻合得很好.推广后的公式具有广泛的适用性,应用范围已扩大,数学模型也更加合理,这对大数据量的三维反演来说,应用价值提高.
如果密度随深度的变化关系复杂,不能单用某一种密度模式来近似,可以从深度上划分为几段,每一段对应于一层,再分别用指数函数或多项式函数来近似.并且在迭代过程中可以加入约束条件,例如已知点的深度、密度的上下限等先验信息,以减少位场反演的多解性.
| [1] | Cordell L. 1973. Gravity analysis using an exponential density-depth function-San Jacinto Graben, California. Geophysics, 38(4):684-690. |
| [2] | Deng J F,Wei W B. 2007. The Three-Dimensional Structure of Lithosphere and Its Evolution in North China (in Chinese). Beijing: Geological Publishing House. |
| [3] | Editorial Staff of Handbook of Gravity Exploration Data Interpretation. 1983. Handbook of Gravity Exploration Data Interpretation. Beijing: Geological Publishing House. |
| [4] | Feng R. 1986. A computation method of potential field with three-dimensional density and Magnetization distributions. Chinese J. Geophys. (in Chinese), 29(4): 399-406. |
| [5] | Guan X P. 1991. An effective and simple approach of subsurface inversion using Parker′s equation. Computing Techniques for Geophysical and Geochemical Exploration (in Chinese), 13(3): 236-242. |
| [6] | Liu C S, Fang S M, Li C F. 1996. Joint gravity-seismic interpretation for Yingxian-Ziboprofile. Seismology and Geology, 18(4): 369-374. |
| [7] | Liu G D, Zeng H L. 2005. Gravity Field and Gravity Exploration. Beijing: Geological Publishing House. |
| [8] | Negi J G, Grade S C. 1969. Symmetric mMatrix mMethod for rapid for gGravity iInterpretation. J. Geophys. Res. , 74(153): 3804-3807. |
| [9] | Oldenburg D W. 1974. The inversion and interpretation of gravity anomalies. Geophysics, 39(4): 526-536. |
| [10] | Parker R L. 1973. The rapid calculation of potential anomalies. Geophys. J. Royal Astr. Sco. , 31(4): 447-455. |
| [11] | Wang J B, Xu M J, Peng R R. 2001. Wavelet separating frequency′s application to the surface inversion of gravity anomalies. Numerical Mathematics A Journal of Chinese Universities (in Chinese), 23(1): 68-72. |
| [12] | Xiao P F, Chen S C, Meng L S, et al. 2007. The density interface inversion of high-precision gravity data. Geophysical and Geochemical Exploration (in Chinese), 31(1): 29-33. |
| [13] | Zhang F X, Zhang F Q, Meng L S. 2005. Using cosine transform for forward modeling and inversion of gravitational anomaly on density interface. Oil Geophysical Prospecting (in Chinese), 40(5): 598-602. |
| [14] | Zhang H Z, Fang J, Zhang Z Z. 2006. Application of wavelet analysis in the interface inversion of gravity field. Geomatics and Information Science of Wuhan University (in Chinese), 31(3): 233-236. |
| [15] | 柴玉璞, 贾继军. 1990. Parker 公式的一系列推广及其在石油重力勘探中的应用前景. 石油地球物理勘探, 25(3): 321-332. |
| [16] | 《重力勘探资料解释手册》编写组. 1983. 重力勘探资料解释手册. 北京: 地质出版社. |
| [17] | 邓晋福,魏文博. 2007. 中国华北地区岩石圈三维结构及演化. 北京:地质出版社. |
| [18] | 冯锐. 1986. 三维物性分布的位场计算. 地球物理学报, 29(4): 399-406. |
| [19] | 刘昌栓, 方盛明, 李长法. 1996. 应县一淄博剖面重力、地震测深联合解释. 地震地质, 18(4): 369-374. |
| [20] | 关小平. 1991. 利用Parker公式反演界面的一种有效方法. 物探化探计算技术, 13(3): 236-242. |
| [21] | 王金波, 许梦杰, 彭瑞仁. 2001. 小波分频在重力异常界面反演计算过程中的应用. 高等学校计算数学学报, 23(1): 68-72. |
| [22] | 刘光鼎, 曾华霖. 2005. 重力场与重力勘探. 北京: 地质出版社. |
| [23] | 肖鹏飞, 陈生昌, 孟令顺等. 2007. 高精度重力资料的密度界面反演. 物探与化探, 31(1): 29-33. |
| [24] | 张凤旭, 张凤琴, 孟令顺. 2005. 基于余弦变换的密度界面重力异常正反演研究. 石油地球物理勘探, 40(5): 598-602. |
| [25] | 张会战, 方剑, 张子占. 2006. 小波分析在重力界面反演中的应用. 武汉大学学报(信息科学版), 31(3): 233-236. |
 2014, Vol. 57
2014, Vol. 57

