2. 中国人民解放军95633部队, 邛崃 611531;
3. 吉林大学通信工程学院, 长春 130012
2. Unit 95633 of PLA, Qionglai 611531, China;
3. College of Communication Engineering, Jilin University, Changchun 130012, China
卡尔曼滤波是一种最优化自回归数据处理算法,它以最小均方误差为估计准则,采用状态转移来反映系统变化的内在规律,以“预估-量测-校正”的顺序递推,从被污染的系统中估计出系统的本来面 目. 自从20世纪60年代初卡尔曼滤波方法(Kalman,1960) 被提出,它在目标跟踪(Thorp,1973)、自动控制(Reid et al.,1984)、地震勘探(Crump,1974; 董敏煜等,1991)、导航(Jo et al.,2006)、气象(Shi et al., 2010)、空间物理(乐新安等,2010)、电力系统(Valverde et al., 2011)、医学(Vullings et al., 2011)和通信(胡志辉 et al,2011)等领域得到了广泛的应用. 在地震勘探领域,卡尔曼滤波主要用于地震资料的反褶积.Crump(1974)首先将卡尔曼滤波引入地震资料的反褶积中来估计反射系数序列,董敏煜等(1991)进一步提出了估计时变子波和自适应时变反褶积,以提高地震勘探资料的分辨率、信噪比和同相轴的连续性.
在地震勘探领域中, 地震记录同相轴的位置信息和质量具有极其重要的作用,对地震资料的处理和解释至关重要. 地震信号中所携带的大部分信息基本上都包含在同相轴中,如:同相轴的t0时间在一定程度上反映界面的深度信息,同相轴的形态反映地震波在介质中的传播速度信息,同相轴内地震子波变化源自地震波传播过程的条件等.同时当前日益复杂的勘探条件下所获得的地震资料信噪比较低,同相轴的检测、识别与追踪日趋困难.为了获取地震资料中的同相轴信息, 国内外已发展了多种不同的检测和拾取方法. 边缘检测法(Bondar,1992; 李红星等,2007; 熊会军等,2009; 杨微等,2011)将地震道集看作为一幅灰度图像,从而利用图像处理中的边缘检测方法来检测同相轴.此类方法得到的同相轴比较模糊,分辨率不高,受噪声因素影响较大,且检出的结果是灰度突变区域的包络线,并不能直接作为同相轴检测结果,还需一些后续处理,如细化处理等.不同于上述二维信号中的线检测技术,Faraklioti,2004 提出基于面检测技术自动提取三维地震数据中的层位信息,其复杂度和计算量更大.神经网络法(Liu et al., 1989; McCormack et al., 1993; Glinsky et al., 2001)利用已知同相轴作标准样本训练网络,利用误差回传法逐步修正神经元之间的连接权值,达到最佳权值分布后即可使用网络处理新的数据.该方法训练过程需要足够多的学习样本,样本的选择存在较大困难,且新样本的学习会影响已训练好的网络,大量的迭代运算导致处理耗时较长.互相关法(Spagnolini,1991)、高阶累积量法(Tugnait,1991; 刘财等,2010)和相干方法(Key et al., 1990)的基本原理都是利用同相轴在地震道间的波形相似性特征来提取同相轴.互相关法由地震道间信号的相关系数计算时间延迟从而进行同相轴拾取,易受噪声影响,且随着计算道的增加空间分辨率下降.由于高阶累积量具有对高斯噪声是“盲的”的特点(高斯噪声的高阶累积量恒为零),高阶累积量同相轴自动拾取方法即使在信噪比很低时仍能有效地拾取同相轴,但该方法需要通过人工手动标定准确地获得种子点的位置才能保证整个同相轴自动拾取过程的准确性.相干算法以采样数据协方差矩阵的本征结构为基础,在双曲线轨迹时窗内进行分解,而时窗在整个共深度点资料上移动,通过同时估计噪声场和信号特征来改善同相轴分辨率.相干算法相应的本征值稳定性较低,且需确定每个时间-速度对下协方差矩阵的本征结构分解来检验该时间-速度对是否存在反射同相轴,计算量大.链匹配法(许建华等,1990)把每道波形用带若干特征的波峰和波谷所组成的链来代表, 将同相轴的拾取转化为各链之间的最优匹配问题. 插值法(卞志彬,2011)是对地震资料先通过手动拾取地震同相轴的一些控制点(种子点),然后通过插值法对控制点数据插值,再用滤波器滤掉插值过程中可能产生的高频异常值.种子点的手动拾取使该方法较难实现自动化.拟合法(周冠雄等,1991)的基本思想是将同相轴视为具有某种动态规律的曲线, 通过一个广义的时间序列来描述, 并用某种模型(如: AR模型)去拟合这个时间序列,其中合适的模型以及波达的时间序列仍是较难确定的,这些都将影响后续的同相轴拟合结果. 概率数据互联法(Woodham et al., 1995a; Woodham et al., 1995b)将要检测的层位信息建模成一个一阶常微分方程组, 通过计算各观测向量的后验概率进行数据互联逐步跟踪层位信息. 其所建立的一阶常微分方程模型是针对地震剖面的层位信息的,而非针对地震反射记录,未利用地震反射波传播的运动特征,且需人工给出跟踪的起始点和终止点深度信息.τ-p变换法(王维红等,2006)利用线性同相轴在τ-p域聚集为一点的特性可大大提高线性同相轴的信噪比,但其仅对直线型的线性同相轴适用.混沌振子检测法(李月等,2005; 赵雪平等,2006; Li et al.,2009)利用修正的Duffing方程建立检测微弱同相轴的混沌振子系统, 根据假设的不同时间-速度对扫描同相轴以构成新子波等时间间隔序列, 最后送入混沌振子系统中依据相态的改变进行检测判决. 该方法在地震资料信噪比极低的情况下仍能较准确地检测到同相轴,但该方法由于需要搜索时间-速度对,且每次搜索时都需求解混沌振子微分方程组,运行效率较低.上述方法中, 多数方法与地震波的运动规律结合较少, 计算量较大且在强随机噪声背景下同相轴的自动拾取有一些困难. 基于此本文提出利用卡尔曼滤波来拾取地震记录同相轴, 结合地震波的运动特征建立一个新的用于跟踪反射地震记录同相轴的卡尔曼滤波系统模型,并通过仿真实验分析不同因素对所建立滤波系统性能的影响.
卡尔曼滤波作为一种数值估计优化方法,与应用领域的背景结合性很强.因此在应用卡尔曼滤波解决实际问题时, 最重要的是根据所应用领域知识建立相应的数学模型,再从这个模型出发进行滤波器的设计与实现工作.在反射波地震勘探领域中,地震反射波时距曲线一般近似为双曲线,其运动方程满足双曲时距方程.考虑均匀水平层状介质,假设地震波在反射界面之上介质中的传播速度为v, 炮点的自激自收时间为t0,各检波器的炮检距分别为x1,x2,…,xk,xk+1,…,xN,各检波道的波达时间分别为t1,t2,…,tk,tk+1,…,tN,则由地震反射波双曲时距方程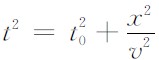 有
有
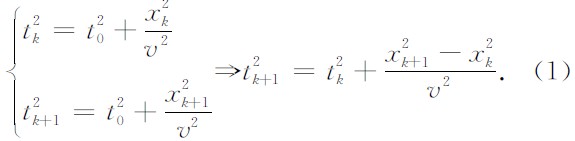
基于该递推方程, 我们建立用于跟踪同相轴的卡尔曼滤波系统模型. 取状态向量
 是地震波由炮点经反射界面传播到第k个检波器过程中的平均传播速度,量测向量
是地震波由炮点经反射界面传播到第k个检波器过程中的平均传播速度,量测向量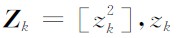 为第k个检波道实际测得的波达时间, 则根据标准的线性卡尔曼滤波模型(Kalman,1960),状态方程可写成
为第k个检波道实际测得的波达时间, 则根据标准的线性卡尔曼滤波模型(Kalman,1960),状态方程可写成
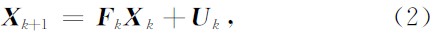
量测方程可写成
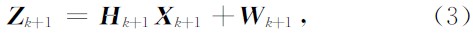
式中,Fk为状态转移矩阵,Hk+1是量测矩阵, 且
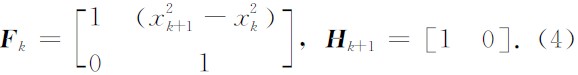
考虑到不可能获得地震波反射的精确模型以及许多不可预测的因素,在上述的状态方程(2)中引入了过程噪声Uk,过程噪声刻画地震波实际在地下传播过程中的运动规律与我们所建立的状态方程模型之间的误差, 例如:我们所建立的状态方程是基于地震波在单一介质中匀速传播以及反射界面为水平的前提条件下的, 而实际地下局部区域介质属性变化会引起地震波传播速度的微小变化,局部反射界面非水平会引起地震波传播方向的微小变化进而影响波达时间等,这些都可看做过程噪声(或称模型误差)来建模. 另外考虑在地震波的接收和测量过程中也会不可避免地存在噪声,在量测方程(3)中引入量测噪声Wk+1,例如:检波器的热噪声、检波器附近风吹草动引起的噪声等都可看做量测噪声(或称观测误差)来建模. 通常假设过程噪声和量测噪声是均值为零的高斯白噪声序列, 同时假定不同检波道的过程噪声、量测噪声是各自相互独立的, 且过程噪声和量测噪声序列之间互不相关.
由于状态向量两分量之间具有一定的相关性,进一步假设过程噪声Uk可用Γkuk表示, 其中过程噪声分布矩阵
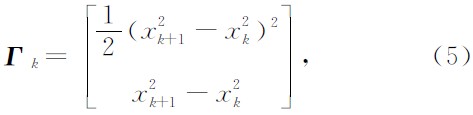
uk是状态向量中到达时分量的误差,可假定为零均值高斯白噪声.
假设第k个检波道的状态估计为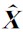 k/k,状态估计的协方差为Pk/k,利用最小均方误差准则可逐一推导上节所建立的跟踪地震记录同相轴的卡尔曼滤波系统模型下的滤波过程. 与常规卡尔曼滤波模型相同,这里首先对状态向量、状态协方差和量测向量进行预测,它们的一步预测分别为
k/k,状态估计的协方差为Pk/k,利用最小均方误差准则可逐一推导上节所建立的跟踪地震记录同相轴的卡尔曼滤波系统模型下的滤波过程. 与常规卡尔曼滤波模型相同,这里首先对状态向量、状态协方差和量测向量进行预测,它们的一步预测分别为
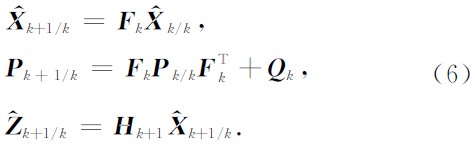
其中
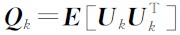 是过程噪声协方差矩阵.根据实际地震记录检测到的第k个检波道的波达时间Zk+1可得量测的预测值和量测值之间的差值(新息)为
是过程噪声协方差矩阵.根据实际地震记录检测到的第k个检波道的波达时间Zk+1可得量测的预测值和量测值之间的差值(新息)为
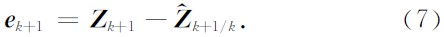
量测的预测协方差(新息协方差)为
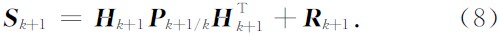
其中
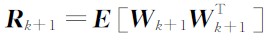 是量测噪声的协方差矩阵.当
是量测噪声的协方差矩阵.当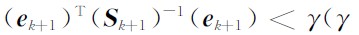 为给定的门限)时,滤波器增益为
为给定的门限)时,滤波器增益为
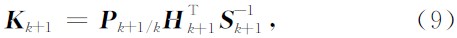
否则滤波器增益为0, 这可避免一些野值对滤波结果的影响. 最后更新状态向量和状态估计的协方差
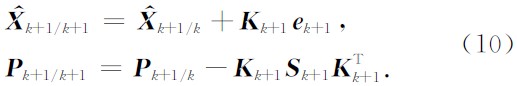
这样就完成了一次卡尔曼滤波的迭代过程.随着迭代次数(地震道数)的增长, 滤波值和同相轴真实值之间的差值会越来越小.
可见经过上述滤波过程不但拾取了同相轴位置(时间)信息,而且同时估计出了地震波在地下介质中的传播速度.
由上节的滤波模型可知, 运用卡尔曼滤波的一个重要前提条件是初始化状态估计和状态估计的协方差. 假设量测噪声Wk是均值为0、方差为σw2的高斯白噪声, 即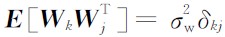 ,过程噪声Uk=Γkuk, uk是均值为0、方差为σu2的高斯白噪声, 即
,过程噪声Uk=Γkuk, uk是均值为0、方差为σu2的高斯白噪声, 即 ,且假设量测噪声与过程噪声相互独立. 此时可采用两点差分法进行初始化, 即利用最先得到的两个量测值Z1和Z2来初始化. 初始状态估计为
,且假设量测噪声与过程噪声相互独立. 此时可采用两点差分法进行初始化, 即利用最先得到的两个量测值Z1和Z2来初始化. 初始状态估计为
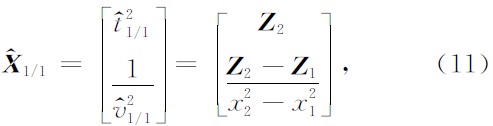
其中x1和x2分别是测得量测值Z1和Z2时所对应的炮检距. 由初始状态估计向量(11)及关于量测噪声和过程噪声的假设, 可推得初始协方差为
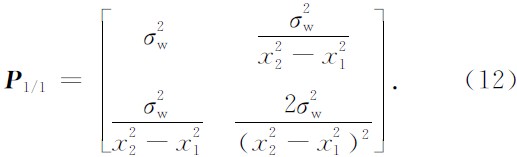
量测噪声的协方差矩阵
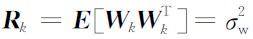 ,过程噪声协方差矩阵
,过程噪声协方差矩阵
 如式(5)所示. 在卡尔曼滤波迭代过程中, 为了简便通常认为量测噪声、过程噪声方差不变, 则各自协方差Rk和Qk也不随k的变化而变化.
如式(5)所示. 在卡尔曼滤波迭代过程中, 为了简便通常认为量测噪声、过程噪声方差不变, 则各自协方差Rk和Qk也不随k的变化而变化.综上所述, 根据反射地震波传播时距方程, 以同相轴各子波到达时间和地震波传播速度的估计量为状态向量, 以观测到的各道地震子波到达时间为量测, 我们建立了跟踪反射同相轴的系统模型和滤波模型, 该模型融入了波达时间、炮检距、层速度等地震波传播过程中的重要物理量, 利用可观测到的各检波道地震子波的到达时间和炮检距逐次进行卡 尔曼滤波迭代, 从而得到滤波后的同相轴估计信息.
建立了用于跟踪地震记录同相轴的卡尔曼滤波系统的数学模型后,本节通过仿真实验分析不同参数下其跟踪滤波性能.
上述用于跟踪地震记录同相轴的卡尔曼滤波系统模型的输入数据是不同的炮检距和在不同炮检距道集上检测到的地震子波的波达时间. 检测波达时间是相关的另外一个研究要点, 限于篇幅在本文的仿真实验中, 仅通过简单地取各道固定窗口内地震信号幅度最大值点所对应的时间作为量测到的各道波达时间, 这在单同相轴的情况下是可行的, 多同相轴情况下的检测可通过门限方法获取.然后将各道波达时间经过平方作为卡尔曼滤波系统的量测数据, 进行滤波跟踪同相轴. 具体仿真步骤如下:
(1)根据给定仿真条件, 合成N道含噪声地震观测记录;
(2)对每道地震信号, 记录下给定窗口内幅度最大值点所对应的时间, 并将该时间平方得到量测数据Zk(k=1,2,…,N);
(3)估计量测噪声Wk的方差σw2和到达时的平方的误差的方差σu2,按照式(11)和(12)初始化
卡尔曼滤波器的状态估计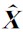 1/1
1/1
和状态估计的协方差P1/1;
(4)按照2.2节中的滤波过程进行预测、滤波,逐步迭代得到滤波后状态向量序列
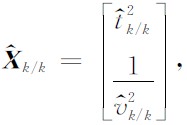 其中的
其中的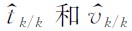 即为经卡尔曼滤波后得到的同相轴第k道的波达时间和速度信息.
即为经卡尔曼滤波后得到的同相轴第k道的波达时间和速度信息.
为了评价所提出方法跟踪滤波同相轴的性能, 考察如下三个评估指标(何友等,2009): 同相轴精度、发散度和收敛速度.
(1)同相轴精度
同相轴精度包括波达时间精度和速度精度. 波达时间精度定义为滤波稳定后波达时间估计的均方根误差, 速度精度定义为滤波稳定后速度估计的均方根误差, 计算公式分别为
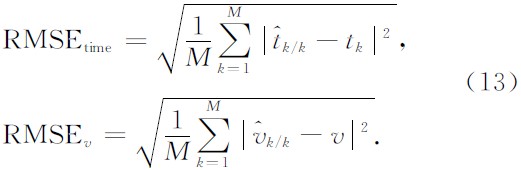
该值越小表明滤波器跟踪滤波精度越高.
(2)发散度η
由于量测噪声以及实际地震波传播过程与所建模型间过程噪声的存在,有时会导致滤波发散,即滤波值和真实值之间的差值随着迭代次数的增加而无限增长.有时即使该差值不无限增长,但BC明显大于检波器的量测误差, 在这种情况下,该滤波结果也是没有实用价值的.因此本文采用如下定义:若从滤波稳定时刻开始连续多道波达时间均方根误差RMSEtime大于发散检验阈值,则认为该次滤波发散,反之认为该次滤波收敛.对发散度的评估在实际应用中通常采用Monte Carlo仿真方法,即发散度定义为Monte Carlo仿真实验中滤波发散次数N0与总仿真次数N之比,即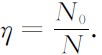 .该值越小说明滤波器正确跟踪同相轴的概率越大.
.该值越小说明滤波器正确跟踪同相轴的概率越大.
(3)收敛速度k0
由于滤波初始阶段数据量少以及噪声的存在, 经常导致滤波不稳定, 表现为状态向量有较强的震荡, 随着数据量增加, 经过多步迭代, 滤波将逐步稳定. 若连续多道波达时间方差小于给定的稳定检验阈值, 则认为滤波稳定. 在滤波发散的情况下考虑稳定的快慢是没有意义的, 因此定义收敛速度为在滤波收敛的条件下滤波达到稳定所需的迭代次数k0,该次数越小则表明滤波器收敛速度越快.
本节首先给出两个利用所提出滤波方法跟踪地震反射记录同相轴的仿真示例,然后通过Monte-Carlo仿真实验较详细地分析不同参数对滤波性能的影响.
(1)简单同相轴
首先考虑简单同相轴的情形,即真实轴为具有单一速度的连续双曲轴.按照3.1节中仿真步骤, 首先依据表1所列参数按双曲时距方程产生各道到达时,合成如图1a所示无噪声地震记录, 其中地震子波采用Ricker子波(Sheriff,1994)w(t)=(1-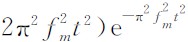 (fm为地震子波的主频), 前100道子波主频取为50 Hz,101-180道主频取为40 Hz,181-256道取为30 Hz. 然后叠加高斯白噪声后形成观测地震记录.图1b给出了一张含噪声记录,其 各道峰值信噪比(PSNR, Peak Signal to Noise Ratio) 为服从[0 dB, 20 dB]上均匀分布的随机数(平均 PSNR=10 dB). 为了计算简便, 这里定义PSNR为
(fm为地震子波的主频), 前100道子波主频取为50 Hz,101-180道主频取为40 Hz,181-256道取为30 Hz. 然后叠加高斯白噪声后形成观测地震记录.图1b给出了一张含噪声记录,其 各道峰值信噪比(PSNR, Peak Signal to Noise Ratio) 为服从[0 dB, 20 dB]上均匀分布的随机数(平均 PSNR=10 dB). 为了计算简便, 这里定义PSNR为
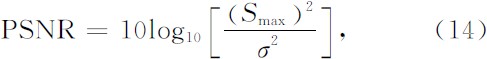
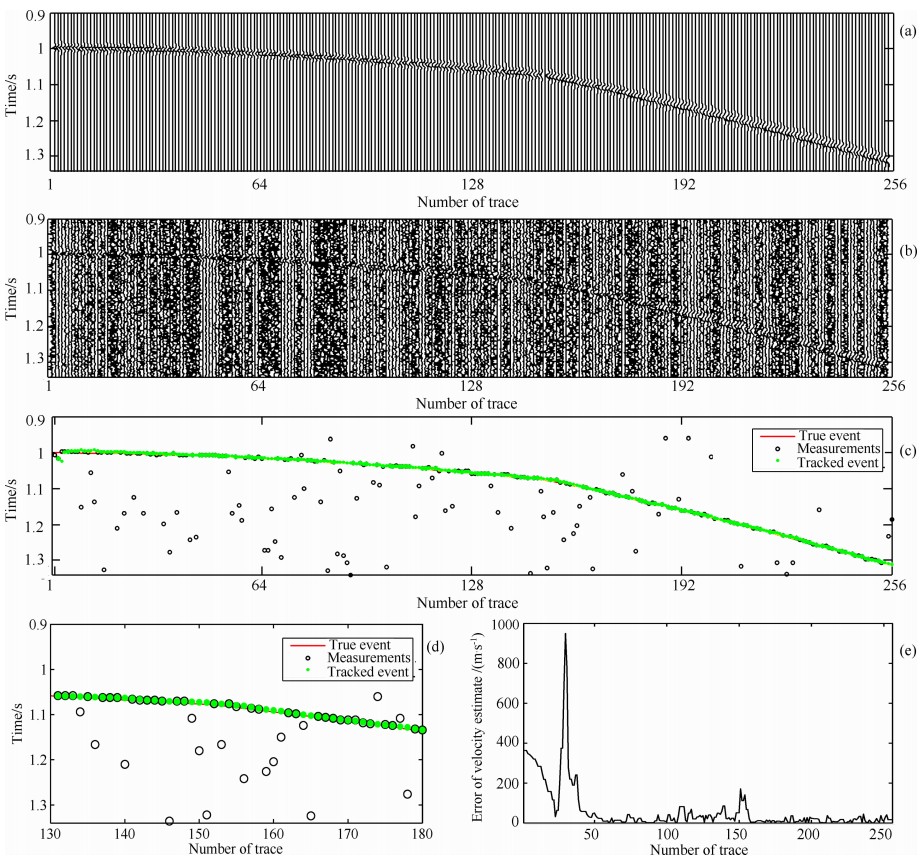
其中Smax是未叠加噪声的地震子波的峰值, σ2是所叠加的高斯白噪声功率. 由图1b可见较强噪声掩盖了同相轴,使同相轴的辨识变得困难. 对每道信号,取出时间窗[0.9 s,1.2 s]内幅度最大值点所在的时间,与每道的炮检距一起作为量测数据来源,然后利用本文方法拾取地震反射同相轴信息. 图1c给出了经本文方法处理后跟踪得到的同相轴, 其中小圆圈表示对每道数据取窗口内最大值检测得到的量测点, 可见部分量测点已偏离真实同相轴(实线)较远, 跟踪得到的同相轴(实心点)起始部分受量测噪声影响较大, 随着迭代次数的增加, 滤波值(实心点)和真实值之间的差值越来越小. 图1d放大显示了图1c中40-70道的检测跟踪结果,从中可清晰地观察到所提出方法极大地抑制了量测噪声,滤波结果较接近真实值.图1e给出了速度估计误差曲线,可见起始部分很不稳定,误差较大,但稳定后误差变小, 这里收敛速度较慢可能是因为各道地震信号所加噪声功率不同,而滤波时为了方便却使用了相同的噪声功率估计值的缘故.
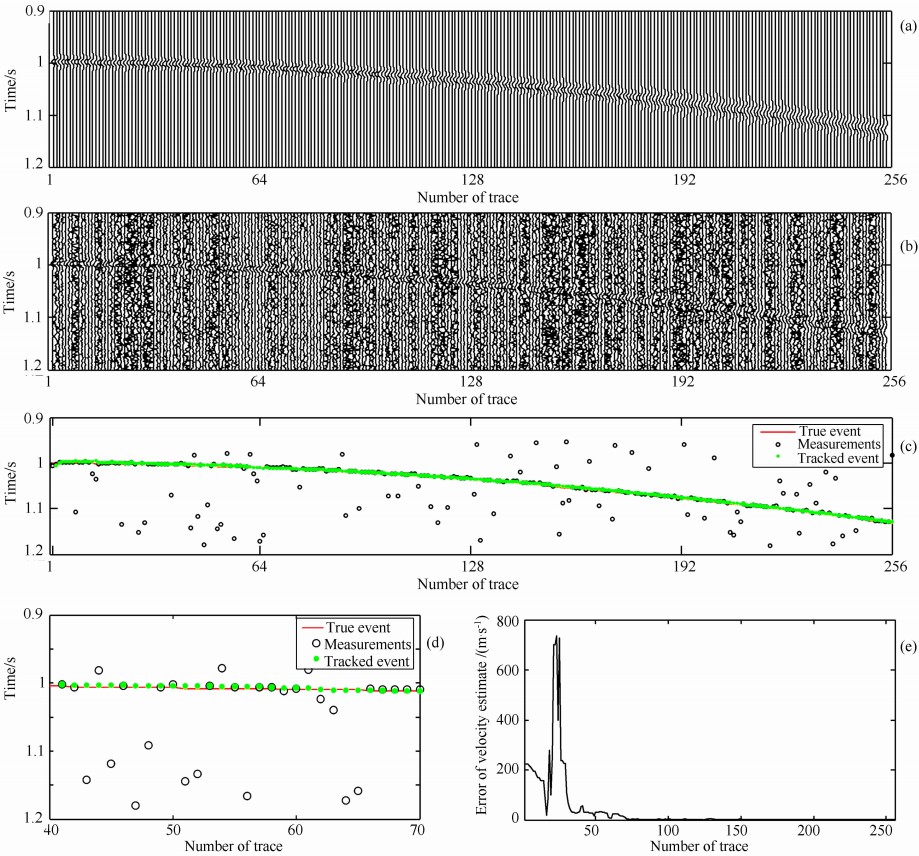 | 图1 简单同相轴的卡尔曼滤波拾取实验示例 (a)无噪声地震记录; (b)含噪声地震记录(平均PSNR=10 dB);(c)检测和跟踪结果; (d)图(c)的局部放大;(e)速度估计误差. Fig.1 A tracking example for a simple event by using Kalman filter (a) Noise-free seismic record;(b) Noisy record (mean PSNR=10 dB);(c) Results of detecting and tracking; (d) Enlarged part of subplot (c);(e) Errors of velocity estimates. |
上例表明对较简单的同相轴本文方法能有效地抑制噪声,拾取出正确的同相轴.为考察本文方法对复杂同相轴情形的有效性,对图1a所示的无噪声 记录,改变地震道1~150的层速度为2000 m/s,令 第151道无有效地震子波,地震道152~256的层速度为 1400 m/s,其他合成参数如表1所示不变.图2a显示了所合成的复杂双曲同相轴的地震记录,从第152道起由于速度变慢同相轴变得更向下倾斜,而不是原来的双曲线形态.图2b叠加了高斯白噪声,图2c显示了对复杂双曲轴的检测和跟踪结果,其中实线表示真实同相轴,小圆圈表示由最大值法找到的代表反射地震子波的量测点,实心点表示通过卡尔曼滤波跟踪得到的同相轴点.由图2c可见,即使在150道附近同相轴的速度发生了突然变换,但跟踪效果依然良好,与真实同相轴基本吻合.图2d放大显示了第150道附近的跟踪情况,图2e显示了每道的速度估计误差,除了初始估计误差较大外,在速度发生变化的第150道左右速度估计误差也较大,但随着迭代的增加误差逐渐减小.这是由于当速度发生变化的时候,虽然状态向量的预测误差较大,但此时新息也将增大,从而修正了预测值,使之逐渐收敛到新的速度.
|
|
表1 产生合成记录所用参数 Table 1 Parameters used to synthesize the seismic record |
 | 图2 复杂同相轴的卡尔曼滤波拾取实验示例 (a) 无噪声地震记录; (b) 含噪声地震记录(平均PSNR=10 dB);(c) 检测和跟踪结果;(d) 图(c)的局部放大;(e) 速度估计误差. Fig.2 A tracking example for a complex event by using Kalman filter (a) Noise-free seismic record;(b) Noisy record (mean PSNR=10 dB);(c) Results of detecting and tracking;(d) Enlarged part of subplot (c);(e) Errors of velocity estimates. |
(3)Monte-Carlo仿真
上面两实验示例给出了卡尔曼滤波方法跟踪较简单和较复杂地震反射同相轴的结果, 由于噪声具有随机性,下面通过Monte-Carlo仿真实验计算3.2节所列各项性能评估指标, 分析不同因素对跟踪滤 波性能的影响, 其中所有Monte Carlo仿真次数均为1000.
a.地震记录信噪比
改变所叠加高斯白噪声的功率,表2列出了对所合成的具有不同PSNR地震记录滤波跟踪后的同相轴各项性能评估指标值.由表2可见,随着PSNR的提高,滤波后同相轴精度越来越高,发散度越来越小,收敛速度也缓慢加快.
|
|
表2 不同PSNR下的性能评估 Table 2 Performances of the proposed method for the cases of different PSNRs |
b.层速度
一般说来,层速度越高同相轴的形态表现为越陡峭, 为了考察本文方法对不同形态同相轴的跟踪能力, 改变表1中层速度值, 其它条件不变, 并固定PSNR=10 dB, 得到表3所列不同层速度下滤波跟踪性能评估指标值. 可见层速度越大, 速度估计精度越差, 收敛速度越慢, 到达时精度和发散度受层速度影响较小. 造成速度估计精度随层速度增大而变差的原因部分上是由于采样间隔(0.02 s)较大的缘故.
|
|
表3 不同层速度下的性能评估 Table 3 Performances of the proposed method for the cases of different velocities |
c.量测噪声标准差参数
在卡尔曼滤波系统中, 一般要事先估计量测噪声标准差, 然后作为一个输入参数传递给滤波过程. 在PSNR=10 dB的条件下, 表4列出了不同量测噪声标准差参数对滤波器性能的影响.可见当该参数较小(如:0.001,0.002)或较大(如:0.05,0.1,1)时会导致各项指标变差, 如:发散度变得较大, 即正确跟踪真实同相轴的概率较低, 因此设定合适的量测噪声标准差参数是十分重要的.
|
|
表4 不同量测噪声标准差参数下的性能评估 Table 4 Performances of the proposed method for the cases of different σw |
d.门限参数γ
门限参数γ影响着当前量测点能否参与本次迭代的滤波更新, γ越大则量测点参与滤波更新的概率就越大.设置门限γ的作用是剔除一些误差较大的量测点对跟踪同相轴的影响.表5列出了相同条件下, 不同γ参数对滤波器性能的影响.可见该参数设置过小(如:3)或过大会导致较大的发散度.前者是由于门限较小会导致部分量测点不能参与滤波更新过程,使滤波仅沿着原始预测方向迭代的缘故;后者是由于门限较大导致过多的误差较大的量测点参与滤波更新的缘故.
|
|
表5 不同门限参数下的性能评估 Table 5 Performances of the proposed method with different parameters γ |
由上可见, 本文方法跟踪滤波性能除受层速度影响较小外,地震记录信噪比以及预设的量测噪声标准差参数和门限参数都会不同程度地影响跟踪性能,适宜参数的选取还需进一步研究.
为了拾取地震反射记录同相轴, 结合地震反射波运动规律,本文建立了跟踪地震记录同相轴的卡尔曼滤波系统,逐一给出系统模型、滤波模型和具体的实施步骤,分析了不同因素对滤波器性能的影响.该方法首先检测可能代表反射地震子波的量测点,减少了后期参与卡尔曼滤波的数据量,从而降低了该方法的计算量;其次该方法所建立的状态方程融入了反射波运动规律,并利用炮检距和检测到的量测点逐次进行卡尔曼滤波迭代,极大限度地利用已知信息和规律,在抑制噪声的同时逐步自动跟踪识别出同相轴,这一点与其它的同相轴拾取方法有较大的不同.仿真实验表明,对简单和复杂同相轴,本文提出的方法能较准确地拾取出同相轴信息.地震记录信噪比的提高、量测噪声标准差参数的准确估计、门限参数的合适选取将会产生较高的同相轴精度、较小的发散度、较快的收敛速度.本文方法的跟踪滤波性能除受层速度影响较小外,上述三个参量都会不同程度地影响着跟踪性能,但作为一种新方法为同相轴的自动拾取开辟了一条新途径. 类似地, 依据不同地震波传播规律, 可以分别建立跟踪直达波、折射波、绕射波等同相轴的一类卡尔曼滤波系统.关于如何选取较合适的参数、如何提高滤波性能以及同时跟踪多同相轴等问题还需进一步研究.
| [1] | Bian Z B. 2011. Study of automatic events extraction on the seismic profiles methods based on the QT platform [Master′s thesis] (in Chinese).Chengdu: Chengdu University of Technology. |
| [2] | Bondar I. 1992. Seismic horizon detection using image processing algorithms. Geophysical Prospecting, 40(7): 785-800, doi:10.1111/j.1365-2478.1992.tb00552.x. |
| [3] | Crump N D. 1974. A Kalman filter approach to the deconvolution of seismic signals. Geophysics, 39(1): 1-13, doi: 10.1190/1.1440408. |
| [4] | Dong M Y, Wang Z H. 1991. Adaptive time-variable deconvolution for seismic data using Kalman predictor model. Chinese J. Geophy. (in Chinese), 34(2): 248-258. |
| [5] | Faraklioti M, Petrou M. 2004. Horizon picking in 3D seismic data volumes. Machine Vision and Applications, 15(4): 216-219, doi: 10. 1007/s00138-004-0151-8. |
| [6] | Glinsky M E, Clark G A, Cheng P K Z, et al. 2001. Automatic event picking in prestack migrated gathers using a probabilistic neural network. Geophysics, 66(5):1488-1496, doi: 10.2172/394450. |
| [7] | He Y, Xiu J J, Zhang J W, et al. 2009. Radar data processing with applications (Second Edition) (in Chinese). Beijing: Publishing House of Electronic Industry. |
| [8] | Hu Z H, Feng J C. 2011. Chaotic communications with multiuser based on unscented Kalman filter. Acta Phys. Sin. (in Chinese), 60(7):070505-1-070505-6. |
| [9] | Jo G N, Choi H S. 2006. Velocity-aided underwater navigation system using receding horizon Kalman filter. IEEE J. Oceanic Engr., 31(3):565-573, doi: 10.1109/JOE.2006.875100. |
| [10] | Kalman R E. 1960. A new approach to linear filtering and prediction problems. Trans. ASME-J. Basic Engr., 82(Series D): 35-45, doi:10.1115/1.3662552. |
| [11] | Key S C, Smithson S B. 1990. New approach to seismic-reflection event detection and velocity determination. Geophysics, 55(8): 1057-1069, doi: 10.1190/1.1442918. |
| [12] | Le X A, Wan W X, Liu L B, et al. 2010. Development of an ionospheric numerical assimilation nowcast and forecast system based on Gauss-Markov Kalman filter-An observation system simulation experiment taking example for China and its surrounding area. Chinese J. Geophys. (in Chinese), 53(4):787-795, doi:10.3969/j.issn.0001-5733.2010.04.003. |
| [13] | Li H X, Liu C, Tao C H. 2007. The study of application of edge measuring technique to the detection of phase axis of the seismic section. Progress in Geophys. (in Chinese), 22(5):1607-1610, doi:10.3969/j. issn.1004-2903.2007.05.041. |
| [14] | Li Y, Yang B J, Badal J, et al. 2009. Chaotic system detection of weak seismic signals. Geophys J. Int., 178(3): 1493-1522, doi: 10.1111/j.1365-246x.2009.04232.x. |
| [15] | Li Y, Yang B J, Zhao X P, et al. 2005. An algorithm of chaotic vibrator to detect weak events in seismic prospecting records. Chinese J. Geophys. (in Chinese), 48(6):1428-1433, doi: 10.3321/j.issn.0001 -5733.2005.06.028. |
| [16] | Liu C, Feng Z H, Xie J E, et al. 2010. A method of automatic events extraction based on fourth-order cumulants. Journal of Jilin University (Earth Science Edition) (in Chinese), 40(5): 1188-1193, doi: 10.3969/j.issn.1671-5888.2010.05.032. |
| [17] | Liu X W, Xue P, Li Y D. 1989. Neural network method for tracing seismic events. 59th Ann. Internat Mtg., Soc. Expi. Geophys. |
| [18] | McCormack M D, Zaucha D E, Dushek D W. 1993. First-break refraction event picking and seismic data trace editing using neural networks. Geophysics, 58(1): 67-78, doi: 10.1190/1.1443352. |
| [19] | Reid R E, Tugcu A K, Mears B C. 1984. The use of wave filter design in Kalman filter state estimation of the automatic steering problem of a tanker in a seaway. IEEE Trans. Auto. Cont., 29(7): 577-584, doi: 10.1109/TAC.1984.1103591. |
| [20] | Sheriff R E. 1994. Encyclopedic dictionary of exploration geophysics. Tulsa: SEG. |
| [21] | Shi X K, Wen J, Liu J W, et al. 2010. Application and improvement of an adaptive ensemble Kalman filter for soil moisture data assimilation. Sci China Earth Sci,53(11):1700-1708, doi:10. 1007/s11430-010-4107-8. |
| [22] | Spagnolini U. 1991. Adaptive picking of refracted first arrivals. Geophy. Prosp.,39(3):293-312, doi:10.1111/j.1365-2478.1991.tb00314.x. |
| [23] | Thorp J S. 1973. Optimal tracking of maneuvering targets. IEEE Trans. Aero. Elec.Sys.,9(4):512-519, doi:10.1109/TAES.1973.309633. |
| [24] | Tugnait J K. 1991. On time delay estimation with unknown spatially correlated Gaussian noise using fourth-order cumulants and cross cumulants. IEEE Trans. Signal Processing,39(6):1259-1267, doi:10.1109/78.136532. |
| [25] | Valverde G, Terzija V. 2011. Unscented kalman filter for power system dynamic state estimation. IET Gener., Transm. & Distrib., 5(1):29-37,10.1049/iet-gtd.2010.0210. |
| [26] | Vullings R, Vries B D, Bergmans J W M. 2011. An adaptive Kalman filter for ECG signal enhancement. IEEE Trans. Biom. Engr., 58(4):1094-1103, doi:10.1109/TBME.2010.2099229. |
| [27] | Wang W H, Shou H, Liu H, et al. 2006. High resolution τ-p transform in linear events wave field separation. Progress in Geophys. (in Chinese),21(1):74-78, doi:10.3969/j.issn.004-2903.2006.01.012. |
| [28] | Woodham C A, Sandham W A, Durrani T S. 1995a. 3-D seismic tracking with probabilistic data association. Geophysics, 60(4):1088-1094, doi:10.1190/1.1443837. |
| [29] | Woodham C A, Sandham W A, Durrani T S. 1995b. Error analysis for the seismic PDA tracker. Geophysics,60(5):1451-1456, doi:10.1190/1.1443879. |
| [30] | Xiong H J, Guan Y P, Yu Y J, et al. 2009. Extraction of cophasal axes on seismic sections based on the edge detection method. Progress in Geophys.(in Chinese),24(6):2250-2254, doi:10.3969/j.issn. 1004-2903.2009.06.045. |
| [31] | Xu J H, Wang S K, Zhao T S. 1990. Picking up the events automatically by chain matching algorithm. Geophy. Prosp. Petr. (in Chinese), 29(2):13-23. |
| [32] | Yang W, Chen K Y. 2011. The seismic reflection cophasal axes checked by using image thin algorithm. Complex Hydrocarbon Reservoirs(in Chinese),4(2):31-34, doi:10.3969/j.issn.1674-4667.2011.02.008. |
| [33] | Zhao X P, Li Y, Yang B J. 2006. The discussion to the resilience items in the Duffing type system used for detecting events. Progress in Geophys.(in Chinese),21(1):61-69, doi:10.3969/j.issn.004-2903.2006.01.010. |
| [34] | Zhou G X, Hu Z C. 1991. An AR-method for automatically tracking syncphase axis of the seismic cross-section graph. Acta Auto. Sin. (in Chinese),17(3):369-362. |
| [35] | 卞志彬. 2011. 基于QT的地震剖面同相轴自动拾取方法技术研究[硕士论文]. 成都: 成都理工大学. |
| [36] | 董敏煜, 王振华. 1991. 地震资料自适应时变卡尔曼反褶积. 地球物理学报, 34(2): 248-258. |
| [37] | 何友,修建娟,张晶炜等. 2009. 雷达数据处理及应用(第二版). 北京:电子工业出版社. |
| [38] | 胡志辉, 冯久超. 2011. 基于UKF的多用户混沌通信. 物理学报, 60(7): 070505-1-070505-6. |
| [39] | 乐新安, 万卫星, 刘立波等. 2010. 基于Gauss-Markov卡尔曼滤波的电离层数值同化现报预报系统的构建--以中国及周边地区为例的观测系统模拟试验. 地球物理学报,53(4):787-795, doi: 10.3969/j.issn.0001-5733.2010.04.003. |
| [40] | 李红星, 刘财, 陶春辉. 2007. 图像边缘检测方法在地震剖面同相轴自动检测中的应用研究. 地球物理学进展, 22(5):1607-1610, doi:10.3969/j.issn.1004-2903.2007.05.041. |
| [41] | 李月, 杨宝俊, 赵雪平等. 2005. 检测地震勘探微弱同相轴的混沌振子算法. 地球物理学报,48(6):1428-1433, doi:10.3321/j.issn.0001-5733.2005.06.028. |
| [42] | 刘财, 冯智慧, 谢金娥等. 2010. 基于四阶累积量的同相轴自动拾取方法. 吉林大学学报(地球科学版), 40(5):1188-1193, doi:10.3969/j.issn.1671-5888.2010.05.032. |
| [43] | 王维红, 首皓, 刘洪等. 2006. 线性同相轴波场分离的高分辨率τ- p变换法.地球物理学进展,21(1):74-78, doi:10.3969/j.issn.004-2903.2006.01.012. |
| [44] | 熊会军, 管业鹏, 于蕴杰等. 2009. 基于图像边缘检测方法提取地震剖面同相轴.地球物理学进展,24(6):2250-2254, doi:10.3969/j.issn.1004-2903.2009.06.045. |
| [45] | 许建华, 王世库, 赵廷寿. 1990. 用链匹配算法自动拾取同相轴. 石油物探, 29(2):13-23. |
| [46] | 杨微, 陈可洋. 2011. 利用图像细化算法检测地震反射同相轴. 复杂油气藏, 4(2):31-34, doi:10.3969/j.issn.1674-4667.2011.02.008. |
| [47] | 赵雪平, 李月, 杨宝俊. 2006. 用于检测同相轴的Duffing 型系统恢复力项的讨论. 地球物理学进展,21(1):61-69, doi:10.3969/j.issn.004-2903.2006.01.010. |
| [48] | 周冠雄, 胡志成. 1991. 地震剖面图同相轴的AR自动追踪方法. 自动化学报, 17(3): 369-362. |
 2014, Vol. 57
2014, Vol. 57

