地球物理学报  2014, Vol. 57 Issue (1): 31-41   PDF    
引用本文
郑伟, 许厚泽, 钟敏, 刘成恕, 员美娟. 基于残余星间速度法精确和快速反演下一代GRACE Follow-On地球重力场. 地球物理学报,2014,57(1): 31-41, doi: 10.6038/cjg20140104   
ZHENG Wei, HSU Hou-Tse, ZHONG Min, LIU Cheng-Shu, YUN Mei-Juan. Precise and rapid recovery of Earth’s gravity field from next-generation GRACE Follow-On mission using the residual intersatellite range-rate method. Chinese J. Geophys. (in Chinese),2014,57(1): 31-41, doi: 10.6038/cjg20140104   
基于残余星间速度法精确和快速反演下一代GRACE Follow-On地球重力场
郑伟1, 许厚泽1, 钟敏1, 刘成恕1, 员美娟2    
1. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室, 武汉 430077;
2. 武汉科技大学理学院, 武汉 430081
投稿日期:2013-1-14  , 2013-12-25 收修定稿.
基金项目：中国科学院知识创新工程重要方向青年人才项目（KZCX2-EW-QN114），国家自然科学基金青年项目（41004006，41202094）、国家自然科学基金重点项目（41131067）和国家自然科学基金面上项目（11173049），国家留学人员科技活动项目择优资助基金（2011），中国科学院青年创新促进会基金（2013），武汉大学地球空间环境与大地测量教育部重点实验室测绘基础研究基金（11-01-02），中国测绘科学研究院地理空间信息工程国家测绘地理信息局重点实验室开放基金（201322），西安测绘研究所地理信息工程国家重点实验室开放基金（SKLGIE2013-M-1-5），中国科学院测量与地球物理研究所重要方向项目（Y309451045）和大地测量与地球动力学国家重点实验室自主项目（Y309491050）联合资助.
作者简介：郑伟，男，1977年生，理学博士，副研究员，硕士生导师，日本京都大学博士后，日本外籍特别研究员，主要从事基于卫星重力测量反演地球、月球和火星重力场的理论和方法等方面研究. E-mail：wzheng@asch.whigg.ac.cn
摘要：基于新型残余星间速度法（RIRM）反演了120阶GRACE Follow-On地球重力场. 第一，由于GPS定轨精度相对较低，通过将激光干涉测距仪的高精度残余星间速度（测量精度10-7 m·s-1）引入残余轨道速度差分矢量的视线分量构建了新型RIRM观测方程. 第二，基于2点、4点、6点和8点RIRM公式对比论证了最优的插值点数. 如果相关系数和采样间隔一定，随着插值点数的增加，卫星观测值的信号量被有效加强，而卫星观测值的误差量也同时增加. 因此，6点RIRM公式是提高下一代地球重力场精度的较优选择. 第三，相关系数对地球重力场精度的影响在不同频段表现为不同特性. 随着相关系数的逐渐增大，地球长波重力场精度逐渐降低，而地球中长波重力场精度逐渐升高. 第四，基于6点RIRM公式，通过30天观测数据和采样间隔5 s，分别利用星间速度和残余星间速度观测值，在120阶次处反演下一代GRACE Follow-On累计大地水准面精度为1.638×10-3 m和1.396×10-3 m. 研究结果表明：（1）残余星间速度观测量较星间速度对地球重力场反演精度更敏感；（2）GRACE Follow-On地球重力场精度较GRACE至少高10倍.
关键词： GRACE Follow-On卫星     残余星间速度法     激光干涉测距仪     下一代卫星重力反演     累计大地水准面精度    
Precise and rapid recovery of Earth’s gravity field from next-generation GRACE Follow-On mission using the residual intersatellite range-rate method
ZHENG Wei1, HSU Hou-Tse1, ZHONG Min1, LIU Cheng-Shu1, YUN Mei-Juan2    
1. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China;
2. College of Science, Wuhan University of Science and Technology, Wuhan 430081, China
Abstract: The Earth's gravitational field from the Gravity Recovery and Climate Experiment (GRACE) Follow-On mission up to degree and order 120 is recovered based on a new residual intersatellite range-rate method (RIRM) by numerical simulation. Due to a low-precision orbit determination by the Global Positioning System (GPS), a new RIRM observation equation is created by introducing the residual intersatellite range-rate with a precision of 10-7 m·s-1 from the interferometric laser ranging (ILR) system into the line-of-sight (LOS) component of the residual orbital velocity difference vector from the twin satellites. The optimal number of interpolation points is comparatively demonstrated by the two-point, four-point, six-point and eight-point RIRM formulas, respectively. If the correlation coefficient and sampling interval are fixed, when the amount of signals from satellite observations is effectively enhanced with increasing the number of interpolation points, the satellite observation errors are simultaneously improved. Therefore, the six-point RIRM formula is a preferred selection for recovering the Earth's gravitational field complete up to degree and order 120. The impact of the correlation coefficient on the accuracy of the Earth's gravitational field recovery exhibits different characteristics in different frequency bands. With the gradual increase of the correlation coefficient, the accuracy of the Earth's gravitational field recovery decreases in the long-wavelength range, while it increases in the medium-long-wavelength range. The study on a comparison of influences of intersatellite range-rate and residual intersatellite range-rate measurements on the accuracies of the Earth's gravitational field recovery from GRACE Follow-On mission is conducted, which indicates that cumulative geoid height errors from GRACE Follow-On are 1.638×10-3 m and 1.396×10-3 m using the six-point RIRM formula, an observation duration of 30 d and a sampling interval of 5 s at degree 120, respectively. The research results show that the sensitivity of satellite gravity recovery using residual intersatellite range-rate measurements is greater than that using intersatellite range-rate measurements, and the accuracy of the Earth's gravitational field recovery from GRACE Follow-On is at least 10 times higher than that from GRACE.
Key words: GRACE Follow-On satellite     Residual intersatellite range-rate method     Interferometric laser ranging system     Next-generation satellite gravity recovery     Cumulative geoid height error    

1 引 言

地球重力场及其时变量反映地球表层及内部物质的空间分布、运动和变化，同时决定着大地水准面的起伏和变化(许厚泽, 2001). 因此，确定地球重力场的精细结构及其时变特性不仅是空间大地测量学、地球物理学、地球动力学、海洋学等的需求，同时也将为寻求资源、保护环境和预测灾害提供重要的信息资源. 基于GRACE卫星精密探测地球中长波静态和长波时变重力场的突出贡献(张捍卫等, 2004; 沈云中等, 2005; 程芦颖和许厚泽, 2006; 周旭华等, 2006; 郑伟, 2006, 2008,2009a,2009b,2009c; Zheng et al., 2011)，美国宇航局(NASA)提出了用于高精度探测地球中短波静态和中长波时变重力场的下一代GRACE Follow-On卫星重力测量计划(Rummel, 2003; Sneeuw, 2005; Bender et al., 2008; Zheng et al, 2008, 2009; Wiese et al, 2009, 2012; 郑伟, 2010, 2012,2013; Loomis et al., 2012).

如表1所示，GRACE Follow-On双星采用近圆、近极和低轨道设计，利用激光干涉测距仪精确测量星间距离(10-6~10-8 m)和星间速度(10-7~10-9 m/s)，基于高轨GPS卫星确定轨道位置和轨道速度，通过星载加速度计感测作用于卫星的非保守力(10-11~10-13 m/s2)，以及依靠非保守力补偿系统(DFCS)平衡非保守力(大气阻力、太阳光压、地球辐射压、轨道高度和姿态控制力等). 基于较低的卫星轨道高度和较高的关键载荷测量精度，利用下一代GRACE Follow-On计划反演地球重力场精度较当前GRACE计划至少提高10倍.

表1 当前GRACE和下一代GRACE Follow-On卫星对比 Table 1 A comparison of current GRACE and future GRACE Follow-On missions

Wolff于1969年首次提出了利用卫星跟踪卫星低低技术(SST-LL)测量地球重力场的新思想(Wolff, 1969). 自此以后，国内外众多学者积极投身于地球重力场反演的理论研究和数值计算之中. 当前，国际通用的卫星重力反演方法主要包括：动力学法、能量守恒法、卫星加速度法、解析/半解析法等. 美国宇航局喷气推进实验室(NASA-JPL)、美国德克萨斯州立大学空间研究中心(UT-CSR)、以及德国波兹坦地学研究中心(GFZ)等研究机构采用动力学法建立了全球重力场模型GGM01S/02S (Reigber et al., 2005; Tapley et al., 2005), EIGEN-GRACE01S/02S(Reigber, 2004; Reigber et al., 2004a), EIGEN-CG01C/03C(Reigber et al., 2004b; Förste et al., 2005), EIGEN-GL04C/04S1(Förste et al., 2008a), EIGEN-5C(Förste et al., 2008b)等. 但动力学法的主要缺点是随着卫星轨道弧长的增加，动力模型的误差将快速累积，而且计算过程较复杂，需要高性能并行计算机支持.

为了有效克服动力学法的缺点，我们于2012年利用1年的GRACE-Level-1B实测数据，基于星间距离插值法和星间速度插值法分别构建了 GRACE-only全球重力场模型WHIGG-GEGM01S/02S(Zheng et al, 2012a,2012b). 为了进一步提高下一代地球重力场的反演精度，我们首次通过将高精度的残余星间速度(测量精度10-7 m/s)引入残余轨道速度差分矢量的视线方向建立了新型残余星间速度法，进而精确和快速反演了下一代GRACE Follow-On地球重力场.

2 残余星间速度观测方程建立

在地心惯性系(ECI)中，基于牛顿插值原理，单星轨道速度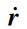的泰勒展开表示如下( Engeln-Mullges and Reutter, 1988):


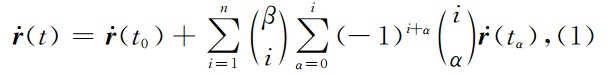
其中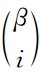，表示二项式系数，，t表示计算点的时刻，t0表示插值点的初始时刻，Δt表示采样间隔，n表示插值点的数量.

单星参考轨道速度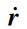o的泰勒展开表示如下:


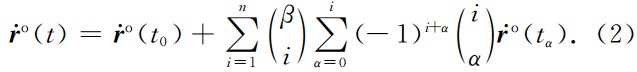
基于公式(1)—(2)，单星残余轨道速度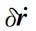的泰勒展开表示如下:


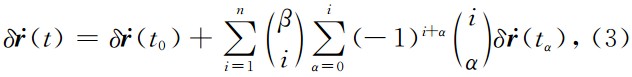
其中

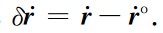
基于公式(3)的一阶时间导数，单星残余轨道加速度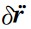的泰勒展开表示如下:


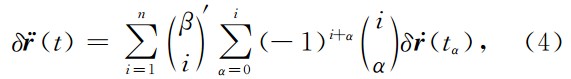
其中，

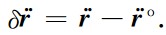
基于公式(4)，双星残余轨道加速度差分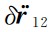的泰勒展开表示如下


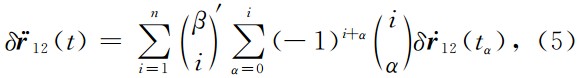
其中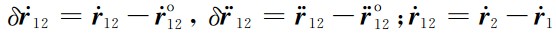和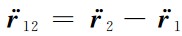分别表示轨道速度差分矢量和轨道加速度差分矢量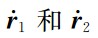， 表示双星的轨道速度矢量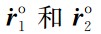，表示双星的参考轨道速度矢量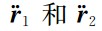，表示双星的轨道加速度矢量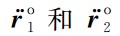，表示双星的参考轨道加速度矢量.

双星残余轨道加速度差分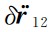的视线分量表示如下：


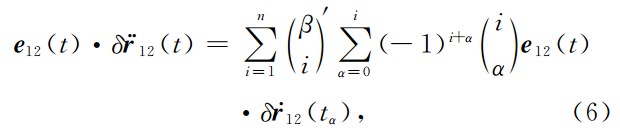
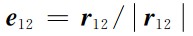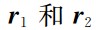其中，表示第一颗卫星指向第二颗卫星的单位矢量，表示双星的观测轨道位置矢量差分，分别表示双星的观测轨道位置矢量.

由于GPS低精度的轨道测量，假如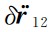被直接使用于公式(6)，地球重力场精度将无法实质性提高. 因此，激光干涉测距仪的高精度残余星间速度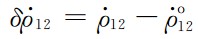的有效引入是进一步提高地球重力场精度的有效手段.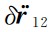可被改写为


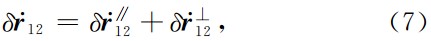
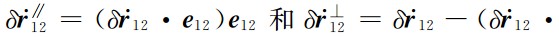
其中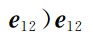，分别表示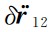的视线分量和垂向分量.

将公式(7)中的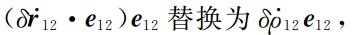并代入公式(6)可得


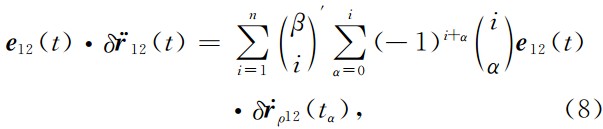
其中，

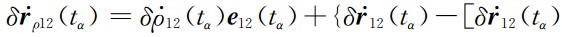
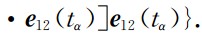
基于公式(8)，2、4、6点和8点残余星间速度公式分别表示如下:


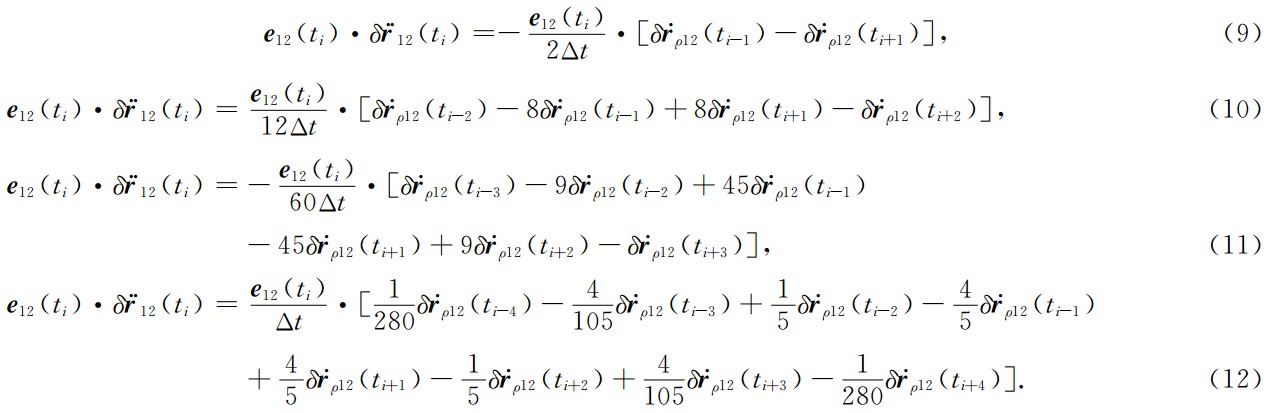
在公式(8)中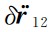，的具体形式表示如下


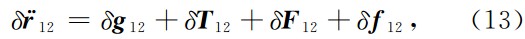
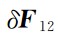
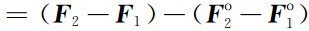其中，表示残余地球扰动位的一阶梯度，表示除地球引力之外的残余保守力差(如日月引力，地球固体潮、海潮、大气潮、极潮汐力，相对论效应等)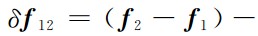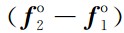，表示残余非保守力差(大气阻力、太阳光压、地球辐射压、轨道高度和姿态控制力等)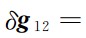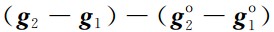，表示残余地心引力差:


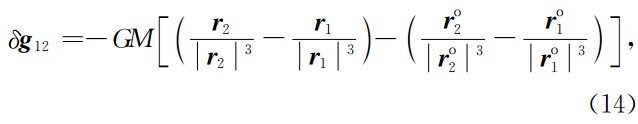
其中，GM表示地球质量M和万有引力常数G的乘积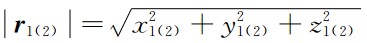，分别表示双星的地心半径，表示轨道位置矢量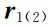的3个分量.

通过将公式(13)和(14)代入(8)，残余星间速度观测方程表示如下：


其中，r,θ,λ分别表示地心半径、地心余纬度和地心经度，Re表示地球平均半径，L表示球函数展开的最大阶数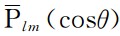；表示正规化的缔合Legendre函数，l表示阶数，m表示次数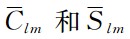；表示待估的地球引力位系数.

3 卫星观测值色噪声模拟

基于残余星间速度观测方程(15)，利用9阶Runge-Kutta线性单步法和12阶Adams-Cowell线 性多步法(刘林, 1992)数值模拟了GRACE Follow- On-A/B双星的实测轨道和参考轨道. GRACE Follow-On-A/B 双星的初始轨道参数如表1所示，其他相关模拟参数如下：先验地球重力场模型EGM2008(实测轨道和参考轨道分别截断至前120阶和30阶)、观测时间30天和采样间隔5 s. 卫星观测值不是相互独立，而具有明显的相关性. 因此，本文在卫星观测值中引入了具有相关性的色噪声. 基于Gauss-Markov模型，卫星观测值色噪声公式表示如下(沈云中, 2000):


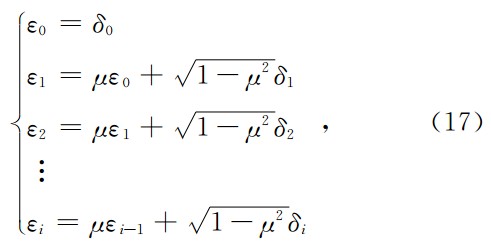
其中，μ表示相关系数；δi(i=1,2,…)表示正态分布的随机白噪声(μ=0)，i表示卫星观测值的数量；εi(i=1,2,…)表示色噪声(0<μ<1).

目前国内外众多科研机构正在积极开展下一代GRACE Follow-On卫星载荷匹配精度指标的需求论证. 为了进一步减少载荷误差对地球重力场精度的负面影响，有效弱化地球时变重力场信号在地表南北向的“条带误差”效应，以及较大程度降低海洋和大气潮汐等高频误差的“混频效应”，国内外学者建议将下一代GRACE Follow-On卫星载荷的精度指标设计为较当前GRACE卫星载荷精度指标提高 1～3个数量级较优. 本文以下一代GRACE Follow-On 卫星载荷精度指标较当前GRACE载荷精度指标提高1个数量级为例开展了数值模拟研究.

3.1 星间距离和星间速度的色噪声

如图1a所示，基于不同的相关系数0≤μ≤0.99和相同的采样间隔5 s，按照公式(17)数值模拟了激光干涉测距仪的星间距离色噪声10-6 m.

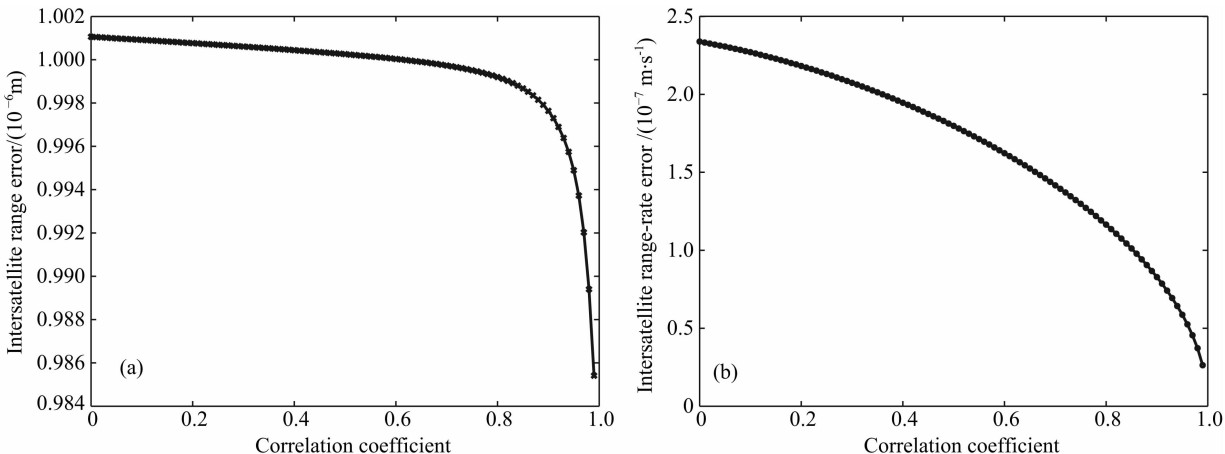图1 基于不同的相关系数和相同的采样间隔5 s模拟的观测值色噪声 (a) 星间距离；(b) 星间速度. Fig.1 Standard deviations using a sampling interval of 5 s and different correlation coefficients (a) Intersatellite range; (b) Intersatellite range-rate.
基于6点牛顿插值公式，星间速度色噪声表示如下


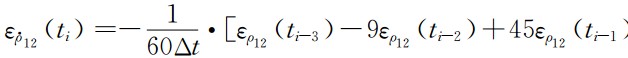
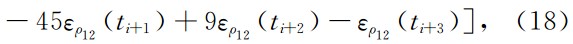
其中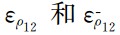，分别表示星间距离和星间速度的色噪声.

图1b表示基于不同的相关系数0≤μ≤0.99和相同的采样间隔5 s计算的星间速度色噪声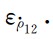.研究结果表明：随着相关系数逐渐增加0~0.99，星间 速度色噪声逐渐减小2.338×10-7 ~0.263×10-7 m/s. 因此，相关系数的适当增加有利于提高星间速度的精度. 由于星间速度的测量精度约为10-7 m/s，因此本文基于相关系数0.80~0.90和采样间隔5 s计算了星间速度的色噪声. 图2表示利用相关系数0.85和采样间隔5 s计算的星间距离和星间速度色噪声.

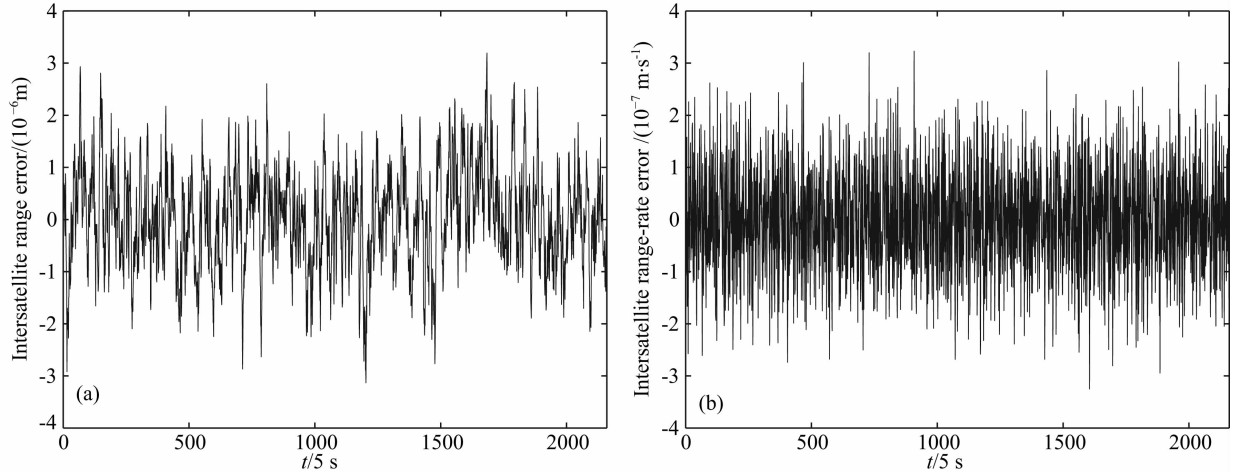图2 基于相关系数0.85和采样间隔5 s模拟的观测值色噪声 (a) 星间距离；(b) 星间速度. Fig.2 Colored noises using a sampling interval of 5 s and a correlation coefficient of 0.85 (a) Intersatellite range; (b) Intersatellite range-rate.
3.2 轨道位置和轨道速度的色噪声

本文基于不同相关系数0≤μ≤0.99和相同采样间隔5 s，分别利用公式(17)和(18)数值模拟了卫星轨道位置和轨道速度的色噪声(视线、垂向和径向)，其中视线方向轨道位置和轨道速度的色噪声如图3所示. 结果表明：随着相关系数的逐渐增加，轨 道位置和轨道速度的色噪声逐渐减小. 基于GRACE Follow-On 卫星的轨道位置(10-3 m)和轨 道速度(10-6 m/s)的测量精度，利用相关系数0.90~0.99 数值模拟了轨道位置和轨道速度的色噪声. 图4表示基于相关系数0.95和采样间隔5 s数值模拟的视线方向轨道位置和轨道速度的色噪声.

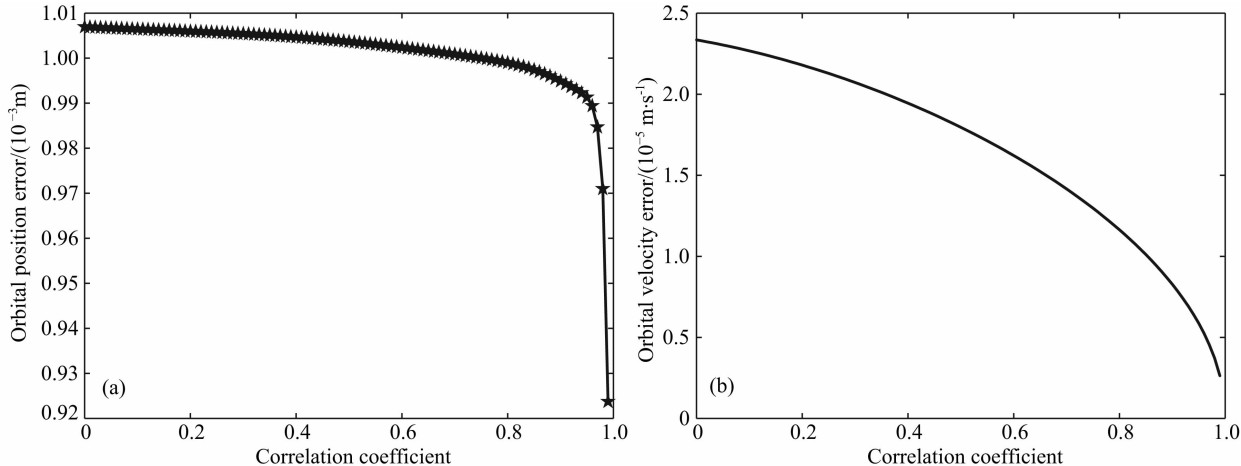图3 基于不同的相关系数和相同的采样间隔5 s模拟的视线方向色噪声 (a) 轨道位置；(b) 轨道速度. Fig.3 LOS standard deviations using a sampling interval of 5 s and different correlation coefficients (a) Orbital position; (b) Orbital velocity.

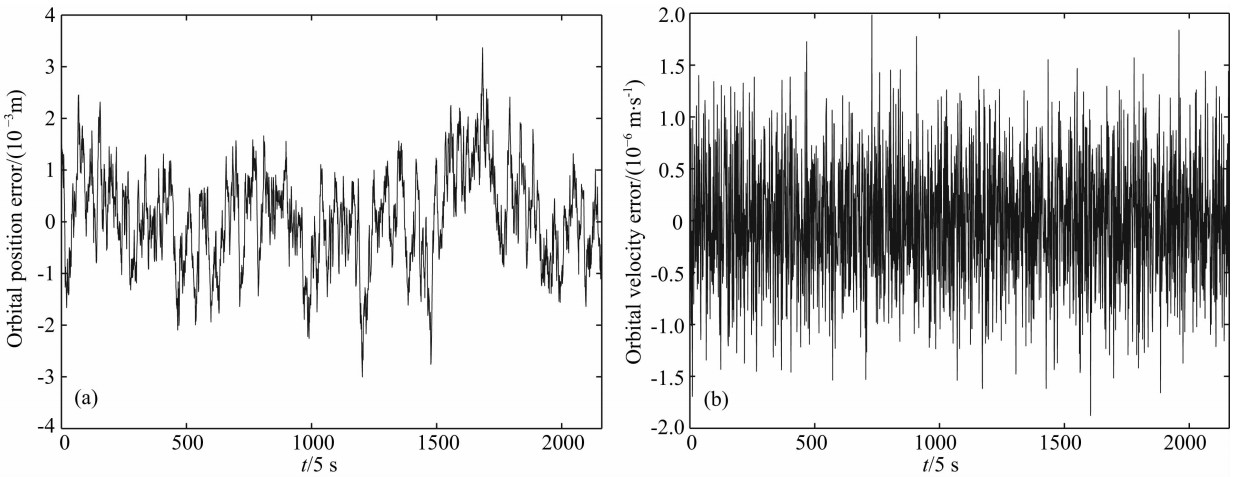图4 基于相关系数0.95和采样间隔5 s模拟的视线方向色噪声 (a) 轨道位置；(b) 轨道速度. Fig.4 LOS colored noises using a sampling interval of 5 s and a correlation coefficient of 0.95 (a) Orbital position; (b) Orbital velocity.
3.3 非保守力的色噪声

基于美国JPL公布的GRACE-Level-1B实测 数据，星载加速度计非保守力的相关系数约为0.85~ 0.95.图5表示基于相关系数0.90和采样间隔5 s，利用公式(17)模拟的加速度计视线方向的非保守力色噪声10-11 m/s2.

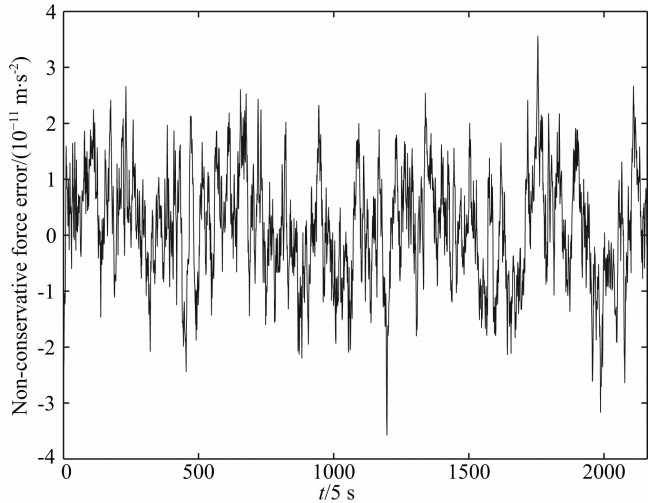图5 基于相关系数0.90和采样间隔5 s模拟的视线方向非保守力色噪声 Fig.5 LOS colored noises of non-conservative force using a sampling interval of 5 s and a correlation coefficient of 0.90
4 结果和讨论

我们于2012年基于传统的星间加速度法开展了插值公式、相关系数和采样间隔对GRACE Follow-On星间加速度精度的影响研究，主要论证了3、5、7点和9点星间距离插值公式和不同相关系数(0~0.99)对星间加速度精度的影响(郑伟等, 2012)；不同于上述研究，本文围绕2、4、6点和8点残余星间速度插值公式和不同卫星观测数据(星间速度、轨道位置、轨道速度和非保守力)相关系数对地球重力场精度的影响开展研究，重点验证了基于新型残余星间速度法提高下一代地球重力场反演精度的可行性.

4.1 星间速度插值点数的选取

如图6所示，圆圈线、十字线、实线和虚线分别表示基于观测时间30天、采样间隔5 s和相关系数(星间速度0.85、轨道位置和轨道速度0.95、以及非保守力0.90)，利用2、4、6点和8点残余星间速度公式，反演累计大地水准面精度，统计结果如表2所示. 当相关系数和采样间隔一定，插值点数的适当增加有利于地球重力场精度的提高. 研究结果表明：第一，在120阶内，基于2点残余星间速度公式的累计大地水准面精度远低于基于4、6和8点残余星间速度公式的精度；第二，基于6点残余星间速度公式的累计大地水准面精度远高于基于2点、4点和8点残余星间速度公式的精度. 总而言之，6点残余星间速度公式是建立下一代高精度和髙阶次全球重力场模型的优选方法之一.

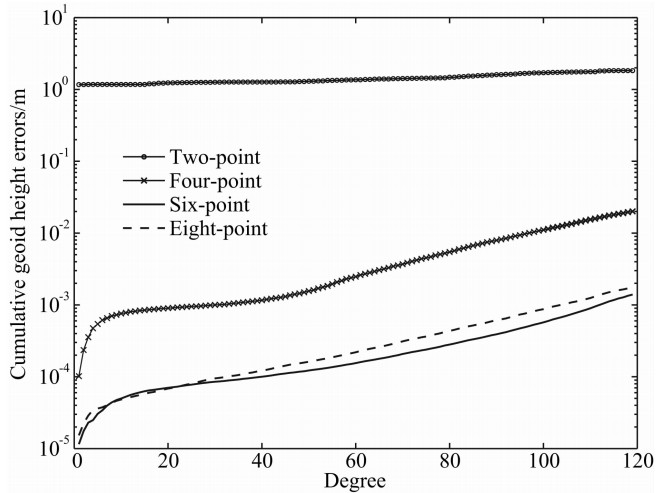图6 基于不同的残余星间速度插值点数反演累计大地水准面精度 Fig.6 Cumulative geoid height errors based on different numbers of interpolation points of residual intersatellite range-rate

表2 基于不同残余星间速度点数的累计大地水准面精度统计结果 Table 2 Statistics of cumulative geoid height error using different numbers of residual intersatellite rangr-rate measurements
4.2 相关系数的影响

图7a表示基于卫星观测时间30天和采样间隔5 s，通过6点残余星间速度公式，利用相关系数(轨道位置和轨道速度0.95、非保守力0.90、星间速度 0.80、0.85和0.90)反演地球引力位系数的精度；图7b表示利用相关系数(星间速度0.85、非保 守力0.90、轨道位置和轨道速度0.90、0.95和0.99) 反演地球引力位系数的精度；图7c表示利用相关系数(星间速度0.85、轨道位置和轨道速度0.95、非保守力0.85、0.90和0.95)反演地球引力位系数的精度. 研究结果表明：相关系数对地球重力场精度的影响在不同频段具有不同的特性. 第一，在地球重力场长波段，随着相关系数减小，地球重力场精度逐渐提高. 基于高相关性的卫星观测值，地球重力场长波段信号强度将被降低，因此在一定程度上将损失地球重力场低频信号精度. 第二，在地球重力场中长波段，随着相关系数的增加，由于卫星观测值的误差逐步减小，因此地球重力场精度逐渐提高. 总而言之，相关系数的优化设计是进一步提高地球重力场精度的关键因素.

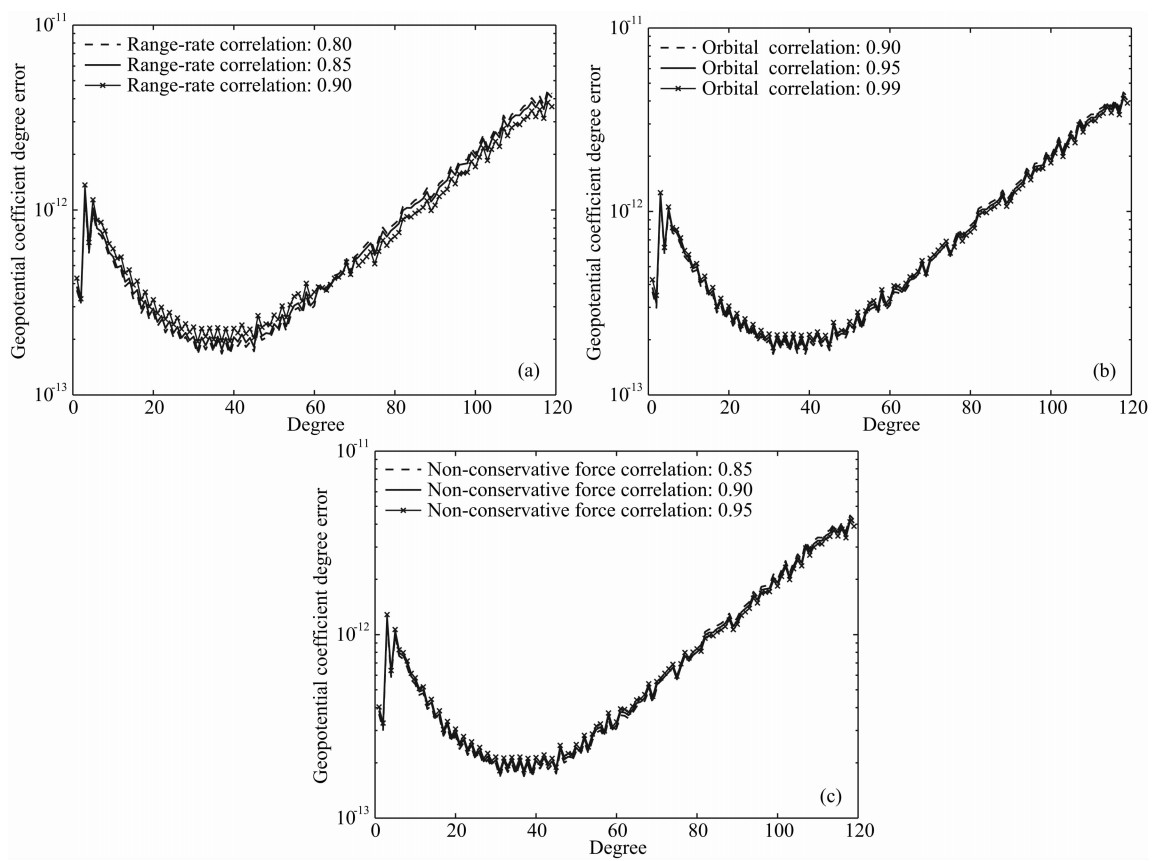图7 基于6点残余星间速度法以及利用不同相关系数和相同采样间隔5 s反演地球引力位系数精度 (a)星间速度；(b)轨道位置和轨道速度；(c)非保守力. Fig.7 Geopotential coefficients degree RMS errors based on the six-point RIRM formula and using a sampling interval of 5 s and different correlation coefficients (a) Intersatellite range-rate; (b) Orbital position and velocity; (c) Non-conservative force.
4.3 地球重力场反演

如图8所示，实线、虚线、十字线和圆圈线分别 表示基于关键载荷误差(激光干涉测距仪的星间速度1×10-7 m·s-1、GPS接收机的轨道位置3×10-3 m和轨道速度1×10-6 m·s-1、加速度计的非保守力3×10-11 m·s-2)，通过6点残余星间速度公式，利用卫星观测时间30天、采样间隔5 s和相关系数(星间速度0.85、轨道位置和轨道速度0.95、非保守力0.90)反演地球引力位系数的精度. 以基于星间速度误差1×10-7 m·s-1反演地球重力场精度为标准，我们分别基于轨道位置误差10-3~10-5 m、轨道速度误差10-6 ~10-8 m·s-1和非保守力误差10-11 ~10-13 m·s-2反演了地球重力场. 研究结果表明：星间速度误差1×10-7 m·s-1对地球 重力场精度的影响与轨道位置误差(2~3)×10-3 m、 轨道速度误差(0.5~1)×10-6 m·s-1和非保守力误差(2 ~ 3)×10-11 m·s-2相匹配. 因此，残余星间速度法是获得下一代重力卫星系统的关键载荷匹配精度指标的有效方法.

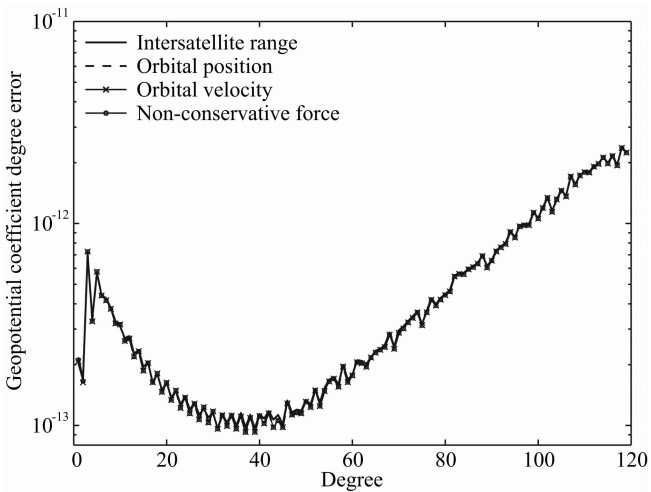图8 基于不同关键载荷精度指标反演地球引力位系数精度 Fig.8 Geopotential coefficients degree RMS errors from the measurement accuracies of different key payloads

如图9和表3所示，十字线表示德国波兹坦地学研究中心(GFZ)公布的120阶GRACE-only地球重力场模型EIGEN-GRACE02S的实测精度，在120阶处累计大地水准面精度为1.893×10-1 m. 虚线和实线表示基于6点残余星间速度公式，通过卫星观测时间30天、采样间隔5 s和相关系数(星间速度0.85、轨道位置和轨道速度0.95、非保守力0.90)，基于关键载荷匹配精度指标(激光干涉测距仪的星间速度1×10-7 m·s-1、GPS接收机的轨道位置3×10-3 m和轨道速度1×10-6 m·s-1、加速度计的非保守力3×10-11 m·s-2)，分别利用星间速度和残余星间速度观测值，反演下一代GRACE Follow-On地球重力场精度；在120阶处，GRACE Follow-On累计大地水准面精度分别为1.638× 10-3 m和1.396×10-3 m. 研究结果表明：(1)基于下一代GRACE Follow-On卫星(虚线)反演地球重力场精度较当前GRACE卫星(十字线)至少提高一个数量级；(2)下一代重力双星的残余星间速度观测量(实线)较星间速度(虚线)对地球重力场反演精度更敏感，理论分析如下：残余星间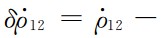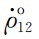速度是星间速度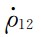扣除参考星间速度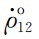后的扰动小量，通过二者的差分计算，星间速度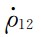和参考星间速度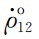之间的公共误差将被大部分消除，因此，基于残余星间速度观测量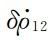有利于提高地球重力场反演精度；(3)残余星间速度法是有效抑制地球重力场的高频噪声，进而精确和快速建立下一代髙阶次地球重力场模型的有效方法.

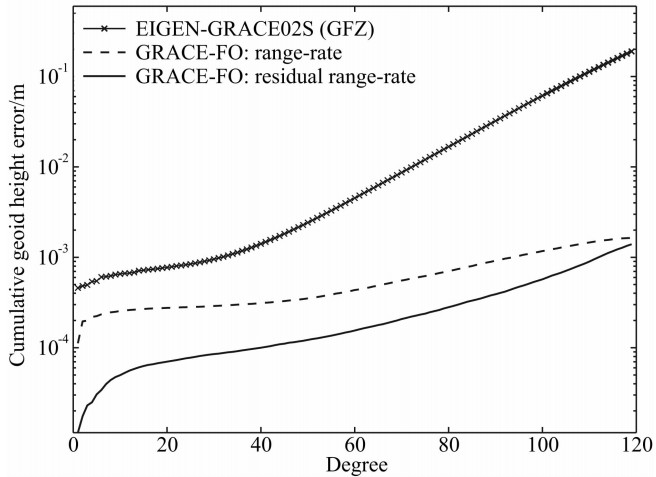图9 基于残余星间速度法反演GRACEFollow-On累计大地水准面精度 Fig.9 Cumulative geoid height errors from GRACE Follow-On using RIRM

表3 基于残余星间速度法反演累计大地水准面精度统计结果 Table 3 Statistics of cumulative geoid heigh errors by RIRM
5 结 论

本文围绕将来GRACE Follow-On卫星重力计划，旨在检验基于新型残余星间速度法进一步提高下一代地球重力场反演精度的可行性. 基于当前和将来GPS定轨精度的限制(10-2~10-3 m)，本文选择下一代GRACE Follow-On卫星载荷精度指标较当前GRACE载荷精度指标提高1个数量级开展了数值模拟研究.

(1)基于2、4、6点和8点残余星间速度公式分别反演了120阶地球重力场精度，结果表明：6 点残余星间速度公式有利于120阶GRACE Follow-On 地球重力场精度的提高；论证了不同卫星观测值相关系数对地球重力场精度的影响，结果表明：随着相关系数的逐渐减小，地球重力场长波信号精度逐渐提高，但中长波信号精度逐渐降低.

(2)开展了星间速度和残余星间速度观测值对下一代GRACE Follow-On地球重力场精度的影响研究，结果表明：下一代重力双星的残余星间速度观测量对地球重力场反演精度的敏感性较星间速度更强.

(3)残余星间速度法是反演下一代高精度和高空间分辨率GRACE Follow-On地球重力场的有效方法. 在GRACE Follow-On卫星成功发射之后，基于残余星间速度法有利于精确建立下一代高阶次全球重力场模型.

致 谢 感谢华中科技大学罗俊院士及匿名评审专家对本文的帮助. 感谢美国宇航局(NASA)等研究机构提供了下一代卫星重力测量计划的相关资料.

参考文献
[1] Bender P L, Wiese D N, Nerem R S. 2008. A possible dual-GRACE mission with 90 degree and 63 degree inclination orbits. In: Proceedings of the third international symposium on formation flying, missions and technologies. ESA/ESTEC, Noordwijk, 1-6.
[2] Engeln-Mullges G, Reutter F. 1988. Numerik-Algorithmen mit ANSI C-Programmen, BI-Wiss, Verlag, Mannheim.
[3] Förste C, Flechtner F, Schmidt R, et al. 2005. A new high resolution global gravity field model derived from combination of GRACE and CHAMP mission and altimetry/gravimetry surface gravity data. Presented at EGU General Assembly 2005, Vienna, Austria, 24-29, April.
[4] Föerste C, Schmidt R, Stubenvoll R, et al. 2008a. The Geo Forschungs Zentrum Potsdam/Groupe de Recherche de Geodesie Spatiale satellite-only and combined gravity field models: EIGEN-GL04S1 and EIGEN-GL04C.   Journal of Geodesy, 82(6): 331-346.
[5] Föerste C, Flechtner F, Schmidt R, et al. 2008b. EIGEN-GL05C-A new global combined high-resolution GRACE-based gravity field model of the GFZ-GRGS cooperation. General Assembly European Geosciences Union. Geophysical Research Abstracts, Vol. 10, Abstract No. EGU2008-A-06944.
[6] Loomis B D, Nerem R S, Luthcke S B. 2012. Simulation study of a follow-on gravity mission to GRACE.   Journal of Geodesy, 86(5): 319-335.
[7] Reigber C. 2004. First GFZ GRACE gravity field model EIGEN-GRACE01S..
[8] Reigber C, Schmidt R, Flechtner F. 2004a. An Earth gravity field model complete to degree and order 150 from GRACE: EIGEN-GRACE02S.   Journal of Geodynamics, 39(1): 1-10.
[9] Reigber C, Schwintzer P, Stubenvoll R, et al. 2004b. A high-resolution global gravity field model combining CHAMP and GRACE satellite mission and surface gravity data: EIGEN-CG01C.   Joint CHAMP/GRACE Science Meeting, GFZ, July 5-7.
[10] Reigber C, Schmidt R, Flechtner F. 2005. An Earth gravity field model complete to degree and order 150 from GRACE: EIGEN-GRACE02S.   Journal of Geodynamics, 39(1): 1-10.
[11] Rummel R. 2003. How to climb the gravity wall.   Space Science Reviews, 108(1): 1-14.
[12] Sneeuw N, Flury J, Rummel R. 2005. Science requirements on future missions and simulated mission scenarios.   Earth, Moon, and Planets, 94(1-2): 113-142.
[13] Tapley B, Ries J, Bettadpur S, et al. 2005. GGM02-An improved Earth gravity field model from GRACE.   Journal of Geodesy, 79(8): 467-478.
[14] Wiese D N, Folkner W M, Nerem R S. 2009. Alternative mission architectures for a gravity recovery satellite Mission.   Journal of Geodesy, 83(6): 569-581.
[15] Wiese D N, Nerem R S, Lemoine F G. 2012. Design considerations for a dedicated gravity recovery satellite mission consisting of two pairs of satellites.   Journal of Geodesy, 86(2): 81-98.
[16] Wolff M. 1969. Direct measurement of the Earth′s gravitational potential using a satellite pair.   Journal of Geophysical Research, 74(22): 5295-5300.
[17] Zheng W, Shao C G, Luo J, et al. 2008. Improving the accuracy of GRACE Earth′s gravitational field using the combination of different inclinations.   Progress in Natural Science, 18(5): 555-561.
[18] Zheng W, Xu H Z, Zhong M, et al. 2009. Physical explanation of influence of twin and three satellites formation mode on the accuracy of Earth′s gravitational field.   Chinese Physics Letters, 26(2): 029101-1-029101-4.
[19] Zheng W, Xu H Z, Zhong M, et al. 2011. Efficient calibration of the non-conservative force data from the space-borne accelerometers of the twin GRACE satellites.   Transactions of the Japan Society for Aeronautical and Space Sciences, 54(184): 106-110.
[20] Zheng W, Xu H Z, Zhong M, et al. 2012a. Efficient accuracy improvement of GRACE global gravitational field recovery using a new inter-satellite range interpolation method.   Journal of Geodynamics, 53: 1-7.
[21] Zheng W, Xu H Z, Zhong M, et al. 2012b. Precise recovery of the Earth's gravitational field with GRACE: Intersatellite Range-Rate Interpolation Approach.   IEEE Geoscience and Remote Sensing Letters, 9(3): 422-426.
[22] 程芦颖, 许厚泽. 2006. 地球重力场恢复中的位旋转效应.   地球物理学报, 49(1): 93-98.
[23] 刘林. 1992. 人造地球卫星轨道力学.   北京: 高等教育出版社, 1-619.
[24] 沈云中. 2000. 应用CHAMP卫星星历精化地球重力场模型的研究[博士论文].   武汉: 中国科学院测量与地球物理研究所, 1-111.
[25] 沈云中, 许厚泽, 吴斌. 2005. 星间加速度解算模式的模拟与分析.   地球物理学报, 48(4): 807-811.
[26] 许厚泽. 2001. 卫星重力研究: 21世纪大地测量研究的新热点.   测绘科学, 26(3): 1-3.
[27] 张捍卫, 许厚泽, 刘学谦. 2004. 固体潮Love数的基本理论和数值结果.   地球物理学进展, 19(2): 372-378.
[28] 郑伟, 邵成刚, 罗俊等. 2006. 基于卫—卫跟踪观测技术利用能量守恒法恢复地球重力场的数值模拟研究.   地球物理学报, 49(3): 712-717.
[29] 郑伟, 许厚泽, 钟敏等. 2008. 基于半解析法有效和快速估计GRACE全球重力场的精度.   地球物理学报, 51(6): 1704-1710.
[30] 郑伟, 许厚泽, 钟敏等. 2009a. GRACE星体和SuperSTAR加速度计的质心调整精度对地球重力场精度的影响.   地球物理学报, 52(6): 1465-1473.
[31] 郑伟, 许厚泽, 钟敏等. 2009b. GRACE卫星关键载荷实测数据的有效处理和地球重力场的精确解算.   地球物理学报, 52(8): 1966-1975.
[32] 郑伟, 许厚泽, 钟敏等. 2009c. 卫星跟踪卫星测量模式中星载加速度计高低灵敏轴分辨率指标优化设计论证.   地球物理学报, 52(11): 2712-2720.
[33] 郑伟, 许厚泽, 钟敏等. 2010. 利用解析法有效快速估计将来GRACE Follow-On地球重力场的精度.   地球物理学报, 53(4): 796-806.
[34] 郑伟, 许厚泽, 钟敏等. 2012. 插值公式、相关系数和采样间隔对GRACE Follow-On星间加速度精度的影响.   地球物理学报, 55(3): 822-832.
[35] 郑伟, 许厚泽, 钟敏等. 2013. 基于下一代四星转轮式编队系统精确和快速反演FSCF地球重力场.   地球物理学报, 56(9): 2928-2935.
[36] 周旭华, 许厚泽, 吴斌等. 2006. 用GRACE卫星跟踪数据反演地球重力场.   地球物理学报, 49(3): 718-723.