随着复杂构造成像及岩性勘探的深入,地震资料叠前偏移成像处理中由不同炮或不同偏移距的偏移结果得到地下反射点对不同角度入射波场的反射强度,进而利用AVO或AVA响应直接识别流体和含油气情况成为一个日益受到关注的环节.
波动方程叠前深度偏移是用较准确的波动理论来描述地震波的传播过程,能正确模拟复杂上覆地层导致的多值走时等复杂的波传播现象和地震波传播的几何扩散现象,因此既可对复杂构造正确成像,又有望得到正确反映地下构造反射强弱的成像幅值.但服务于复杂构造成像的波动方程叠前深度偏移多是通过分炮偏移实现的,且每炮偏移实现时需要对原始炮集做镶边处理以满足偏移孔径的要求;这种数据集组织方式易于得到叠加剖面,但由这些炮集偏移结果抽取随偏移距变化的共反射点(CRP)道集将产生巨大的硬盘存储需求.此外,既然真正反映地下构造物性参数对比的是随入射角变化的角度域成像道集,人们就希望能由分炮偏移结果直接得到角道集.
已发展了一系列通过炮域波动方程叠前深度偏移产出角度域成像道集的方法.这些方法可归纳为如下两类:一是在应用成像条件前对入射和反传波场进行局部平面波分解,对每对平面波分别成像[1-3];二是在炮域偏移的成像条件中应用空间移动或时间移动的成像条件,进而通过倾斜叠加等角度变换方法得到角度道集[4-6].第一种方法需对逐个成像点进行局部平面波分解,将单点的成像转换成一个成像矩阵,三维问题的计算量难以承受;第二种方法尽管计算量较第一种有所减少,但空间移动或时间移动的成像条件导致成像空间巨大,计算和内存需求随之增加,三维问题的成像空间将变为五维.两种方法均不能考虑炮点覆盖不均匀导致的成像幅值误差,且波场延拓的空间采样限制了角道集的有效频率范围.
本文在文献[7]所发展的单程波算子地震波入射角计算方法的基础上,通过计算震源入射波场与地层界面夹角,发展了由炮域偏移的结果直接通过部分叠加得到角道集的方法;该方法通过应用“保幅”的反褶积成像条件和考虑角度区间内累加的炮数,解决了炮点覆盖不均匀导致的成像幅值误差问题.与前述两类方法相比,这一方法所需的计算量及内存几乎可以忽略,角道集的有效频率范围也与偏移剖面相同,因而更适于现行的计算能力和工业资料的实际情况.
本文首先简述基于单程波算子的地震波入射波之波前面法线、地层界面倾角估计以及以此为基础的地震波入射角计算方法,然后建议了一种考虑炮点覆盖不均匀的基于反褶积成像条件的直接累加生成角度域成像道集的方法,最后给出了实际应用的计算流程和基于角道集改善地震成像效果的实用方法.文中算例表明,这一炮域波动方程深度偏移直接产生角道集方法既能剔除复杂上覆地层的影响,又可补偿观测系统非均匀覆盖对成像幅值的影响;而与常规炮域波动方程叠前深度偏移相比,并不增加过多内存需求与计算量.
2 反射角计算 2.1 基于单程波算子的入射波之波前面法线计算单程波算子是通过对标准的声波方程进行分解而得到的,一般情况人们总是沿垂直方向分解单程波算子.单程波算子可正确模拟复杂介质中地震波的单向传播,与标准的声波(双程波)方程相比,单程波算子沿其分解方向不发生地震波反射.由于这一特征,单程波算子所得到的简谐波场就对应着地震波传播过程中的波前面.地震波场的波数是与波前面的法线方向相联系的,而波场的空间导数又与波数存在着对应关系,因此,我们可利用求取空间导数前后简谐波场的变化,简单求得全场的地震波入射角方向.
由单程波方程可知,频率-波数域下行的波场
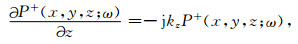
|
(1) |
其中j是单位虚数,kz是垂直波数,ω是角频率,x和y是水平位置坐标,z是深度坐标,由频散关系得

|
(2a) |

|
(2b) |

|
(2c) |
式中k=ω/c(x,y,z)为波数,c(x,y,z)是空间各位置处的介质波速,角度θx,θy,θz分别是空间位置(x,y,z)处波前面法线与水平坐标轴x,y以及深度轴z的夹角.以z方向为例,将(2a)式代入(1)式并做离散的时域傅氏反变换,且令时间t=0,可得

|
(3) |
式中符号Re代表求复波场值的实部.若令

脉冲响应


|
(4a) |

|
(4b) |
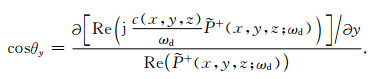
|
(4c) |
由此可得到(xs,ys,0)处炮点的出射波在(x,y,z)点的入射波之波前面法线[7]:

|
(5) |
基于局部结构的张量分析(local structure tensors)为简单信号提供了一个较简洁的描述其方向的方法.这里所谓的简单信号,是指该信号在局部范围内只能沿一个方向变化.对于这类信号,可以把它的局部方向定义成一个张量Ts,该张量的大小是由信号的维数来确定的.比如,对于3D信号,其局部方向可以表示为3×3的张量.Van Vliet和Verbeek[8]利用一阶梯度张量计算了2D情况下的局部地层倾角.在这里,我们沿用一阶梯度张量的方法给出3D情况下一阶梯度张量表达式:

|
(6) |
式中fx,fy,fz分别表示偏移数据体沿x,y,z方向上的一阶导数,〈〉表示高斯平滑.我们依据这一张量可以获取地下介质某点所在地层的切平面及其法线方向:矩阵TS的最大特征值对应的特征向量描述了我们所需要的地层法线方向;而其它两个特征向量组成的平面即为地层的切平面.在炮域波动方程叠前深度偏移提取角道集的研究中,首先将所有单炮的叠前深度偏移结果叠加得到整个工区的偏移数据体,然后应用该偏移数据体采用这一方法计算得到地下介质(x,y,z)点处地层界面法向量为n(x,y,z)=(cosαx,cosαy,cosαz),则结合2.1节得到的炮点(xs,ys,0)处出射波在(x,y,z)点的入射波之波前面法线,可计算入射地震波与地层界面法线的夹角:

|
(7) |
就反射波偏移成像而言,震源入射波场与反射界面法线的夹角,即入射角,就是反映偏移道集AVA特征的角度.基于此角度的角道集完全反映了由界面波阻抗和泊松比对比决定的随角度变化的界面反射特征[9-10].获得此类角道集是正确应用反射幅值特性的基础,也一直是各种偏移方法的努力方向.
基于第2节获得的反射角,可以按反射角对炮域偏移结果直接累加来得到角道集.有学者从理论上证明[11],若按反射角对炮域偏移结果直接累加,基于相关成像条件的炮域偏移结果恰可得到“保幅”的角道集.这里的保幅指的是正确补偿了地震波的几何扩散效应,并没有考虑补偿黏性吸收和薄层散射[12].但实际应用中由于炮、检点的离散分布和非均匀覆盖,因而难以满足文献[11]的应用条件.实际上,在地震资料的整个处理流程中,如何更好地解决观测系统非均匀覆盖对幅值影响,一直是一个重要的研究课题.
本文因此建议了一种可同时处理几何扩散效应和观测系统非均匀覆盖的“保幅”的角道集生成方法.角道集是按反射角对炮域偏移结果直接累加形成的;在偏移成像中用反褶积成像条件来补偿几何扩散,同时应用统计按角度累加过程中落入不同角度区间内的炮数的方法来剔除观测系统非均匀覆盖的影响.
炮域偏移的反褶积成像条件可表达为

|
(8) |
式中PU(x,y,z,mΔω)和PD(x,y,z,mΔω)分别是深度延拓后频率域炮点和检波点波场,l1Δω和l2Δω分别对应地震数据有效频带的下、上限;令T0是地震记录的时长,则频率采样Δω=2π/T0.引入参数β是为了保持地震子波不变,三维偏移时β=jmΔω,二维偏移时
式(8)中的波场相除可进一步表达为

|
(9) |
式中上标*代表共轭.为避免式(9)中除法计算的不稳定,我们在除法中应用了如下的级数展开近似式:

|
(10) |
当x趋于零,式(10)仍可得到稳定的结果,而当0.6<x≤1.2时,式(10)的近似有很好的精度.利用式(10),我们发展了稳定的相除算法,令式(9)中实数的分母为A(x,y,z,mΔω),由(10)式可得

|
(11) |
式中A0(z)是A(x,y,z,mω)在深度z上的平均值.该式既保证了稳定性,又可以得到光滑的相除结果.将式(11)代入(9)再代入(8),可保证反褶积成像条件的稳定.
叠加是压制随机噪音的有效手段,对地震资料整个处理流程,叠加起到了关键的作用;但叠加也改变了地震资料的幅值特征,特别是在观测系统非均匀覆盖的情况下.解决观测系统非均匀覆盖是地震资料处理中一直受到关注的问题,目前尚没有非常有效的方法.在生成角度道集的过程中,为获得较高信噪比的角道集,也需要采用叠加处理,即保证有足够多的反射角(每个角度对应一个炮点)落在一个角度区间内.对等间距的角度区间而言,即使是规则的三维观测系统,由于(各向同性情况下)不考虑方位角,落在各个角度区间内的炮点数也是不相同的.
由于采用反褶积成像条件,可认为每个单炮偏移结果对应某一个角度的(有限带宽)的反射系数;因此,在累加过程中统计落入不同角度区间内的炮数,可籍此剔除非均匀覆盖对角道集幅值的影响.具体实现如下:定义角度采样间距Δγ,对每一成像点定义一个一维数组,数组长度小于90/Δγ;对全部炮循环,对每炮的偏移结果,读取由上节得到的该炮点震源对各成像点的地层界面法向量夹角γ,计算l=1+int{γ/Δγ},将各成像点的幅值累加到对应数组的l元素上,同时统计累加到元素上的炮数;完成对全部炮循环,然后用统计得到的各元素上的累加炮数除各成像点对应数组中的各元素值.这样就得到各成像点随角度变化的成像幅值.需要指出的是,这一操作并不能简单推广应用到常规的叠加处理;以炮域偏移的叠加过程为例,由于不能保证任一炮记录的偏移结果对某一同相轴有实质的贡献,简单的统计、剔除并不能消除非均匀覆盖的影响.
4 计算流程和改善波动方程成像效果结合炮域波动方程偏移流程以及集群式并行机的软硬件分布特点,提出了如图 1所示的一种直接由炮域偏移得到角道集的实现流程.这一流程具有如下几个特点:首先,就各成像点震源入射波场与地层界面的夹角的计算环节而言,因其使用了与波动方程炮域叠前深度偏移处理完全相同的偏移速度模型和单程波算子,因此得到的角度更真实地反映了入射波与反射波之间的夹角;而其所需计算量仅为单个频率的震源波场延拓加上求导及平滑、插值等处理,与叠前偏移的全频带波场延拓相比,几乎可以忽略;其次,这一环节主要的计算(图 1中两虚线箭头中间部分所示)均是在集群并行机计算节点上并行进行的,因而可获得较高的计算效率.就这一实现流程的内存需求而言,各成像点震源入射波场与地层界面的夹角的计算环节所需内存与单炮偏移基本相同,且这一操作与单炮偏移是先后进行的,不需要额外的内存,这克服了空间移动或时间移动的成像条件产生角道集方法巨大内存需求导致不能应用于大规模工业数据的障碍.本文流程是先对单炮偏移结果直接在各个计算节点部分叠加,然后在主节点对部分叠加结果进行叠加产生各成像点的角道集,这一实现方法规避了首先由炮集偏移结果抽取共成像点道集,然后再结合入射角信息将共成像点道集转化为角道集时产生的巨大文件存储及数据交换需求.

|
图 1 直接由炮集成像结果得到角道集的实现流程图 Fig. 1 Flow chart of angle gather obtained directly from shots gather prestack migration result |
与现行各类波动方程偏移生成角道集的方法相比,本文提出的方法几乎不增加额外计算量和内存需求,可容易与现行炮域偏移流程结合,获得有较好幅值特征的角道集.本文方法获得的角道集,除服务于叠前岩石物理参数反演,还可用于进一步改善偏移成像效果.
就改进偏移成像效果而言,现行积分法偏移流程都包括一个后续的剩余动校及拉伸切除步骤;这一步骤将存在微小弯曲的同相轴拉平并切除无法拉平和存在拉伸畸变的部分.尽管剩余动校量较小,但它使得同相轴的波峰和波谷对得更齐,因而在叠加过程中更好地保持了高频成分;而切除也提高了成像的信噪比.但对常规的炮域偏移而言,由于产出的是随炮点变化的CIG道集,同相轴的弯曲没有一定的规律,有效成像段并不一定在中心部分,将工业界经常使用的剩余动校及拉伸切除应用于炮域波动方程偏移就产生了困难.而提取角道集后使得在炮域波动方程叠前深度偏移处理中应用剩余动校和拉伸切除变得与Kirchhoff积分偏移一样容易.就本文提取的角道集而言,其剩余动校量可定量描述为

|
(12) |
式中z是零角度处同相轴的深度,γ是角度.在1.0附近对ρ进行扫描并将角道集沿角度叠加,可得到不同ρ值对应的能量谱,由能量谱中拾取最大能量对应的ρ,由式(12)计算不同角度处同相轴的移动量Δz,同时将大角度处的无效信息切除,这样就简单地实现了剩余动校及拉伸切除.
5 数值算例 5.1 三维层状介质模型为验证本文发展的方法能够得到相对保幅的角道集,文中设计了一个四层的水平层状均匀速度模型,将层位按照从上到下排列,分别编号为1,2,3,4.各层位深度-厚度及速度密度信息见表 1,其中第3层为一个低速薄层.
|
|
表 1 水平层状模型层位深度-厚度、速度及密度信息 Table 1 The depth-thickness, velocity and density of 3-D layered model |
先应用声波方程正演方法生成理论炮集记录[14],然后按照图 1所示流程,可由各单炮偏移结果直接得到角道集.图 2a给出了典型空间位置上本文方法求得的入射角的等值线图.图 2b展示了某CDP点未进行覆盖不均匀补偿的角道集;对这一角道集进行覆盖不均匀补偿后则示于图 2c.图 2b的角道集没有进行覆盖不均匀补偿,因此这一角道集的幅值特征完全受到非均匀覆盖的控制,小角度照明弱,中等角度照明强;可容易地在三维积分法偏移的CRP道集中观察到这一特征.而覆盖不均匀补偿后的图 2c则正确反映了界面的AVA反射特征.

|
图 2 三维层状介质模型角道集提取实例 (a)典型单炮的入射角等值线图;(b)未进行覆盖非均匀补偿的角道集;(c)进行覆盖非均匀补偿后的角道集. Fig. 2 3-D layered medium angle gather generating example (a) angle field of a typical shot; angle gather obtained before (b) and after (c) heterogeneous illumination compensation. |
图 3进一步给出在三个界面处,图 2c所示角道集反映的AVA特性与理论值的对比,可见两者拟合得很好;大角度出现偏差是因为本文正演结果的长偏移距数据有限导致的.

|
图 3 表 1中三个反射界面的计算(虚线)和理论(实线)反射强度比较 (a)第一个界面;(b)第二个界面;(c)第三个界面. Fig. 3 Comparisons of theoretical (solid line) and estimated (dashed line) amplitude (a) Firstlayer; (b) Secondlayer; (c) Thirdlayer. |
本节将文中提出的波动方程叠前深度偏移直接生成角道集流程应用于我国东部油田某地区满覆盖11.2km2的三维开发地震数据.这一数据集观测系统如下:地表接收数据约为3600个共炮点道集,每炮16×168=2688道,接收点间距inline方向为40m,crossline方向为160m;炮点间距inline方向为120m,crossline方向为40m,记录长度为6s.
利用图 1所示流程,由该数据集3600个炮集偏移结果直接生成了满覆盖区各成像点的角道集.出于计算效率以及计算精度的考虑,流程中的炮集深度偏移及入射角计算中的波场延拓均采用了最优分裂Fourier方法[15-17].对这一实际资料,我们继续应用了文中建议的改进偏移成像效果方法,即进行了剩余动校及拉伸切除.
图 4a展示了某成像点初始的角道集,在1.0附近对ρ进行扫描并将角道集沿角度叠加,可得如图 4b所示的能量谱,由能量谱中拾取最大能量对应的ρ,由式(12)计算不同角度处同相轴的移动量Δz,可将图 4a所示的角道集转换到图 4c,比较两个图可见同相轴变得更加平直.由图 4c可见,大角度处已无有效信息,因此可将它们如图 4d所示那样切除.图 5展示了满覆盖区由剩余动校前后角道集叠加得到的数据体抽取的深度为750 m的水平切片对比.比较可见在图 5a显示的经过剩余动校后的水平切片上,信噪比得到较大提高,断层及断点显示更为清晰.

|
图 4 典型角道集(a)及其ρ扫描(b)、剩余动校(c)和切除(d) Fig. 4 A typical angle gather (a) and its scan of ρ (b), RNMO (c) and mute (d) |

|
图 5 深度为750m的水平切片剩余动校前(b)、后(a)对比 Fig. 5 Comparisons of slices at depth of 750m before (b) and after (a) RNMO |
我们将所生成的角道集与这一地区的17口测井数据进行了AVA特性对比.图 6给出了某一井点处所生成的角度域成像道集与典型层位的AVA特性曲线对比,其中理论曲线的计算参数中,速度与密度信息是由测井数据得到的,泊松比参数是由有关地层的经验参数给出的.图 6a为该点所有深度(自地面至深度为5000m)的角度域成像道集;图 6b与图 6c为图中所示的深度处典型层位的AVA特性曲线与依据测井信息计算的理论曲线对比.考察可见,所生成的角度域道集与理论计算曲线变化趋势吻合较好,从而表明所生成的角度域成像道集展现了良好的AVA特性.

|
图 6 某井点处角道集与典型层位的AVA特性曲线 (a)某井点处本文方法得到的角道集;(b)深度为0.95km处由该角道集提取的AVA特性曲线(实线)与测井数据计算得到的AVA特性曲线(虚线)对比;(c)深度为1.07km处由该角道集提取的AVA特性曲线(实线)与测井数据计算得到的AVA特性曲线(虚线)对比. Fig. 6 Angle gather at some well and its AVA characteristic curves (a) Angle gather at some well computed with the proposed scheme; (b) Comparisons of AVA characteristic curves of a typical layer at the depth of 0.95km between the angle gather (solid line) and the well logging data (dashed line); (c) Comparisons of AVA characteristic curves of a typical layer at the depth of 1.07km between the angle gather (solid line) and the well logging data (dashed line). |
本文给出了基于炮域波动方程叠前深度偏移结果直接生成角道集的方法.该方法可将炮域偏移结果直接转换成反映界面AVA特征的角道集.文中也分别建议了校正因炮点覆盖不均匀导致的成像幅值误差的方法和基于角道集改善波动方程深度偏移成像效果的方法.与现行各类提取角道集方法相比,本文方法计算效率高,内存需求及存储需求甚少,可灵活应用于二维和三维问题,更适用于工业规模资料.文中给出了该方法的实际应用流程和三维资料的应用实例.理论及实际数值算例表明,本文方法提取的角道集真实反映了界面的AVA特征,而改善偏移成像效果的方法提高了偏移剖面的信噪比.较大规模的实际三维资料应用表明,本文方法已具备了较好的工业资料应用能力.本文方法可为直接识别油气的AVA反演提供高质量的数据.
| [1] | Xie X, Wu R. Extracting angle domain information from migrated wavefield. 72nd Annual International Meeting, SEG, Expanded Abstracts, 2002:1360-1363. |
| [2] | Wu R, Chen L. Prestack depth migration in angle-domain using beamlet decomposition: Local image matrix and local AVA. 73rd Annual International Meeting, SEG, Expanded Abstracts, 2003:973-976 |
| [3] | Soubaras R. Angle gathers for shot-record migration by local harmonic decomposition. 73rd Annual International Meeting, SEG, Expanded Abstracts, 2003:889-892. |
| [4] | Rickett J E, Sava P C. Offset and angle-domain common image point gathers for shot-profile migration. Geophysics , 2002, 67(3): 883-889. DOI:10.1190/1.1484531 |
| [5] | Sava P C, Fomel S. Angle-domain common-image gathers by wavefield continuation methods. Geophysics , 2003, 68(3): 1065-1074. DOI:10.1190/1.1581078 |
| [6] | Biondo B. Angle-domain common-image gathers from anisotropic migration. Geophysics , 2007, 72(2): S81-S91. DOI:10.1190/1.2430561 |
| [7] | 张剑锋, 张辉, 刘礼农. 单程波算子地震波入射角计算. 地球物理学报 , 2013, 56(3): 953–960. Zhang J F, Zhang H, Liu L N. Incident angle field estimation: a one-way propagator approach. Chinese J. Geophys. (in Chinese) , 2013, 56(3): 953-960. |
| [8] | van Vliet L J, Verbeek P W. Estimators for orientation and anisotropy in digitized images. Proceedings of the First Annual Conference of the Advanced School for Computing and Imaging ASCI'95, Heijen (The Netherlands), 1995:442-450. |
| [9] | Aki K, Richards P G. Quantitative Seismology. San Francisco: W. H. Freeman & Co., 1980. |
| [10] | de Bruin C G M, Wapenaar C P A, Berkhout A J. Angle dependent reflectivity by means of prestack migration. Geophysics , 1990, 55: 1223-1234. DOI:10.1190/1.1442938 |
| [11] | Zhang Y, Xu S, Bleistein N, et al. True-amplitude, angle-domain, common-image gathers from one-way wave-equation migrations. Geophysics , 2007, 72(1): S49-S58. DOI:10.1190/1.2399371 |
| [12] | Zhang J F, Wapenaar C P A. Wavefield extrapolation and amplitude-variation-with-angle migration in highly discontinuous media. Geophysical Journal International , 2003, 155: 327-339. DOI:10.1046/j.1365-246X.2003.02039.x |
| [13] | Antoine G, Alejandro V, Dimitri B, et al. Smoothing imaging condition for shot-profile migration. Geophysics , 2007, 72(3): S149-S154. DOI:10.1190/1.2712113 |
| [14] | Gao H, Zhang J. Parallel 3-D simulation of seismic wave propagation in heterogeneous anisotropic media: a grid method approach. Geophysical Journal International , 2006, 165: 875-888. DOI:10.1111/gji.2006.165.issue-3 |
| [15] | Liu L N, Zhang J F. 3D wavefield extrapolation with optimum split-step Fourier method. Geophysics , 2006, 71(3): T95-T108. DOI:10.1190/1.2197493 |
| [16] | Zhang J F, Liu L N. Optimum split-step Fourier 3D depth migration: Developments and practical aspects. Geophysics , 2007, 72(3): S167-S175. DOI:10.1190/1.2715658 |
| [17] | 张剑锋, 卢宝坤, 刘礼农. 波动方程深度偏移的频率相关变步长延拓方法. 地球物理学报 , 2008, 51(1): 221–227. Zhang J F, Lu B K, Liu L N. Frequency-dependent varying-step depth extrapolation scheme for wave equation based migration. Chinese J. Geophys. (in Chinese) , 2008, 51(1): 221-227. |
 2013, Vol. 56
2013, Vol. 56


